Конспект урока по Алгебре «Решение простейших и некоторых типов тригонометрических уравнений» 10 класс

План-конспект урока

Учитель: Дорофеева Л.И.

Предмет: математика.

Класс: 10 класс.

Тема урока: «Решение простейших и некоторых типов тригонометрических уравнений».

Продолжительность: 45мин.

Тип урока: урок обобщения и систематизации знаний обучающихся.

Цели урока:

• образовательные – обеспечить повторение, обобщение и систематизацию материала темы, создать условия контроля усвоения знаний и умений

• развивающие – содействовать развитию у учащихся мыслительных операций: умение анализировать, сравнивать; формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения; отрабатывать навыки самооценивания знаний и умений, выбора задания, соответствующего их уровню развития.

• воспитательные – вырабатывать внимание, самостоятельность при работе на уроке; способствовать формированию активности и настойчивости, максимальной работоспособности.

Оборудование: доска; карточки для индивидуальной работы учащихся; таблица ответов для проверки индивидуальных заданий.

Краткий план урока:

1.Оргмомент, цель урока – 2 мин

2.Устная работа – 6 мин

3. Проверка домашнего задания – 2 мин

4.Фронтальное решение задачи – 3-4 мин

5.Самостоятельная работа по карточкам – 10 мин

6.Самоконтроль– 2 мин

7.Разбор различных типов заданий – 6-7 мин.

8.Коррекция знаний и умений – 5 мин

9.Подведение итогов урока, выставление оценок.- 2-3 мин

10. Домашнее задание – 2 мин.

Конспект урока.

1. Оргмомент. Эпиграф занятия: «Без уравнения нет математики как средства познания природы» (академик Александров П. С.).

Приветствие учащихся. Постановка цели урока.

- Добрый день! Я рада всех Вас видеть. Сегодня у нас необычный урок, а необычен он тем, что у нас сегодня гости.

Ребята, мы разобрали с Вами простейшие 4 типа тригонометрических уравнений. Сегодня нам предстоит повторить и применить полученные знания и умения при решении различных заданий. Перед Вами стоит задача-показать свои знания и умения по решению тригонометрических уравнений. Все виды работ на уроке будут оценены ,результаты занесены в лист учёта знаний.

2.Устная работа. (Финк-райт-раунд робин-«подумай,-запиши-обсуди в команде». Ученики обдумывают ответы на определённые вопросы, записывают и по очереди высказывают свои ответы)

- Повторим формулы корней простейших тригонометрических уравнений.

№1

1. Каково будет решение уравнения cos x = a при a > 1?

2. При каком значении a уравнение cos x = a имеет решение?

3. Какой формулой выражается это решение?

4. На какой оси откладывается значение a при решении уравнения cos x = a?

5. В каком промежутке находится arccos a?

6. Каким будет решение уравнения cos x = 1?

7. Каким будет решение уравнения cos x = -1?

8. Каким будет решение уравнения cos x = 0?

9. Чему равняется arccos (-a)?

№2

1. Каково будет решение уравнения sin x = a при a > 1?

2. При каком значении a уравнение sin x = a имеет решение?

3. Какой формулой выражается это решение?

4. На какой оси откладывается значение a при решении уравнения sin x = a?

5. В каком промежутке находится arcsin a?

6. Каким будет решение уравнения sin x = 1?

7. Каким будет решение уравнения sin x = -1?

8. Каким будет решение уравнения sin x = 0?

9. Чему равняется arcsin (-a)?

№3

1. В каком промежутке находится arctg a?

2. В каком промежутке находится arcctg a?

3. Чему равняется arctg (-a)?

4. Чему равняется arcctg (-a)?

5. Какой формулой выражается решение уравнения tg x =a?

6. Какой формулой выражается решение уравнения ctg x =a?

7. Каким будет решение уравнения tg x = 1, tg x = 0

8. Каким будет решение уравнения ctg x = 1, ctg x =0

3.Проверка домашнего задания.

- Вспомним домашнее задание (заранее на экране написано решение домашнего задания).У кого есть вопросы?

4 .Установите соответствие между уравнением и его корнями:

А. 2 sin x = 1

1.

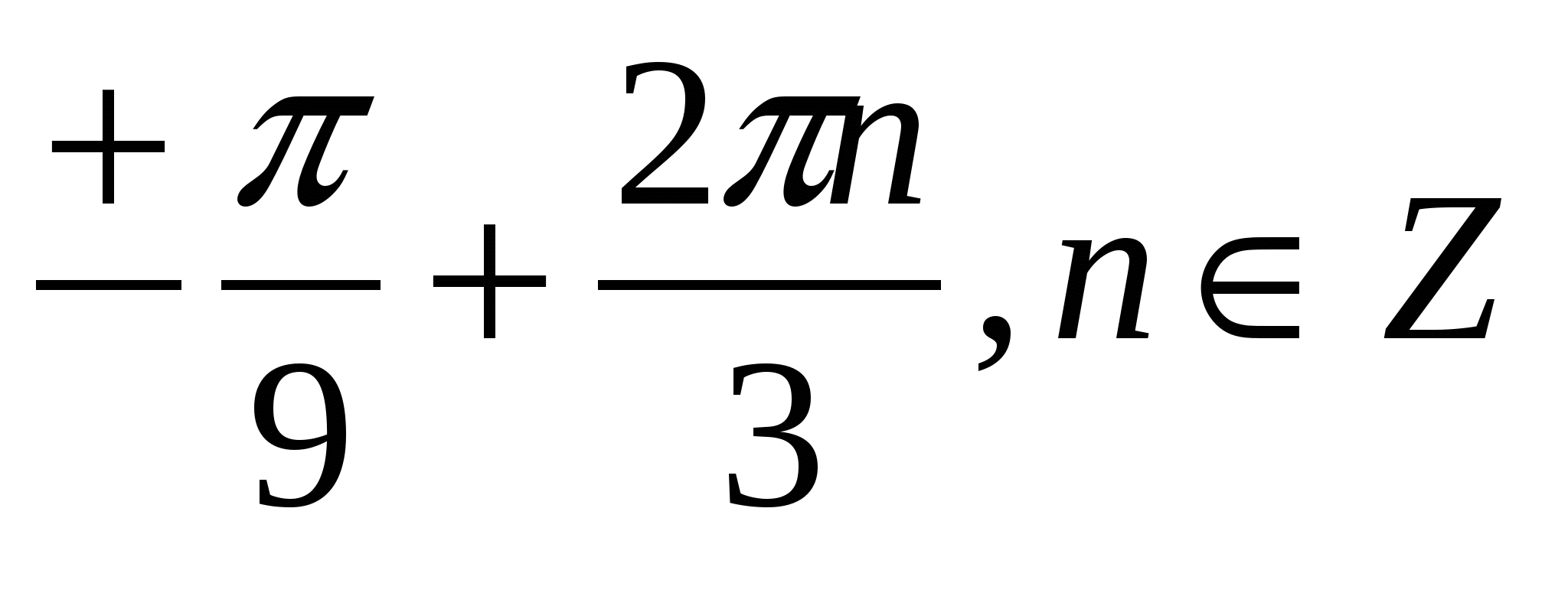
Б. 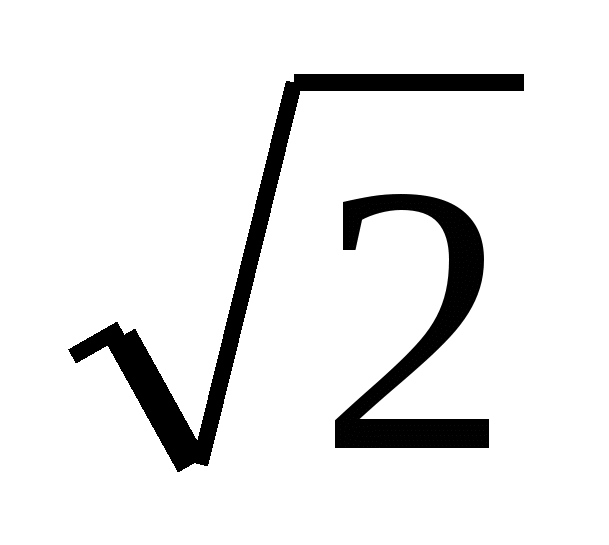sin x = 1

2.

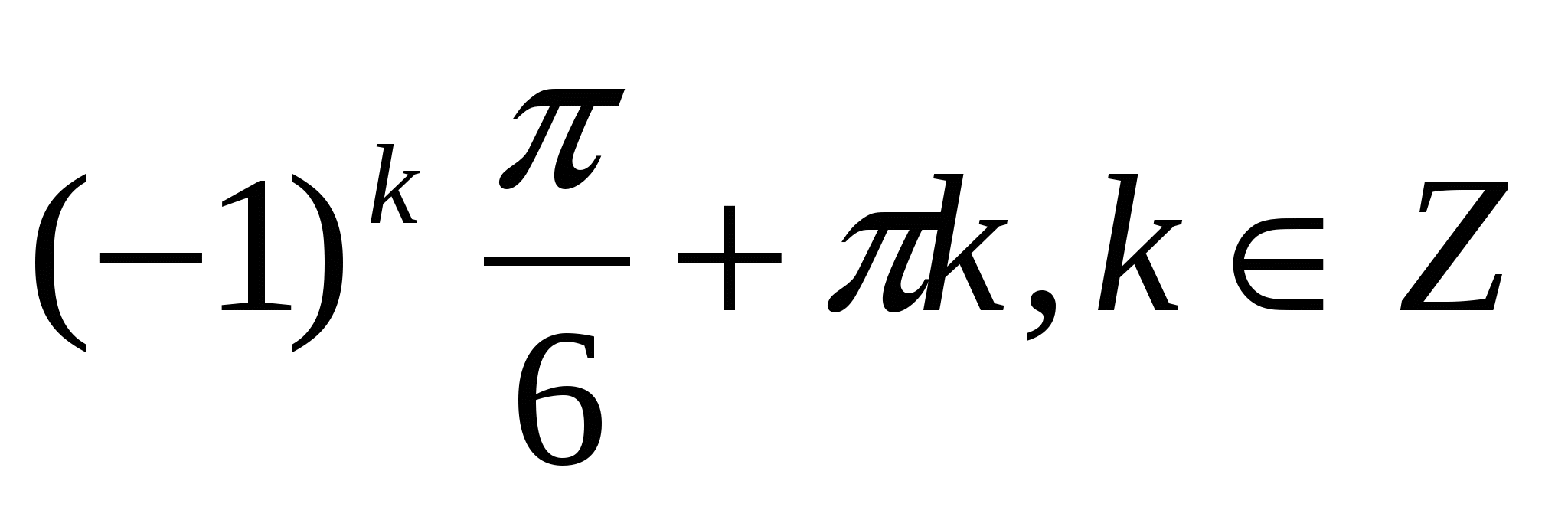
В. – 2 cos x = 1

3.

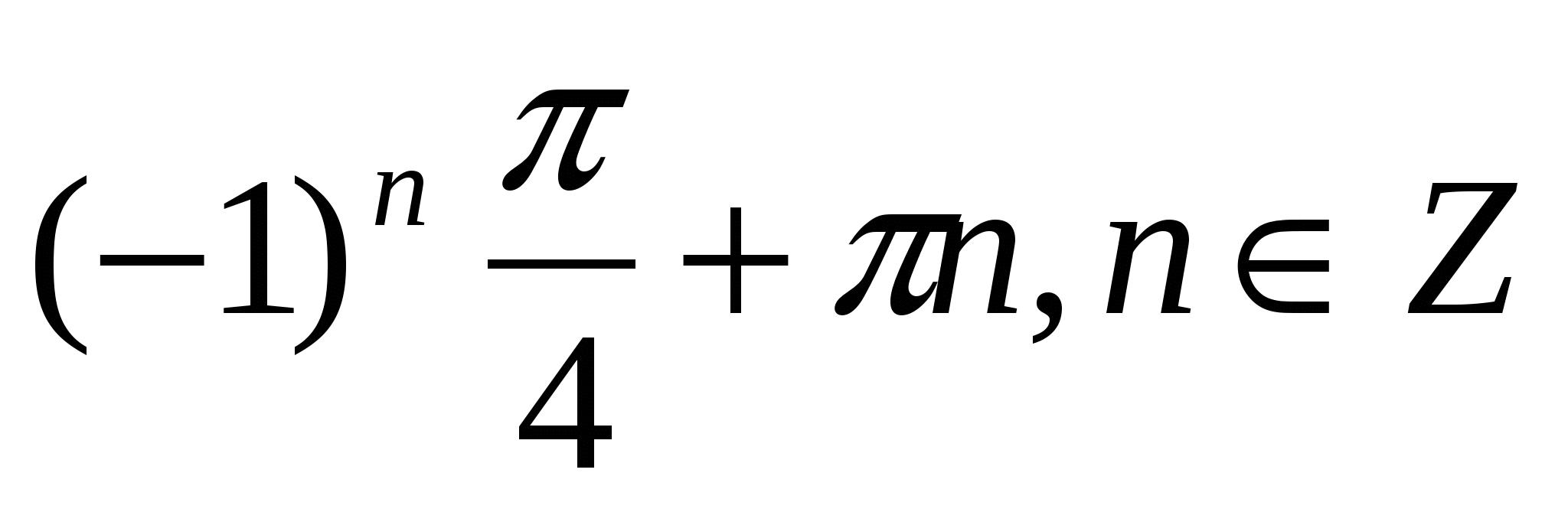
Г. cos3x =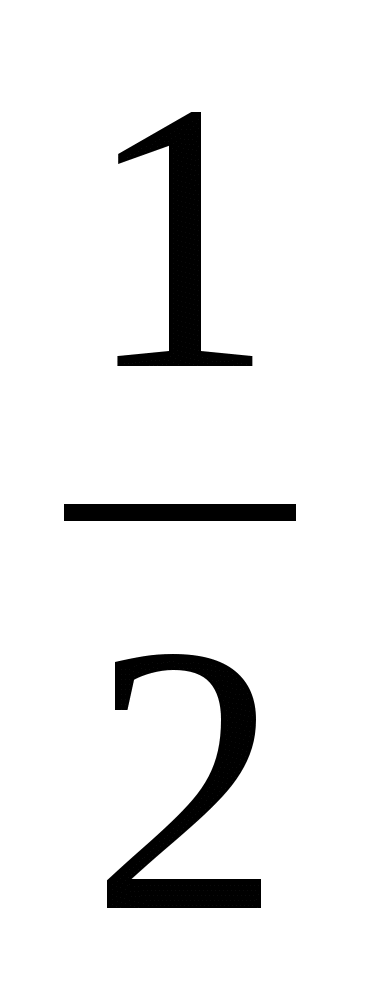

4.

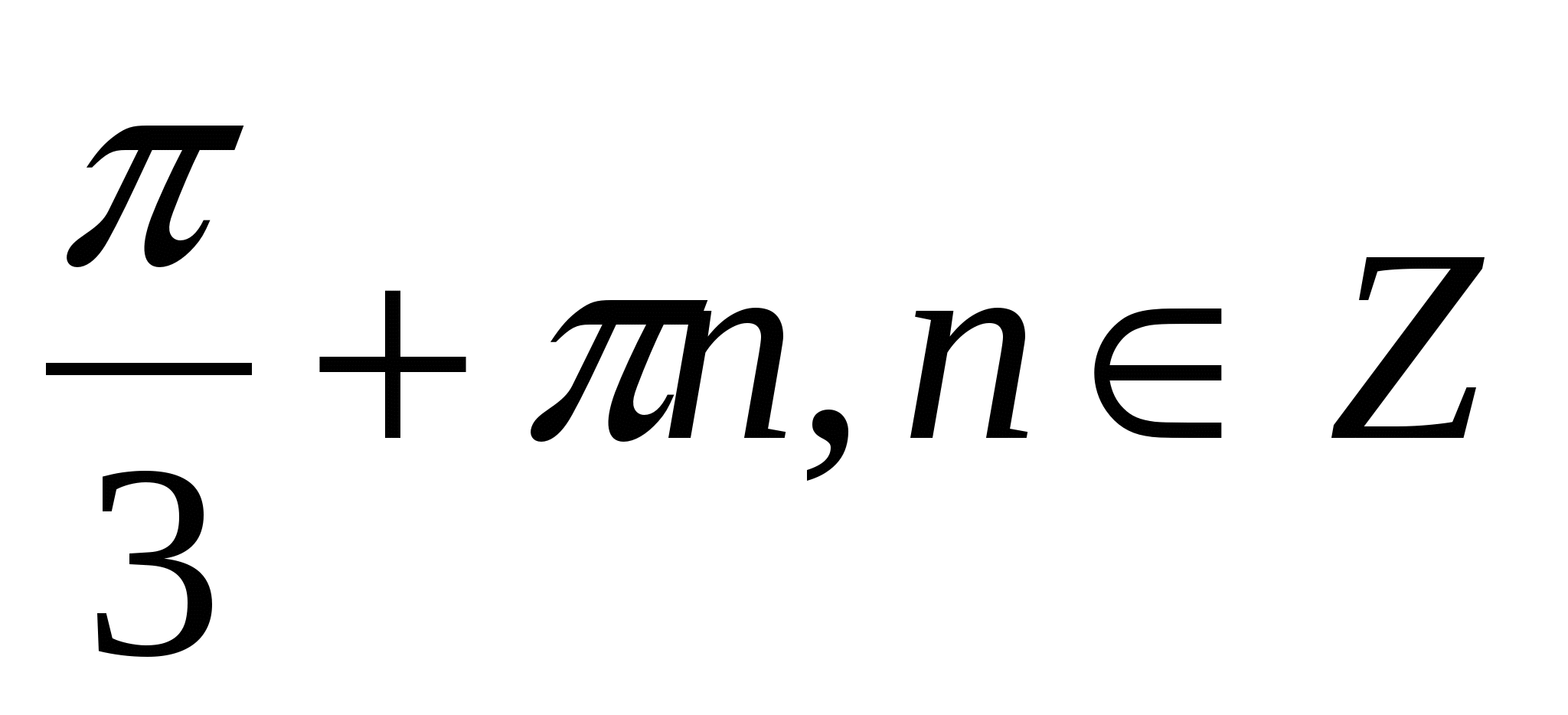
Д. 2 tg x =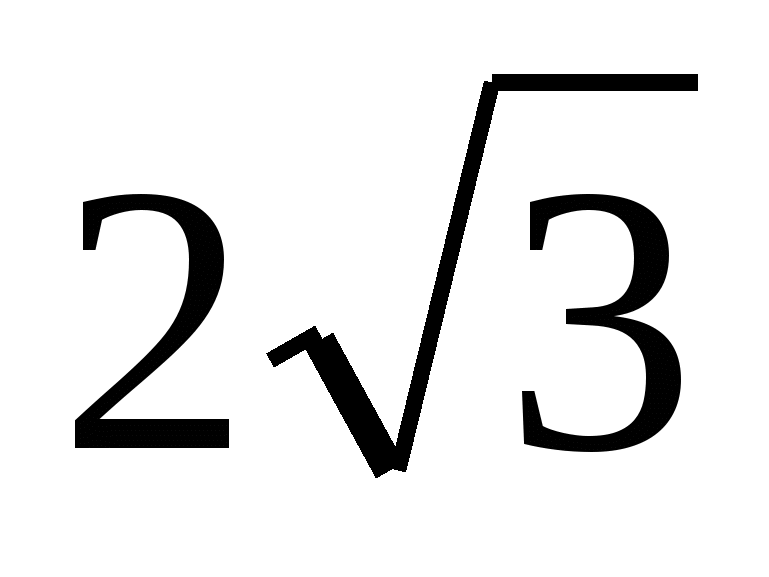

5.

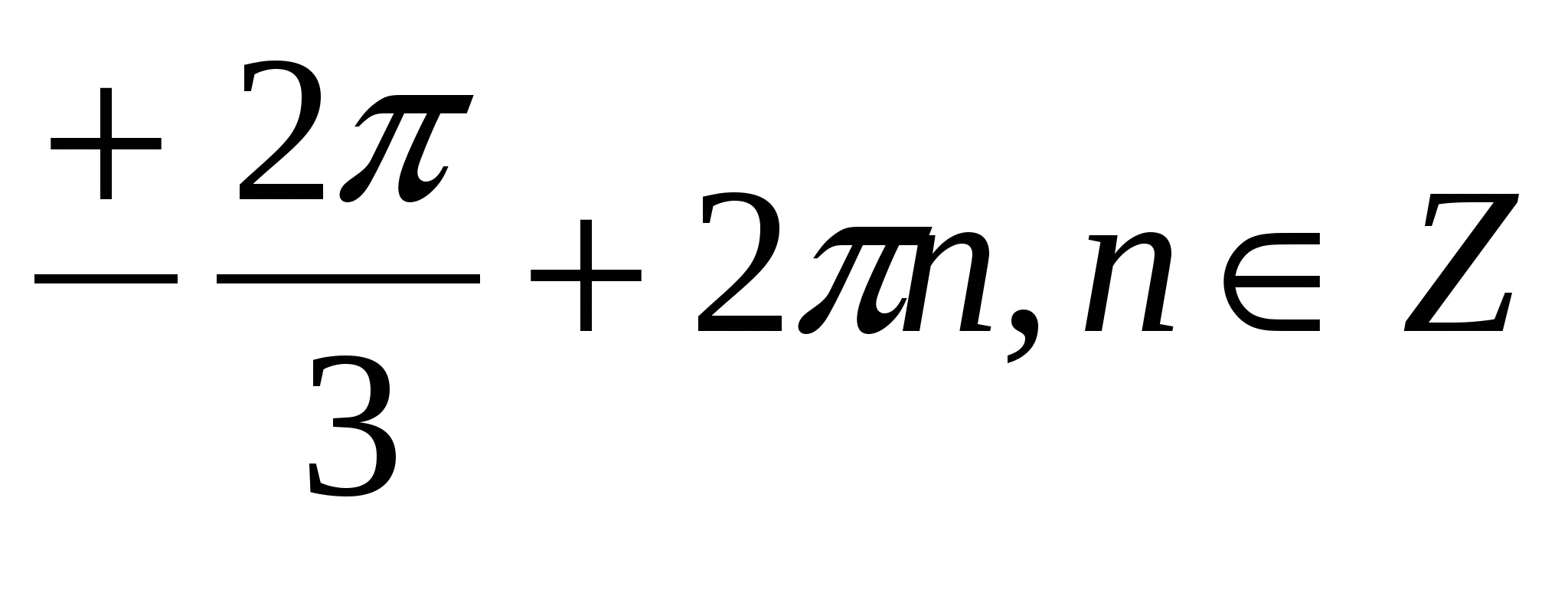
А

Б

В

Г

Д

5. Самостоятельная работа.

Учитель: Ребята, а теперь, прежде чем приступить к самостоятельной работе, вспомним основные методы решения тригонометрических уравнений.

*На экране проецируются основные виды тригонометрических уравнений, методы их решений

1. Введение новой переменной.

2sin²x – 5sinx + 2 = 0.

Пусть sinx = t, |t|≤1,

Имеем: 2t² – 5t + 2 = 0.

2. Разложение на множители

2sinx cos5x – cos5x = 0;

cos5x (2sinx – 1) = 0.

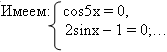
3. Однородные тригонометрические уравнения.

I степени

a sinx + b cosx = 0, (a,b ≠ 0).

Разделим на cosx ≠ 0.

Получаем ии решаем: a tgx + b = 0; …

II степени

a sin²x + b sinx cosx + c cos²x = 0.

1) если а ≠ 0, разделим на cos²x ≠0

имеем: a tg²x + b tgx + c = 0.

2) если а = 0, то

имеем: b sinx cosx + c cos²x =0; разделим на cos²x ≠0

получаем и решаем

b tgx + c = 0

(Раунд тэйбл- учащиеся по очереди выполняют письменную работу по кругу на одном листе бумаги)

- Теперь проверьте свои знания и умения по данной теме.

Учащимся предлагается выполнить самостоятельную работу по карточкам на 3 команды

I команда

II команда

III команда

Решите уравнения:

1).

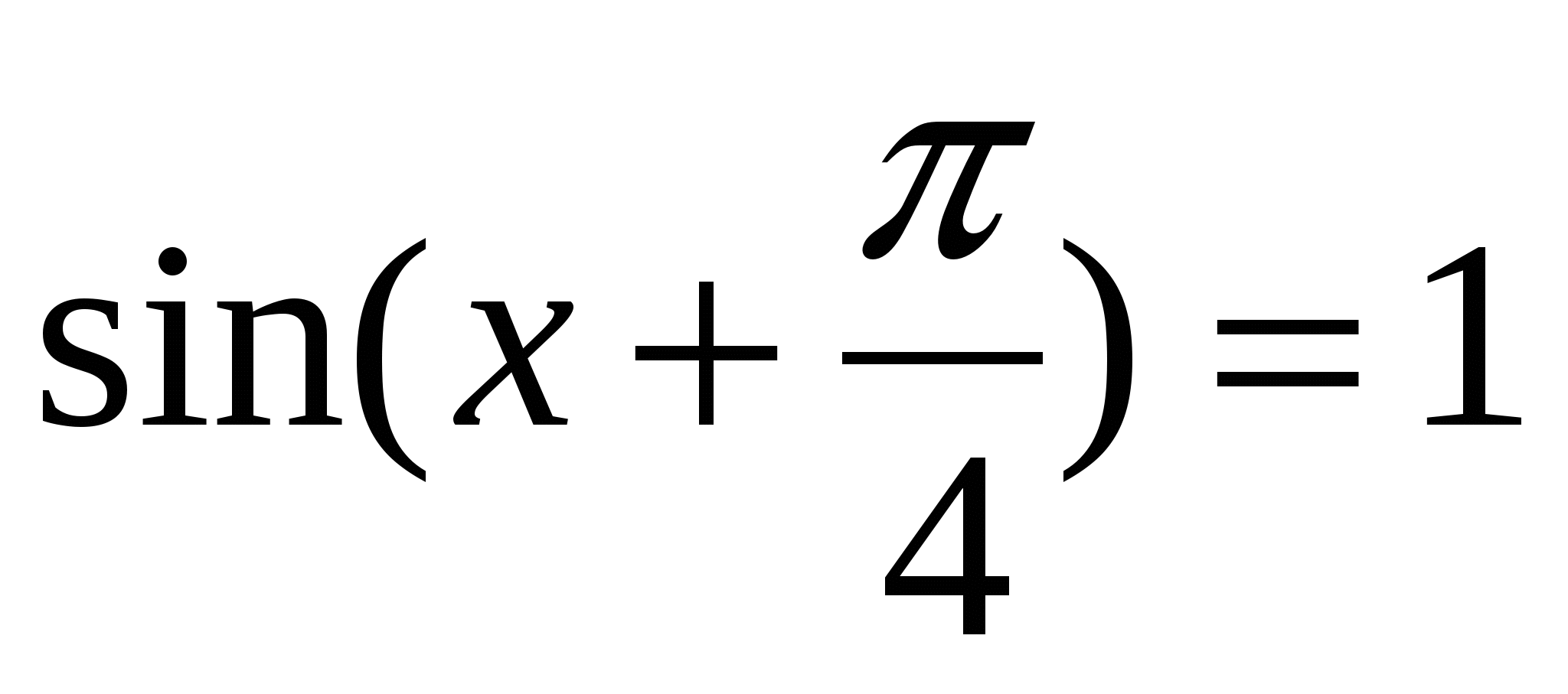
2)

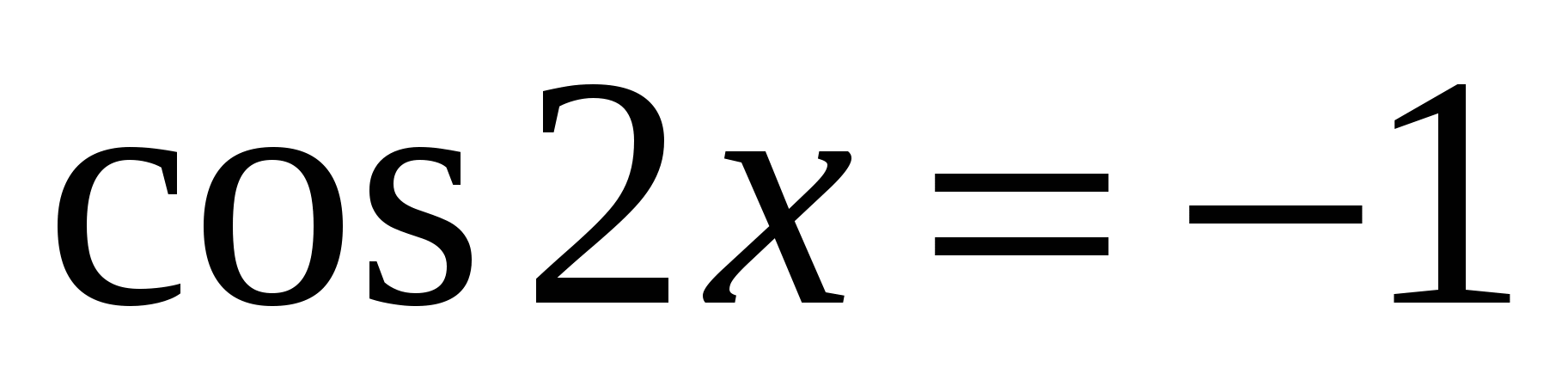
3) ctg 2 x= - 1

4). 2sin²x – 5 sin x + 2 = 0

5). 2 sin x ∙ cos x – 3sin x = 0

Решите уравнения:

1).

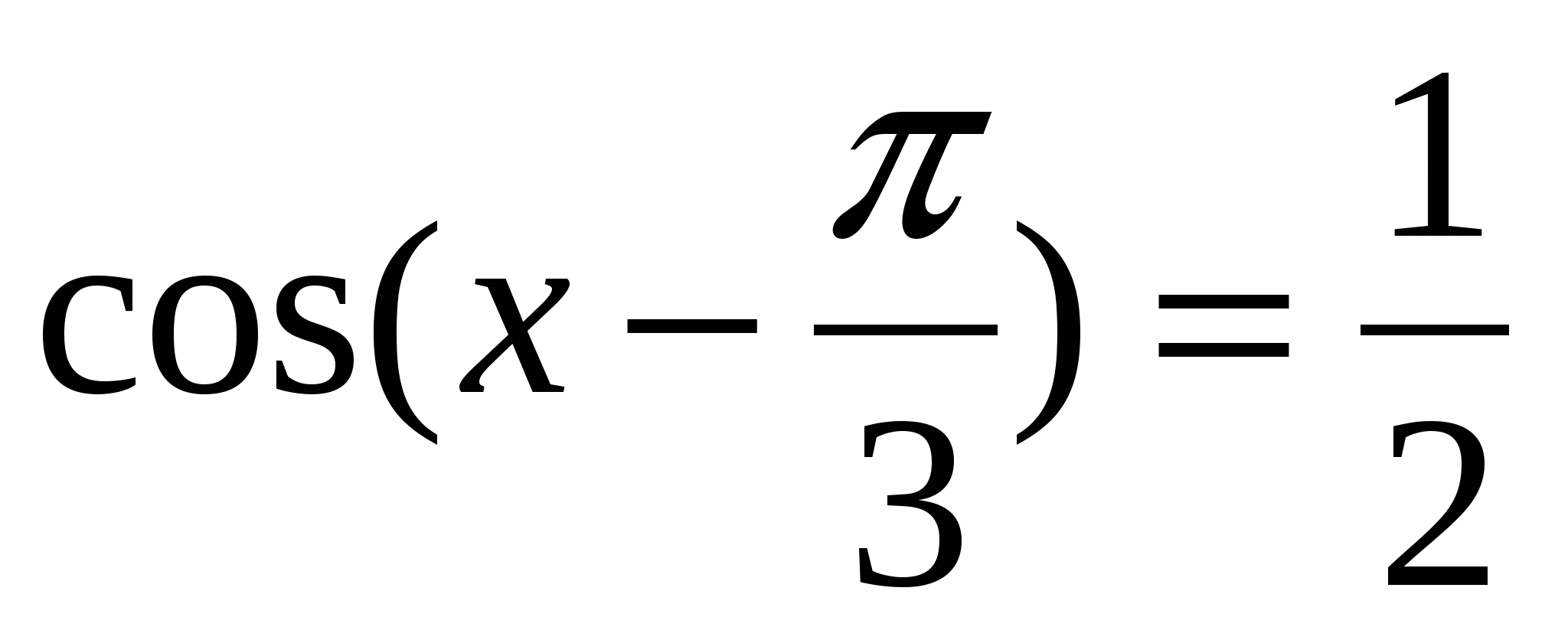
2).

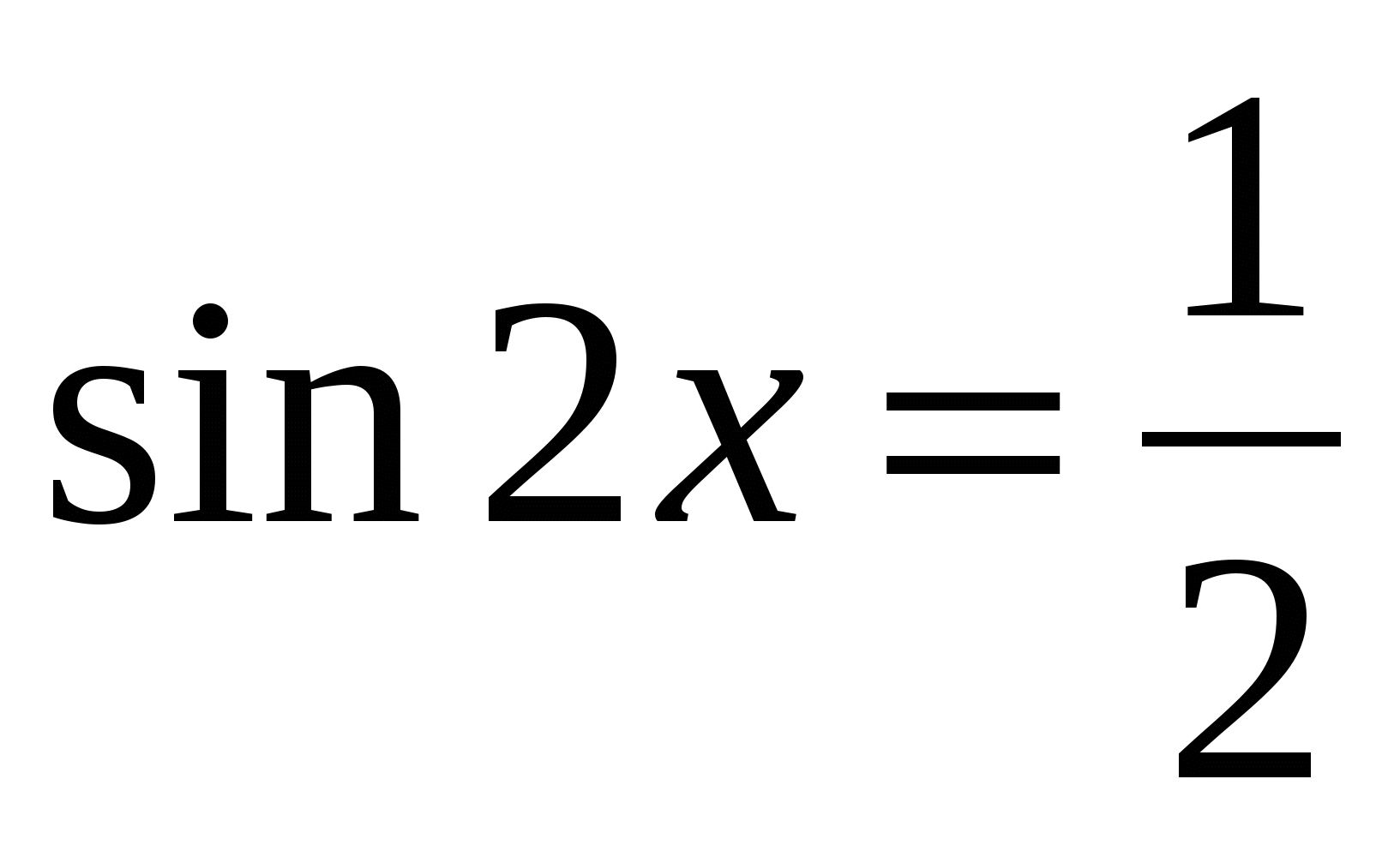
3)

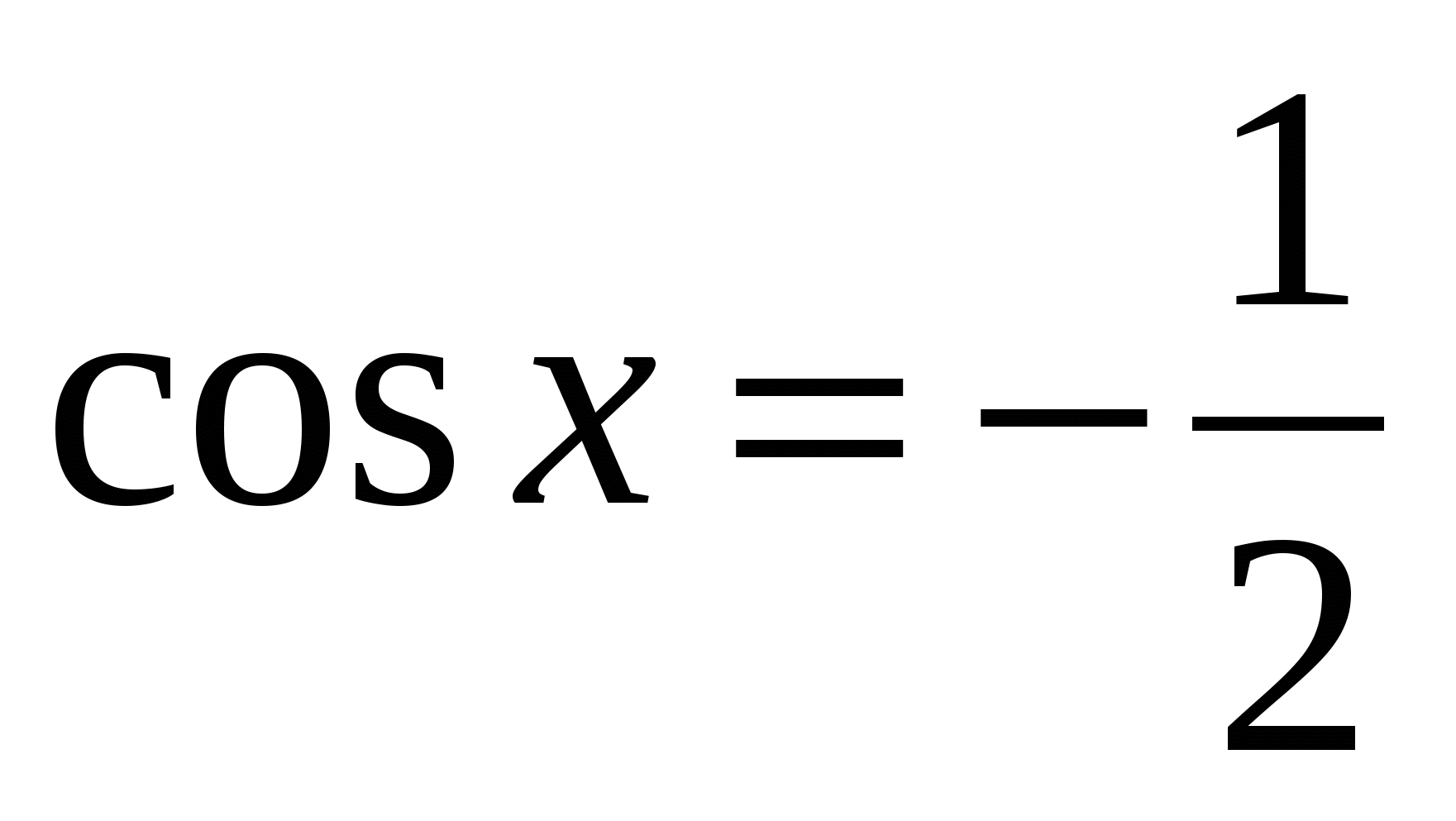
4)cos²x + 3cos x = 0

5). 2 sin² x + 3cos x = 0

Решите уравнения:

1)

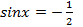
2)

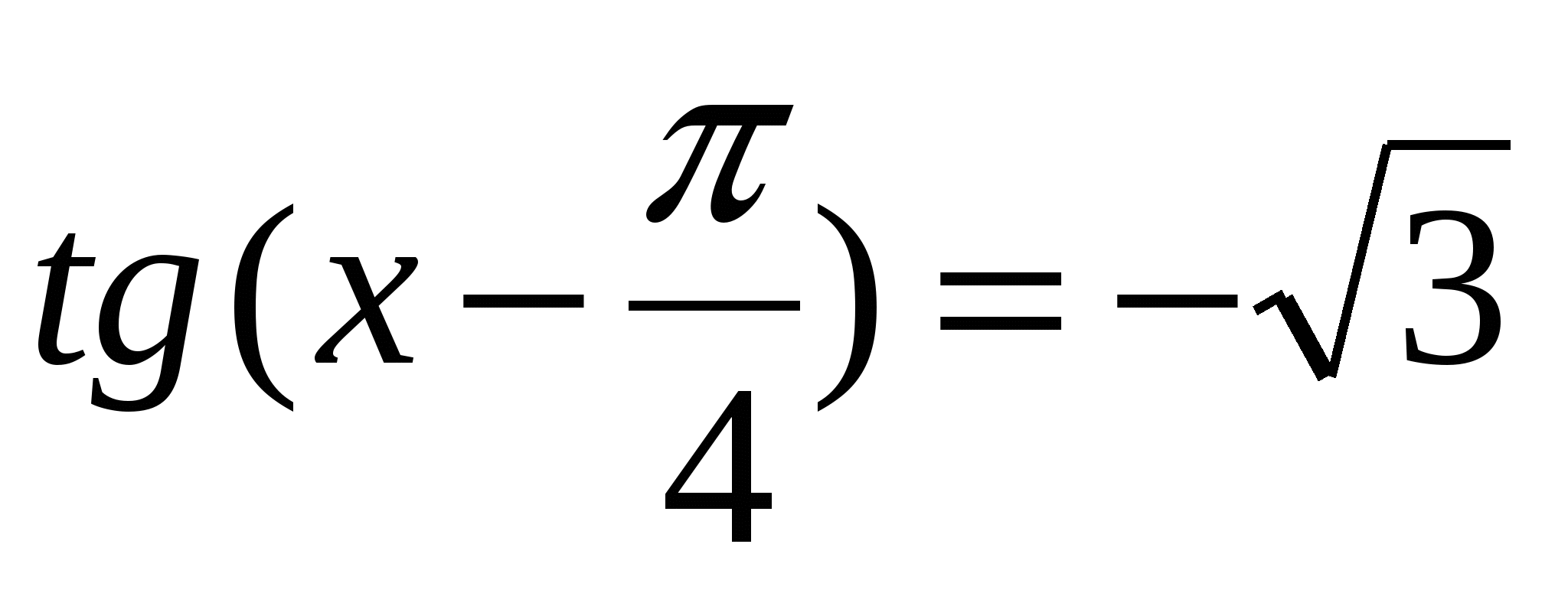
3)

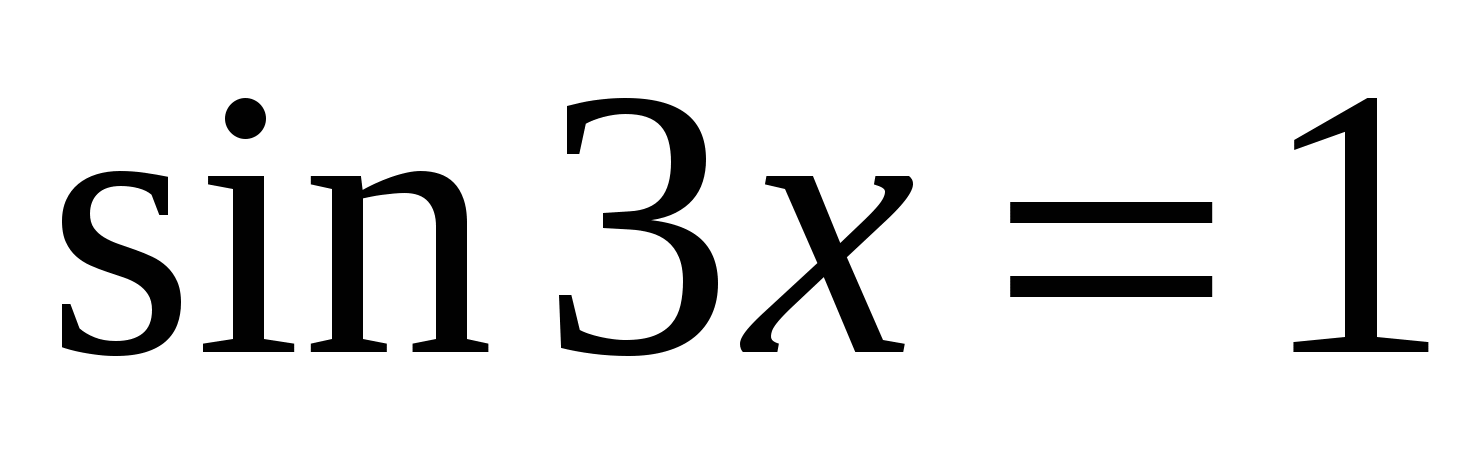
4) sin2 х + 5 sin х - 6 =0.

5) 2 sin x+ 3 cos x = 0.

6. Самоконтроль.

- На партах- таблица ответов.

- Проверьте результаты своей работы по таблице и оцените ее.

Проводится сравнительный анализ результатов работы.

7. Разбор различных типов заданий.

2 сильных ученика приглашаются к доске для индивидуальной работы. Им выдаются карточки с заданиями, которые они решают на доске.

1. Сколько корней имеет уравнение cos²x + sin x = cos 2x + 2 ……….

В это время остальные эти же задания выполняют на месте

8. Коррекция знаний и умений.

Учащиеся, допустившие ошибки в самостоятельной работе, выполняют работу над ошибками. Ребята, которые выполнили самостоятельную работу верно, выполняют то же задание , что на доске

9. Подведение итогов урока, выставление оценок.

- Итак, сегодня мы проверили знания и умения решения простейших тригонометрических уравнении и первых 4 типов и уравнений, приводимых к ним. Рассмотрели примеры применения их при выполнении различных типов заданий, что вам потребуется при сдаче ЕГЭ.

Я уверена, что у вас сложилось более полное представление о тригонометрических уравнениях и разнообразии способов их решения, и с решением тригонометрических уравнений большинство из вас справится.

- Что нового узнали на уроке?

- Испытывали ли вы затруднения при выполнении самостоятельной работы?

- Испытывали ли вы затруднения при выборе самостоятельной работы?

- Какие проблемы у вас возникли по окончании урока?

Комментирование результатов работы учащихся. Выставление оценок.

Дифференцированное домашнее задание. Задание выводится на экран, в факультативе загружается файлом

Решите уравнения

Оценка «3»:

1. 

2. 

3. 

Оценка «4»:

1. 

2. 

Оценка «5»:

1. Найдите наибольший отрицательный корень уравнения

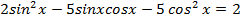
Учитель: Спасибо вам за насыщенную работу на уроке. Я благодарю всех, кто принял активное участие в работе. Урок окончен. До свидания!