Тема: «Решение систем уравнений» 9 класс
Цели:
образовательная: оперирование основными понятиями, входящими в изучаемую тему; закрепление навыков решения систем уравнений различными методами и выработка умений пользоваться всеми методами решения систем уравнений; решение типовых и повышенного уровня сложности задач по теме;
развивающая: побуждение учащихся к творческому, нестандартному мышлению через нестандартные вопросы и задания; развитие рефлексивных навыков;
воспитательная: приобретение веры в себя, в свои потенциальные возможности; умение ставить перед собой цель, планировать деятельность; развитие навыков работы в группе, формирование культуры оформления.
Ход урока
1.Организационный момент
Сегодня мы поговорим о методах решения систем уравнений. Мы знаем, что правильно выбранный метод часто позволяет существенно упростить решение, поэтому все изученные нами методы всегда нужно держать в зоне своего внимания, чтобы решать конкретные задачи наиболее подходящим методом.
2.Актуализация знаний
Перечислите методы решений систем уравнений.
Подберите наиболее подходящий метод для решения следующих систем уравнений:
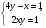 ;
;  ;
; 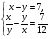 ;
;  .
.
Игровой момент
В библейской легенде голубка приносит Ною весть о том, что бог сменил гнев на милость и что потоп кончился. Выражение «Голубь мира» приобрело особую популярность после того, как голубь, несущий в клюве оливковую ветвь, был использован художником при создании эмблемы для Всемирного конгресса сторонников мира (1949 г.). 
Решите системы уравнений. Используя найденные ответы, узнайте методом исключений фамилию художника, создавшего эту эмблему.
I вариант 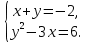 II вариант
II вариант 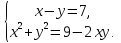
Сальвадор Дали
Александр Дейнека
Пабло Пикассо
(-2;0), (1;-3)
(5; -2), (2;-5)
(-2;5), (-5;2)
Ответы: I вариант (-2; 0), (1; -3)
II вариант (5; -2), (2;-5)
Вывод: Пабло Пикассо.
Учитель: Пикассо-и-Руис, Пабло испанец. Годы жизни: 1881 - 1973. Великий художник 20-го века, живописец, рисовальщик, скульптор, график, керамист. Жил и работал в Париже и разных окрестностях Франции. В Эрмитаже - 35 картин, богатое собрание графики, а также произведения керамики.
3.Исследовательская работа (в группах).
Подготовительная работа

НОМЕР
1
2
3
4
5
6
ОТВЕТ
2
3
1
4
нет
1
Задание.
При каких значениях параметра а система уравнений имеет три решения?
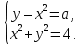
Решение: парабола y= x2 +a будет иметь с окружностью x2 + y2 = 4 три общие точки только в случае а = - 2.
Ответ: а = - 2
4.Решение примеров с «изюминкой»
Учитель записывает все три системы на доске и выслушивает предложения учащихся об их решении, затем вызывает трех человек к доске.
1.Решить систему уравнений: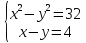
Решение.
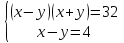
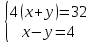 ( изюминка)
( изюминка)
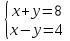
Получили простейшую систему; применяя метод алгебраического сложения, получим:
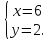
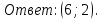
2. Решить систему уравнений: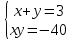
Решение.
Изюминка состоит в том, что решения этой системы можно подобрать, как корни приведенного квадратного уравнения ( по теореме Виета).
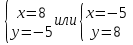
Ответ: (8;-5); (-5;8).
3. Решить систему уравнений: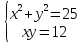
Решение.
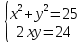

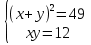 ( изюминка)
( изюминка)
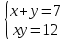 или
или 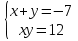
 решаем, как пример 2.
решаем, как пример 2.
 (3;4); (4;3); (-3;-4); (-4;-3).
(3;4); (4;3); (-3;-4); (-4;-3).
5.Дифференцированная самостоятельная работа
( Самостоятельные и контрольные работы по алгебре и геометрии для 9 класса. Ершова А.П., Голобородько В.В.)

6.Итог урока
1.Наш урок подошел к концу. Чем мы сегодня занимались на уроке, что нового узнали?
Благодарю всех за проделанную работу
Порой задача не решается,
Но это, в общем, не беда.
Ведь солнце все же улыбается,
Не унывай никогда.
Друзья тебе всегда помогут
Они с тобой, ты не один.
Поверь в себя – и ты все сможешь,
Иди вперед и победишь.
7.Домашнее задание (индивидуальное домашнее задание по карточкам).
(Индивидуальное домашнее задание по теме: "Системы рациональных уравнений" Горина Л.В.
http://metodisty.ru/m/files/view/individualnoe_domashnee_zadanie_po_teme-_-sistemy_racionalnyh_uravnenii)