
РЕШЕНИЕ СЛОЖНЫХ ЛОГАРИФМИЧЕСКИХ НЕРАВЕНСТВ

Цель урока:
Сформировать умения учащихся решать сложные логарифмические неравенства, а также неравенства смешанного типа.
Не допускать ошибок в проводимых преобразованиях. Следить за тем, чтобы каждое действие не расширяло и не сужало область допустимых значений неравенства, то есть не приводило ни к потере, ни к приобретению посторонних решений.
Развитие у учащихся логического мышления . Умение учащихся оперировать такими понятиями, как система неравенств (пересечение множеств), совокупность неравенств (объедение множеств), осуществлять отбор решений неравенства, руководствуясь его областью допустимых значений
Освоение всеми учащимися алгоритмов решения сложных логарифмических неравенств, закрепление теоретических знаний при решении конкретных примеров;
Развитие культуры научных и учебных взаимоотношений между учениками и между учениками и учителем; воспитание навыков совместного решения задач.
«В науке нет широкой столбовой дороги,
и только тот может достигнуть её сияющих вершин,
кто не страшась усталости,
карабкается по её каменистым тропам.»
К. Маркс
Ход урока
Организационный момент (формулировка темы, постановка целей и задач урока перед учащимися, план хода урока)
Актуализация опорных знаний проводится в форме беседы по лекционному материалу по данной теме.
Понятие сложного логарифмического неравенства
Под сложным логарифмическим неравенством понимают неравенство вида 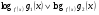 , где
, где 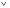 – один из знаков неравенств:
– один из знаков неравенств: 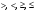 .
.
Алгоритм решения сложного логарифмического неравенства
Так как при 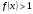 функция
функция 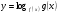 является возрастающей, а при – убывающей, то для решения сложного логарифмического неравенства необходимо рассмотреть два случая, т. е. решить совокупность двух систем:
является возрастающей, а при – убывающей, то для решения сложного логарифмического неравенства необходимо рассмотреть два случая, т. е. решить совокупность двух систем:

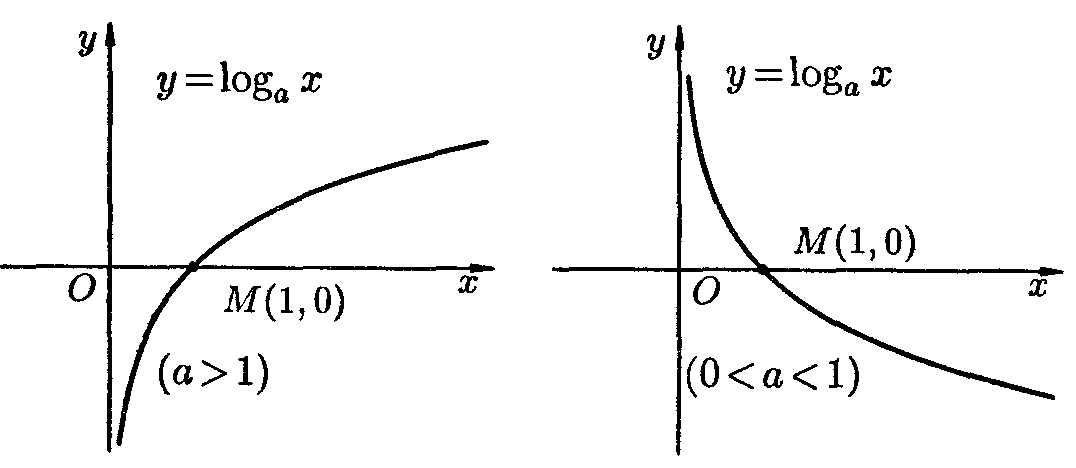
Решение сложных логарифмических неравенств методом эквивалентной замены их одной системой неравенств
Решение сложных логарифмических неравенств совокупностью двух систем можно значительно упростить, применяя эквивалентную замену:
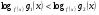

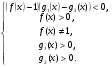
Решение задач:.
Пример 1.
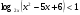
Решается двумя способами(совокупностью двух систем; эквивалентной системой) на доске разными учениками одновременно. Далее проводится обсуждение каждого из методов решения, определяется более рациональный
.Решение:
1 способ
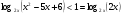
Данное неравенство равносильно совокупности двух систем рациональных неравенств:
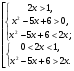
x
6
3
2
1

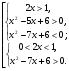
x
6
1

0
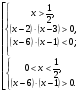
Решение совокупности:
x
6
3
2
1

0
Ответ. 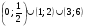 .
.
2 способ
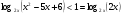
Данное неравенство равносильно системе рациональных неравенств:
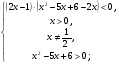
x
6
3
2
1

0
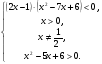
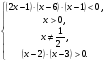
Ответ. 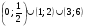 .
.
Пример 2. Решите логарифмическое неравенство:
![\[ \log_{x+1}(x^3+3x^2+2x)<2. \]](http://doc4web.ru/uploads/files/49/49067/hello_html_m3cd487f1.png)
Решается учеником на доске с комментариями
Решение. Область допустимых значений неравенства определяется следующей системой:
![\[ \begin{cases} x+1>0, \\ x+1\ne 1,\\ x(x+1)(x+2)>0 \end{cases}\Leftrightarrow x\in (0;+\mathcal{1}). \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_2.png)
Видно, что в области допустимых значений выражение, стоящее в основании логарифма, всегда больше единицы, а потому равносильным по теореме 2 будет переход к следующему неравенству:
![\[ x^3+3x^2+2x<x^2+2x+1\Leftrightarrow x^3+2x^2-1<0\Leftrightarrow \]](http://doc4web.ru/uploads/files/49/49067/hello_html_22bb921c.png)
![\[ (x+1)(x^2+x-1)<0\Leftrightarrow \]](http://doc4web.ru/uploads/files/49/49067/hello_html_12b0f8ab.png)
![\[ x\in\left(-\mathcal{1};-\frac{1+\sqrt{5}}{2}\right)\cup\left(-1;\frac{\sqrt{5}-1}{2}\right). \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_3.png)
С учетом области допустимых значений получаем окончательный ответ:
![\[ x\in\left(0;\frac{\sqrt{5}-1}{2}\right). \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_4.png)
Пример 3 .
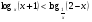
Решается учеником на доске с комментариями
Решение:
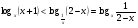
Данное неравенство равносильно системе рациональных неравенств:
x
-1

0
1
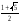
2
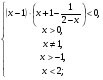
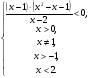
Ответ. 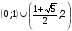 .
.
Пример 4. Решите неравенство 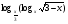 ≥ 0.
≥ 0.
Решение. Заменим данное неравенство равносильной системой, используя метод рационализации
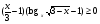
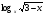 > 0
> 0
3 – x > 0
x > 0
x ≠ 3
x ≠ 1
(x – 3)(x – 1)(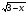 - 1) ≥ 0
- 1) ≥ 0
(x – 1)(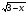 - 1) > 0
- 1) > 0
x > 0
x ≠ 3
x ≠ 1
(x – 1)(3 – x –x2) ≤ 0
(x – 1)(3 – x – 1) > 0
x < 3
x > 0
x ≠ 1
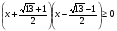
1 < x < 2
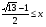 < 2.
< 2.
При решении неравенства (х – 1)(х – 2) < 0 системы учтены условия x < 3, x > 0, x ≠ 1. Условие 1 < x < 2 позволяет исключить множитель x – 1 > 0 в первом неравенстве системы.
Ответ: 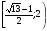 .
.
Пример 5. Решите неравенство:
![\[ \frac{2\log_3(x^2-4x)}{\log_3 x^2}\leqslant 1. \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_5.png)
Решение.
Область допустимых значений неравенства определяется системой неравенств:
![\[ \begin{cases} x^2-4x>0, \\ x^2>0, \\ x^2\ne 1 \end{cases}\Leftrightarrow x\in(-\mathcal{1};-1)\cup(-1;0)\cup(4;+\mathcal{1}). \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_6.png)
I способ. Воспользуемся формулой перехода к новому основанию логарифма и перейдем к равносильному в области допустимых значений неравенству:
![\[ \log_{x^2}(x^2-4x)^2\leqslant 1. \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_7.png)
Неравенство будет равносильно двум системам. Первой:
![\[ \begin{cases} x\in(-1;0), \\ (x^2-4x)^2\geqslant x^2 \end{cases}\Leftrightarrow \begin{cases} x\in(-1;0), \\ x^2(x-5)(x-3)\geqslant 0 \end{cases}\Leftrightarrow \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_8.png)
![\[ x\in (-1;0). \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_9.png)
И второй:
![\[ \begin{cases}x\in(-\mathcal{1};-1)\cup(4;+\mathcal{1}), \\ x^2(x-5)(x-3)\leqslant 0 \end{cases}\Leftrightarrow x\in(4; 5]. \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_10.png)
Итак, окончательный ответ:
![\[ x\in(-1;0)\cup(4;5]. \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_11.png)
II способ. Решаем методом интервалов. Преобразуем неравенство к виду:
![\[ \frac{2\log_3(x^2-4x)-\log_3 x^2}{\log_3 x^2}\leqslant 0\Leftrightarrow \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_12.png)
Вычтем из знаменателя 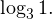 Это ничего не изменит, поскольку
Это ничего не изменит, поскольку 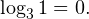
![\[ \frac{\log_3(x^2-4x)^2-\log_3 x^2}{\log_3 x^2-\log_3 1}\leqslant 0 \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_15.png)
С учетом того, что выражения  и
и  — одного знака при
— одного знака при ![]() в области допустимых значений имеет место следующий равносильный переход:
в области допустимых значений имеет место следующий равносильный переход:
![\[ \frac{(x^2-4x)^2-x^2}{x^2-1}\leqslant 0\Leftrightarrow \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_19.png)
![\[ \frac{(x^2-5x)(x^2-3x)}{x^2-1}\leqslant 0. \]](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_20.png)
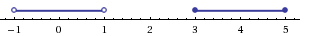
Множество решений данного неравенства
Итак, ![x\in(-1;1)\cup [3;5],](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_21.png) а с учетом области допустимых значений получаем тот же результат:
а с учетом области допустимых значений получаем тот же результат: ![x\in(-1;0)\cup (4;5].](/wp-content/uploads/images/konspekt_uroka_po_algebre_reshenie_slozhnih_logarifmicheskih_neravenstv_doc_22.png)
Подведение итогов урока. Рефлексия.
Домашнее задание.
Решите неравенство
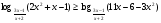 .
.
Ответ: 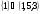
Решите неравенство
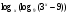 < 1.
< 1.
Ответ: (log310; + 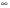 ).
).
Решите неравенство
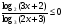 .
.
Ответ: 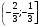 .
.