Разработка урока по математике в 10 классе.
Тема: «Решение тригонометрических уравнений»
Цель:
Систематизировать и обобщить знания учащихся
Совершенствовать навыки решения тригонометрических уравнений
Ход урока:
Организационный момент.
Задание на внимательность.
Дан набор букв. Нужно вычеркнуть буквы, которые стоят на четных местах. Получится высказывание.
Мйацтуекмеантгишкщузнхеълфьызвяаипзруочладтдьжняачбслмюидтаьябкю
Айкцэуткоеднеглшащезтхсъофсыевда ( Математику нельзя изучать, наблюдая, как это делает сосед. Нивей)
Устный счет. Вычисли (задания написаны на доске или слайде):
sin30º; cos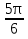 ; sin90º; cos120º; cos180º
; sin90º; cos120º; cos180º
arcsin(-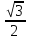 ); arccos(-
); arccos(-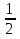 ); 2sin15°cos15°; cos2
); 2sin15°cos15°; cos2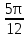 - sin2
- sin2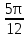 ;
; 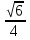 +
+  .
.
Найди ошибку.
cos2x – sin2x = 1; cos2x + sin2x = sin2x ; cos2x = 2sinxcosx; cos2x = 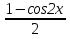 ; sin2x =
; sin2x = 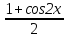 .
.
Даны уравнения:
х2 + 5х – 6 = 0
sinx =
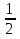
2cosx = -
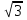
x2 + 7x = 0
ctgx = -1
sinx = 1
3sinx = 9
Выполните задания:
На сколько групп можно разделить эти уравнения?
Решите устно квадратные уравнения.
Из тригонометрических уравнений выберите лишнее. Почему?
Решите устно тригонометрические уравнения.
Вывод темы и цели урока совместно с учащимися.
На доске написано решение уравнения, но с ошибками. Реши у себя в тетради правильно и сравни с образцом на слайде или на доске.
sin2x + 2cosx – sinx – 1 = 0
2sinxcosx + 2cosx – (sinx + 1) = 0
2cosx(sinx + 1) – (sinx + 1) = 0
(sinx + 1)2cosx = 0
sinx + 1 = 0 2cox = 0
sinx = -1 cosx = 0
x = 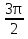 + n, n€Z; x = 2n, n€Z
+ n, n€Z; x = 2n, n€Z
Физкультминутка.
Решение уравнения на доске (1 ученик), остальные в тетрадях.
Решите уравнение 2cos2x – sin2x = 0 и определите корни, которые принадлежат промежутку х€ (-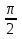 ; 3].
; 3].
Продолжи решение уравнения и определи, сколько корней имеет уравнение на промежутке [-2; 2].
1 + sinx +cosx + sin2x + cos2x = 0
1 + sinx + cosx + 2sinxcosx + cos2x – sin2x = 0
sinx + cosx + 2sinxcosx + 2cos2x = 0
Подведение итога урока. Мне приходилось делить время между политикой и уравнениями. Однако уравнения, по-моему, важнее. Политика только для данного момента, а уравнения будут существовать вечно. (А.Энштейн)
Блиц – опрос. (Если утверждение верно – то «да», если неверно – то «нет»)
sinx = 0,5 x = (-1)n
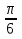 + n, n€Z
+ n, n€Zcosx = 0 x =
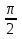 + 2n, n€Z
+ 2n, n€Zsin2x = sinxcosx
tgx = -1 x = -
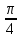 + n, n€Z
+ n, n€Zcosx + sin2x = cosx(1 + 2sinx)
Взаимопроверка. ( нет ошибок – «5», 1 ошибка – «4», 2 ошибки – «3», 3 ошибки и больше – «2»)