МБОУ СОШ №6 г.Пушкино
Открытый урок: «Решение задач с помощью дробных рациональных уравнений»
Учитель: Горшкова Н.Н.
Урок №2 (по теме).
С помощью рациональных уравнений решается целый ряд задач, которые возникают не только на страницах учебника математики, но и в жизни. Однако, для того, чтобы решить рациональное уравнение, его ещё необходимо уметь правильно составить. Поэтому на данном уроке мы не только рассмотрим примеры решения рациональных уравнений как таковых, но и примеры математического моделирования задачи, которое приводит к возникновению соответствующих рациональных уравнений.
Тема: Решение задач с помощью дробных рациональных уравнений.
Цель: Уметь решать задачи на движение, движение по реке, на работу, сводящиеся к составлению дробных рациональных уравнений.
Тип урока: Урок формирования умений и навыков.
План урока:
№
Этап урока
Содержание (цель) этапа
Время
(мин)
1
Организационный момент.
Нацелить учащихся на урок.
1
2
Проверка домашнего задания.
Коррекция ошибок.
4
3
Изучение нового материала.
Познакомить учащихся с решением текстовых задач с помощью дробных рациональных уравнений.
8
4
Тренировочные упражнения.
Формировать умения решать задачи на движение с помощью дробных рациональных уравнений.
15
5
Самостоятельная работа обучающего характера.
Проверить сформированность умений составлять дробные рациональные уравнения по условию задачи.
15
6
Подведение итогов урока.
Обобщить теоретические сведения, полученные на уроке.
1
7
Сообщение домашнего задания.
Разъяснить содержание домашнего задания.
1
Ход урока
2. Проверка домашней работы.
№ 623 (учащийся у доски)
Цена,
руб
Кол-во билетов
Стоимость,
руб
«Надежды»
x
240/x
240
«Удачи»
x-5
240/(x-5)
240
Уравнение составим, зная, что билетов «Удачи» купили на 4 больше чем билетов «Надежды
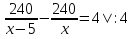
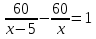
x2-5x=300
x2-5x-300=0
x1= -15 (не является решением задачи)
x2=20
Ответ: 20 руб.
Учитель:
Решение текстовых задач обычно осуществляется в несколько этапов.
Учащиеся:
Введение неизвестной величины;
Составление уравнения;
Решение полученного уравнения;
Отбор решений по смыслу задачи - т.е. проверка ответа.
Объяснение нового материала. Решение задач.
№ 627
-
v (км/час)
t (час)
S (км)
Против течения
x-2
6/(x-2)
6
Озеро
x
15/x
15
Пусть vсоб = x км/час, тогда
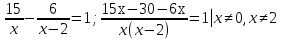9x-30=x2-2x;
x2-11x+30=0;
x1=5
x2=6
Ответ: 5 км/час или 6 км/час
Тренировочные упражнения.
№ 629
v
t
S
По течению
20+x
22/(x+20)
22
Против теч.
20-x
36/(20-x)
36
vсоб=20 км/час
vтеч.р.= x км/час
Составим уравнение, зная, что всего времени потрачено 3 часа.
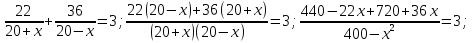14x+1160=1200-3x2;3x2+14x-40=0;
D1=49+120=169;
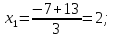
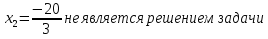
Ответ: 2 км/час
№632
Произв. труда
t
Объем работы
I
1/(x+5)
x+5
1
II
1/x
x
1
Составим уравнение, зная, что вместе они выполняют работу за 6 часов
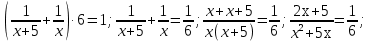
x2+5x=12x+30;
x2 - 7x - 30=0 ;
x1=10;
x2=-3 не является решением задачи
I: 10+5=15 (часов)
II: 10 (часов)
Ответ: 15 часов; 10 часов
Самостоятельная работа (работа в парах).
Вариант I.
Первый рабочий за час делает на 2 детали больше, чем второй, и заканчивает работу над заказом, состоящим из 143 деталей, на 2 часа раньше, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Два велосипедиста одновременно отправляются в 70-километровый пробег. Первый едет со скоростью на 3 км/ч большей, чем второй и прибывает к финишу на 3 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Два комбайна убрали поле за 4 дня. За сколько дней мог убрать поле каждый комбайн, если одному из них для выполнения этой работы потребовалось бы на 6 дней меньше, чем другому?
Вариант II.
Два велосипедиста одновременно отправляются в 80-километровый пробег. Первый едет со скоростью на 2 км/ч большей, чем второй и прибывает к финишу на 2 часа раньше второго. Найти скорость велосипедиста, пришедшего к финишу вторым. Ответ дайте в км/ч.
Первый рабочий за час делает на 3 детали больше, чем второй, и заканчивает работу над заказом, состоящим из 340 деталей, на 3 часа раньше, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Две машинистки, работая совместно, могут перепечатать рукопись за 8 ч. Сколько времени потребовалось бы каждой машинистке на выполнение этой работы, если одной для этого потребуется на 12 ч больше, чем другой?
У доски двое учащихся решают К-6 Б1, в то время как класс выполняет самостоятельную работу.
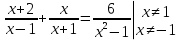(x+1)(x+2)+x(x-1)=6
x2+3x+2+x2-x=6
2 x2+2x-4=0
x2+x-2=0
D=1+2∙4=9
x1= -2
x2 =1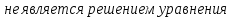 
Ответ: x=-2
6x2+60x=120x+1200-120x
x2+10x-200=0
x1=-20 не является решением задачи
x2=10
Ответ: 10 км/час
7. Домашние задание.
№№ 627, 636(а), 624, 702
На оценку 705*
Дополнительные задания (при наличии времени)
№ 638
x2-10x+q=0
x1-x2=6
q=?
Решение:
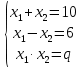
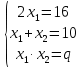
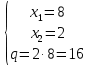
Ответ: 16
№636(б)
Доказать, что
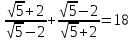
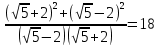
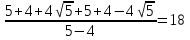
18=18
Применение дробных рациональных уравнений. Решение задач (Ершова А.П. 1999).
№2
№1
№3
V
t
S
По теч.
x+2
60/(x+2)
60
Озеро
x
36/x
36
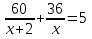
5x2-86x-72=0
D1=2209
x1=18
x2=-0.8 не является решением задачи
Ответ: 18 км/час
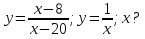
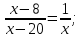
x2-8x=x-20;
x2-9x+20=0;
x1=5
x2=4
Ответ: 4;5
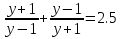
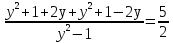
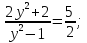4y2+4=5y2-5;
y2=9;
y1,2=±3
Ответ: ±3
Литература
1. С.А.Теляковский, Учебник по алгебре для 8 класса общеобразовательных учреждений, «Просвещение», М., 2007
2. А.П.Ершова, В.В.Голобородько, Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса, «Илекса», М., 2001
Т.М. Ерина, Поурочное планирование по алгебре к учебнику Макарычева Ю.М. и др. «Алгебра 7 класс», изд. «Экзамен», М., 2008