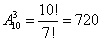Презентацию к уроку вы можете скачать по ссылке http://gomonova.ucoz.ru/load/konspekt_i_prezentacija_k_uroku_matematiki_quot_sochetanija_i_razmeshhenija_quot/1-1-0-29
Урок по теме «Сочетания и размещения»
Организационная информация
Тема урока: «Сочетания и размещения».
Предмет: алгебра и начала анализа.
Класс: 11.
Автор урока: Гомонова Галина Васильевна, учитель математики.
Образовательное учреждение: ГБОУ СОШ п. Масленниково Хворостянского района Самарской области.
Методическая информация
Методологическая база:
программа: Математика. 5 – 6 классы. Алгебра. 7 – 9 классы. Алгебра и начала анализа. 10 – 11 классы. Авторы – составители И.И. Зубарева, А.Г. Мордкович. Москва: Мнемозина, 2009 год.
УМК:
А.Г.Мордкович. Алгебра и начала математического анализа. 10 – 11классы. В 2 ч. Ч. 1. Учебник;
А.Г.Мордкович и др. Алгебра и начала математического анализа. 10 – 11классы. В 2 ч. Ч. 2. Задачник;
И.Р.Высоцкий, И.В.Ященко. ЕГЭ 2012. Математика. Задача В10. Теория вероятностей. Рабочая тетрадь/Под редакцией А.Л.Семенова, И.В.Ященко. Москва. Издательство МЦНМО, 2012;
Задача В10. Открытый банк заданий по математике. ЕГЭ 2012.
интернет – источники:
http://ru.wikipedia.org/wiki/%CA%EE%EC%E1%E8%ED%E0%F2%EE%F0%E8%EA%E0;
http://wiki.kemedu.ru/index.php5/%D0%9A%D1%80%D0%B0%D1%81%D0%BE%D1%82%D0%B0_%D0%BA%D0%BE%D0%BC%D0%B1%D0%B8%D0%BD%D0%B0%D1%82%D0%BE%D1%80%D0%B8%D0%BA%D0%B8;
http://festival.1september.ru/articles/595703/;
http://www.bestreferat.ru/referat-198511.html;
http://festival.1september.ru/articles/585278/;
http://artalbum.org.ua/ru/category/clipart?catid=73;
http://www.74rif.ru/CaF2-1.html;
http://www.testsoch.com/urok-sochetaniya-i-razmeshheniya/.
Тип урока: комбинированный.
Длительность: 2 учебных часа.
Цель урока: рассмотреть основные понятия теории комбинаторики.
Задачи урока:
образовательные: научить воспроизводить общие правила комбинаторики и типы соединений, уметь применять теоретические знания при решении задач;
воспитательные: воспитание умения слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, настойчивости в достижении цели и заинтересованности в конечном результате труда;
развивающие: развитие умения анализировать, обобщать изучаемые факты, выделять и сравнивать существенные признаки, выбирать наиболее эффективные способы решения задач в зависимости от конкретных условий; рефлексия способов и условий действия; контроль и оценка процесса и результатов деятельности.
Используемые технологии: развивающее обучение, групповая технология, ИКТ, элементы исследовательской деятельности, элементы блочного изучения тем.
Оборудование и материалы для урока: компьютер, проектор, презентация по теме «Что такое комбинаторика? Истоки комбинаторики», презентация по теме «Комбинаторика в реальной жизни», презентация по теме «Решение комбинаторных задач», экран.
План урока:
1) Организационный момент.
2) Повторение и закрепление пройденного материала.
3) Изучение нового материала.
3.1. Сообщение 1 группы.
3.2. Сообщение 2 группы.
3.3. Сообщение 3 группы.
3.4. Решение задач по теме «Сочетания и размещения».
4) Итоги урока.
5) Домашнее задание.
Ход урока
1. Организационный момент
Приветствие учеников, сообщение темы и цели урока
2. Повторение и закрепление пройденного материала
Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
Контроль усвоения материала (письменный опрос).
Вариант 1
1. Достоверное событие и его вероятность.
2. а) В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 7 очков. Результат округлите до сотых.
б) В чемпионате по гимнастике участвуют 40 спортсменок: 12 из Аргентины, 9 из Бразилии, остальные — из Парагвая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Парагвая.
в) В среднем из 500 садовых насосов, поступивших в продажу, 4 подтекают. Найдите вероятность того, что один случайно выбранный для контроля насос не подтекает.
Вариант 2
1. Невозможное событие и его вероятность.
2. а) В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 9 очков. Результат округлите до сотых.
б) В чемпионате по гимнастике участвуют 64 спортсменки: 20 из Японии, 28 из Китая, остальные — из Кореи. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Кореи.
в) Фабрика выпускает сумки. В среднем на 170 качественных сумок приходится шесть сумок со скрытыми дефектами. Найдите вероятность того, что купленная сумка окажется качественной. Результат округлите до сотых.
Ответ: вариант 1. 2. а) 0,17; б) 0,475; в) 0,992.
вариант 2. 2. а) 0,11; б) 0,25; в) 0,97.
3. Изучение нового материала
Класс разделен на группы, которые занимались сбором информации, оформлением и представлением на уроке результатов своего труда (выступление учащихся с итогами своей работы).
1 группа (найти информацию о том, какие факторы (причины) способствовали появлению науки комбинаторики, какие ученые стояли у самых истоков возникновения).
2 группа (найти информацию о том, существует ли комбинаторика в реальной жизни, если да, то в каких отраслях применяется).
3 группа (найти информацию о том, какие задачи называются комбинаторными и как можно их решить, рассмотреть каждый метод решения и сделать подборку нескольких задач, решаемых конкретным методом).
1 группа.
Представителям самых различных специальностей приходиться решать задачи, в которых рассматриваются те или иные комбинации, составленные из букв, цифр и иных объектов.
При рассмотрении простейших вероятностных задач нам приходилось подсчитывать число различных исходов (комбинаций). Для небольшого числа элементов такие вычисления сделать несложно. В противном случае такая задача представляет значительную сложность. ( слайд 1)
Комбинаторикой называют область математики, которая изучает вопросы о числе различных комбинаций (удовлетворяющих тем или иным условиям), которые можно составить из данных элементов.
Комбинаторика - раздел математики, в котором изучаются простейшие «соединения». Перестановки - соединения, которые можно составить из n предметов, меняя всеми возможными способами их порядок; число их Размещения - соединения, содержащие по m предметов из числа n данных, различающиеся либо порядком предметов, либо самими предметами; число их Сочетания - соединения, содержащие по m предметов из n, различающиеся друг от друга, по крайней мере, одним предметом (в современном толковом словаре изд. «Большая Советская Энциклопедия»).
С задачами, в которых приходилось выбирать те или иные предметы, располагать их в определенном порядке и отыскивать среди разных расположений наилучшие, люди столкнулись еще в доисторическую эпоху, выбирая наилучшее положение охотников во время охоты, воинов – во время битвы, инструментов – во время работы. (слайд 2)
Термин «комбинаторика» был введён в математический обиход Лейбницем, который в 1666 году опубликовал свой труд «Рассуждения о комбинаторном искусстве». (слайд 3)
Первоначально комбинаторика возникла в XVI в в связи с распространением различных азартных игр. (слайд 4)
Основы комбинаторики и теории вероятностей создали и разработали французские математики XVII века Пьер Ферма и Блез Паскаль.
(слайд 5)
Комбинаторные мотивы можно заметить в символике китайской «Книги Перемен» (V век до н. э.). По мнению её авторов, всё в мире комбинируется из различных сочетаний мужского и женского начал, а также восьми стихий: земля, горы, вода, ветер, гроза, огонь, облака и небо. Историки отмечают также комбинаторные проблемы в руководствах по игре в Го и другие игры. Большой интерес математиков многих стран с древних времён неизменно вызывали магические квадраты. (слайд 6)
В XII веке индийский математик Бхаскара в своём основном труде «Лилавати» подробно исследовал задачи, связанные с перестановками и сочетаниями, включая перестановки с повторениями.
(слайд 7)
В Западной Европе ряд глубоких открытий в области комбинаторики сделали два еврейских исследователя, Авраам ибн Эзра (XII век) и Леви бен Гершом (он же Герсонид, XIV век). Ибн Эзра обнаружил симметричность биномиальных коэффициентов, а Герсонид дал явные формулы для их подсчёта и применения в задачах вычисления числа размещений и сочетаний. (слайд
Джероламо Кардано написал математическое исследование игры в кости, опубликованное посмертно. Теорией этой игры занимались также Тарталья и Галилей. (слайд 9)
Помимо азартных игр, комбинаторные методы использовались (и продолжают использоваться) в криптографии — как для разработки шифров, так и для их взлома. (слайд 10)
Блез Паскаль много занимался биномиальными коэффициентами и открыл простой способ их вычисления: «треугольник Паскаля». Хотя этот способ был уже известен на Востоке (примерно с X века), Паскаль, в отличие от предшественников, строго изложил и доказал свойства этого треугольника
ученик Лейбница Якоб Бернулли, один из основателей теории вероятностей, изложил в своей книге «Искусство предположений» (1713) множество сведений по комбинаторике. (слайд 11)
В этот же период формируется терминология новой науки. Термин «сочетание» впервые встречается у Паскаля. Термин «перестановка» употребил в указанной книге Якоб Бернулли. Бернулли использовал и термин «размещение». (слайд 11)
После появления математического анализа обнаружилась тесная связь комбинаторных и ряда аналитических задач. Абрахам де Муавр и Джеймс Стирлинг нашли формулы для аппроксимации факториала. (слайд 12)
В начале XX века начала развиваться комбинаторная геометрия: были доказаны теоремы Минковского — Радона, Радона, Хелли,Юнга, Бляшке, а также строго доказана изопериметрическая теорема. На стыке топологии, анализа и комбинаторики были доказаны теоремы Борсука — Улама и Люстерника — Шнирельмана. Во второй четверти XX века были поставлены проблема Борсука ипроблема Нелсона — Эрдёша — Хадвигера. В 1940-х годах оформилась теория Рамсея. Отцом современной комбинаторики считается Пал Эрдёш, который ввёл в комбинаторику вероятностный анализ. Внимание к конечной математике и, в частности, к комбинаторике значительно повысилось со второй половины XX века, когда появились компьютеры. Сейчас это чрезвычайно содержательная и быстроразвивающаяся область математики. (слайд 13)
3.2. 2 группа. (слайд 1)
Замечательно, что наука, которая начала с рассмотрения азартных игр, обещает стать наиболее важным объектом человеческого знания. Ведь большей частью жизненные вопросы являются на самом деле задачами из теории вероятностей.
П. Лаплас
Области применения комбинаторики:
учебные заведения (составление расписаний) (слайд 2)
сфера общественного питания (составление меню)
лингвистика (рассмотрение вариантов комбинаций букв)
география (раскраска карт) (слайд 3)
спортивные соревнования (расчёт количества игр между участниками)
производство (распределение нескольких видов работ между рабочими)
агротехника (размещение посевов на нескольких полях) (слайд 4)
азартные игры (подсчёт частоты выигрышей)
химия (анализ возможных связей между химическими элементами)
экономика (анализ вариантов купли-продажи акций) (слайд 5)
криптография (разработка методов шифрования)
доставка почты (рассмотрение вариантов пересылки)
3.3. 3 группа
Задачи, в которых идет речь о тех или иных комбинациях объектов, называются комбинаторными. (слайд 1)
Правило сложения: если некоторый объект А можно выбрать m способами, а другой объект В можно выбрать n способами, то выбор « либо А, либо В» можно осуществить m + n способами. (слайд 2)
Например:
На тарелке лежат 5 яблок и 4 апельсина. Сколькими способами можно выбрать один плод?
По условию задачи яблоко можно выбрать пятью способами, апельсин – четырьмя. Так как в задаче речь идет о выборе «либо яблоко, либо апельсин», то его, согласно правилу сложения, можно осуществить 5+4=9 способами.
Давайте рассмотрим такую задачу: сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза? (слайд 3)
Решение: для того, чтобы не пропустить и не повторить ни одно из чисел, будем записывать их в порядке возрастания. Сначала запишем числа, начинающиеся с цифры 1, затем с цифры 4, и, наконец, с цифры 7:
14, 17, 41, 47, 71, 74.
Ответ: 6.
Этот метод называется перебором вариантов. Таким образом, их трех данных цифр можно составить всего 6 различных двузначных чисел.
Эту задачу можно решить и другим способом. Его название – дерево возможных вариантов. Для этой задачи построена специальная схема. (слайд 4) (слайд 5)
Ставим звездочку. Она будет обозначать количество возможных вариантов.
Далее отводим от звездочки 3 отрезка. В условии задачи даны 3 цифры – 1, 4, 7.
Ставим эти цифры на концах отрезков. Они будут обозначать число десятков в данном числе.
Далее от каждой цифры проводим по 2 отрезка.
На концах этих отрезков записываем также цифры 1, 4, 7. Они будут обозначать число единиц.
Рассмотрим, какие числа получились: 14, 17, 41, 47, 71, 74. То есть всего получилось 6 чисел.
Ответ: 6.
Эта схема действительно похожа на дерево, правда «вверх ногами» и без ствола.
Правило умножения: если объект А можно выбрать m способами и если после каждого такого выбора объект В можно выбрать n способами, то выбор пары (А,В) в указанном порядке можно осуществить m ∙ n способами. (слайд 6)
Сколько двузначных чисел можно составить из цифр 1,4,7, используя в записи числа каждую из них не более одного раза?
Эту задачу можно решить по-другому и намного быстрее, не строя дерева возможных вариантов. Рассуждать будем так. Первую цифру двузначного числа можно выбрать тремя способами. Так как после выбора первой цифры останутся две, то вторую цифру можно выбрать из оставшихся цифр уже двумя способами. Следовательно, общее число искомых трехзначных чисел равно произведению 3∙2, т.е. 6.
Сколько пятизначных чисел можно составить из цифр 5, 9, 0, 6?
По правилу умножения получаем: 4∙4∙4∙4=256 чисел.
(слайд 7)
Перестановки – соединения, каждое из которых содержит n различных элементов, взятых в определенном порядке. (слайд
Pn=n! = 1 · 2 · 3 · … · (n-2) · (n-1) · n
Задача. (слайд 9)
Сколькими способами можно расставить на полке семь различных книг?
Решение:
Число таких способов равно числу перестановок из семи элементов,
т.е. P7 = 7! = 1 · 2 · 3 · … · 7 = 5040.
Ответ: 5040.
Задача. (слайд 10)
Имеются 10 различных книг, три из которых – справочники. Сколькими способами
Можно расставить эти книги на полке так, чтобы все справочники стояли рядом?
Решение:
Т.к. в справочники должны стоять рядом, то будем рассматривать их как одну книгу. Тогда на полке надо расставить 10 – 3+1=8 книг. Это можно сделать P8 способами. Для каждой из полученных комбинаций можно сделать P3 перестановок справочников.
Поэтому число способов расположения книг на полке равно произведению:
P8 · P3 = 8! · 3! = 40320 · 6 =241920.
Ответ: 241920.
Размещения – соединения, отличающиеся друг от друга составом элементов или их порядком, каждая из которых содержит k элементов, взятых из n различных элементов.
Порядок следования элементов важен.
Число размещений из n элементов по k обозначают символом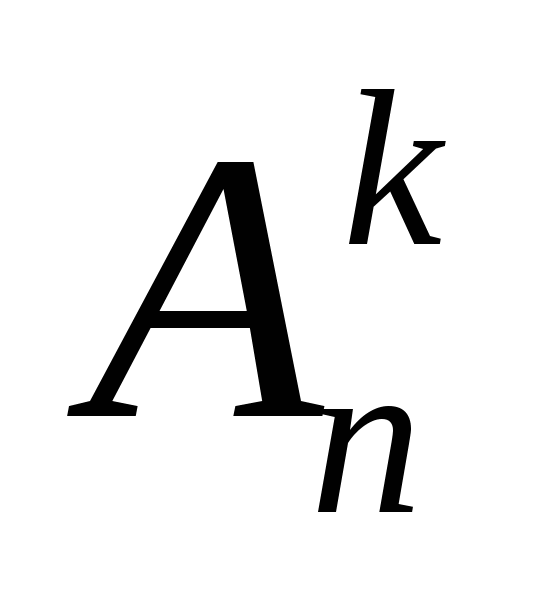 
(читается: А из n по k). (слайд 11)
Сочетания – соединения, отличающиеся друг от друга по крайней мере одним элементом, каждое из которых содержит k элементов, выбранных из n различных элементов.
Порядок следования элементов неважен.
Число сочетаний из n элементов по k обозначают символом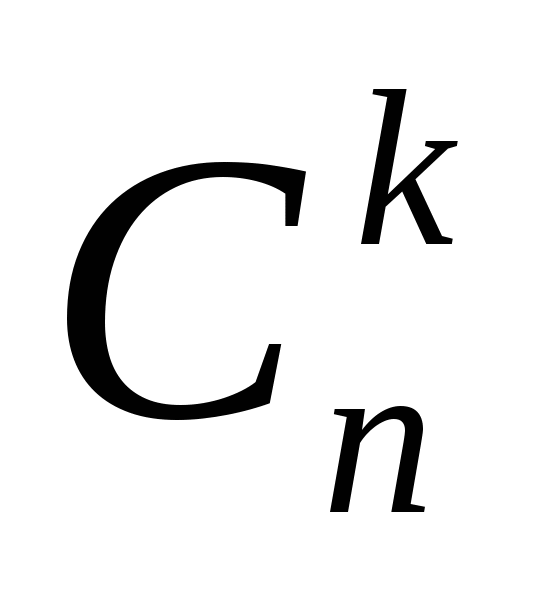 
(читается: С из n по k). (слайд 12)
(слайд 13)
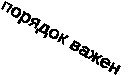
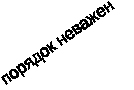
сочетания
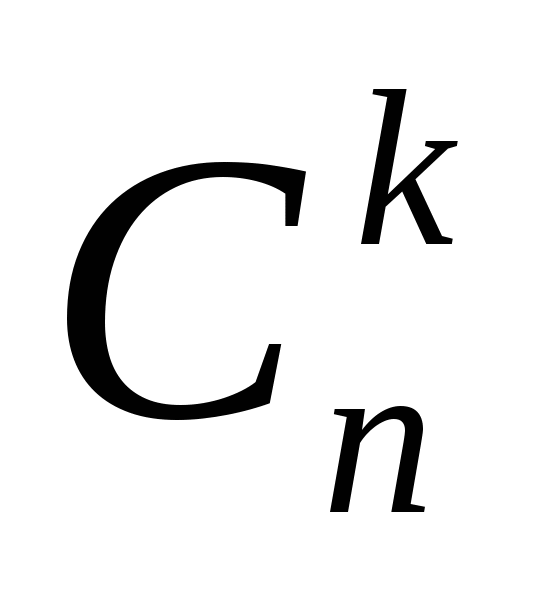
перестановки размещения
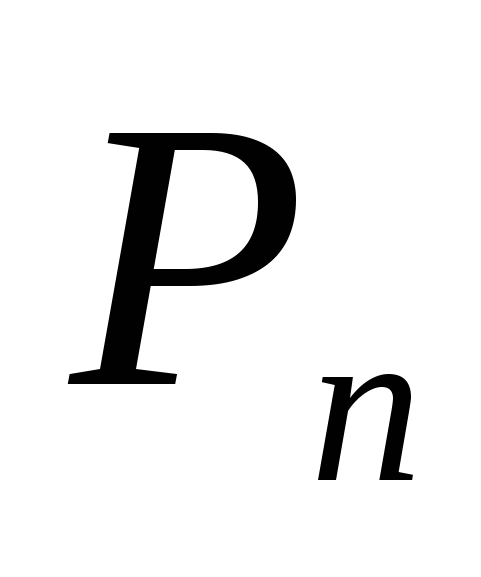
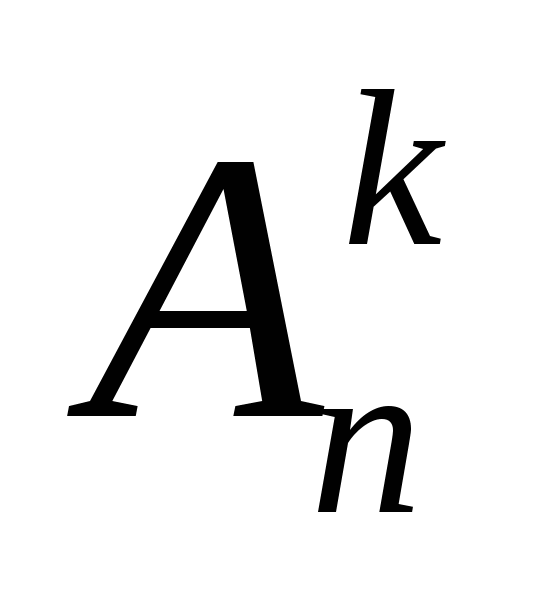
Вопросы.
Сколькими способами можно выбрать 5 учеников из 30 для дежурства в столовой; актив класса (староста, культорг, редактор стенгазеты, организатор спортивных мероприятий) – 4 человека из 30; 7 монет из 10 данных монет; 10 карт из колоды в 32 карты?
Ответ:
5 учеников из 30 для дежурства в столовой можно выбрать
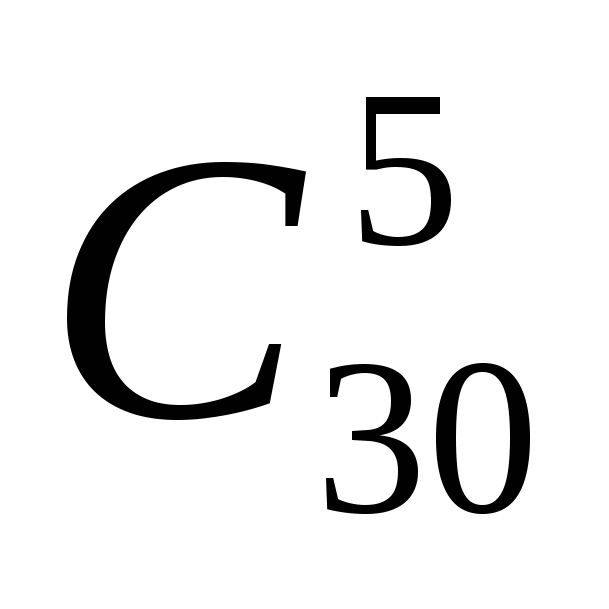способами; 7 монет из 10 данных монет можно выбрать 
способами; 10 карт из колоды в 32 карты 
способами (в этих случаях порядок не важен, и поэтому мы используем сочетания).Для состава актива класса важно, кто именно будет старостой, кто – культоргом, кто – редактором стенгазеты и кто будет отвечать за спорт. Поэтому следует использовать размещения: нужный выбор (4 человека из 30) можно произвести
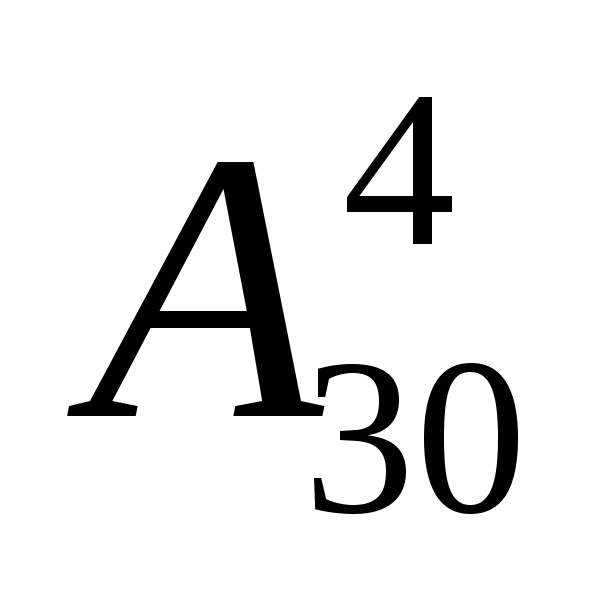способами.
Для любых натуральных чисел n и k, таких, что k
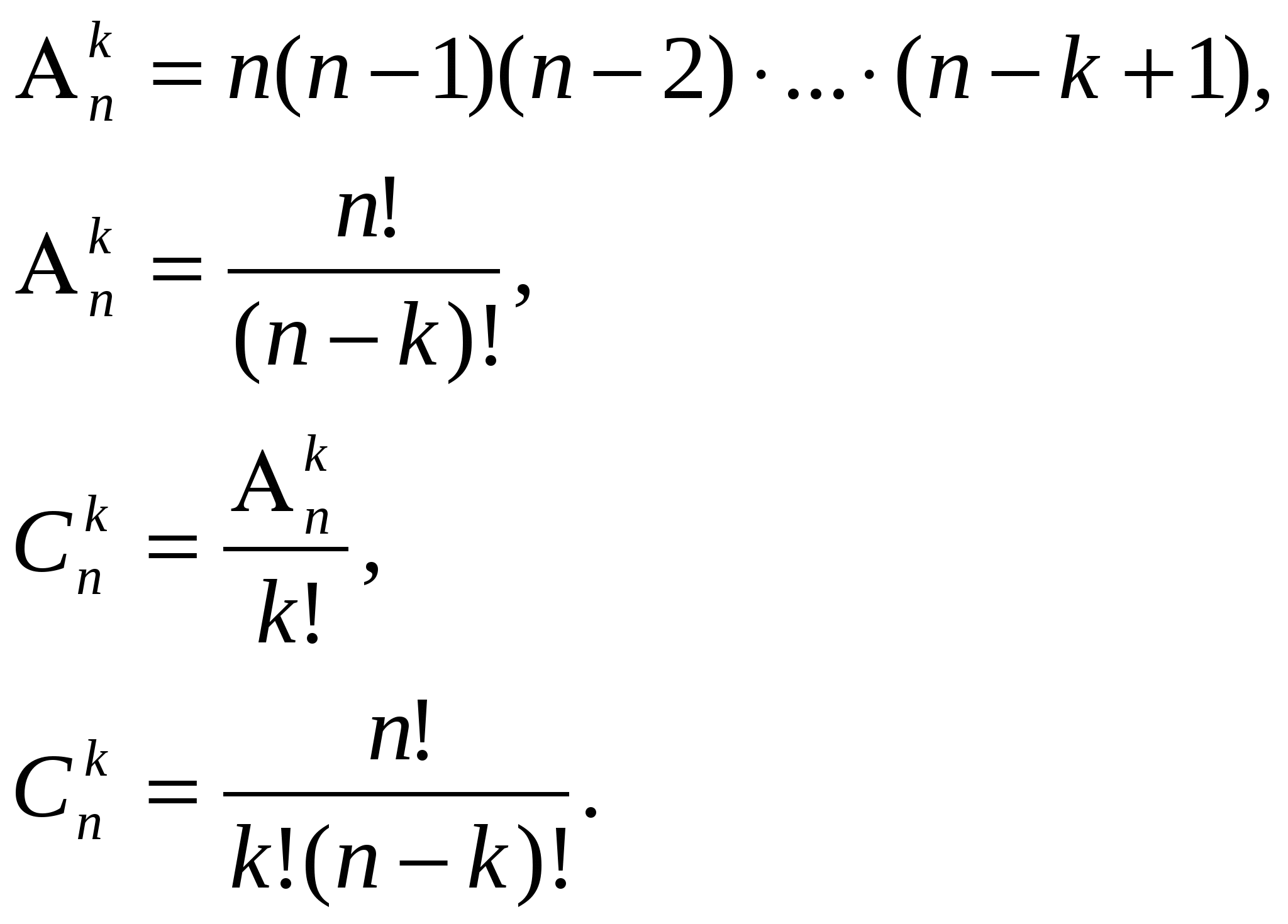(слайд 14)
Задача. (слайд 15)
Сколько трехзначных чисел с различными цифрами можно составить из цифр 0, 1, 2, 3, 4, 5?
Р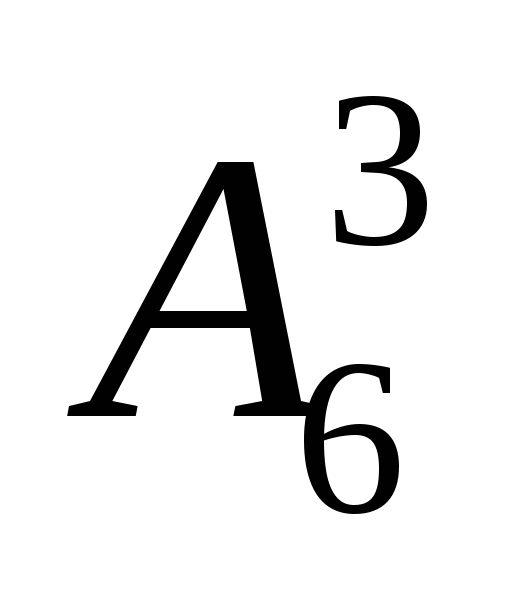
ешение:
И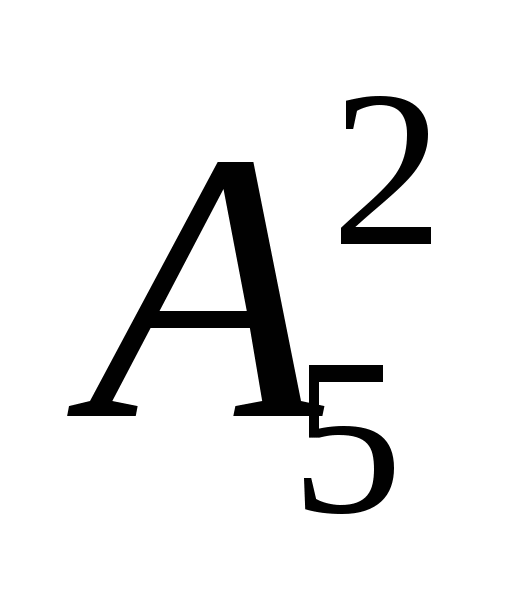
з шести данных цифр можно составить чисел, но среди них будут и трехзначные числа, начинающиеся с нуля (чего, естественно, быть не может). Посчитаем количество таких чисел. В них на первом месте стоит нуль. Значит, на оставшиеся две позиции размещают оставшиеся пять цифр. Поэтому таких чисел будет
С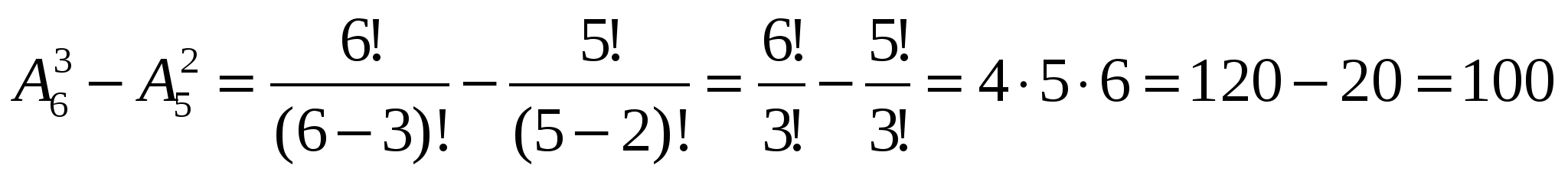
ледовательно, искомых чисел можно получить:
Ответ: 100.
Задача. (слайд 16)
Сколько существует трехзначных чисел, в которых цифры различные и нечетные.
Решение:
Н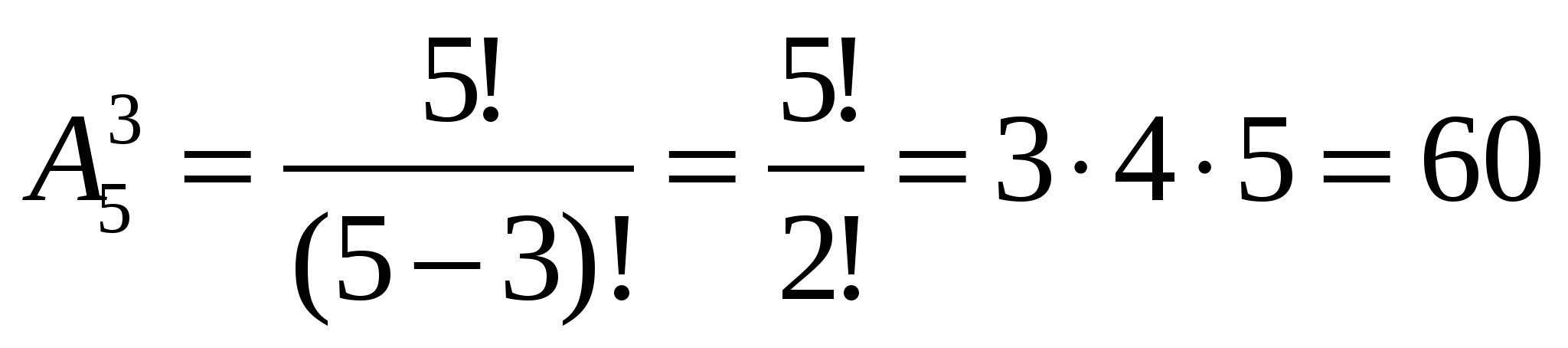
ечётных цифр пять: 1,3,5,7,9. Их надо разместить на три позиции. Поэтому количество искомых чисел равно числу размещения.
Ответ: 60.
Задача. (слайд 17)
Найти число диагоналей n – угольника.
Решение:
И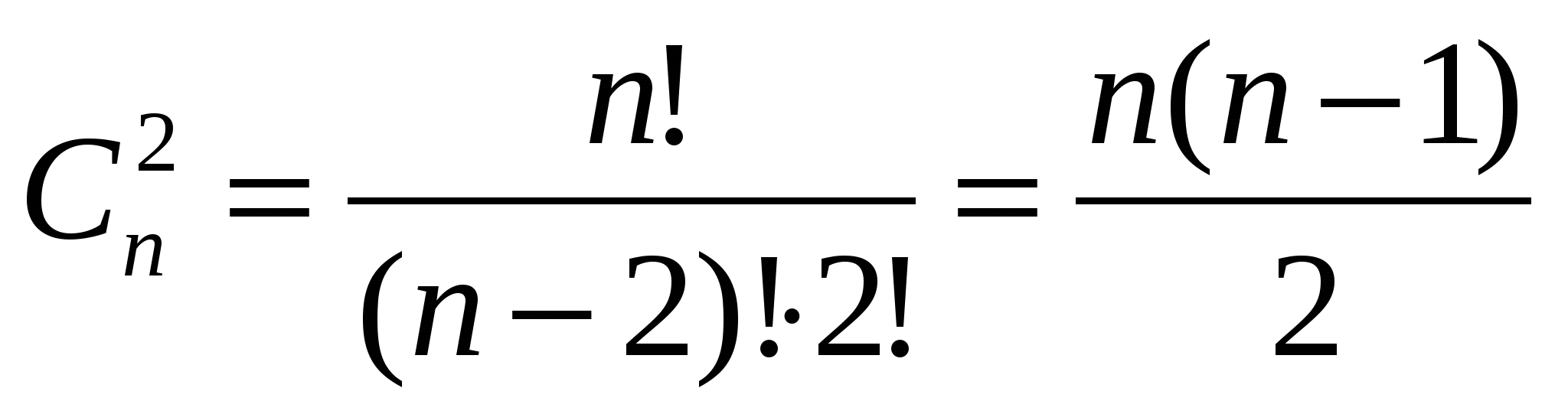
меем n точек плоскости, из которых никакие три не лежат на одной прямой. Соединим эти точки попарно всеми возможными способами. Будем иметь
отрезков. Из этих отрезков n отрезков являются сторонами многоугольника. Тогда диагоналей будет: В соответствии с полученной формулой имеем: у треугольника 0 диагоналей, у четырехугольника 2 диагонали, у пятиугольника 5 диагоналей, у шестиугольника 9 диагоналей и т.д.
Задача. (слайд 18)
Сколькими способами можно составить расписание на вторник, если изучаются 10 предметов и должно быть 6 уроков (порядок уроков неважен).
Р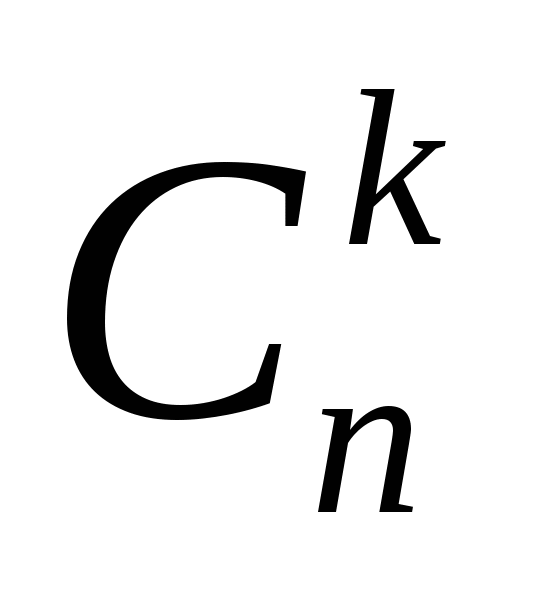
ешение:
И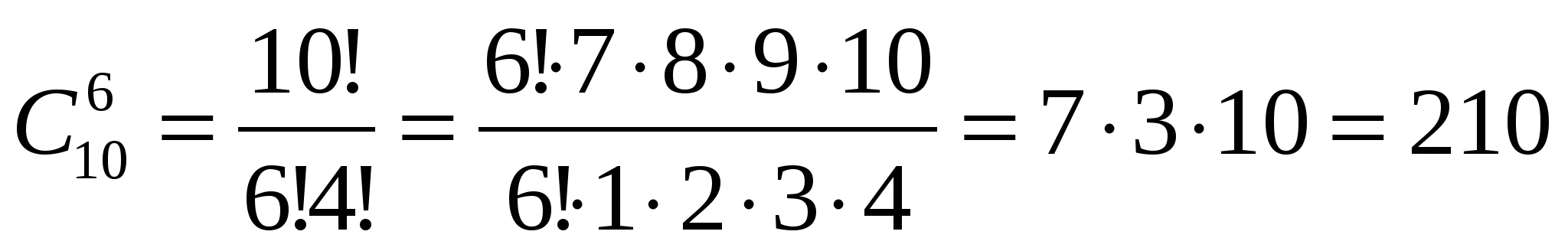
спользуем формулу для числа сочетаний из n элементов по k и получим
способов.
Ответ: 210.
3.4. Решение задач в группах.
А теперь перейдем к работе в группах. Ваша задача: решить задачи, оформить их в тетрадях и рассказать о проделанной совместной работе. Листочки с заданиями на столах. Помогайте друг другу при решении. (Учитель, в процессе работы учащихся, оказывает помощь каждой группе).
Задачи для решения на закрепление нового материала
Задача № 1. Сколькими способами могут быть расставлены 5 участниц финального забега на 5-ти беговых дорожках?
Решение:
Р5 = 5!= 1 ∙2 ∙3 ∙4 ∙5 = 120 способов.
Ответ: 120 способов.
Задача №2. Сколько трехзначных чисел можно составить из цифр 1,2,3, если каждая цифра входит в изображение числа только один раз?
Решение:
Число всех перестановок из трех элементов равно Р3=3!, где 3!=1 · 2 · 3=6. Значит, существует шесть трехзначных чисел, составленных из цифр 1,2,3.
Ответ: 6 чисел.
Задача № 3. Сколькими способами четверо юношей могут пригласить четырех из шести девушек на танец?
Решение:
Два юноши не могут одновременно пригласить одну и ту же девушку. И
варианты, при которых одни и те же девушки танцуют с разными юношами,
считаются разными, поэтому:
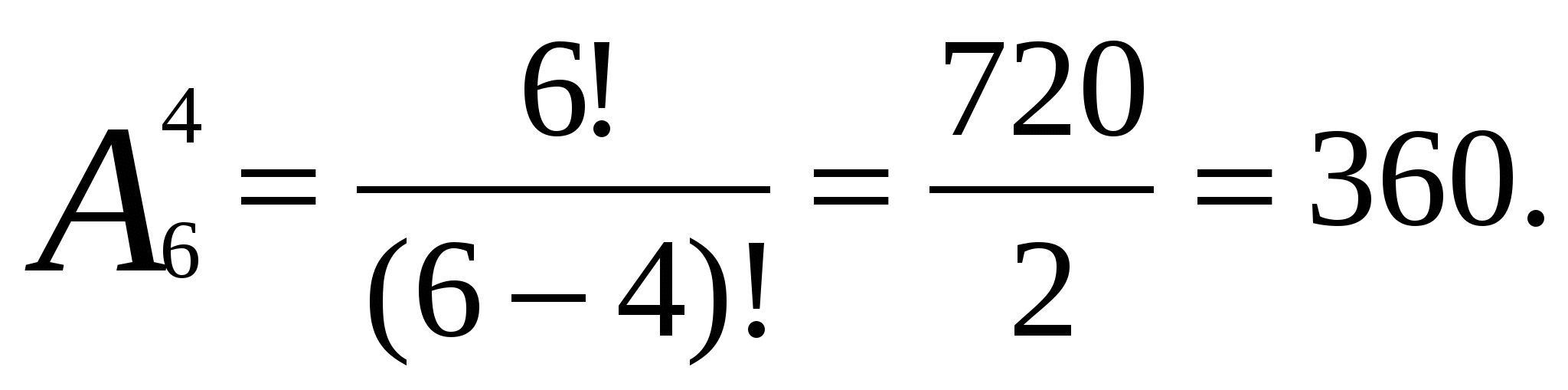
Ответ: 360.
Задача № 4. Сколько различных трехзначных чисел можно составить из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 при условии, что в записи числа каждая цифра используется только один раз?
Решение:
В условии задачи предложено подсчитать число всевозможных комбинаций из трех цифр, взятых из предположенных девяти цифр, причём порядок
расположения цифр в комбинации имеет значение (например, числа 132 и 231 различные). Иначе говоря, нужно найти число размещений из девяти элементов по три. По формуле числа размещений находим:
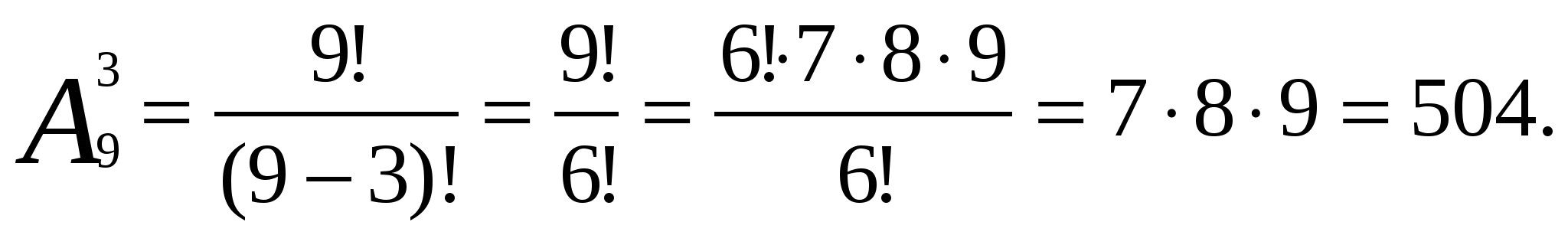
Ответ: 504 трехзначных чисел.
Задача №5. Сколькими способами из 7 человек можно выбрать комиссию, состоящую из 3 человек?
Решение:
Чтобы рассмотреть все возможные комиссии, нужно рассмотреть все возможные 3 – элементные подмножества множества, состоящего из 7 человек. Искомое число способов равно
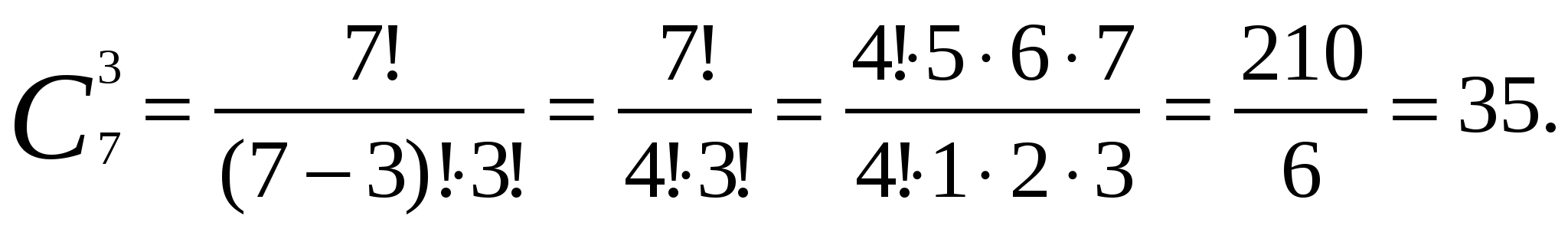
Ответ: 35 способов.
Задача № 6. В соревновании участвуют 12 команд. Сколько существует вариантов распределения призовых (1, 2, 3) мест?
Решение:
А123 = 12 ∙11 ∙10 = 1320 вариантов распределения призовых мест.
Ответ: 1320 вариантов.
Задача № 7. На соревнованиях по лёгкой атлетике нашу школу представляла команда из 10 спортсменов. Сколькими способами тренер может определить, кто из них побежит в эстафете 4100 м на первом, втором, третьем и четвёртом этапах?
Решение:
Выбор из 10 по 4 с учётом порядка: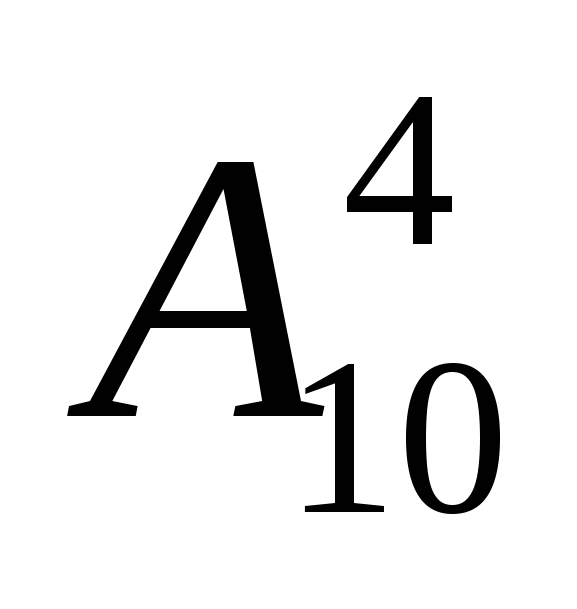 
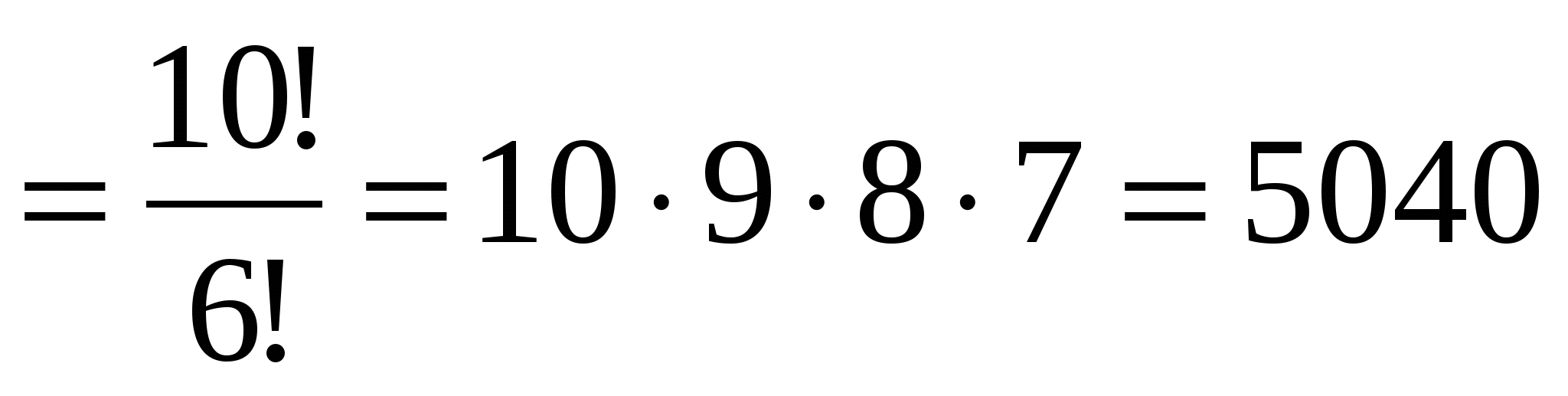способов.
Ответ: 5040 способов.
Задача № 8. Сколькими способами можно выложить в ряд красный, черный, синий и зеленый шарики?
Решение:
На первое место можно поставить любой из четырех шариков (4 способа), на
второе – любой из трех оставшихся (3 способа), на третье место – любой из
оставшихся двух (2 способа), на четвертое место – оставшийся последний шар.
Всего 4 · 3 · 2 · 1 = 24 способа. Р4 = 4! = 1 · 2 · 3 · 4 = 24. Ответ: 24 способа.
Задача № 9. Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 6 книг?
Решение:
Выбор 6 из 10 без учёта порядка: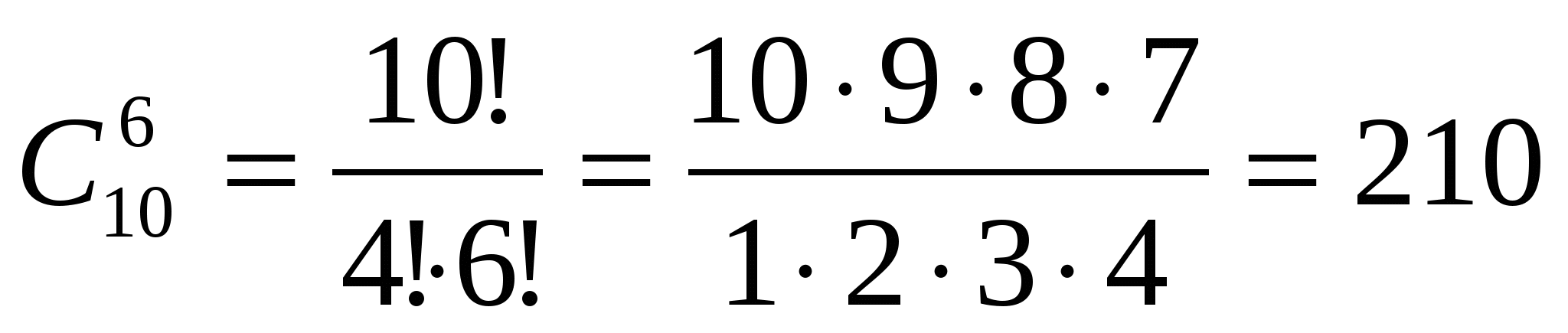 
способов.
Ответ: 210 способов.
Задача № 10. В 9 классе учатся 7 учащихся, в 10 - 9 учащихся, а в 11 - 8 учащихся. Для работы на пришкольном участке надо выделить двух учащихся из 9 класса, трех – из 10, и одного – из 11 . Сколько существует способов выбора учащихся для работы на пришкольном участке?
Решение:
Выбор из трёх совокупностей без учёта порядка, каждый вариант выбора из
первой совокупности (С72) может сочетаться с каждым вариантом выбора из
второй (С93) и с каждым вариантом выбора третьей (С81) по правилу умножения получаем:
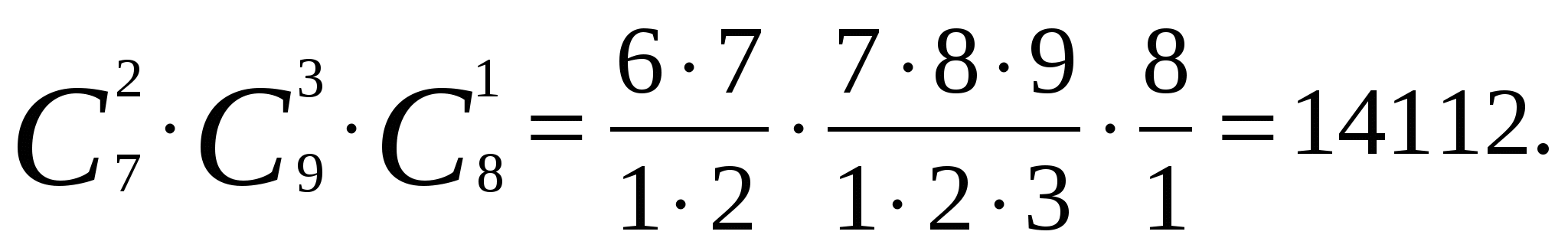
Ответ: 14 112 способов.
Задача № 11. Девятиклассники Женя, Сережа, Коля, Наташа и Оля побежали на перемене к теннисному столу, за которым уже шла игра. Сколькими способами подбежавшие к столу пятеро девятиклассников могут занять очередь для игры в настольный теннис?
Решение:
Первым в очередь мог встать любой девятиклассник, вторым – любой из оставшихся троих, третьим – любой из оставшихся двоих и четвёртым – девятиклассник, подбежавший предпоследним, а пятым – последний. По правилу умножения у пяти учащихся существует 5· 4321=120 способов занять очередь.
Ответ: 120 способов.
Отчет групп о проделанной работе.
4. Итоги урока
Ученики проговаривают, что нового узнали на уроке. Учитель оценивает работу ребят. При выходе из кабинета каждый ученик выбирает прямоугольник по цвету, соответствующему надписями “всё понятно и усвоено”, “трудно и не всё понятно”, “не понятно и не усвоено”, и опускает в соответствующий конверт.
5. Домашнее задание
1 вариант.
Решить задачи:
1. Сколькими способами можно из 6 человек составить комиссию, состоящую из двух человек?
2. В соревновании участвуют 10 человек. Сколькими способами могут распределиться между ними места?
3. Сколькими способами можно расставить на полке 4 различные книги?
4. Сколько различных словарей необходимо переводчику, чтобы он мог переводить с любого из 5 языков – русского, английского, немецкого, французского, испанского – на любой другой из этих языков?
5. Пять человек обменялись друг с другом фотографиями. Сколько всего фотографий было?
6. На плоскости отмечены 6 точек. Каждые две точки соединили отрезком. Сколько получилось отрезков?
2 вариант
Решить задачи:
1. Сколькими способами можно переставить 5 различных геометрических фигур?
2. Пять человек пожали друг другу руки. Сколько было рукопожатий?
3. За свои рисунки ученик получил две положительные оценки. Какими они могут быть? Сколько вариантов?
4. Сколько флагов можно составить из трех разных цветов, если имеются полосы синего, белого, красного цветов?
5. В понедельник в пятом классе 5 уроков. Сколькими способами можно составить расписание на понедельник?
6. Из десяти учащихся надо выбрать старосту, физорга и культорга. Сколькими способами это можно сделать?
Ответы и решения:
I вариант
II вариант
1. 
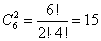
2. 
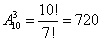
3. Pn=4!=24
4. Pn=5!=120
5. Pn=5!=120
6.
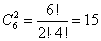
1. Pn=5!=120
2. 
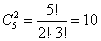
3. положительные оценки: 4, 5.
22=4
4. Рn=3!=6
5. Pn=5!=120
6.
