Урок в 8 классе по алгебре с применением технологии критического мышления в процессе преподавания математики.
Тема: «Способы решения квадратного уравнения. Использование частных соотношений коэффициентов»
Учитель: Гусак Валентина Арсентьевна КГУ «Новосветловская средняя школа».
Цели: -расширить знания способов решения квадратных уравнений, повторить теорему Виета, изучить свойства коэффициентов;
-подготовить учащихся к выполнению теста;
-воспитывать коллективизм, поддержку в командах;
-развивать логическое мышление, быстроту, сообразительность;
-учить грамотной математической речи;
-формировать у учащихся умение прислушиваться к ответам своих товарищей,отстаивать свое решениеесли уверены вправильности ответа.
Оборудование и раздаточный материал: проектор, компьютер, карточки с заданиями и сигнальные карточки, стикеры, ватманы, магниты.
План урока:
Этапы урока
Время, мин
Приемы и методы
1. Этап актуализации знаний.
2. Мотивация учебной проблемы
5
Беседа учителя
3. Основное содержание урока. Формирование и закрепление у учащихся представления о свойствах коэффициентов квадратного уравнения.
4. Проверка понимания материала темы.
15
8
Групповая работа. Изучение темы и составление постеров, вопросов высокого и низкого порядков.
5. Закрепление изученного материала.Формирование умений и навыков.
6. Ассоциации.
3
3
Защита постеров. Ответы на вопросы
7. Проверка усвоения знаний.
5
Ранжирование по признакам, работа по карточкам. Проверка решений.
8. Рефлексия
3
Пожелание. «Дартс».
Ход урока
Этап
Время
Деятельность учителя
Деятельность учащихся
Ресурсы
Эмоциональный настрой на урок.
3
Встать в круг. Игра летает, не летает.
На дворе весна, апрель месяц. Вернулись перелетные птицы.
На столах лежат карточки, найдите какие перелетные птицы к нам прилетели, образуйте группы по 6 человек.(4 группы)
Формируют группы:
скворцы, цапли, грачи, лебеди.
картинки с птицами
журавли, ласточки, скворцы, цапли.
Этап актуализации знаний. Мотивация учебной проблемы. Постановка целей
- я знаю что коэффициенты обладают определенными свойствами
- я могу применять данные свойства при решении уравнений
-я могу объяснить товарищам в решении уравнений, как используются данные свойства.
2
Мы с вами уже изучили некоторые способы решения квадратных уравнений. Обсудите в группе и назовите эти способы. Заполним «Понятийное колесо».
Каждая группа назовите по одному способу. И заполните понятийное колесо.
Сегодня мы расширим представление о способах решения квадратных уравнений, используя свойства коэффициентов.
Сформулируем цели урока, чего вы должны достичь сегодня.
На кругах пишут способы решения квадратного уравнения:
1. Решение неполного квадратного уравнения
2. Выделения квадрата двучлена
3.С помощью формулы
4. Графически
5. С помощью теоремы Виета.
6. Используя формулы сокращенного умножения
7. По формуле с четным коэффициентом.
8. Другое.
круги по колличеству групп.
8 по 4=32, магниты 10 шт.
Стадия осмысления.
Формирование и закрепление представления о свойствах коэффициентов квадратного уравнения.
5
10
В восьмом классе, учащиеся знакомятся с квадратными уравнениями и способами их решения. При этом, как показывает опыт, большинство учащихся при решении полных квадратных уравнений применяют только один способ – формулу корней квадратного уравнения. Для учеников, хорошо владеющих навыками устного счета, этот способ явно нерационален. Решать квадратные уравнения учащимся приходится часто и в старших классах, а там тратить время на расчет дискриминанта просто жалко.
Тема «Свойства коэффициентов» в курсе алгебры рассматривается после изучения темы «Решение квадратного уравнения по формуле».
прием «Зигзаг».
Каждый в группе получает ресурс, один из трех, пронумерованный 1,2,3.
Каждый знакомится с материалом и формируются новые группы по 6 человек (с №1, с №2, с №3).
на постерах
«Зигзаг» (один из вариантов использования приемов). Класс разделен на четверки, у каждого школьника номер от 1 до 4. Дети работают с текстом, каждый сосредоточен на части с соответствующим номером, затем первые номера объединяются с первыми, вторые – со вторыми и т.д. для обсуждения своей части текста, составления схемы рассказа по теме и выбора представителя, который проведет итоговую презентацию. Вернувшись в свою группу, школьники по схеме рассказывают о своей части текста, слушают других, делают записи в тетрадях, затем эксперты от каждого номера проводят презентации своих тем, все остальные вносят уточнения и дополнения.
Ресурсы (№1,№2, №3) на 4 группы.
Проверка понимания материала темы
8
Группе «Цапля» предоставляется возможность защитить свой постер.
Остальным участникам подготовить по два вопроса для осмысления и закрепления данной темы.
Защита постера и ответы на вопросы.
Когда целесообразней изучать свойство коэффициентов, до или после изучения теоремы Виета?
маркеры, 6 ватманов.
Закрепление изученного материала. Формирование умений и навыков.
3
Найдите три признака, общих для данных свойств и три отличия.
Какое слово созвучно со свойством, в котором несколько раз мы слышим и произносим «ца», дробь «це» на «а». Подумайте, на что похоже по произношению, выглядит единица как, произносится как…и это слово уже сегодня звучало в аудитории?
В природе существуют несколько видов цапли. Есть белая цапля и серая цапля. Как вы думаете, какую цаплю можно соотнести к какому из свойств?
Группы отвечают:
1. Используются все три коэффициента
2. К сумме (с+а)…. 3.Похожие формулы корней.
(с+а)+-в
+-1
+-с/а.
Диалогическая беседа. Обсуждение слайда.
слайд «Цапля белая и серая»
6. Ассоциации
3
Какое слово созвучно со свойством, в котором несколько раз мы слышим и произносим «ца», дробь «це» на «а». Подумайте, на что похоже по произношению, выглядит как, произносится как…«Цапля».
Обсудите и назовите, что есть общего и в чем различия между белой и серой цаплей? Назовите по оному признаку и соотнесите с цаплями.
Выглядит, как…
Звучит, как…
При условии: а+в+с=о
«Цапля» белая
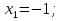

При условии:
а-в+с=о
«Цапля» серая
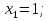
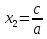
7.Проверка усвоения знаний.
5
-5х² - 8х – 3=0
3х2-10х+7=0
4х2-11х+7=0
-2х2-4х+6=0
3х² + 11х – 4=0
х² - 4х +3=0
3х² - 2х – 5=0
х² + 7х – 8=0
х² + 6х – 7=0
х² - 7х + 10=0
Выполните задание. Разложите в три колонки уравнения, решаемые по свойству «белой цапли», «серой цапли» и по формуле, через дискриминант.
Назови корни уравнений.
ресурс 4.
8. Рефлексия.
3
Подведем итог нашей работы в виде игры в «Дартс».
На стикерах напишите 1 пожелание и 1 замечание и приклейте в один из секторов.
Пишут пожелания.
стикеры, плакат.
РЕСУРС №1
Использование частных соотношений коэффициентов.
Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.
Корни квадратного уравнения, сумма всех коэффициентов которого равна нулю
Если в квадратном уравнении сумма всех его коэффициентов равна нулю (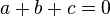 ), то корнями такого уравнения являются
), то корнями такого уравнения являются 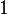 и отношение свободного члена к старшему коэффициенту
и отношение свободного члена к старшему коэффициенту 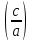 .
.
Доказательство
Способ 1. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):
D=b2-4ac= (-(a+c))2-4ac=a2+2ac+c2-4ac=a2-2ac+c2=(a-c)2
Да, это так, ведь при любых действительных значениях коэффициентов 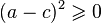 , а значит и дискриминант неотрицателен. Таким образом, если
, а значит и дискриминант неотрицателен. Таким образом, если 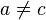 , то уравнение имеет два корня, если же
, то уравнение имеет два корня, если же  , то оно имеет только один корень. Найдём эти корни:
, то оно имеет только один корень. Найдём эти корни:
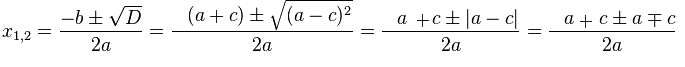

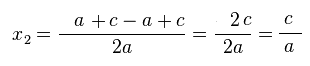
В частности, если а=с, то корень будет один: 1.
Отсюда, прежде, чем решать уравнение стандартными методами, следует проверить применимость к нему этой теоремы: сложить все коэффициенты данного уравнения и посмотреть, не равна ли нулю эта сумма.
РЕСУРС №2
Использование частных соотношений коэффициентов.
Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.
Корни квадратного уравнения, в котором сумма старшего коэффициента и свободного члена равна второму коэффициенту
Если в квадратном уравнении 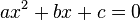 сумма первого коэффициента и свободного члена равна второму коэффициенту:
сумма первого коэффициента и свободного члена равна второму коэффициенту: 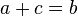 (речь идёт об уравнении с вещественными коэффициентами), то его корнями являются
(речь идёт об уравнении с вещественными коэффициентами), то его корнями являются 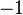 и число, противоположное отношению свободного члена к старшему коэффициенту
и число, противоположное отношению свободного члена к старшему коэффициенту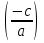 .
.
Доказательство
Способ 2. Сначала выясним, действительно ли такое уравнение имеет два корня (в том числе, два совпадающих):
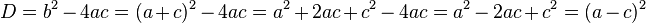 .
.
Да, это так, ведь при любых действительных значениях коэффициентов 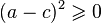 , а значит и дискриминант неотрицателен. Таким образом, если
, а значит и дискриминант неотрицателен. Таким образом, если 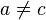 , то уравнение имеет два корня, если же
, то уравнение имеет два корня, если же  , то оно имеет только один корень. Найдём эти корни:
, то оно имеет только один корень. Найдём эти корни:
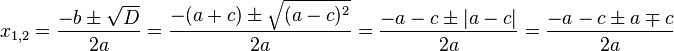 .
.
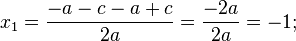
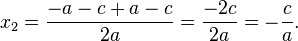
В частности, если  , то корень будет один:
, то корень будет один: 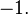
Отсюда, прежде, чем решать какое-либо квадратное уравнение, следует проверить возможность применения к нему этой теоремы: сравнить сумму старшего коэффициента и свободного члена со вторым коэффициентом.
РЕСУРС №3
Использование частных соотношений коэффициентов.
Существуют частные случаи квадратных уравнений, в которых коэффициенты находятся в соотношениях между собой, позволяющих решать их гораздо проще.
Пусть дано квадратное уравнение ах2 + bх + с = 0, где а ≠ 0.
Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю),
то х1 = 1,
х2 = 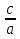
Доказательство
Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение
x2 + 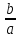 x +
x + 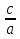 = 0.
= 0.
Согласно теореме Виета
x1•x2 = 1• 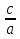
x1 + x2 = - 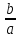 .
.
Если же а – b + с = 0, откуда b = а + с, то:
х1 = -1,
х2 = - 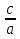
Доказательство
Согласно теореме Виета
x1•x2 = - 1• ( - 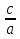 ),
),
x1 + x2 = - а + 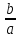 = -1 –
= -1 – 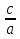 .
.
т.е. х1 = -1 и х2 = - 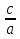 , что и требовалось доказать.
, что и требовалось доказать.