Разработка урока математики в 7-м классе по теме "Сумма и разность многочленов"
Цели урока:
Ввести понятие суммы и разности многочленов. Составить и использовать алгоритм сложения и вычитания многочленов.
Развивать умение решения типовых задач, связанных с преобразованием многочленов, развивать умение делать выводы.
Способствовать воспитанию культуры общения.
Ход урока
1. Организационный: подготовка учащихся к работе
2 . Актуализация опорных знаний:
1. Проверка домашнего задания: проводится в виде самопроверки по готовым ответам.
2. Фронтальный опрос по ранее изученному теоретическому материалу:
- что называют многочленом,
- что называют степенью ненулевого многочлена,
- какие члены многочлена называют подобными?
Четко проговариваем следующие определения:
- многочлен- это сумма одночленов;
- степенью ненулевого многочлена называют наибольшую из степеней одночленов, входящих в этот многочлен, когда он приведен к стандартному виду;
- ненулевые одночлены стандартного вида называются подобными, если они равны или если они отличаются своими коэффициентами.
3. Самостоятельная работа :
Учащимся предлагается записать только ответы.
1. Привести подобные члены многочлена:
Р3-2р2+Зр5+р3-4р2+7;
2ad-4dc+16+6da-16+5cd;
3m2n-5mn+m2n2-4mn+8m2n.
2. Определить степень многочлена:
6f5mn2+5vn 6b-7+3a 3b;
4m 5n 6+7Ьск-25+а 2t 2.







Ребята меняются тетрадями. Учителем вывешивается на доску лист с критериями оценки:
“5” - 6 верно
“4” - 5 верно
“3” - 4 верно
Осуществляется взаимопроверка учащимися, используя слайд готовых ответов, который появляются на интерактивной доске.

Подводится итог выполнения самостоятельной работы через опрос какое количество учащихся на какую отметку выполнили работу.
Учитель: “Умение приводить подобные слагаемые нам понадобится при нахождении суммы и разности многочленов. Итак, тема урока “Сумма и разность многочленов”
3 . Изучение нового материала.
На доске записана тема урока, и затем пошаговые рассуждения, к которым приходят учащиеся под руководством учителя при объяснении темы урока.
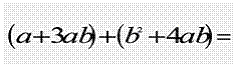
Опираясь на ранее изученный материал (раскрытие скобок, когда перед скобками стоит знак +) , упрощаем следующее выражение : (a+3ab)+(b2+4ab).
Получаем многочлен a+3ab+b2+4ab.
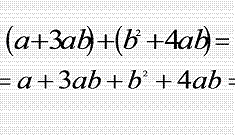
Учитель: “Чем является первое слагаемое?”
Ученик: “Многочленом”.
Учитель: “Чем является второе слагаемое?”
Ученик: “Многочленом”.
Учитель: “Чему равна сумма многочленов?”
Ученик: “Сумма многочленов равна многочлену, членами которого являются все члены данных многочленов”.
Учитель: “В данном выражении необходимо привести подобные члены многочлена, привести в стандартный вид полученный многочлен”.
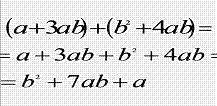
Аналогично вводим понятие разности многочленов.

Откроем учебник на странице и найдем правило, как найти разность многочленов”.
Учащиеся несколько раз прочитывают правило.
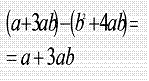
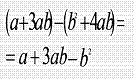
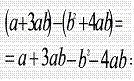
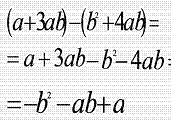
Далее рассматривается как вычисляется по правилу разность многочленов. (Повторяем правило раскрытия скобок, когда перед скобками стоит знак “ - ” ).
Учитель: “ Используя выполненные задания, давайте сформулируем алгоритм нахождения суммы и разности многочленов”.
Учащиеся:
Раскрыть скобки.
Привести подобные члены многочлена.
Преобразовать многочлен к стандартному виду.
По ходу предложения правильных шагов на доске появляется алгоритм.

Учитель: “Запишем данный алгоритм в тетради (он также записан на доске)”.
4 . Первичное закрепление нового материала.
Учитель: “Применяя данный алгоритм, переходим к решению задач”.
Разбор у доски заданий из учебника
Самостоятельная работа.
учащиеся выполняют в тетрадях работу по карточкам
одновременно с классом 2 ученика решают на закрытой доске задание из учебника
Проверяем самостоятельно с проверкой ответов.
Дополнительно: тем, кто решает быстрее С-8 дидактический материал стр.15 вариант 1
5 . Информация о домашнем задании.
Учитель: “Задания, которые предлагаю для выполнения дома, аналогичны тем, что мы прорешали сегодня в классе”.
6 . Итог урока.
Итог урока через ответы на вопросы:
Что называют суммой (разностью многочленов)?
Сформулируйте правила раскрытия скобок, перед которыми стоит знак “-” (“+”).
Каков алгоритм нахождения суммы (разности) многочленов?