Конспект урока по алгебре и началам анализа в 11 классе.

Учитель математики высшей категории
Юдинцева Валентина Николаевна
ШМОКУ СОШ с углублённым изучением
отдельных предметов пгт Ленинское
Шабалинского района Кировской области.
2014 год.
Тема: «Свойства функций»
Цели:
Образовательная: обобщить и систематизировать знания по теме «Свойства функций» для подготовки ребят 11 класса к сдаче ЕГЭ по математике.
Развивающая: развивать аналитические способности и логическое мышление, учить адаптироваться в новой ситуации при решении нестандартных заданий.
Воспитательная: формировать активность личности школьника, взаимопомощь, коллективизм.
Оформление кабинета:
На доске:
Тема урока.
Правила мастерской.
Алгоритм исследования функций.
задания для устной работы.
На столах: 
Памятка для командира.
Карточки с заданиями для группы.
Номер и название группы (для индукции).
Карточки для самостоятельной работы.
Карточки для индивидуального домашнего задания.
На отдельном столе:
Карточки с формулами различных функций для определения места ученика.
3 конверта с надписями «всё понятно и усвоено», «трудно и не всё понятно», «не понятно и не усвоено».
Ход урока.
Этап урока
Время
Деятельность учащихся
1.Индукция.
3 мин.
Дети заходят в класс, каждый берёт карточку с формулой функции, определяет её вид и садится за тот стол, где стоит соответствующее название функции:
Логарифмическая ( например:
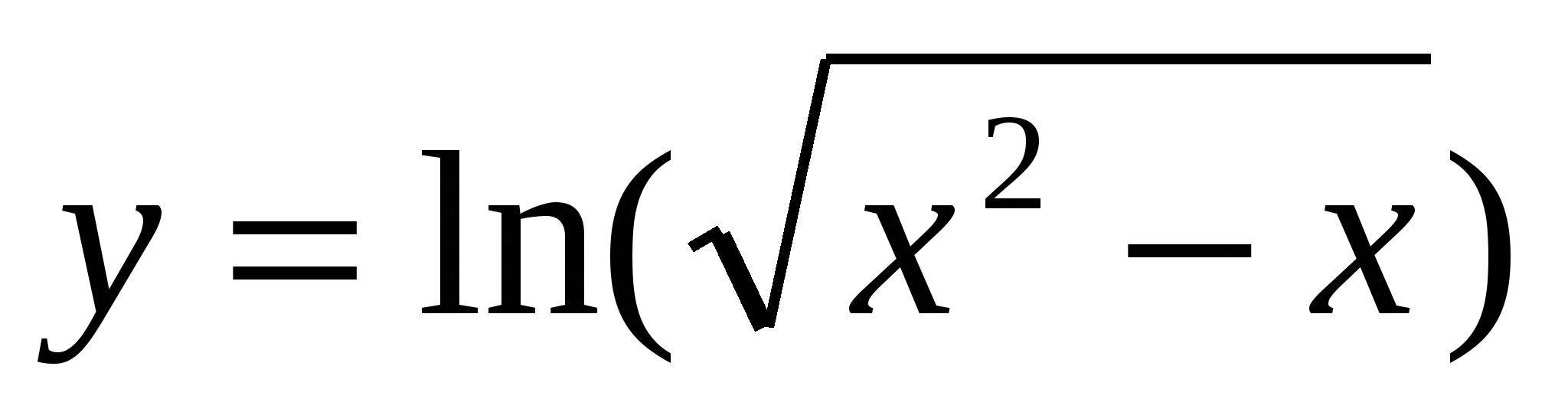
 )
)Показательная ( например:
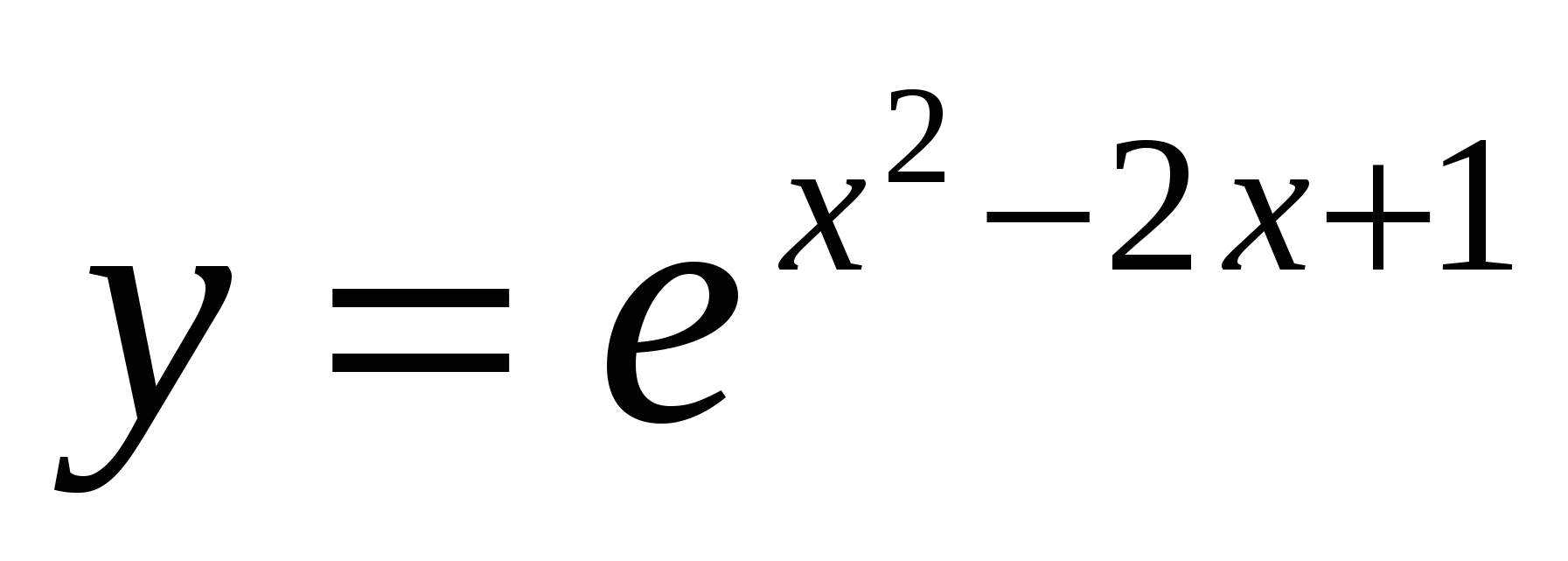 )
)Квадратичная ( например:
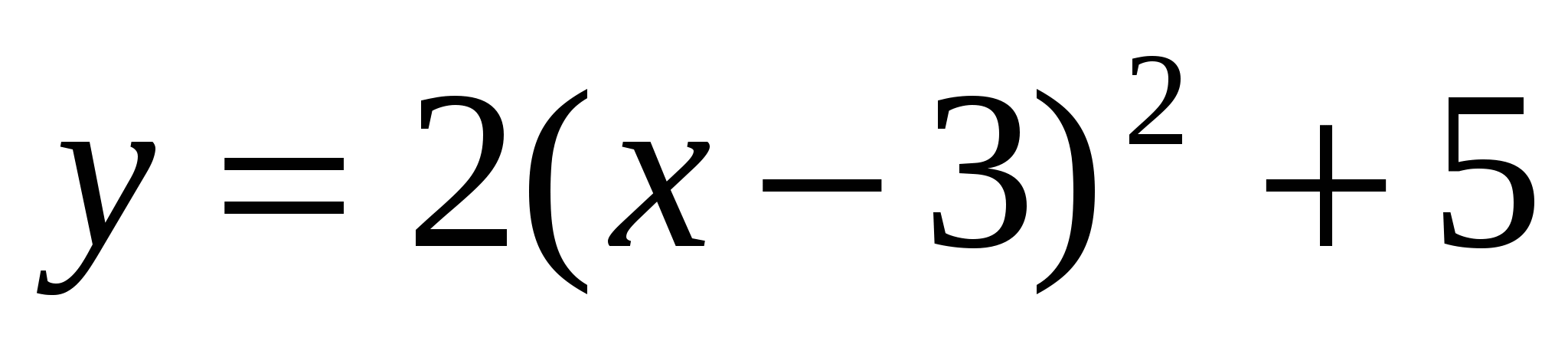 )
)Дробная рациональная ( например:
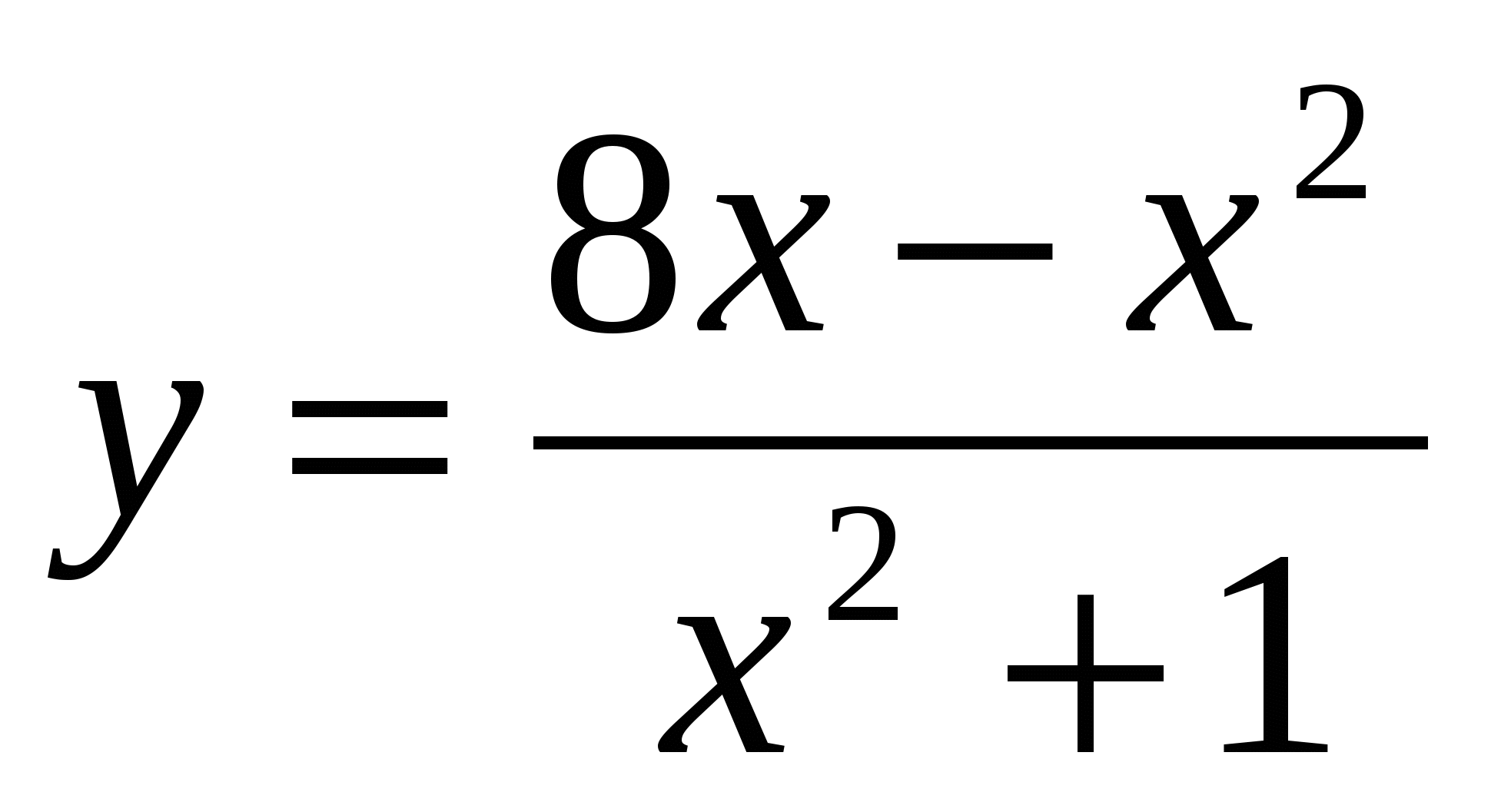 )
)Иррациональная (например:
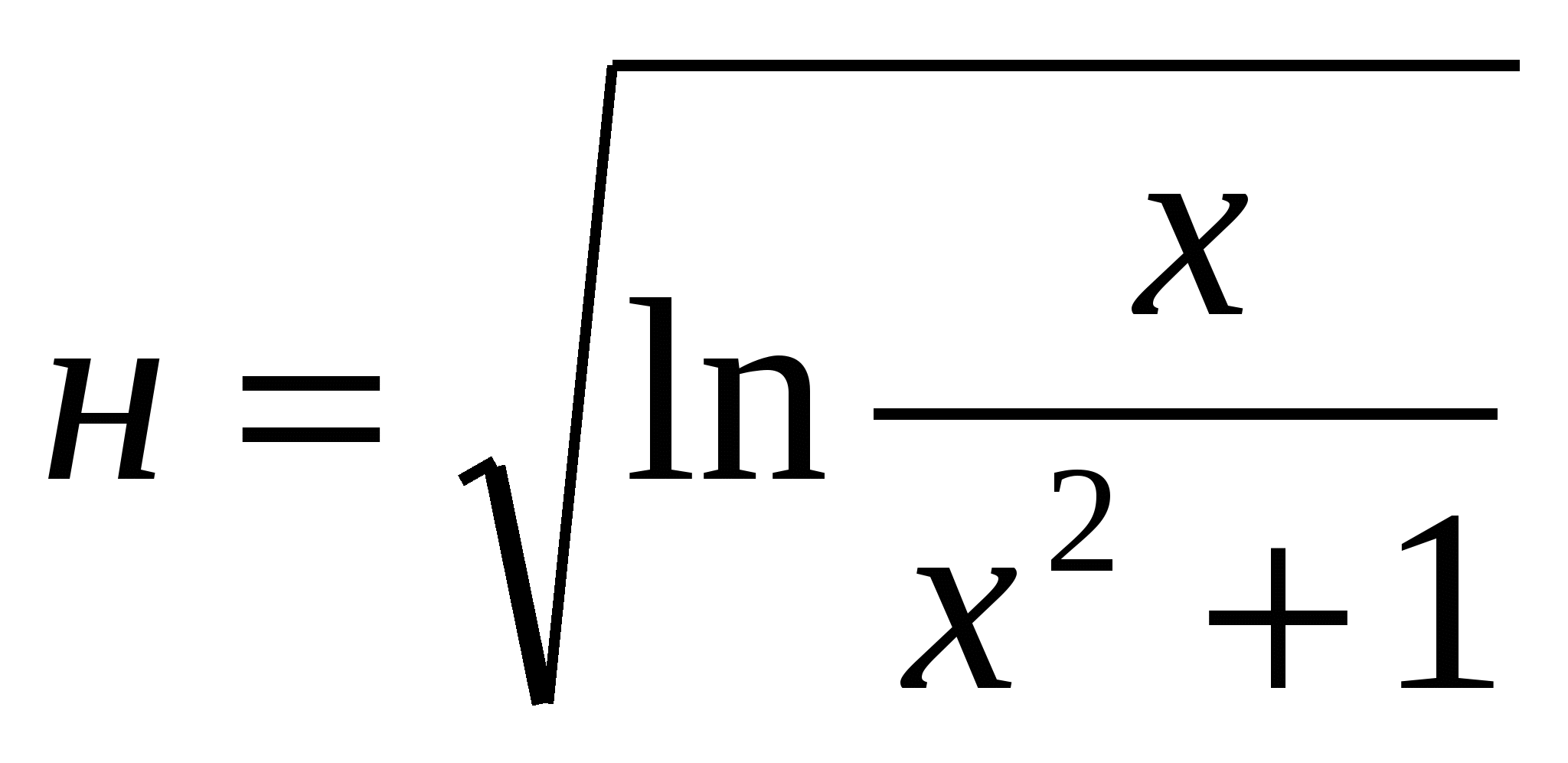 )
)Тригонометрическая (например:
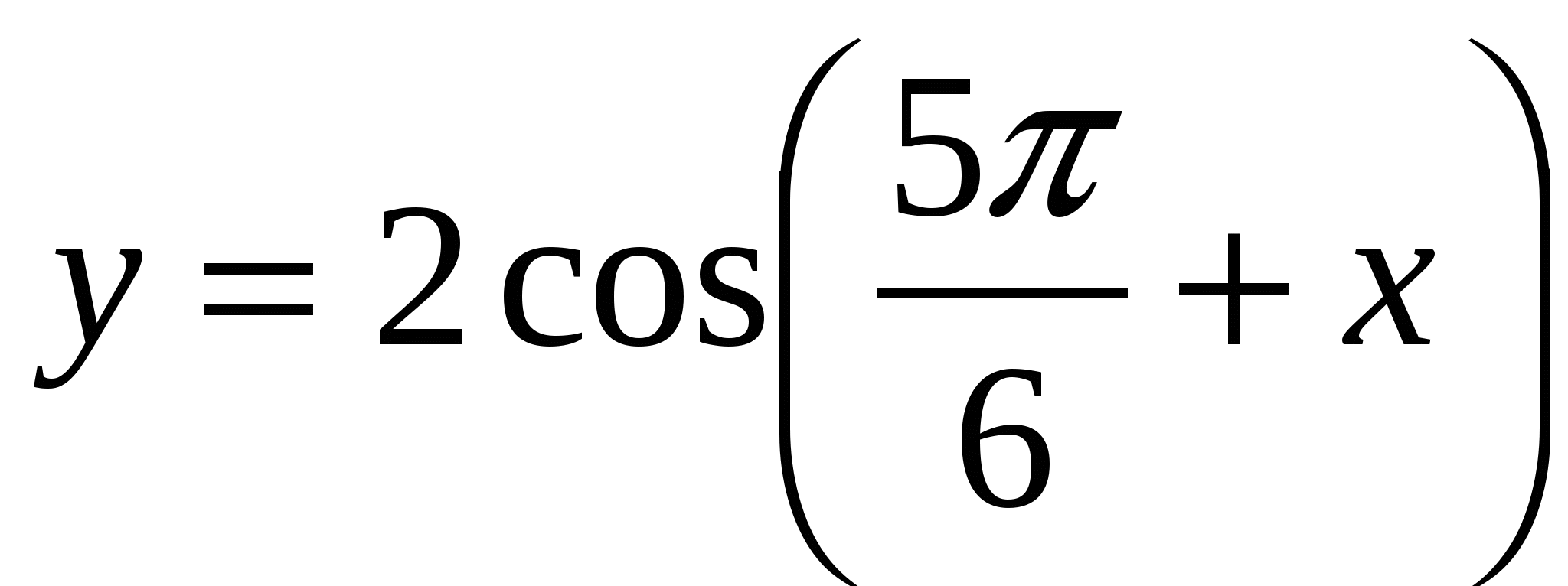 )
)
2.Орг.
момент.
2мин.
Сообщение цели мастерской, плана работы, выбор командиров групп, запись в тетрадях числа и темы урока.
3.Реконструк ция.
Устная
работа.
5мин.
Дать определение логарифма и логарифмической функции.
Перечислить свойства функции
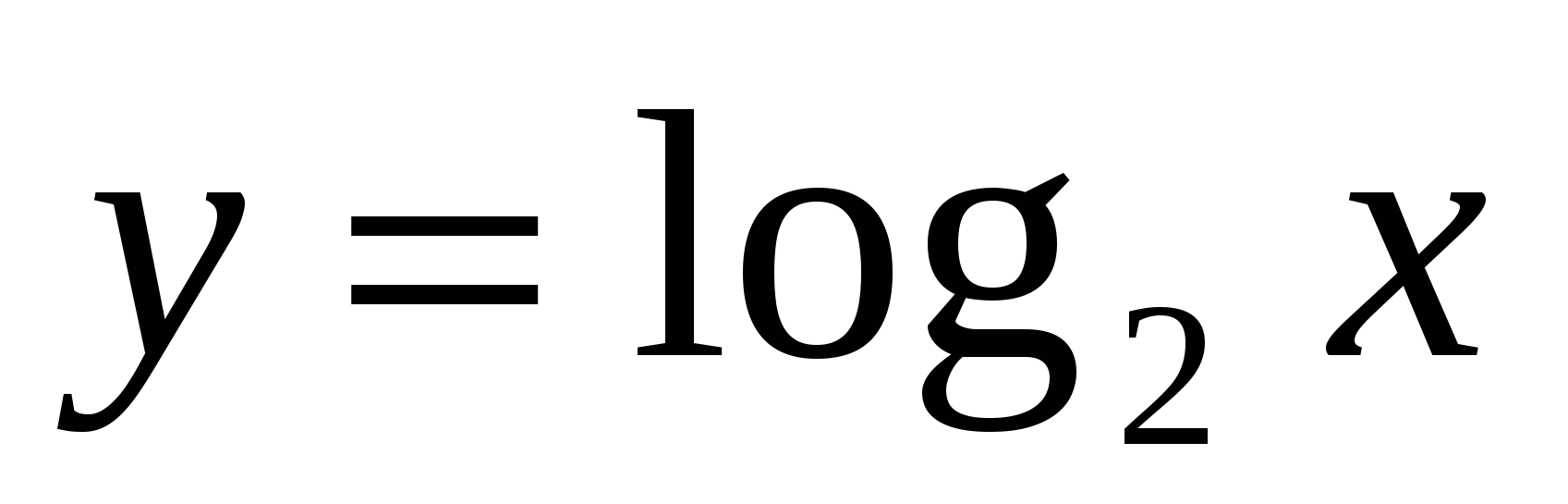 .
.Перечислить свойства функции
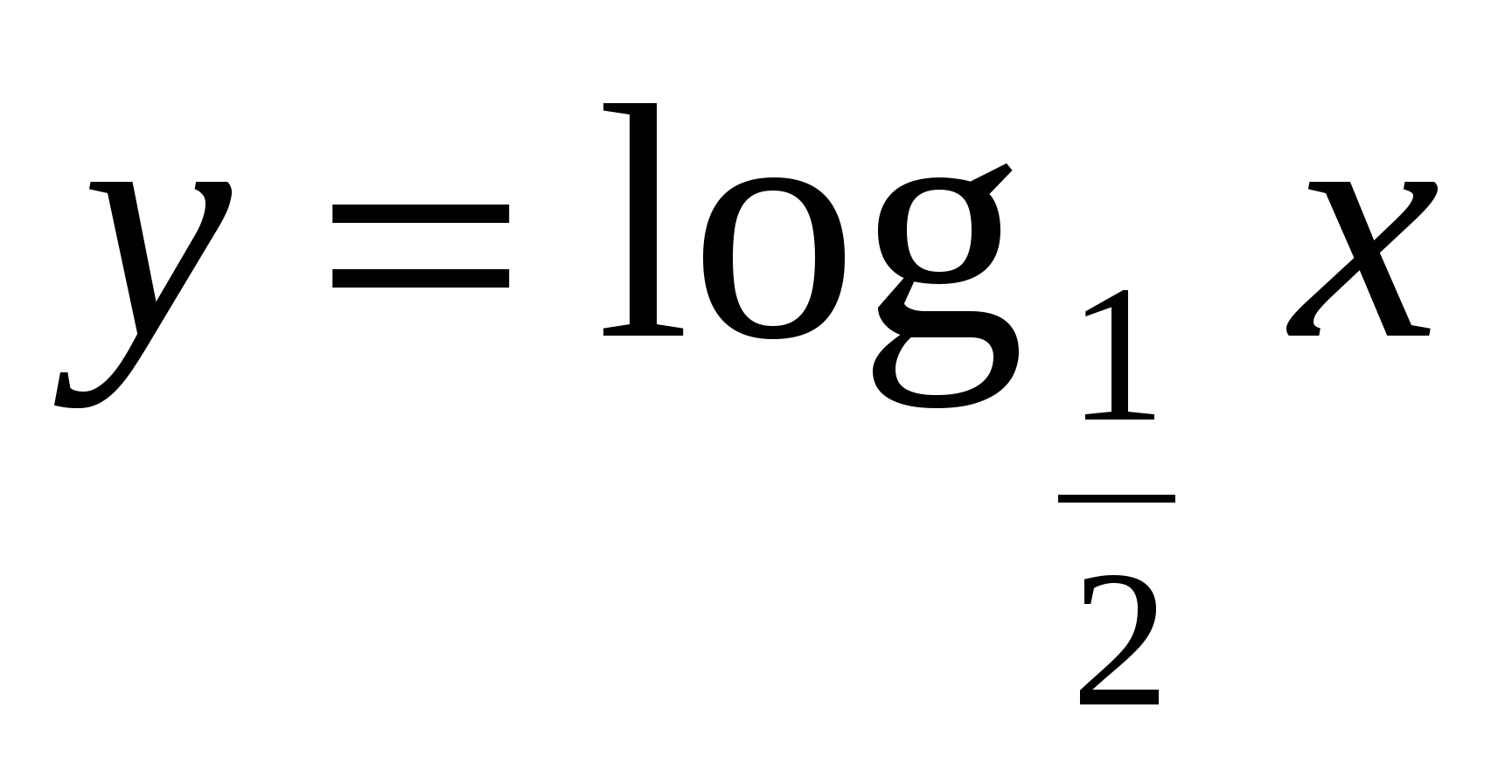
Перечислить и записать на доске свойства логарифмов.
Вычислить: log216 ; log162 ; log381 ; log⅛2 ;
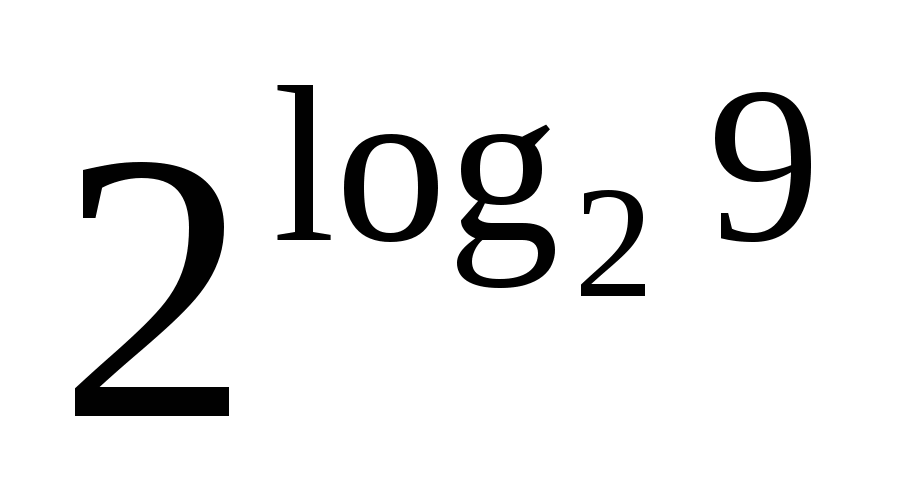 ;
; 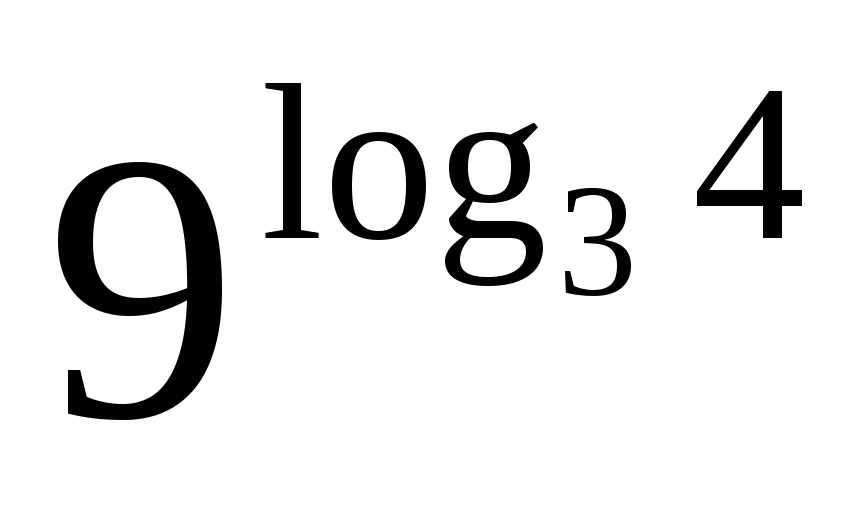 ;
;
Log321 – log37 ; lg25 + lg4 ; log95 ∙ log53 ; lg2 + 2lg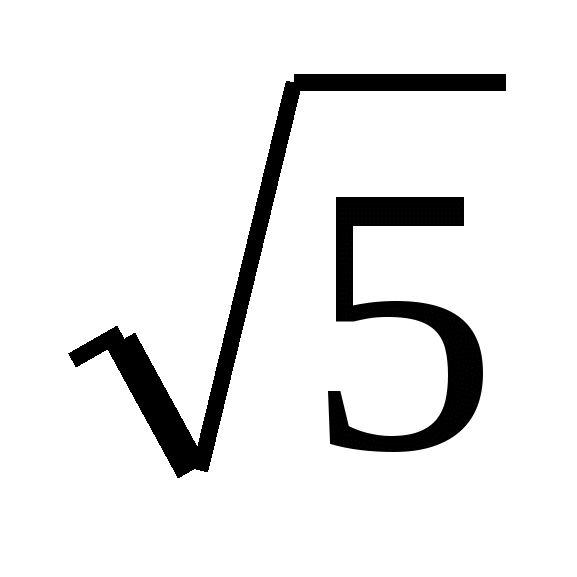 .
.
Найти х : log9x = log94 ; log43x = log45 ; 5x = 2 ; log2(-x) = 0.
4.Реконструк
ция. Работа
в группах.
5мин.
Задание общее для всех: вычислить logab, где а = рm, b = pn, используя
формулу перехода к новому основанию.
(Вывод нового свойства 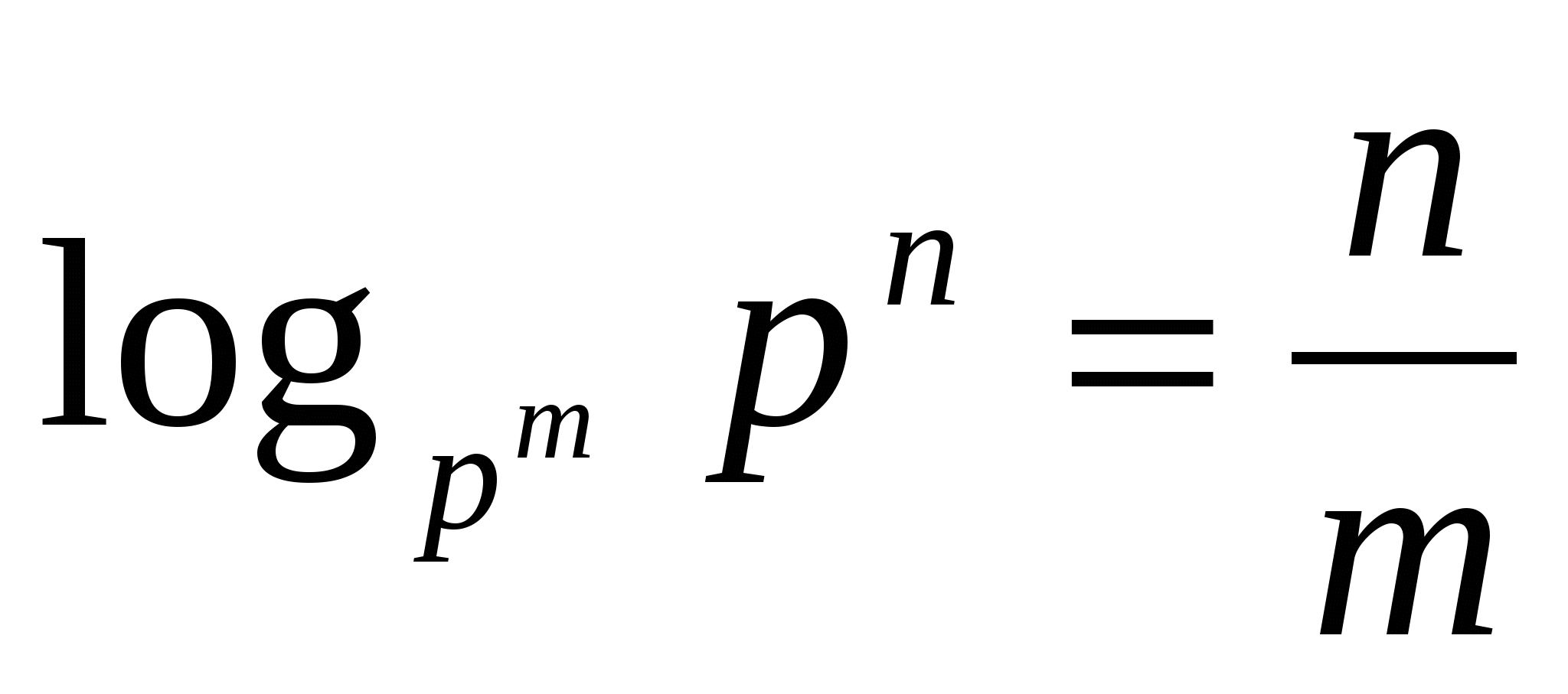 ). А потом вычислить по одному выражению: 1 – 3 группы, используя определение логарифма,
). А потом вычислить по одному выражению: 1 – 3 группы, используя определение логарифма,
4 – 6 группы, используя новое свойство.
Задание для 1 и 4 групп: 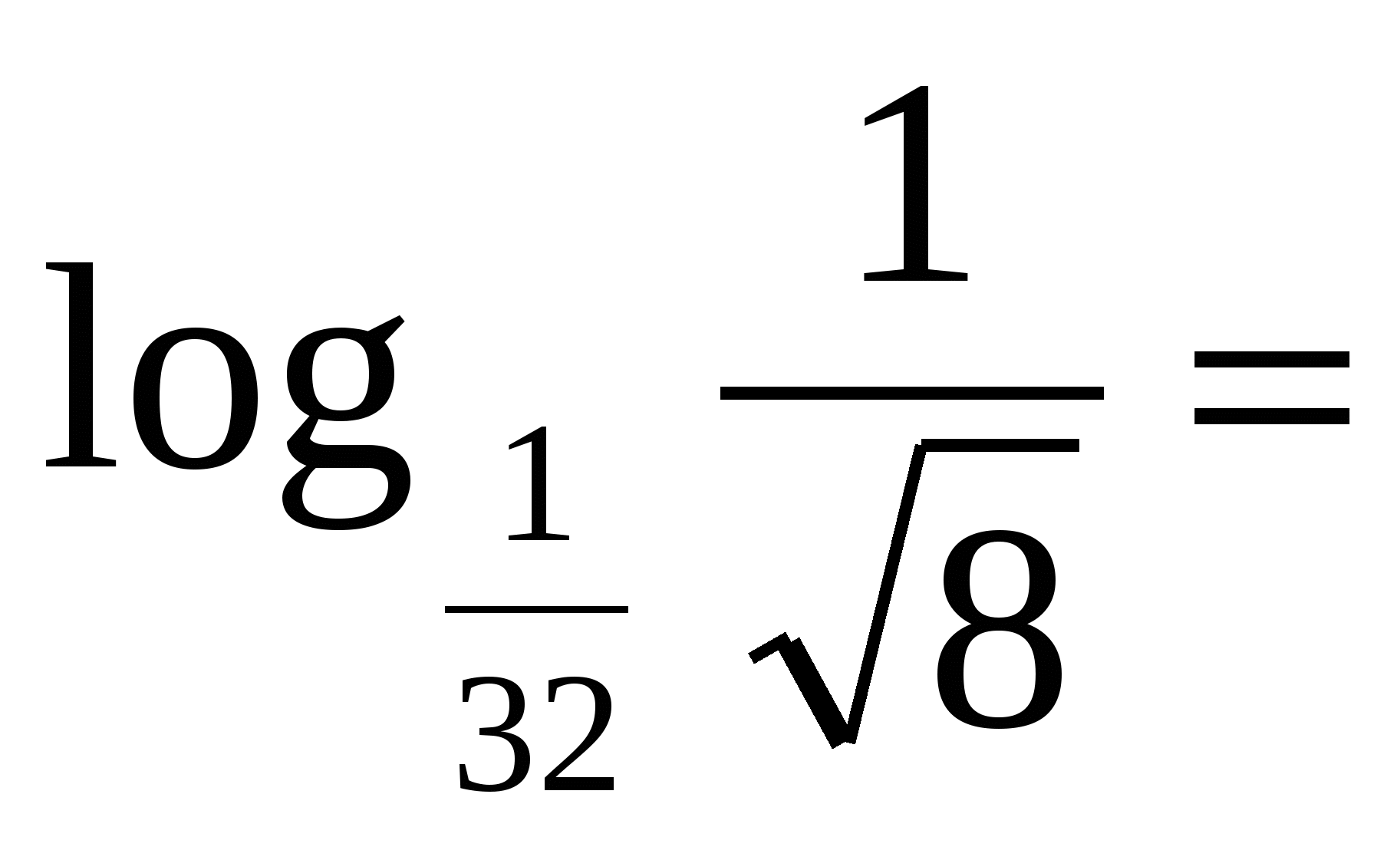
Задание для 2 и 5 групп: 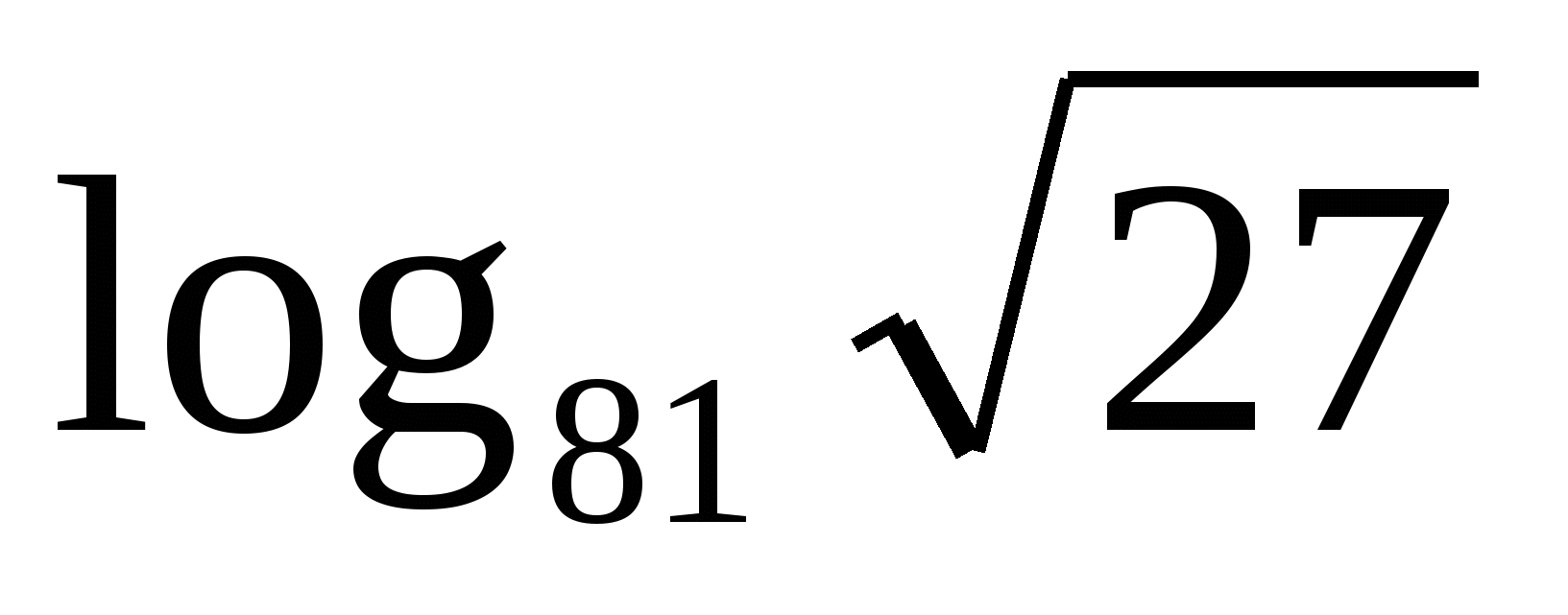 =
=
Задание для 3 и 6 групп: 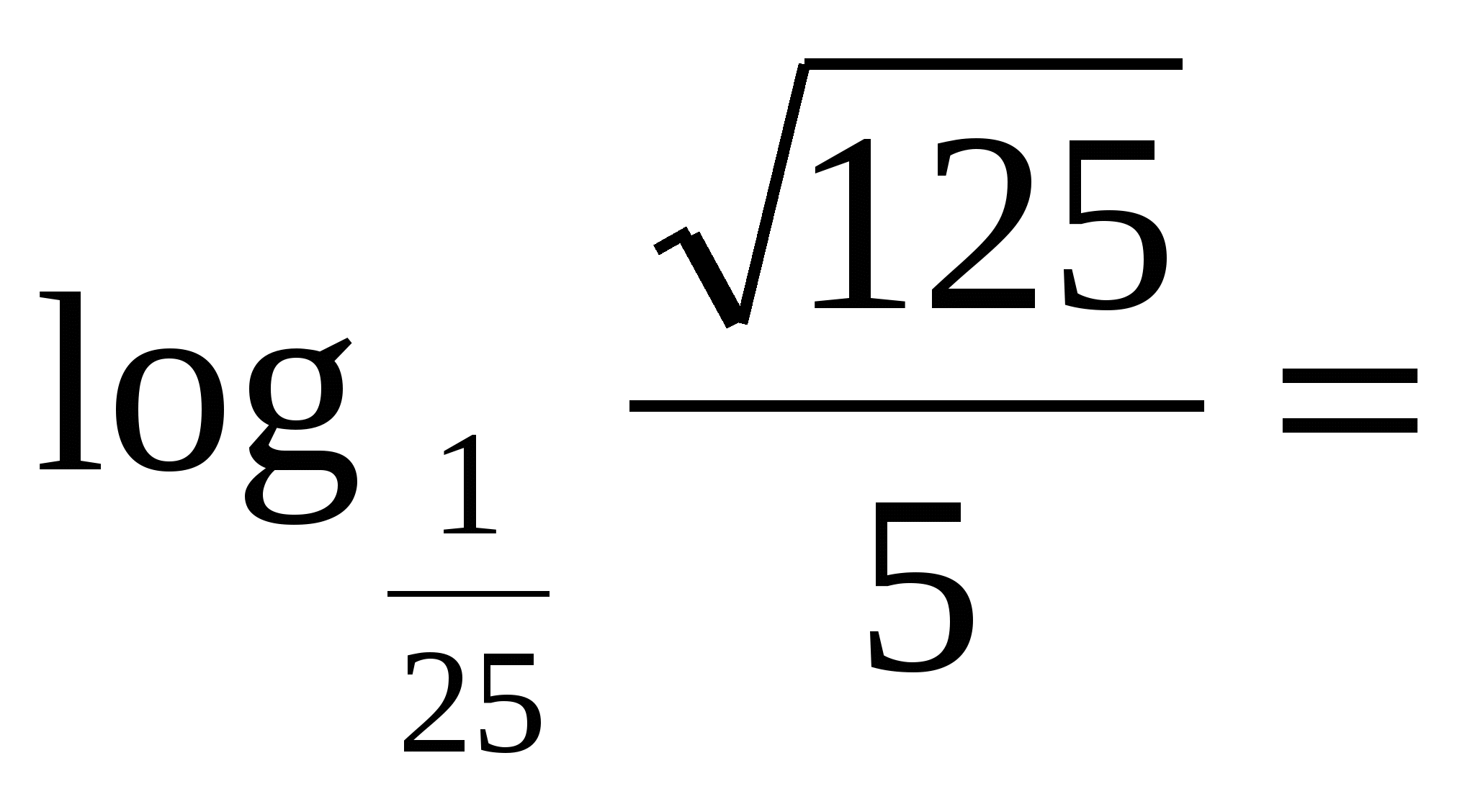
5.Афиширо-
вание и со-
циализация.
5мин.
Два представителя выходят к доске, показывая своё решение. Остальные ребята записывают в тетрадь оба способа и делают вывод, что с помощью свойства вычисление идёт быстрее.
6.Реконструк
ция
7мин.
Рассказать схему исследования функций ( перечислить свойства, а потом открыть написанную на доске).
Дать определения области определения и области значений функции.
Сформулировать определения чётной и нечётной функций.
Сформулировать определения возрастающей и убывающей функций.
Сформулировать определение нуля функции.
7.Деконструк
кция
10мин.
Ребята берут карточку с заданием (для каждой группы разное). Они должны решить в группе и представить решение на доске.
При каких х не определена функция
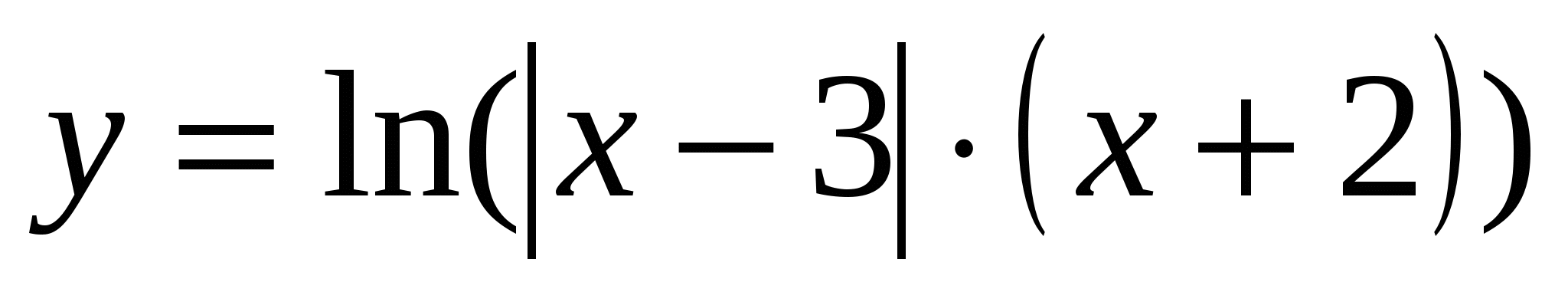 ? Найдите наибольшее целое число, не входящее в область определения функции.
? Найдите наибольшее целое число, не входящее в область определения функции.На каком множестве совпадают функции
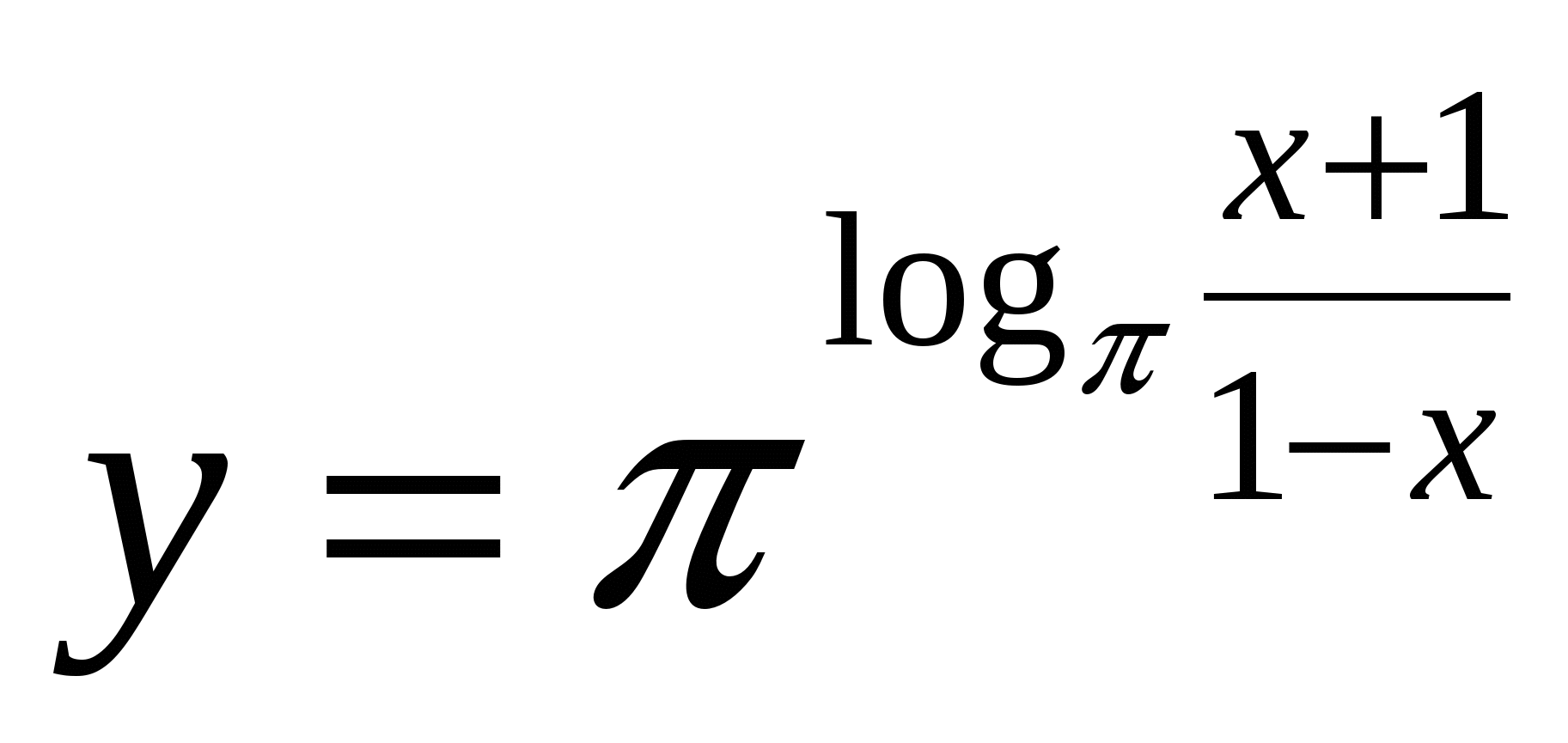 и
и 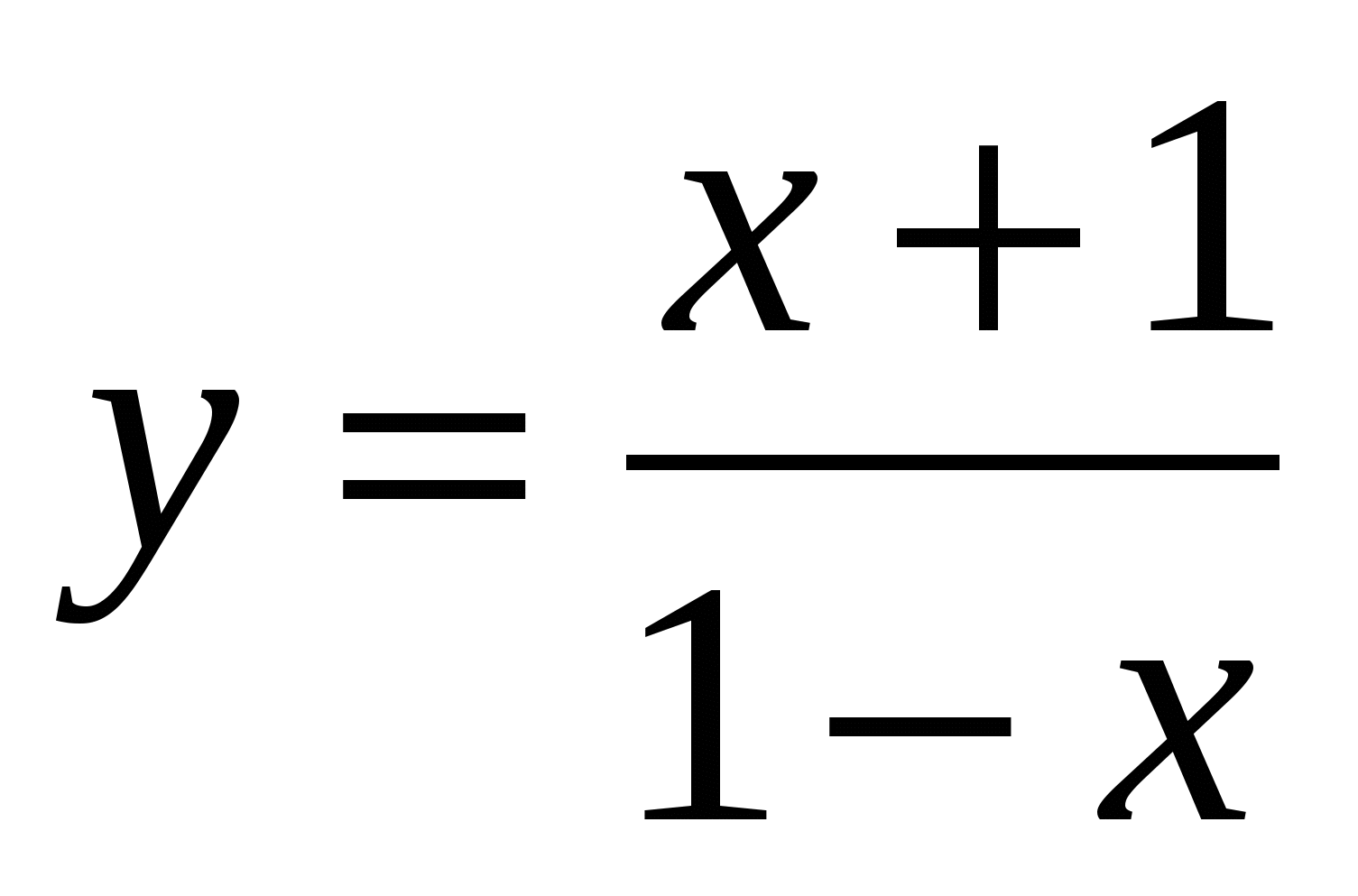 ?
?На каком множестве не существует ни одна из функций
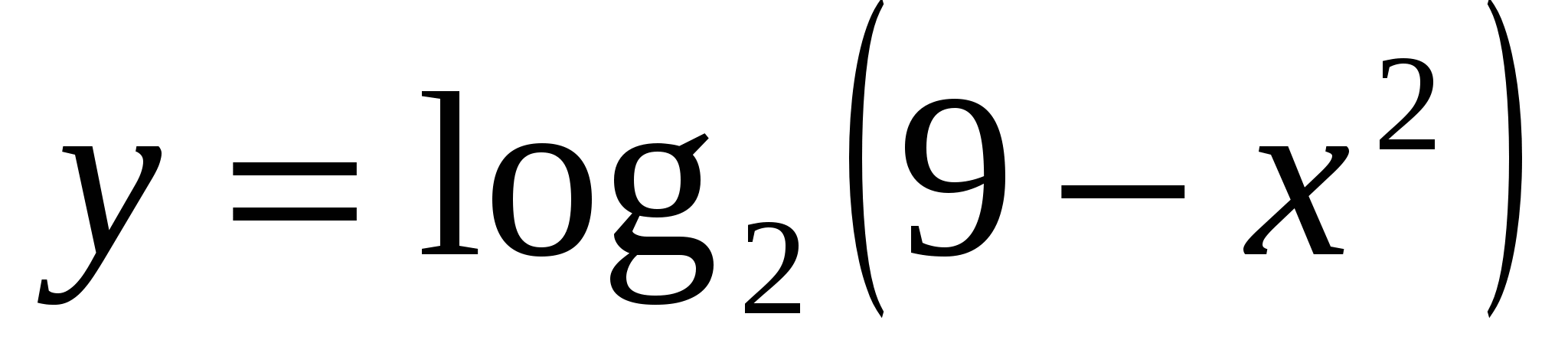 и
и 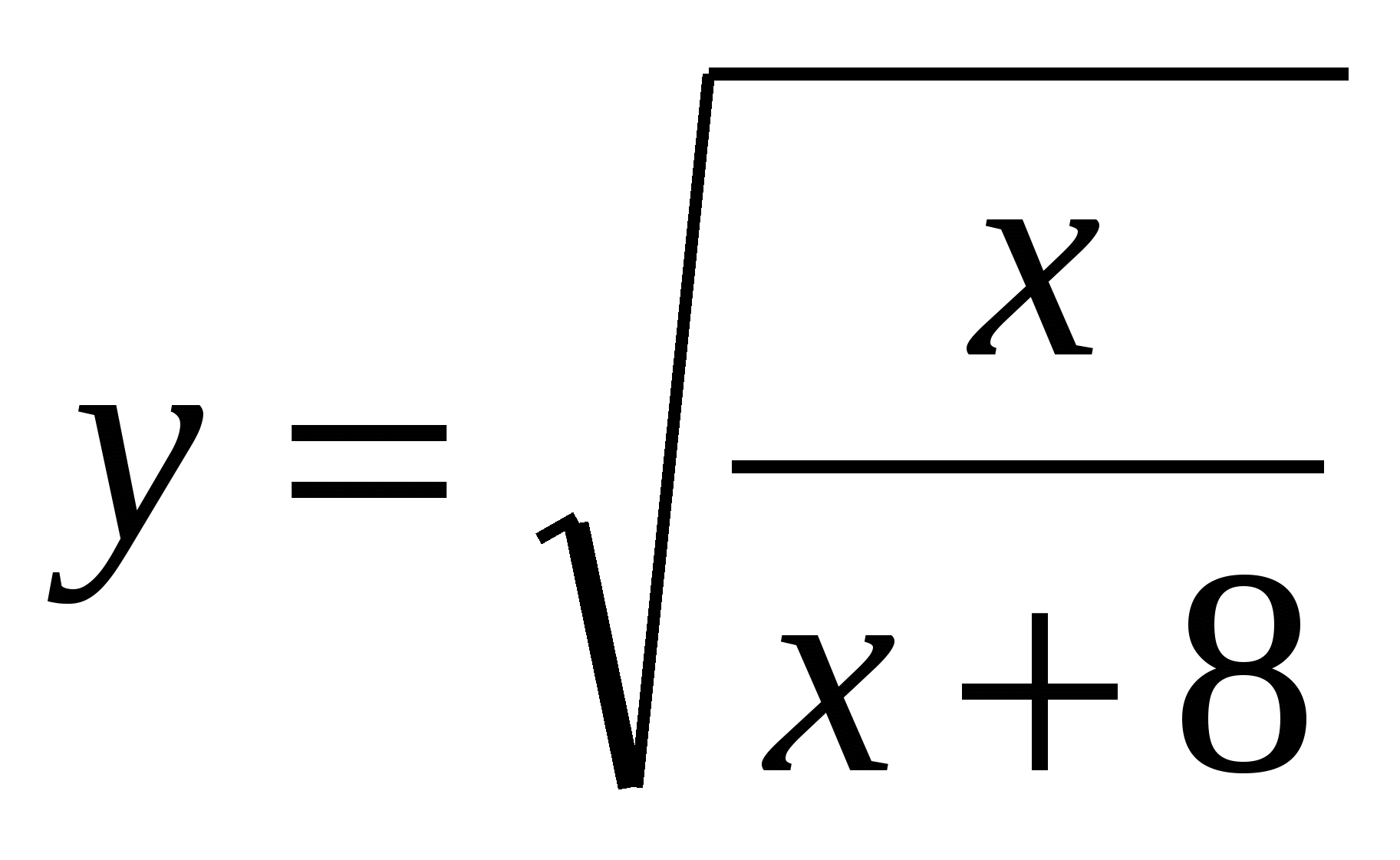 ?
?
Найти число нулей функции
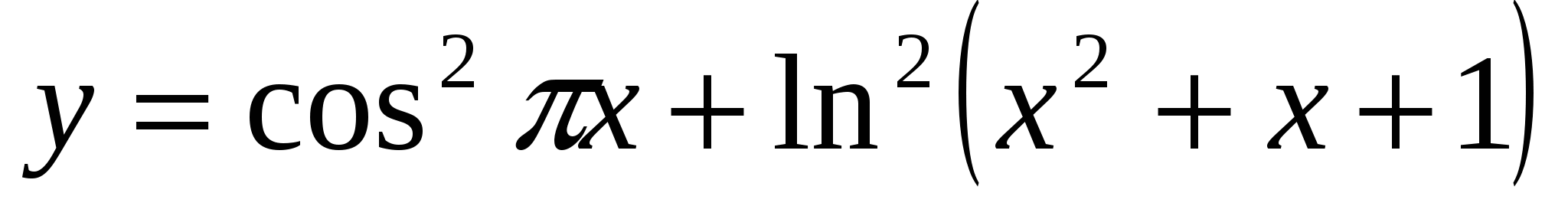 .
.Найти число нулей функции:
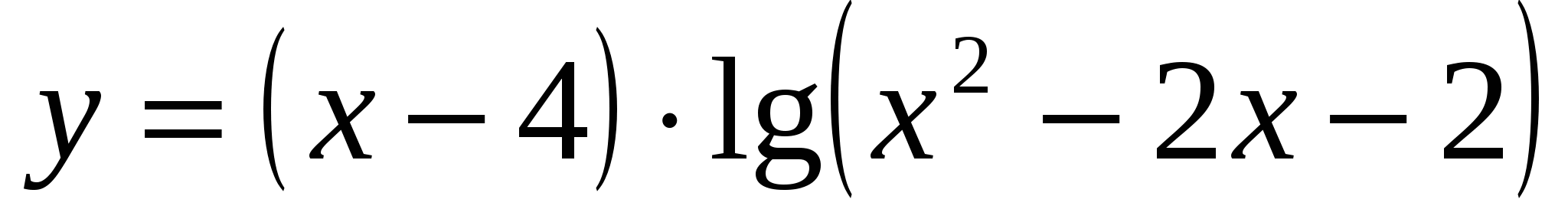 .
.Найдите количество целых чисел, принадлежащих области определения функции
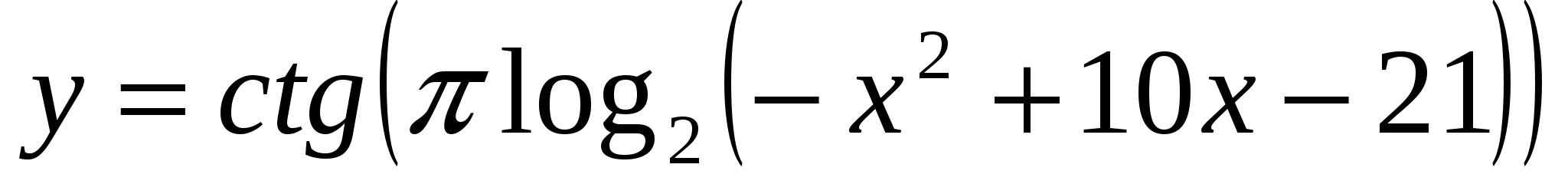 .
.
8.Афиширо-
вание
15мин.
Каждая группа представляет своё решение с полным объяснением. Среди них обязательно найдётся такая группа (например 6), которой потребуется помощь других групп. Если появляются вопросы и сомнения в решении, то ребятам из других групп предлагается предложить решение или высказать гипотезы.
9.Деконструк
ция. Разрыв.
Инсайт.
5мин.
Всем группам предлагается одно задание: исследовать на чётность функцию
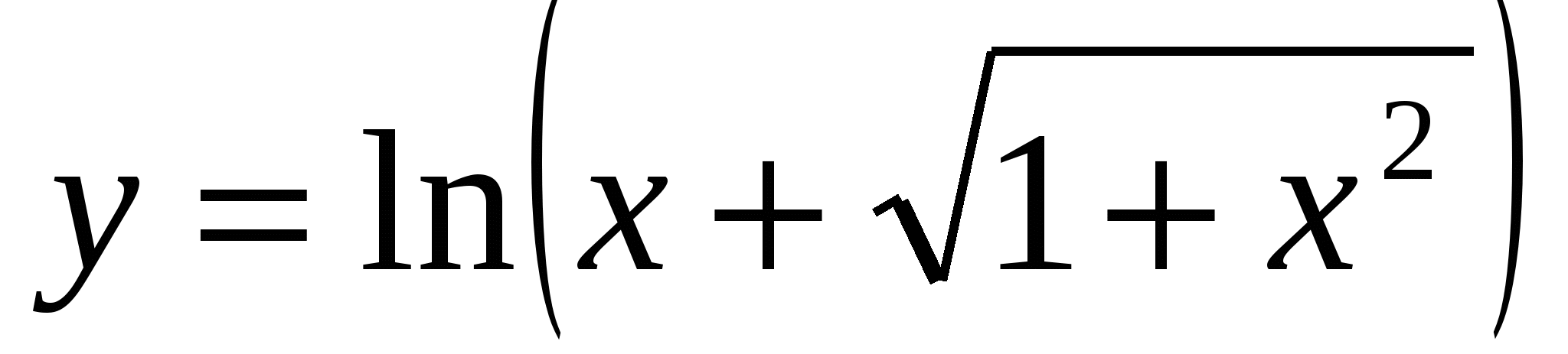 . Ребята обсуждают решение в группах и предлагают разные способы решения. Доказав, что область определения функции симметрична (множество R), приступают к проверке равенств f(-x) = f(x) и f(-x) = -f(x), но заходят в «тупик» и получают функцию общего вида. Тогда вопрос выносится на обсуждение в классе и выясняется, что необходимо применить тождественные преобразования и свойства логарифмов. Функция оказывается нечётной.
. Ребята обсуждают решение в группах и предлагают разные способы решения. Доказав, что область определения функции симметрична (множество R), приступают к проверке равенств f(-x) = f(x) и f(-x) = -f(x), но заходят в «тупик» и получают функцию общего вида. Тогда вопрос выносится на обсуждение в классе и выясняется, что необходимо применить тождественные преобразования и свойства логарифмов. Функция оказывается нечётной.
10. Инсайт.
5мин.
Детям даётся новое задание, идёт аналогичная работа.
Функция f(x) периодична с периодом Т = 11. Решите неравенство f(x) ≥ 0, если f(x) = 11x – x2 для всех х  [ 0;11].
[ 0;11].
11.Социализа
ция общеклассная
2мин.
Подводятся итоги работы на уроке, объясняется индивидуальное домашнее задание, которое будет дано каждому ученику с учётом запросов, знаний и способностей (карточки приготовлены заранее и раздаются детям во время самостоятельной работы). Дети оценивают свою работу и работу других групп. Пример одной карточки для домашней работы:
1. Повторить монотонность функции, знакопостоянство, нахождение нулей функции и точек пересечения графика функции с осями координат.
2. Найдите количество целых чисел, принадлежащих множеству значений функции 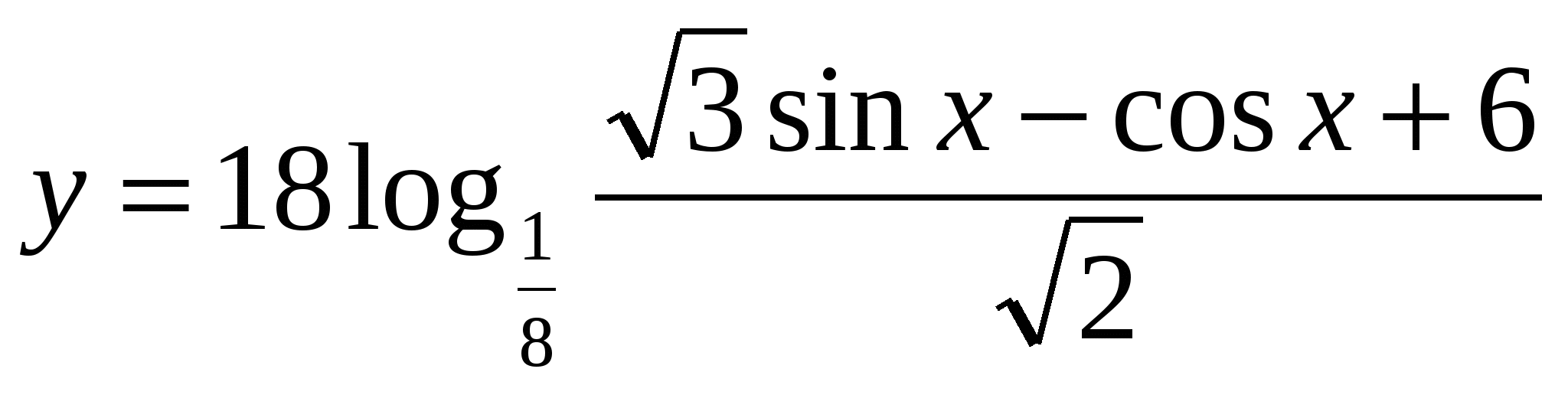 .
.
3. Найдите наименьшее значение функции 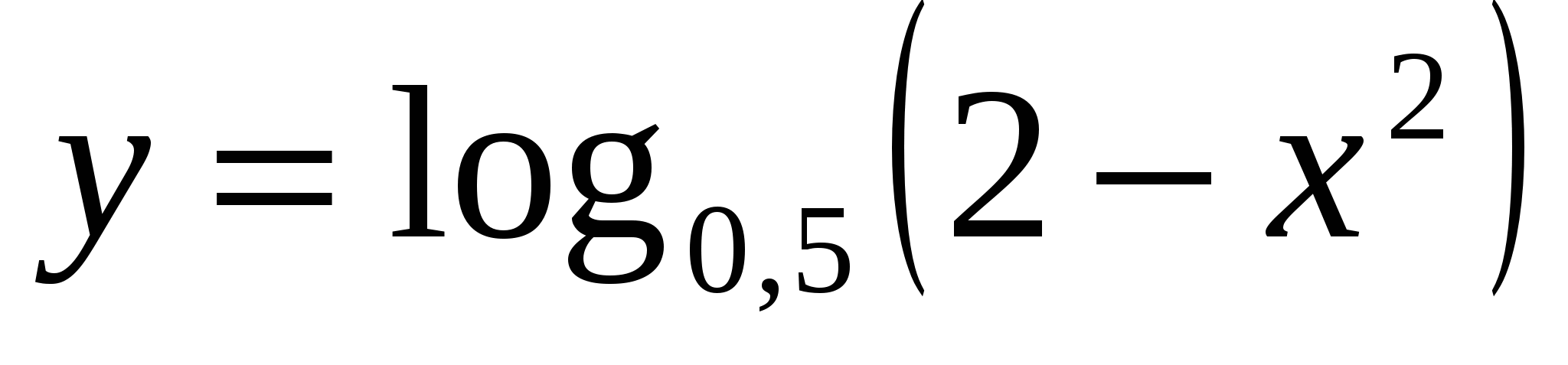 .
.
4. Найдите наибольшее целое число, не входящее в область определения функции 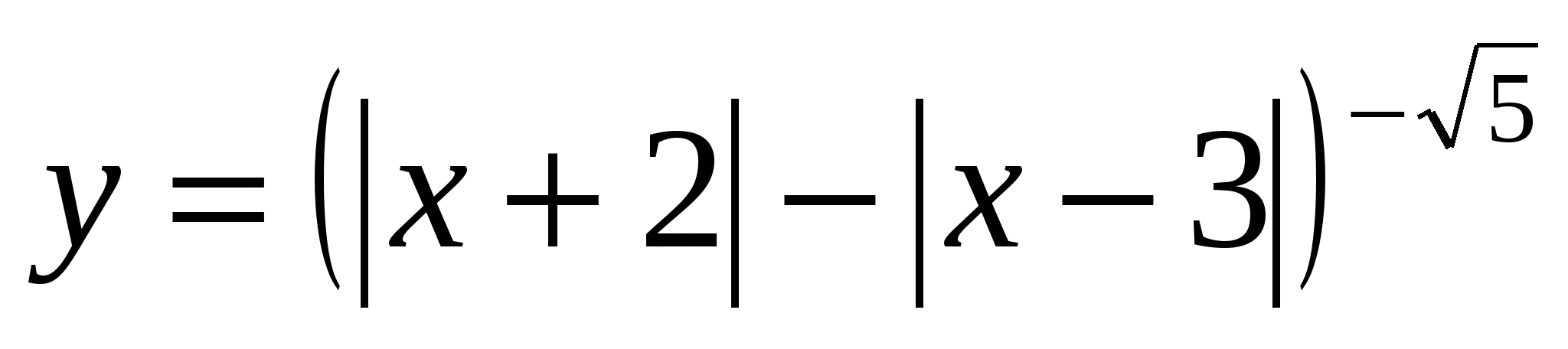 .
.
12.Рефлексия
Самостоятель
ная работа.
Остав-
шееся
время
1. Дан график функции. Укажите промежуток, которому принадлежит наименьшее значение функции а) [-3;0]; b) [-2;8] ; c) [5;10]; d) [1;3].
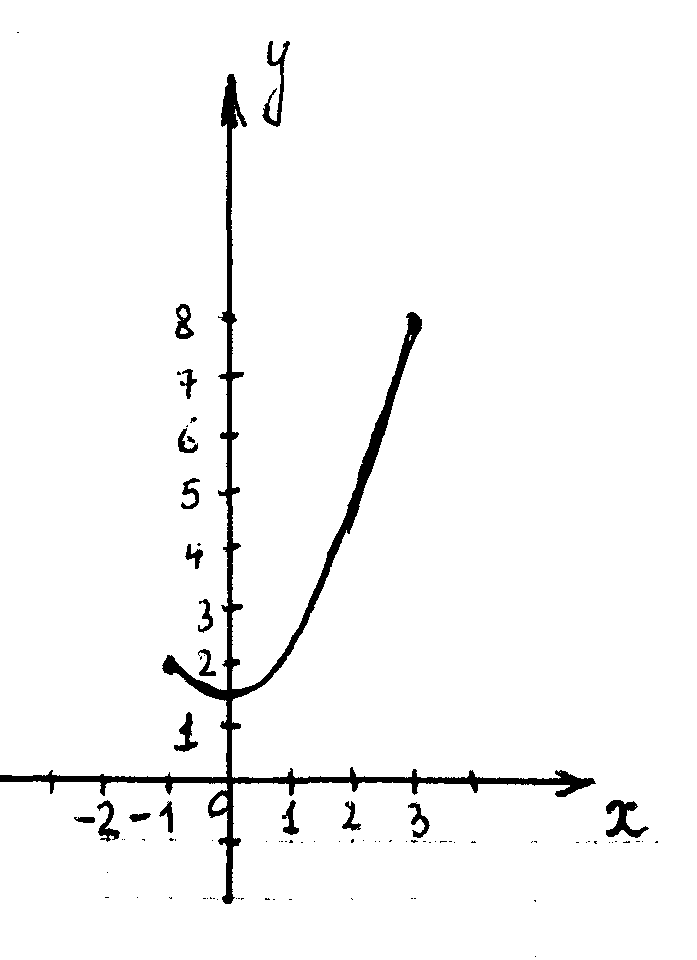
Найдите нули функции
 .
.Найдите количество целых чисел, принадлежащих области определения функции
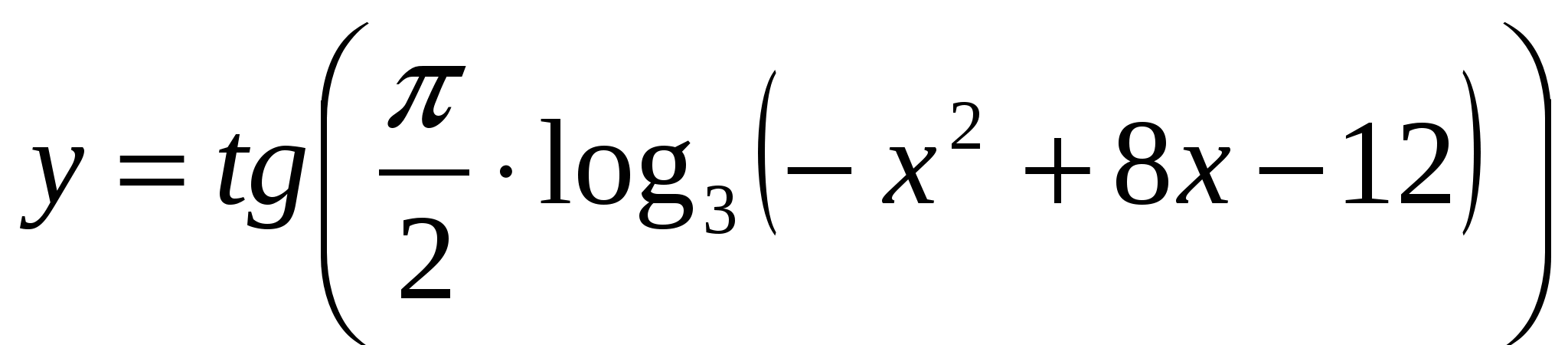 .
.Исследовать функцию на чётность
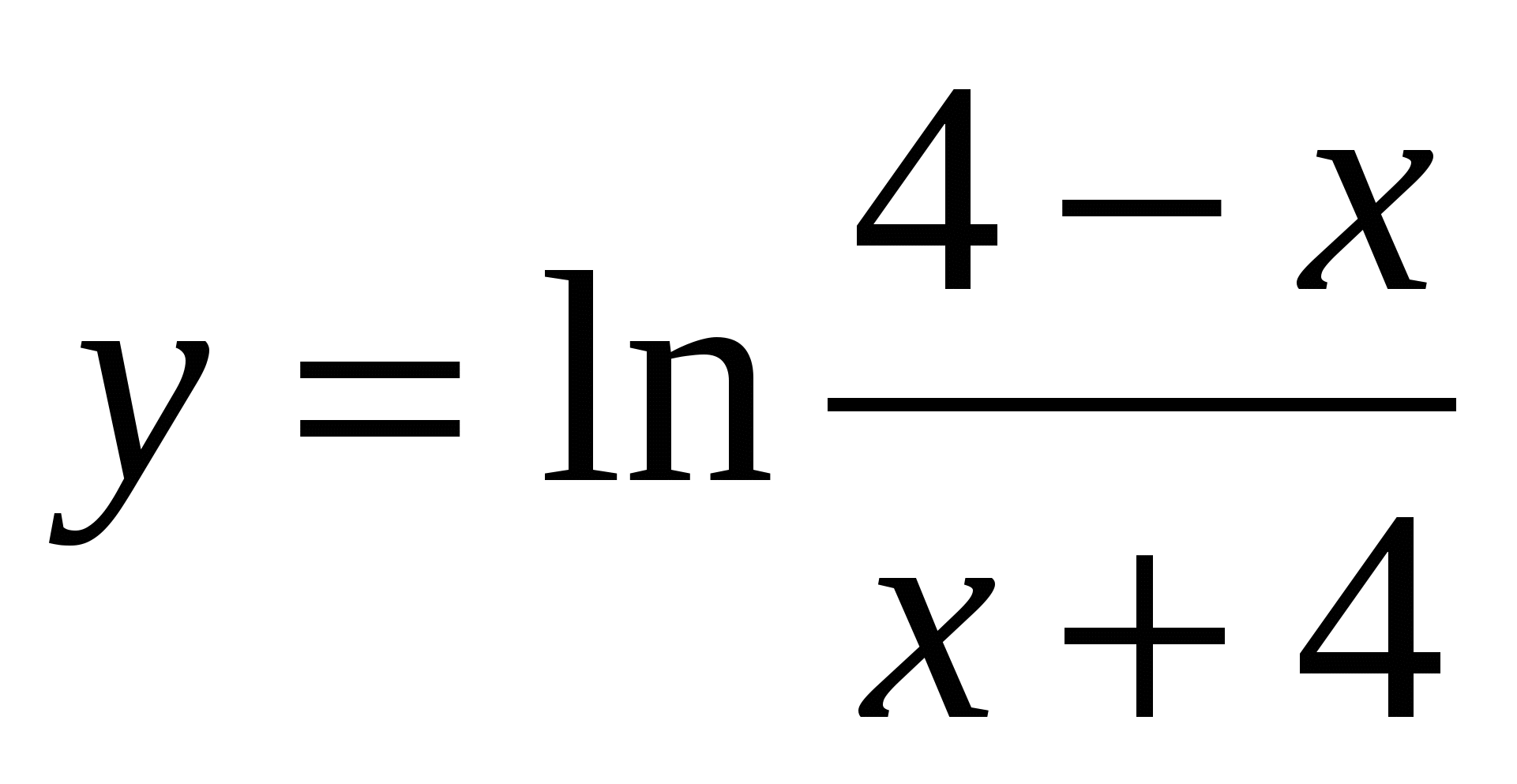 .
.
13.Рефлексия.
2мин.
Со звонком ребята сдают листочки с самостоятельной работой на отдельный стол, вкладывая в конверт с соответствующей надписью.