Урок по алгебре и началам анализа в 11 классе
Тема: Свойства логарифмов.
Цель:
Организовать работу учащихся по изучению и применению свойств логарифмов.
Способствовать овладению учащимися основными алгоритмическими приемами применения изученных свойств при вычислении логарифмов, развитию внимания, мышления и памяти в процессе воспроизведения и применения формул.
Содействовать формированию коммуникативных навыков при работе в парах, привитию ответственного отношения к учебе.
Учебное обеспечение: Колмогоров А.Н. Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений. - М.: Просвещение, 2007.
Оборудование: мультимедийный компьютер, рабочие карты урока, карточки с заданиями.
№ п/п
Этап урока
Время
I
Организационный момент
2 мин
II
Повторение. Решение заданий части А (ЕГЭ)
5 мин
III
Актуализация знаний. Постановка проблемы.
Сообщение «Логарифмы в природе»
4 мин
IV
Постановка целей и задач урока
2 мин
V
Изучение нового материала
8 мин
VI
Работа в парах
20 мин
VII
Домашнее задание
1 мин
VIII
Итог урока
3 мин
ХОД УРОКА
Организационный момент. Объяснение учителя порядка работы. Знакомство с рабочей картой урока.
РАБОЧАЯ КАРТА УРОКА
ФИ учащегося __________________________________
№ п/п
Этапы урока
Задание
Отметка о выполнении
1
Организационный момент
Соберись.
Настройся на урок.
2
Повторение. Тест (ЕГЭ часть А)
«3»
3 – 4 верных ответа
«4»
5 верных
ответов
«5»
6 верных ответов
3
Ознакомление с новым материалом
Смотри.
Слушай.
Вспоминай.
Записывай.
4
Выполнение заданий на применение формулы логарифма произведения
«3»
«4»
«5»
5
Выполнение заданий на применение формулы логарифма частного
«3»
«4»
«5»
6
Выполнение заданий на применение формулы логарифма степени
«3»
«4»
«5»
7
Формула перехода логарифма к другому основанию
«3»
«4»
«5»
Доп.
Задание на применение всех формул
8
Самооценка за урок
«3»
«4»
«5»
9
Домашнее задание:
п.37 весь, свойства знать
«3»
№ 494 аб,
495 аб, 496 ав
«4»
№ 494 вг, 495 вг, 496 бг, 497 вг
«5»
Глава V. Задачи на повторение, п.7, № 66
10
Итог урока. Рефлексия.
Повторение. Решение заданий части А ЕГЭ. Выполнить задания с выбором ответа, сделать самопроверку (Приложение 1). Отметить количество допущенных ошибок.
Актуализация знаний. Проблема: Как найти значение такого выражения? (Приложение 2).
Постановка целей и задач урока. Повторить свойства степени, определение логарифма, процитировать слова Дж. Непера.
На прошлом уроке вы ознакомились с понятием логарифма, рассмотрели основные примеры нахождения логарифмов. Но чтобы успешно использовать на практике операцию логарифмирования, необходимо познакомиться со свойствами этой операции. Итак, тема урока «Свойства логарифмов». Формулируем цели урока.
Изучение нового материала. Обсуждение свойств идет с использованием презентаций при активном участии детей. Свойства записываются в тетради. Продумывается название свойства. Уточняется область определения входящих в формулы буквенных величин. Добавляются полезные, изученные ранее, свойства (частные случаи).
Самостоятельная работа учащихся. Работа некоторых учащихся у доски.
VIII . Итог урока. Рефлексия.
Выполнил ли задания намеченного уровня сложности?
Если не выполнил – почему?
Кто перешел на более высокий?
Что нужно сделать дома?
Карточка 1
Карточка 2
log a 1 =
log a a =
log a 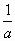 =
=
log a a =
a =
log a а m =
а m =
log a а m =
log a (xy) =
log a  =
=
log a xp =
log a b = 
5. Самостоятельная работа проверочного характера
Ребята, вам даются задания, которые вы должны выполнить. Получив ответы к каждому заданию, внизу таблицы выберите свои ответы и рядом с заданием, в пустые клеточки впишите соответствующие значения букв.
Вариант 1
1.
Вычислите  , если
, если 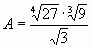 ;
;
2.
Вычислите 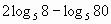 ;
;
3.
Вычислите 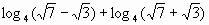 ;
;
4.
Вычислите 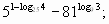
5.
При каких значениях х имеет смысл выражение 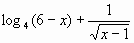 ;
;
Е
Ю
Б
И
Р
Г
Н
П
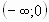
-1
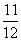
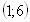
1
-6,5
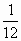
2
Вариант 2
1.
Вычислите 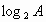 , если
, если  ;
;
2.
Определите знак разности 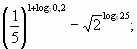
3.
Вычислите 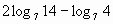
4.
При каких значениях х имеет смысл выражение  ;
;
5.
Вычислите 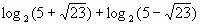 ;
;
Ю
Е
Б
И
Р
Г
Н
П
-1
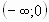
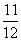
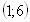
1
-6,5
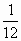
2
Проверка ответов самостоятельной работы.
У 1-го варианта получилось Бюрги, у 2-го варианта – Непер. Это фамилии двух известных математиков: шотландца Джона Непера (1550 – 1617) и швейцарца Иобстома Бюрги (1552 – 1632), которыми одновременно и независимо друг от друга были изобретены логарифмы.
Немного из истории логарифмов
Логарифмы были придуманы для ускорения и упрощения вычислений.
Бурное развитие науки, техники и мореплавания в эпоху Возрождения, быстрое развитие астрономии и усложнение арифметических выкладок настоятельно требовали новых способов вычислений, которые позволили бы ускорить вычисления, сделать их доступными более широкому кругу людей.
К концу XVI в. астрономы, например, пользовались 10-тизначными таблицами тригонометрических функций. Значит, им приходилось производить многочисленные выкладки с 10-значными числами. Выкладки эти отнимали очень много времени и не всякому были под силу.
Нужен был способ ускорить вычисления.
Этим способом или, как говорят, вспомогательным вычислительным аппаратом, явились логарифмы.
Почва для развития логарифмов была подготовлена всем предшествующим развитием математики.
У древнегреческого ученого Диофанта в зачаточной форме есть действия над степенями одного и того же основания; французской ученый Оресм (XIV в.) вводит дробные показатели; другой французский ученый Шюке (XV в.) ввел нулевой и отрицательный показатель; фламандский ученый XVI в. Стевин составил таблицы процентных расчетов.
Таким образом, к концу XVI в. были подготовлены условия создания логарифмов.
Идея логарифма, т.е. идея выражать числа в виде степени одного и того же основания, принадлежит Михаилу Штифелю. (Предвосхищение этой идеи можно видеть у Архимеда.) Но во времена Штифеля математика была не столь развита и идея логарифма не нашла своего развития.
Логарифмы были изобретены позже одновременно и независимо друг от друга шотландским ученым Джоном Непером (1550-1617) и швейцарцем Иобстом Бюрги (1552-1632).
Первым опубликовал работу Непер в 1614 г. под названием “Описание удивительной таблицы логарифмов”. Теория логарифмов Непером была дана в достаточно полном объеме, способ вычисления логарифмов дан наиболее простой, поэтому заслуги непера в изобретении логарифмов больше, чем у Бюрги.
Бюрги работал над таблицами одновременно с Непером, но долгое время держал их в секрете и опубликовал лишь в 1620 г.