Конспект урока по Алгебре «Умножение разности двух выражений на их сумму» 7 класс

«Умножение разности двух выражений на их сумму»

ТЕМА: «Умножение разности двух выражений на их сумму».

Цели урока:

Образовательные:

- способствовать созданию условий для введения формулы сокращённого умножения (а – b)(а + b) = а² – b²;

- способствовать формированию умения распознавать формулу (а – b)(а + b) = а² – b² и применять ее в несложных случаях, обобщать и исследовать полученные результаты, контролировать свою деятельность.

Воспитательные: - формирование умений выделять главное,

переносить знания в новую ситуацию, сопоставлять факты,

анализировать;

- укрепление «нужности» математики в сознании ученика;

- способствовать развитию мышления, памяти, речи;

- расширение кругозора учащихся (компонент НРК).

Развивающие: - с помощью интересных форм работы на уроке содействовать повышению активности учащихся на уроке, воспитанию интереса к математике;

- создать условия для формирования у учащихся коммуникативых навыков, умения работать в паре, объективно оценивать свои знания и умения.

ТИП УРОКА: урок ознакомления с новым материалом.

ФОРМА ПРОВЕДЕНИЯ УРОКА:

ФОРМЫ ОРГАНИЗАЦИИ ПОЗНАВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ: индивидуальная, фронтальная, парная.

МЕТОДЫ ОБУЧЕНИЯ НА УРОКЕ: частично-поисковый, наглядно-иллюстративный, словесный.

ФОРМЫ РЕАЛИЗАЦИИ МЕТОДОВ НА УРОКЕ:

1. Беседа.

2. Парная работа.

3. Практическая работа.

ЛОГИЧЕСКИЕ МЕТОДЫ ОБУЧЕНИЯ: анализ, индуктивный метод.

СИСТЕМА КОНТРОЛЯ: самоконтроль.

СРЕДСТВА ОБУЧЕНИЯ: индивидуальный раздаточный материал; учебник; тетрадь; ТСО.

ХОД УРОКА

I. Организационный момент.

Здравствуйте, дети!

Сегодня у нас с вами 30 минут общения, 30 минут сотрудничества, 30 минут движения вперед, 30 минут открытий, 30 минут, надеюсь, плодотворной работы. И если вы готовы со мной работать, то хлопните, пожалуйста, два раза в ладоши. (Если вяло - зарядка).

Итак, вперед!

Начать урок я хотела бы с высказывания одного из великих ученых - Б.Паскаля: «Величие человека в его способности мыслить» (слайд 1). Давайте вместе покажем, как мы умеем мыслить. А ДЛЯ ЭТОГО нам нужно (слайд 2):

1. Повторить изученные ранее формулы.

2. Познакомиться с еще одной формулой сокращенного умножения и научиться ее применять.

Кроме того, мы сегодня займемся строительством. А что мы вместе построим, увидим в конце урока.

Блез Паскаль

фр. Blaise Pascal

Блез Паскаль (автор Филипп де Шампень)

Род деятельности:

математик, философ, литератор, физик

Дата рождения:

19 июня 1623(1623-06-19)

Место рождения:

Клермон-Ферран, Овернь

Дата смерти:

19 августа 1662(1662-08-19) (39 лет)

Место смерти:

Париж

II. Актуализация опорных знаний.

Вспомните, что вы изучали на прошлых уроках. (Формулы).

Как они называются? (ФСУ).

А почему же они называются формулами сокращенного умножения? Вспомните русский язык и поясните, что значит сократить. (Сделать короче).

Оказывается, ФСУ гораздо больше и применять их можно при выполнении различных заданий: при решении уравнений, доказательстве тождеств, вычислении значений выражений. И всему этому мы будем учиться на уроках алгебры.

А сейчас мы заложим первый кирпич нашего будущего здания.

1. У каждого на парте лежит рабочий материал в той последовательности, в которой вы будете выполнять задания. Кроме того, отдельно лежит лист контроля, где вы после каждого выполненного задания проставите себе оценку.

Сейчас возьмите таблицу №1 и заполните ее, выбрав буквы, соответствующие верным и неверным равенствам (слайд 3).

а) (0,4x³y²)²=0,16x⁶y⁴

б) (3m⁵)²=9m⁷

Таблица №1

Верные равенства

Неверные равенства

в

а

д

б

г

в) (3а²)²=27а⁴

г) (0,5ав²)²=0,25ав⁴

д) (0,1ху³)²=0,01х²у⁶

Обведите в кружок верные ответы. (Обсуждение ошибок.)

Оцените себя: 3 верных ответа – «3»; 4 верных ответа – «4»; 5 верных ответа – «5». Поставьте оценку в лист контроля в первом столбце «Работа с таблицей №1».

(В мозаике открывается одна часть - слайд 4).

1. Следующий кирпич-это результат выполнения 2-го задания.

Вспомним известную фразу «Казнить нельзя помиловать». Где будем ставить запятую? От нее зависит жизнь человека. Очень важно и в математике не только правильно решать, но и говорить. Квадрат суммы или сумма квадратов, разность квадратов или квадрат разности…Человек, далекий от математики, возможно и не заметит принципиальной разницы, но мы то знаем, что эти действия приводят к соверщенно разным результатам.

Каждое из следующих выражений запишите в соответствующий столбец таблицы:

(7а+3с) ²; а²-в²; х²+у²; (5x-2y)² (слайд 5).

Таблица №2

Сумма квадратов выражений

Квадрат суммы выражений

Разность квадратов выражений

Квадрат разности выражений

х²+у²

(7а+3с) ²

а²-в²

(5х-2у) ²

Прочитайте эти выражения вслух.

Проверьте и оцените себя: 2 верных ответа – «3»; 3 верных ответа – «4»; 4 верных ответа – «5». Оценку выставляют в лист контроля во второй столбец «Работа с таблицей №2» .

(В мозаике открывается вторая часть - слайд 6).

3) Откройте тетради, запишите число и выполните следующее задание: запишите в виде выражения (слайд 7):

а) квадрат суммы 3а и ;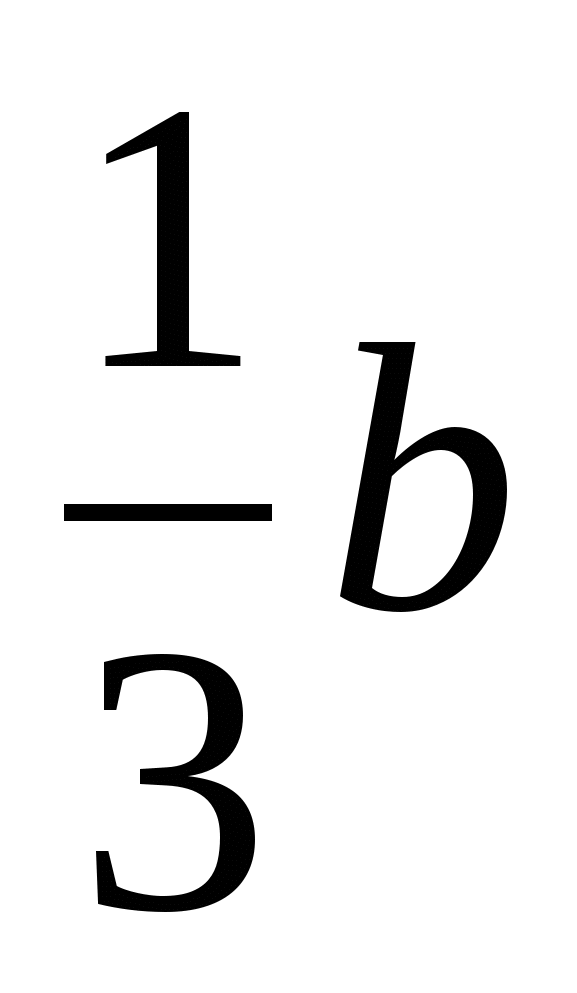

б) сумму квадратов 0,5m и 5,3n;

в) произведение суммы выражений 8х и 4у и разности этих выражений.

Проверьте и оцените себя: 1 верный ответ – «3»; 2 верных ответа – «4»; 3 верных ответа – «5». Оценку выставляют в лист контроля во второй столбец «Работа с таблицей №2» .

(В мозаике открывается третья часть - слайд 8).

III. Введение нового материала.

Заполним таблицу, для этого надо выполнить умножение многочленов (слайд 9).

Один из учеников у доски заполняет первую строчку, а другой – вторую. Остальные записывают в тетради все произведения.

Выполните умножение.

1.

2.

3.

а-5

2+а

1-а

1.

а+5

а² – 25

а² + 7а + 10

– а² – 4а + 5

2.

2-а

– а²+7а – 10

4 – а²

а² – 3а + 2

Ответьте на вопросы:

- Как называются выражения, которые вы получили? (Многочлены.)

- Произведения каких двучленов вам легче было выполнять? ((а-5)(а+5);(2-а)(2+а)).

- Кому еще так показалось?

- Как вы думаете, почему было легче? (При приведении подобных встречаются противоположные слагаемые).

- Приведите свои примеры подобных произведений. Можете быстро назвать результат умножения?

- Можете ли вы обобщить все примеры одной формулой?

- Запишите эту формулу в тетрадь.

- Что мы умножали? (Сумму и разность двух выражений).

- Что мы получили в результате? (Разность квадратов этих выражений).

- Попробуйте сформулировать записанное вами равенство (слайд 10).

- А теперь сформулируйте тему нашего урока. («Умножение разности двух выражений на их сумму).

- Формулу, которую вы записали, можно назвать тождеством? (Да).

- А как мы можем доказать эту формулу? (Умножив два многочлена).

(а – b)(a + b) = a² – ab + ab – b² = a² – b². (Выполняет у доски ученик, слайд 11).

(Дети записывают в тетрадь).

- Применим данную формулу на практике.

Рассмотрим записанные выражения (слайд 12):

1. (2а + в)(в – 2а) и 4а² – в²

2. (а² – в)(а² + в) и а⁴ + в²

3. (4 – а²)(а² + 4) и 16 – а⁴

Скажите, между какими из них можно поставить знак равно, чтобы получилось тождество?

-От чего зависит расположение квадрата каждого выражения? (Смотрим на разность двух выражений).

-Можно ли полученную формулу назвать формулой сокращенного выражения? Почему?

(Да. Так как вычисления сокращаются из-за наличия противоположных слагаемых).

(В мозаике открывается четвертая часть - слайд 13).

IV. Физкультминутка. Мы замечательно поработали, пора отдохнуть. А как вы знаете, лучший слайд 1 отдых – это смена деятельности. (Один из учеников проводит зарядку «Солнышко лучистое» - слайд 14-15).

V.Закрепление нового материала.

1. Теперь поработаем в парах. Откройте учебник на странице 162, прочитайте формулировку тождества и расскажите ее друг другу по очереди. (Поработать над формулировками в статистических парах в режиме взаимообучения).

Оцените ответ друг друга и поставьте оценку в четвертый столбец «Знание формулы».

2) Выполните самостоятельную работу по вариантам (слайд 16). Проверьте работы друг друга и оцените в листке контроля в пятом столбце «Карточка». (Самостоятельно работать в режиме взаимообучения в парах). Без ошибок – «5», с одной ошибкой – «4», с двумя ошибками – «3».

Карточка 1

Выполнить умножение

(m-n)(m+n)=

(x-5)(x+5)=

(2a-8)(2a+8)=

Карточка 2

Выполнить умножение

(с-p)(c+p)=

(3-y)(3+y)=

(5b-6)(5b+6)=

3)Формулу можно также применить для удобного и быстрого счёта (слайд 18):

(100 – 1)(100 + 1) = 100² – 1² = 10000 – 1 = 9999.

Как сказал Паскаль: «Предмет математики настолько серьезен, что полезно не упустить случая сделать его немного занимательным» (слайд 17).

А вот вам – разминка для ума: как одним движением сократить число 9999 в 1,5 раза? Попробуйте применить формулу для нахождения данного произведения.

37*43 = (40 + 3)(40 – 3) = 40² – 3² = 1600 – 9 = 1591. (Выполняет у доски ученик).

4)Решите № 858 (у доски 2 ученика).

VI. Итоги урока.

Настало время подвести итоги. В листе контроля каждый себе поставил оценку за отдельно взятые задания. Как вывести оценку за урок? (Среднее арифметическое - слайд 19).

Лист контроля Ф.И.

Работа с таблицей №1

Работа с таблицей №2

Запись выражений на математическом языке

Знание новой формулы, умение ее сформулировать

Карточка

Оценка за урок

-Что нового изучили на уроке? (ФСУ).

- Сформулируйте новое тождество.

- Где применяется эта ФСУ? (При упрощении выражений, для быстрого счета).

- На что нужно обращать особое внимание при записи разности квадратов? (При записи первого квадрата смотрим на разность).

Передайте ваши листы контроля, таблицы №1 и №2, карточку на первую парту, скрепив скрепкой. Не забудьте подписать листы контроля.

Карточка с домашним заданием остается у вас. Обратите внимание, в этой карточке есть творческое задание.

Задание на дом.

Пункт 34, № 857, 861(а,в,д) – на «4»;

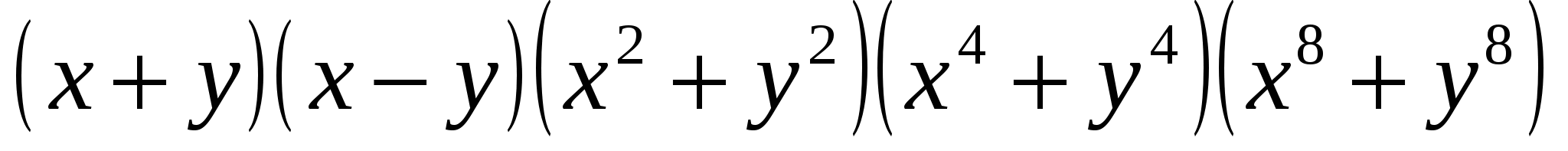– на «5».

Творческое домашнее задание (для тех, кто интересуется).

Очень давно в Древней Греции жили и работали замечательные ученые: математики, философы, астрономы, физики, которые всю свою жизнь отдали служению науке. Начиная с VI века до н. э., у древнегреческих математиков встречаются общие утверждения о тождественном преобразовании многочленов, применении формул и правил. Но тогда было принято все алгебраические утверждения выражать в геометрической форме. Вместо сложения чисел говорили о сложении отрезков, произведение двух чисел сравнивали с площадью, трех чисел - с объемом и т. д.

Ваша задача: найти в тексте учебника примеры, которые иллюстрируют способы доказательства известных вам трёх ФСУ при помощи геометрических чертежей и рассказать остальным учащимся о них.

Сейчас я вам расскажу одну притчу.

Шел мудрец, а навстречу ему три человека, которые под горячим солнцем везли тележки с камнями для строительства. Мудрец остановился и каждому задал по вопросу. У первого спросил: «Что ты делал целый день?». И тот с ухмылкой ответил, что целый день возил проклятые камни. У второго мудрец спросил: «А что ты делал целый день?», и тот ответил: «А я добросовестно выполнял свою работу». А третий улыбнулся, его лицо засветилось радостью и удовольствием: «А я принимал участие в строительстве храма!».

-Ребята! Давайте попробуем оценить каждый свою работу за урок.

-Кто работал так, как первый человек, кладет перед собой синий квадратик.

-Кто работал добросовестно, кладет перед собой зеленый квадратик.

-Кто принимал участие в строительстве «Храма Знаний» - красный квадратик.

Помните, в начале урока, мы задались целью построить здание? Кто построил свой «Храм Знаний» - молодцы! Остальные, я уверена, обязательно достроят свой храм на следующий уроках! Желаю вам терпения и трудолюбия!

На нашей картине открыто 4 части. Вы уже догадались, что изображено на ней? (Кремль) Пусть «Храм Знаний» каждого из Вас станет таким же величественным и красивым, как каждый из архитектурных памятников Казанского Кремля (слайд 20).

СПАСИБО ЗА УРОК! (слайд 21)

8