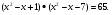Открытый урок по алгебре в 9 классе.
Тема: Уравнения, приводимые к квадратным.
Цели урока: 1) обобщение и углубление знаний учащихся по решению квадратных уравнений;
2) способствовать формированию умений применять различные способы решения уравнений;
3) развить творческие способности учащихся путем решения заданий, содержащих модули и параметры.
Ход урока:
Вводная беседа.
При решении уравнений учащиеся нередко совершают ряд преобразований, которые приводят к ошибочным выводам.
Например:
1. РУ х(х+3)=2х
Решение:
Делим обе части уравнения на х:
Х+3=2,
Х= -1.
При этом решении потеряли корень Х=0. В чем ошибка?
Разделили на Х, а переменная Х может быть равной 0. А на нуль делить нельзя.
Ответ: -1; 0.
2. РУ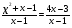 
Решение:
Т.к. знаменатели обеих частей одинаковы, то
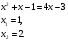
При таком решении появился посторонний корень Х=1. Где ошибка?
Общий знаменатель не может равняться 0.
Ответ: Х=2.
Чтобы не допустить подобные ошибки, нужно знать правила равносильных переходов при решении уравнений.
Устный опрос.
Какие уравнения называются уравнениями 1 степени?
Как решить линейные уравнения?
Сколько решений может иметь линейное уравнение?
Какое уравнение называется уравнением второй степени?
Приведенное квадратное уравнение?
Как решается квадратные уравнения?
Сколько корней может иметь квадратное уравнение?
если Д > 0, то квадратное уравнение имеет 2 корня.
если Д = 0, то один корень.
если Д < 0, то нет корней.
Какая существует связь между корнями и коэффициентами квадратного уравнения?
Составить приведенное квадратное уравнение, если
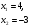
10.Как разложить на множители квадратный трехчлен?
3. Объяснение новой темы.
Сегодня мы будем решать уравнения, приводимые к квадратным, и уравнения 3 и 4 степеней. В их решении большой вклад внесли итальянские математики 16 века.
Сципион Даль Ферро (1465-1526) и его ученик Фиори
Николо Тарталья (1499-1557)
Историческая справка об этих ученых.
Рассмотрим одно из уравнений итальянских математиков:
1.РУ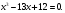 
Решение:
Это уравнение можно решить по формуле Кардано для решения уравнений вида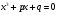 
, что чревато сложными вычислениями.
Можно решить методом разложения на множители левой части уравнения.
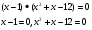
Ответ: 1; -4; 3.
2. РУ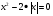 
Решим это уравнение различными способами:
метод разложения на множители.
если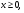 
то 
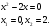
оба значения удовлетворяют условию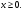 
если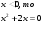 
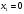- не удовлетворяет условию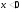 
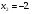
Ответ: 0; -2; 2.
графический способ
Строим график функции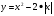 
и ищем абсциссы точек пересечения графика с осью oх.
3) Метод введения новой переменной.
Пусть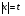 
, тогда
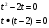
РУ
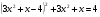
Это уравнение тоже можно решить несколькими способами.
Введем новую переменную
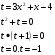
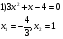
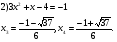
Можно решить методом разложения на множители :
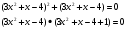
и т.д.
4. Рассмотрим уравнение, предложенное на ЕГЭ в 9 – ом классе:
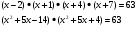
Пусть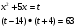
и т. д.
4. Итог урока.
Сегодня мы с вами рассмотрели уравнения, приводимые к квадратным, ознакомились с различными способами их решения. Эта работа будет продолжена на следующих уроках.
Домашнее задание:
РУ
5. 
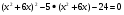
6. 
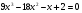
7. 
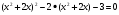
8. 