Муниципальное бюджетное общеобразовательное учреждение
«Средняя общеобразовательная школа № 8»
Рузаевского района Республики Мордовия
Конспект урока по алгебрев 11 классе«Применение производной для решения задач»»
подготовила
учитель математики
Гаврилова Марина Александровна
г. Рузаевка
2013
«Применение производной для решения задач»
Организационный момент
Мы заканчиваем изучение темы «Производная». Сегодня на уроке нам предстоит обобщить, систематизировать и углубить знания о производной.
Мне бы хотелось взять эпиграфом к нашему уроку высказывание Конфуция: Три пути ведут к знанию: путь размышления – это путь самый благородный,
путь подражания – это путь самый легкий и
путь опыта – это путь самый горький.
Таким образом, на уроке мы будем размышлять, подражать и набираться опыта.
Начнем урок с проверки вашего домашнего задания. Внимание на экран!
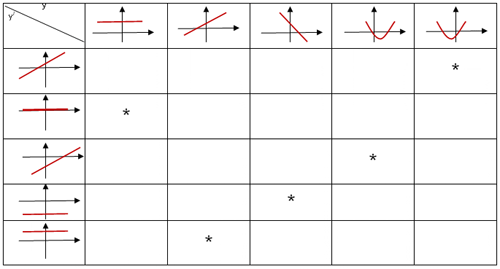
1) Даны графики функции и графики производных. Для каждой из функций, графики которых изображены в верхнем ряду, найдите график ее производной.
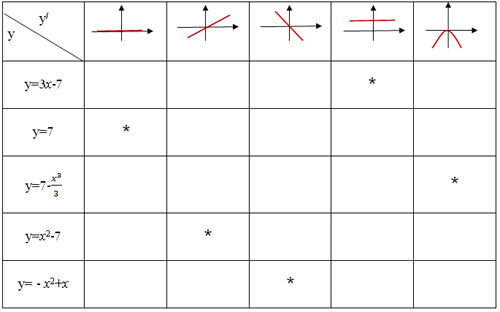
2) Найдите пары “функция – график производной этой функции”.
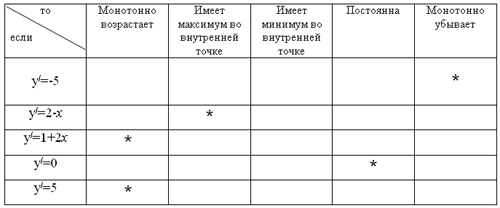
3)Завершите фразы: “Если на отрезке [1; 3] производная ……., то на этом отрезке функция …….
В ходе проверки домашнего задания мы еще раз убедились, что свойства функции и её график связаны с производной.
Сегодня на уроке нам предстоит рассмотреть различные типы заданий В8 и способы их решения. Наша цель – научиться решать задания любой степени сложности, связанные, так или иначе, с исследованием функции по графику её производной. В ЕГЭ задания такого типа повторяются из года в год, причём формулировки вопросов постоянно изменяются.
Тема урока «Применение производной для решения задач». Откройте тетради, запишите число, классная работа.
1 тип задач условно назовем « монотонность функции и производная». Вспомним
Как монотонность функции связана с производной?
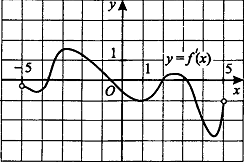
1.На рисунке изображен график производной на отрезке [-5;5 ] Исследуйте функцию y = f(x) на монотонность и в ответе укажите число промежутков убывания функции.
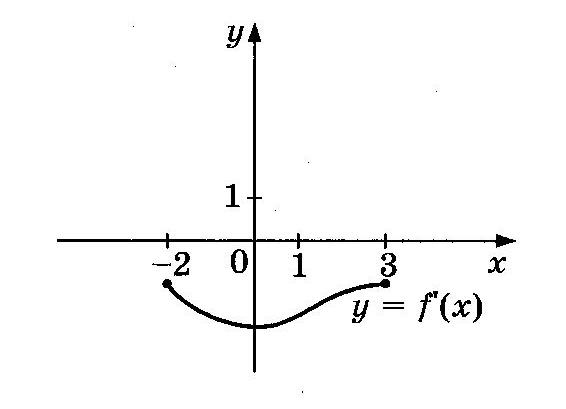
Расскажите алгоритм отыскания наибольшего и наименьшего значений функции y=f(x), непрерывной на отрезке [a;b].
2.Функция у=f(x) определена на отрезке [-2;3]. На рисунке изображен график производной функции у =f `(x). В какой точке отрезка функция принимает наименьшее значение?
Какие точки называются критическими?
Какие точки называются токами экстремума?
Как исследовать функцию на экстремум
3.На рисунке изображен график производной. Исследуйте функцию y = f(x) на монотонность и в ответе укажите число точек эктремума.
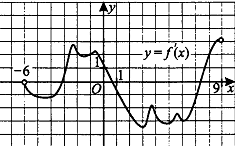
3а) Чему равна точка максимума? 3б) Чуму равнв точка минимума?
4.На рисунке изображён график функции y=f(x) и отмечены девять точек на оси абсцисс: x1,x2,x3,…,x9. В скольких из этих точек производная функции f(x) отрицательна, положительна?
Итак, рассмотрев типовые задачи 1 группы можно сказать, что для их решения нужно помнить о том, как связаны монотонность функции и ее производная.
2 тип задач - на применение геометрического смысла производной
В чем состоит геометрический смысл производной?
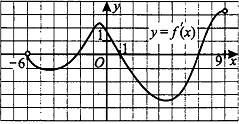
5.На рисунке изображен график производной. Исследуйте функцию y = f(x) на монотонность и в ответе укажите число точек, в которых касательные наклонены под углом 450 к положительному направлению оси Ох.( под углом 135 гр)
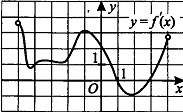
6. На рисунке изображен график производной функции у = f ` (x). Найдите количество точек, в которых касательные к графику функции y =f(x) параллельны прямой у= 2х – 3 или совпадают с ней.
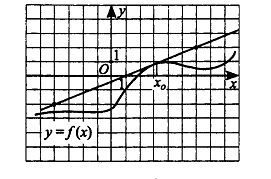
7) На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции y=f(x) в точке х0.
Значение производной функции f(x) в точке х0 равно tga — угловому коэффициенту касательной, проведенной к графику этой функции в данной точке. Чтобы найти угловой коэффициент, выберем две точки А и В, лежащие на касательной, абсциссы и ординаты которых — целые числа. Теперь определим модуль углового коэффициента. Для этого построим ∆ABC. Важно помнить, что тангенс острого угла прямоугольного треугольника — это отношение противолежащего катета к прилежащему.
8)Ещё одна задача – с акцентом на выбор треугольника
9)Третья задача – выбор угла.
Не сможете ли вы предложить другой способ решения данных задач?
Задание можно выполнить двумя способами. Первый – используя равенство f `(x0) = tg α , где α – угол, образованный касательной к графику функции в точке х0 с положительным направлением оси Ох, второй – используя f `(x0) = k, где k – угловой коэффициент касательной.
Подведем итог решения задач второго типа: не смотря на разнообразные формулировки задач, их решение сводится к равенству f `(x0) = tg α = k
3 тип задач – на применение механического смысла производной
Вспомним, в чем заключается физический смысл производной. 7.Точка движется прямолинейно по закону x(t) = 2t3 + t – 3. Найти скорость в момент времени t. В какой момент времени скорость будет равна 7 м/с (х – координата точки в метрах, t – время в секундах). Как вы думаете как её решить? (Обсудить решение и вызвать ученика для оформления).
6. Самостоятельная работа(10 минут) Проверим, то как вы усвоили способы решения рассмотренных задач с помощью тестирования в режиме on line . Займите рабочие места за компьютерами и перейдите по ссылке, которую вы видите на экране. В режиме тренировки попробуйте решить задания В8 из нескольких вариантов, выбранных случайным образом.
8. Подведение итогов. (3 мин)Что вы можете сказать о свойствах функции, читая график ее производной?
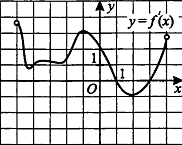
9.Домашнее задание: По рисунку составить и записать 3 задачи с их решениями, аналогичные тем, что были рассмотрены на уроке.
Сегодня мы с вам рассмотрели задания по теме «Производная», наиболее часто встречающиеся в ЕГЭ. Чем больше разнообразных методов решения подобных задач вы будите знать, тем легче вам будет решать нестандартные задания, что, несомненно, придаст вам уверенности в себе и поможет успешно пройти итоговую аттестацию.
Урок окончен!