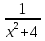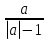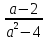«Допустимые значения переменных»
конспект урока по алгебре
в 8 классе
Цели урока:
Образовательные:
1. знать определение допустимых значений переменной в выражении;
2. уметь выполнять числовые подстановки в буквенные выражения и находить их значения;
3. уметь находить область определения целых и дробных выражений.
Развивающие:
Развитие логического мышления,
Расширение кругозора учащихся,
Развитие приемов умственной деятельности, памяти, внимания, умения сопоставлять, анализировать, делать выводы.
Повышение информационной культуры учащихся, интереса к предмету математика
Развитие познавательной активности, формированию навыков самоконтроля, мотивации к учению, потребности к самообразованию.
Воспитательные:
Воспитание чувства ответственности, взаимопонимания, взаимоподдержки, уверенности в себе.
Ход урока.
Организационный момент
Повторение изученного материала (учащиеся выполняют задания на листах, затем фронтальное обсуждение полученных ответов).
Выражение, составленное из __________________________________________________
с помощью действий ___________________________________________________________
называется целым выражением.
Составить и записать:
А) 2 целых выражения__________________________________________________
Б) 2 дробных выражения________________________________________________
3. Даны рациональные выражения:
1) 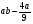 ; 2)
; 2) 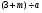 ; 3)
; 3) 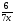 ; 4)
; 4) 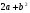
Обведите в кружок целые выражения.
4.Соединить линиями части фраз, соответствующих друг другу
Если в выражении НЕТ деления на выражение с переменной, то это
5.Тоже соедини:
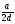
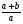
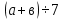
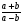
Изучение нового материала.
ДРОБНОЕ ВЫРАЖЕНИЕ
ЦЕЛОЕ ВЫРАЖЕНИЕ
ДРОБНОЕ ВЫРАЖЕНИЕ
ЦЕЛОЕ ВЫРАЖЕНИЕ

 1) Каким действием можно проверить сложение? Приведите примеры.
1) Каким действием можно проверить сложение? Приведите примеры.
2) А как проверить умножение, деление?
3) Сколько будет 8:0? Давайте проверим. Хоть один ответ найдем. Сделаем вывод.
 Есть в математике дроби, которые мы называем алгебраическими (рациональными):
Есть в математике дроби, которые мы называем алгебраическими (рациональными):
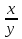 ;
; 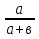 ;
;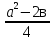 . Числитель и знаменатель алгебраической дроби – многочлены (в частности, одночлены и числа).
. Числитель и знаменатель алгебраической дроби – многочлены (в частности, одночлены и числа).
 Посчитаем:
Посчитаем:
Пример
Найти числовое значение алгебраической дроби
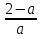 при а=-1.
при а=-1.
Решение:
Если а=-1, то 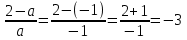 .
.
Ответ: -3
Найдите числовое значение алгебраической дроби:
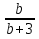 при b=-2.
при b=-2.
Решение:
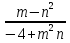 при m=1, n=2
при m=1, n=2
Решение:
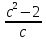 при с=0,2
при с=0,2
Решение:
4)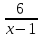 при х=1
при х=1
Решение:
 Алгебраическая дробь не имеет смысла при тех значениях букв, при которых знаменатель дроби обращается в нуль.
Алгебраическая дробь не имеет смысла при тех значениях букв, при которых знаменатель дроби обращается в нуль.
Примеры
При каких значениях переменной имеет смысл выражение:
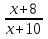
Решение
x+10 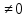
x 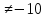
Имеет смысл при всех х, кроме
х=-10.
Решение
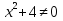 ни при каких x. Имеет смысл при любом значении x.
ни при каких x. Имеет смысл при любом значении x.
Задания
При каких значениях а имеет смысл дробь:
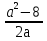
Решение
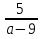 +
+ 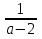
Решение
Решение
Решение
 Все значения переменных, при которых выражение имеет смысл, называется допустимыми значениями переменных.
Все значения переменных, при которых выражение имеет смысл, называется допустимыми значениями переменных.
Закрепление изученного материала
Соедини линиями
Выражения
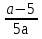
Не имеют смысла при
а=0
а=5
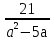 а=-5
а=-5
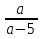 а=5 и а=0
а=5 и а=0
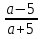 а=5 и а=-5
а=5 и а=-5
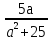
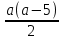
Найти допустимые значения переменных
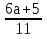 ;
; 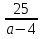 ;
; 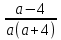 ;
; 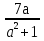
Подведение итогов урока
«Микрофон». Продолжите фразу «Сегодня я узнал (а)»
Поставьте себе оценку за урок.