Конспект урока по алгебре в 8 классе «Решение квадратных уравнений»

Конспект урока по алгебре в 8 классе

Тема урока: «Решение квадратных уравнений»

Тип урока: урок обобщения и систематизации знаний.

Цель урока:

Образовательные цели урока:

1. систематизировать и обобщить знания по теме «Решение квадратных уравнений»,

2. продолжить формирование умений решать квадратные уравнения;

3. расширить представления учащихся о методах решения квадратных уравнений,

Развивающие цели урока:

1. продолжить развитие математического мышления, памяти, внимания; устной и письменной математической речи учащихся; умений анализировать, сравнивать, обобщать;

2. развитие любознательности и познавательного интереса к предмету.

Воспитательные цели урока:

1. воспитывать культуру умственного труда и информационную культуру;

2. потребность добиваться успехов в приобретении знаний;

Оборудование и материалы:

1. Мультимедийный проектор.

2. Презентация по теме “Квадратные уравнения”

3. Дидактическое пособие

Структура урока:

1. Организационный момент.

2. Мотивация учебной деятельности учащихся и постановка целей урока;

3. Актуализация опорных знаний

4. Решение задач (обобщение и систематизация понятий, усвоение системы знаний и их применение для объяснения новых фактов и выполнения практических заданий);

5. Итог урока;

6. Постановка домашнего задания;

7. Рефлексия.

Ход урока

1. Организационный момент.

Проверить готовность к уроку.

Здравствуйте ребята, садитесь.

1. Мотивация учебной деятельности учащихся и постановка целей урока

Я хочу начать наш урок с задачи. (Читаю условие задачи, делаю акцент на словах)

Высоту над землей подброшенного вверх мяча можно вычислять по формуле

h(t) = 2 + 12t - 5t² , где h - высота в метрах, t - время в секундах, прошедшее с момента броска. сколько секунд мяч будет находиться на высоте более 6 метров?

- Как вы думаете это задача описывает реальную ситуацию? (да)

- Задача из повседневной жизни?

- Давайте посмотрим внимательно, реальную ситуацию описывает формула.

На что она похожа из алгебры? (на квадратное уравнение).

- Это значит, что данную задачу как и многие другие можно решить средствами математики, в данном случае, чтобы решить задачу нужно решить квадратное уравнение.

Итак, тема нашего урока: «Решение квадратных уравнений»

- Открываем тетради, записываем число, классная работа, тему урока: «Решение квадратных уравнений» (Я записываю тему вместе с детьми на доске)

- Тема «Квадратные уравнения» нам знакома?

(да, мы уже решали квадратные уравнения)

- как вы думаете, зачем нам с вами этот урок?

(для того чтобы вспомнить о квадратных уравнениях и методах решения квадратных уравнений)

Совершенно верно, сегодня на уроке мы обобщим все полученные ранее знания по теме «Квадратные уравнения», а еще познакомимся с двумя новыми методами решения квадратных уравнений.

- С темой урока определились, а какие цели мы перед собой поставим?

Что мы должны знать и уметь делать?

(- знать: как выглядит квадратное уравнение, какими методами его можно решить;

- уметь: решать квадратное уравнение различными методами)

Молодцы!

1. Актуализация опорных знаний.

А теперь давайте вспомним какие уравнения относятся к квадратным

- Вашему вниманию представлены различные уравнения, назовите те из них которые являются квадратными.

1. 4х² + 7х + 3 = 0 (Ответ: х1=-3/4, х2=-1) (по формулам корней)

2. x⁴-17x²+16=0

3. x(4x+7) = -3

4. 2x² + 16x + 14 = 0 (Ответ:x1 = - 7 и x2 = - 1) (по формуле Виета, по формулам корней, графическим методом)

5. x²+4x-5=0 (Ответ:х1=1, х2=-5) ( по сумме коэф)

6. 2х² – 11х + 15 = 0 (ответ: у1 = 5 х1 = 5/2 x1 = 2,5,у2 = 6 x2 = 6/2 x2 = 3) (метод переброски).

7. 157х²+20х-177=0 (по формуле a+b+c=0)

8. 203х²+220х+17=0 (по формуле a+c=b)

9. 2х²-9х-5=0 (Ответ: y1=10,y2=-1, x1=5,x2=-0,5) (метод переброски).

10. 3(2-3x)-4=5-11x

Прежде чем вспомнить все известные нам способы решения квадратных уравнений посмотрите, у вас на столах лежат памятки с основными методами решения квадратных уравнений.

- назовите все известные вам способы решения квадратных уравнений

1. по формулам корней мы решаем

2. по формулам Виета подбираем корни

3. графический метод

4. свойства четного второго коэффициента

4. Решение задач

Перейдем к решению квадратных уравнений. Решая квадратные уравнения мы знаем что одно и тоже уравнение можно решить различными методами. Графические метод трудоемкий, поэтому решим его с помощью программы построения графиков, тем самым проверим корни уравнения.

Записанные уравнения, решают два человека у доски и один человек на компьютере.

Молодцы, правильно решили, корни совпали.

Итак, вы решали уравнения и каждый из вас использовал разный метод, это самые распространенные методы, но не единственные, есть еще несколько. С этими методами познакомились самостоятельно Евгения Бондаренко и Анастасия Дехтяренко и они хотят с вами поделиться этими методами.

Евгения Бондаренко расскажет вам о способе «переброске» старшего коэффициента.

Примеры:

А) 2x²-9x-5=0

Б) 2x²+8x-10=0

Спасибо Женя, теперь сами пробуем решить уравнения этим способом. Решать будем по группам, а ассистенты вам будут помогать.

Анастасия Дехтяренко расскажет нам о приемах устного решения квадратных уравнений.

ax² + bx + c = 0.

1.Если a + b + c = 0, x₁ = 1, x₂ = с/а

2.Если a - b + c = 0, а+с=b

x₁= - 1, x₂ = -с/а

Примеры:

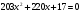
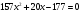А)

Б)

Спасибо Настя, теперь сами пробуем решить уравнения этим способом. Решать будем по группам, а ассистенты вам будут помогать.

Молодцы, отлично справились с заданием.

Спасибо девочкам за работу.

5.Итог урока.

А теперь вернемся к нашей задаче, и решим квадратное уравнение любым из методов.

Высоту над землей подброшенного вверх мяча можно вычислять по формуле h(t) = 2 + 12t - 5t² , где h - высота в метрах, t - время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте более 6 метров?

Решение квадратного уравнения. Анализируя условие, вы заметили, что для ответа на вопрос необходимо найти промежуток времени, когда камень находился на высоте не менее 6 м, то есть те значения t, при которых h(t) ≥ 6.

Решая полученное уравнение

2 + 12t - 5t² = 6

-5t² + 12t -4 =0

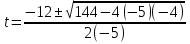
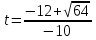
t₁= 0,4c

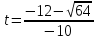
t₂ = 2c

t₁ - t₂= 2c-0,4c = 1,6 c

получаем t ∈ [0,4; 2].

Длина полученного промежутка равна t₁ - t₂= 2c-0,4c = 1,6 секунд.

Ответ: 1,6 с.

В начале урока мы ставили перед собой цели:

- вспомнить о квадратных уравнениях,

-повторить основные методы решения квадратных уравнений,

-познакомиться с новыми методами решения.

Все цели были достигнуты? (Да)

Молодцы ребята, вы сегодня отлично поработали, у нас осталось несколько минут до звонка, предлагаю вам написать синквейн по теме нашего урока сегодня и выразить свое отношение к уроку.

Домашнее задание у вас есть на раздаточном материале. Ваша задача будет дома решить эти уравнения удобным для вас методом.

Спасибо за урок, до свидания!

5