КОНСПЕКТ УРОКА ПО АЛГЕБРЕ
В 8 КЛАССЕ
ТЕМА УРОКА: «РЕШЕНИЕ НЕРАВЕНСТВ С ОДНОЙ ПЕРЕМЕННОЙ»
Современные образовательные технологии, применяемые на уроке:
Технология групповой деятельности.
Технология уровневой дифференциации на основе обязательных результатов.
Технология проблемного обучения.
Основная цель: Сформировать умение решать линейные
неравенства с одной переменной.
Применяемые методы: Устная работа учащихся
Поисковая работа в группах. Творческая работа.
Самостоятельная работа с самопроверкой.
Средства обучения: учебное пособие «Алгебра 8 класс», авторы Ю.Н.Макарычев и др. М. «Просвещение», 2008, карточки для работы в группах.
I этап работы. Устная работа со всем классом.
В таблице приведены неравенства, их геометрические интерпретации и записи соответствующих числовых промежутков, но все перепутано. Восстановить истинную картину.
Неравенство
Графическая иллюстрация
Решение
х<5
х5
5<х
4. 5х
1.
2.
3.
4.
[5;+)
(5; +]
(-;5]
4. (-;5)
Какие из указанных чисел 2; 5; 11; 7 являются решениями неравенства
2х-15>0 ?
Решить неравенства:
а) 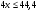 ; в)
; в)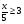 ; д)
; д)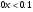 ;
;
б) 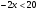 ; г)
; г)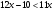 ; е)
; е)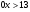 .
.
Комментарии к устной работе.
При выполнении первого задания использую карточки с номерами от 1 до 4.
Даю указания ученикам: можно использовать 2 способа: подстановку и отыскание промежутка.
Ответы:
а) х(-;11,1]; д) на коэффициент при х нельзя делить, поэтому решать
б) х(-10;+ ); с помощью здравого смысла: подставить различные
в) х[15;+ ); значения х и сделать вывод: х – любое число.
г) х(-;10); Ответ: нет решения
е) рассуждения аналогичные.
II этап работы. Поисковая работа в группах.
Класс делю на группы: по 4 человека в группе. Предлагаю задание: Решить неравенство:
1-я и 2-я группы: 1) 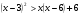 ;
;
3-я и 4-я группы: 2) 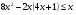 ;
;
5-я и 6-я группы: 3)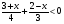 .
.
После решения заданий, один из группы выходит к доске защищать свое решение. Решающие такое же задание в другой группе, могут что-то дополнить, пояснить. Остальные записывают решение в тетрадь.
Решения:
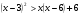 ; 2)
; 2) 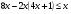 ;
;
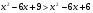 ;
; 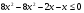 ;
;
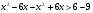 ;
; 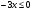 ;
;
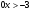
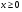
Ответ: (-; +).
Ответ: [0; +).
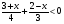 ;
;
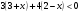 ;
;
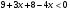 ;
;
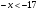 ;
;
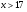
Ответ: (17; +).
III этап работы.
''Слабых'' и ''средних'' способностей учащиеся выполняют
самостоятельную работу по вариантам (учебник 1 вариант №№ 841 (д), 844 (а), 849 (а); 2 вариант №№ 841 (е), 844 (в), 849 (б)..
''Сильные'' ученики – решение задач творческого характера..
На языке неравенств не редко формулируется постановка задачи во многих приложениях математики. Например, многие экономические задачи сводятся к исследованию систем линейных неравенств с большим числом переменных.
Задача 1. В типографию поступил для печати новый учебник алгебры 8 класса. Но, к сожалению, в компьютере произошел сбой, и одно из заданий стало выглядеть следующим образом: ''С помощью калькулятора найти значение выражения 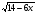 при следующих значениях переменных: 5; -2; -8,3; 10,63; -0,5; 3;
при следующих значениях переменных: 5; -2; -8,3; 10,63; -0,5; 3; 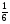 ''. Типографские корректоры заметили, что уже при х=5 в приведенном выражении получаются странные вещи. Что происходит с выражением при х=5? Как узнать, нет ли еще лишних чисел в данном упражнении?
''. Типографские корректоры заметили, что уже при х=5 в приведенном выражении получаются странные вещи. Что происходит с выражением при х=5? Как узнать, нет ли еще лишних чисел в данном упражнении?
Решение.
Вспомнить свойство арифметического квадратного корня: 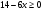
Ответ: (-; 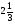 ]. Значит, лишнее следующие числа: 5; 8,3; 10,63; 3.
]. Значит, лишнее следующие числа: 5; 8,3; 10,63; 3.
Задача 2. В уравнении 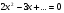 во время перемены кто-то стер одно число. Учитель стал восстанавливать уравнение и поставил на свободное место букву m. Уравнение стало выглядеть так:
во время перемены кто-то стер одно число. Учитель стал восстанавливать уравнение и поставил на свободное место букву m. Уравнение стало выглядеть так: 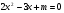
Найти m , если m – натуральное и уравнение имеет 2 различных корня.
Решение.
D 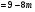 > 0. т.е. 9-8m > 0
> 0. т.е. 9-8m > 0
-8m > -9
m<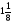
Ответ: единственно возможное решение m = 1. Значит, перед уроком было записано уравнение 
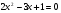 .
.
Задача 3. Решить уравнение 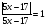
Решение.
Что значит равенство дроби единице?
Это значит, что числитель равен знаменателю, т.е.
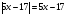 , т.е.
, т.е. 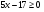
Выражение не может принимать значение 0, т.к. стоит в знаменателе дроби, т.е. 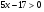 .
.
Ответ: (3,4; +)
IV этап работы. Сдача тетрадей с самостоятельной работой. Подведение итогов урока. Выставление оценок. Комментирование домашнего задания.
На дом предлагается разноуровневое задание по свободному выбору учащихся. На следующий день домашнее задание оценивается следующим образом: I уровень – ''3'', II уровень – ''4'', III уровень – ''5''.
Домашнее задание.
I уровень: №№ 842, 845 (а,в).
II уровень: Выполнить задания 1 уровня сложности + задание поискового плана: подобрать из учебной литературы задачу, решаемую с помощью линейного неравенства и решить ее.
III уровень: Выполнить задания 1 уровня + создание собственной задачи, решение которой основано на применении решения линейного неравенства и решить ее.