КОНСПЕКТ УРОКА ПО АЛГЕБРЕ В 8 КЛАССЕ
ПО ТЕМЕ «СВОЙСТВА АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ».
Современные образовательные технологии, применяемые на уроке:
Технология групповой деятельности.
Технология проблемного обучения.
Цель урока. Изучить свойства арифметического квадратного корня из произведения и дроби. Сформировать умение применять их для вычисления значений квадратных корней.
Тип урока: усвоение нового материала.
Методы обучения: исследовательская деятельность учащихся, работа в группах, взаимопроверка результатов работы.
Средства обучения: учебное пособие «Алгебра 8 класс», авторы Ю.Н.Макарычев и др. М. «Просвещение», 2008, карточки для работы в группах.
План урока.
Проверка домашнего задания. Подготовка к восприятию нового материала – 5 минут.
Исследовательская деятельность учащихся. Работа в парах.
а) Пробы – разбор частных случаев. Выводы – 5 минут
б) Выдвижение гипотезы – 3 минуты.
в) Проверка гипотезы. Вывод – 7 минут.
Решение упражнений – проверка актуальности гипотезы – 10 минут.
Самостоятельная работа – 5 минут.
Проверка ответов в соответствии с приведенными учителем решениями через компьютер – 3 минуты.
Домашнее заданий с комментированием – 2 минуты.
Проверка домашнего задания. Подготовка к восприятию нового материала.
Из данных равенств выберите верные.
0,64 = 0,8; 81 = -9; 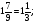 0,016 = 0,04; -121 = -11; -49 = -7.
0,016 = 0,04; -121 = -11; -49 = -7.
2) Имеет ли смысл выражение: - 0,25; -0,36; (-3,1)2; (-4,8); (-1)3; (-1)4.
3) При каких значениях переменных имеет смысл выражение:
3а; -5х; 8с; -10b; 2-х; х 2 ; х3 ; (4-х); -х2 ; -х3 .
Исследовательская деятельность учащихся. Работа в группах.
1 группа
1) Сравнить значения выражений: 16 4 и 16 4 ;
25 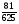 и
и 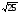
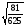 ;
;  и
и 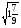
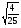 .
.
Сделать выводы.
Выдвинуть гипотезу о том, что
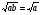
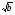 , где а0, b0 (1)
, где а0, b0 (1)Проверить гипотезу, ответив на следующие вопросы:
Согласно определению арифметического квадратного корня, доказать, что выполняются следующие условия:
а) правая часть равенства (1) – неотрицательное число;
б) квадрат правой части равенства (1) равен подкоренному выражению.
4) Сделать выводы, сформулировать свойство квадратного корня из произведения.
2 группа
1) Сравнить значения выражений: 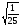 и
и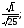
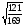 и
и 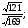
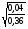 и
и 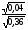
Сделать выводы.
2)Выдвинуть гипотезу о том, что 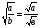 , где а0, b0 (2)
, где а0, b0 (2)
Проверить гипотезу, ответив на следующие вопросы:
Согласно определению арифметического квадратного корня, доказать, что выполняются следующие условия:
а) Правая часть равенства (2) – неотрицательное число;
б) квадрат правой части равенства (1) равен подкоренному выражению.
Сделать выводы, сформулировать свойство квадратного корня из дроби.
Решение упражнений – проверка актуальности гипотезы.
№ 369 (а, д), 370 (г, д), 374 (а, в, д, ж), 376 (а, д), 386 (а, ж) – в тетрадях и у доски с подробным объяснением.
Обучающая самостоятельная работа с последующей проверкой у доски.
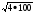 5)
5) 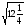
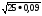 6)
6) 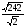
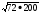 7)
7) 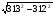
4) 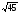
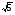
5. Домашнее задание: п. 16, № 371, 375, 377 (а,в,д), 386 (б,г,д), 3 карточки с творческими заданиями.
Карточки для работы в группах.
Карточка № 1.
Сравнить значения выражений: 16 4 и 16 4 ;
25 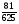 и
и 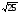
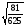 ;
;  и
и 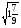
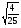 .
.
Сделать выводы.
Карточка № 2.
Сравнить значения выражений: 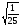 и
и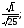
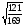 и
и 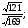
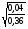 и
и