Конспект урока по Алгебре «Вычисление производных функций» 10 класс

План урока по математике (алгебре) в 10 «А» классе 12.12.2007г.

ТЕМА: Вычисление производных функций.

ЦЕЛЬ УРОКА: 1) Закрепить изученный материал по нахождению производных в ходе выполнения упражнений; проверить знания учащихся по данной теме.

2) Содействовать развитию математического мышления;

3) Воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели. Побуждать учеников к самоконтролю своей деятельности.

ОБОРУДОВАНИЕ: Мультимедиапроектор, ПЭВМ (мобильный), программа-презентация «Открытый урок», выполненная в среде Power Point.

Ход урока

I. Организационный момент.

Сообщить тему урока и сформулировать цели на данный урок.

II. Актуализация знаний.

а) Устные тематические вопросы.

? Что такое приращение аргумента, функции?

? Что такое производная?

? Каков механический смысл производной?

? Каков геометрический смысл производной?

б) Письменно.

По чертежу найти угловой коэффициент секущей.

Решение.

График функции 1 (прямая) пересекает график функции 2 в двух точках с координатами (1;1) и (3;9).

Поэтому ∆х=х₂-х₁=3-1=2 ∆у=у₂-у₁=9-1=8

К= ∆у/∆х= 8/2=4 Ответ: 4

в) Повторить схему нахождение производной по определению и найти по определению производную функции:

у=5х+1

Решение.

f (х +∆х)=5(х + ∆х) + 1= 5х+5∆х+1

∆ у= f(х +∆ х)-f(х) = 5х+5∆х+1-5х-1=5∆х

∆у/∆х= 5∆х/∆х=5

Ответ: f’(х)=5

г) Повторить производные табличные и правила дифференцирования;

(используется таблица мультимедиа: производные функций)

III. Решение задач.

1. Вычислить устно производные следующих функций:

а) у = 2х+1 Ответ: 2

б) у = 5х-6 Ответ: 5

в) у = х²+2х-1 Ответ:2х+2

г) у = 3х²-4х Ответ: 6х-4

д) у = 5х³ Ответ:15х²

е) у = 6х⁷+х⁴ Ответ:42х⁶+4х³

ж) у = 10х⁵ Ответ:50х⁴

2) Найти производную функции в точке (самостоятельно):

у=2х³+8х в точке х=2.

Решение:

Найдём у`=(2х<sup>3</sup> +8х)`= 6х² +8

y`(2) = 6 *2² +8= 4*6+8= 32

Ответ: у`(2) =32.

Результат проверить, выдав решение на «мультимедиапроекторе».

3)Пауза! ФМ! Провести ФМ для снятия напряжения с глаз:

«Быстро поморгать. Закрыть глаза и посидеть спокойно, медленно считая до 5. Повторить 4-5 раз»

4) Техника вычисления производных:

У доски выполнить вычисления следующих производных функций:

а) у = 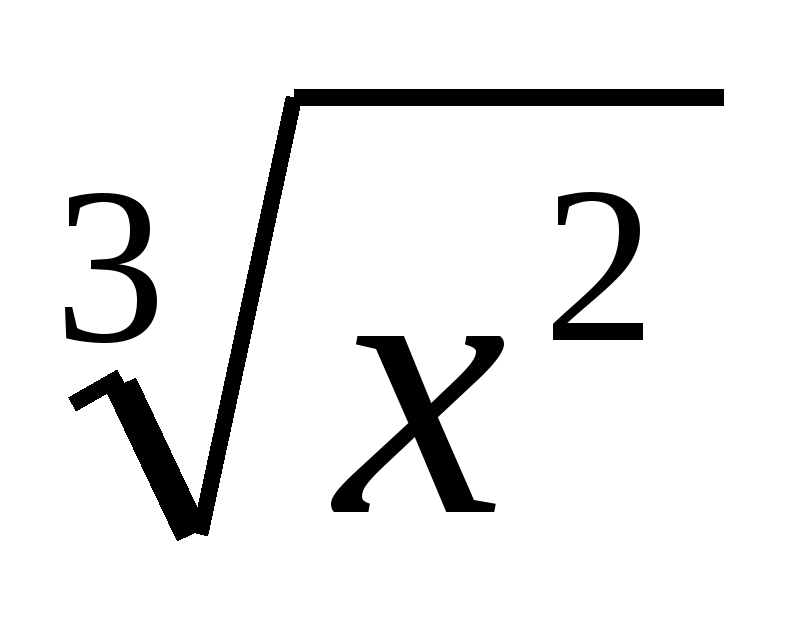Решение

(у)’ = ()’ =()’ =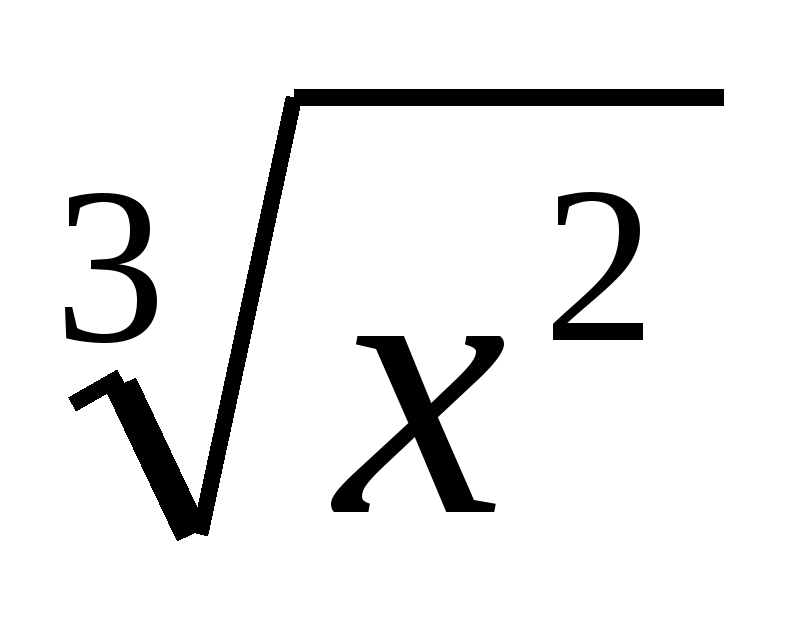

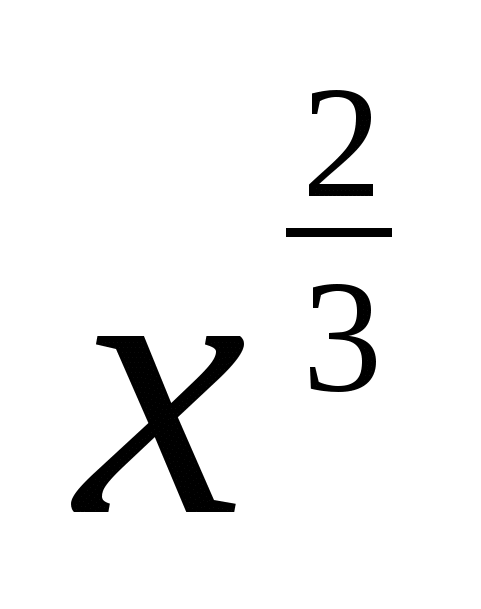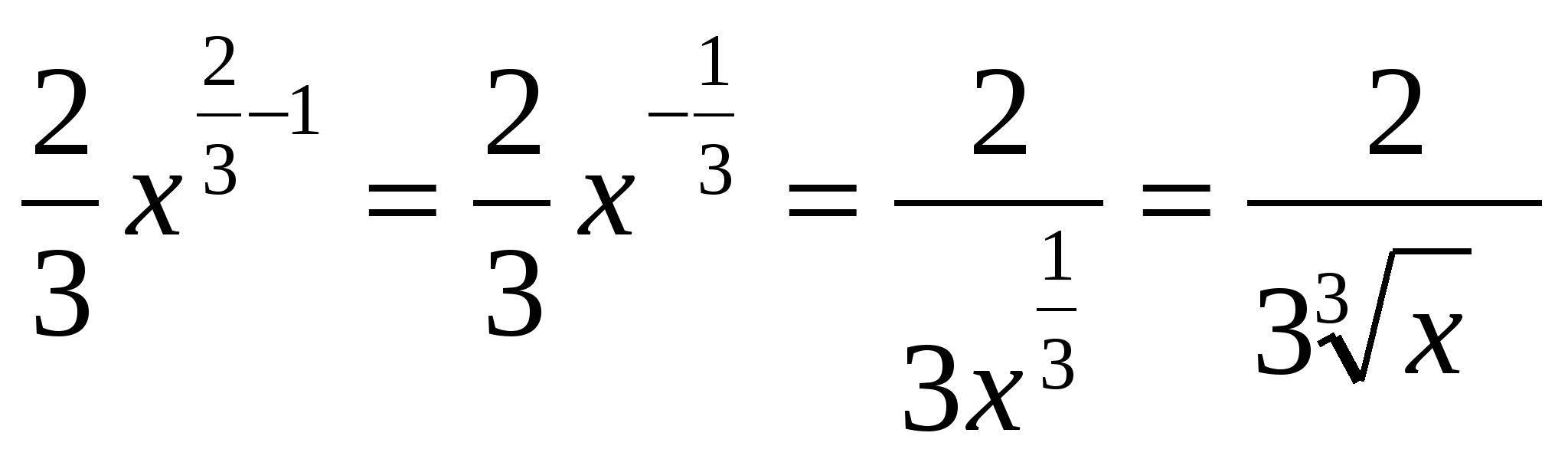
б) у= (х² +2х-5)*( 2х-3)

у`= (х²+ 2х-5)’*(2х-3)+(х²+2х-5)*(2х-3)’=(2х+2)*(2х-3)+2(х²+2х-5)=4х²-6х+

+4х-6+2х²+4х-10=6х²+2х-16

Ответ: 6х²+2х-16.

При быстром темпе работы можно вычислить производную этой функции двумя способами.

в) у= 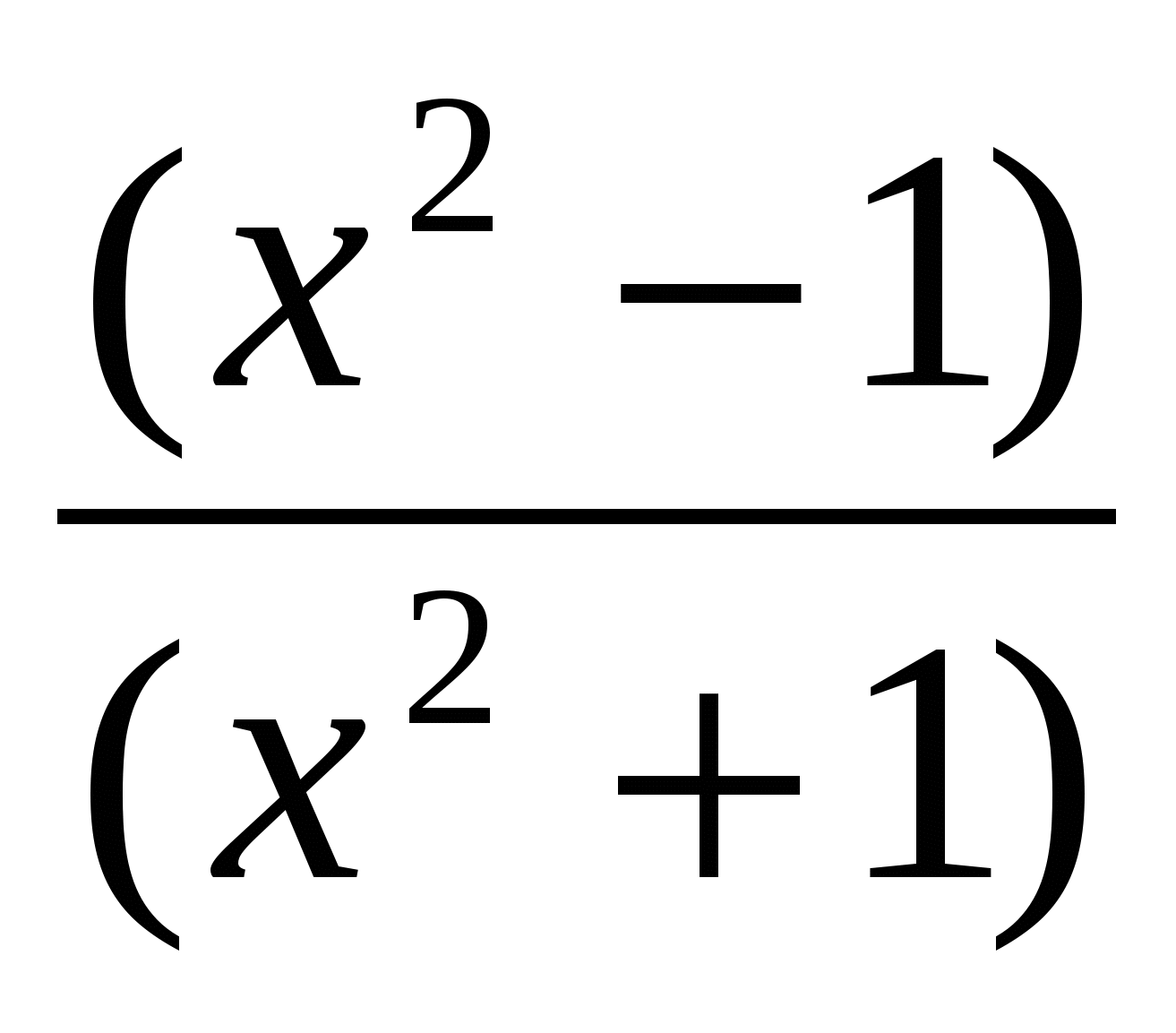Решение

у' = ()’=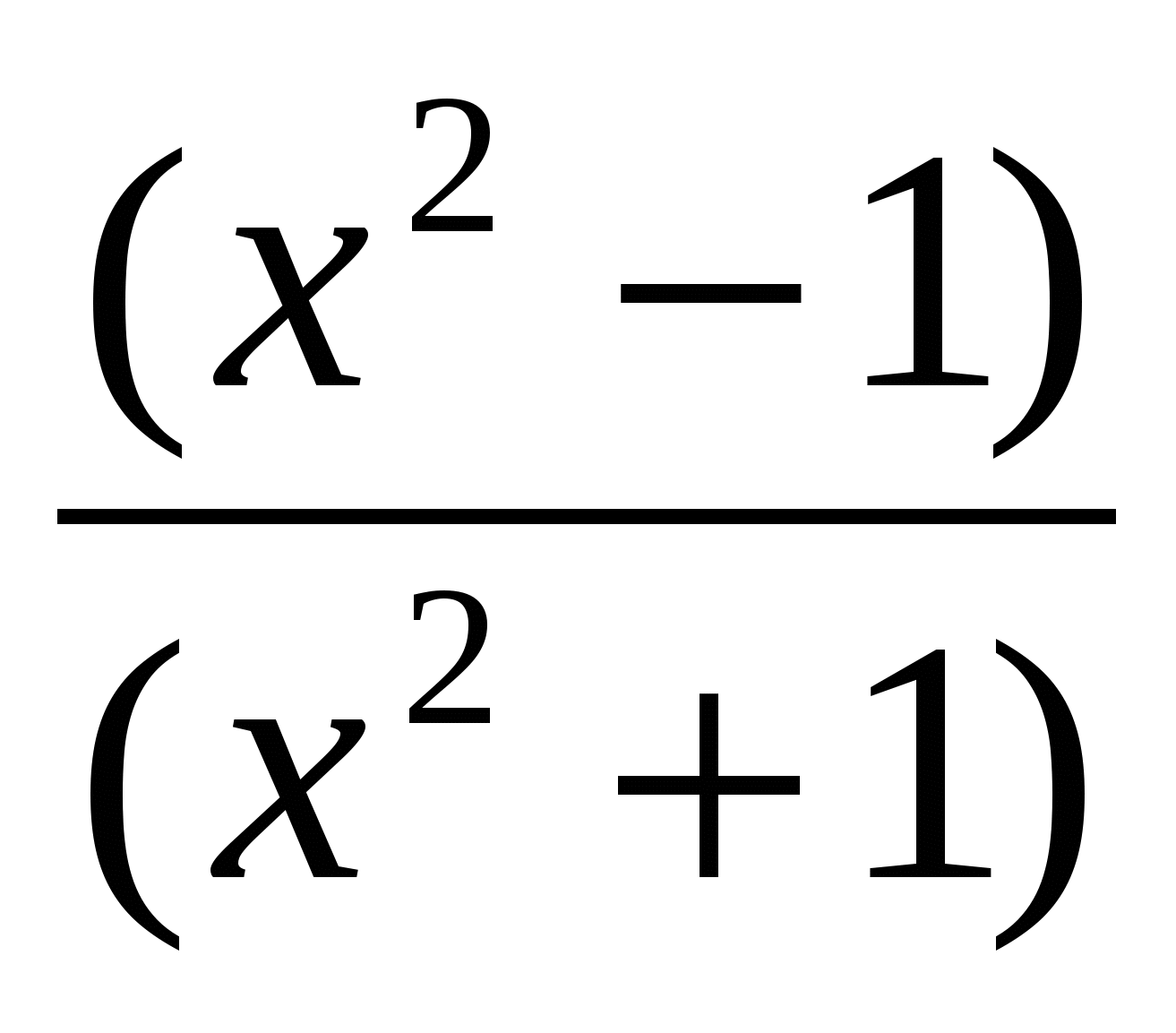

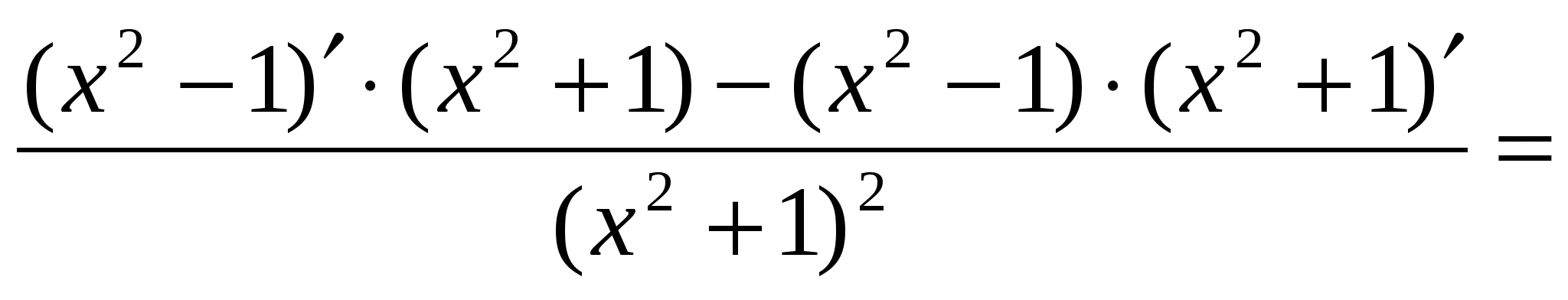
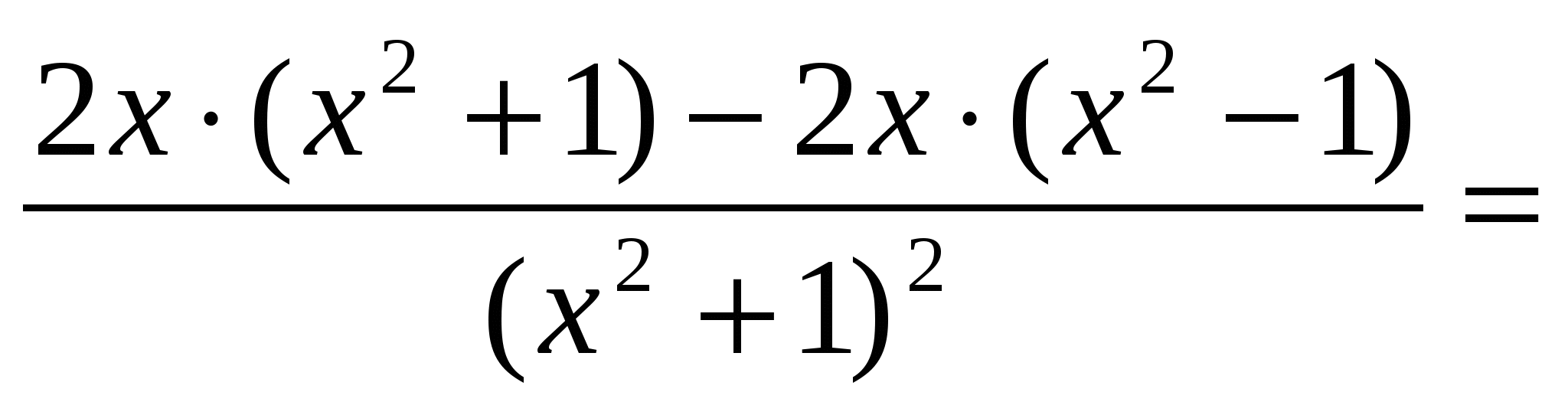
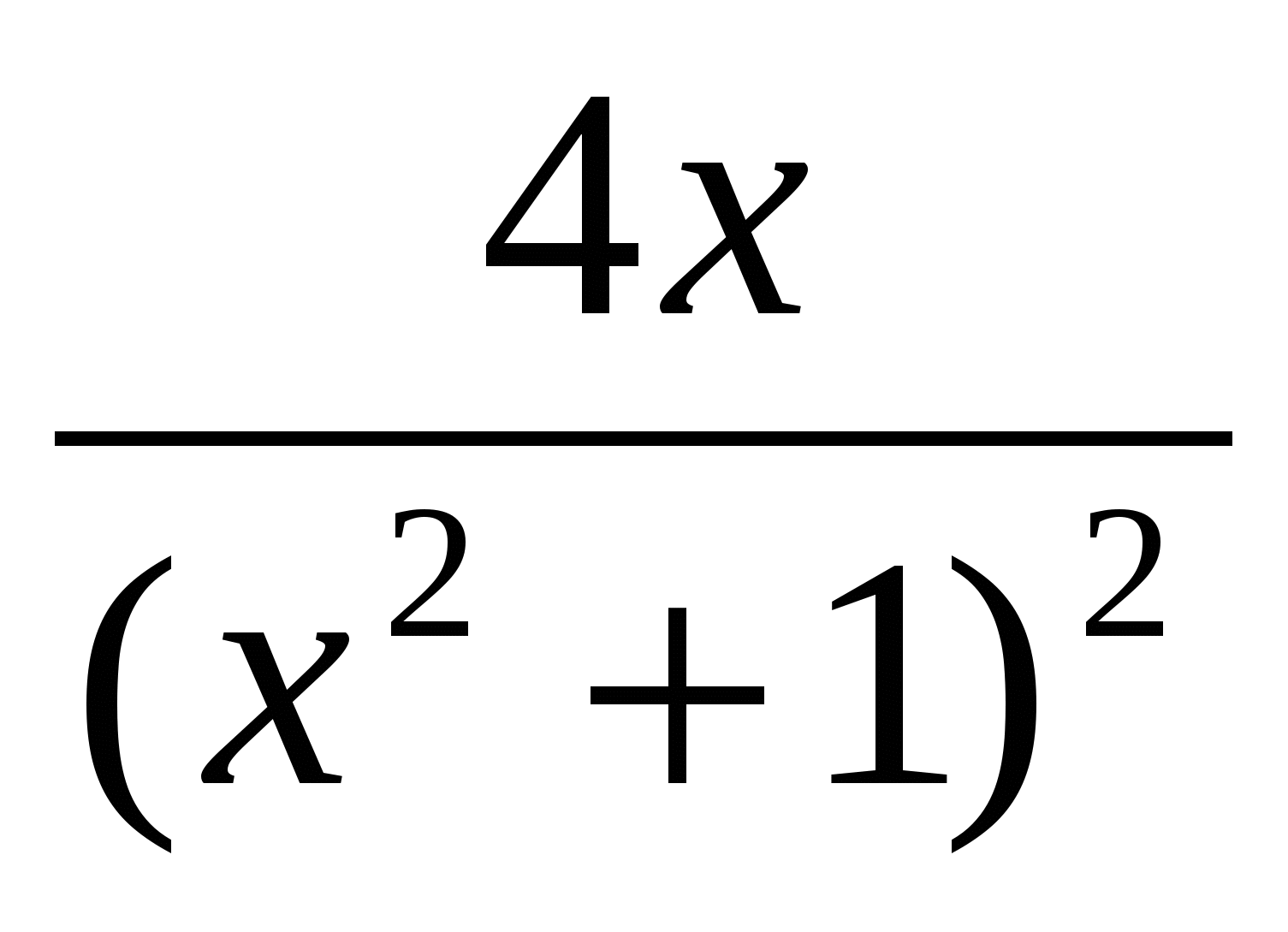
Ответ: у’ =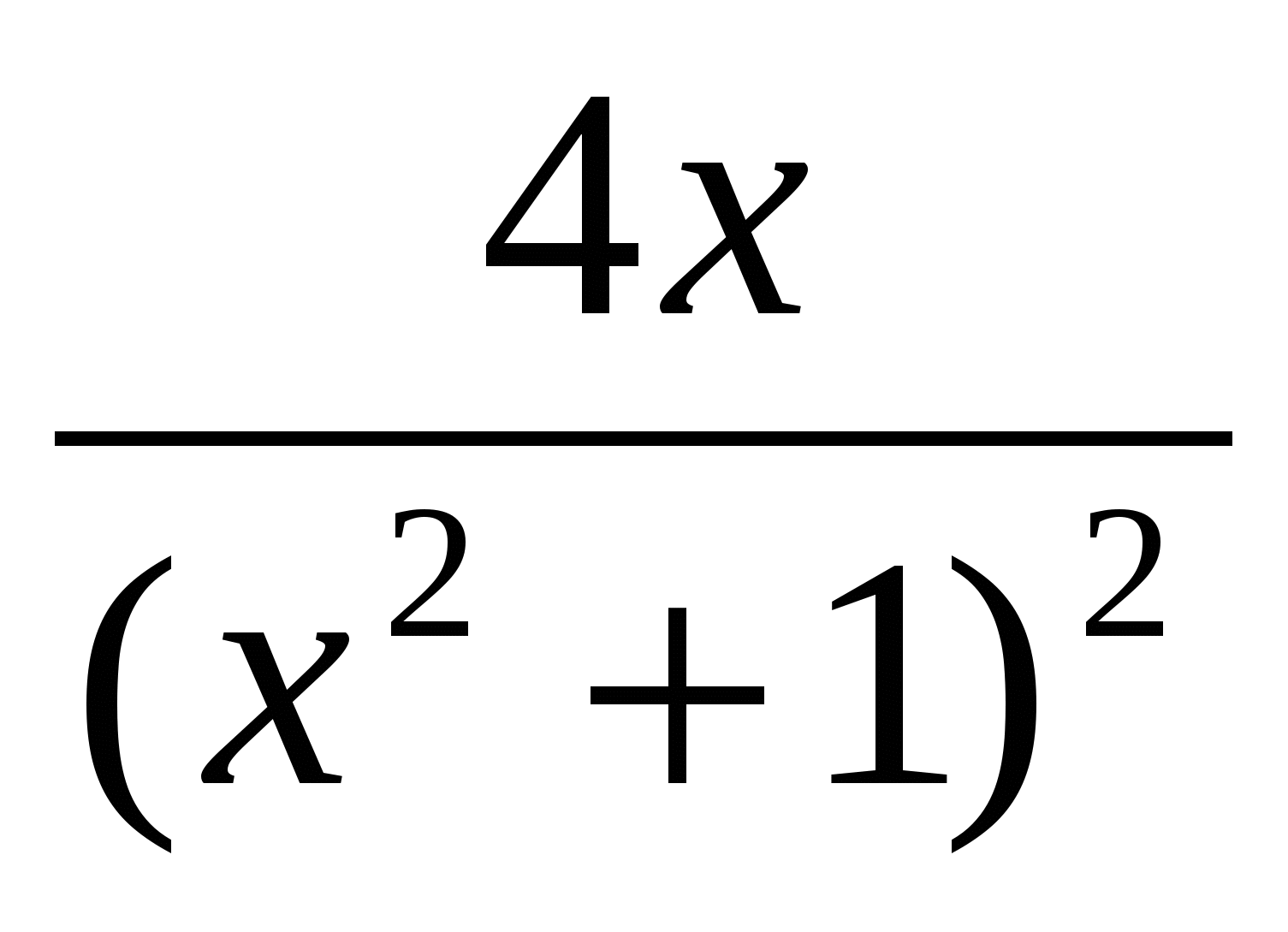

5)Краткая историческая справка.

Дифференциальное исчисление создано Ньютоном и Лейбницем в конце 17 столетия. Понятие производной встречалось в работах итальянского математика Тартальи, здесь появилась касательная в ходе изучения вопроса об угле наклона, при котором обеспечивается наибольшая дальность полёта снаряда.

В 17 веке на основе учения Г.Галилея о движении активно развивалась кинематическая концепция производной. Различные изложения встали встречаться в работах у Декарта, Роберваля, Грегори, а также в работах Ньютона.

Историческая справка сопровождается показом портретов учёных и лёгкой релаксирующей музыкой.

6) Самостоятельная работа.

Задание: найти производные функций.

у = 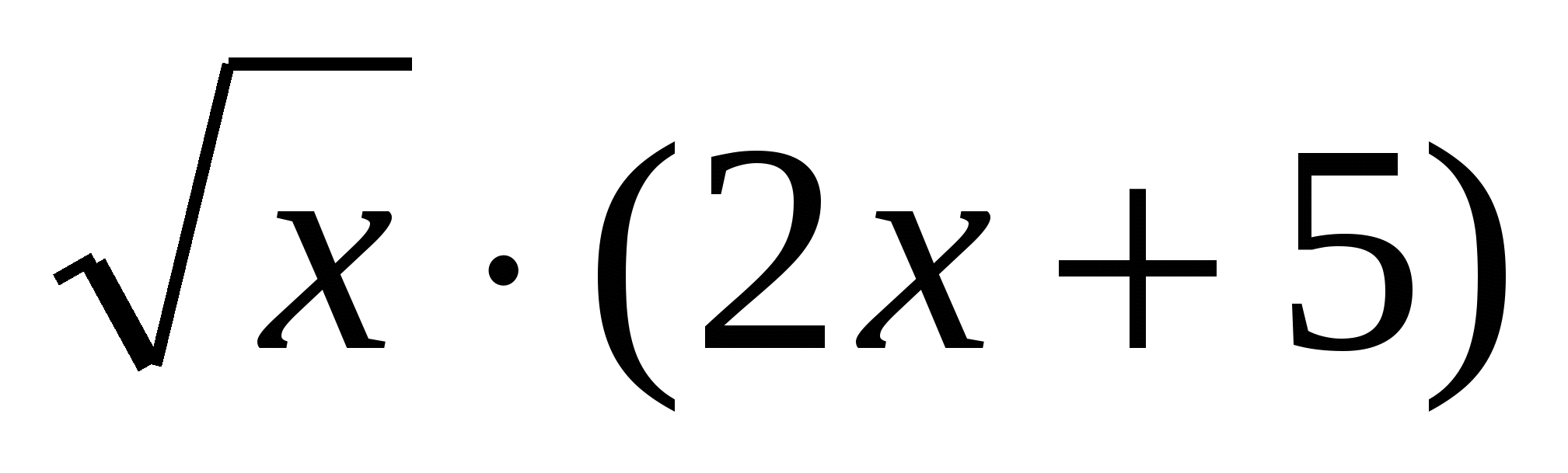у = х(х – 1) (0)

у = (2х-3)/(х+2) у = х/(х +1) (0)

у = (2х² + 4х)(3х - 1)

Производные функций с пометкой (0) дать учащимся для самостоятельной работы, которые являются отстающими в обучении

IV. Подведение итогов урока.

Отметить, в какой мере достигнуты цели урока, оценить работу учащихся на уроке.

V. Домашнее задание.

В учебнике: стр. 134 упр. №22 (35;36;50;56)

Записать в тетради: найти производные функций:

У = (4х² – 6)(2х – 3)

У = (х + 1)/ 2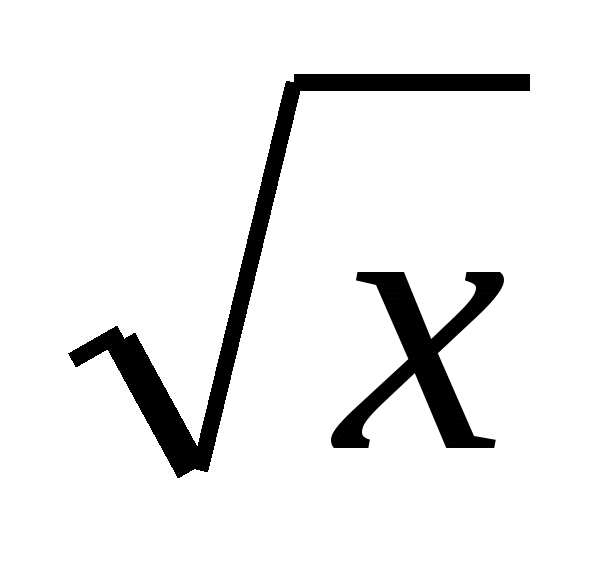

У = 5х² +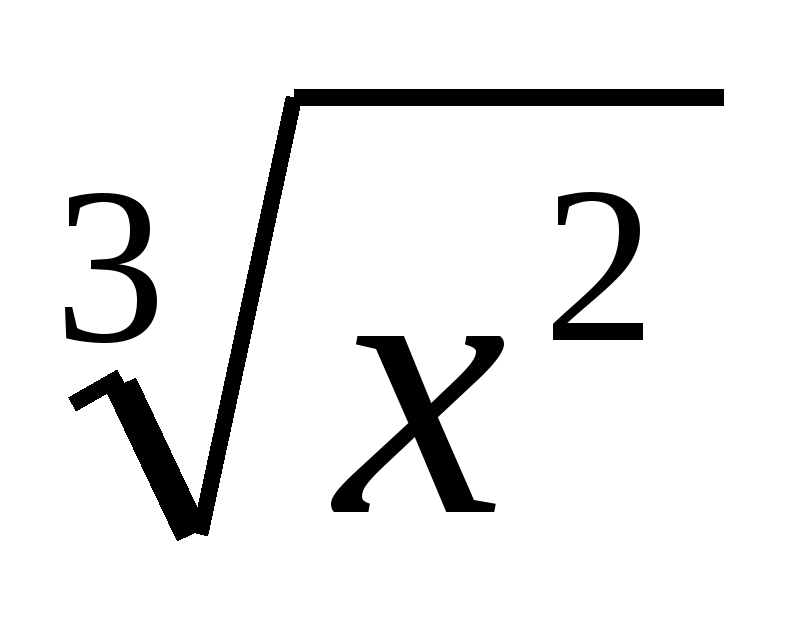

P.S. 1) Программа-презентация урока прилагается на электронном носителе.

2) Следующей рассматриваемой темой курса является: «Производная сложной функции»