Конспект урока по Алгебре «Взаимно обратные числа»

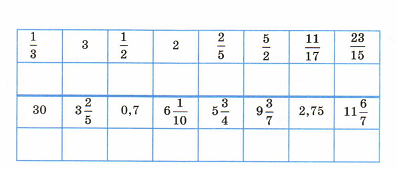
Урок 59. Взаимно обратные числа

Цели: отрабатывать навык нахождения чисел, обратных данным, умения решать уравнения нового типа; формировать навык умножения дробей; повторить порядок действий; воспитывать уважительное отношение к труду товарищей.

Ход урока

1. Организационный момент

2. Проверка домашнего задания

№ 591 (б)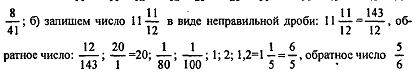

№ 592 (а,в)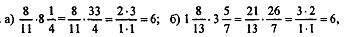

№ 593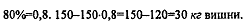

1. Устный счет

1. Сообщение темы урока

• Сегодня мы продолжим работать со взаимно обратными числами.

1. Изучение нового материала

1. Подготовительная работа.

• Приведите примеры взаимно обратных чисел. (Записать на доске и воспользоваться при составлении следующих заданий.)

• Работа над новой темой.

• Найдите значение выражений:

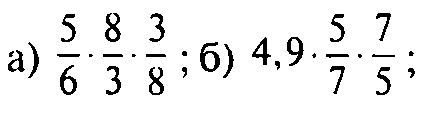
• Какой вывод можно сделать? (Если число х сначала умножить на некоторое число а, а потом умножить на число, обратное а, то получится опять число х.)

1. Закрепление изученного материала

1. № 577 (г—е) стр. 94 (на обратной стороне доски и в тетрадях, самопроверка).

• Как доказать, что данные числа являются взаимно обратными? (Выполнить умножение, если произведение этих чисел равно 1, то числа являются взаимно обратными.)

(Ответ: г) да; д) нет; е) нет.)

1. № 579 стр. 95 (у доски и в тетрадях).

• На чем основано решение таких выражений?

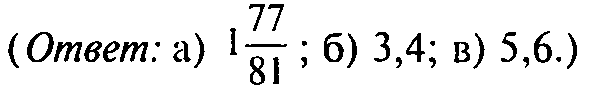
1. Решите уравнения (самостоятельно, взаимопроверка).

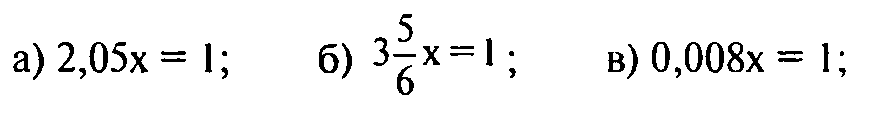
1. Физкультминутка

2. Работа над задачей

№ 588 стр. 96 (на обратной стороне доски и в тетрадях, самопроверка).

• Прочитайте задачу. Что известно? Что надо узнать?

• Запишите краткую запись. Главный вопрос задачи обведите в кружок. Решите задачу самостоятельно.

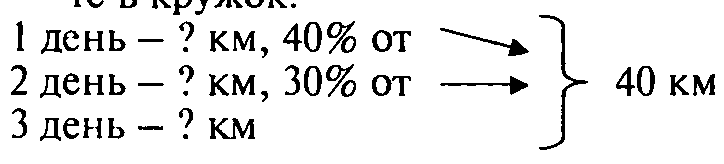
Решение:

1. способ

1. 40% = 0,4 30 % = 0,3

2. 40 • 0,4 = 16 (км) — турист прошел в 1 день.

3. 40 • 0,3 = 12 (км) — турист прошел во 2 день.

4. 40 - (16 + 12) = 12 (км) - турист прошел в 3 день.

1. способ

100% - весь путь

1. 100 — (40 + 30) = 30% — турист прошел в 3 день.

2. 30% = 0,3

3. 40 • 0,3 = 12 (км) — турист прошел в 3 день.

• Кто решил другим способом?

(Ответ: 12 км.)

1. Повторение изученного материала

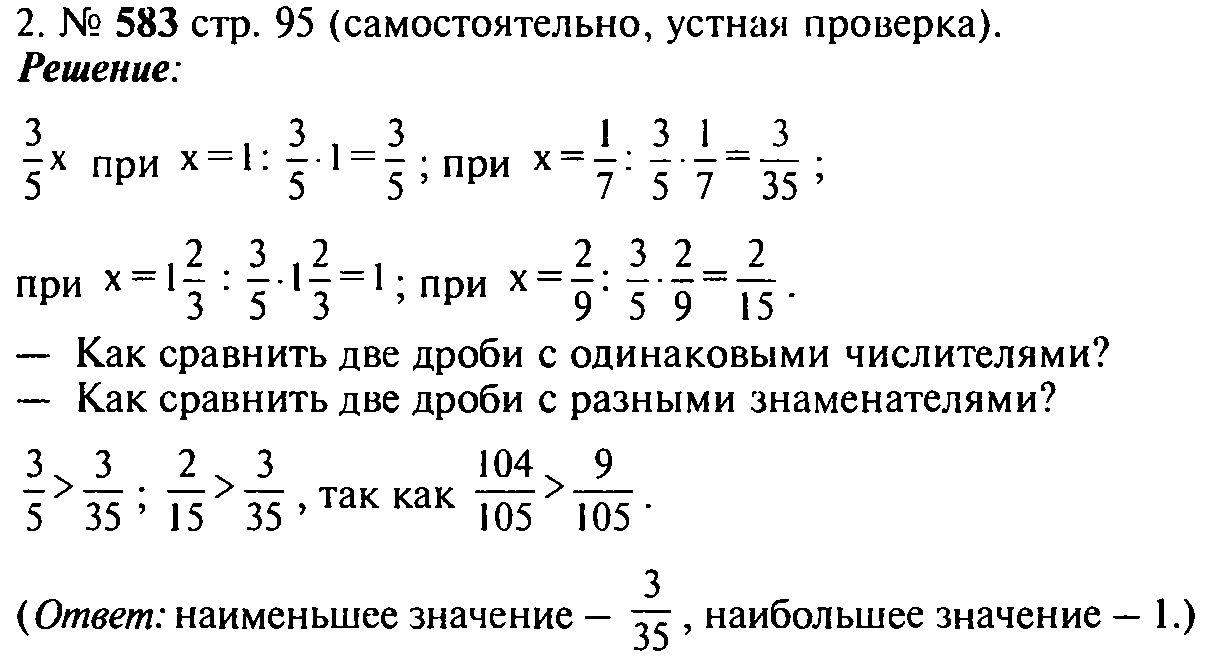
1. Подведение итогов урока

• Какие числа называют взаимно обратными?

• Как записать число, обратное натуральному числу?

• Как записать число, обратное смешанному числу?

Домашнее задание

№ 592 (г-д), 594