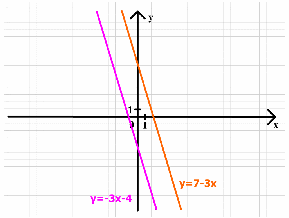
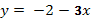
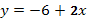
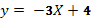
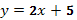
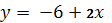
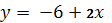
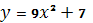
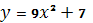
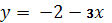
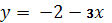
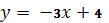
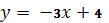
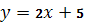
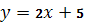
Открытый урок по алгебре в 7 классе на тему: «Взаимное расположение графиков линейной функции»
Напомните пожалуйста, что мы изучали на прошлом уроке?
Дайте определение линейной функции.
Что такое х, у, к, в?
Что является графиком линейной функции?
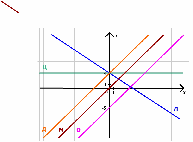
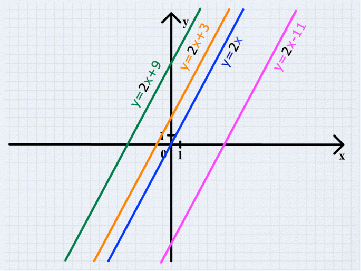
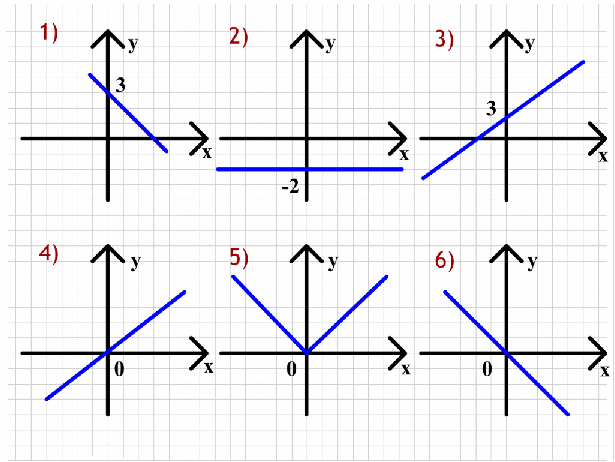
Рассмотрите чертежи, показанные на доске и ответьте на вопросы.
1. Графики функций, у которых к > о расположены на …
2. Графики функций, у которых к < о расположены на …
3. Графики функций, у которых к = о расположены на …
На каких чертежах расположены графики линейных функций?
5. График прямых пропорциональностей даны на чертежах …
6. На каких чертежах изображены графики функций, у которых коэффициент «в» равен 3.
Мы вспомнили графики линейных функций. А сейчас я попрошу вас посмотреть на формулы, задающие функции и среди них выбрать лишнюю:
Эти формулы есть у вас на листочках. Подчеркните лишнюю.
Обоснуйте свой ответ.
Итак, графиком линейной функции является прямая.
Как могут располагаться прямые на плоскости ,относительно друг друга?
А можете ли вы ответить на этот вопрос, глядя на эти формулы, не строя графики?
Проблема?
Как вы думаете, чем мы с вами будем заниматься?
Какая цель урока? Тема урока?
Запишите тему урока.
А сейчас я попрошу вас снова вернуться к формулам и распределить их в два столбика, по какому либо признаку.
Запишем в первый столбик функции, у которых к = 2, во второй к = -3:
А сейчас будем работать в группах. Задание:
Одна группа строит в одной системе координат графики первого столбца и график функции у = -1,5х+3
Вторая группа строит в одной системе координат графики второго столбца и график функции у = 1,5х+3
Итак, еще раз, какая перед вами стоит проблема?
- Как не строя график функций, определить их взаимное расположение? Перед началом вспомним, правила работы в группе.(далее идет работа в группах и представление каждой группы).
Алгоритм определения взаимного расположения графиков линейных функций.
Найти угловые коэффициенты.
Сравнить эти коэффициенты.
Если к1 = к2, то прямые параллельны
Если к1 ≠ к2, то прямые пересекаются
Итак, вы сейчас вывели способ , с помощью которого можно, не строя графики линейных функций, определить их взаимное расположение (слайд 4 и 5).
СЛАЙД 4
СЛАЙД 5
Переходим к следующему этапу урока. Выясним, всем ли было все понятно. У меня на доске, а у вас на листочках даны функции:
у = 5х – 3
у = - 3х – 4
у = 3 – 2х
у = 3х
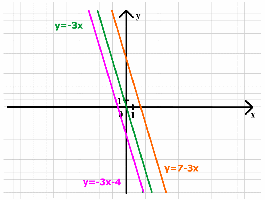
а) Среди функций выберете ту, которая будет параллельна графику функции у = 7 – 3х ( слайд 6). Ответ у = -3х– 4
СЛАЙД 6
б) Задайте формулой функцию, график которой параллелен данной и проходит через начало координат. Ответ у = -3х.
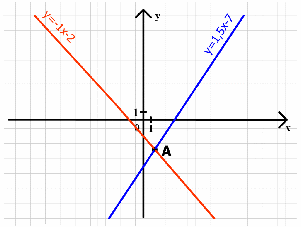
в) Среди функций выбери ту, которая пересечет график функции
у = х + 3 в точке с координатами ( 0; 3 ). Слайд 7. Ответ у = 3 – 2х.
СЛАЙД 7
г) Задайте формулой функцию, график которой параллелен у = х+ 3 и пройдет через точку ( 0;-2). Ответ у = х – 2.
Подведем итог урока:
Что вам было известно из прошлых уроков?
Какая проблема возникла на этом уроке?
Удалось ли вам разрешить эту проблему?
Какой алгоритм или способ мы сегодня вывели?
И на закуску!
Расшифруйте слово, записанное на доске. Для этого в квадратиках впишите букву, соответствующую графику заданной функции. Слайд 8 и 9
СЛАЙД 8
СЛАЙД 9