Тип урока: урок обобщения и систематизации знаний.
Цель урока: обобщить, систематизировать и расширить знания, умения и навыки учащихся при решении задач по теме: «Арифметическая и геометрическая прогрессии.
Задачи урока:
Образовательные:
обобщить, систематизировать и расширить ранее полученные знания и умения у учащихся при решении задач по теме: «Арифметическая и геометрическая прогрессии»;
проверить полноту и осознанность усвоения знаний учащихся по теме.
Воспитательные:
актуализировать навыки аккуратности при решении задач;
развитие математической речи;
воспитывать ответственность;
развить интерес учащихся к предмету.
Развивающая:
расширить и углубить развитие познавательных процессов личности;
развивать навыки самоконтроля, взаимоконтроля, умение работать индивидуально;
развитие памяти, внимания, мышления, математической речи.
Ход урока
1. Организация начала урока.
Цель: кратковременный организационный момент; быстрое включение учащихся в ритм работы; полная готовность класса к уроку.
Метод: устное приветствие, создание атмосферы психологического комфорта.
Проверить готовность учащихся к уроку.
Устное приветствие.
Цель урока: обобщить, систематизировать и расширить ранее полученные знания и умения при решении задач по теме: «Арифметическая и геометрическая прогрессии».
Провести проверочную работу по теме в форме теста.
2. Проверка теоретических знаний
Цель: проверить знания , умения учащихся по теме «Формулы арифметической и геометрической прогрессии».
Ученикам заранее на парты выдаются таблицы.
Учащимся предлагается заполнить таблицу.
Прогрессии
Арифметическая прогрессия
Геометрическая прогрессия
1. Формула n-первых членов прогрессии
2. Характеристическое свойство
3. Сумма n-первых членов прогрессии
Проверка формул.
Через 5 минут на экране появляются формулы арифметической и геометрической прогрессии. Ученики проверяют формулы.
Прогрессии
Арифметическая прогрессия
Геометрическая прогрессия
1. Формула n-первых членов прогрессии
an=a1 + d(n-1)
bn = b1*qn-1
2. Характеристическое свойство
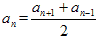
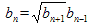
3. Сумма n-первых членов прогрессии
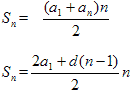
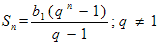
3. Проверка домашнего задания.
4. Историческая справка .
Последовательности (сообщение)
Фундаментальную роль числа в природе определил еще Пифагор своим утверждением "Все есть число". Поэтому математика являлась одной из основ религии последователей Пифагора (пифагорейского союза). Пифагорейцы считали, что бог Дионис положил число в основу мировой организации, в основу порядка; оно отражало единство мира, его начало, а мир представлял собой множество, состоящее из противоположностей. То, что приводит противоположности к единству, и есть гармония. Гармония является божественной и заключается в числовых соотношениях.
Слово «прогрессия» латинского происхождения (progressio), буквально означает «движение вперед» ( как и слово «прогресс») и встречается впервые у римского автора Боэция (V-VI вв.).
Прогрессии известны издавна, а потому нельзя сказать, кто их открыл. Ведь и натуральный ряд – это арифметическая прогрессия. Во время раскопок в Египте был найден папирус, который датируется 2000 г. до н.э., но и его было переписано из другого, еще более раннего, отнесенного к ІІІ тысячелетию до н.э. Ученые расшифровали текст папируса, содержание некоторых задач дает возможность отнести их к задачам на прогрессии.
В вавилонских текстах рассказывается о том, что увеличение освещенной части лунного диска на протяжении первых пяти дней происходит по закону геометрической прогрессии со знаменателем 2, а в следующие десять дней – по закону арифметической прогрессии с разностью 16.
Задачи на прогрессии встречаются в одной из древнейших памяток права – «Русской правде», составленной при Киевском князе Ярославе Мудром (ХІ ст.). В этом документе есть статья, посвященная вычислению приплода от 22 овец за 12 лет при условии, что каждая овца ежегодно приносит одну овцу и два барана. Так же содержатся сведения о приплоде от пчел за определенный промежуток времени, о количестве зерна, собранного на определенном участкае земли и др. Эти задачи не имели хозяйственного значения, а были результатом развития интереса к математике и математическому содержанию данных задач.
О том, как давно была известная геометрическая прогрессия, свидетельствует и легенда об истории изобретения шахмат. Изобретатель шахмат, ученый Сета, попросил в награду у индийского царя Сирама за свое изобретение столько пшеничных зерен, сколько их получится, если на первую клеточку шахматной доски положить одно зерно, на вторую – два, на третью- четыре, т.е. чтобы число зерен все время удваивалось. Рассказывают, что индийский царь Сирам рассмеялся, услышав, какую награду попросил у него изобретатель шахмат.
Сколько зёрен должен был получить изобретатель шахмат? (Учащиеся должны подсчитать дома)
S64 = 264 – 1 = 18 446 744 073 709 551 615.
18 квинтильонов 446 квадрильонов 744 триллиона 73 миллиарда (биллиона) 709миллионов 551 тысяча 615.
Современники сказали бы так:
S64 = 1, 84• 1019 – стандартный вид данного числа.
Если бы царю удалось засеять пшеницей площадь всей поверхности Земли, считая и моря , и океаны, и пустыни, и Арктику с Антарктикой, то получить удовлетворительный урожай, то за пять лет он смог бы рассчитаться с просителем. Такое количество зерен пшеницы можно собрать лишь с площади в 2000 раз большей поверхности Земли. Это превосходит количество пшеницы, собранной человечеством до нашего времени.
Чтобы разместить это зерно в амбаре, то его размеры будут: высота 4 м, ширина 10м, длина будет 30 000 000км- вдвое больше, чем расстояние от Земли до Солнца
5. Устная работа:
Найти неизвестные члены прогрессии
Дано
Найти
Арифметическая прогрессия
a1=4, a2=6
a3=?
Арифметическая прогрессия
х1=5, х30=15
Сумму первых тридцати членов.
Геометрическаяпрогрессия
b1=8, b2=4
Знаменатель g?
Геометрическаяпрогрессия
b1=9, b2=3
b3=?
Геометрическаяпрогрессия
b1=1, g=-2
b3=?
6. Закрепление знаний учащихся:
Цель: Расширить и углубить знания учащихся по теме: «Арифметическая и геометрическая прогрессии».
«Умение решать задачи – практическое искусство, подобное плаванию или катанию на лыжах, или игре на фортепиано; научиться этому можно лишь, подражая избранным образцам и постоянно тренируясь»,- говорил Д.Пойа.
1.Задача. Три числа составляют арифметическую прогрессию. Найдите эти числа, если их сумма равна 27, а при уменьшении первого числа на 1, уменьшении второго на 3 и при увеличении третьего на 3, получили геометрическую прогрессию.
Дано: а1 + а2 + а3 = 27 –сумма трёх членов арифметической прогрессии; а1 - 1; а2 - 3; а3 + 3- геометрическая прогрессия
Найти: а1; а2; а3.
Р
 ешение.
ешение. 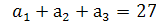 ,
, 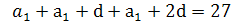 ,
,
q = 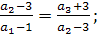
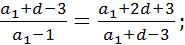
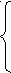
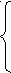
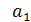 =9 – d,
=9 – d, 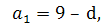
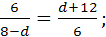 (8 - d)(d + 12)=36.
(8 - d)(d + 12)=36.
d2 + 4d - 60=0,
d1=6, d2=-10.
Если d1=6, то 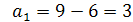 ;
; 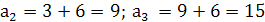 .
.
Если d2=-10, то 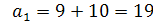 ;
; 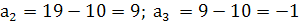 .
.
Ответ: если арифметическая прогрессия 3; 9; 15, то геометрическая прогрессия 2; 6; 18.
Если арифметическая прогрессия 19; 9; -1, то геометрическая прогрессия 18; 6; 2.
7. Проверочная работа (тест)
Приложение 1.
Цель: Проверить ЗУН учащихся по теме: «Арифметическая и геометрическая прогрессия».
Дифференцированный контроль знаний учащихся.
Метод: индивидуальный.
Учащимся даны тесты по теме: « Арифметическая и геометрическая прогрессия».
Учитель объясняет, как оформлять тестовые задания.
Учащиеся выполняют проверочную работу в тестовой форме (время 15 минут)
Проверка теста проходит самостоятельно, ответы по вариантам появляются на экране по мультимедиа проектору.
Проверочная работа (тест)
1 вариант
1) Б 3
2) А 11
3) В 0
4) Б ±2
5) Б 10
2 вариант
1) Б 1
2) Б 320
3) В 0
4) В 2
5) Б 5
8. Подведение итогов урока. Обобщение полученных результатов.
Какое задание вызвало наибольшее затруднение?
Какое значение для Вас имеют знания, полученные сегодня?
9. Домашнее задание
Четыре числа составляют геометрическую прогрессию. Если из первого числа вычесть 11, из второго 1, из третьего 3, а из четвертого 9, то получится арифметическая прогрессия. (Ответ:27;9;3;1)
Задание на повторение: №660(б)