Муниципальное образовательное учреждение «Средняя общеобразовательная школа №16»
города Губкина Белгородской области
Конспект урока по алгебре и началам анализа в 11 классе
«Логарифм и его свойства»
подготовила
учитель математики
Неворотова Ольга Васильевна
г. Губкин 2011
Тема: «Логарифм и его свойства»
Цели урока:
· закрепить понятие логарифма числа;· повторить основное логарифмическое тождество, основные свойства логарифмов.
Оборудование урока.
1. Проектор2. Индивидуальные карточки с заданиями.3. Плакаты: а) ответы для игры «Поле чудес»; б) задания «На выбор»; в) задания «Проверь себя»; г) задания «Вспомним экзамены прошлых лет».
На доске записана тема урока; необходимо знать определение логарифма числа, основное логарифмическое тождество; уметь использовать эти понятия при вычислениях, при решении уравнений.
Ход урока
I. Определение логарифма числа, основное логарифмическое тождество, основные свойства логарифмов
Учитель сообщает цели урока, вызывает к доске ученика для работы с карточкой по заданиям, подобным заданным на дом.
· При каких значениях x выражения имеют смысл:
а) Решите уравнения: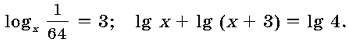 
б) Вычислите: log7 7; log3 1.
в) Запишите основное логарифмическое тождество.
Задание 1. устный счет. (Работает весь класс.)
1) Прочитайте (с готовой кодограммы) определение логарифма и вычислите следующие логарифмы:
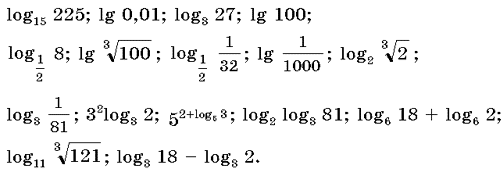
2) Заслушивается ответ ученика, работающего у доски. Вопрос. Что использовалось при решении уравнений?[Определение логарифма, свойства логарифма.]
Задание 2. Программированный контроль. (Материал для проведения контроля заранее приготовлен на доске. Работают все ученики класса.)
· При каких значениях x существует данный логарифм?· При каких значениях x имеет смысл данное выражение?
Задание
Варианты ответа
Вариант 1
Вариант 2
1
2
3
4
5
log5 (7 – x)
log5 (x – 7)
x > 7
0 < x < 7
x < 7
x 7
x 7
log2 (9 – x2)
log3 (x2 – 16)
x <– 3, x> 3
x <– 4, x> 4
– 3 < x < 3
– 4 < x < 4
– 4 x 4
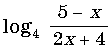
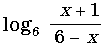
x <– 2, x> 5
x > – 5, x < – 2
– 1 < x < 6
– 2 < x < 5
x <– 2, x> 6
log3 (x2 – 4x + 4)
log7 (x2 – 6x + 9)
– 2 < x < 2
x R, x 2
x > 3
x R, x 3
x R
II. Решение уравнений
Задание 3. (К доске приглашаются три ученика, которые работают по индивидуальным карточкам, остальные учащиеся по вариантам выполняют задания, написанные на доске.)
Вариант 1
1. Вычислите выражения: а) log6 4 + log6 9; б)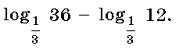 
2. Решите уравнение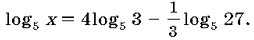 
Вариант 2
1. Вычислите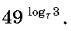 
2. Решите уравнения:
а) log3 (2x + 
= log3 (x – 2); б) log4 (2x + 4) = 2.
Вариант 3
1. Вычислите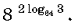 
2. Решите уравнения:
а) 
б) 53x+2 = 7.
Учащиеся, опрошенные по индивидуальным карточкам и по программированному контролю, приступают к работе в тетрадях по плакату «На выбор».
Задание 4. Работа с плакатом «На выбор».
1. Найдите области определения функций:
а) y = 7x + lg (6 – 3x); б)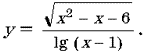 
2. Вычислите:
а)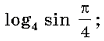 
б)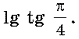 
3. Вычислите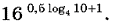 
4. Найдите log3 6, если log3 2 = a.
Все остальные учащиеся принимают участие в игре «Поле чудес».
Задание 5. Игра «Поле чудес». На доске записаны следующие числа:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42, а на плакате – буквы и ответы к упражнениям в индивидуальных карточках.
е
л
т
з
ш
д
м
2
-2
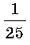
1
40
25
8
с
и
ь
н
о
р
3
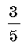
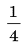
10
24
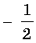
ч
а
у
ж
б
ы
200
-5
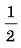
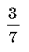
9
Ученики получают 2 или 3 индивидуальные карточки с заданиями (в каждой карточке одно задание). Выполнив задание, они ищут в таблице букву, которой соответствует ответ. Если такая буква есть, то называют номер карточки, и под этим номером на доске пишется буква. Если ответ неправильный – СТОП ИГРА! – ученику предлагается переделать задание.
Номер задания
Задание
Ответ
Номер задания
Задание
Ответ
1
Решите уравнениеlog3 (3x – 5) = log3 (2x – 3)
2
22
Решите уравнение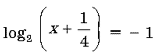
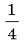
2
Решите уравнение log5 125 = x
3
23
Решите уравнение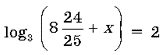 
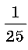
3
Вычислите log0,5 4 – 2
-2
24
Вычислите 24log2 log2 log2 16
24
4
Вычислите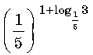 
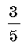
25
Вычислите 2lg 100 000
10
5
Вычислите 103–lg 5
200
26
Решите уравнение lg 2 + lg (x + 2) = lg (x – 1)
-5
6
Вычислите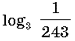 
-5
27
Вычислите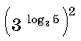 
25
7
Вычислите lg 3000 – lg 3
3
28
Решите уравнение log0,04 5 = x
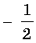
8
Вычислите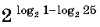 
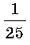
29
Решите уравнение log7 (2x + 1) = 2
24
9
Вычислите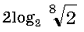 
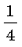
30
Вычислите 
10
Вычислите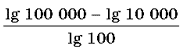 
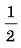
31
Вычислите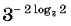 
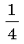
11
Вычислите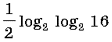 
1
32
Вычислите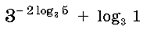 
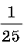
12
Решите уравнение lg (9x + 10) = 2
10
33
Вычислите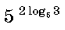 
9
13
Решите уравнение 3lg 2 + lg (x + = lg 48 – lg 2 – 5
-5
34
Вычислите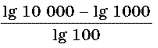 
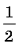
14
Решите уравнение log5 x = – 2
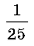
35
Вычислите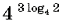 
8
15
Вычислите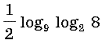 
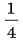
36
Вычислите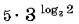 
10
16
Решите уравнение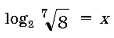 
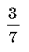
37
Вычислите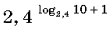 
24
17
Вычислите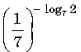 
2
38
Вычислите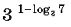 
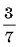
18
Решите уравнение log2 (x + 6) = 2
-2
39
Решите уравнение lg (6x + 3) = lg (x – 22)
-5
19
Решите уравнениеlg 40 – lg 2 = lg (10 – 2x)
-5
40
Вычислите lg 20 + lg 5
2
20
Решите уравнение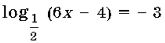 
2
41
Вычислите 
40
21
Вычислите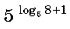 
40
42
Вычислите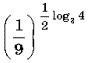 
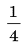
Задание 6. Работа с плакатом «С экзаменов». (Учащиеся выполняют в тетрадях экзаменационные задания предыдущих лет.)
1. Установите, при каких x существуют логарифмы:
а) 
б) log5 (x2 – 6x + 8); в) log4 (2x2 + 9x).
2. Решите уравнения:
а) log7 (x – 1) = log7 2 + log7 3;б) log3 (2x + 1) = log3 13 + log3 3;в)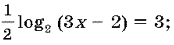 
г)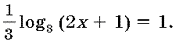 
Задание 7 (устное). Работа с плакатом «Проверь себя».
1) 
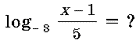2) log5 (121 – x2), (121 – x2) 0, x – 11, x 11.3) 
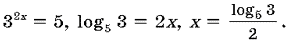4) 
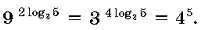5) lg x2 = 2lg x.
Это задание позволит учителю проверить внимание учащихся, их знания.
III. Подведение итогов урока. Задание на дом
Список использованной литературы
Алгебра и начала математического анализа. 10-11 классы. Учебник. Колмогоров А.Н. и др. (2008, 384с.).
Алгебра и начала математического анализа. 11 класс. Учебник. Никольский С.М. и др. (2009, 464с.).
Алгебра и начала математического анализа. 11 класс. Дидактические материалы. Потапов М.К., Шевкин А.В. (2008, 189с.).
Алгебра и начала математического анализа. 11 класс. Тематические тесты. Шепелева Ю.В. (2009, 108с.).
Алгебра и начала математического анализа. 11 класс. Книга для учителя. Потапов М.К., Шевкин А.В. (2009, 256с.).