конспект урока по теме «Рациональные числа как бесконечные десятичные дроби.» 8 класс | Лучшие рефераты, дипломные, курсовые работы

МБОУ гимназия №2 г. Гурьевска

Калининградской области

Конспект урока алгебры в 8-м классе

"Рациональные числа как бесконечные десятичные дроби."

Подготовила: Матвеева Надежда Витальевна,

учитель математики

Гурьевск - 2013

Конспект урока алгебры в 8-м классе "Рациональные числа как бесконечные десятичные дроби."

Цели урока:

Дидактическая цель: Ознакомить с понятием бесконечная периодическая десятичная дробь, с правилами перевода бесконечных периодических дробей в обыкновенные дроби.

Воспитательная цель: Развитие умений применять знания в нестандартных ситуациях. Обучение навыкам контроля и самоконтроля.

План урока.

Постановка цели урока.
Самостоятельная работа.
Знакомство с таблицей преобразования обыкновенных дробей в десятичные.
Решение упражнений.
Знакомство с правилами преобразования периодической дроби в обыкновенную.
Итог урока.
Домашнее задание.

Ход урока

1. Постановка цели урока.

Сегодня мы с вами продолжим изучение рациональных чисел. Познакомимся с новыми представителями десятичных дробей – бесконечными периодическими дробями, рассмотрим задания, при выполнении которых появляются различные виды десятичных дробей..

Самостоятельная работа.

(3 ученика на доске выполняют задания по карточкам.)

1 ученик. Преобразовать обыкновенную дробь 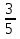в десятичную.

2 ученик. Преобразовать обыкновенную дробь 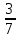в десятичную.

3 ученик. Преобразовать обыкновенную дробь 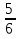в десятичную.

Задание для класса: Преобразовать обыкновенные дроби в десятичные:

, , ,

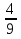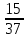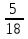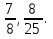
Проверка: один из учащихся проговаривает ответы с комментариями, остальные проверяют свои результаты в своих тетрадях, ставя “+” или “-”.

Заслушиваются ответы учащихся, выполнявших задания на карточках. Предлагается прокомментировать получившиеся результаты. Оцениваются ответы у доски и учащихся, комментировавших решения.

Ставится перед учащимися вопрос: «Почему получились такие различные результаты?», « В каком случае будут получаться сходные результаты?»

3. Учащимся демонстрируется таблица преобразования обыкновенных дробей в конечные, бесконечные чистые периодические, бесконечные смешанные периодические десятичные дроби. (Раздаточный материал на каждую парту по 1-2 штуки.)

Числа, которые делятся только на себя и на 1, называются ПРОСТЫМИ. Самое маленькое простое число 2. Самого большого не существует.

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, …

8=2∙2∙2 12=2∙2-3 34=2∙17 90=2∙3∙3∙5 625=5∙5∙5∙5

Есть и 2-ки, и 5-ки и другие простые числа

Нет 2-ек, нет 5-ок

только другие простые числа

Только 2-ки или

только 5-ки или

2-ки и 5-ки вместе

5,2(45) ; 12,42(4) ; 0,5(083)

12,(3) ; 4,(12) ; 0,(369)

4,12 ; 32,5 ; 0,475

Бесконечная смешанная периодическая десятичная дробь

Бесконечная чистая периодическая десятичная дробь

Конечная десятичная дробь

З н а м е н а т е л ь

О б ы к н о в е н н а я д р о б ь

Под руководством учителя учащиеся знакомятся с содержанием нового материала в таблице.

В каком случае десятичная дробь получится конечной десятичной? Приведите примеры.
В каком случае десятичная дробь получится бесконечной чисто периодической? Приведите примеры.
В каком случае десятичная дробь получится бесконечной смешано периодической? Приведите примеры.

Обсуждение ответов. По окончании работы можно выборочно поставить оценки.

4. Решение упражнений.

1).Определите какая получится дробь в результате преобразования в десятичную?

2). Преобразовать в десятичную дробь:

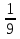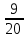а) б) ; в)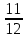

5. Знакомство с правилами преобразования бесконечной периодической дроби в обыкновенную дробь.

Правило 1.

Для преобразования дробной части чистой периодической дроби в обыкновенную, следует в числителе обыкновенной дроби записать её период, а в знаменателе написать столько 9, сколько цифр в периоде, сохранив неизменной целую часть дроби.

Пример 1.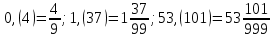

Правило 2.

Для преобразования смешанной периодической дроби в обыкновенную дробь:

Запишем натуральное число, которое получится из дробной части, если не обращать внимание на запятую и на скобки;
Запишем натуральное число, составленное из цифр, стоящих до периода;
Разность этих чисел будет числителем искомой обыкновенной дроби;
Знаменатель же этой дроби будет содержать столько 9, сколько цифр в периоде, и столько нулей, сколько цифр до периода.
Целую часть дроби сохраним неизменной.

Пример 2.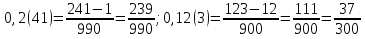

Работа с учебным пособием : № 9.15, 9.16(а,б); 9.19, 9.22(а,б) (Алгебра. 8 класс в 2 ч. Ч. 2. Под ред. А.Г. Мордковича.)

6. Итог урока:

1) Как преобразовать обыкновенную дробь в десятичную?

2)Какие возможны случаи? При наличии каких условий полученная дробь окажется конечной десятичной? Чистой периодической? Смешанной периодической?

3) Как преобразовать десятичную дробь в обыкновенную?

7. Задание на дом. № 9.15, 9.16(в,г); 9.19, 9.22(в,г)

Список литературы:

Мордкович А.Г., Александрова Л.А., Мишустина Т.Н., Тульчинская Е.Е.. Алгебра. 8 класс. В 2ч. – 11-е изд., - М.: Мнемозина, 2009.
Глейзер Г.И. История математики в школе: пособие для учащихся 7-8 кл. / М.: Просвещение, 1982./
Ершова А.П., Голобородько В.В. Алгебра. 8 класс. Самостоятельные и контрольные работы / А.П. Ершова, В.В. Голобородько, А.С. Ершова. М.: ИЛЕКСА, 2007.
Клименченко Д.В. Задачи по математике для любознательных / Д.В. Клименченко. – М.: Просвещение, 2007/
Математика: еженедельное приложение к газете «Первое сентября».
Математика в школе: ежемесячный научно-методический журнал.
Олимпиадные задания по математике. 5-8 классы: 500 нестандартных задач для проведения конкурсов и олимпиад: развитие творческой сущности учащихся / авт.-сост. Н.В. Заболотнева.- Волгоград: Учитель, 2006./
Перельман Я.И. Занимательная алгебра / М.: Наука, 1975./
Пичурин Л.Ф. За страницами учебника алгебры: пособие для учащихся / Л.Ф. Пичурин. – М.: Просвещение, 2005./
Черкасов О.Ю. Математика. Справочник / О.Ю. Черкасов, А.Г. Якушев. – М.: АСТПРЕСС ШКОЛА, 2006./