Разработка темы:

Решение квадратных уравнений

Учитель – Тхайшаова Н.Г.

Тема: Квадратные уравнения. Способы их решения.

Цель: Научить решать квадратные уравнения различного вида разными способами.

Количество часов уроков: 2 урока (спаренные ).

План

1. Повторение темы «Линейные уравнения»

2. Новый материал. Тема: «Квадратные уравнения»

1. Полные квадратные уравнения;

2. Неполные квадратные уравнения;

3. Из истории квадратных уравнений;

4. Решение неполных квадратных уравнений;

5. Способ выделения квадрата двучлена при решении полных кв. уравнений;

6. Графический способ решения полных квадратных уравнений;

7. Вывод формул для решения полных кв. уравнений;

8. Теорема Виетта (для полных кв. уравнений при а=1 и при а ≠1)

1. Обобщение темы.

2. Задания к зачету.

3. Викторина.

4. Итог урока и домашнее задание.

Ход урока.

1. Вспомним виды уравнений.

(я пишу уравнение, а ребята называют его вид)

1. 5х-3=2+4х

2. 3х²-14=8х-х²

3. х³+27=0

4. ах+в=с-х

5. ах²+вх=с

Сделаем вывод, что такое уравнение. Всякое равенство, содержащее неизвестную величину, обозначенную какой-либо буквой, называется уравнением.

Так что же такое решить уравнение? Решить уравнение – это значит найти все его корни или убедиться в их отсутствии.

Например: уравнение ½=0 не имеет решения.

Для решения уравнений вызываю трех учеников.

1. 3х-2=5х+4

Ответ: х=-3

1. |х-1 | +2=3

решение: |х-1 |=

Следовательно, решение уравнения разбивается на решение двух систем.

а)

не является решением уравнения, т.к. 0,5<1

в)

Т.к. ¾<1, то x=¾ является решением уравнения.

Ответ: ¾

1. (3х+4в)+(7в+2х)=13в и указать при каких «в» корень уравнения положительное число.

х=16в, при в >0 корень уравнения х >0

Ответ: 16в, корень уравнения положительное число, при в >0.

1. Новый материал.

Изучение темы «Квадратные уравнения»

1. Что же такое квадратные уравнения? Какие они бывают? (даем опрос)

2. Уравнения вида ах²+вх=0 ,ах²=0,ах²+с=0 , где а, в, с – некоторые числа, отличные от нуля, называются неполными квадратными уравнениями.

3. Немного истории.

4. Рассмотрим решение неполных квадратных уравнений.

а) ,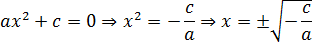

где (- ) < 0

Пример 8х²-8=0

х²=1

х=±1

Ответ: +1

2х²=0

х²=0/2

х²=0/2

х²=0

х=0

Ответ: х=0

в)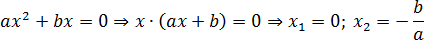

Пример 5х²-2х=0

х(ах+в)=0

х=0 или х=0,4

Ответ: 0; 0,4

1. Пример 1 решить уравнение

х² + 8х - 33=0 (а≠в)²=а²+2ав+в²

х² + 8х – 33 = (х² + 2х × 4+16) – 16 - 33=(х+4)² - 49

(х+4)² - 49=0

(х+4)² = 49

х+4=±

х+4 = ±7

х = -4±7

итак х₁=-4+7

х₁=3

х₂=-4-7

х₂=-11

Ответ: 3; -11

Пример 2 решить уравнение

2х² - 9х+4=0

2(х² - х+2)=0 равноценно уравнению х² - х+2=0

х²- +2=(х² - 2х + ) - + 2 = (х - )² - = (х - )² -

(х - )² - = 0

х₁= + = 4

х₂= - =0,5

Ответ: 4; 0,5

1. Графический способ решения уравнения

1. Вывод формул для решения неполных квадратных уравнений.

Если в=2к, то формула (2) примет вид:

, где Д = к² - ас

Пример1 2х²-5х+2=0

х₁=2

х₂=0,5

Пример 2 х²-6х+9=0

в=6 - четное число

к=-6÷2=-3

Д=0

х= = =3

Любое квадратное уравнение (полное) можно привести к виду x²+pх+q делением обеих частей уравнения на q≠0. Такое уравнение называется приведенным квадратным уравнением. Корни приведенного квадратного уравнения можно найти по формуле

где а=1; в=р; с=q

Пример 2х² - 8х - 42=0

х² + 4х - 21=0

Используя формулу (1) получим

х₁=3; х₂=-7

Ответ: 3; -7

1. Рациональные корни квадратных уравнений нетрудно находить устно, использовав теорему Виетта.

Теорема Виетта:

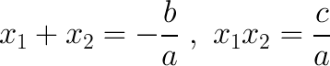
Теорема Виетта для приведения квадратного уравнения.

х²+px-q=0

х₁+x₂=-p

х₁*x₂=q

1. Свести данное уравнение

ах²+вх+с=0

у²+ву+ас=0

а²х²+вах+ас=0 умножить обе части на «а» и обозначить ах=у

у²+ву+ас=0 1)решить по теореме Виетта

2)разделить каждый корень на «а»

Примеры 2х²-3х-9=0

(2х)²-3*2х-18=0/2

2х=у

у²-3у-18=0

у₁=-3; у₂=6

х₁=- ; х₂=3

1. 4х²-х-5=0/4

(4х)²-4х-20=0

4х=у

у²-у-20=0

у₁= 5; у₂ = - 4

х₁= =1 ¼; х₂ = - = - 1

а – в + с = 0; х₁ = - 1 ; х₂ = -

Ответ : 1 ¼; -1

1. Обобщение темы.

Сделаем обобщение пройденной на уроке темы в виде таблиц, которые занесем в карточки индивидуального пользования.

Таблица 1. Полные квадратные уравнения.

Доп. условия

Корни уравнения

ах²+вх+с=0

Пример

1) в - четное

, к= ½,

где Д=к²-ас

5х²-6х-8=0

Д₁=9+40=49

х₁= ; х₁=2

х₂= ; х₂=-0,8

2) в - нечетное

,

где Д=в²-4ас

2х²-5х+2=0

Д=25-16=9

х₁= ; х₁=2

х₂= ; х₂=0,5

3) а=1

в=р

е=q

х²+4х-5=0

х=-2±

х=-2±3

х₁=-5; х₂=1

Таблица 2. Неполные квадратные уравнения.

Уравнение

Корни уравнения

Пример

1) ах²=0

х=0

2х²=0; х=0

2) ах²+вх=0

х₁=0

х₂= -

5х²+4х=0

х=0; х= -

3) ах²+с=0

х=± √ - ,

где <0

7х²-3=0

х=±√

Таблица 3. Теорема Виетта.

Уравнение

Условие

Пример

ах²+вх+с=0

х₁+х₂= -

х₁∗х₂ =

2х²- 9х+10=0

у₁=5; у₂=4

х₁=2,5; х₂=2

x²+рх+q=0

х₁+х₂ =-p

х₁∗х₂ =q

х²+5х+6=0

х₁= - 2; х₂= - 3

1. Задания к зачету.

Запишем уравнения для самостоятельного решения.

1. 3х + 8=18 - 2х

2. 5 - |1-3х | = 4х

3. (2х - 4а)+(4х + 5а)=19а

4. х² - 11х - 60=0

5. х² - 6х + 9=0

6. 2х² - 5х + 2=0

7. - 4х²+7х + 2=0

8. 25=26х - х²

9. - 11х=11

10. =

11. 0,7х²=1,3х+2

12. х²=2х-7

13. у²-10у-25=0

14. 299х²+100х=500-101х2

15. 3р²+3=10р

16. 4х²=7х+7,5

17. (3х-1)(х+3)=х(1+6х)

18. 5х²=0

19. 6х²-16х=0

20. 7х²+5=0

21. 8х²-1=0

22. 3х²-3х+1=0

23. 2х²-3х-1=0

24. у²=52у-576

25. (х+1)²=7918-2х

1. Викторина.

Теперь, когда мы закончили изучение темы урока, проведем небольшую викторину.

(за верный ответ выдается красный жетон. Ученикам, имеющим 10 жетонов ставится «5», имеющим 8,9 жетонов – «4».)

Вопросы викторины.

1. Как называется уравнение? (показываю заранее подготовленные карточки).

Уравнения: а) 5х² - 6х+1=0

б) х² -7х+5=0

в) 5х² -1=0

Ответ: а) полное квадратное уравнение

б) приведенное квадратное уравнение

в) неполное квадратное уравнение

1. Как называется выражение и какой буквой обозначается. (показываю карточки).

Выражение: а) в²-4ас

б) к²-ас

а) Д₁ дискриминант

б) Д₁ дискриминант

1. Указать правильный ответ при решении уравнения.

5х²+3=0

1. Решений нет

2. ±

3. ±

1. Решить устно:

х²+16х+63=0

1. 9; 7

2. -9; 7

3. -7; 9

4. -7; -9

1. Решить устно:

3х²-4х-4=0

1. 6; -2

2. 2; -6

3. - ; 2

4. ; -2

1. Назвать корни квадратного уравнения:

х²-4х+3=0

1. 3; 1

2. 21

3. 1; 2; 3

4. 1; 2

1. Решить уравнение

3х²-7х+4=0

2. 1 ; 1

3. -1 ; -1

4. -1 ; 1

Правильные ответы к вопросам 3-7.

3 а) ; 4 d) ; 5 c); 6 a); 7 b)

1. Итог урока и домашнее задание.

Запишем домашнее задание.

1. Вывод формул корней квадратного уравнения.

2. Теорема Виетта (с доказательством)

3. Решить уравнения:

1. 3(х-5) - 2х=6х

2. - = 1

3. |х - 1 | +5=6х

4. 2(х + а)-3х=5а

5. 8х²-1=0

6. 8х²+8=0

7. 5х² - 4х+5=0

8. 5х² - 4х-1=0

9. х² - 4х - 5=0

10. 2х^{2 —} 3+2=0

11. х²-9х-10=0