Контрольная работа № 1. Векторы
1 вариант.
1. Начертите два неколлинеарных вектора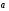 
и 
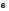. Постройте векторы, равные:
а)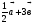 
; б)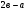 
2. На стороне ВС ромба АВСD лежит точкаК такая, что ВК = КС, О – точка пересечения диагоналей. Выразите векторы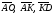 
через векторы 
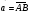и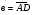 
.
3. В равнобедренной трапеции высота делит большее основание на отрезки, равные 5 и 12 см. Найдите среднюю линию трапеции.
4.* В треугольнике АВС О – точка пересечения медиан. Выразите вектор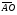 
через векторы 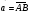и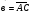 
.
2 вариант
1. Начертите два неколлинеарных вектора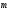 
и 
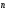. Постройте векторы, равные:
а)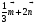 
; б)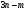 
2. На стороне СD квадрата АВСD лежит точка Р такая, что СР = РD , О – точка пересечения диагоналей. Выразите векторы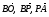 
через векторы 
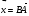и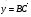 
3. В равнобедренной трапеции один из углов равен 600, боковая сторона равна 8 см, а меньшее основание 7 см. Найдите среднюю линию трапеции.
4. * В треугольнике МNK О – точка пересечения медиан,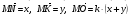 
. Найдите число k.
Контрольная работа № 2. Метод координат.
1 вариант.
1. Найдите координаты и длину вектора 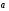, если 
.
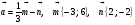2. Напишите уравнение окружности с центром в точкеА (- 3;2), проходящей через точку В (0; - 2).
3. Треугольник МNK задан координатами своих вершин: М (- 6; 1), N (2; 4), К (2; - 2).
а) Докажите, что Δ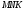
- равнобедренный;
б) Найдите высоту, проведённую из вершины М.
4. * Найдите координаты точки N, лежащей на оси абсцисс и равноудалённой от точек Р и К, если Р( - 1; 3 ) и К( 0; 2 ).
2 вариант.
1). Найдите координаты и длину вектора 
, если 
.
2). Напишите уравнение окружности с центром в точке С ( 2; 1 ), проходящей через точку D ( 5; 5 ).
3). Треугольник СDЕ задан координатами своих вершин: С (2; 2), D (6; 5), Е (5; - 2).
а) Докажите, что Δ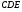
- равнобедренный;
б) Найдите биссектрису, проведённую из вершины С.
4. * Найдите координаты точки А, лежащей на оси ординат и равноудалённой от точек В и С, если В( 1; - 3 ) и С( 2; 0 ).
Контрольная работа № 3.
Соотношения между сторонами и углами треугольника.
1 вариант
В треугольнике АВС
А = 450,
В = 600, ВС =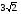 
Найдите АС.
Две стороны треугольника равны
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
* В ΔАВС АВ = ВС,
САВ = 300, АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.
2 вариант
В треугольнике СDE
С = 300,
D = 450, СЕ =
Найдите DE.
Две стороны треугольника равны
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
* В ромбе АВСD АК – биссектриса угла САВ,
ВАD = 600, ВК = 12 см. Найдите площадь ромба.
Контрольная работа № 4.
Длина окружности и площадь круга.
1 вариант
1. Найдите площадь круга и длину ограничивающей его окружности, если сторона правильного треугольника, вписанного в него, равна 
2. Вычислите длину дуги окружности с радиусом 4 см, если её градусная мера равна 1200. Чему равна площадь соответствующего данной дуге кругового сектора?
3. Периметр правильного треугольника, вписанного в окружность, равен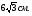
Найдите периметр правильного шестиугольника, описанного около той же окружности.
2 вариант
1. Найдите площадь круга и длину ограничивающей его окружности, если сторона квадрата, описанного около него, равна 6 см.
2. Вычислите длину дуги окружности с радиусом 10 см, если её градусная мера равна 1500. Чему равна площадь соответствующего данной дуге кругового сектора?
3. Периметр квадрата, описанного около окружности, равен 16 дм. Найдите периметр правильного пятиугольника, вписанного в эту же окружность.
Контрольная работа № 5.
Движения.
1 вариант
1. Начертите ромб АВСD. Постройте образ этого ромба:
а) при симметрии относительно точки С;
б) при симметрии относительно прямой АВ;
в) при параллельном переносе на вектор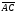 
;
г) при повороте вокруг точки D на 600 по часовой стрелке.
2. Докажите, что прямая, содержащая середины двух параллельных хорд окружности, проходит через её центр.
3. * Начертите два параллельных отрезка, длины которых равны.начертите точку, являющуюся центром симметрии, при котором один отрезок отображается на другой.
2 вариант
1. Начертите параллелограмм АВСD. Постройте образ этого параллелограмма:
а) при симметрии относительно точки D;
б) при симметрии относительно прямой CD;
в) при параллельном переносе на вектор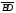 
;
г) при повороте вокруг точки А на 450 против часовой стрелки.
2. Докажите, что прямая, содержащая середины противоположных сторон параллелограмма, проходит через точку пересечения его диагоналей.
3.* Начертите два параллельных отрезка, длины которых равны. Постройте центр поворота, при котором один отрезок отображается на другой.