По учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год
Контрольная работа №1 по алгебре в 9 классе
по теме «Функции и их свойства, квадратный трехчлен»
Вариант 1
• 1. Дана функция f (х) = 17х - 51. При каких значениях аргумента f (х) =0, f (х) < 0, f (х) > 0? Является ли эта функция возрастающей или убывающей?
• 2. Разложите на множители квадратный трехчлен: а) х2 -14х +45; б) 3у2 +7у-6.
•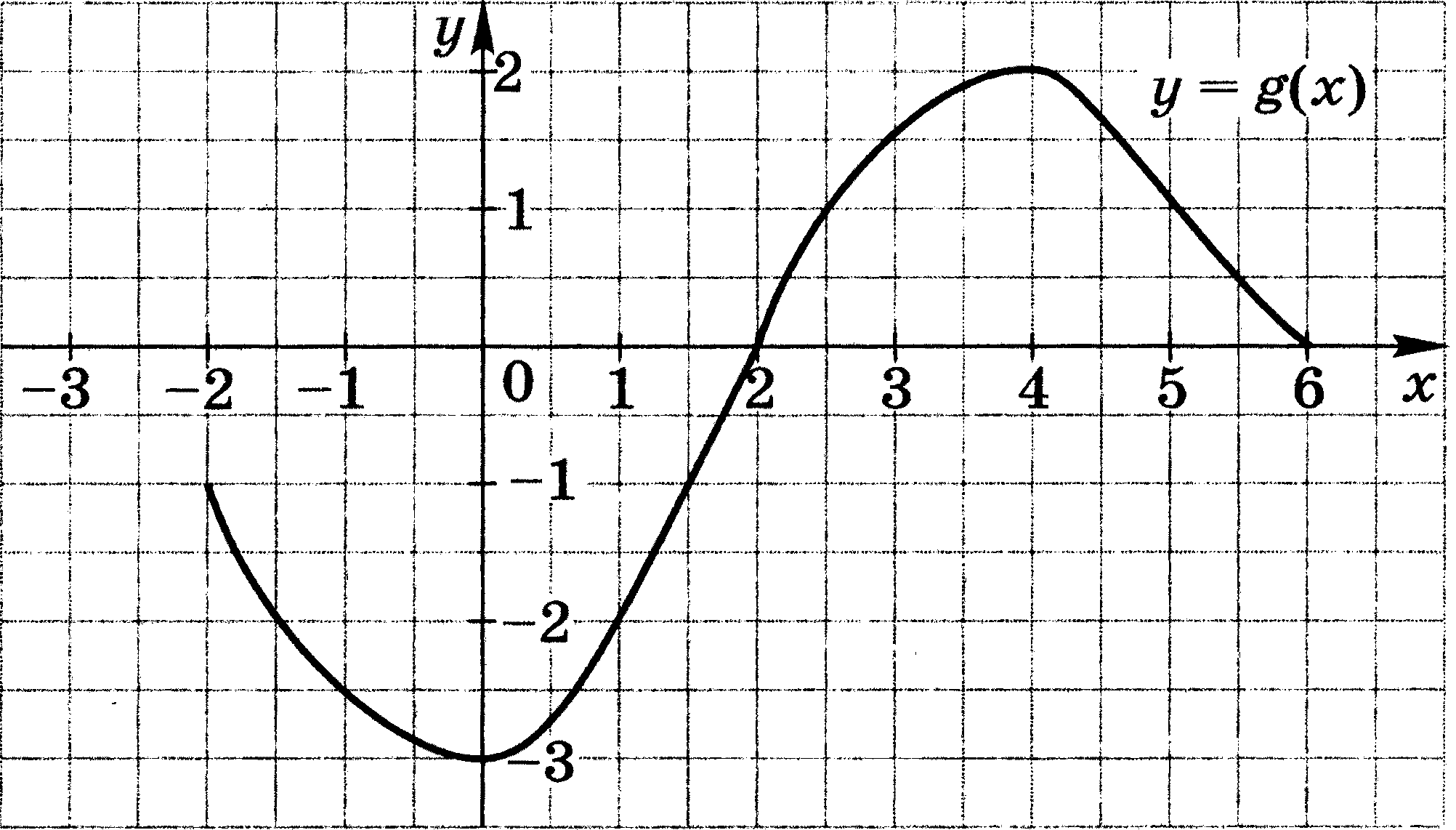 3. Сократите дробь
3. Сократите дробь 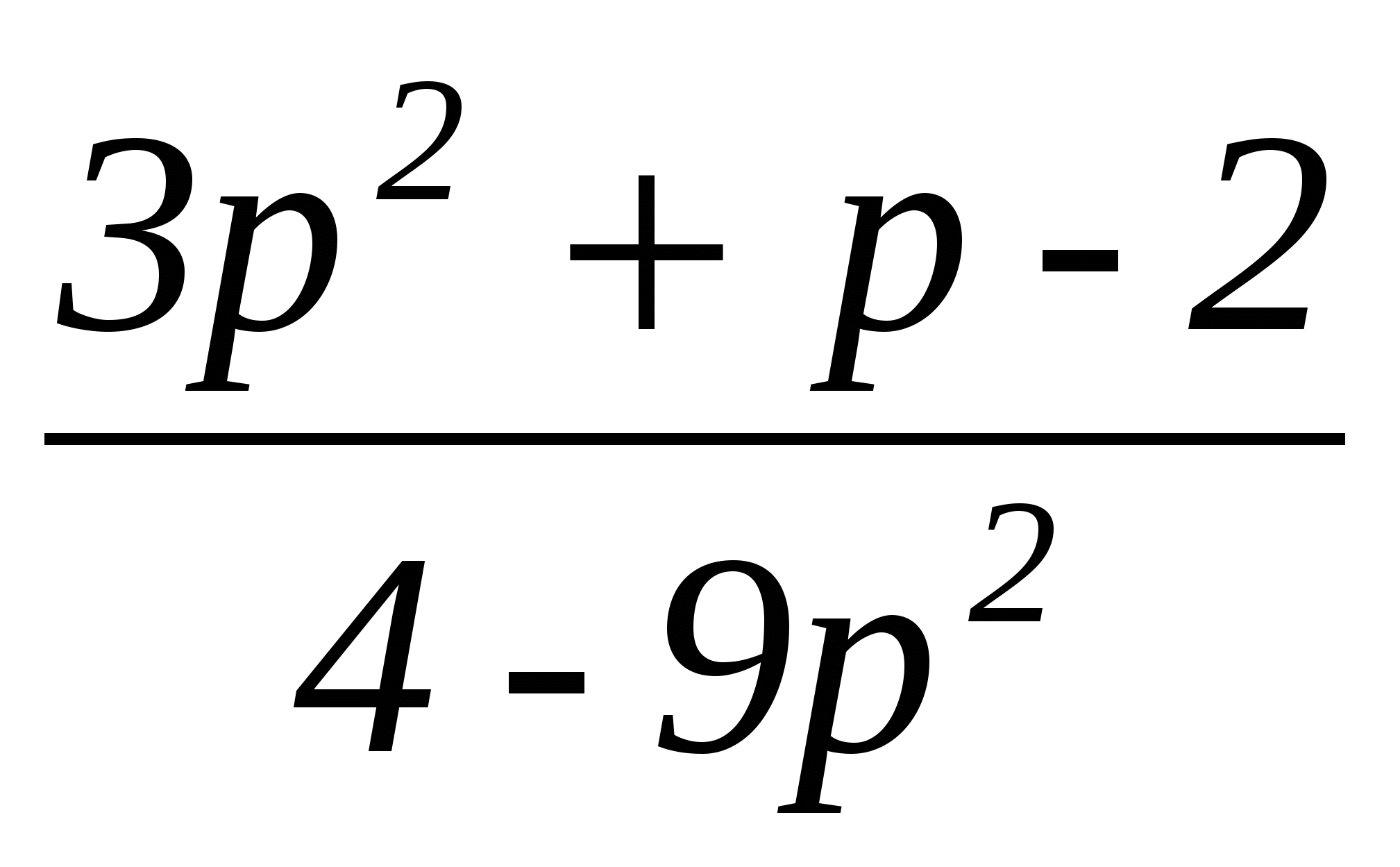 .
.
4
Рис. 1
. Область определения функции g (рис. 1) отрезок [-2; 6]. Найдите нули функции, промежутки возрастания и убывания, область значений функции.5. Сумма положительных чисел а и b равна 50. При каких значениях а и b их произведение будет наибольшим?
Вариант 2
• 1. Дана функция g(х) = -13х + 65. При каких значениях аргумента g(х) = 0, g (х) < 0, g (х) > 0? Является ли эта функция возрастающей или убывающей?
• 2. Разложите на множители квадратный трехчлен: а) х2-10х+21; б) 5у2+9у-2.
•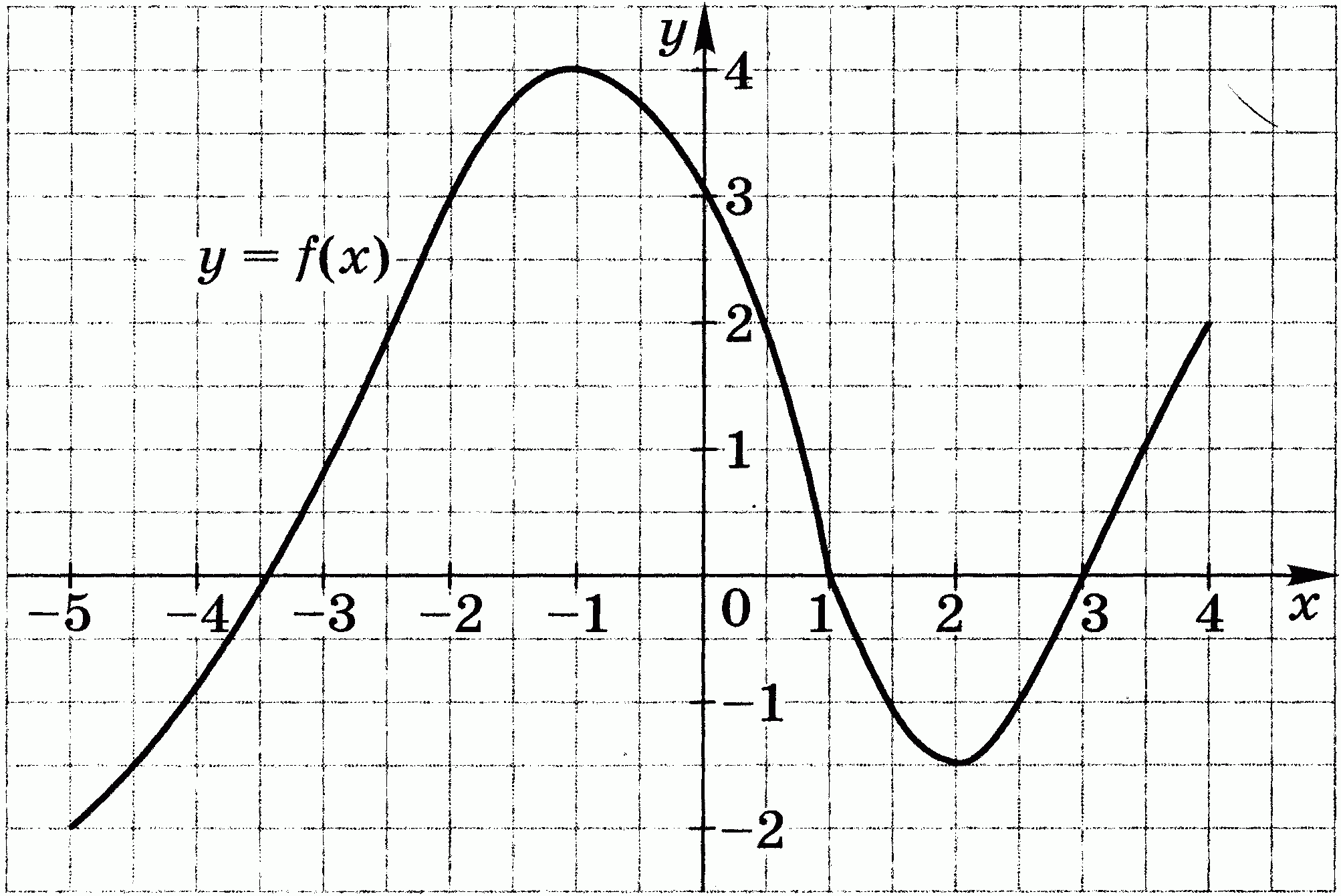 3. Сократите дробь
3. Сократите дробь 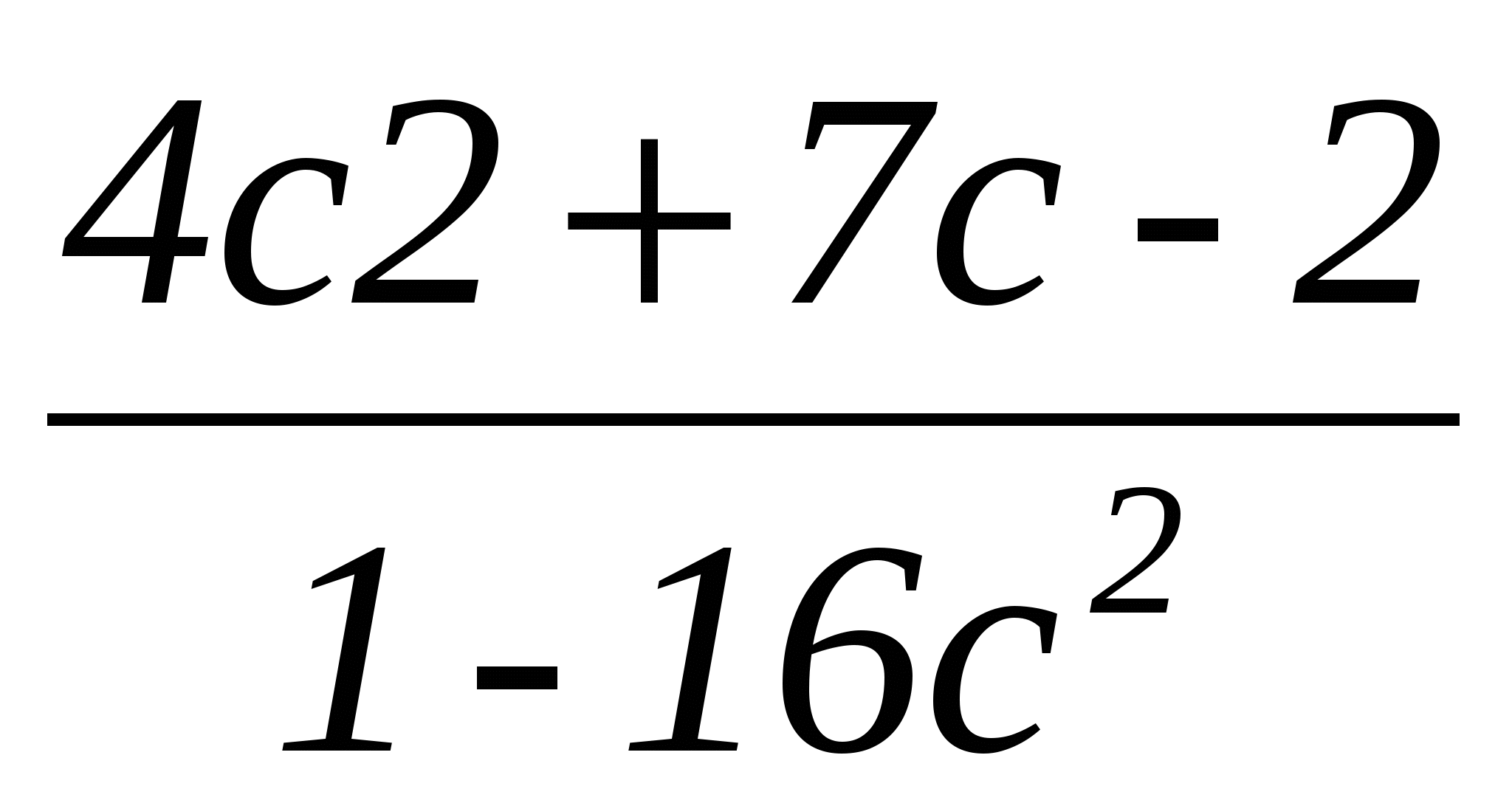 .
.
4. Область определения функции f (рис. 2) отрезок [-5; 4]. Найдите нули функции, промежутки возрастания и убывания, класть значений функции.
5
Рис. 2
. Сумма положительных чисел с и d равна 70. При каких значениях с и d их произведение будет наибольшим?
По учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год
Контрольная работа №2 по алгебре в 9 классе
по теме «квадратичная функция и ее график»
Вариант 1
• 1. Постройте график функции у = х2 - 6х + 5. Найдите с помощью графика:
а) значение у при х = 0,5; б) значения х, при которых у = -1;
в) нули функции; промежутки, в которых у > 0 и в которых у < 0;
г) промежуток, на котором функция возрастает.
• 2. Найдите наименьшее значение функции у = х2 - 8х + 7.
• 3. Найдите область значений функции у = х2 - 6х - 13, где x 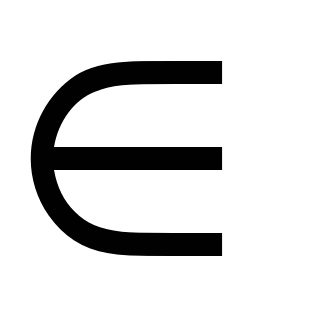 [-2; 7].
[-2; 7].
4. Не выполняя построения, определите, пересекаются ли парабола у =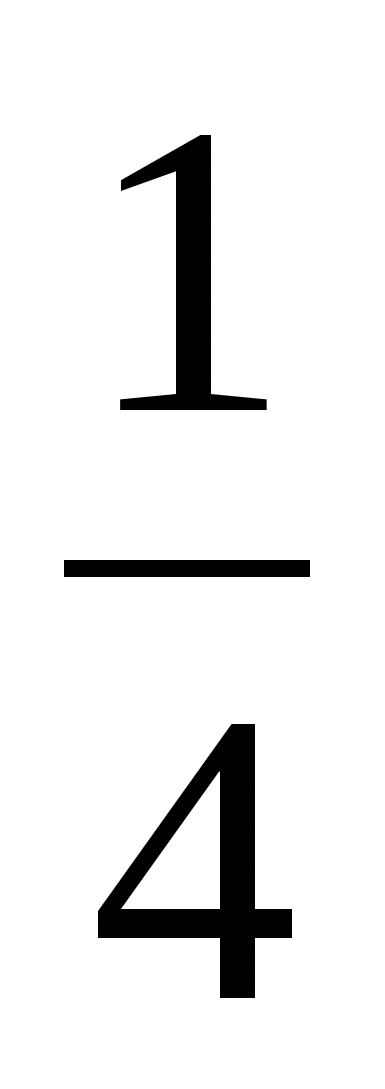 х2 и прямая у = 5х -16. Если точки пересечения существуют, то найдите их координаты.
х2 и прямая у = 5х -16. Если точки пересечения существуют, то найдите их координаты.
5. Найдите значение выражения 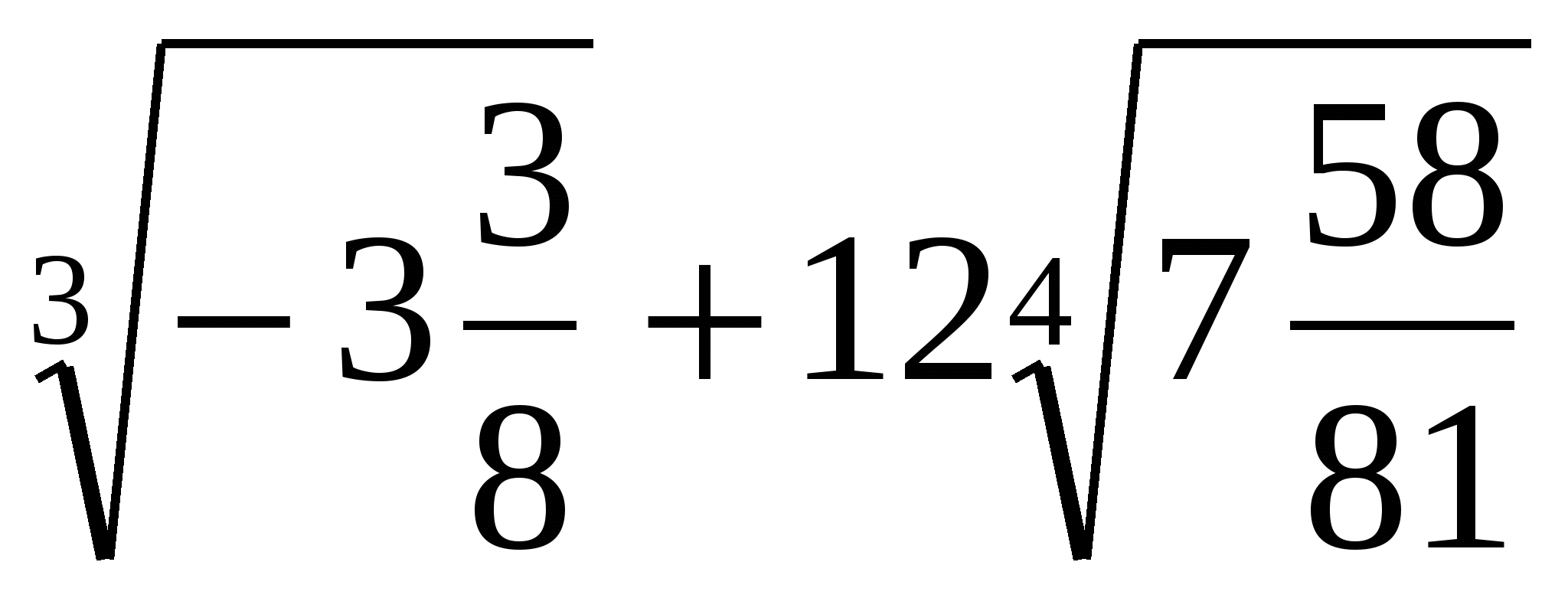 .
.
Вариант 2
• 1. Постройте график функции у = х2 - 8х + 13. Найдите с помощью графика:
а) значение у при х = 1,5; б) значения х, при которых у = 2;
в) нули функции; промежутки, в которых у > 0 и в которых y < 0;
г) промежуток, в котором функция убывает.
• 2. Найдите наибольшее значение функции у = -х2 + 6х – 4.
3. Найдите область значений функции у = x2 - 4х - 7, где х 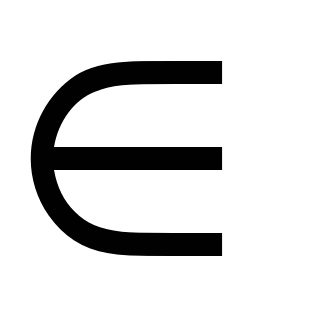 [-1; 5].
[-1; 5].
4. Не выполняя построения, определите, пересекаются ли парабола у =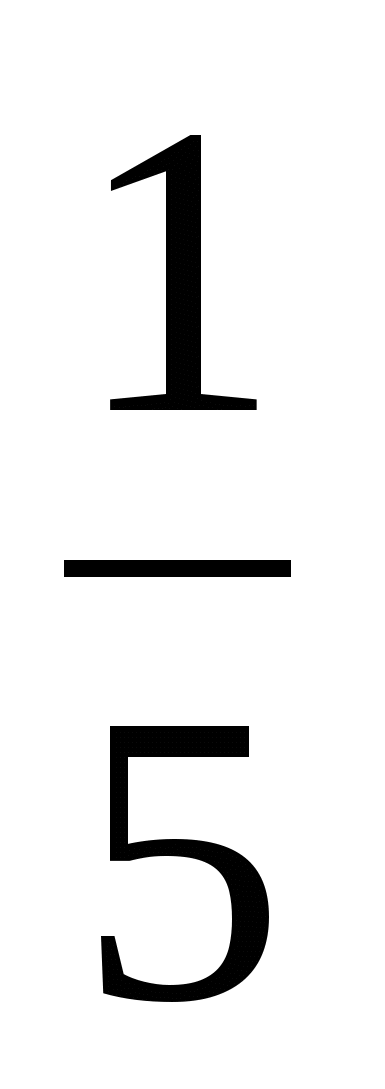 х2 и прямая у =20-3х. Если точки пересечения существуют, то найдите их координаты.
х2 и прямая у =20-3х. Если точки пересечения существуют, то найдите их координаты.
5. Найдите значение выражения 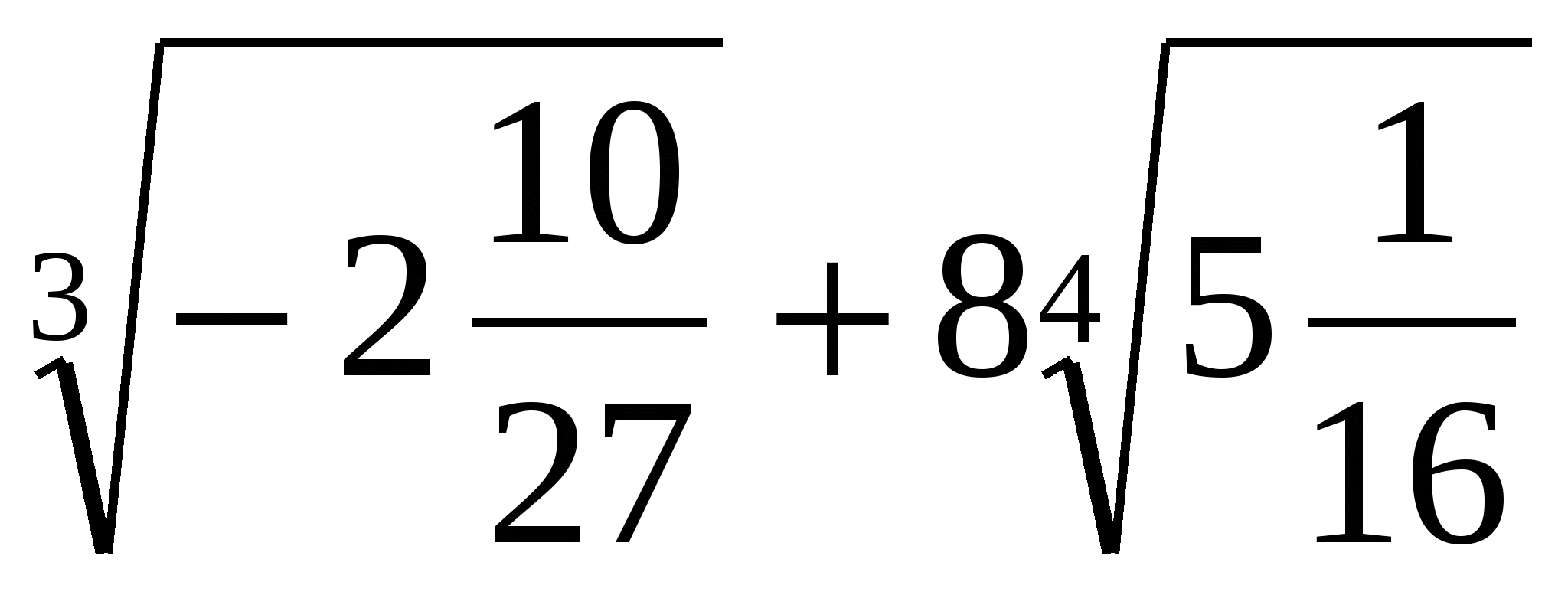 .
.
По учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год
Контрольная работа №3 по алгебре в 9 классе
по теме «Уравнения и неравенства с одной переменной»
Вариант 1
• 1. Решите уравнение: а) х3 - 81х = 0; б) 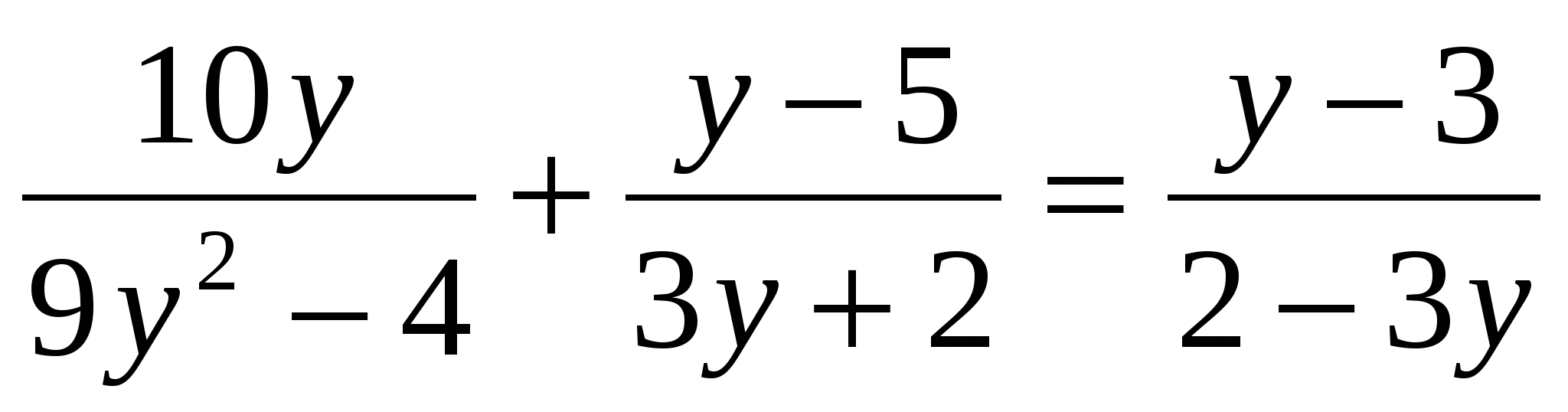 .
.
•2. Решите неравенство: а) 2х2 - 13х + 6 < 0; б) х2 > 9.
• 3. Решите неравенство методом интервалов:
а) (х +  (х - 4) (х - 7) > 0; б)
(х - 4) (х - 7) > 0; б)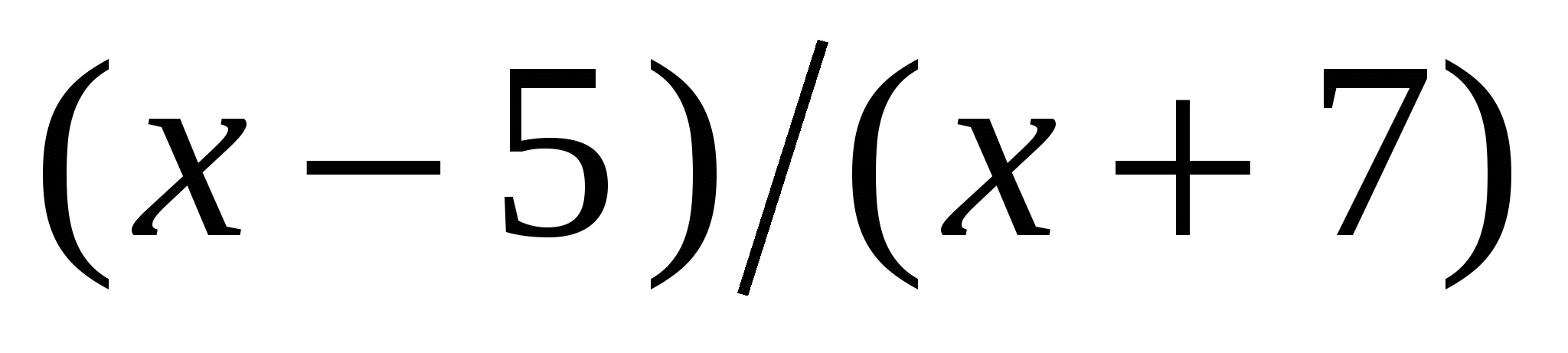 < 0.
< 0.
• 4. Решите биквадратное уравнение х4 - 19х2 + 48 = 0.
5. При каких значениях т уравнение 3х2 + тх + 3 = 0 имеет два корня?
6. Найдите область определения функции 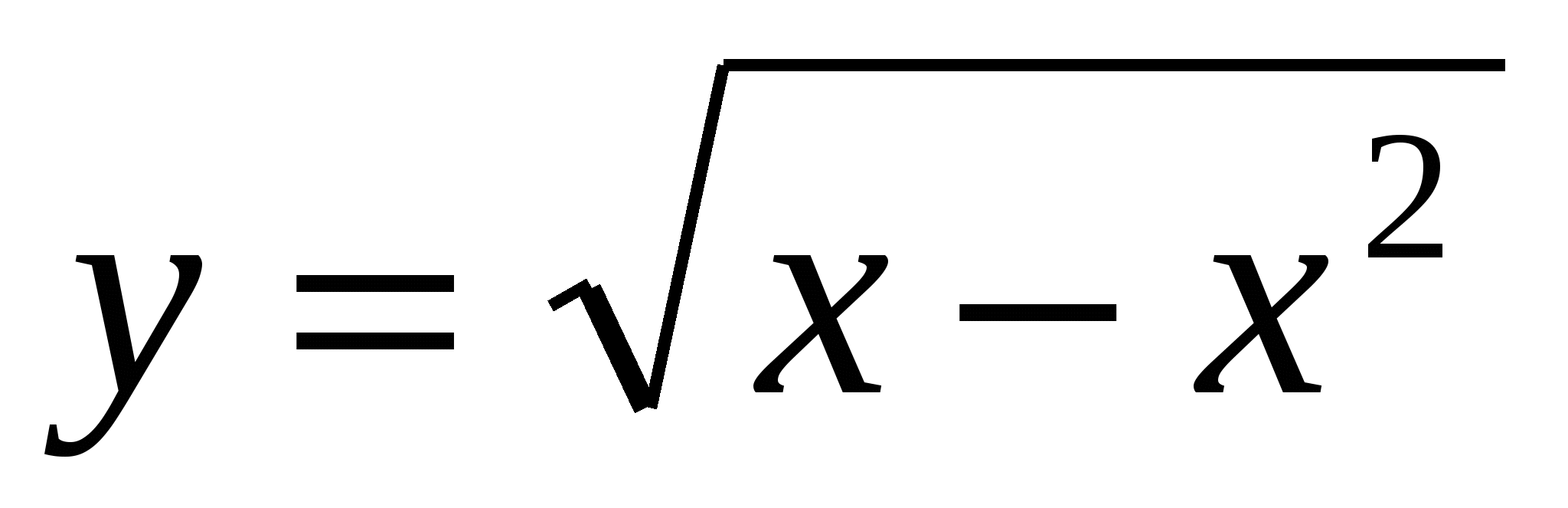 .
.
7. Найдите координаты точек пересечения графиков функций у = 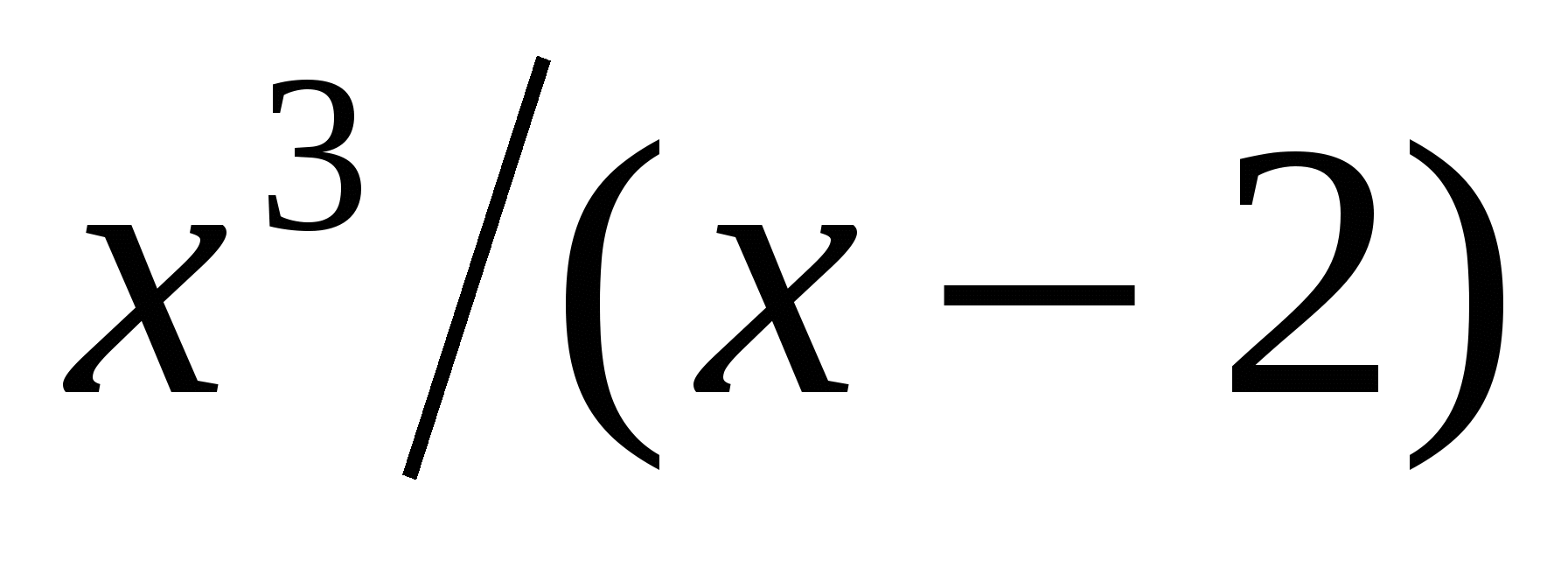 и y = x2 - 3x+1.
и y = x2 - 3x+1.
Вариант 2
• 1. Решите уравнение: а) x3 - 25x = 0; б) 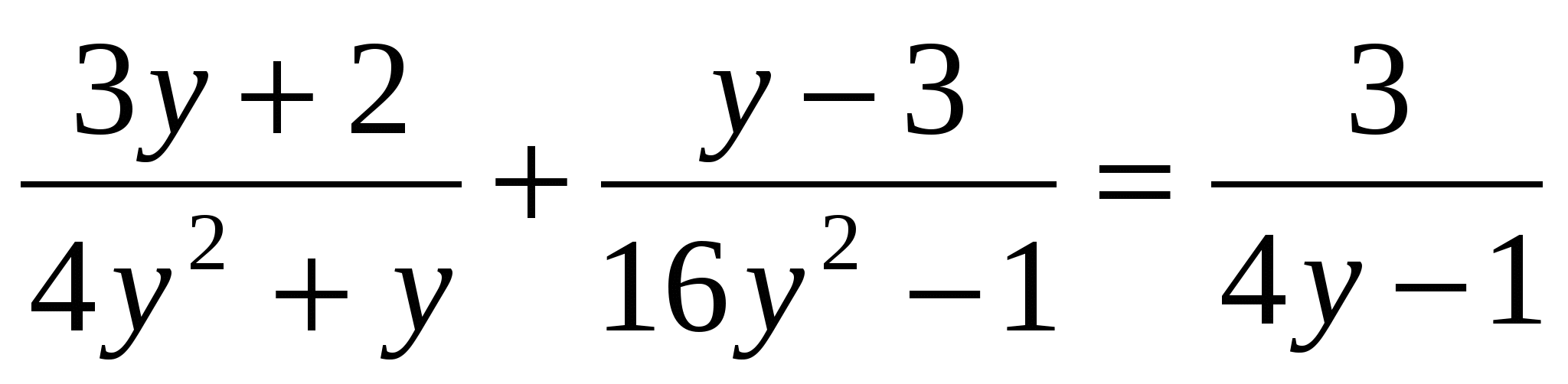 .
.
• 2. Решите неравенство: а) 2х2 - х - 15 > 0; б) х2 < 16.
•3. Решите неравенство методом интервалов:
а) (х + 11) (х + 2) (х - 9) < 0; б) 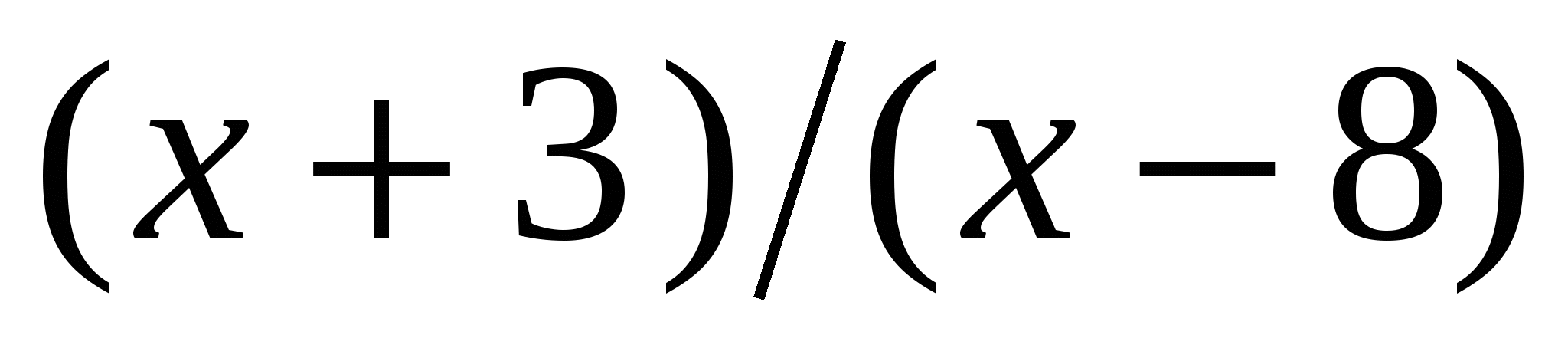 > 0.
> 0.
• 4. Решите биквадратное уравнение х4 - 4х2 - 45 = 0.
5. При каких значениях п уравнение 2х2 + пх + 8 = 0 не имеет корней?
6. Найдите область определения функции 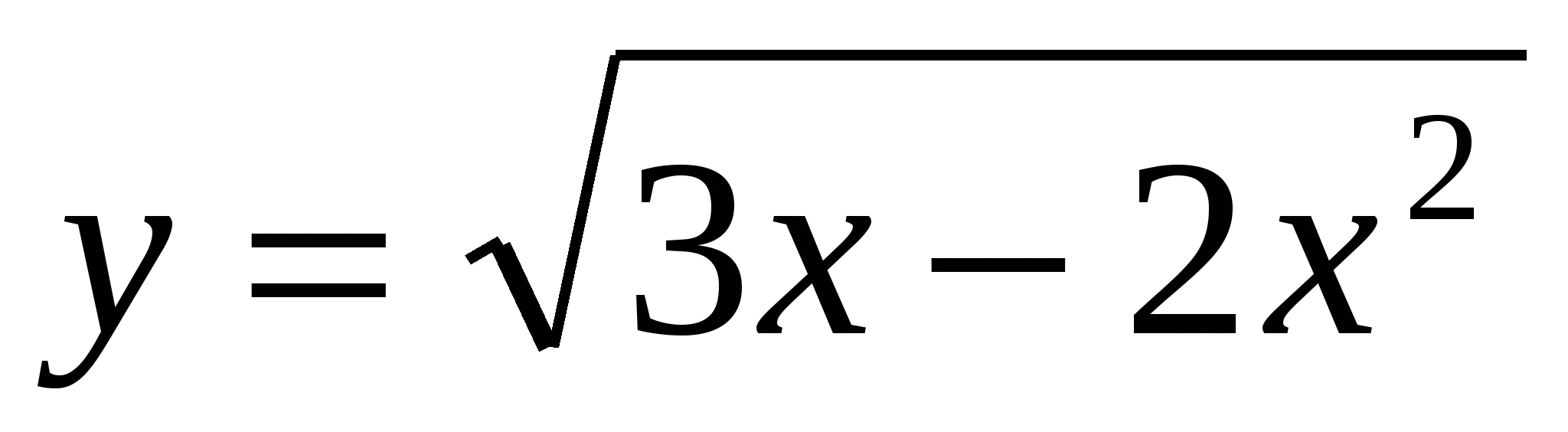
7. Найдите координаты точек пересечения графиков функций y = 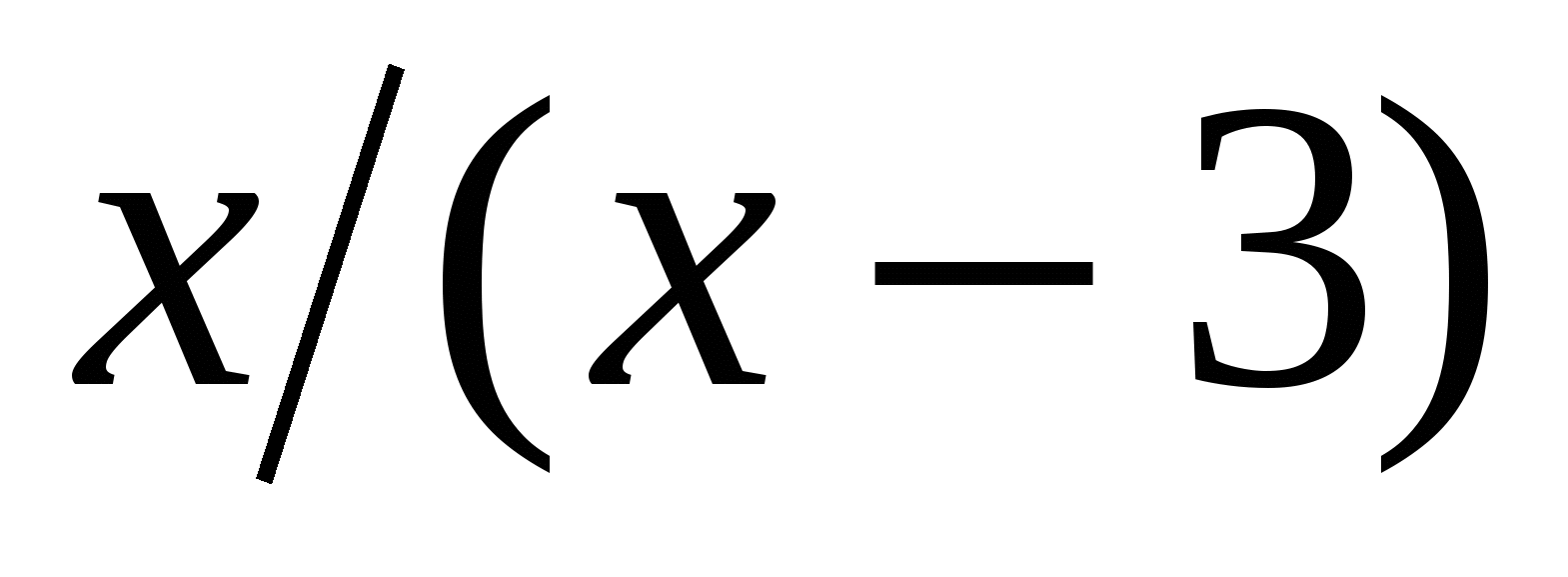 и y =
и y = 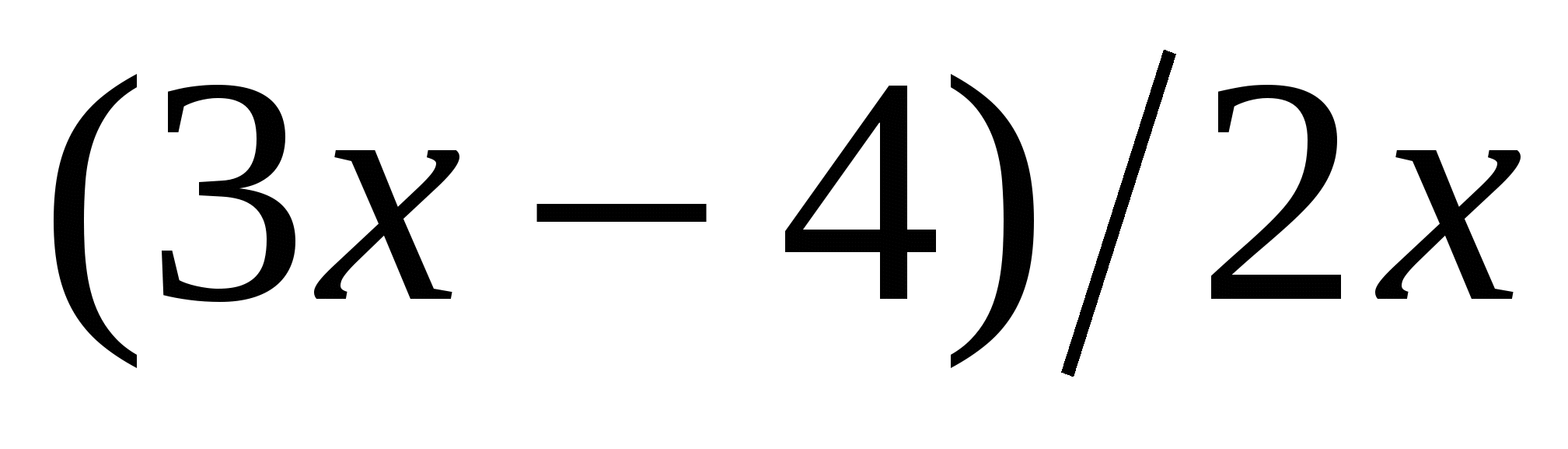 .
.
По учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год
Контрольная работа №4 по алгебре в 9 классе
по теме «Уравнения и неравенства с двумя переменными»
Вариант 1
• 1. Решите систему уравнений:
1. Решите систему уравнений:
2x + y = 7,
х2 - у = 1.
• 2. Периметр прямоугольника равен 28 м, а его площадь равна 40 м2. Найдите стороны прямоугольника.
•3. Изобразите на координатной плоскости множество решений системы неравенств:
х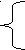 2 + у2
2 + у2 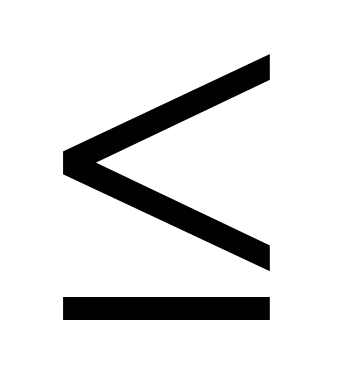 9,
9,
y 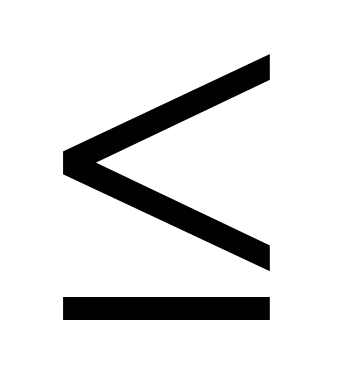 x + 1.
x + 1.
4. Не выполняя построения, найдите координаты точек пересечения параболы у = х2 + 4 и прямой х + у = 6.
5. Решите систему уравнений:
2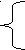 y - х = 7,
y - х = 7,
х2 – ху - у2= 20.
Вариант 2
• 1. Решите систему уравнений
1. Решите систему уравнений
x - 3y = 2,
xy + y = 6.
• 2. Одна из сторон прямоугольника на 2 см больше другой стороны. Найдите стороны прямоугольника, если его площадь равна 120 см2.
•3. Изобразите на координатной плоскости множество решений системы неравенств:
x 2 +у2
2 +у2 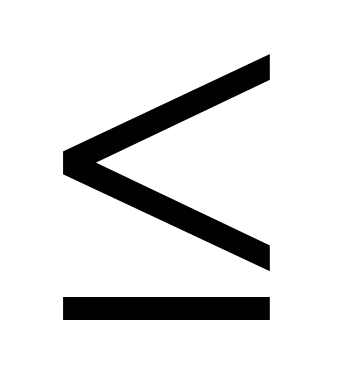 16,
16,
х + у 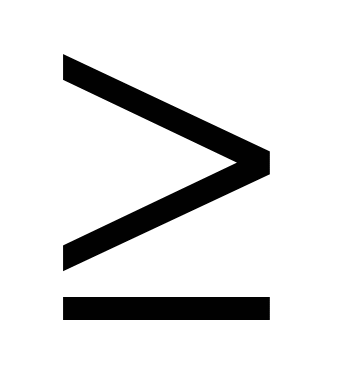 -2.
-2.
4. Не выполняя построения, найдите координаты точек пересечения окружности х2 + у2 = 10 и прямой х + 2у = 5.
5. Решите систему уравнений:
y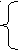 - 3x = l,
- 3x = l,
х2 - 2ху + у2 = 9.
По учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год
Контрольная работа №5 по алгебре в 9 классе
по теме «Арифметическая прогрессия»
Вариант 1
• 1. Найдите двадцать третий член арифметической прогрессии (аn), если а1 = -15 и d = 3.
• 2. Найдите сумму шестнадцати первых членов арифметической прогрессии: 8; 4; 0; ....
3. Найдите сумму шестидесяти первых членов последовательности (bn), заданной формулой bn = 3п - 1.
4. Является ли число 54,5 членом арифметической прогрессии (аn), в которой а1 = 25,5 и а9 = 5,5?
5. Найдите сумму всех натуральных чисел, кратных 3 и не превосходящих 100.
Вариант 2
• 1. Найдите восемнадцатый член арифметической прогрессии (аn),, если а1 = 70 и d = -3.
• 2. Найдите сумму двадцати первых членов арифметической прогрессии: -21; -18; -15; ....
3. Найдите сумму сорока первых членов последовательности (bn), заданной формулой bn = 4п - 2.
4. Является ли число 30,4 членом арифметической прогрессии (аn), в которой а1 = 11,6 и а15 = 17,2?
5. Найдите сумму всех натуральных чисел, кратных 7 и не превосходящих 150.
По учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год
Контрольная работа №6 по алгебре в 9 классе
по теме «Геометрическая прогрессия»
Вариант 1
• 1. Найдите седьмой член геометрической прогрессии (bn), если b1 = -32 и q =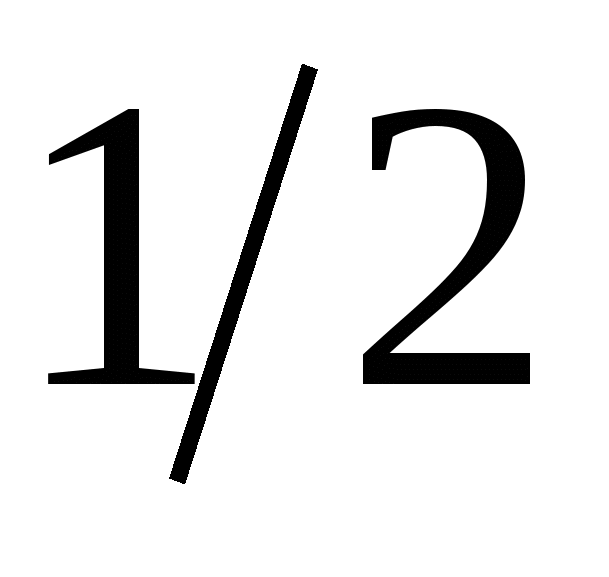 .
.
• 2. Первый член геометрической прогрессии (bn), равен 2, а знаменатель равен 3. Найдите сумму шести первых членов это прогрессии.
3. Найдите сумму бесконечной геометрической прогрессии: 24; -12; 6; ....
4. Найдите сумму девяти первых членов геометрической прогрессии (bn), с положительными членами, зная, что b2 = 0,04 и b4 = 0,16.
5. Представьте в виде обыкновенной дроби бесконечную десятичную дробь: а) 0,(27); б) 0,5(6).
Вариант 2
• 1. Найдите шестой член геометрической прогрессии (bn), если b1 = 0,81 и q = - 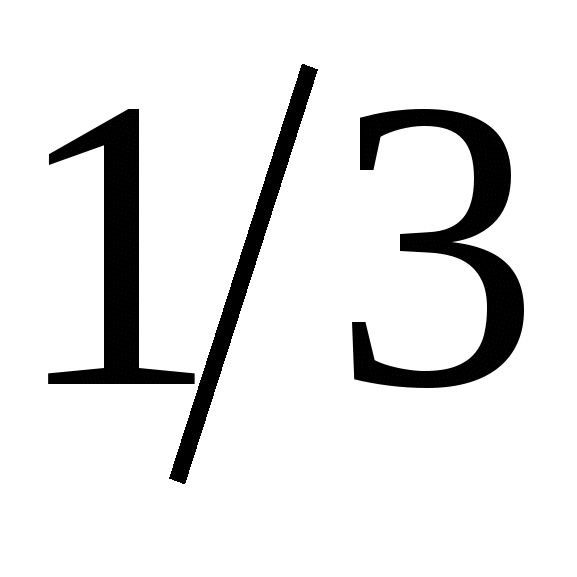 .
.
• 2. Первый член геометрической прогрессии (bn), равен 6, а знаменатель равен 2. Найдите сумму семи первых членов это прогрессии.
3. Найдите сумму бесконечной геометрической прогрессии: -40; 20; -10; ... .
4. Найдите сумму восьми первых членов геометрической прогрессии (bn), с положительными членами, зная, что b2 = 1,2 и b4 = 4,8.
5. Представьте в виде обыкновенной дроби бесконечную десятичную дробь: а) 0,(153); б) 0,3(2).
По учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год
Контрольная работа №7 по алгебре в 9 классе
по теме «Элементы комбинаторики и теории вероятности»
Вариант 1
• 1. Сколькими способами могут разместиться 5 человек в салоне автобуса на пяти свободных местах.
• 2. Сколько трехзначных чисел, в которых нет одинаковых цифр, можно составить из цифр 1, 2, 5, 7, 9?
• 3. Победителю конкурса книголюбов разрешается выбрать две книги из 10 различных книг. Сколькими способами он может осуществить этот выбор?
• 4. В доме 90 квартир, которые распределяются по жребию. Какова вероятность того, что жильцу не достанется квартира на первом этаже, если таких квартир 6?
5. Из 8 мальчиков и 5 девочек надо выделить для работы на пришкольном участке 3 мальчиков и 2 девочек. Сколькими способами это можно сделать?
6. На четырех карточках записаны цифры 1, 3, 5, 7. Карточки перевернули и перемешали. Затем наугад последовательно положили эти карточки в ряд одну за другой и открыли. Какова вероятность того, что в результате получится число 3157?
Вариант 2
• 1. Сколько шестизначных чисел можно составить из цифр 1, 2, 3, 5, 7, 9 без повторений цифр?
• 2. Из 8 учащихся класса, успешно выступивших на школьной олимпиаде, надо выбрать двух для участия в городской олимпиаде. Сколькими способами можно сделать этот выбор?
• 3. Из 15 туристов надо выбрать дежурного и его помощника. Какими способами это можно сделать?
• 4. Из 30 книг, стоящих на полке, 5 учебников, а остальные художественные произведения. Наугад берут с полки одну книгу. Какова вероятность того, что она не окажется учебником?
5. Из 9 книг и 6 журналов надо выбрать 2 книги и 3 журнала. Сколькими способами можно сделать этот выбор?
6. На пяти карточках написаны буквы а, в, и, л, с. Карточки перевернули и перемешали. Затем наугад последовательно эти карточки положили в ряд и открыли. Какова вероятность того, что в результате получится слово "слива"?
По учебнику « Алгебра 9 класс» Авторы: под редакцией Ю.Н. Макарычева, Н.Г. Миндюк, К.И.Нешкова, С.Б. Суворова. Издательство: М., «Просвещение», 2008 год
Итоговая контрольная работа по алгебре в 9 классе
Вариант 1
• 1. Упростите выражение: 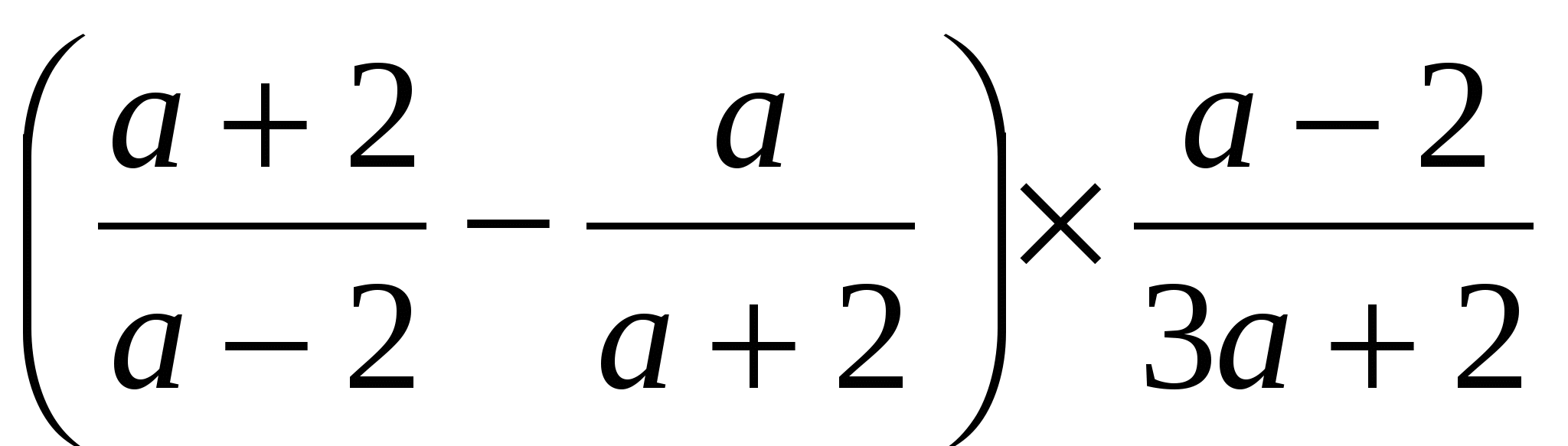 .
.
•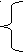 2. Решите систему уравнений:
2. Решите систему уравнений:
x - у = 6,
ху = 16.
• 3. Решите неравенство:
5х - 1,5 (2х + 3) < 4х + 1,5.
•4. Представьте выражение 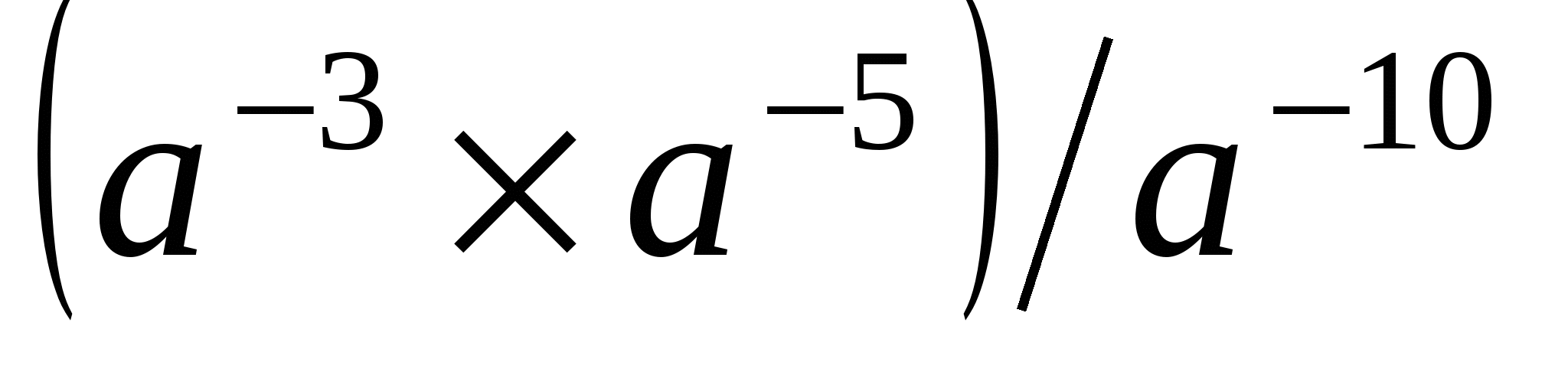 в виде степени с основанием а.
в виде степени с основанием а.
5. Постройте график функции у = х2 - 4. Укажите, при каких значениях х функция принимает положительные значения.
6. В фермерском хозяйстве под гречиху было отведено два участка. С первого участка собрали 105 ц гречихи, а со второго, площадь которого на 3 га больше, собрали 152 ц. Найдите площадь каждого участка, если известно, что урожайность гречихи на первом участке была на 2 ц с 1 га больше, чем на втором.
Вариант 2
• 1. Упростите выражение: 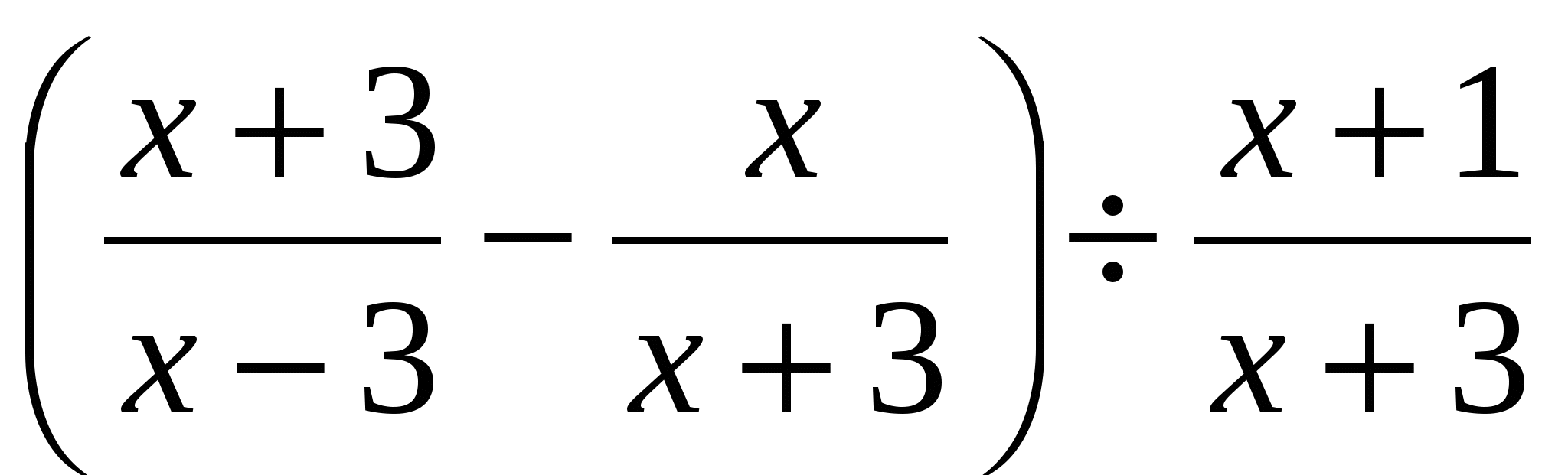 .
.
•2. Решите систему уравнений:
x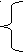 - у = 2,
- у = 2,
ху = 15.
• 3. Решите неравенство:
2х - 4,5 > 6х - 0,5 (4х - 3).
•4. Представьте выражение 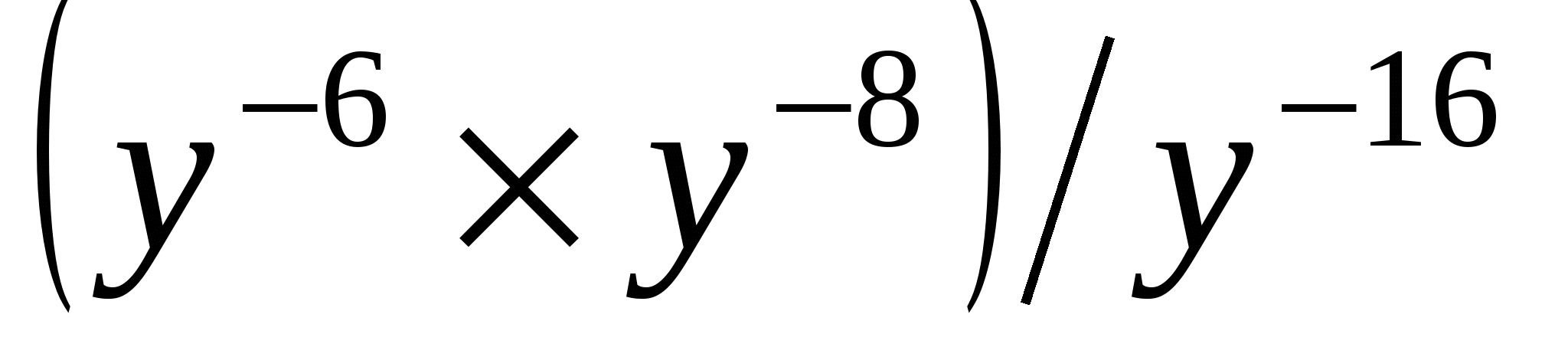 в виде степени с основанием у.
в виде степени с основанием у.
5. Постройте график функции у = -х2 + 1. Укажите, при каких значениях х функция принимает отрицательные значения.
6. Из пункта А в пункт В, расстояние между которыми 45 км, выехал велосипедист. Через 30 мин вслед за ним выехал второй велосипедист, который прибыл в пункт B на 15 мин раньше первого. Какова скорость первого велосипедиста, если она на 3 км/ч меньше скорости второго?