ГБПОУ Строгановский колледж
Контрольная работа по алгебре и началам математического анализа
Тема «Первообразная функции и интеграл»
2 курс системы НПО и 1 курс СПО
на базе основного образования
Разработано преподавателем математики
Пешковой Ольгой Алексеевной
Контрольная работа по теме «Первообразная функции и интеграл. Применение интеграла» ориентирована на учебник Ш.А.Алимова и др. «Алгебра и начала анализа» 1 и 2 курса колледжей по профессиям технического и естественно-математического профилей.
Контрольная работа предназначена для самостоятельной внеаудиторной работы.
Контрольная работа включает в себя 10 вариантов заданий одинакового уровня сложности. Вариант определяется последними цифрами номера зачетной книжки студента /или порядкового номера в журнале теоритических занятий/.
Работа выполняется студентом в отдельной тетради с соответствующим оформлением титульного листа. На титульном листе указывается дисциплина, название контрольной работы, номер варианта, фамилия, имя и отчество студента, группа.
Оформление работы должно соответствовать «Единым требованиям оформления письменных работ по математике».
Правильное выполнение каждого задания оценивается 1 баллом. Максимально возможное количество баллов за контрольную работу – 12. Для того чтобы работа была зачтена, необходимо выполнить все задания и набрать не менее 8 баллов.
Задание 1. Найти первообразные следующих функций
1 вариант
а) у = 1 б) 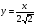 в) у =3sin x г)
в) у =3sin x г) 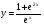 д)
д) 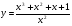 е) y = sin 2x + 2cos 3x
е) y = sin 2x + 2cos 3x
2 вариант
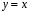 б)
б) 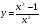 в)
в) 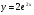 г)
г) 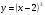 д)
д) 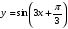 е)
е) 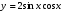
3 вариант
а) 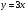 б)
б) 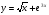 в)
в) 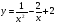 г)
г) 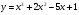 д)
д) 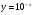 е)
е) 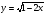
4 вариант
а) 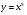 б)
б) 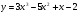 в)
в) 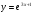 г)
г) 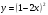 д)
д) 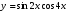 е)
е) 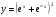
5 вариант
а) 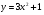 б)
б) 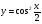 в)
в) 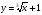 г)
г) 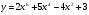 д)
д) 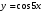 е)
е) 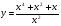
6 вариант
а) 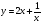 б)
б) 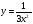 в)
в) 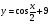 г)
г) 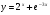 д)
д) 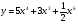 е)
е) 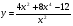
7 вариант
а) 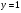 б)
б) 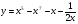 в)
в) 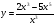 г)
г) 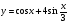 д)
д) 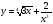 е)
е) 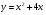
8 вариант
а) 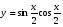 б)
б) 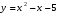 в)
в) 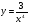 г)
г) 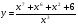 д)
д) 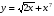 е)
е) 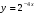
9 вариант
а) 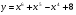 б)
б) 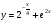 в)
в) 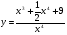 г)
г) 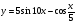 д)
д) 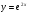 е)
е) 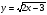
10 вариант
а) 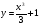 б)
б) 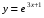 в)
в) 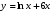 г)
г) 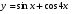 д)
д) 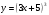 е)
е) 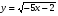
Задание 2 Вычислить площадь фигуры ограниченной линиями
1 вариант
а) x = -1 x = 2 y = 0 y = x2 – 1
б) y = 0 y = 1 – x2
2 вариант
x = 0 x = 3 y = 0 y = - x2 + 1
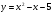 y = x - 2
y = x - 2
3 вариант
a) x = 1 x = 2 y = 0 y = x2 + 1
b)
4 вариант
x = -1 x = 1 y = 0 y = x2 - 2
5 вариант
x = 1 x = 4 y = 0 y = x - 1
6 вариант
x = 1 x = 4 y = 0 y = 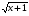
7 вариант
x = 0 x = 2 y = 0 y = x3
8 вариант
x = 1 x = 2 y = 0 y = 2x2
9 вариант
x = -1 x = 2 y = 0 y = 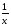
10 вариант
x = 1 x = 2 y = 0 y = 2x
Задание 3 Вычислить определенный интеграл
1 вариант
а) 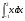 б)
б) 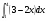 в)
в) 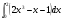 г)
г) 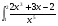
2 вариант
а) 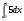 б)
б) 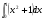 в)
в) 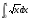 г)
г) 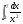
3 вариант
а) 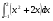 б)
б) 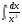 в)
в) 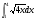 г)
г) 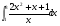
4 вариант
а) 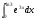 б)
б) 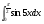 в)
в) 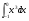 г)
г) 
5 вариант
а) 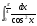 б)
б) 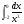 в)
в) 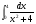 г)
г) 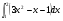
6 вариант
а) 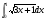 б)
б) 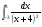 в)
в) 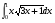 г)
г) 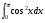
7 вариант
а) 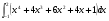 б)
б) 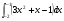 в)
в) 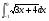 г)
г) 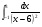
8 вариант
а) 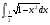 б)
б) 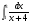 в)
в) 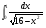 г)
г) 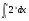
9 вариант
а) 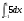 б)
б) 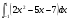 в)
в) 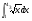 г)
г) 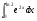
10 вариант
а) 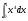 б)
б) 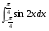 в)
в) 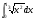 г)
г) 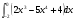
Задание 4 Найти общее решение дифференциального уравнения
1 вариант а) 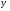 ’=x2 б) y’= y
’=x2 б) y’= y
2 вариант а) y’= 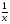 б) y’= 2y
б) y’= 2y
3 вариант а) y’= sin x б) y’=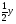
4 вариант а) y’ = 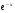 б) y’ = y2
б) y’ = y2
5 вариант а) y’ = 2x + 1 б) y’ = -5y
6 вариант а) y’ = x2 + x б) y’ = = y
7 вариант а) y’ = sin x б) y’ = 5y
8 вариант а) y’ = 2 cos x б) y’ = 6y
9 вариант а) y’ = 5x4 б) y’ = 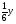
10 вариант а) y’ = -6x б) y’ = - y
Задание 5 Найти частное решение дифференциального уравнения
1 вариант а) y’ = x2 y(2 ) = 1
2 вариант а) y’ = 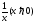 y(e ) = 1
y(e ) = 1
3 вариант а) y’ = e-x y(0) = -2
4 вариант а) y’ = 2cos x y(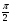 ) = 3
) = 3
5 вариант а) y’ = 3x + 2 y(1) = 4
6 вариант а) y’ = x3 y(1) = 3
7 вариант а) y’ = 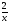 y(-1) = 2
y(-1) = 2
8 вариант а) y’ = x + 2x2 y(1) = 1
9 вариант а) y’ = x3 + 1 y(-1) = 2
10 вариант а) y’ = 2 – 3x y(1) = 6
Задание 6 Вычислить значения скорости V(t) м/с и перемещения S(t) м материальной точки за время t c, если ускорение
1 вариант a(t) = 3t + 2 t = 3 c
2 вариант a(t) = - 3t + t2 t = 1 c
3 вариант a(t) = 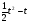 t = 2 c
t = 2 c
4 вариант a(t) = -2t3 + 4 t = 2 c
5 вариант a(t) = 2t2 – 3 t = 1 c
6 вариант a(t) = -6 + t3 t = 4 c
7 вариант a(t) = 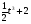 t = 5 c
t = 5 c
8 вариант a(t) = 3x5+2 t = 1 c
9 вариант a(t) = -2x3 – 4 t = 4 c
10 вариант a(t) = 3 + 4t3 t = 2 c
Задание 7 Вычислить объем тела, полученного вращением графика функции y = f (x) вокруг оси Ох
1 вариант f(x) = x3 + 2 a = 0 b = 2
2 вариант f(x) = - x2 + 1 a = 1 b = 2
3 вариант f(x) = 2 – 2x3 a = - 1 b = 0
4 вариант f (x) = 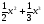 a = 1 b = 4
a = 1 b = 4
5 вариант f(x) = x2 + 1 a = 1 b = 3
6 вариант f(x) = 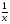 a = 2 b = 3
a = 2 b = 3
7 вариант f(x) = 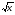 a = 1 b = 4
a = 1 b = 4
8 вариант f(x) = cos x a = 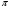 b =
b = 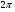
9 вариант f(x) = sin x a = 0 b = 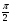
10 вариант f(x) = x + 1 a = 2 b = 4
Задание 8 Найти неопределённые интегралы
1 вариант
а) 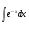 б)
б) 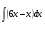 в)
в) 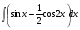 г)
г) 
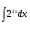
2 вариант
а) 
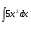 б)
б) 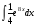 в)
в) 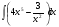 г)
г) 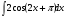
3 вариант
а) 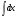 б)
б) 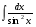 в)
в) 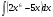 г)
г) 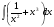
4 вариант
а) 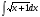 б)
б) 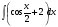 в)
в) 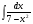 г)
г) 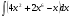
5 вариант
а) 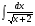 б)
б) 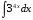 в)
в) 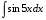 г)
г) 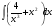
6 вариант
а) 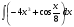 б)
б) 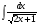 в)
в) 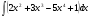 г)
г) 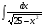
7 вариант
а) 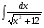 б)
б) 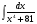 в)
в) 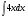 г)
г) 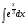
8 вариант
а) 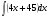 б)
б) 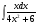 в)
в) 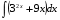 г)
г) 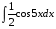
9 вариант
а) 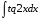 б)
б) 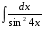 в)
в) 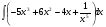 г)
г) 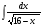
10 вариант
а) 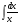 б)
б) 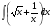 в)
в) 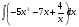 г)
г)