ОГБОУ «Смоленская специальная (коррекционная)
общеобразовательная школа I и II видов»
Центр дистанционного образования
Смоленск
Конспект урока по алгебре в 8 классе «Квадратные корни.
Арифметический квадратный корень»
подготовила
учитель математики
Швечкова Алеся Михайловна
Смоленск
2012
Тема: «Квадратные корни. Арифметический квадратный корень».
Цели: ввести понятия квадратного корня и арифметического квадратного корня; сформировать умение извлекать квадратные корни; развивать логическое мышление, смекалку.
Оборудование: компьютер, презентация, интерактивная доска scriblink.
План урока:
Организационный момент.
Устная работа.
Объяснение нового материала.
Формирование умений и навыков.
Итоги урока.
Домашнее задание.
Ход урока:
Организационный момент.
Сообщение темы и целей урока.
(слайд 1)
Устная работа.
Вычислите:
а) 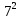 ; б)
; б) 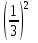 ; в)
; в) 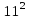 ; г)
; г) 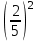 ;
;
д) 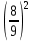 ; е)
; е) 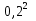 ; ж)
; ж) 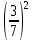 ; з)
; з) 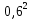 .
.
(слайд 2)
Объяснение нового материала.
Введение понятия квадратного корня.
Рассмотрим задачу о нахождении стороны квадрата по его площади.
Пусть площадь квадрата равна 64 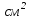 . Чему равна длина стороны этого квадрата?
. Чему равна длина стороны этого квадрата?
Обозначим длину стороны квадрата (в сантиметрах) буквой х. Тогда площадь квадрата будет 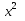 см². По условию площадь равна 64 см², значит х²=64.
см². По условию площадь равна 64 см², значит х²=64.
Корнями уравнения х²=64 являются числа: 8 и — 8. Действительно, 8²=64 и (-8)²=64. Так как длина не может выражаться отрицательным числом, то условию задачи удовлетворяет только один из корней — число 8. Итак, длина стороны квадрата равна 8 см.
Корни уравнения х²=64, т.е. Числа, квадраты которых равны 64, называют квадратными корнями из числа 64.
(слайд 3)
Задание. Вместо пустых клеточек поставьте числа так, чтобы равенства были верными:
²=16 ²=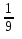 ²=100
²=100
Определение. Квадратным корнем из числа а называют число, квадрат которого равен а.
Задание: выяснить, является ли число n квадратным корнем из числа m, если:
а) n=5, m=25; в) n=0,3, m=0,9;
б) n= - 7, m=49; г) n=6, m= - 36.
(слайд 4)
Введение понятия арифметического квадратного корня.
Учащиеся должны усвоить существенный признак данного понятия — арифметический квадратный корень является неотрицательным числом (то есть необходимо знание того, что равенство 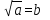 означает одновременно выполнение двух условий: b²=a и b≥0).
означает одновременно выполнение двух условий: b²=a и b≥0).
Число 8 — неотрицательный корень уравнения х²=64 — называют арифметическим квадратным корнем из 64. Иначе говоря, арифметический квадратный корень из 64 — это неотрицательное число, квадрат которого равен 64.
Определение. Арифметическим квадратным корнем из числа а называется неотрицательное число, квадрат которого равен а.
Задание: определить, является ли число n арифметическим квадратным корнем из числа m, если:
а) n=8, m=64; в) n=0,2, m=0,4;
б) n= - 3, m=9; г) n=0,4, m=0,16.
(слайд 5)
Физкультминутка. Гимнастика для глаз: быстро поморгать, закрыть глаза и посидеть спокойно, медленно считая до 5 (повторить 4–5 раз).
Историческая справка.
Обратим внимание на совпадение в терминах — квадратный корень и корень уравнения. Это совпадение неслучайно. Уравнения вида х²=а исторически были первыми сложными уравнениями, и их решения были названы корнями по метафоре, что из стороны квадрата, как из корня, вырастает сам квадрат. В дальнейшем термин «корень» стал употребляться и для произвольных уравнений.
Название «радикал» тоже связано с термином «корень»: по-латыне корень — radix (он же редис — корнеплод). Также слово «радикальный» в русском языке является синонимом слова «коренной». Происхождение же символа √ связывают с написанием латинской буквы r.
(слайд 6)
Основное свойство арифметического квадратного корня.
Вычислите значения следующих выражений:
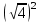 ,
, 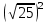 ,
, 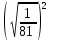 .
.
Сформулируйте вывод:
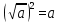 , если а≥0
, если а≥0
(слайд 7)
Формирование умений и навыков.
Найдите значение арифметического квадратного корня:
а) 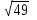 ; б)
; б) 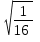 ; в)
; в) 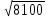 ; г)
; г) 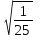 ; д)
; д) 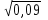 ; е)
; е) 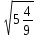 .
.
Найдите значение выражения:
а) 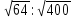 ; б)
; б) 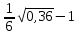 ; в)
; в) 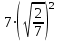 ; г)
; г) 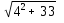 .
.
Укажите натуральные значения n, при которых является натуральным числом значение выражения
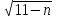
(Решение: чтобы значение выражения 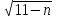 являлось натуральным числом, подкоренное выражение должно быть равно 1, 4 или 9. Получаем 3 случая:
являлось натуральным числом, подкоренное выражение должно быть равно 1, 4 или 9. Получаем 3 случая:
11 — n=1 11 — n=4 11 — n=9
n=10 n=7 n=2
Эти же значения можно было найти подбором.
Ответ: 2, 7, 10.)
(слайд 
Итоги урока.
Что называется квадратным корнем из числа а?
Сколько квадратных корней может быть из числа а?
Что такое арифметический квадратный корень из числа а?
Имеет ли смысл запись
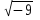 ? Почему?
? Почему?
(слайд 9)
6. Домашнее задание:
Найдите значение выражения:
а) 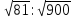 ; б)
; б) 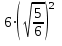 ; в)
; в) 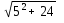 .
.
(слайд 10)
Презентация в картинках
Слайд 1:

Слайд 2:

Слайд 3:

Слайд 4:

Слайд 5:

Слайд 6:

Слайд 7:

Слайд 8:

Слайд 9:

Слайд 10:

Список использованной литературы:
Алгебра. 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.Б. Суворовой / авт.-сост. Т.Ю. Дюмина, А.А. Махонина. - Волгоград: Учитель, 2011. - 399 с.