Муниципальное общеобразовательное учреждение

Средняя общеобразовательная школа № 34 города Томска

Программа

элективного курса по выбору

для предпрофильной подготовки

в 9 классе«Линейная алгебра»

Подготовила

учитель математики

Пихтовникова Светлана Александровна

Томск 2010

Линейная алгебра: решение систем уравнений матричным способом

Программа элективного курса.

9 класс.

Пихтовникова Светлана Александровна,

учитель математики,

высшей категории

МОУ СОШ № 34 города Томска

Пояснительная записка.

Содержание курса соответствует целям предпрофильного обучения, который направлен на достижение нового качества обучения математике с учетом современных требований в условиях организации предпрофильной подготовки и введение профильного обучения, на предварительное самоопределение учащихся в отношении собственного профильного направления в образовании.

• Дает обучающимся возможность реализовать свой интерес к выбранному предмету;

• Помогает уточнить готовность и способность обучающихся осваивать выбранный предмет на повышенном уровне;

• Создает условия для подготовки к экзаменам по выбору (будущее профилирующие);

• Создает условия для осознанного и успешного выбора профиля выпускником основной школы.

Содержание учебного материала включает темы, полезные для дальнейшего выбора профиля обучения.

• Программа содержит все знания, необходимые для достижения запланированных целей.

• включены прогрессивные научные знания и наиболее ценный опыт практической деятельности человека.

• применима для различных групп (категорий) школьников, что достигается обобщённостью включённых в неё знаний, их отбором в соответствии с общими для всех учащихся задачами предпрофильного обучения, модульным принципом построения программы. Доля необобщённых знаний: частного опыта, фактов, информации сведена в программе к минимуму.

• Содержание направлено на передачу знаний, необходимых для формирования компетенции в предметной области, а также зрелости в выборе профиля обучения.

• Предполагается применение активных методов обучения, использование ИКТ.

• Изучение всех последующих знаний обеспечивается предыдущими, наличие связей между частными и общими знаниями.

• Способ развёртывания содержания избирается в зависимости от стоящих в программе целей (формирования теоретического или эмпирического мышления).

• Обеспечивается степенью операциональности описания тех знаний, которые предполагается сформировать, а также выделением результатов подготовки по каждой из ведущих тем или по программе в целом.

• Возможность в любой момент обучения установить степень достижения промежуточных и итоговых результатов обучения и выявить сбой в прохождении программы.

• Делается крен в сторону "абитуриентской" математики. Этому способствует набор тем, рассматриваемых в процессе изучения курса.

Цели курса:

Выявление интересов, проверка возможностей ученика на основе широкой палитры небольших курсов, охватывающих основные области знания, позволяющие составить представление о характере профессионального труда людей на основе личного опыта

(«Концепция профильного обучения»)

Выявление и формирование средствами математики направленности личности, ее профессиональных интересов.

- Формирование деятельностных способностей учащихся: способностей к самоопределению, самореализации, рефлексии собственной деятельности.

- Формирование и развитие мышления.

- Овладение комплексом математических знаний, умений и навыков.

- Решение полезных задач для подготовки к ЕГЭ, в том числе и абитуриентского плана

Задачи :

• Оказать психолого-педагогическую помощь в приобретении школьниками представлений о жизненных, социальных ценностях, в том числе, связанных с профессиональным становлением;

• Обеспечить индивидуализацию обучения;

• Дать возможность реализовать свои образовательные запросы;

• Формировать способности принимать адекватное решение о выборе дальнейшего направления образования, пути получения профессии.

• Уметь решать системы уравнений различными способами как школьного курса так и способами высшей школы (линейная алгебра);

• Уметь применять ЗУН при решении трудных заданий, из ЕГЭ, практических задач.

Распределение программного материала по времени с учётом его достаточности для

• качественного изучения и получения запланированных результатов;

• устранения возможных сбоев;

применения наиболее эффективных методов обучения. Нахождение наиболее «короткого» пути качественного изучения материала.

Преобладающие методы обучения:

• Проблемный;

• Исследовательский;

• Практикумы;

• Самостоятельная работа обучающихся;

• Уроки с компьютерной поддержкой;

• Лекционные занятия;

• Проектный;

• Коллективная работа, проблемная группа по методу проекта.

Предпрофильное обучение элективных курсов осуществляется в форме:

• Лекционных занятий;

• Практикумов;

• Уроки исследования;

• Уроки с использованием ИКТ;

• Защита проектов, творческих заданий, рефератов.

Технологии обучения.

Так как в основу организации предпрофильного обучения заложены основные идеи личностно – ориентированного подхода в овладении системой ЗУН, то наиболее эффективными в условиях ППО и профильной школы, а также для организации данного элективного курса в школе являются:

• Обучение укрупненными дидактическими единицами;

• КСО (в парах: контроль и самоконтроль, проблемные группы);

• Технология полного усвоения знаний (есть разные уровни заданий, контрольные тесты, дидактический материал, все сделал только тогда - к следующему);

• Компьютерные технологии;

• ТРИЗ (технические решения изобретательных задач) ;

• Технология проектного обучения.

Дидактические принципы организации УВП на элективных курсах по математике являются принципами развивающего обучения:

1. Принцип деятельности: ученик

является не объектом, а субъектом деятельности Технология деятельностного метода:

1.Самоопределение к деятельности

2.Актуализация знаний

3.Постановка учебной задачи

4.Построение проекта выхода из затруднения

5.Первичное закрепление во внешней речи

6.Самостоятельная работа с самопроверкой по эталону

7.Включение в систему знаний и повторение

8.Рефлексия деятельности (итог урока)

2. Принцип вариативности: самостоятельный выбор учащимися вариантов своего профиля

3. Принцип минимакса: Разведение уровня подачи материала и уровня требований к его освоению. Разноуровневое содержание курса. 4. Принцип психологической комфортности: Снятие стрессобразующих факторов учебного процесса, создание доброжелательной атмосферы, ориентированной на реализацию идей педагогики сотрудничества. 5. Принцип творчества: Максимальная ориентация на творческое начало в учебной деятельности учащихся, приобретение ими собственного опыта творческой деятельности.

1) Самоопределение к деятельности: положительный настрой на работу 2) Актуализация знаний: подготовка мышления учащихся к проектировочной деятельности. Этап завершается осмыслением затруднений в индивидуальной деятельности3) Постановка учебной задачи: выявление и фиксация причины затруднений. Постановка цели урока, связанной с устранением причины затруднения. Формулировка темы урока.

4) Построение проекта выхода из затруднения: Построение нового способа действия на основе выбранного метода решения учебной задачи Этап завершается фиксацией решения учебной задачи5) Первичное закрепление во внешней речи: Решение типовых заданий на новый способ действий с проговариванием способа решения во внешней речи

6) Самостоятельная работа с самопроверкой поэталону: Самостоятельное выполнение заданий на новый способ действий и их самопроверка по эталону. Организация ситуации успеха.

7) Включение в систему знаний и повторение: Выполнение заданий, где новый способ действий используется как шаг в более общем алгоритме решения.Решение заданий на тренировку ранее изученных алгоритмов, с целью подготовки введения нового знания. Рефлексия деятельности (итог урока): Самооценка детьми собственной деятельности.Соотнесение полученных результатов с поставленной целью деятельности.Цель дальнейшей деятельности.

Методами учета и оценки результатов обучения являются тестирование, входной контроль(+ итоговый), рейтинг итоговый, а также возможно составление

учебного портфолио по математике :

-работы ученика, как классные самостоятельные, так и домашние;

- прикладные математические проекты (индивидуальные или групповые);

- решения сложных занимательных задач;

- решение задач из учебника, выполненных самостоятельно сверх учебной программы;

- математическое сочинение по сложным вопросам темы;

-математический реферат с историческим содержанием;

- фотографии или зарисовки наглядных пособий по учебным темам, моделей, изготовленных учащимся или группой учащихся;

- копии статей из журналов, книг или Интернет, прочитанных учащимся по конкретной теме;

- задачи, составленные самими учащимся;

- уровень реальных достижений и описание причин в случае недостижения целей;

- графические работы учащихся, выполненные по данным темам;

- описание экспериментов и лабораторных работ, выполненных учащимся как индивидуально, так и в группе;

- тексты докладов, прочитанных учеником на конференциях;

- копии работ учащегося, выполненные на элективных курсах;

- дипломы, поощрения, награды по математике;

- лист целей, которых учащийся хотел бы достигнуть после изучения учебной темы; уровень реальных достижений и описание причин в случае недостижения целей.

- заметки учителя по наблюдению за данным учащимся на уроках математики;

- листы проверок учителя с комментариями (участие в работе класса, посещаемость, уровень и качество выполнения работ);

- математическая характеристика, включающая количественные и качественные результаты;

- отзывы других учителей, администрации, родителей, одноклассников, общественных организаций и др.

Критерии оценки портфолио (описание предполагаемых результатов):

• Развитость математического мышления (гибкость, рациональность, оригинальность мышления);

• сформированность умения решать задачи;

• сформированность прикладных умений (способность решать практические проблемы, прикладные задачи);

• развитость коммуникативных умений (умение работать в малых группах, умение выступать с математическими докладами, сформированность письменного математического языка, умение чётко и аргументированно излагать свою мысль, грамотность в оформлении решений задач и доказательств теорем, умелое использование графиков, диаграмм, таблиц и т.д.);

• сформированность навыков самоконтроля и самооценки (самокритичность, умение работать над ошибками, реалистичность в оценке своих способностей…)

Уровни итоговой оценки.

• Самый высокий уровень (“отлично”). Учебные портфолио характеризуются всесторонностью в отражении основных категорий и критериев оценки. Содержание свидетельствует о больших приложенных усилиях и очевидном прогрессе учащегося по уровню развития его математического мышления, умения решать задачи, прикладных и коммуникативных умений, наличия высокого уровня самооценки и творческого отношения к предмету. В содержании и оформлении портфолио ярко проявляются оригинальность и изобретательность.

• Высокий уровень (“хорошо”). Портфолио демонстрирует солидные математические знания и умения учащегося, но, в отличие от предыдущего, в нём могут отсутствовать некоторые элементы из необязательных категорий, а также может быть недостаточно выражена оригинальность в содержании и отсутствовать творческий элемент в оформлении.

• Средний уровень (“удовлетворительно”). В портфолио основной акцент сделан на обязательной категории, по которой можно судить об уровне сформированности программных знаний и умений. Отсутствуют свидетельства, демонстрирующие уровень развития творческого математического мышления, прикладных умений, способностей к содержательной коммуникации на языке математики (как устном, так и письменном).

• Слабый уровень (“неудовлетворительно”). По портфолио трудно получить общее представление о математических способностях учащегося. В нём представлены отрывочные задания из разных категорий, отдельные листы с неполностью выполненными заданиями, образцы попыток выполнения графических работ и т.п. Практически невозможно определить прогресс в обучении и уровень сформированности качеств, отражающих основные цели курса и критерии оценки.

ТЕМАТИЧЕСКОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА.

№

Тема

Кол.час

Вид занятий

1

Основные понятия

1

Лекция

2

Уравнение с двумя переменными и его график

1

Практикум,

Лаб работа

3

Система уравнений с двумя переменными

1

Лекция

4

Метод подстановки

2

Лекция

Практикум в компьют классе

5

Метод алгебраического сложения

2

Лекция

Практикум в компьют классе.

Зачет .

6

Другие способы решения систем уравнений

1

Практикум в компьют классе.

7

Решение задач

2

Лекция

Зачет .

Творч. отчет

8

Определители. Свойства и вычисления

• Общие понятия

• Свойства

• Вычисления определителя

1

Лекция +

практикум

9

Матрицы и действия над ними

• Виды матриц

• Линейные операции

• Нелинейные операции

• Обратная матрица

• Матричные уравнения

• Ранг матрицы

1

Лекция

10

Системы линейных уравнений

• Общие понятия

• Метод Крамера

• Матричный метод

• Метод Гаусса

• Однородные системы

4

Лекция

Практикум

Защита Творч. Работ,

проектов

Защита проектов

1

Формой итогового контроля являются рефераты, проекты, практикумы в компьютерном классе, презентации которые проходят на уроках в своем, чужом классах, на элективных курсах, на школьной и городской НПК.

Темы проектов:

1. Экскурс в историю решений систем уравнений;

2. Сравнительная характеристика подачи способа подстановки в различных учебных пособиях;

3. Сравнительная характеристика подачи способа алгебраического сложения в различных учебных пособиях;

4. Графический способ решения систем уравнений;

5. Различные способы решения систем уравнений;

6. Составление базы заданий по различным способам решений;

7. Составление базы практических, прикладных, исторических задач по данной теме.

8. Решение одной системы уравнений всеми известными и возможными способами

Темы рефератов:

1. Матрицы и действия над ними;

2. Решение систем уравнений методом Крамера;

3. Решение систем уравнений методом Гаусса;

4. Решение систем уравнений матричным методом.

5. Собственные векторы и собственные значения матриц;

6. Определители. Свойства и вычисления.

7. Системы уравнений и их способы решений.

Содержание блоков:

1. Основные понятия систем линейных уравнений, и уравнений второй степени с двумя переменными ;

2. решение систем уравнений различными способами:

• рассматриваются системы линейных уравнений ;

• системы уравнений второй степени с двумя переменными;

• системы содержащие параметры, из ЕГЭ.

1. Решение практических, прикладных задач.

2. Решение систем линейных уравнений с двумя переменными с помощью определителей, первоначальное знакомство с матрицами.

3. Основное знакомство с матрицами и действиями над ними;

4. Решение систем уравнений:

• Методом Крамера;

• Матричным методом;

• Методом Гаусса;

Рассмотрение однородных систем.

Курс предполагает использование следующих материальных образовательных ресурсов:

• Раздаточный материал по темам;

• Работа на ПЭВМ в компьютерном классе, компьютерных программ;

• Наглядный материал, по теме решение систем уравнений графическим способом.,

Практикум.

Задания по теме «Решение систем разными способами»

Это хорошо решить!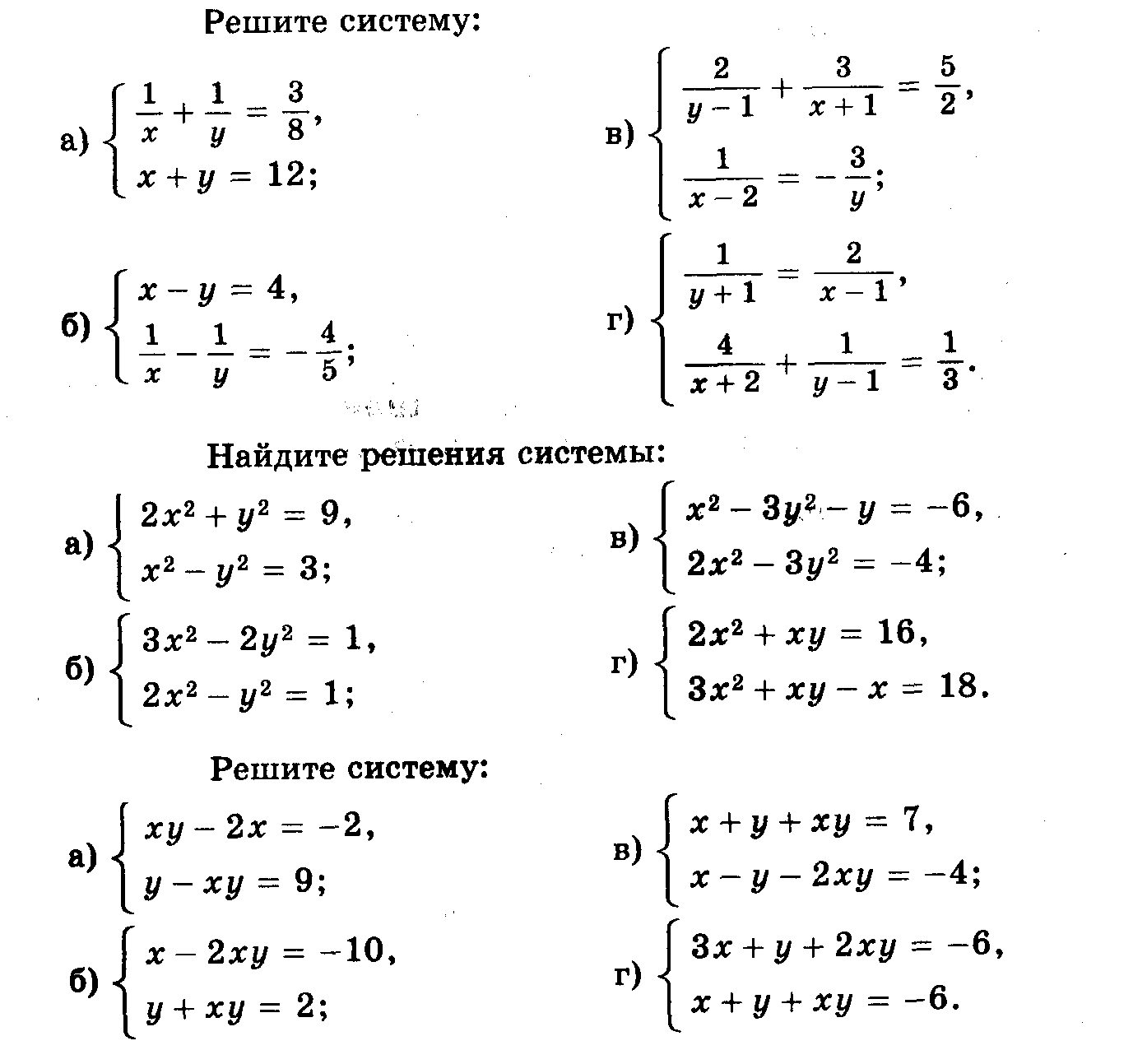

П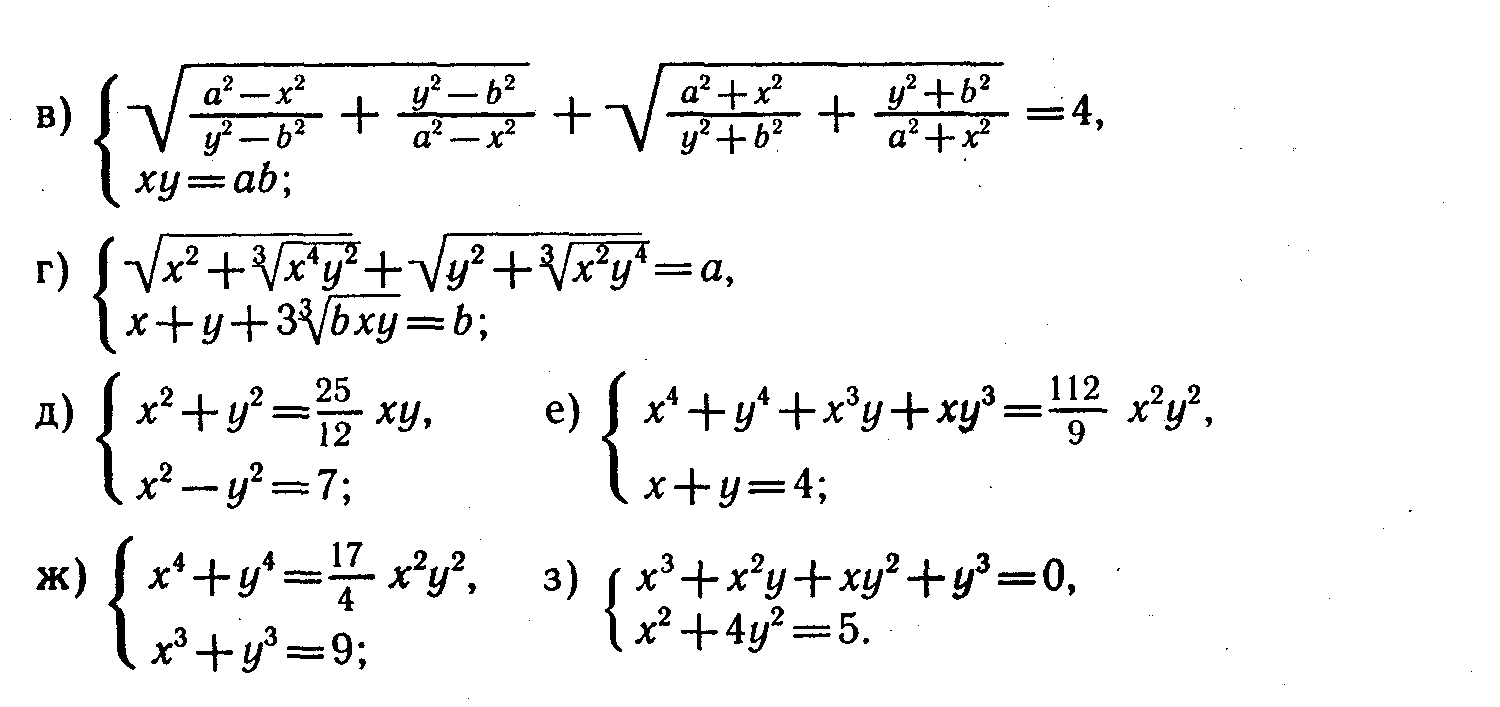опробуй свои силы!

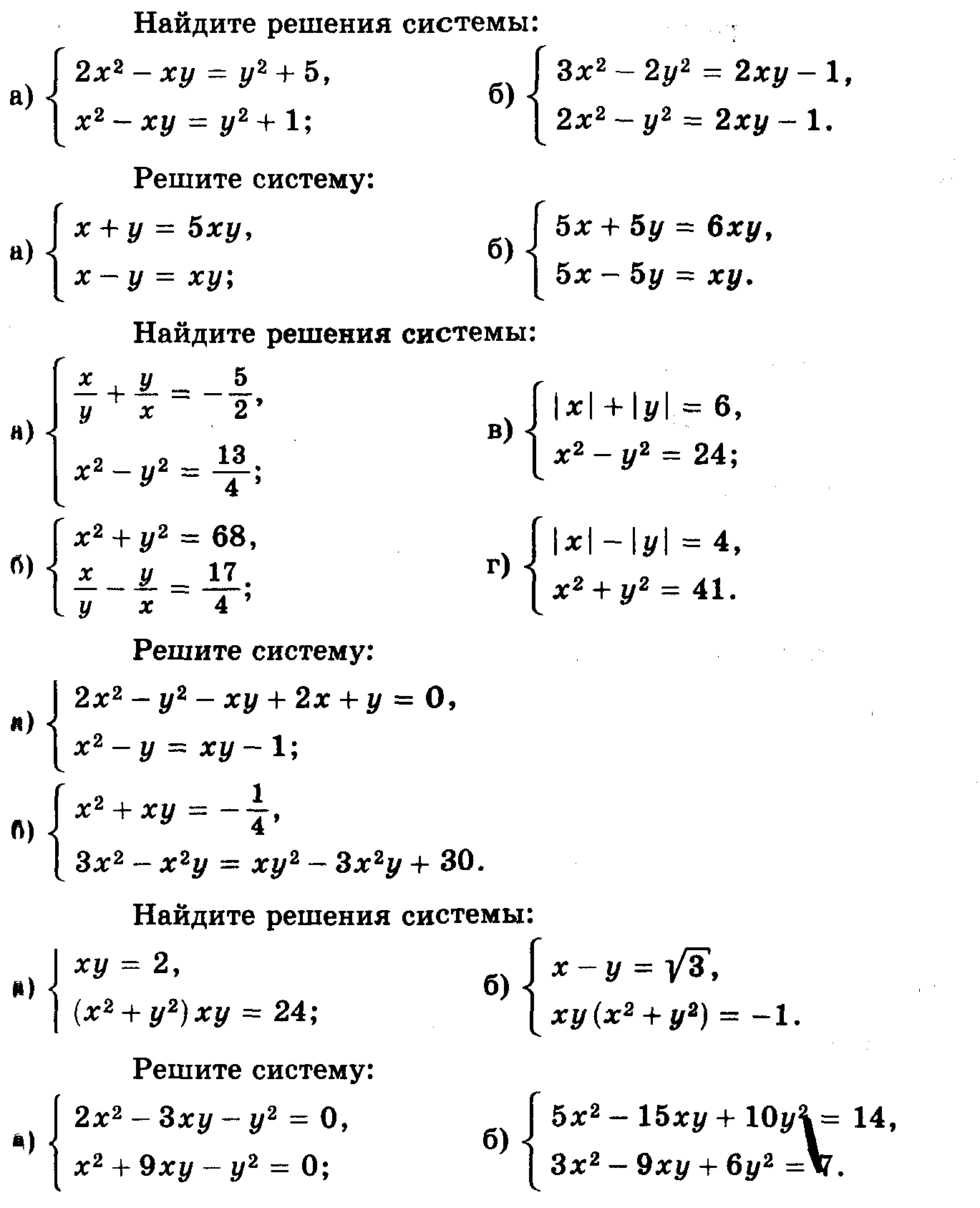
Задания по теме «Теорема Крамера»

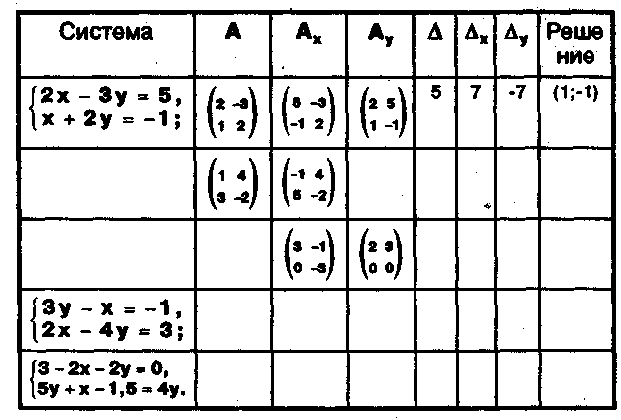
Задание.

Заполните пропуски в таблице

Задание.

Решите системы уравнений, используя формулы Крамера:

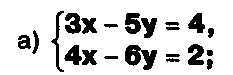
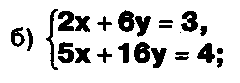
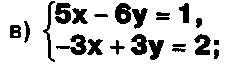
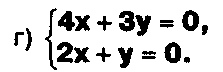
Задание.

Выясните, какие из следующих систем можно решить с помощью формул Крамера, и решите их, а если нет, то решите их любым другим способом:

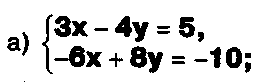
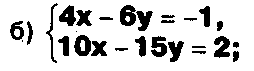
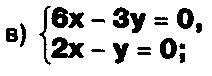
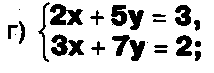
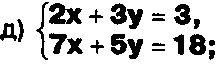
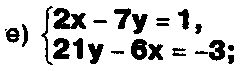
Задание.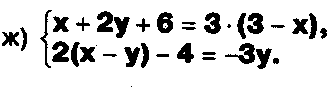

Даны системы. Не решая их, определите чис­ло решений, т.е. определите по внешнему виду систем, какие из них

- совместные;

• несовместные;

- определенные;

- неопределенные?

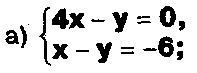
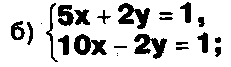
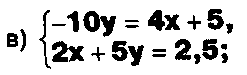
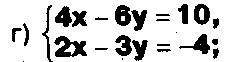
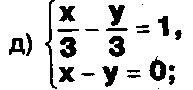
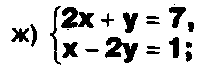
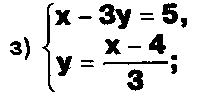
Задание.

Вычислите определители матриц:

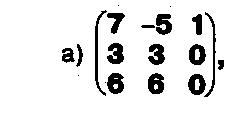
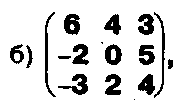
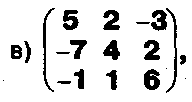
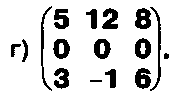
Задание.

Решите системы:

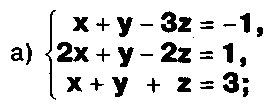
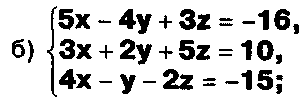
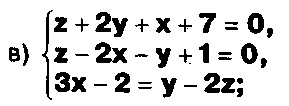
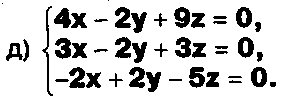
Задание.

Даны системы. Не решая их, определите, ка­кие из них являются совместными? Несовмест­ными? Определенными? Неопределенными? Затем решите их.

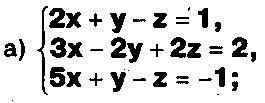
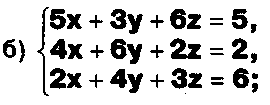
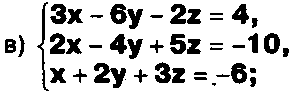
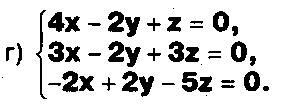
Задание.

Дано одно уравнение системы, припишите к нему другое уравнение так, чтобы полученная система:

- не имела решений;

- имела единственное решение;

- имела бесконечное число решений.

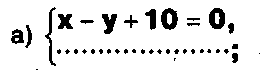
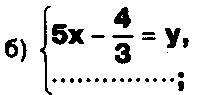
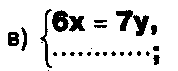
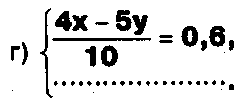
Задание.

Может ли система

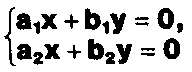
а) иметь единственное решение;

б) иметь бесконечное множество решений;

в) не иметь решений?

Какими должны быть коэффициенты в каждом возможном случае?

Задание.

Найти все значения параметра а, при которых система не имеет решений:

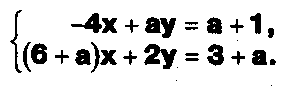
Задание 4.

Дана система

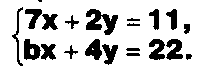
Найдите такие значения Ь, при которых сис­тема имела бы:

- единственное решение,

• бесконечное число решений.

Задание.

а) Определите, при каких значениях парамет­ра k система

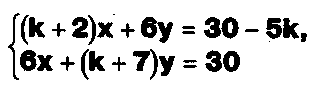
имеет бесконечное число решений.

б) Определите, при каких значениях параметра k система

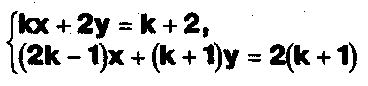
не имеет решений.

Задание . . .Дана система с параметром а :

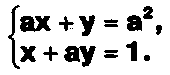
Объясните предложенное решение: 1-й шаг.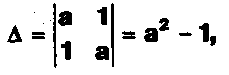

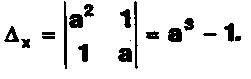
2-й шаг.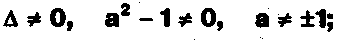

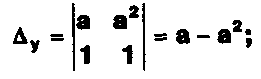
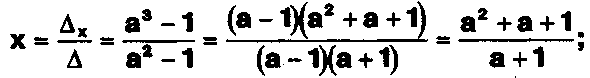
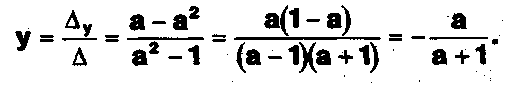
3-й шаг.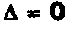при а = 1 или а =-1. а) а = 1,

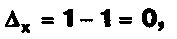
1 х + у = 1,

у = 1 - х, х - любое;

б)а = -1,

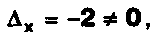решений нет.

Задание.

Решите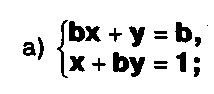системы с параметром:

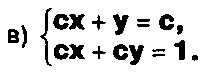
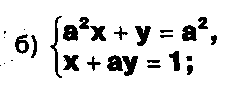
Задание.

Найти все значения параметра с, при которых система не имеет решений:

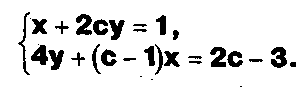
Задание.

Решите систему с параметрами а и Ь:

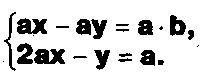
Задание.

Решите систему используя параметр k.

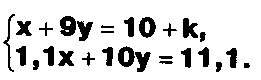
ЛИСТ КОНТРОЛЯ

1. Как вывести формулы Крамера для решения системы двух линейных уравнений с двумя неизвестными?

2. Как решать систему двух линейных уравнений с двумя неизвестными, если нельзя пользоваться формулами Крамера?

3.Какая система линейных уравнений называется совместной? несовместной? определенной? неопределенной?

4.Как формулируется теорема Крамера?

5.Как вычислить определитель второго порядка?

6. Как вычислить определитель третьего порядка?

7. В каком случае система двух линейных уравнений с двумя неизвестными имеет единст­венное решение?

8.В каком случае система трех линейных уравнений с тремя неизвестными имеет единственное решение?

9.В каком случае система двух линейных уравнений с двумя неизвестными имеет беско­нечное число решений?

10.В каком случае система трех линейных уравнений с тремя неизвестными имеет беско­нечное число решений?

11.В каком случае система двух линейных уравнений с двумя неизвестными не имеет решений?

12.В каком случае система трех линейных уравнений с тремя неизвестными не имеет решений ?

13. Как решать определенную систему трех линейных уравнений с тремя неизвестными?

14.Что называется решением уравнения с n неизвестными?

15. Как решать уравнение с n неизвестными, если хотя бы один из коэффициентов при неиз­вестных отличен от нуля?

Задания по теме «Метод Гаусса»

ЗАДАНИЕ .

Решите системы уравнений:

*• *

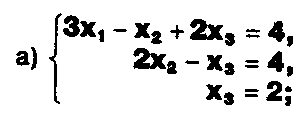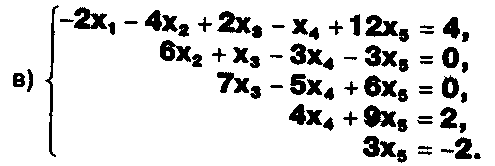
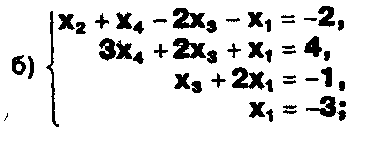
ЗАДАНИЕ .

а) Прокомментируйте 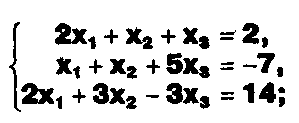решение системы:

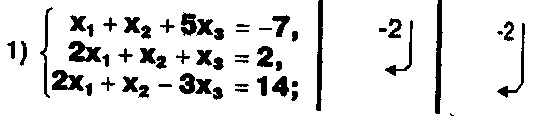
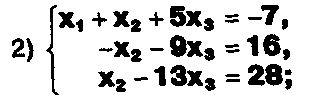
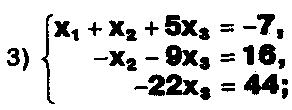
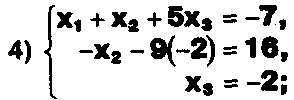
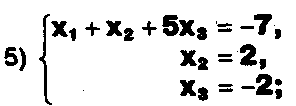
x₁ = 1,

6) x₂= 2, x₃ = -2.

б) Решите систему

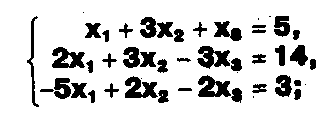
в)Равносильны ли системы а) и б)?

ЗАДАНИЕ .

а) Решите системы уравнений:

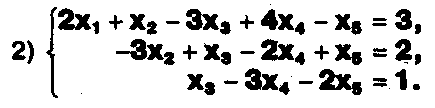
б) Составьте аналогичные по внешнему виду системы из трех уравнений с четырьмя, пятью и шестью неизвестными и решите их.

ЗАДАНИЕ .

При решении систем методом Гаусса были получены системы:

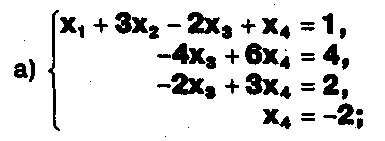
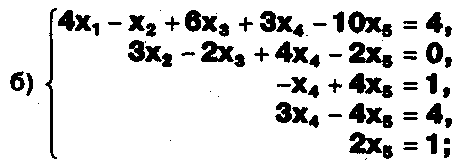
Можно ли утверждать, что первая система совместна и неопределенна, а вторая - несов­местна? Закончите решения этих систем.

ЗАДАНИЕ .

а) Решите систему

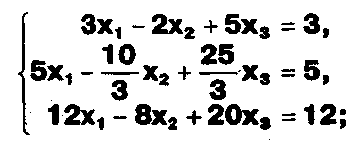
б) Верно ли, что система из а) равносильна сис­теме

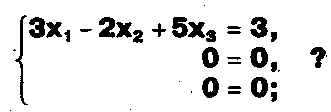
в) Верно ли, что система из а) равносильна сис­теме, имеющей общее решение:

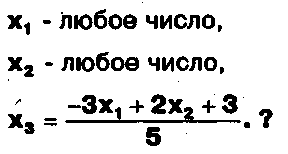
ЗАДАНИЕ .

Решите системы уравнений:

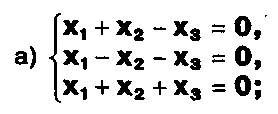
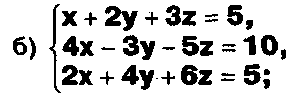
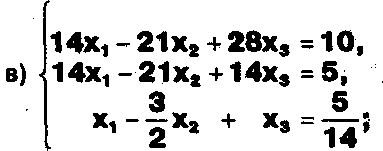
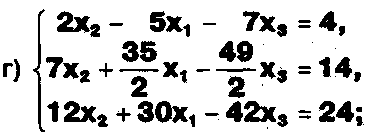
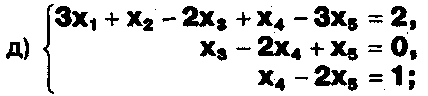
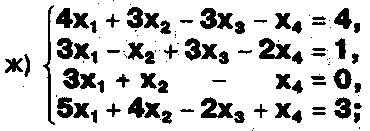
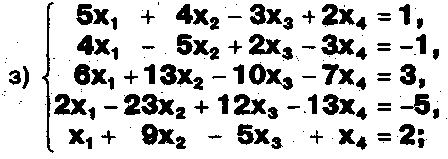
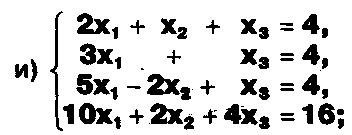
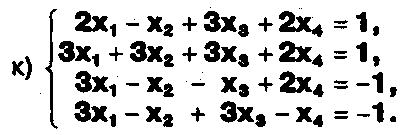
ЗАДАНИЕ .

Решите системы уравнений:

?

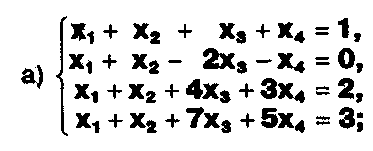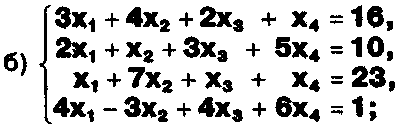
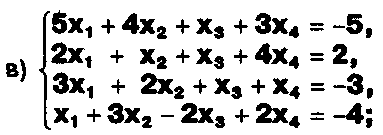
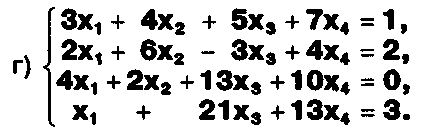
ЗАДАНИЕ .

Доказать, что система уравнений

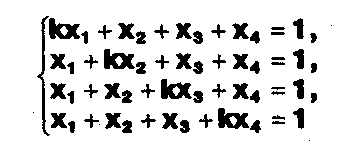
при k, отличном от 1 и -3, имеет единственное решение.

ЗАДАНИЕ.

Доказать, что система уравнений

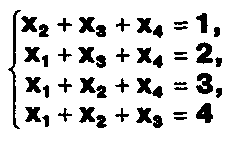
имеет единственное решение. Найти это реше­ние.

ЗАДАНИЕ .

Доказать, что система уравнений

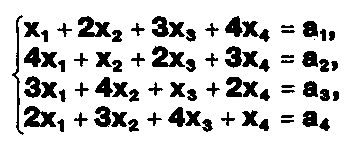
имеет единственное решение. Найти это решение.

ЗАДАНИЕ .

При каком условии система уравнений

;

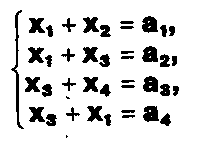имеет единственное решение? Найти это решение.

ЗАДАНИЕ.

Доказать, что система уравнений

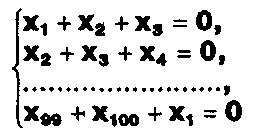
имеет единственное нулевое решение (т.е. x₁ = х₂ =К = х₁₀₀ = О).

ЛИСТ КОНТРОЛЯ.

1.Какие две системы называются равносильными?

2. Каковы способы перехода к равносильным системам?

3. В чем состоит прием доказательства равносильности двух систем?

4. Как можно проверить равносильность определенных систем?

5.Как можно проверить равносильность неопределенных систем?

6.Каким методом можно решить системы линейных уравнений с любым числом неизвестных?

7. В чем состоит метод Гаусса?

Список использованной литературы:

1. А.Г .Мордкович, Алгебра 7,М.: Мнемозина,2006

2. А.Г Мордкович., Алгебра 9, М.: Мнемозина,2006

3. Ю.Н Макарычев., Н.Г Миндюк, Алгебра 9. Учебник с углубленным изучением математики. М.: Мнемозина 2003

4. В.С Крамор, Повторяем и систематизируем школьный курс алгебры и начал анализа.

5. Л.И Терехина., И.И Фикс. Высшая математика. Линейная алгебра. Аналитическая геометрия. Ч.1,Изд-во «Дельтаплан», 2002, Томск.

6. Ш.А Алимов, Алгебра 7, М.: Мнемозина,2006

7. Ш.А Алимов, Алгебра 9, М.: Мнемозина,2006

8. А.С Солодовников, Г.А Торопова. Линейная алгебра с элементами аналитической геометрии. Учебное пособие для учащихся сред.сп5ец.учеб.заведений – М.: Высшая школа,1987

9. ТГУ, механико- механический факультет. Составители: О.Н. Балыкина, О.М. Биматова, Л.Г. Плеханова, Е.П.Шамова. Сборник задач по математике. Часть 1. Элементы линейной алгебры…

10. И.Ф.Шарыгин. Факультативный курс по математике. Учебное пособие для 10 класса средней школы.

11. С.К.Росошек, Л.Б. Хают, И.Е.Малова. Системы уравнений., Томск,2003