Методические пособия по тригонометрии
для учащихся 10-11 классов и студентов СПО
преподаватель Маркина О.А.
Санкт-Петербургского ГБПОУ «Педагогического колледжа №8»


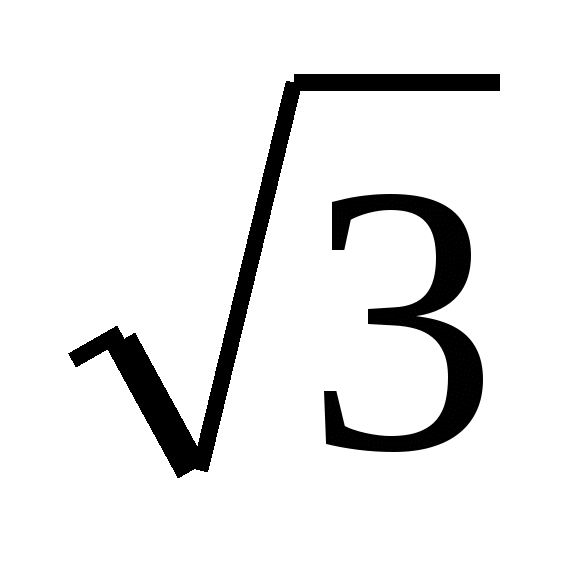 tg
tg
Значения тригонометрических функций
sin
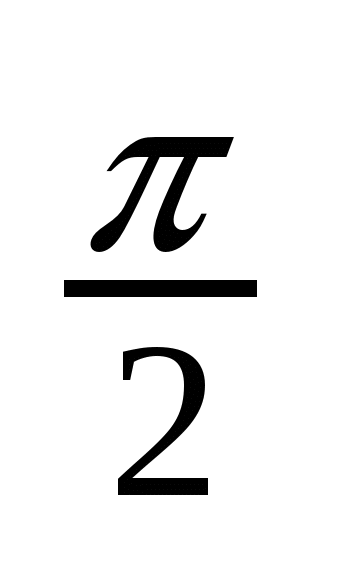
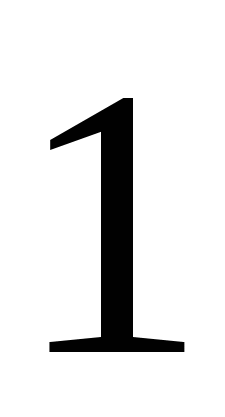
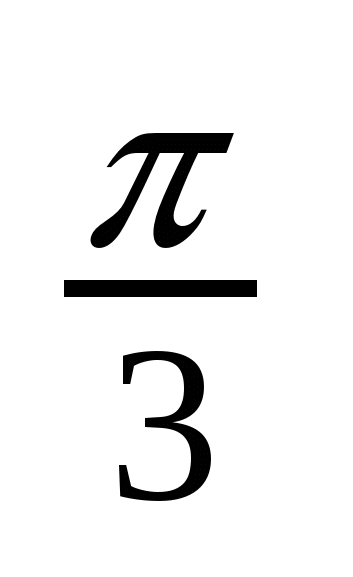

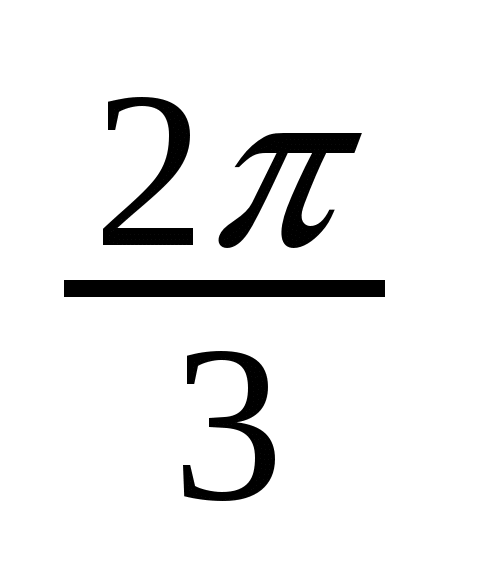
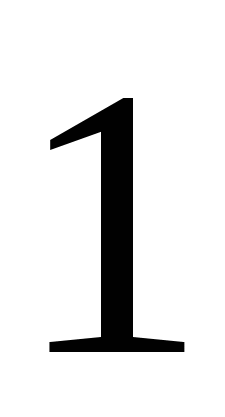

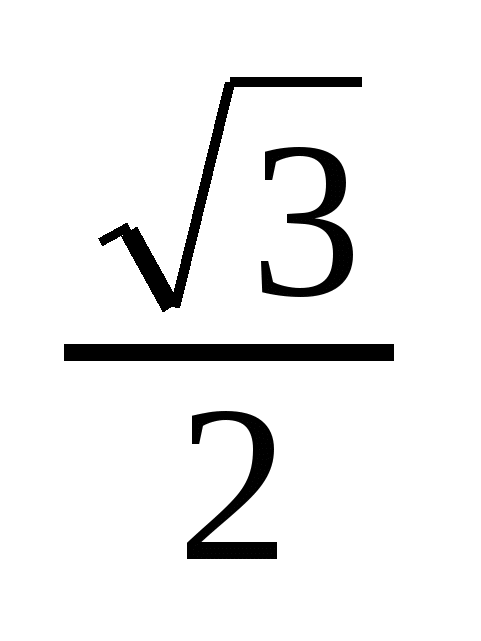
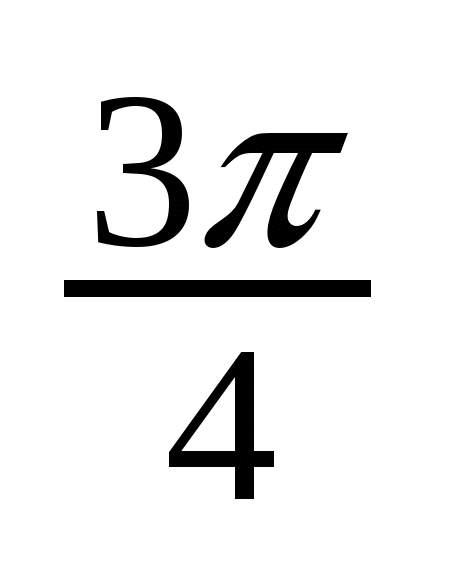








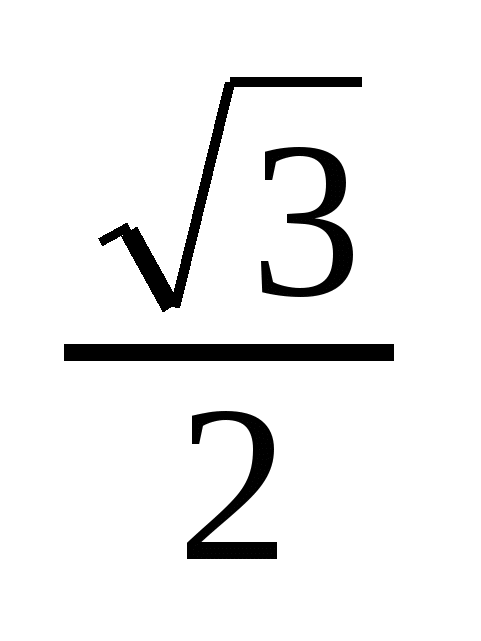
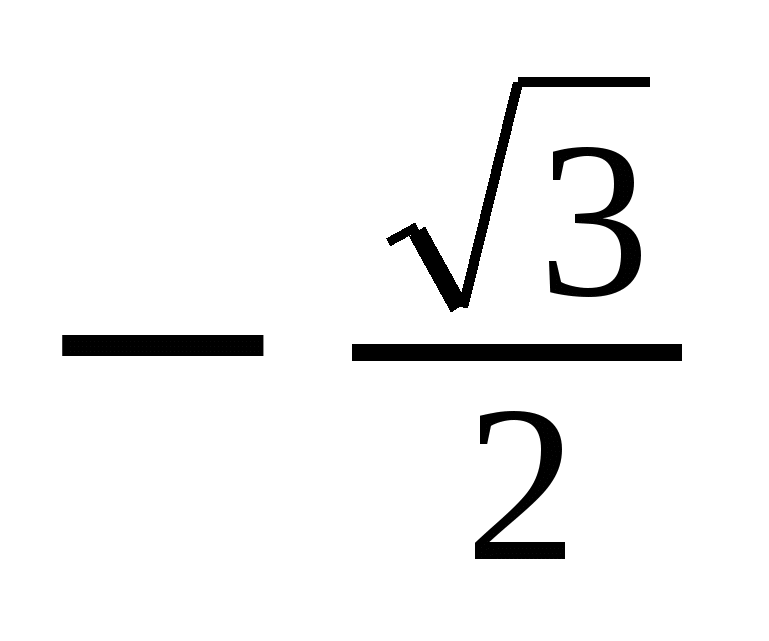
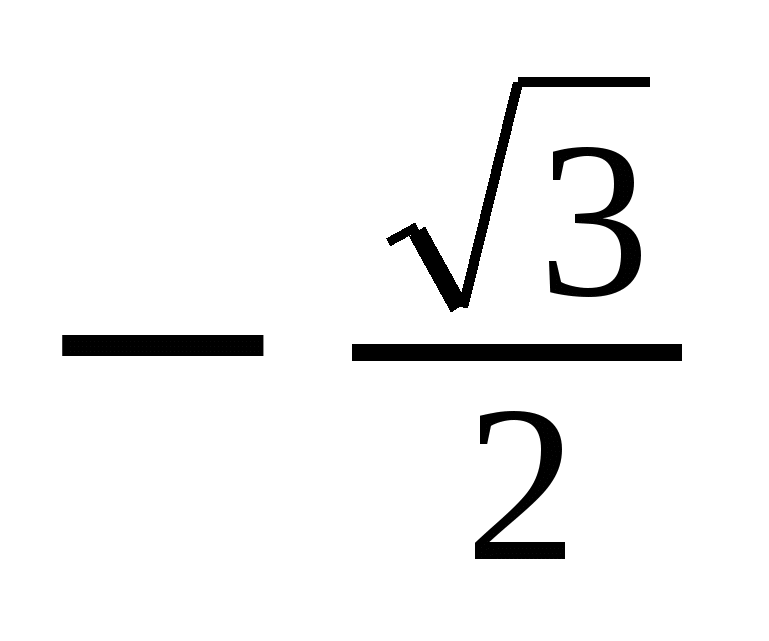
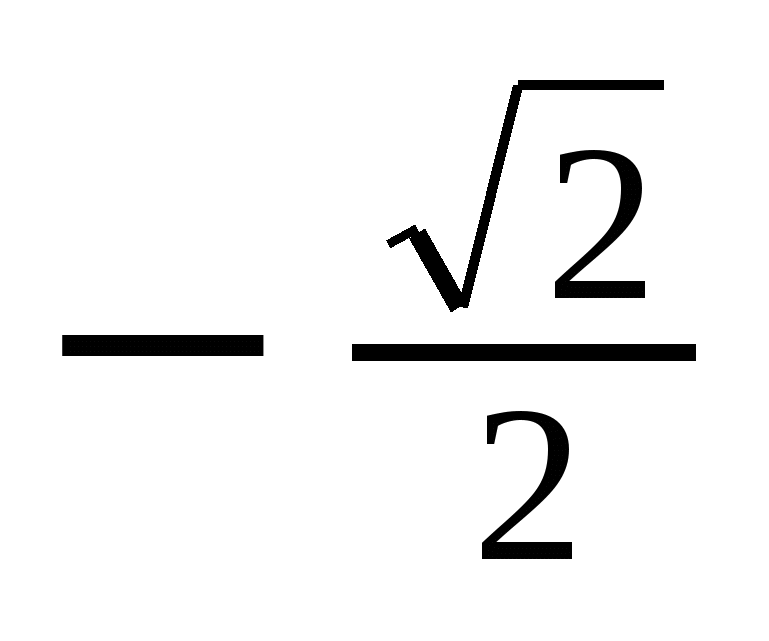
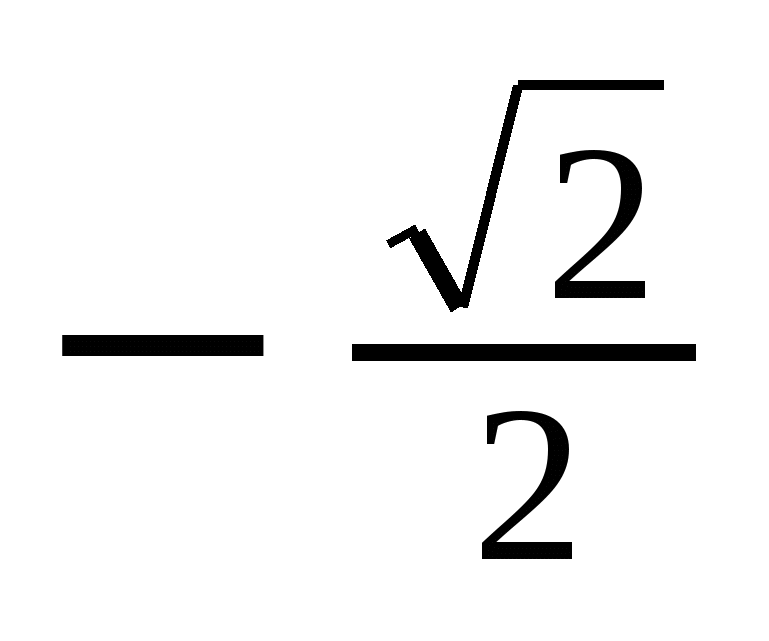
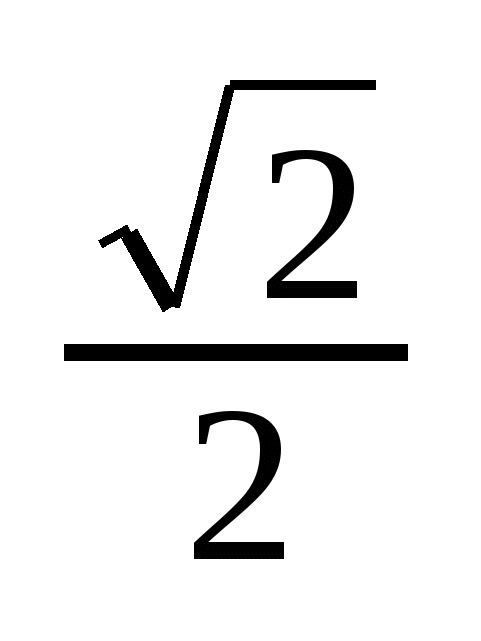
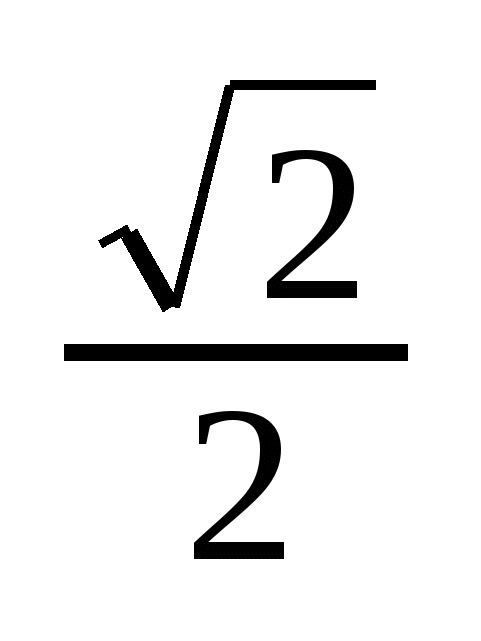


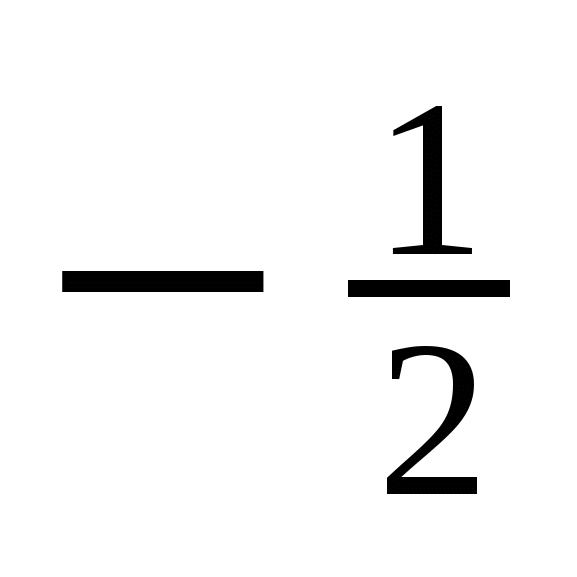
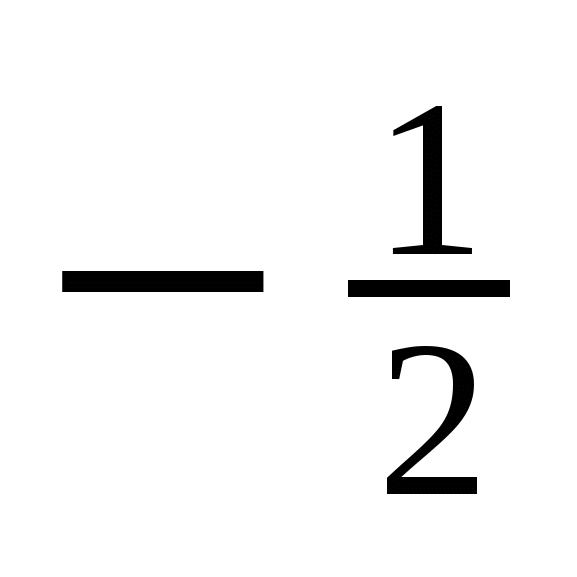
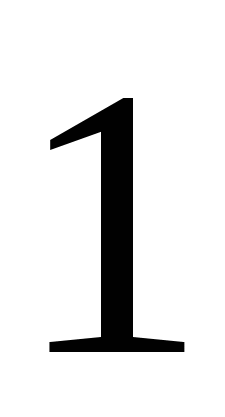
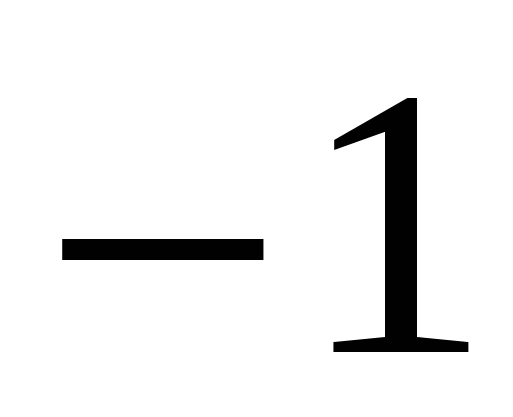
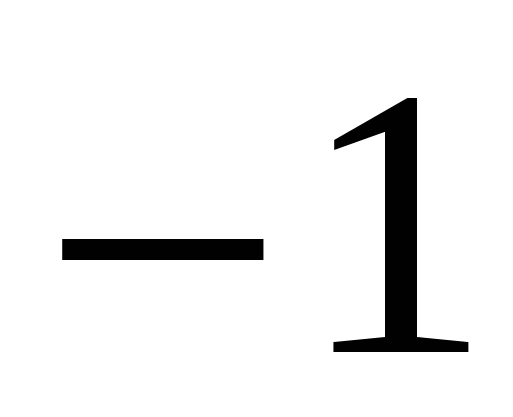
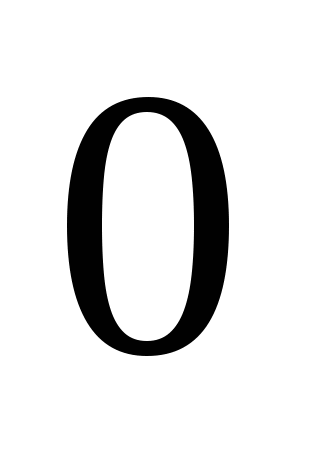
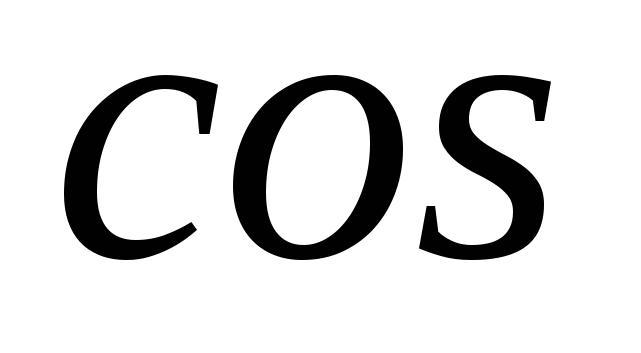
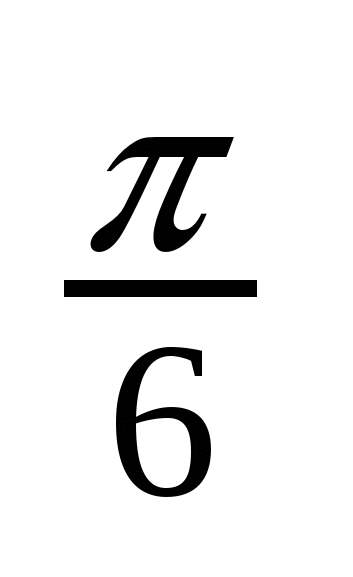
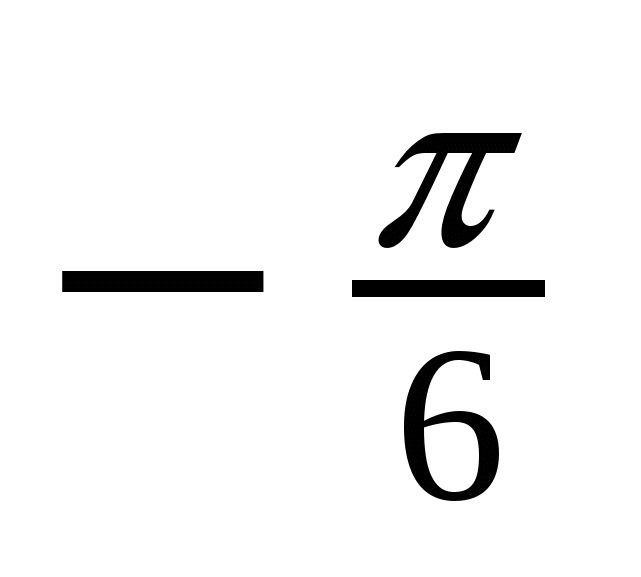
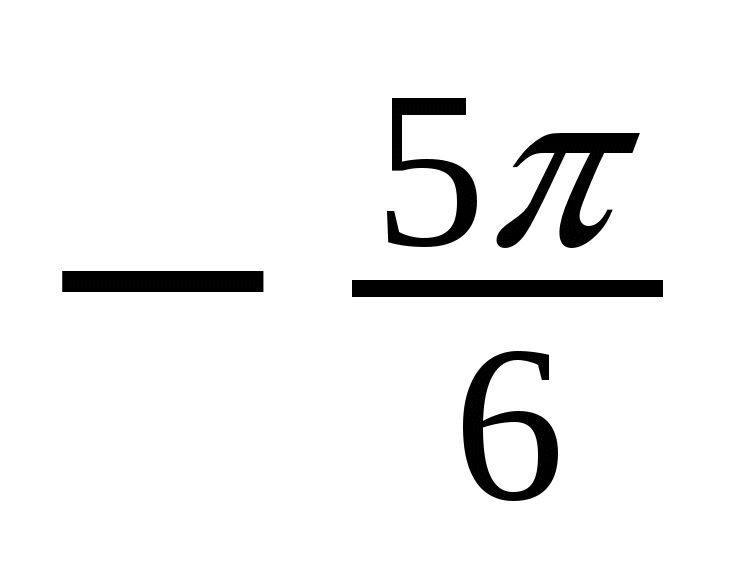
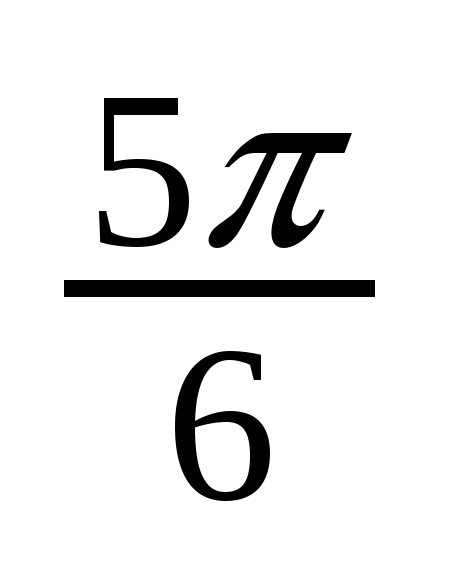
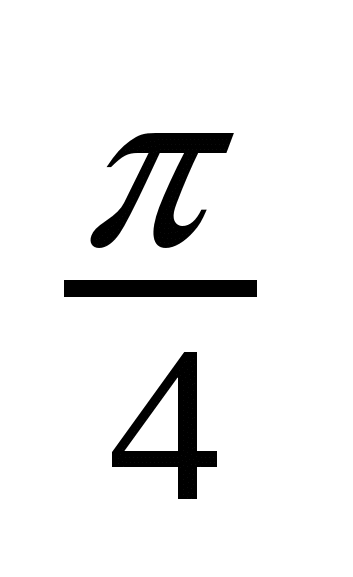
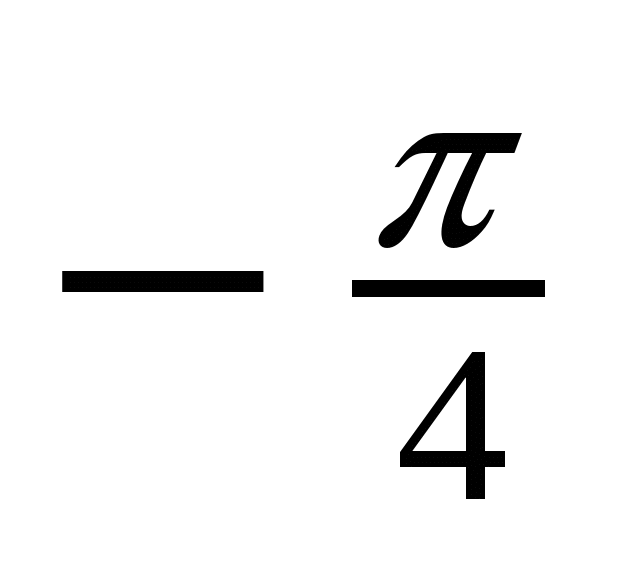
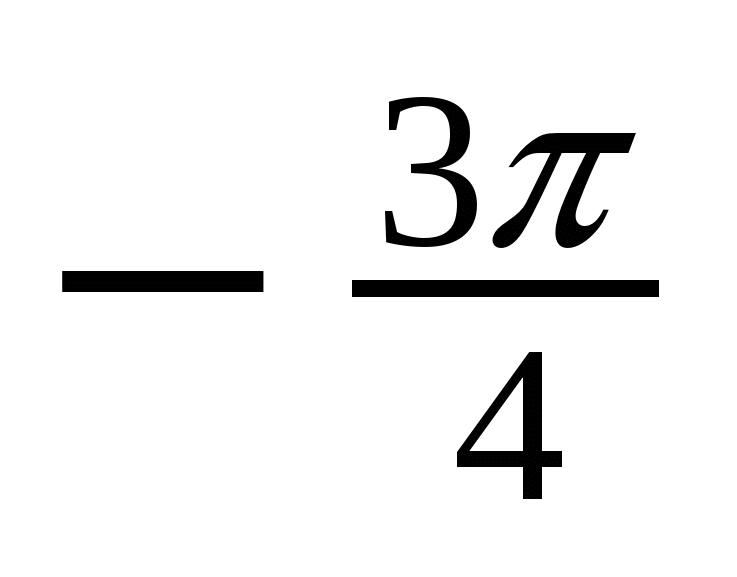



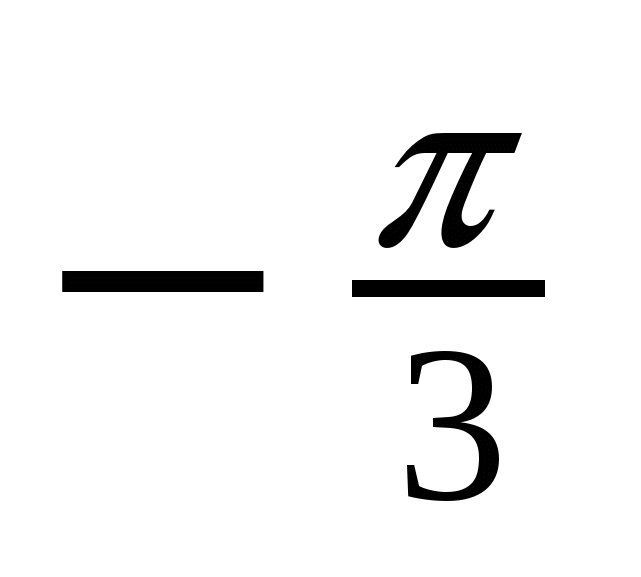
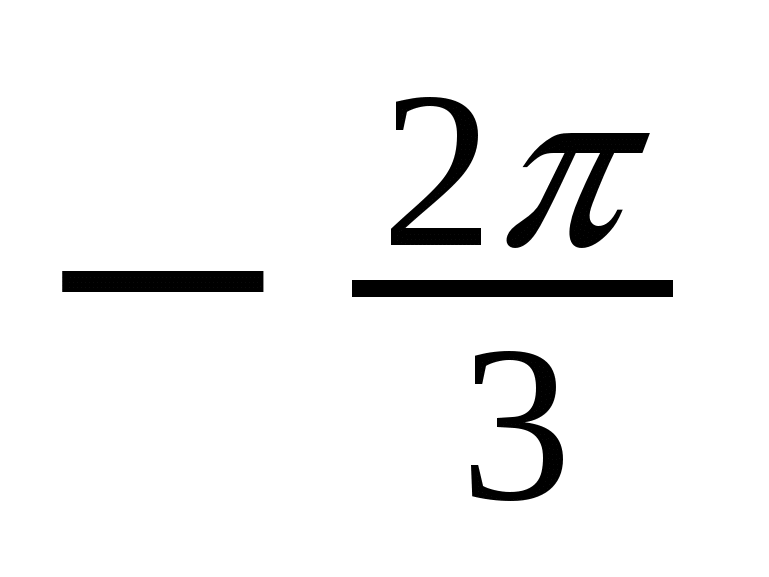
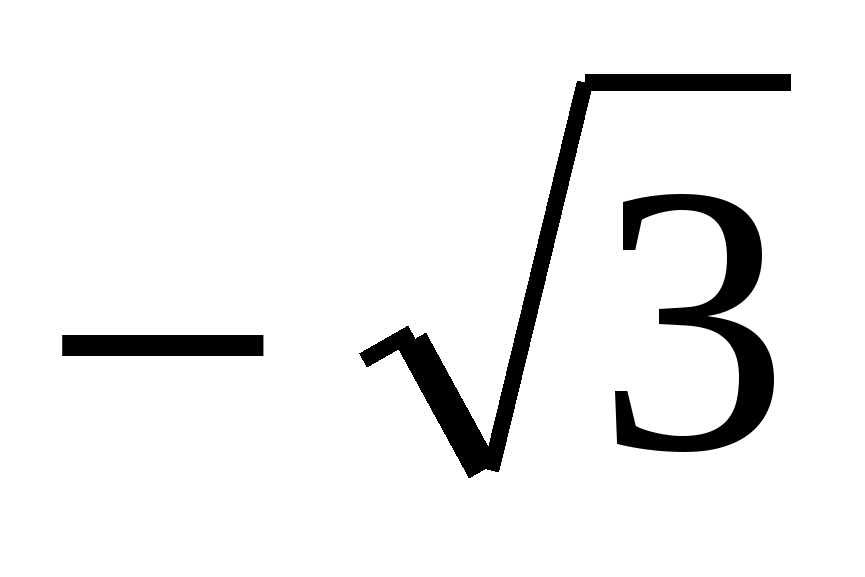
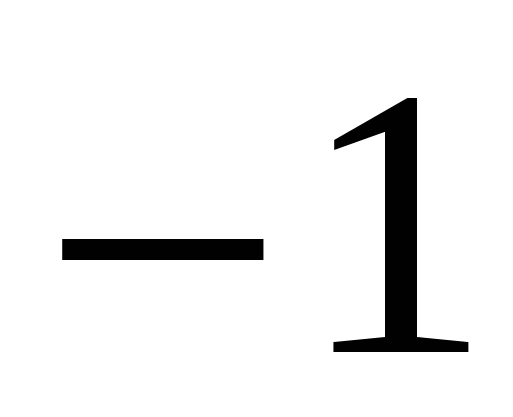
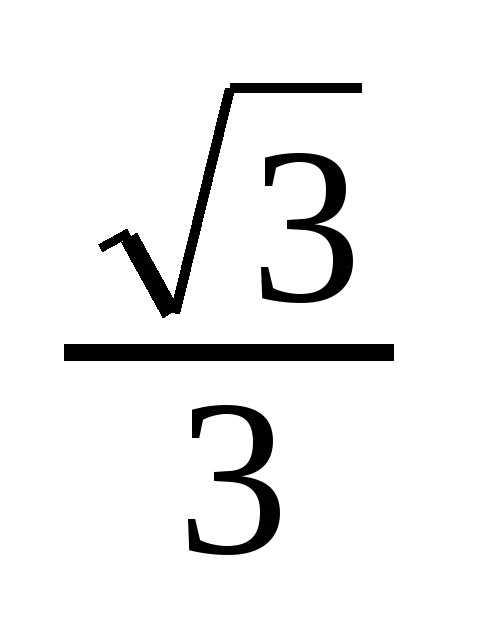
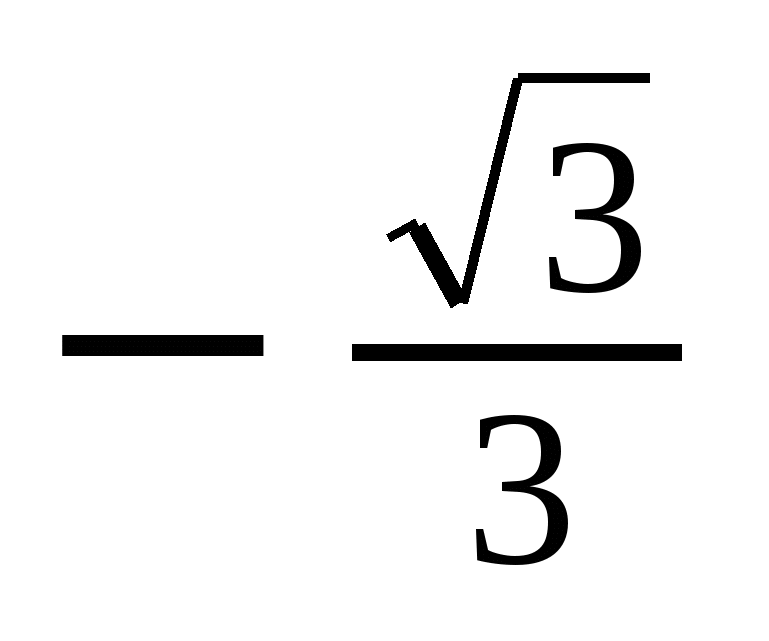

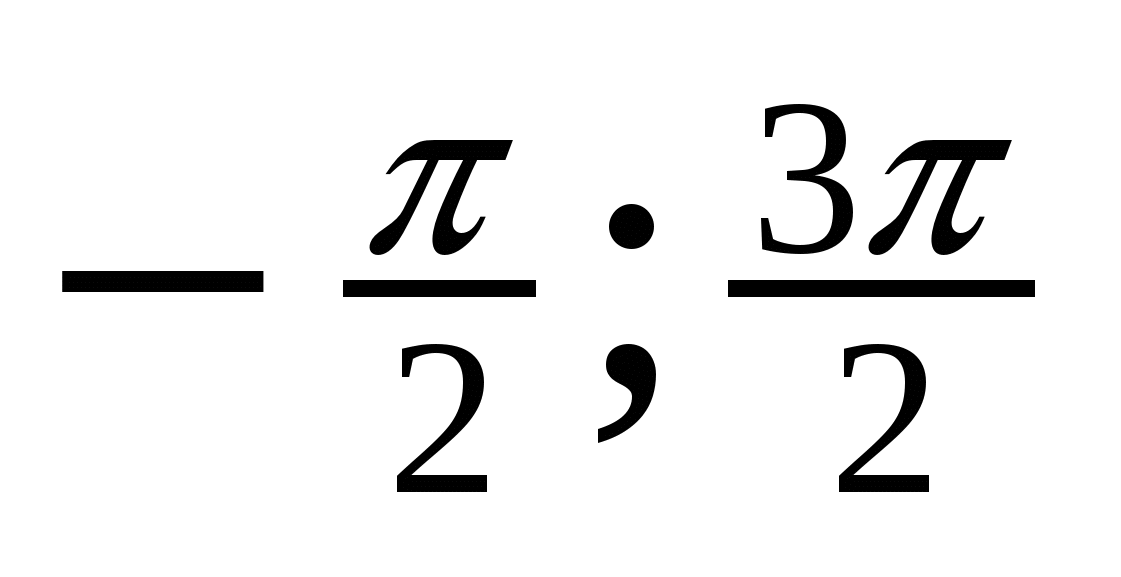
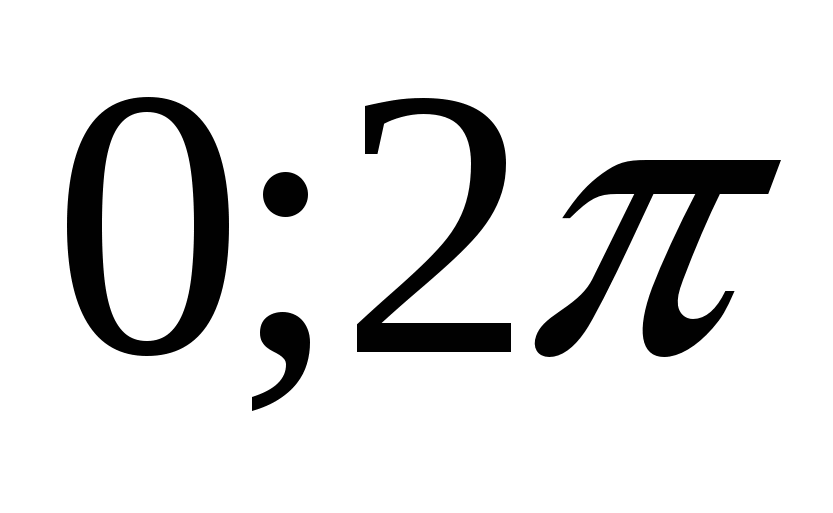




Решение тригонометрических уравнений
sin x = a, -1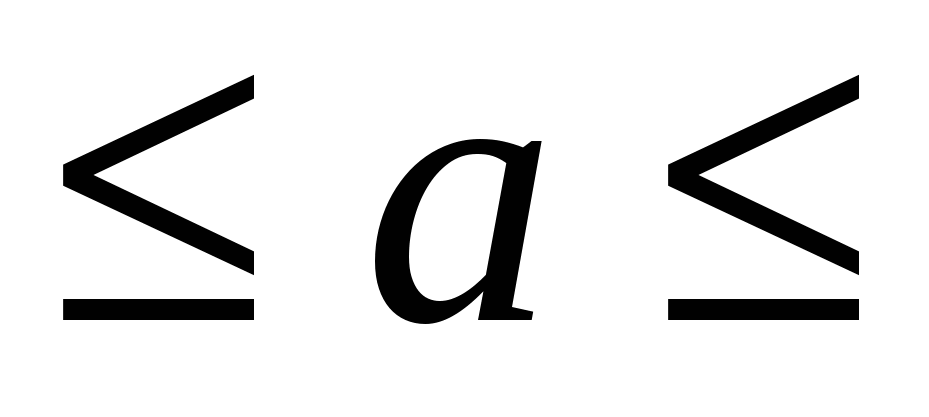 1
1
x = (-1)n arcsin a + n, n
n, n Z
Z
arcsin (-a) = - arcsin a
Частные случаи:
sin x = 0 x =  n, n
n, n Z
Z
sin x = 1 x = 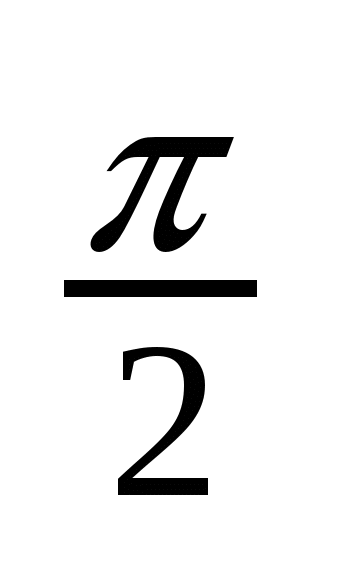 +2
+2 n, n
n, n Z
Z
sin x = - 1 x = 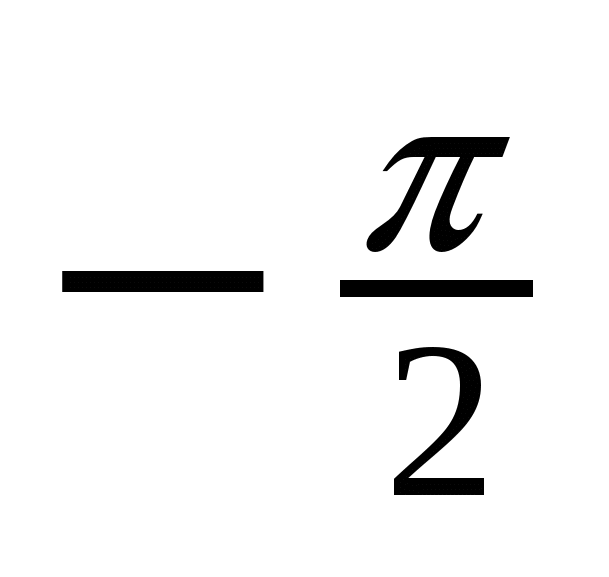 +2
+2 n, n
n, n Z
Z
tg x = a, x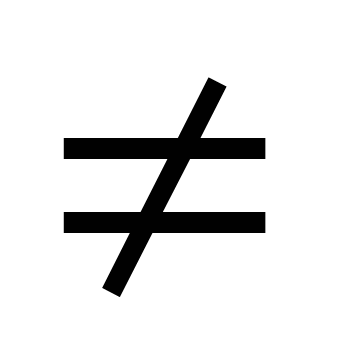
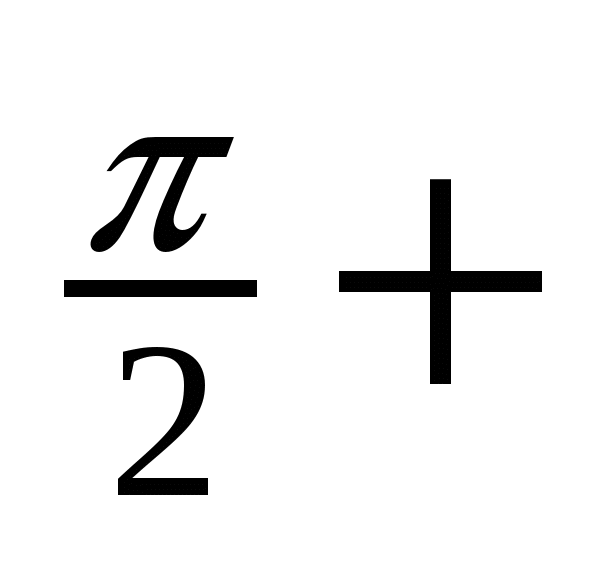
 n, n
n, n Z
Z
x = arctg a +  n, n
n, n Z
Z
arctg (-a) = - arctg a
Частные случаи:
tg x = 0 x =  n, n
n, n Z
Z
tg x = 1 x =  +
+ n, n
n, n Z
Z
tg x = -1 x = 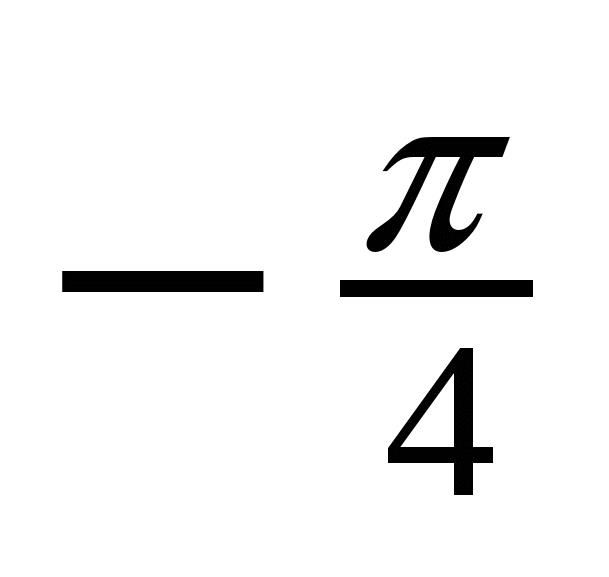 +
+ n, n
n, n Z
Z
cos x = a, -1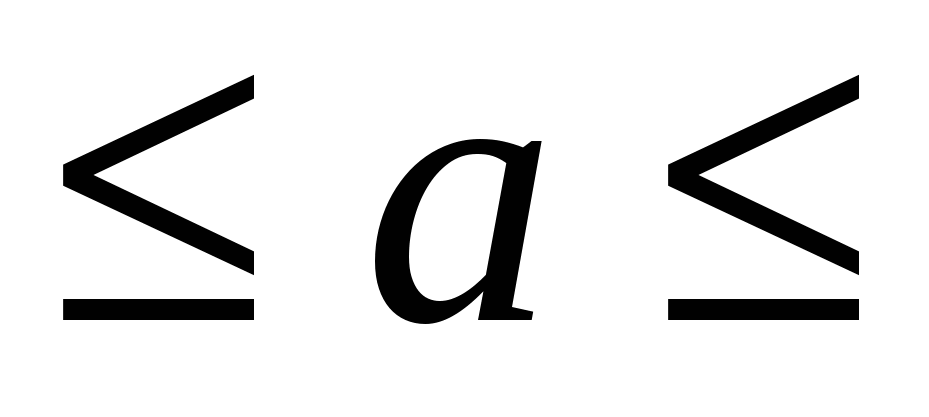 1
1
x = 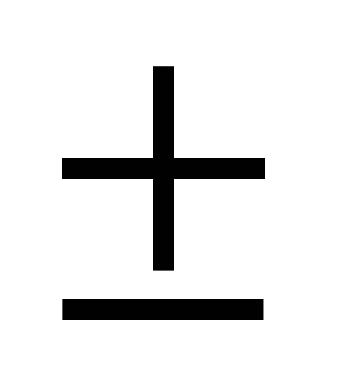 arccos a +2
arccos a +2 n, n
n, n Z
Z
arccos (-a) =  - arccos a
- arccos a
Частные случаи:
cos x = 0 x = 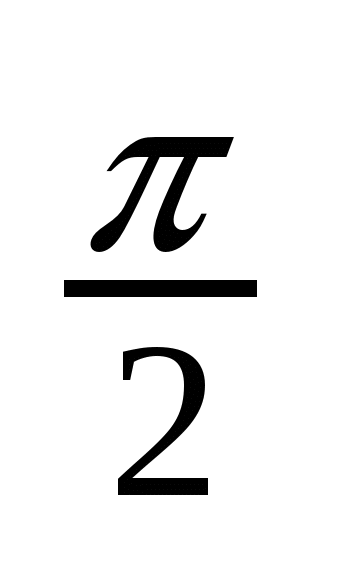 +
+ n, n
n, n Z
Z
cos x = 1 x =2 n, n
n, n Z
Z
cos x = -1 x = +2
+2 n, n
n, n Z
Z
ctg x = a, x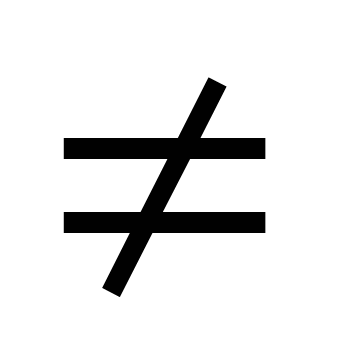
 n, n
n, n Z
Z
x = arcctg a +  n, n
n, n Z
Z
arcctg (-a) =  - arcctg a
- arcctg a
Частные случаи:
ctg x = 0 x = 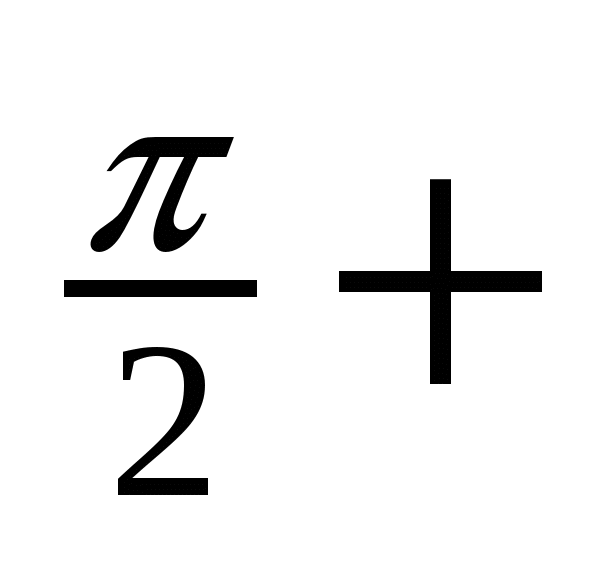
 n, n
n, n Z
Z
ctg x = 1 x =  +
+ n, n
n, n Z
Z
ctg x = -1 x = 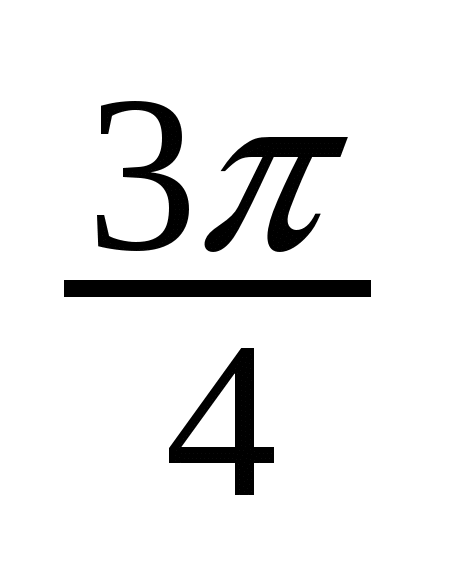 +
+ n, n
n, n Z
Z
Основные тригонометрические тождества
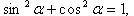
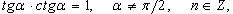
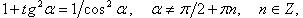
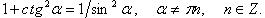
Выражение тригонометрических функций через одну из них того же аргумента
(выбор знака перед корнем зависит от того, в какой четверти находится угол 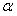 )
)
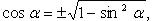
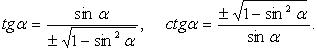
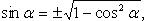
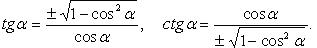
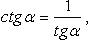
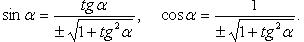

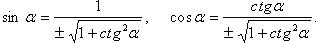
Формулы сложения
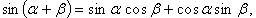
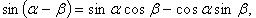
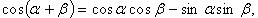
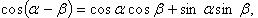
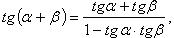
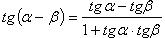
Преобразование суммы тригонометрических функций
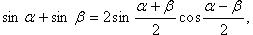
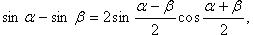
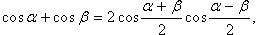
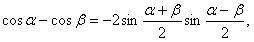
Преобразование произведения тригонометрических функций в сумму
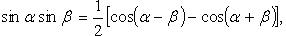
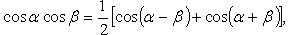
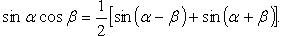
Тригонометрические функции двойного и тройного аргумента
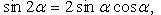
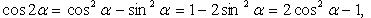
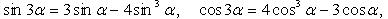
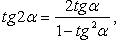
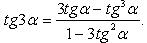
Преобразование степеней синуса и косинуса
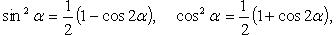
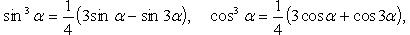
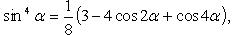
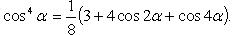
Знаки тригонометрических функций

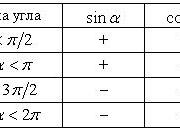
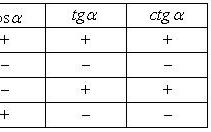
Список литературы:
Учебник для 10-11 классов общеобразовательных учреждений
под редакцией Ш.А. Алимова, Ю.М. Колягина, Ю.В. Сидорова
Москва, “Просвещение” 2006 год.
Дорофеев Г.В. «Математика» ДРОФО, Москва, 2002, 160с.