Муниципальное бюджетное образовательное учреждение
«Средняя общеобразовательная школа № 7» им. О.Н. Мамченкова
г. Елизово, Камчатский край
Обобщающий урок математики в 10 классе
по теме
«Свойства логарифмов. Логарифмические и показательные уравнения и неравенства»»
Подготовила
учитель математики
Шатова Марина Николаевна
г. Елизово
2013 год
(алгебра и начала анализа, 10 класс, УМК «МГУ – школе», С.Н. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин )
Цели урока:
1.Систематизация и углубление знаний учащихся; обобщение свойств логарифмов, логарифмической и показательной функций; установление связей с наиболее трудными вопросами теории при решении уравнений и неравенств.
2.Развивитие мыслительной деятельности учащихся через решение разнотипных задач и находить наиболее рациональные способы решения.
3.Развитие у учащихся навыков самостоятельного поиска решения нестандартных уравнений и неравенств, умение работать в группах, навыков самоконтроля.
Оборудование: интерактивная доска, маркерная доска, раздаточный материал для работы в группах.
Ход урока.
1.Организационный момент.
Разделить класс на 3 группы.
2.Определение темы и целей урока.
Посмотрите на уравнения и неравенства, записанные на доске. Чем мы будем сегодня заниматься на уроке? Попробуйте сформулировать тему нашего урока. Есть ли в её названии математические термины, которые вам незнакомы? Тогда возникает вопрос: «Чему же мы должны сегодня научиться на уроке, что узнать нового?» Посмотрите более внимательно на задания, которые вам предстоит выполнить во время урока и попробуйте сформулировать задачи нашего урока.
Сообщение плана работы на уроке:
Теоретическая разминка «Повторение – мать учения».
Вычислительная разминка «Проверь себя» (работа в парах).
Работа в группах «Получи пятёрку».
Работа в группах «Тёмная лошадка».
3.Актуализация опорных знаний и умений учащихся.
Теоретическая разминка «Повторение – мать учения».
а) Заполнить на доске таблицу (работа 2-х учащихся) (работа на интерактивной доске):
Функция
Показательная у = …
Логарифмическая у = …
№
Основание
Свойство
а > 1
0 < а <1
а > 1
0 < а <1
1.
D (f)
2.
E (f)
3.
Характ. точка
4.
Монотонность
5.
Знакопостоянство
6.
Чётность, нечётность
7.
График функции
(схематично)
б) Устная работа с остальными учащимися. Ответьте на вопросы:
Что называется логарифмом положительного числа b по основанию а?
Какие уравнения называются простейшими показательными, логарифмическими уравнениями?
Назовите основные способы решения показательных уравнений.
Назовите основные способы решения логарифмических уравнений.
На чём основано решение показательных и логарифмических неравенств?
4. Работа в парах. Вычислительная разминка «Проверь себя».
Работая в парах, заполните таблицу:
Выражение
Значение выражения
Свойство логарифмов
lg 120 - lg 12
1
ln 1 - 7
- 7
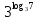+ 2
9
.
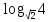4
.
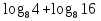2
.
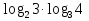2
.
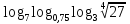0
5.Математический диктант «Спешите видеть и ответить» с взаимопроверкой.
1.Перед вами уравнения и неравенства:
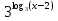= 5; 7
= 
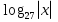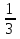; 3; - 3 
> 0; (- 1; 0)U(0; 1)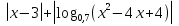
= 0; 3
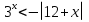; Ø
х + 2)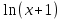 
= 0. 0
Верно ли моё утверждение:
Корнем уравнения № 1 является положительное число. +
Уравнение № 2 имеет один корень. –
Решением неравенства № 3 является интервал ( - 1; 1). –
Корнем уравнения № 4 является корень уравнения (
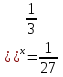. +Решением неравенства № 5 является любое действительное число. –
Уравнение № 6 имеет два корня: - 2 и 0. –
2.Укажите номер «лишнего» выражения:
;
;
;
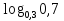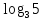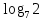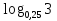. (значение данного выражения отрицательно)
3.Укажите номер строки в данных математических рассуждениях, в которой допущена ошибка. Объясните свой выбор:
(
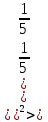;lg
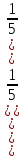;2 lg
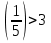lg(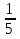
) : lg(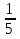); (lg() 
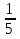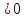, поэтому знак неравенства надо изменить)2
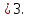
6.Работа в группах «Получи пятёрку».
Работая в группах и помогая друг другу, выполните следующие задания.
1.Решите неравенство и укажите наименьшее целое решение неравенства
(
(- 2; +
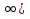; - 1
2.Решите неравенство и укажите наименьшее целое положительное решение неравенства
4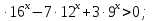
(- 
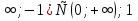
3.Решите неравенство и найдите сумму наименьшего целого и наибольшего целого решений неравенства
(
+ 
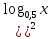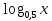- 6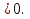 
(0,25; 8); 8
7.Работа в группах «Тёмная лошадка».
Перед вами три уравнения:
= 
;
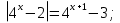
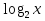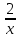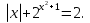
Попробуйте, работая в группах и помогая друг другу, составить план решения каждого уравнения. Если вы будете испытывать трудности при выполнении данного задания, то обсудите ответы на следующие вопросы:
а) К уравнению какого вида можно отнести уравнение № 1? Можно ли его решить, используя один из способов решения уравнения указанного вида? Что не позволяет применить известный способ решения? Как можно избавиться от модуля? Попробуйте, работая в группах, составить план решения данного уравнения, решите его.
б) Можно ли уравнение № 2 отнести к логарифмическим уравнениям? Почему? Укажите ОДЗ переменной данного уравнения. Рассмотрите функци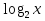и у = и у = 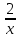на указанной ОДЗ, что можно сказать о монотонности данных логарифмической функции и обратной пропорциональности? Используя данный вывод, определите количество корней уравнения, попробуйте подобрать его. Данный способ решения уравнения называется функционально-графическим. Оформите решение данного уравнения.
в) Можно ли решить уравнение № 3 способами, используемыми при решении уравнений № 1 и № 2. Попробуйте это обсудить в группе. Есть более рациональный способ решения данного уравнения. Попытайтесь оценить значение каждого слагаемого, значение суммы, когда будет достигаться? Данное уравнение можно решить, оценивая значения левой и правой частей уравнения. Решите данное уравнение.
8.Рефлексия учебной деятельности на уроке.
Организуется рефлексия и самооценка учащихся, соотносятся цель учебной деятельности учащихся и результатами, достигнутыми на уроке.
9.Д/з:карточка.
1.Решите уравнение:
1).
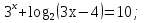
2).
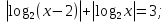
2.Решите неравенство:
