Урасова Наталья Николаевна
МКОУ Крутовская ООШ
Серафимовичского района
Волгоградской области
Учитель математики
Обобщающий урок по алгебре в 8 классе
по теме «Квадратные уравнения»
Девиз нашего урока: «Силу уму придают упражнения, а не покой».
Александр Поуп - английский поэт 18 века.
Цели урока:
Закрепить умение решать квадратные уравнения различными способами.
Развивать сообразительность, логическое мышление, умение анализировать.
Воспитывать любовь к математике, интерес к точным наукам.
Оборудование к уроку: карточки с заданиями, карточки с
формулами, тесты, лист результативности ученика, презентация к уроку
Ход урока:
(слайд 2)
(слайд 3)
Организация класса. (2 мин.)
Актуализация опорных знаний: (11 мин.)
(слайд 4)
математическое домино (3 мин.)
Учащиеся работают в парах, задают вопросы по пройденной теме и с помощью домино дают ответы. Учащиеся по очереди читают вопрос и дают ответ и сразу же задают вопрос своему однокласснику.
Вписать в лист результативности в Таблицу 1 баллы.
(по 1 за правильный ответ)
(слайд 5)
Работа со словами. (2 мин.)
Учащиеся вставляют пропущенные буквы в слова:
дискриминант, коэффициент,
Франсуа Виет_, приведенное квадратное уравнение, неполное квадратное уравнение.
(слайд 5). Проверка
Вписать в лист результативности в Таблицу 1 баллы.
(по 1 за правильный ответ).
(слайд 6)
Работа с формулами. (1 мин.)
Учащиеся выбирают из множества представленных формул на только те, по которым можно решать квадратные уравнения.
D = в² – 4ас х = 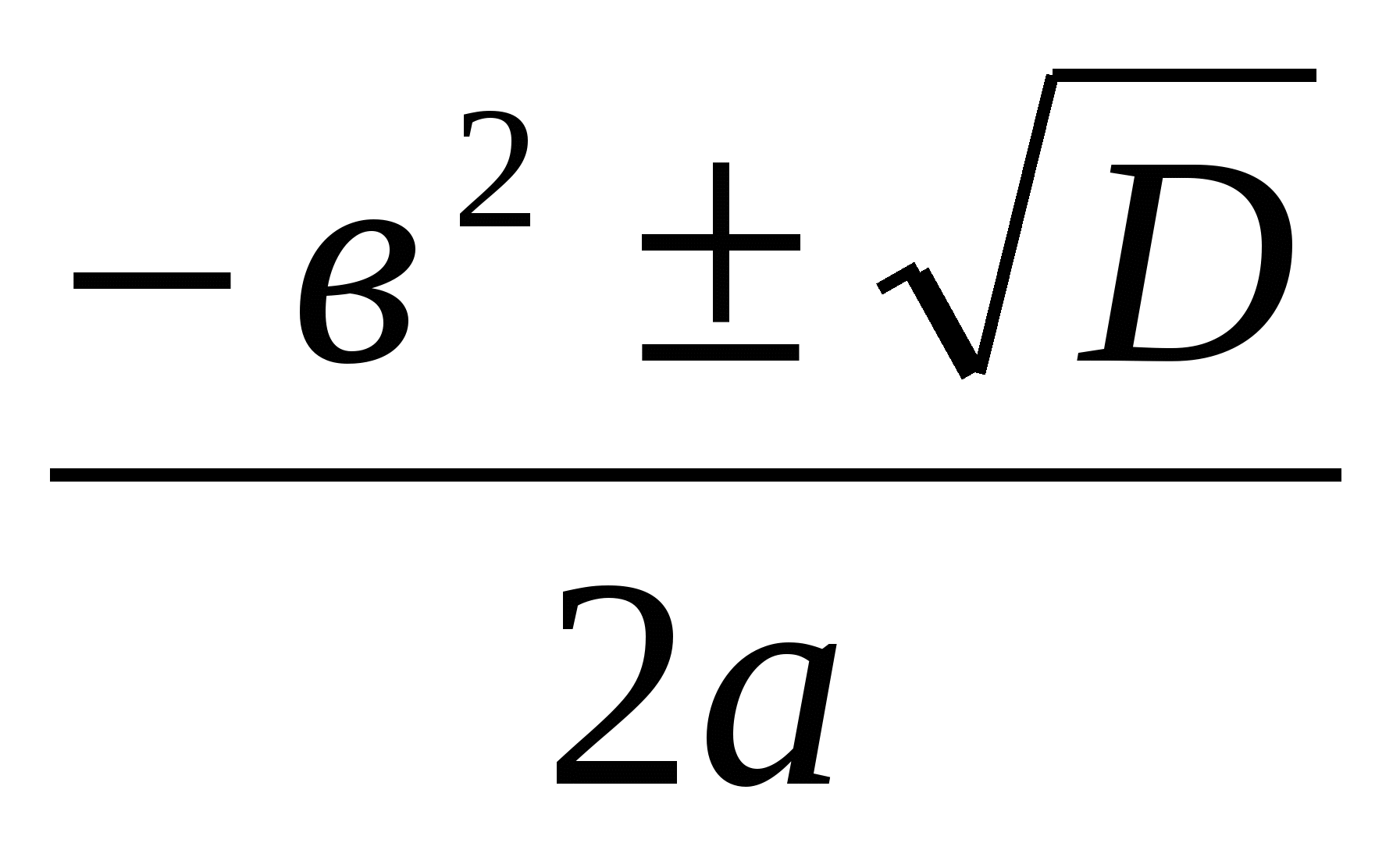
Д = 2 R L = П Д
D1 = k² ─ ас х = 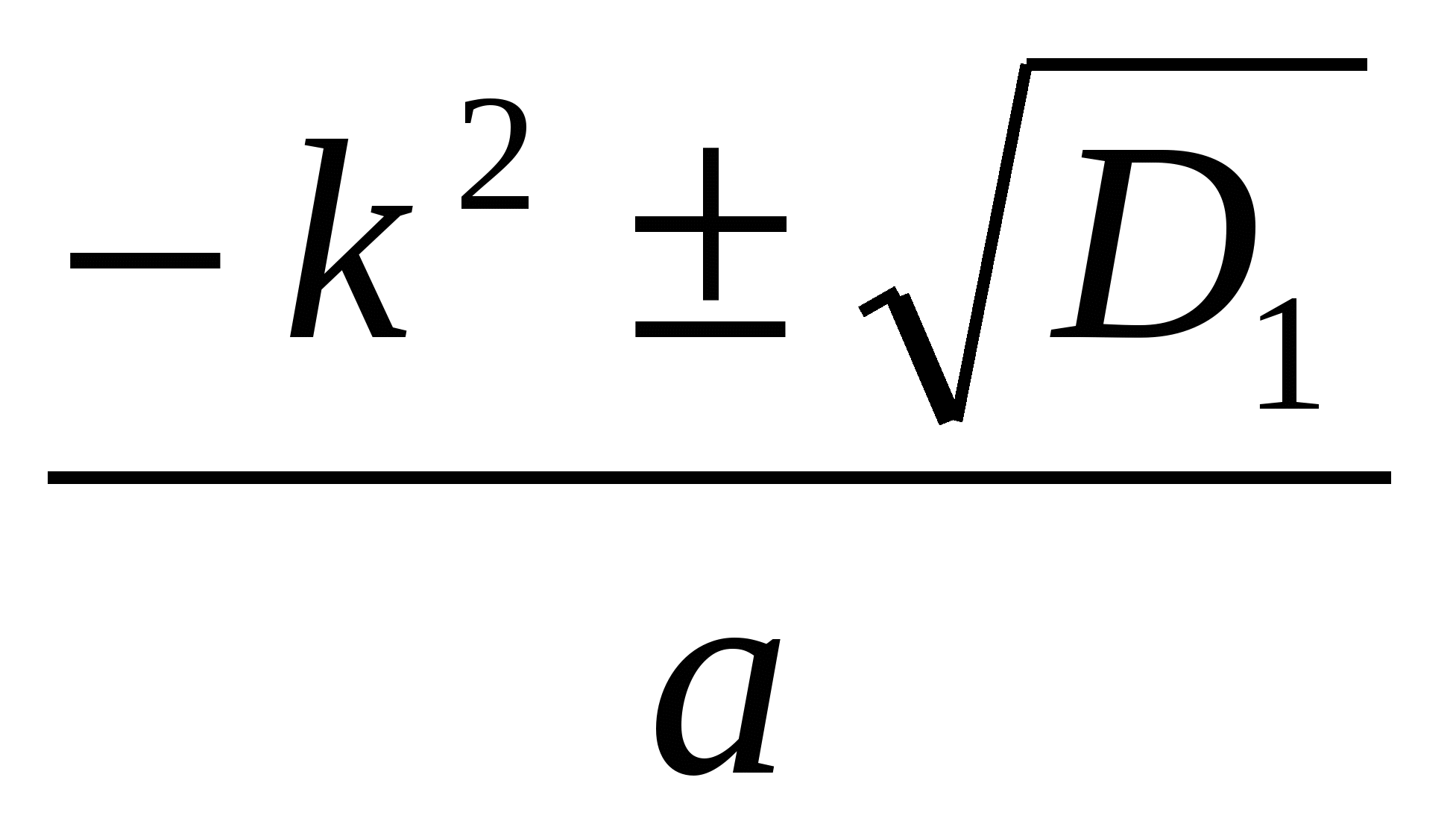
S = V t S = П R²
(слайд 6). Проверка
Вписать в лист результативности в Таблицу 1 баллы.
(по 1 за правильный ответ).
(слайд 7)
Работа с уравнениями. (5 мин.)
На экране появляются два столбика  уравнений:
уравнений:
А) 2х² – х + 3 = 0 Д) х² - 9х = 0
Б) 4х + х² - 1 = 0 Е) 2х – 5 = 0
В) 0,3 - 0,2х - х² = 0 Ж) 5х² = 0
Г) -7х + х2 - 0,5 = 0 З) 49х² = 0
Учащимся предлагается ответить на следующие вопросы:
Напишите коэффициенты квадратных уравнений.
Какое из этих уравнений не является квадратным?
Назовите неполные квадратные уравнения.
Назовите приведенные квадратные уравнения.
Какие уравнения можно решить по формуле корней квадратного уравнения?
(слайд 8). Проверка
Вписать в лист результативности в Таблицу 1 баллы.
(по 1 за правильный ответ). Итого max количество балов 22.
Самостоятельная работа. (12 мин.)
(слайд 9)
Каждый ученик выполняет посильные ему задания.
Карточка
1. Решите уравнения:
а) 5х² + 8х – 4 = 0
б) 25х² – 4 = 0
в) 6х² = 18х
Вписать в лист результативности в Таблицу 2 баллы.
(по 1 за правильный ответ).
2. Найдите два последовательных натуральных числа, произведение которых равно 132.
Вписать в лист результативности в Таблицу 2 баллы.
( 3 балла за правильный ответ).
3. Найти корни квадратного уравнения х² +3х – 40=0 по теореме Виета.
Вписать в лист результативности в Таблицу 2 баллы.
( 3 балла за правильный ответ).
4. Составить уравнение по его корням: х1 = 2 и х2 = - 5.
Вписать в лист результативности в Таблицу 2 баллы.
( 3 балла за правильный ответ). Итого max количество балов 12.
(слайд 10). Взаимопроверка.
Ответы на экране.
1. а) -2; 0,4
б) 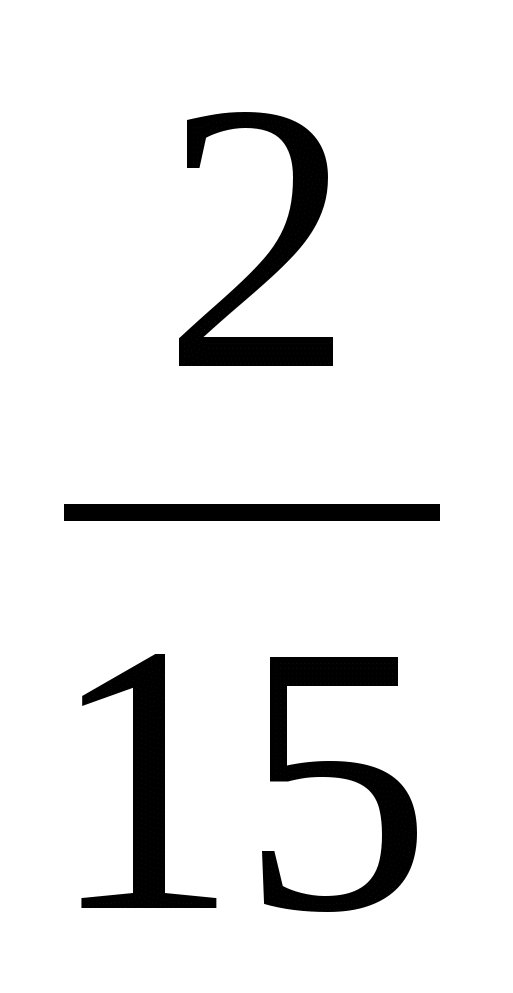 ; -
; -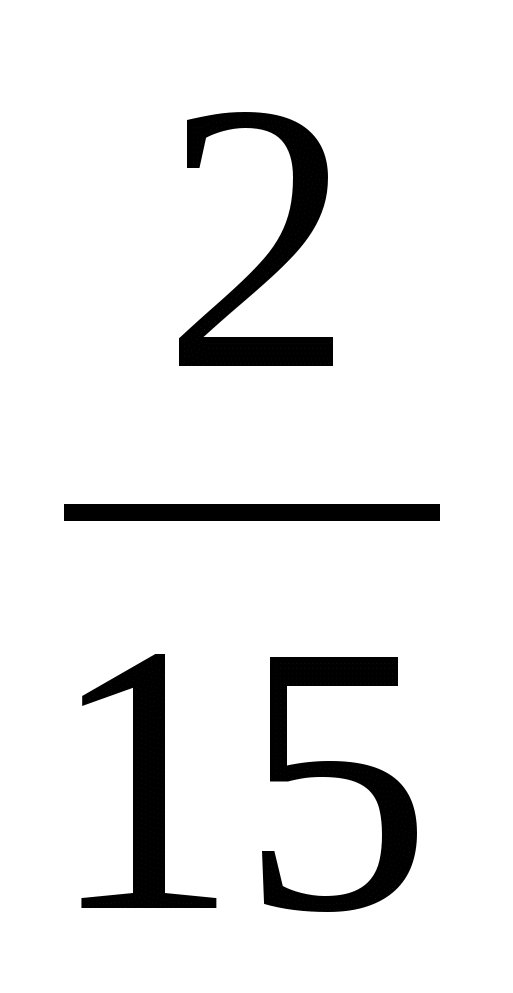
в) 0; 3
г) -2; 4
11 и 12.
– 8 и 5
х2 +3х-10=0
Устная работа. (3 мин.)
(слайд 11)
На доске написаны 4 пары квадратных уравнений:
 70х² - 175х + 70 = 0 |
70х² - 175х + 70 = 0 | 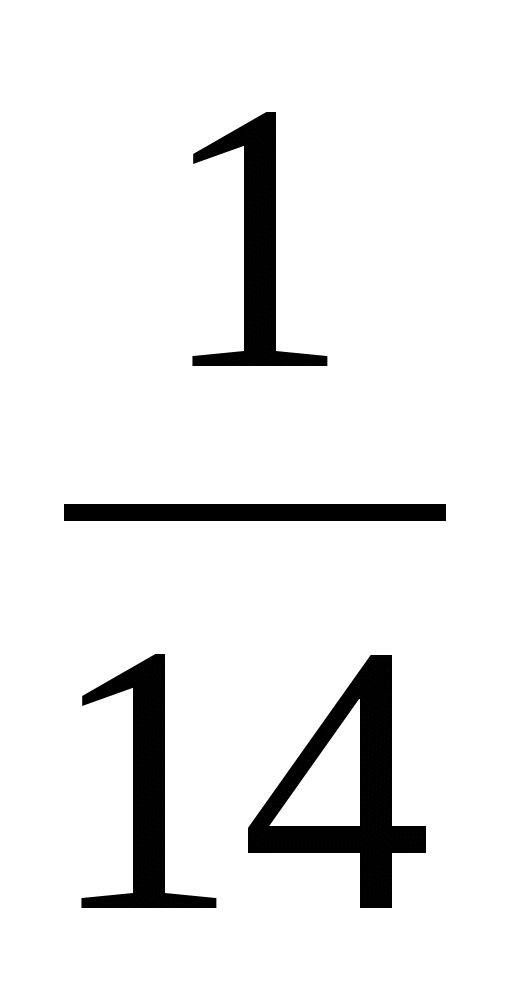 х² -
х² - 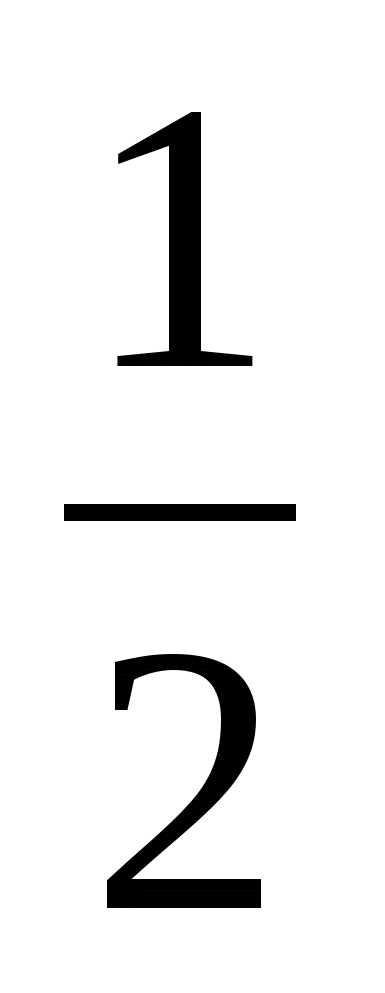 х +
х + 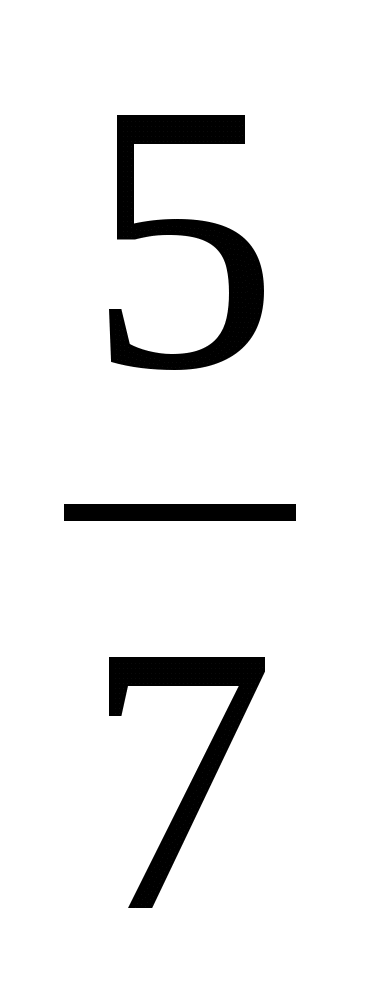 = 0 |
= 0 |
2х² - 5х + 2 = 0 х² - 7х + 10 = 0
0,6х² - 0,8х + 0,2 = 0 | -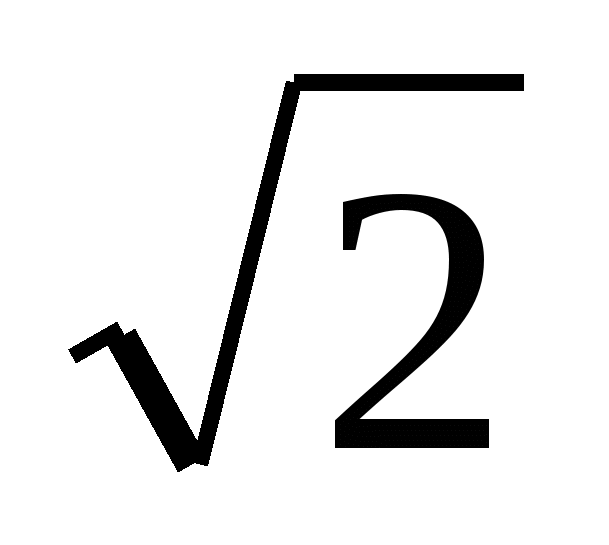 х² -
х² - 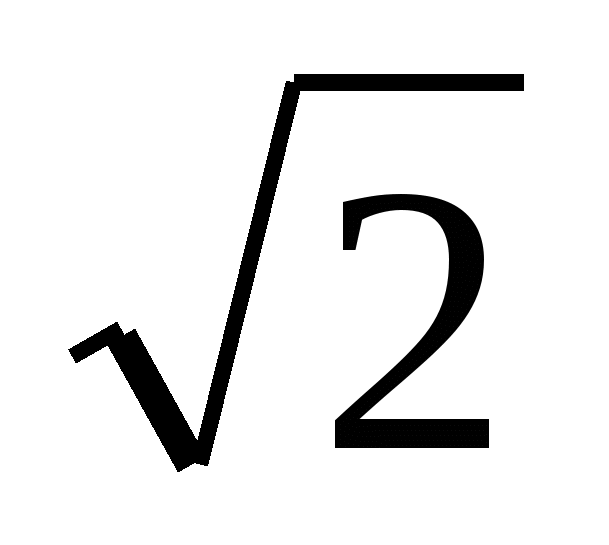 х +
х + 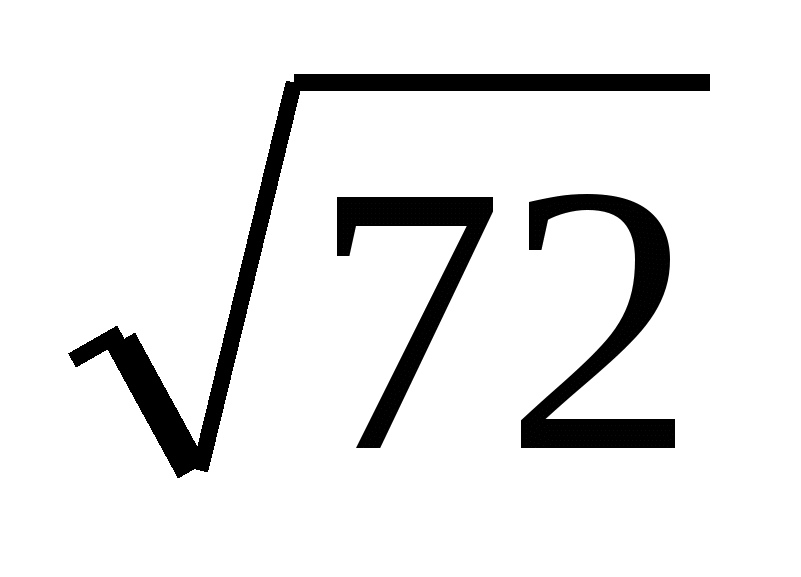 = 0 |
= 0 |
3х² - 4х + 1 = 0 х² + х – 6 = 0
(слайд 12)
Учащимся предлагается ответить на следующие вопросы:
Какое уравнение из пары вам хотелось бы решить?
____________________________________________
Можно ли от первого уравнения перейти ко второму?
____________________________________________
Если да, то как это сделать?
____________________________________________
Какое из этих уравнений можно решить по теореме Виета?
____________________________________________
(слайд 13). Проверка
Вписать в лист результативности в Таблицу 3 баллы.
( по 1 баллу за правильный ответ). Итого max количество балов 4.
Проверка знаний. (10 мин.)
(слайд 14)
Тест.
Какое из предложенных уравнений является квадратным уравнением?
А. 8х² + 4 – х³ = 0 Б. 2х³ – 5х² + 1 = 0
М. 4х – 9 + 2х² = 0 Н. х² + 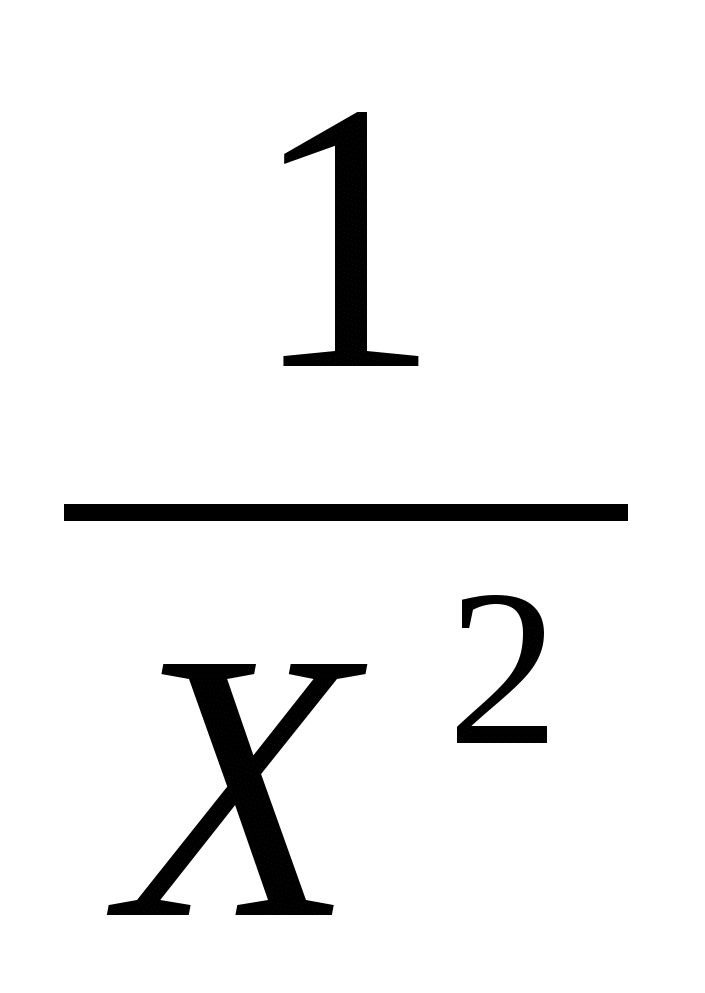 – 2 = 0
– 2 = 0
2. Сколько корней имеет квадратное уравнение, если дискриминант
меньше нуля?
К. два корня С.один корень О.не имеет корней
3. Какое из чисел -2, -1, 3, 5 является корнем уравнения
4х² – 11х – 3 = 0 ?
А. -1 О. -2 Л. 3 К. 5
4.Чему равна сумма корней уравнения:
7х² - 19х + 4 = 0
Е. 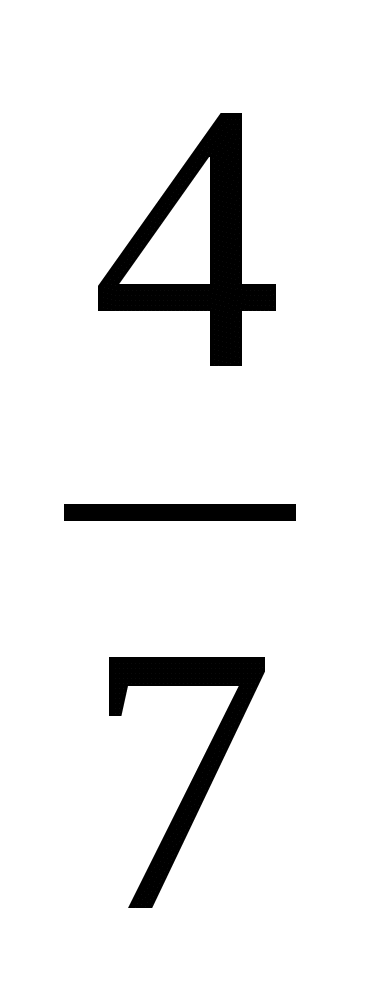 Б. -
Б. -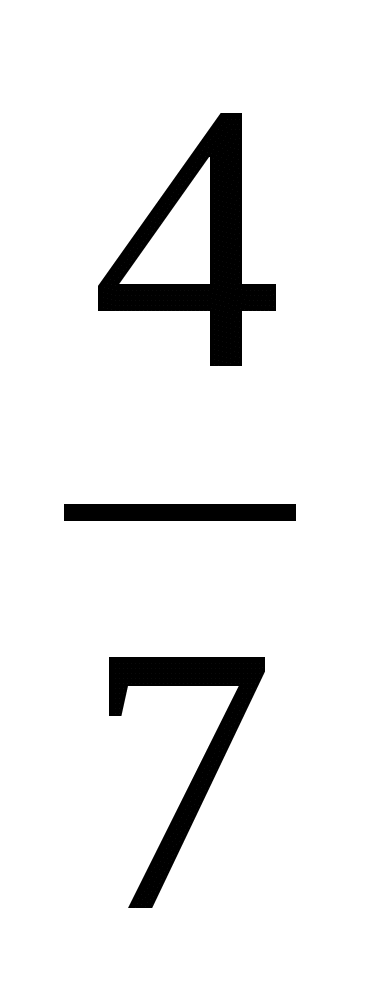 В. -
В. -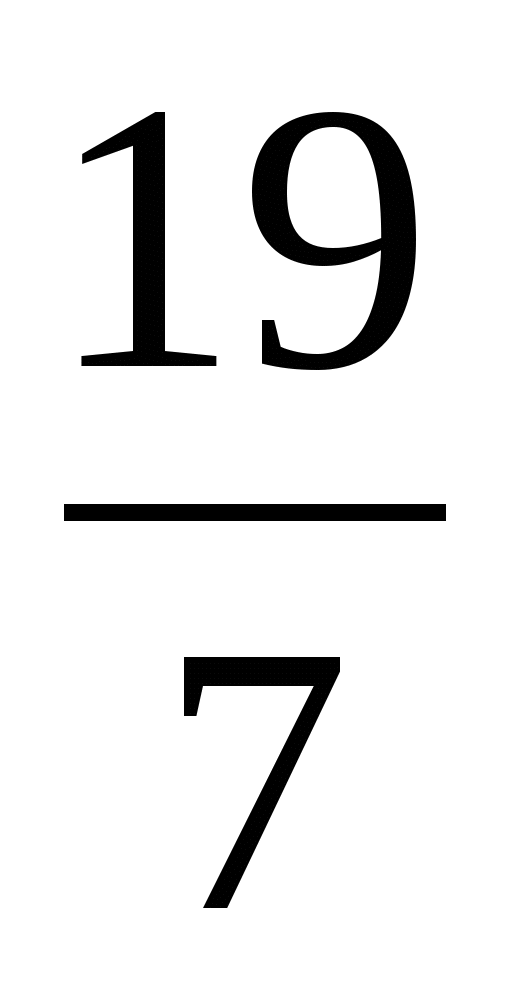 О.
О. 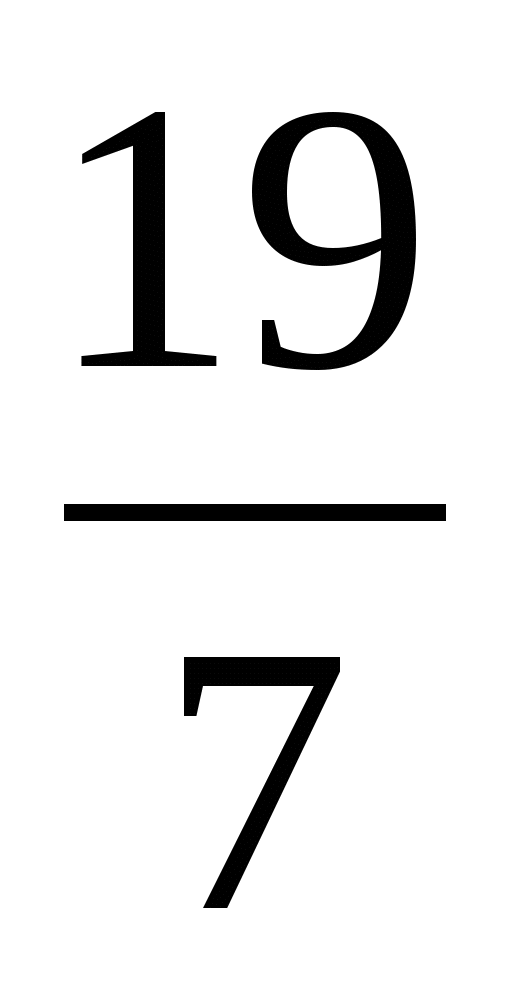
Какое из предложенных квадратных уравнений не имеет корней?
А. 4х² – 3х – 4 = 0 В. 9х² + 6х + 1 = 0
Б. х² + 4х + 3 = 0 Д. 5х² – х + 1 = 0
6. Чему равна сумма корней уравнения
х² ( х - 4 ) – ( х - 4 ) = 0
А. 18 В. 16 Г. 6 Е. 4
7. При каких значениях параметра р квадратное уравнение
2х² – 7х + 3р = 0 имеет только один корень?
А. Нет таких значений. Н. 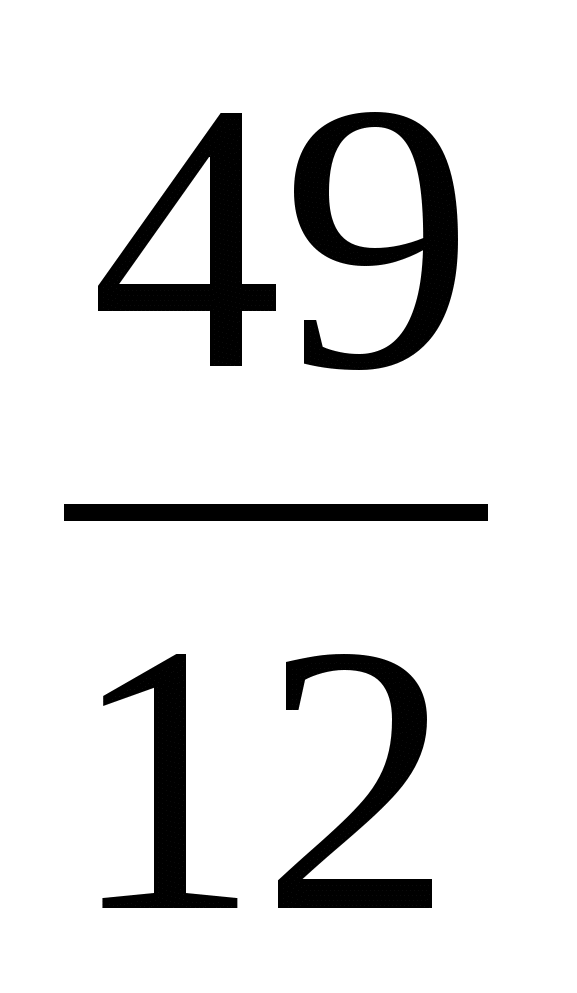 Ц.
Ц. 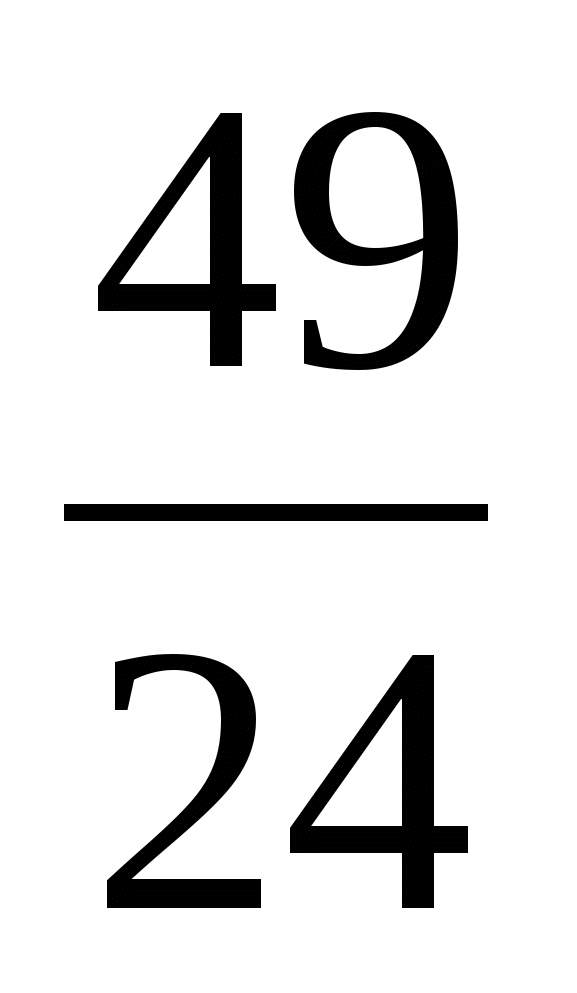 Г. -
Г. -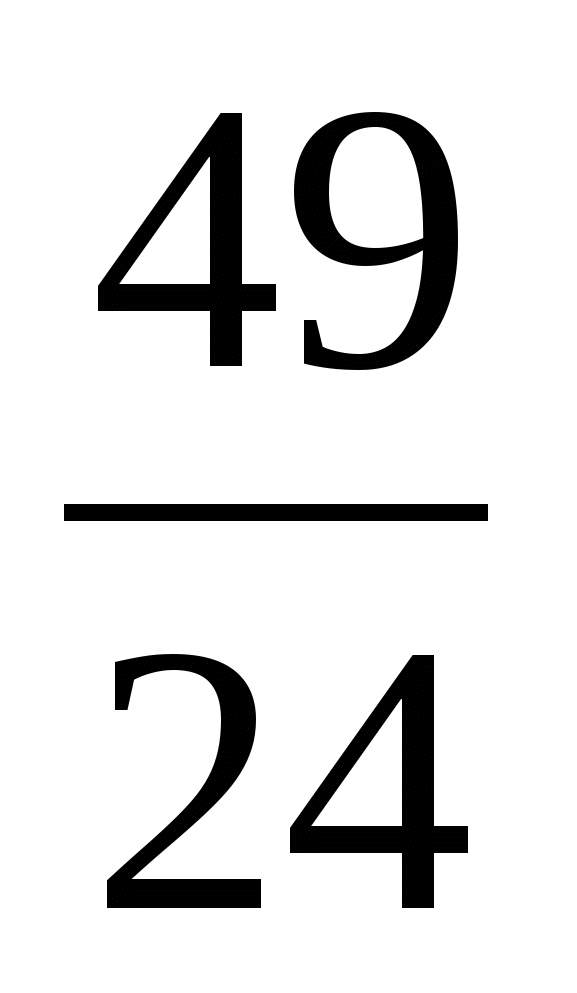
(слайд 14). Проверка
Ответы на экране.
1-М 2-О 3-Л 4-О 5-Д 6-Е 7-Ц
Вписать в лист результативности в Таблицу 4 баллы.
( по 1 баллу за правильный ответ). Итого max количество балов 7.
Итог урока. (2 мин.)
(слайд 15)
- Повторим алгоритм решения квадратных уравнений.
(слайд 16)
менее 23 балов оценку получим на следующем уроке.
23 - 30 балов – «3»
31 - 38 балов – «4»
39 - 47 балов – «5»
(слайд 17)
- Молодцы, ребята! Вы справились с поставленной задачей!
(слайд 18)
Спасибо! До новых встреч!