Павлюк Ирина Владиславовна
учитель математики
МБОУ гимназия №19 г. Липецка
Методическая разработка «Особые приёмы при решении трансцендентных неравенств методом интервалов»
Алгебра и начала анализа
11 класс
«ЗАМЕНА НА ЭКВИВАЛЕНТНОЕ ВЫРАЖЕНИЕ» ПРИ РЕШЕНИИ ТРАНСЦЕНДЕНТНЫХ НЕРАВЕНСТВ МЕТОДОМ ИНТЕРВАЛОВ
Павлюк Ирина Владиславовна,
учитель математики МОУ гимназии №19 г. Липецка,
стаж работы 23 года, высшая квалификационная категория
Без сомнения, одна из основных задач учителя математики – развивать самостоятельное мышление учеников. Но приходиться признать тот факт, что даже усердные ученики часто не могут продвинуться дальше применения отработанных методов. Очевидно, что чем большем запасом наработанных «стандартных положений» владеет ученик, тем выше отодвигается его личная планка эвристического уровня.
Представляется полезным приведение в систему приёмов решения трансцендентных неравенств методом интервалов.
Методическая разработка
Тема урока*. Метод интервалов в решении трансцендентных неравенств.
Цели урока:
Выработка творческого подхода к использованию теоретического материала вообще и свойств монотонных функции в частности.
Овладение новым методом решения трансцендентных неравенств.
Развитие навыков решения неравенств.
Программно-методическое обеспечение: Математика. ЕГЭ-2006. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2005. - [1],
Математика. ЕГЭ-2009. Часть II. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2009. - [2].
План урока:
Постановка цели урока.
Разбор домашнего задания и постановка проблемы.
Актуализация знаний.
Формулирование положений нового метода.
Решение неравенств из домашней работы новым способом.
Самостоятельное (с обсуждением и корректировкой) решение неравенств.
Решение задач с использованием рассматриваемого метода.
Итоги урока и домашнее задание.
Ход урока.
Постановка цели урока.
В классе (раздать задания):
К пункту 6:
№2 а) 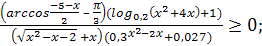 б)
б) 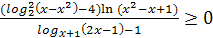 .
.
К пункту 7:
№3 Функция 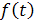 определена, строго возрастает и отрицательна на всей числовой прямой. Найдите все значения х, удовлетворяющие неравенству
определена, строго возрастает и отрицательна на всей числовой прямой. Найдите все значения х, удовлетворяющие неравенству
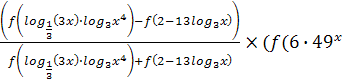 +20
+20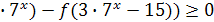 . ([1], Вариант10 С3).
. ([1], Вариант10 С3).
№4 Найдите все значения x при каждом из которых выполняется хотя бы одно из неравенств 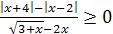 или
или 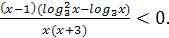 ([2], Вариант5 С3)
([2], Вариант5 С3)
Анализ домашней работы
На предыдущем уроке учащимся было предложено в домашней работе продумать возможные пути решения неравенств:
№1 а) 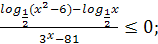 б)
б) 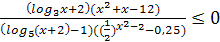 .
.
№1 (а) 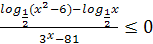
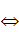
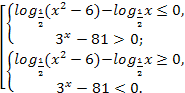
№1 (б)
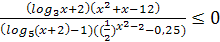
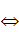
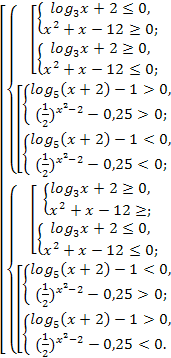
Очевидно, что решения получаются громоздкими и следует поискать другой поход.
3. Актуализация знаний.
Заметим, что множители, входящие в левые части неравенств содержат выражения, соответствующие монотонным функциям (логарифмической и показательной). Вспомним определения возрастающей и убывающей функций.
Опр.1: Функция 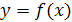 называется возрастающей, если для
называется возрастающей, если для 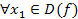 и
и 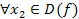 имеет место
имеет место 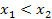
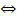
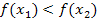 .
.
Опр.2: Функция 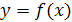 называется убывающей, если для
называется убывающей, если для 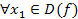 и
и 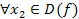 имеет место
имеет место 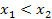
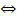
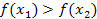 .
.
4. Решение неравенств из домашней работы новым способом.
№1 (а)
Выражение из неравенства
Соответствующая функция
Эквивалентное выражение
Условия
f(t)
D(f)
монотонность
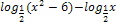
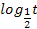
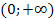
убывающая
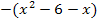
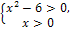
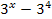
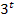
R
возрастающая
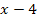
нет
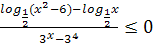
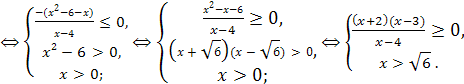
Ответ. 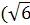 ;3]
;3]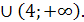
№1 (б)
Выражение из неравенства
Соответствующая функция
Эквивалентное выражение
Условия
f(t)
D(f)
монотонность
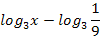
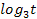
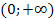
возрастающая
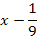
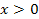
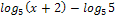
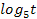
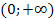
возрастающая
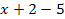
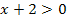
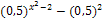
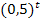
R
убывающая
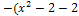 )
)
нет
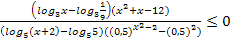
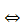
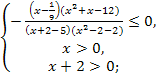
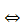
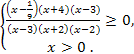
Ответ. 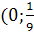 ]
]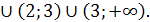
№2 (а)

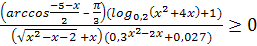
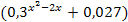 , причём
, причём 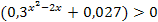 при
при 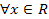
Одз: 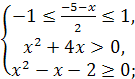
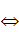
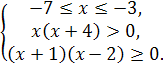 Итак,
Итак, 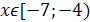 .
.
Отметив, что при 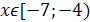 :
: 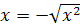 , получим уравнение
, получим уравнение
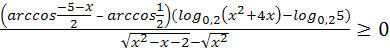 .
.
Функция 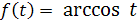 - убывающая с
- убывающая с 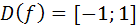 , функция
, функция 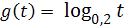 - убывающая с
- убывающая с 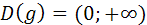 , функция
, функция 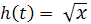 - возрастающая с
- возрастающая с 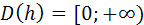 .
.
Заменив выражение 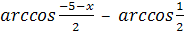 на эквивалентное -(
на эквивалентное -(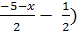 , выражение
, выражение 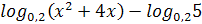 на эквивалентное
на эквивалентное 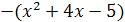 и выражение
и выражение 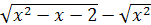 на эквивалентное
на эквивалентное 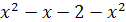 , и учитывая Одз, получим равносильную систему:
, и учитывая Одз, получим равносильную систему:
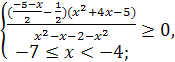
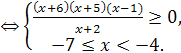
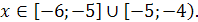
Ответ. 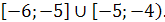
№2(б) 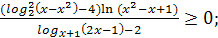
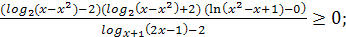
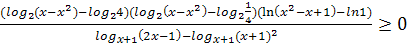 .
.
Логарифмическая функция 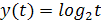 на
на 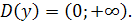
Заметим, что для существования решения неравенства необходимо выполнение условия 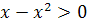 , то есть
, то есть 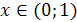 . А при
. А при 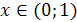 :
: 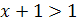 и логарифмическая функция с соответствующим основанием возрастает на своей области определения.
и логарифмическая функция с соответствующим основанием возрастает на своей области определения.
Получим равносильную систему:
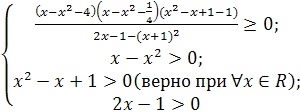
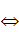
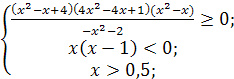 Учитывая, что
Учитывая, что 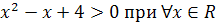 и
и 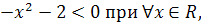 получим
получим 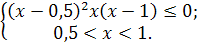
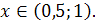
Ответ. 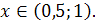
5. Самостоятельное (с обсуждением и корректировкой) решение неравенств.
№2 (а)

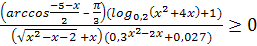
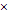
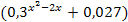 , причём
, причём 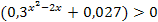 при
при 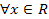
Одз: 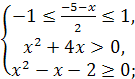
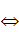
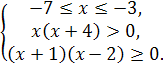 Итак,
Итак, 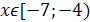 .
.
Отметив, что при 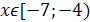 :
: 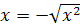 , получим уравнение
, получим уравнение
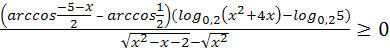 .
.
Функция 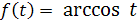 - убывающая с
- убывающая с 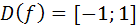 , функция
, функция 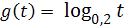 - убывающая с
- убывающая с 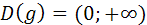 , функция
, функция 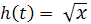 - возрастающая с
- возрастающая с 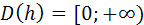 .
.
Заменив выражение 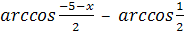 на эквивалентное -(
на эквивалентное -(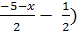 , выражение
, выражение 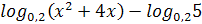 на эквивалентное
на эквивалентное 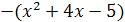 и выражение
и выражение 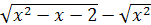 на эквивалентное
на эквивалентное 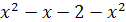 , и учитывая Одз, получим равносильную систему:
, и учитывая Одз, получим равносильную систему:
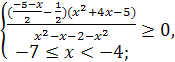
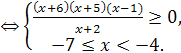
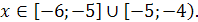
Ответ. 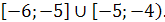
№2(б) 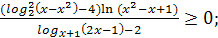
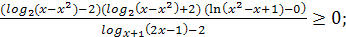
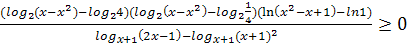 .
.
Логарифмическая функция 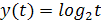 на
на 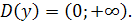
Заметим, что для существования решения неравенства необходимо выполнение условия 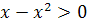 , то есть
, то есть 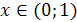 . А при
. А при 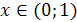 :
: 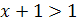 и логарифмическая функция с соответствующим основанием возрастает на своей области определения.
и логарифмическая функция с соответствующим основанием возрастает на своей области определения.
Получим равносильную систему:
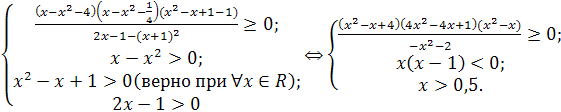 Учитывая, что
Учитывая, что 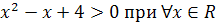 и
и 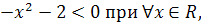 получим
получим 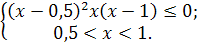
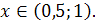
Ответ. 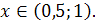
6. Решение задач с использованием рассматриваемого метода.
№3 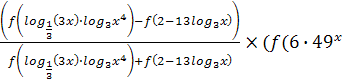 +20
+20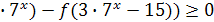 .
.
Так как по условию 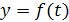 – возрастающая функция и
– возрастающая функция и 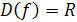 , то можем заменить
, то можем заменить 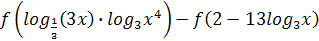 на эквивалентное
на эквивалентное 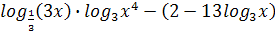 , а
, а 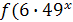 +20
+20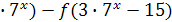 - на эквивалентное
- на эквивалентное 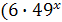 +20
+20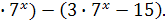
Кроме того по условию 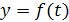 принимает только отрицательные значения, то
принимает только отрицательные значения, то 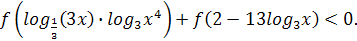
Получим неравенство, равносильное заданному:
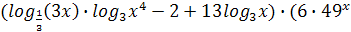 +20
+20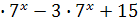 )
)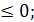
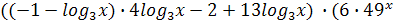 +17
+17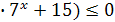 .
.
Учитывая, что 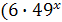 +17
+17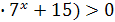 при
при 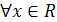 , получим:
, получим:
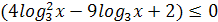 ; (
; (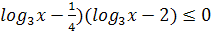 ;
; 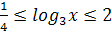 ;
; 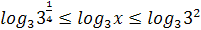 .
.
Так как 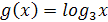 - возрастающая функция с
- возрастающая функция с 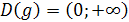 , то получим равносильную систему:
, то получим равносильную систему: 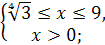
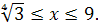
Ответ. [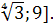
№4
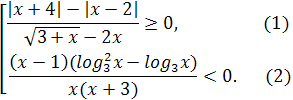
Рассмотрим неравенство (1). С учётом необходимого условия 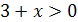 получим
получим 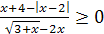 , что равносильно совокупности
, что равносильно совокупности
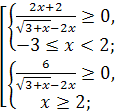
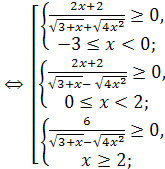
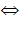
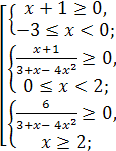
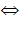
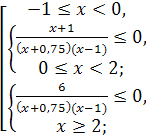
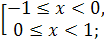
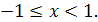
Рассмотрим неравенство (2).
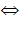
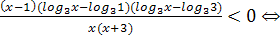
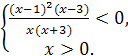
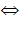
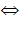
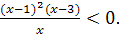
Итак, 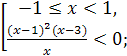
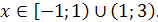
Ответ. 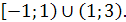
7. Итоги урока и домашнее задание.
№5 Найдите все значения x, удовлетворяющие неравенству 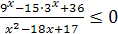 , при каждом из которых выполняется хотя бы одно из неравенств
, при каждом из которых выполняется хотя бы одно из неравенств 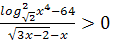 ,
, 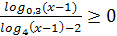 . ([2], Вариант6 С3)
. ([2], Вариант6 С3)
№6 Функция 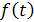 определена и строго убывает на всей числовой прямой. Найдите все значения x, удовлетворяющие неравенству
определена и строго убывает на всей числовой прямой. Найдите все значения x, удовлетворяющие неравенству
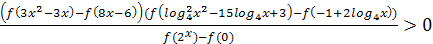 . ([1], Вариант10 С3).
. ([1], Вариант10 С3).
Программно-методическое обеспечение: Математика. ЕГЭ-2006. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2005. - [1],
Математика. ЕГЭ-2009. Часть II. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2009. - [2].
* Материал рассчитан на 2 часа (сдвоенный урок)