Открытый урок по алгебре
Тема: «Решение задач с помощью рациональных уравнений»
Класс: 8 «Б»
Предмет: Алгебра
Цели урока:
Обучающая:
закрепление понятия дробного рационального уравнения;
составление математической модели задачи, перевод условия задачи с обычного языка на математический;
проверка уровня усвоения темы путем проведения проверочной работы.
Развивающая:
развитие умения правильно оперировать полученными знаниями, логически мыслить;
развитие интеллектуальных умений;
развитие умения принимать решения.
Воспитательная:
воспитание познавательного интереса к предмету;
воспитание самостоятельности при решении учебных задач;
воспитание воли и упорства для достижения конечных результатов.
Задачи:
1) актуализировать знание решения дробных рациональных уравнений, умение решать задачи при помощи рациональных уравнений; добиться усвоения алгоритма решения задач;
2) - Познавательные: овладение основами логического и алгоритмического мышления;
Регулятивные: развитие умения читать и записывать информацию в виде различных математических моделей, планировать действия в соответствии с поставленной задачей;
Коммуникативные: строить высказывания, аргументировано доказывать свою точку зрения;
Личностные: развитие навыков сотрудничества со сверстниками,
3) - воспитывать чувство товарищества.
Оборудование: презентация, конспект урока, компьютер, проектор.
Ход урока:
1. Организационный момент.
Здравствуйте, ребята.
Прозвенел звонок - начинается новый урок , на котором будем учиться математике, а значит жизни. Ведь жизнь перед нами ставит постоянно много вопросов, задач, на которые надо найти ответ непременно и именно только нам . И от правильности найденного решения зависит порою очень многое в жизни .Бывает так, что жизнь ошибок не прощает…
Математика считается царицей всех наук, потому что……?… «ум, который решает все наши жизненные вопросы, в порядок приводит», ……. через умения мыслить , анализировать, сопоставлять, делать выводы, считать. Все эти мыслительные процессы и помогают нам найти правильное решение жизненных проблем. Очень хорошо развиваются эти мыслительные процессы при решении разного рода школьных задач. Задачам отводится много места ,как в школьном курсе математики, так и на экзамене по математике в 9 классе и на ЕГЭ в 11классе.
Ещё начиная с начальной школы, вы учились решать разные , теперь уже не сложные для вас ,задачи. С каждым годом вы узнавали всё новые и новые методы и способы их решения. Сегодня мы будем решать задачи, решение которых сводится к дробным рациональным уравнениям.
Итак, тема урока «Решение задач с помощью рациональных уравнений»
(Ученики записывают тему урока, которая была закрыта доской)
Актуализация знаний.
Фронтальный опрос, устная работа с классом.
-Исходя из темы урока, чтобы решать сами задачи первоначально надо уметь решать рациональные уравнения, которые включают в себя…..целые уравнения и дробно-рациональные.
-Слайд1
-Скажите, что вы видите на этом слайде? ( Уравнения)
- Правильно. Какие это уравнения? ( Дробно-рациональные)
- а могу я сказать, что это рациональные уравнения? ( Да. Т.к. рациональные включают в себя и дробно-рациональные вместе с целыми)
- Какие уравнения называют рациональными?
-Назовите алгоритм решения дробно-рациональных уравнений?
Решите устно данные уравнения.
Слайды1-3.

Решение задач.
-Прежде чем приступать к решению задачи необходимо несколько раз внимательно прочитать условие задачи, и ответить для себя на ряд вопросов. Каких?
( Тип задачи - объекты, участвующие в ней, - величины, характеризующие эти объекты - связи между этими величинами – какую величину обозначим за х)
-Получив ответы на эти вопросы, далее или составляем краткую запись в том виде, как нам удобно, а затем математическую модель, или, логически рассуждая, составляем математическую модель задачи, предварительно все велечины выразив через введенную переменную х)
Рассмотрим задачу1
Идет коллективный анализ условия задачи и составление математической модели. Возможны несколько вариантов составления уравнения. Все их записываем на доске.
Работу с математической моделью у доски проводит ученик, выбрав то уравнение, которое ему ближе.

После того, как решение задачи завершено, проговариваем большие этапы в решении этой задачи:
Назовите этапы решения задачи.
(1.Составление математической модели.
2.Работа с составленной моделью.
3. Ответ на вопрос задачи)
- Мы решили задачу на движение. Какой тип задач по своей сути и ходу решения очень похож на рассмотренные задачи на движение?
( Задачи на работу)
Пример 2 Слайд 5
Прочитав условие задачи на слайде, ученики, работая в паре, составляют краткую запись условия задачи и озвучивают свое решение с места .
Учитель показывает презентацию до уравнения.
-Какое же уравнение ,из предложенных мною, является математической моделью данной задачи? (ученики выбирают верное уравнение)

Ученики составляют уравнение, соответствующее условию задачи на местах и выбирают верное из предложенных учителем.
-Как можно по-другому назвать процесс составления уравнения по задачи?
- Как вы можете образно назвать это уравнение для нашей задачи?
-Какие еще задачи на движения мы с вами ранее решали?
( Ученики называют разные типы, но учитель останавливается на движении по течению и против)
- Какие в этих задачах участвуют величины?
Пример 3.

Ученики на месте решают предложенную задачу, кто первый справился, тот решение уравнения демонстрирует на доске, а другой справившейся с заданием ученик комментирует составление таблицы
.
--- Составьте сами задачу, используя эти же данные, где бы вариантов составления уравнения было бы намного меньше.!!!!!!
4. Выполнение контролирующего задания
Индивидуальная работа выполняется на листочках.
Работа оценивается
На «3» за правильно выполненное 1 задание;
На «4» - за 1-2;
На «5»- за 1-3( в 3-ем задании достаточно только составить уравнение.
Вариант 1.
Выполните тест, выбрав в заданиях 1-2 ответы под цифрами 1,2,3 или 4 ( ответы указаны в рамке),а в задании 3 запишите получившийся у вас результат в виде целого числа или десятичной дроби. Желаем удачи.
Решите уравнение:
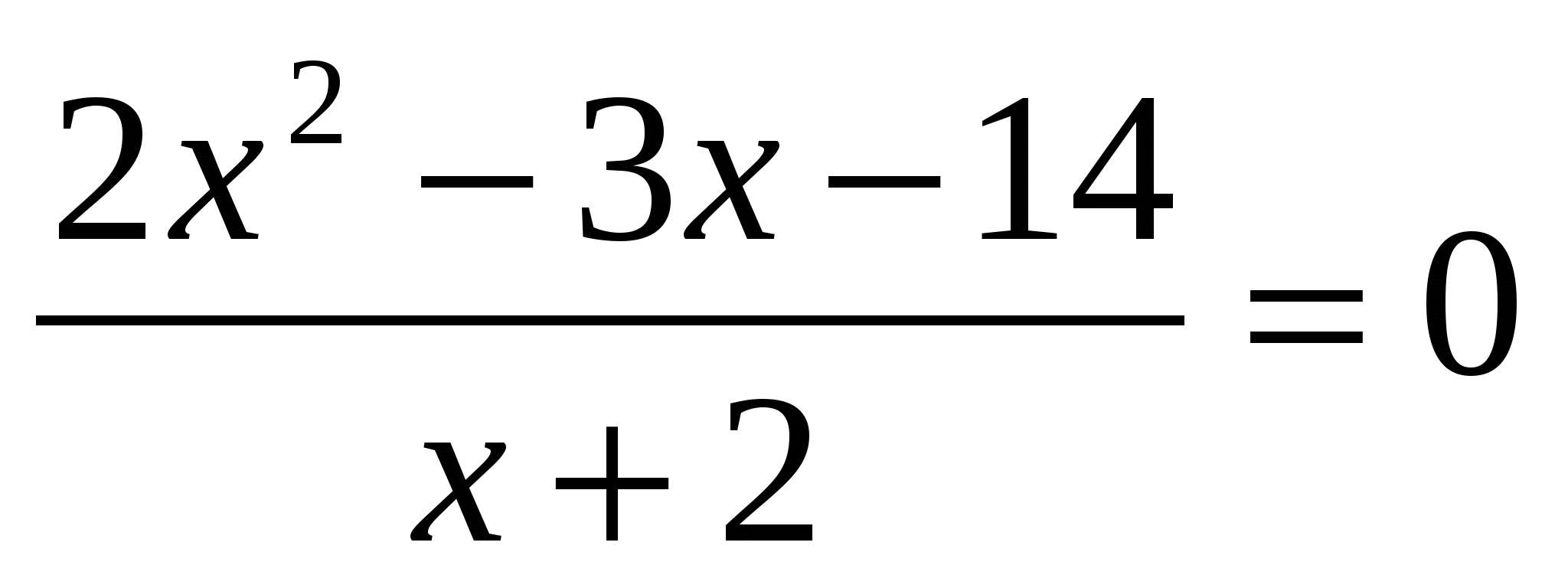
-
1) 7 ; -2 ; 2) 7 ; 3) 3,5 ; 4) 3,5 ; -2
Прочитав условие задачи, составьте уравнение, которое ему соответствует:
Теплоход прошёл 108 км по течению реки и 84 км против течения, затратив на весь путь 8ч. Найдите собственную скорость теплохода, обозначив её х км/, если скорость течения реки 3 км/ч
-
1)
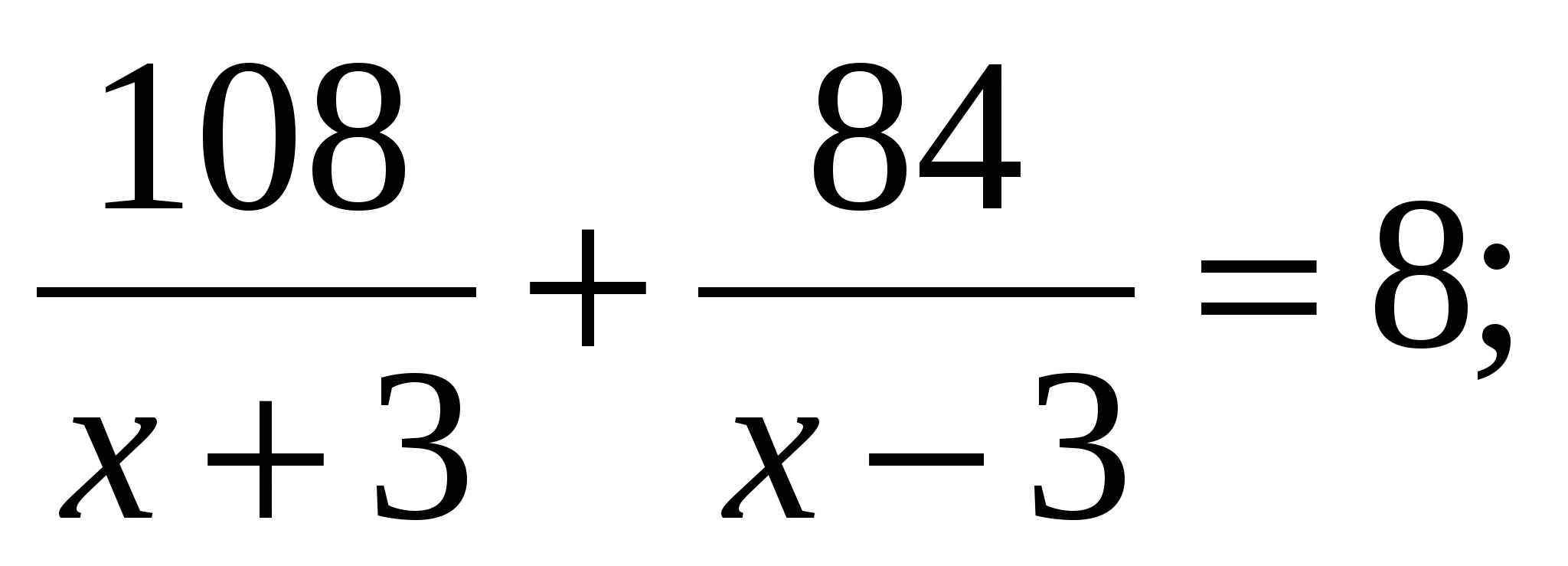 ; 2)
; 2) 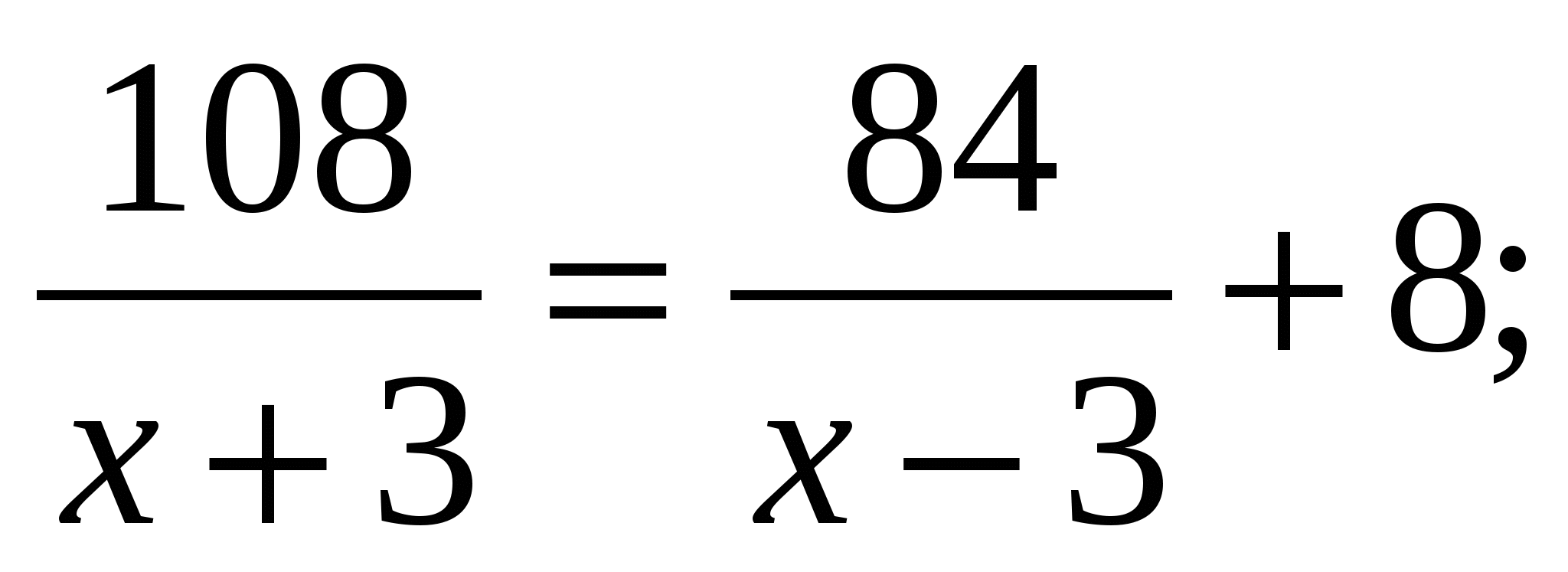 ;
; 3)
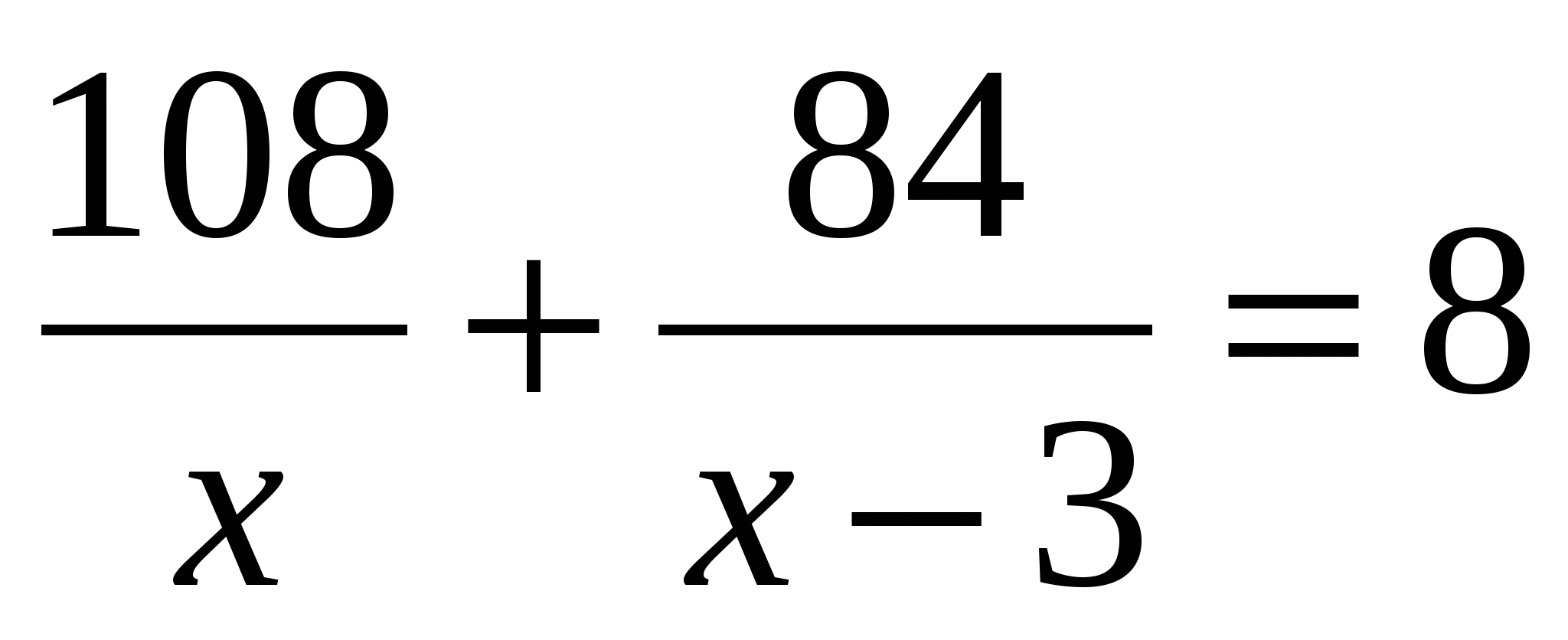 ; 4)
; 4) 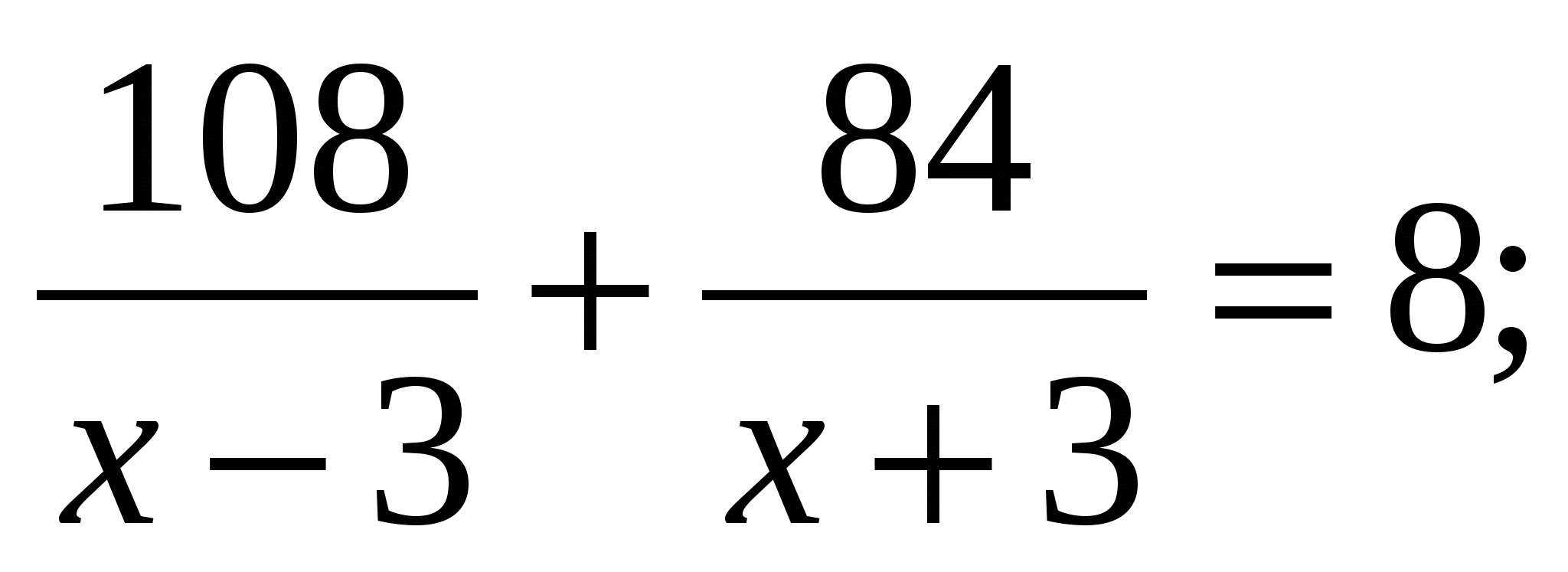
3.Решите задачу, составив уравнение:
Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?
Ответ: ___________
Вариант 2.
Выполните тест, выбрав в заданиях 1-2 ответы под цифрами 1,2,3 или 4 ( ответы указаны в рамке),а в задании 3 запишите получившийся у вас результат в виде целого числа или десятичной дроби. Желаем удачи.
Решите уравнение:
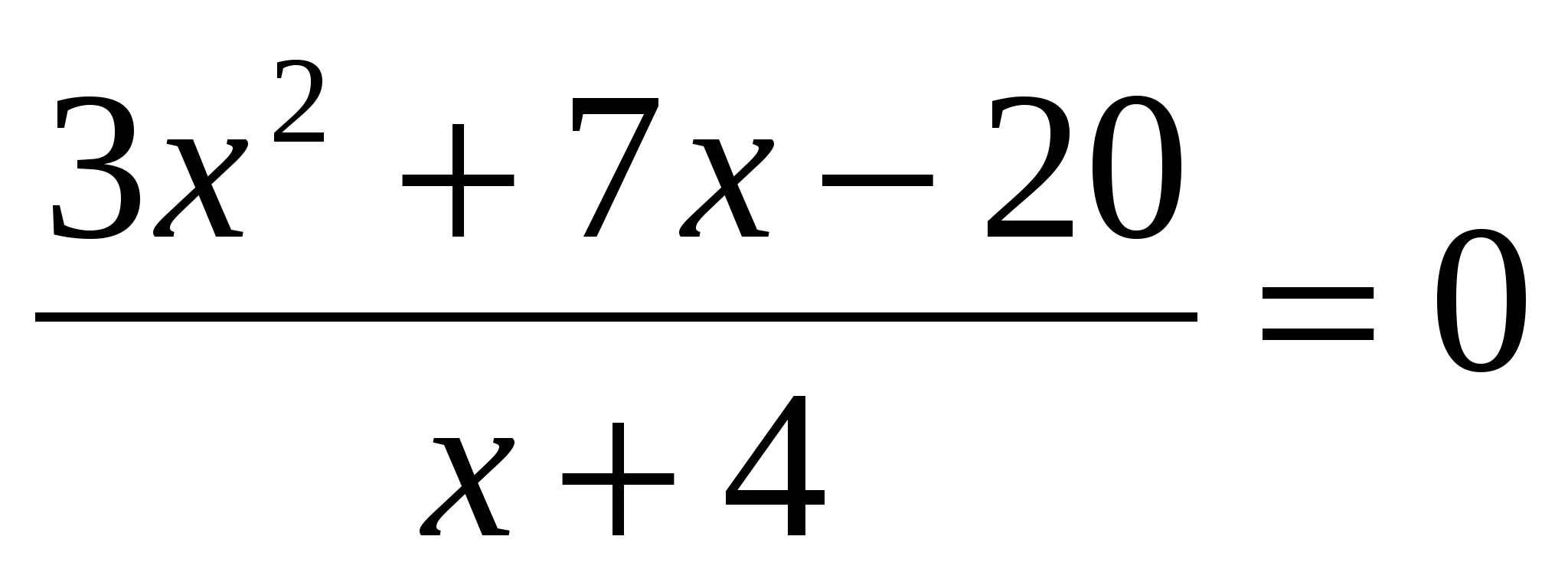
-
1)
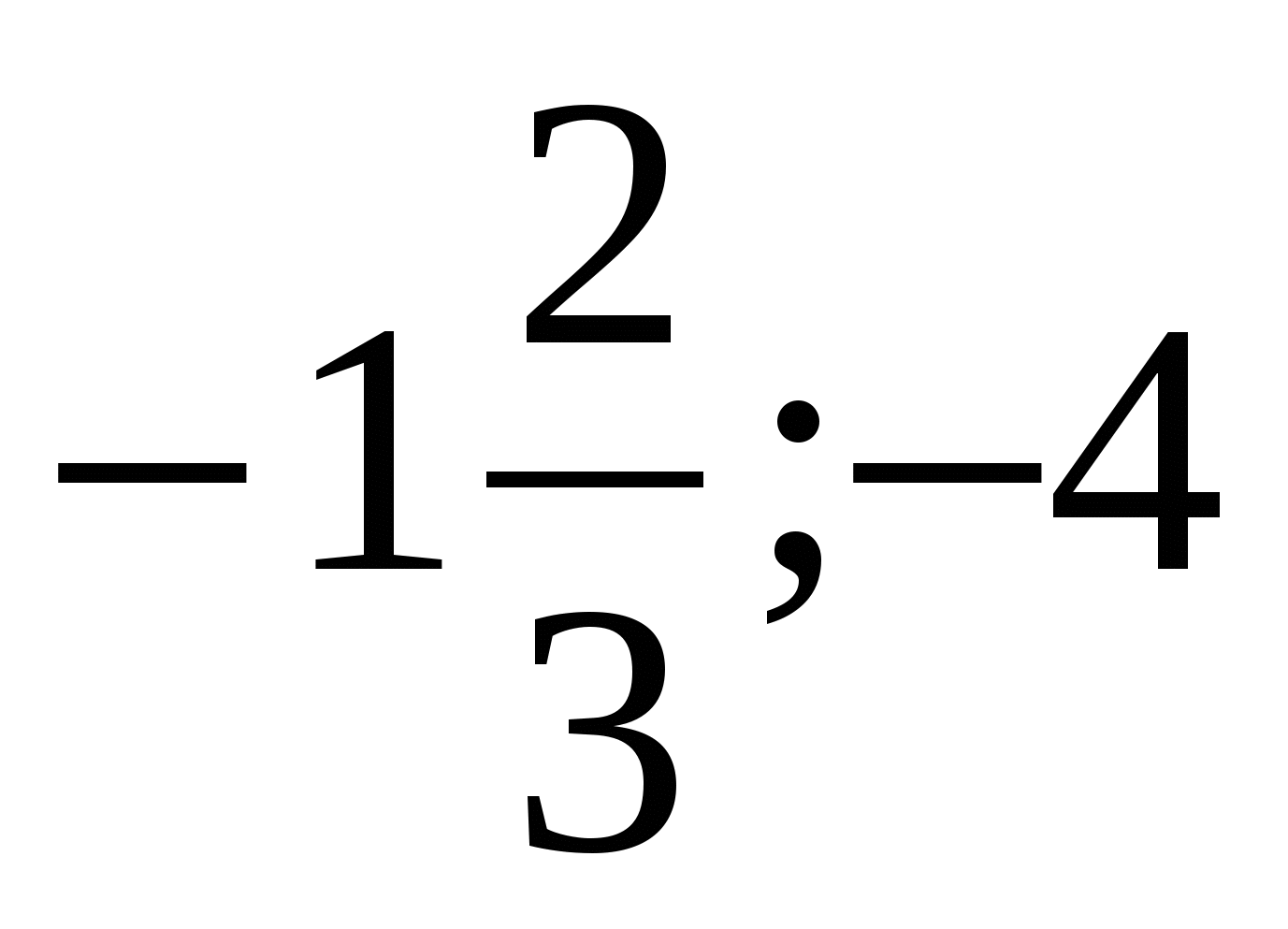 ; 2)
; 2) 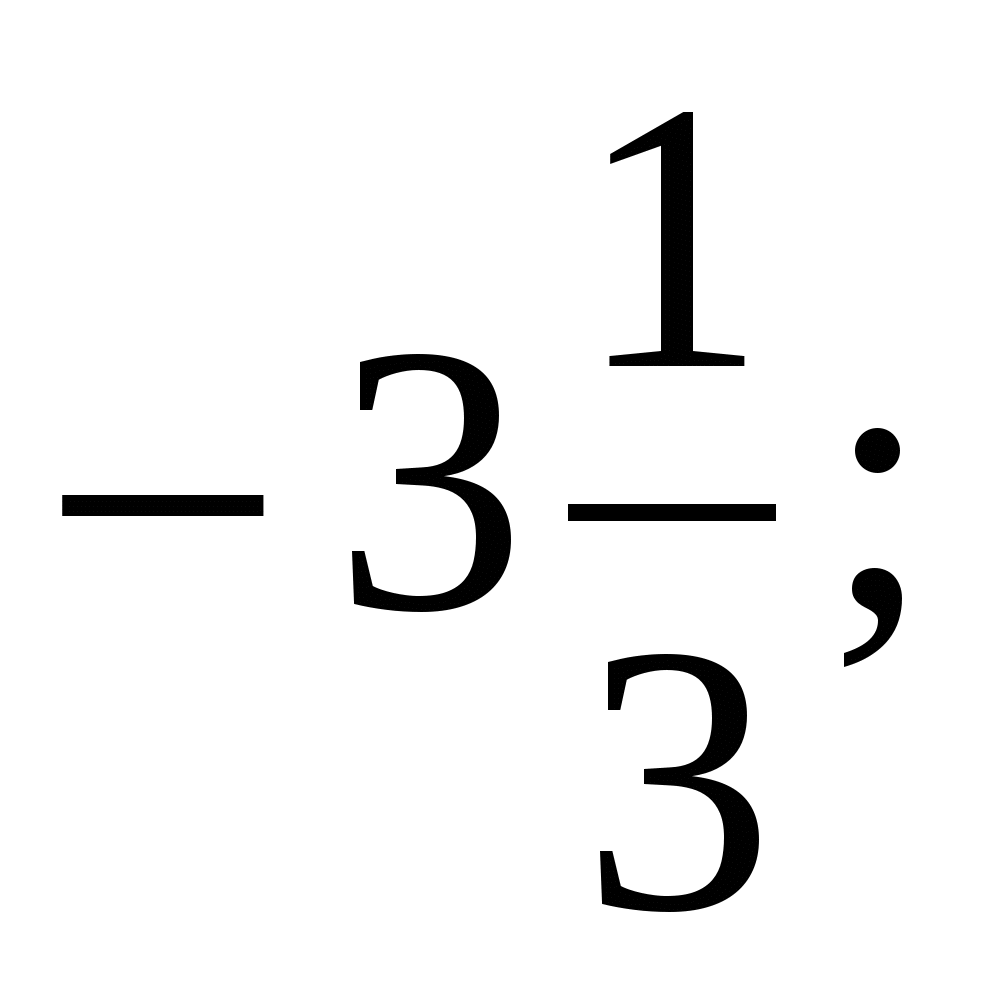 ; 3)
; 3) 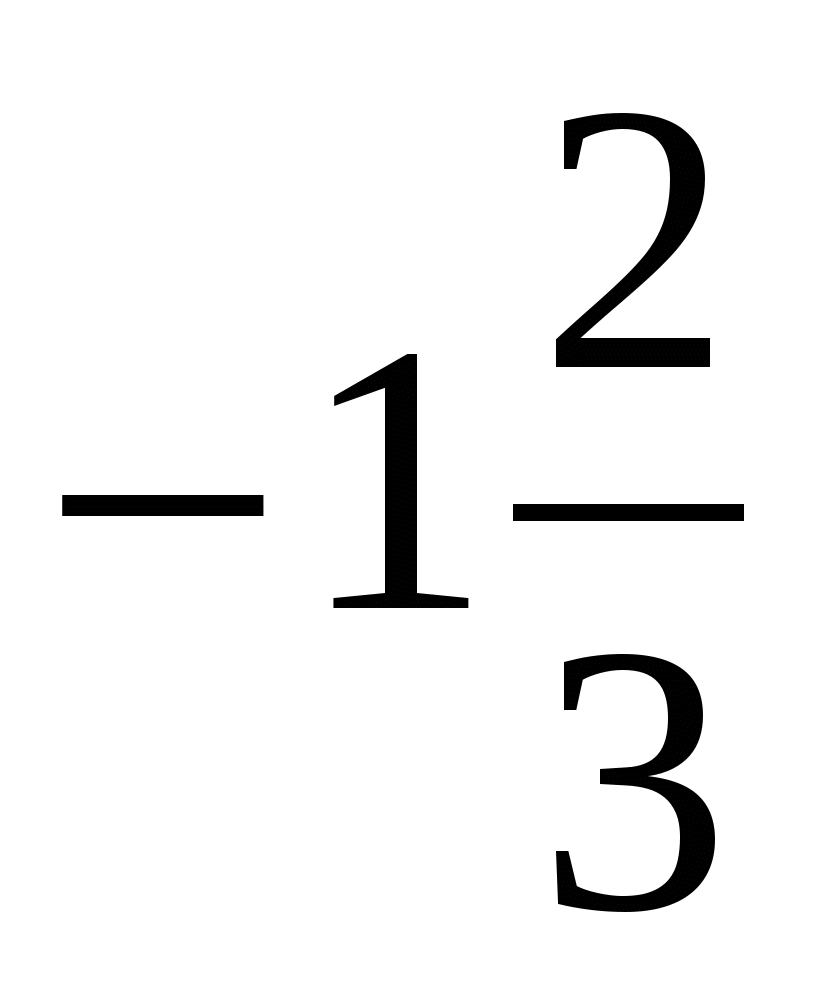 ; 4)
; 4) 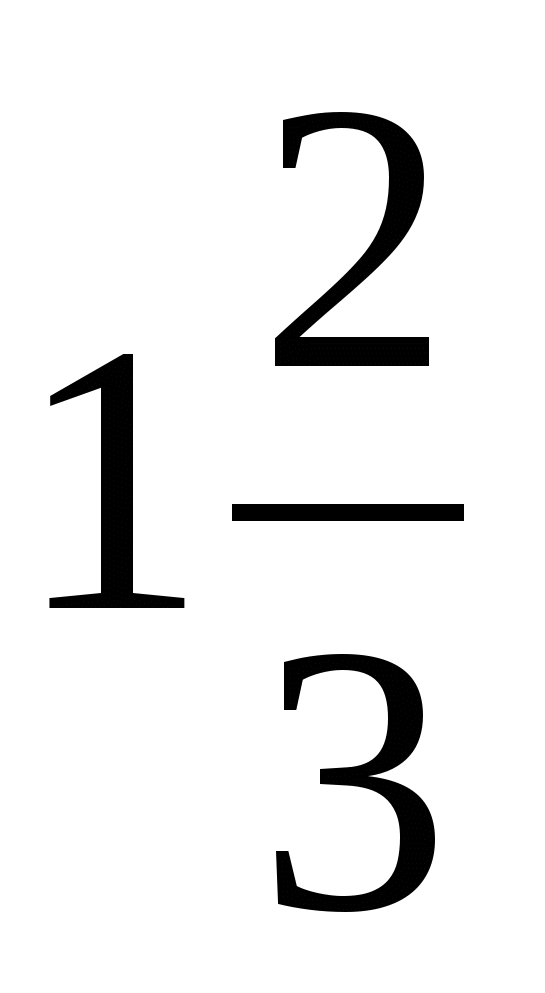
Прочитав условие задачи, составьте уравнение, которое ему соответствует:
Моторная лодка прошла 56 км против течения реки и 32 км по течению, затратив на весь путь 3ч. Найдите собственную скорость лодки, обозначив её через х км/ч, при условии, что скорость течения реки равна 1км/ч.
-
1)
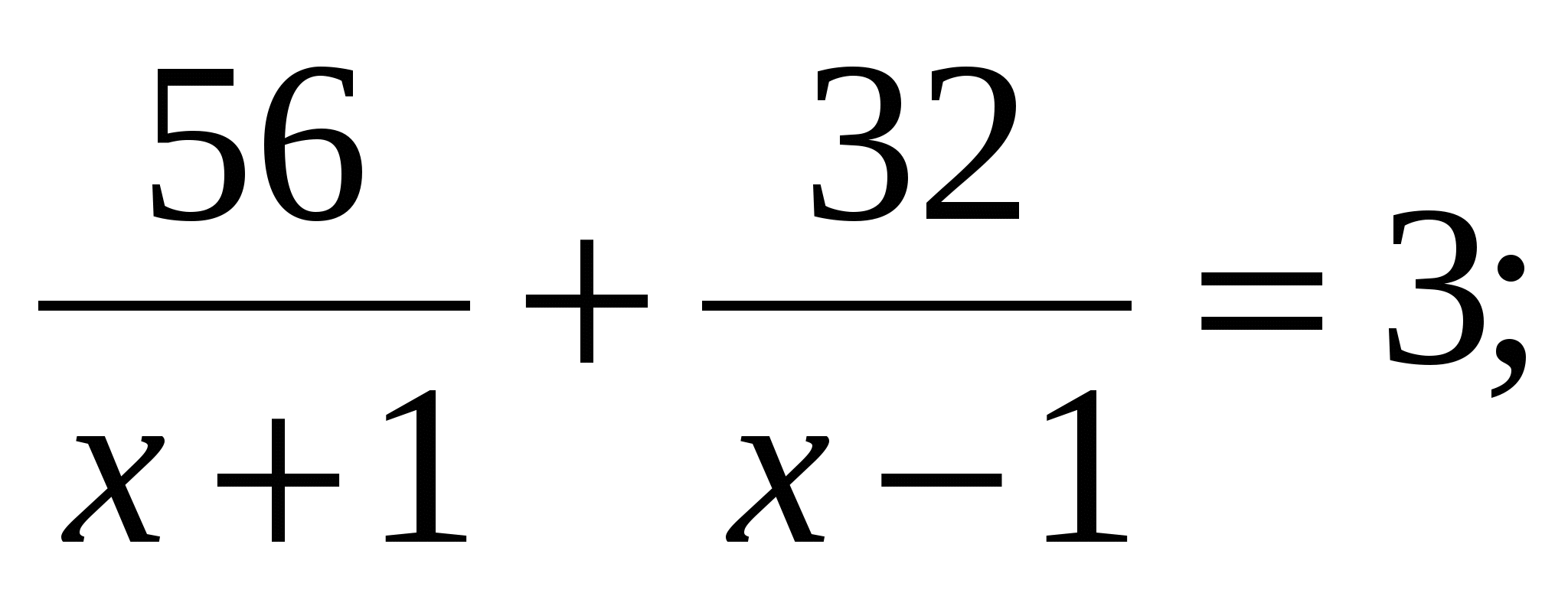 ; 2)
; 2) 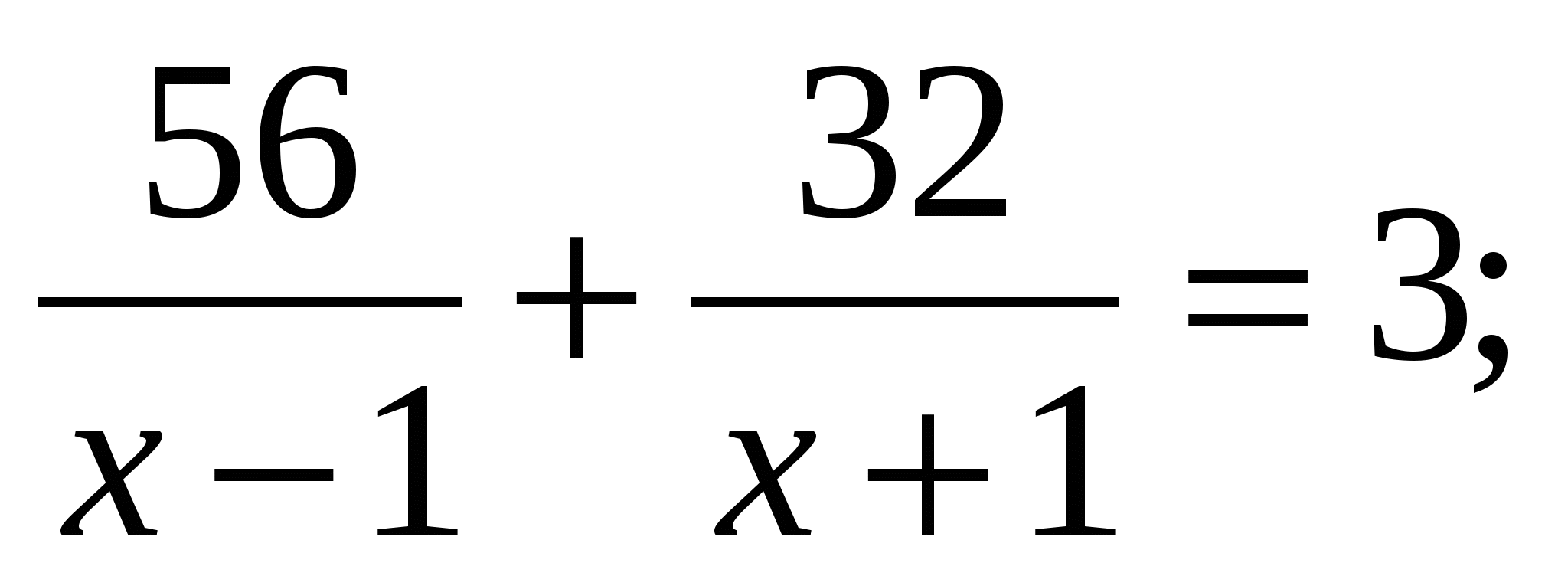 ;
; 3)
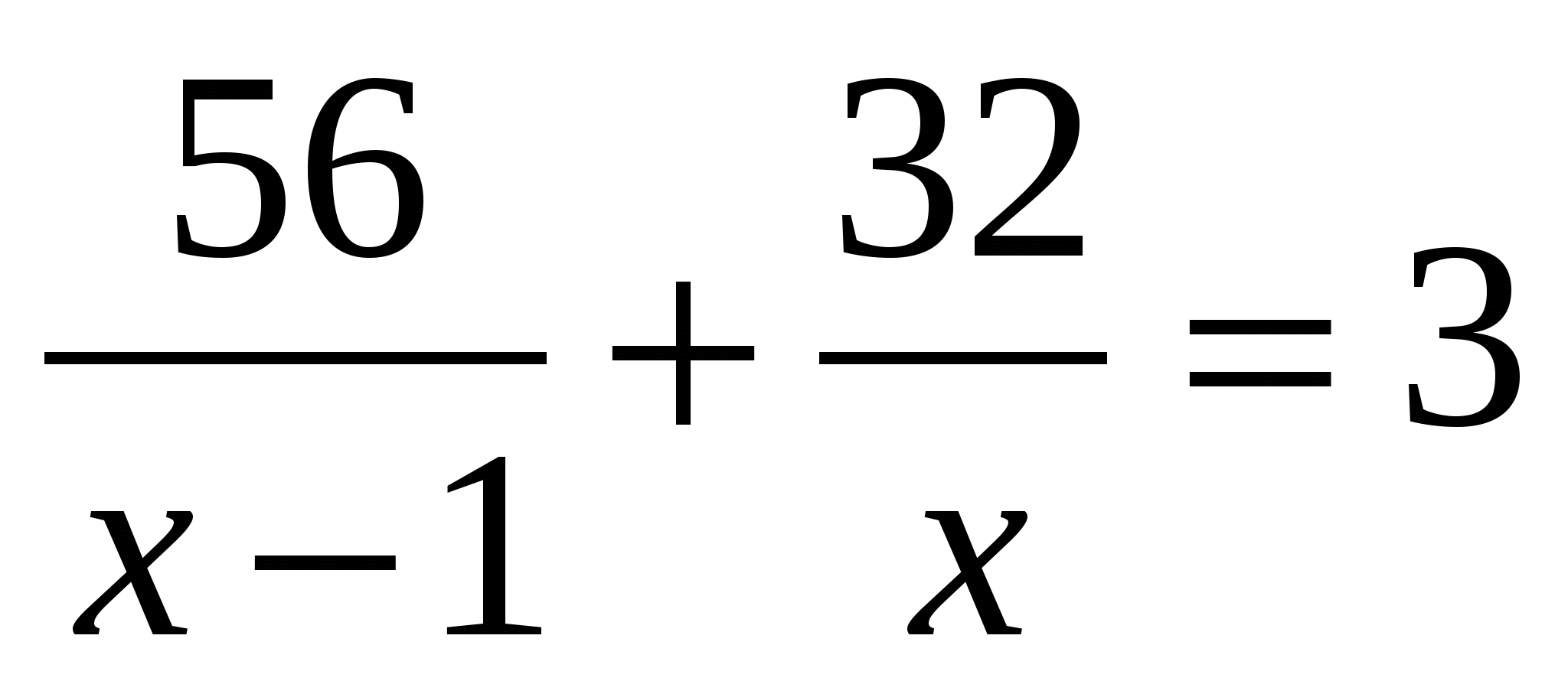 ; 4)
; 4) 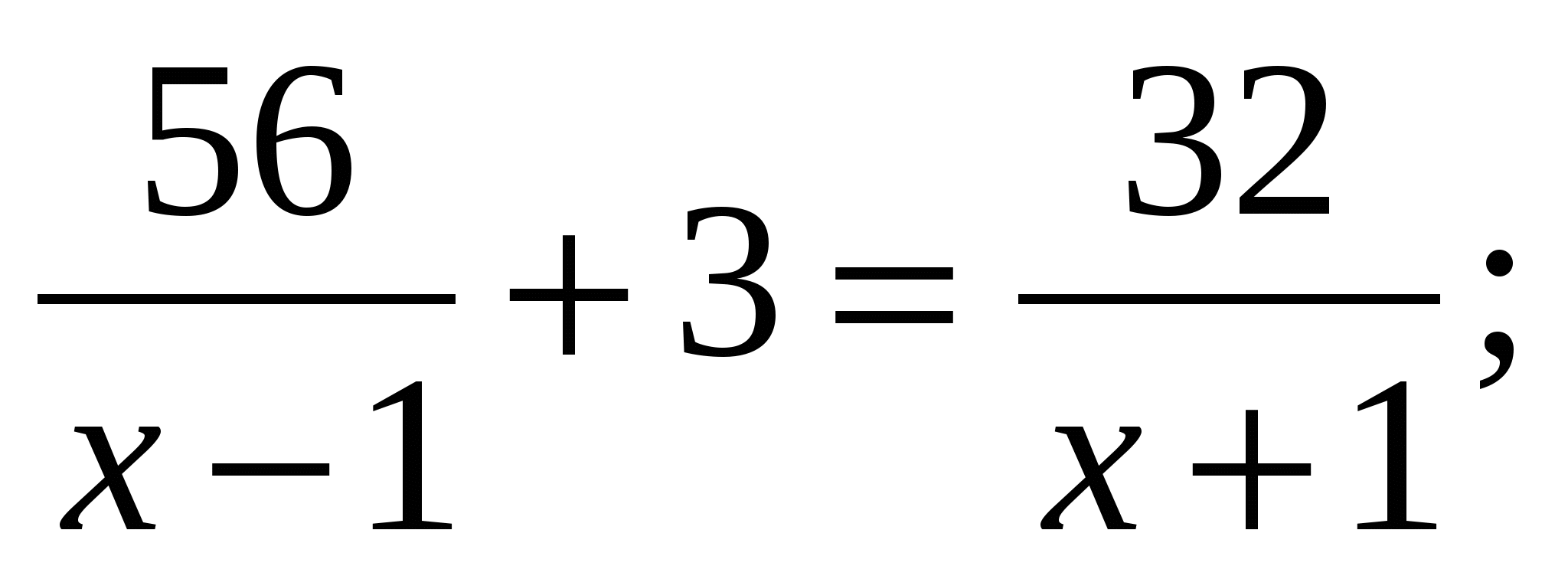
3.Решите задачу, составив уравнение:
Заказ на 156 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает первый рабочий, если известно, что он за час делает на 1 деталь больше?/ч.
Ответ: ___________
5.Домашнее задание . слайд 7
Решить в тетрадях 3любых задачи разного типа из «Открытого банка задач» или из адреса http://mathege.ru:8080/or/ege/ShowProblems?posMask=2048
6.Рефлексия на уроке.
Что нового вы узнали на уроке?
- Оцените себя на уроке
Слайд81 .
Молодцы. Спасибо за урок.