




























План-конспект урока по теме:
«Логарифмические уравнения и способы их решения» (10 кл.)
Автор:
Филиппова Е.М.,
учитель МБОУ СОШ №1
г.Новочеркасска
2012-2013
Урок получения новых знаний
Цель урока: сформировать умения решать логарифмические уравнения разных типов на основе применения определения логарифма, свойств логарифмов и общих методов решения уравнений.
Задачи: а) общенаучная – выбирать рациональные способы решения уравнений, владеть приемами монолога и диалога речи;
б) воспитательная – формировать толерантные отношения к чужой точке зрения, способности работать индивидуально и в группе;
в) развивающая – отрабатывать аналитические навыки (выделять главное, делать выводы, систематизировать, сравнивать); развивать способности к само- и взаимоконтролю.
Оборудование: телевизор, документ-камера.
Ход урока
I. Организационный момент.
II. Этап актуализации знаний. Устно (через документ-камеру по слайдам) вычислить:
1) а) 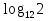 +
+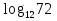 ; б)
; б)  -
-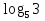 ; в)
; в) 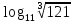 .
.
(учащиеся комментируют выбранный ответ)
2) б) Решить уравнения:
а) 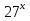 =
=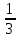 ; б)
; б) 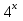 =
=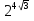 ; в)
; в)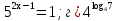 =х+1; д)
=х+1; д) 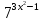 =-49
=-49
е) 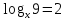 ; ё)
; ё)  .
.
3) в) При каких значениях х существует выражение:
а) 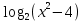 ; б)
; б) ; в)
; в) 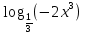 ; г)
; г)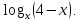
III. Этап изучения нового материала.
Работа над определением логарифмического уравнения.
Учитель: «Рассмотрим равенства»:
1) Слайд 4 а) 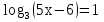 ; б)
; б)  0;
0;
в) 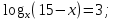 г)
г) 
Вопросы учащимся:
- Где находится переменная? Как называются такие уравнения?
- Как вы думаете, какова тема урока?
2) Рассмотрим способы решения логарифмических уравнений.
Запись на слайде: Что представляет собой эта запись?
I. 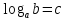
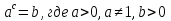
Решим уравнение: (решение осуществляется на доске учеником под руководством учителя, при этом учащийся задает вопросы)
1)  ОДЗ 5х-6
ОДЗ 5х-6 0, х
0, х  1,2
1,2
По определению Логарифма имеем:
5х-6=3  х=1,8 (в качестве образца)
х=1,8 (в качестве образца)
Ответ: 1,8.
Самостоятельно классу предлагается закрепить I способ.
2 ученика работают на переносных досках самостоятельно.
Решить уравнение:
2)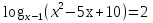

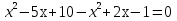 -3х=-9 х=3
-3х=-9 х=3
ОДЗ: 
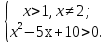
3 удовлетворяет ОДЗ. Ответ:3.
II. 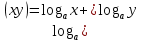 ;
;
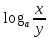 =
=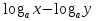 ;
;
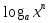 =n
=n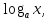 если a
если a 0, a
0, a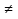 1, x
1, x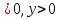
3) II способ. Постановка проблемы (задачи).
Решить уравнение: 1) 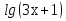 -
- =1.
=1.
Вопросы:
- Возможно ли решение I способом? Обоснуйте.
- Каким свойством возможно воспользоваться?
- Решите II способом (комментируются решения учащихся у доски).
Решение уравнения:
ОДЗ: 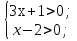
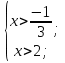 х
х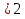
Представим уравнение в виде:
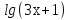 =1+
=1+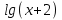 или
или 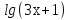 =
=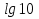 +
+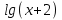
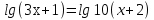 3х+1=10х+20 х=3
3х+1=10х+20 х=3
Здесь ОДЗ не расширен
Проверка х=3
Л.ч. 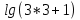 -
-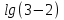 =
=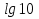 -
-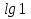 =1
=1
П.ч. 1 1=1
Ответ: 3.
Метод потенцирования – он широко применяется при решении логарифмических уравнений. Но при решении уравнений этим способом расширяется область допустимых значений переменной, поэтому здесь нужна проверка полученных корней.
Для закрепления II способа.
2) +
+ =
=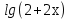
Решение:
 +
+ =
=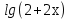
ОДЗ: 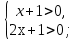
 х
х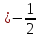
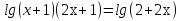
ОДЗ расширено, т.к. произведение (х+1)(2х+1)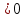 возможно при:
возможно при:
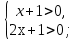 и
и 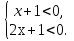
(х+1)(2х+1)=2+2х
2
 2
2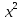 +х-1=0, х1=-1; х2=
+х-1=0, х1=-1; х2=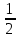
-1 не входит в ОДЗ, это посторонний корень
Проверка: х=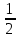
Л.ч. 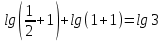
П.ч. 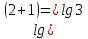
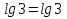
Ответ: 0,5.
3) III способ – замена переменной.

Вопросы учащимся:
- Каким способом решаем? Ученик у доски с классом.
Решение:

ОДЗ: х-1 0 х
0 х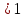
Пусть 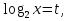 тогда уравнение примет вид:
тогда уравнение примет вид:
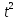 -2t-3=0 t1=-1, t2=3
-2t-3=0 t1=-1, t2=3
Вернемся к переменной х:
 =-1 х-1=0,5 х=1,5
=-1 х-1=0,5 х=1,5
 =3 х-1=8 х=9
=3 х-1=8 х=9
Оба корня входят в ОДЗ, но лучше сделать проверку корней.
IV этап. Закрепление полученных знаний.
Работа по группам (состав до 5 человек)
Распределение по группам, назначение консультантов осуществляет учитель.
Слайд 5 Решить уравнения
1)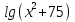 -
-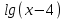 =2 (х=5; х=95)
=2 (х=5; х=95)
2)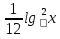 =
=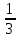 -
-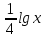 (0,0001;10)
(0,0001;10)
3)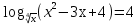 (2)
(2)
Учащиеся работают в группах, 3 ученика самостоятельно на переносных досках.
Затем комментируются ответы уравнений, решённых на доске. Проверка решения носит фронтальный характер, т.к. представители разных групп могут участвовать в обсуждении решения.
V. Итоги урока.
Вопросы классу:
1) Какова была цель урока?
2) Какие уравнения решали?
3) Способы их решения?
4) В полной ли мере реализована тема урока? Все ли свойства логарифмов учтены при решении уравнений?
Домашнее задание направлено на закрепление изученного на уроке материала.
д/з: п.19, задачи 1-4; №337(2,4), 340(2), 378(1), 379(4).
Остальные способы решения логарифмических уравнений рассматриваются на следующих двух уроках. Для систематизации и обобщения материала данной темы учащимся предлагается выполнить задания из презентации.