План-конспект урока «Уравнения, приводимые к квадратным. Биквадратное уравнение»

Тема урока: «Уравнения, приводимые к квадратным. Биквадратное уравнение.

Тип урока: Урок обобщения и закрепления полученных знаний.

Цели урока:

Образовательные: повторить, полученные знания по теме: «Квадратные уравнения», ввести понятие биквадратного уравнения, алгоритм его решения.

Развивающие: развивать умения применять имеющиеся у учащихся знания в измененной ситуации, расширить знания учащихся о городах и народах Поволжья, об ученых – математиках, живших и работавших в этих городах.

Воспитательные: способствовать выработке у учащихся желания и потребности применения изучаемых факторов.

Этапы урока:

1. Организация начала урока.

2. Самостоятельная работа.

3. Устная работа.

4. Работа по тестам (работа в парах).

5. Изучение нового материала.

6. Подведение итогов урока.

7. Информация о домашнем задании.

Ход урока.

1. Организация начала урока.

Слайд 1. (Звучит песня «Школьный корабль»). Все присутствующие встают.

Учитель:

Здравствуйте, садитесь. Сегодня у нас с вами не совсем обычный урок, а урок- путешествие. Мы отправимся в плавание по Волге – матушке, по великой русской реке. Путь наш будет не прост, но знания, полученные вами на уроках должны помочь вам в прокладывании курса.

Сегодня мы с вами должны вспомнить формулы корней квадратного уравнения, ввести понятие биквадратного уравнения и научиться его решать.

Откройте тетради и запишите тему урока «Биквадратное уравнение».

1. Проверка навыков решения квадратных уравнений (самостоятельная работа).

Слайд 1.

Покачиваясь у причала Северного речного порта нашей родной Москвы. Вас ожидает красавец – теплоход. Чтобы попасть на него, вы должны купить билет. Для этого нужно решить 4 уравнения.

Слайд 3.

1 вариант 2 вариант

х² – 9 = 0 х² – 25 = 0

х² + 4х = 0 х² – 3х = 0

6х² = 0 4х² = 0

3х² – 3х + 4 = 0 х² + 8х + 7 = 0

Учитель:

Работаете по вариантам. Два человека решают у доски эти же уравнения. Те, кто решил быстрее решают ребусы о Волге:

1. Выполняя ходы шахматным конем, прочитать название одного из волжских городов.

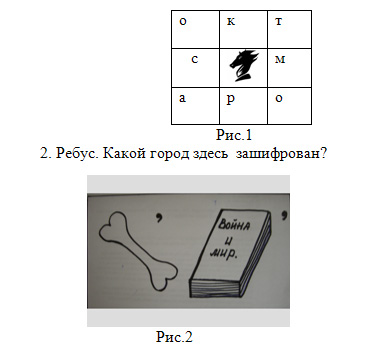
Контролерами становятся сами ребята, они обмениваются тетрадями и карандашами, проверяют друг у друга решение по записям учеников, решивших у доски.

Слайд 4.

Обменяйтесь тетрадями, возьмите карандаши и проверьте ответы. Поднимите руки, кто все уравнения решил верно – занимаете VIP - каюты; кто сделал одну ошибку – занимают каюты бизнес класса; две ошибки, три ошибки – занимают каюты эконом класса; все решил неверно – драят палубу.

1. Устная работа.

Учитель:

Дорогие пассажиры! Команда корабля приветствует Вас на борту нашего теплохода. Во время путешествия вас будет сопровождать экскурсовод Анастасия Блинова.

Экскурсовод:

От причала Северного речного порта нашей любимой столицы, города-героя Москвы, мы начинаем путешествие по Волге. Волга – крупнейшая река Европы, ее длина более 3,5 тысяч км, она принимает воды 260 притоков. Начинаясь тоненьким ручейком на Валдайской возвышенности, она заканчивается могучим потоком, несущим свои воды в Каспийское море. Без нее немыслима наша история, культура, экономика.

Учитель: Мы оправляемся в путешествие. Чтобы узнать название города, в котором мы сделаем свою первую остановку, вы должны ответить на вопросы.

Слайд 5.

1. Степень уравнения ах² + вх + с = 0?

2. Как называют уравнение вида ах² + вх + с = 0?

3. Квадратное уравнение, в котором а = 1 называют…?

4. Название выражения в² – 4ас?

5. Число корней квадратного уравнения при Д = 0?

6. Когда необходимо применять формулу вычисления корней ?

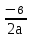7. Уравнение р(х) = 0, где р(х) – рациональное выражение называют…?

8. Расскажите алгоритм решения рационального уравнения.

В это время два ученика работают у доски с заданиями по карточкам.

Задание 1.

Один из корней уравнения х² + 11х + с = 0 равен -3. Найдите другой корень уравнения и свободный член.

Задание 2.

Сократите дробь .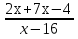

Слайд 6.

Экскурсовод:

Итак, впереди Ярославль, он протянулся на 30 км вдоль Волги. Ярославль был основан князем Ярославом Мудрым в 1010 году. Здесь можно увидеть Спасо-Преображенский собор- древнейшее здание Ярославля (15 в), именно в нем была найдена рукопись «Слово о полку Игореве». Живописные пейзажи Ярославля увековечены многими русскими художниками, здесь Саврасов писал картины «Волга», «Грачи прилетели».

А еще в Ярославле родился известный ученый – математик Александр Михайлович Ляпунов (1857- 1918), он родился в Ярославле в семье директора ярославского Демидовского лицея. Отец обучал его быстрому счету, составлению географических карт. После смерти отца семья перебралась в Нижний Новгород, где Александра взяли сразу в 3 класс гимназии, которую он окончил с золотой медалью и поступил на математическое отделение Петербургского университета. Он защитил магистерскую, а затем и докторскую диссертацию, в 1900 году он избран членом Петербургской Академии наук. Он внес большой вклад в теорию вероятностей, в теорию фигур равновесия, решение дифференциальных уравнений.

1. Работа по тестам.

Слайд 7.

Учитель: Мы отплываем дальше. Перед вами тест. Решив его, вы найдете название города, в котором будет наша следующая остановка.

Тест.

1. Найдите коэффициенты уравнения 4х²+ х – 1 = 0

и) а = 4; в = -1; с = -1 к) а = 4; в = 1; с = -1 л) а = 1; в = 4; с = -1

2. Найдите приведенное квадратное уравнение

п) 5х² – 6х – 8 = 0; р) 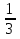х² + х - 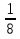= 0; о) х² – 0,5х + 2 = 0

3. Квадратное уравнение не имеет решения, если:

с) Д <0; т) р) Д> 0

4. Найдите дискриминант квадратного уравнения 2х² + 3х – 1 = 0

с) -17; т) 17; р) 1

5. Решите уравнение =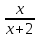

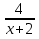
Р) 4; с) 2; -2; т) -2.

6. Решите уравнение =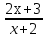

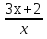
м) -2; -4; н) -2; 4 о) -4; -1

7. Найдите сумму корней квадратного уравнения х² + 2х – 5 = 0

м) -2; н) 2; о) 5

Найдите произведение корней квадратного уравнения 7х + 15х² + 24= 0

а) 24 б) – 24 в) 7

В это время два ученика работают у доски с заданиями.

Задание 1.

Решите уравнение 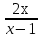– 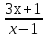+ 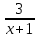= 0.

Задание 2.

Решите уравнение 2х(х -4) + 15 = 3(х² + 5).

Экскурсовод:

Мы приближаемся к Костроме. Кострома основана в 1152 году князем Юрием Долгоруким для охраны северо-восточных рубежей Руси, впервые в летописи упоминается в 1213 году. Облик этого старинного русского города известен нам по многим кинофильмам. Здесь снимались «Жестокий романс», «Снегурочка». В основе названия города лежит финское слово «кострум» - крепость. В окрестностях Костромы зимой 1612 года Иван Сусанин завел поляков в непроходимые болота. В 17 веке Кострома стала третьим по величине городом России после Москвы и Ярославля. Сейчас в Костроме живут около 300 тысяч человек. Главный исторический памятник Костромы – Ипатьевский монастырь, он расположен в месте слияния двух рек Волги и Костромы. Он был основан в 130 году, в монастыре была найдена знаменитая Ипатьевская летопись – основной источник об истории Древней Руси. Кострому посещал при вступлении на престол каждый царь из династии Романовых.

Костромская земля – родина советского математика – Ладыженской Ольги Александровны – члена-корреспондента АН СССР. Она окончила Московский университет, работала в Ленинградском математическом институте им. В.А. Стеклова. Ее труды по дифференциальным уравнениям с частным производным, функциональному анализу и их приложения к задачам математической физики вклад в развитие математической науки.

Следующий пункт нашего путешествия – Нижний Новгород. Чтобы попасть в него должны решить уравнение.

1. Изучение нового материала.

Слайд 8.

х⁴ – 17х² + 16 = 0.

Что это за уравнение? Как его решить?

Уравнение вида а х⁴ + вх² + с = 0 называют биквадратным уравнением, где х – переменная, а а, в и с – некоторые числа («би» - два, т.е. как бы дважды квадратное уравнение).

Для того чтобы решить это уравнение вводят новую переменную у = х². Т.к. х⁴ = (х²)² = у², то заданное уравнение можно записать в виде у² – 17у + 16 = 0.

Д = (-17)² – 4* 1* 16 = 289 – 64 = 225 > 0 – 2 решения

у₁ = 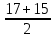= 16 у₂ = 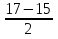= 1

С учетом замены имеем:

х² = 16 х² = 1

х₁ = 4; х₂ = - 4; х₃ = 1; х₄ = -1.

Ответ: 4; -4; 1; -1.

Слайд 9.

Алгоритм решения биквадратного уравнения.

1. Ввести новую переменную t = х².

2. Решить, получившееся квадратное уравнение.

3. С учетом замены решить следующие уравнения.

4. Записать ответ.

Слайд 10.

Вот мы в Нижнем Новгороде, городе с 1,5 млн. населением. Нижний Новгород основан в 1121 году, с 1248 года городом правил Александр Невский; именно здесь в 1611 году по призыву гражданина Кузьмы Минина стало собираться народное ополчение под предводительством князя Пожарского. В начале 16 века здесь был построен Кремль, который с тех пор никогда не был захвачен. Нижний Новгород – родина известного русского писателя Максима Горького, здесь похоронен известный изобретатель Кулибин. В Нижнем Новгороде родились известные математики: Лобачевский В.И., Стеклов В.А., Боголюбов Н.Н.

Владимиру Андреевичу Стеклову принадлежат важные исследования по теории дифференциальных уравнений, математическому анализу, теории упругости и гидромеханике. Он является основателем школы математической физики при АН СССР, который сейчас носит его имя.

Учитель:

Следующий пункт назначения Казань, чтобы туда попасть нужно решить № 868 (в,г) задачника.

Слайд 11.

Казань недавно отметила свое тысячелетие. Город был основан булгарами в месте падения в Волгу реки Казань и назывался булгарами – Джаидом, впоследствии он становится столицей Казанского ханства, в 1552 году Иван Грозный присоединил Казань к Русскому Государству. В Казани много интересного. Казанский Кремль – уникальный архитектурный памятник, включенный в список мирового наследия ЮНЕСКО (построен в 16 веке), его башня Сююмбике стала архитектурной эмблемой Казани (ее копию можно увидеть на здании Казанского вокзала в Москве). В 1804 году в Казани был основан университет. В нем учились Л.Н. Толстой, В.И. Ленин, работали Бутлеров, Бехтерев. Ректором университета был выдающийся математик Николай Иванович Лобачевский. Лобачевского по праву считают создателем неевклидовой геометрии, ему принадлежит ряд ценных работ по математическому анализу, метод приближенного решения уравнений любой степени. В 1846 году Лобачевский был снят с поста ректора, тяжело заболел, умер в Казани в 1856 году.

1. Подведение итогов. Выставление оценок.

Ответьте на вопросы:

- Сегодня на уроке я узнал…

- Сегодня на уроке я повторил…

- Сегодня на уроке я закрепил…

А в конце урока мне бы хотелось вам напомнить: «Никогда не считай, что ты знаешь все, что тебе уже больше нечему учиться. Учитесь, добывайте новые знания, и они вам всегда пригодятся».

1. Домашнее задание.

Прочитать на странице 132- 135 учебника.

№ 868 (а,б); № 871 (а).