Міністерство освіти України
Львівський державний університет ім. І. Франка
Факультет прикладної математики
та інформатики
Кафедра теорії оптимальних
процесів.
Звіт
про виконання індивідуального завдання № 3
“Побудова кривих регресій методом парабол”
з курсу
"Теорія імовірностей та математична статистика"
Виконав: студенти групи ПМП-32
Ковальський Д., Шевчук А.
Керівник: Сеньо П.С.
Львів – 1998
Теоритичні відомості
Лінійна залежність є найпростішою і в більшості випадків є початковим, першим наближенням до істини. Часто потрібно встановити більш адекватну залежність між компонентами наприклад двомірного випадкового вектора, яка як правило не лінійна.
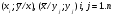Так як у вибіркових данних присутні випадковості, то початковий вигляд нелінійної залежності можна приблизно уявити побудувавши на міліметровому папері сукупність точок
Ми будемо шукати залежність у вигляді y = a0 + a1x + … + akxk , де а0, …, аk – початкові моменти.
Ця передумова обумовлюється теоремою Вейерштраса про наближення будь-якої функції многочленом відповідного степеня (многочленом Берштейна).
Складність полягає в тому, що як правило в статистиці многочлени степеня k > 4 не використовуються, а початкові моменти вище четвертого дають великі похибки, а експериментальних данних багато, отже не можна провести многочлен який би проходив через всі вибіркові точки. Тому параболу будемо будувати таку, щоб сума квадратів відхилень вибіркових значень була найменшою.
Розглянувши пари (xi,yi) скористаємося формулами:
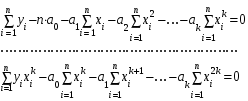Розв'язавши дану систему, отримаємо рівняння шуканої параболи.
Найбільшу величину похибки при апроксимації початкових данних шукатимемо за наступною формулою:
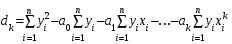
Приклад дії програми
Початкові данні:
x
o
1
2
3
4
y
1
1.5
1.7
2.1
5.9
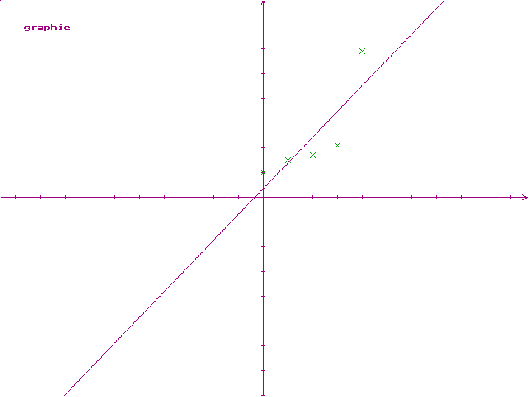
При виборі степеня k=1 результат отримано наступний:
а0 = 0.36
а1 = 1.04
d = 4.776
Графік:
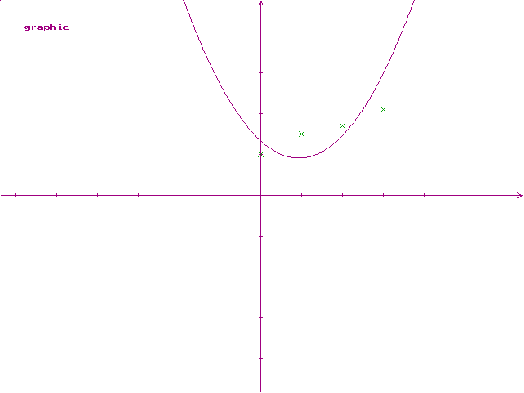
При k=2:
a0 = 1.3314; a1 = -0.9029; a2 = 0.4857; d= 1.4731
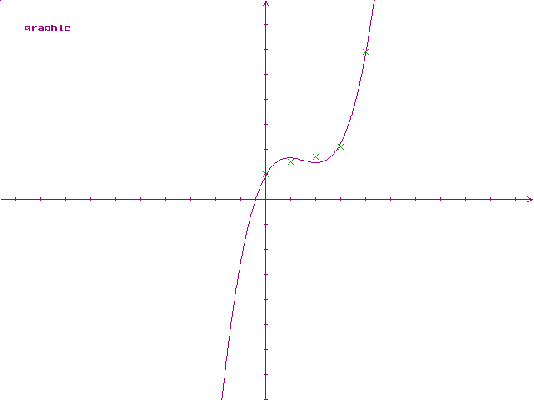
При k=3:
a0 = 0.9614; a1 = 1.7488; a2 =-1.3643; a3 =-0.3083; d= 0.1041
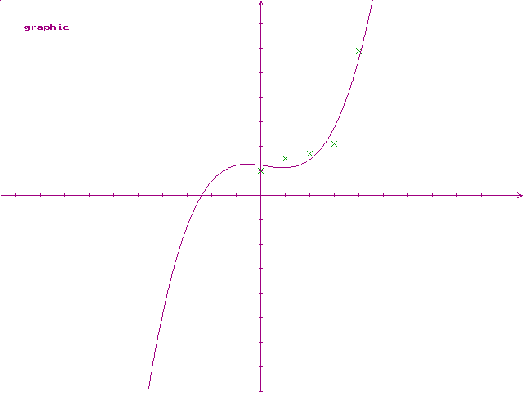
При k=4:
a0 = 1.2250; a1 = -0.1381; a2 =-0.0495; a3 =0.090; a4 =-0.0002; d= 0.7906
Текст програми (Borland Pascal 7.0):
uses crt, graph;
var xn,yn:array[1..30] of real; n:integer; chr:char; a: array [1..5] of real;
function stepin (x:real; i:integer):real;
var j:integer; temp:real;
begin
temp:=1;
for j:=1 to i do
begin
temp:=temp*x;
inc (i);
end;
stepin:=temp;
end;
procedure xyread;
var fl:text; i:integer;
begin
TextBackground(3);
TextColor(0);
clrscr;
assign (fl,'3.txt');
reset (fl);
writeln ('Програма знаходження кривих регресiй методом парабол');
writeln ('Шевчук А., Ковальський Д. ПМП-32, 1998');
{ writeln ('Esc for Exit');}
writeln;
writeln;
writeln (' x', ' y');
writeln ;
i:=1;
while not EOF (fl) do
begin
read (fl,xn[i]);
read (fl,yn[i]);
writeln ('x[',i,']=',xn[i]:0:2,' ',' y','[',i,']=',yn[i]:0:2);
inc (i); n:=i-1;
end;
writeln;
writeln ('Тиснiть ENTER для продовження');
close (fl);
repeat
chr:=readkey;
if ord(chr)=13 then break;
until false;
end;
procedure obchysl;
var k :integer; i,j,h:integer;
sx: array [1..6] of real;
sy: array [1..2] of real;
sxy: array [1..3] of real;
matr: array [1..5, 1..5] of real;
b: array [1..5] of real;
s: real;
d:real;
m,v:word;
gd,gm,ch,cv:integer;
x,y:real;
chr:char;
ex:boolean;
{процедура ўнўцўалўзацў• системи кординат}
procedure initgrah(m:word);
var i:integer;
begin
setbkcolor(white);
setcolor(magenta);
ch:=getmaxx div 2 ;
cv:=getmaxy div 2 ;
line(1,cv,getmaxx,cv);
line(getmaxx,cv,getmaxx-6,cv-3);
line(getmaxx,cv,getmaxx-6,cv+3);
line(ch,1,ch,getmaxy);
line(ch,1,ch-3,6);
line(ch,1,ch+3,6);
i:=0;
while ch+i*m<=getmaxx-6 do
begin
line(ch+i*m,cv+2,ch+i*m,cv-2);
line(ch-2,cv+i*m,ch+2,cv+i*m);
line(ch-i*m,cv+2,ch-i*m,cv-2);
line(ch-2,cv-i*m,ch+2,cv-i*m);
i:=i+1;
end;
end;
begin
writeln;
writeln;
writeln ('Крива регресii описуэться рiвнянням y=g(x), де');
writeln ('g(x)=a[0] + a[1]*x + ... + a[k]*x^k');
writeln ('Введiть cтепiнь k (k < = 4):');
readln (k);
for i:=k+1 to 5 do
a[i]:=0;
for i:=1 to 6 do
begin
sx[i]:=0;
for j:=1 to n do
sx[i]:=sx[i] + stepin (xn[j], i);
end;
for i:=1 to 2 do
begin
sy[i]:=0;
for j:=1 to n do
sy[i]:=sy[i] + stepin (yn[j], i);
end;
for i:=1 to 3 do
begin
sxy[i]:=0;
for j:=1 to n do
sxy[i]:=sxy[i] + yn[j] * stepin (xn[j], i);
end;
b[1]:=sy[1];
for j:=2 to k+1 do
matr[1,j]:=sx[j-1];
for i:=2 to k+1 do
b[i]:=sxy[i-1];
for i:=2 to k+1 do
for j:=1 to k+1 do
matr[i,j]:=sx[j+i-2];
matr[1,1]:=n;
{ МЕТОД ГАУСА РОЗВ'ЯЗАННЯ С.Л.А.Р. }
{ прямий хiд методу гауса }
for i:=1 to k do
for j:=i+1 to k+1 do
begin
matr[j,i]:= -matr[j,i]/matr[i,i];
for h:=i+1 to k+1 do
matr[j,h]:=matr[j,h]+matr[j,i]*matr[i,h];
b[j]:=b[j]+matr[j,i]*b[i];
end;
{ обернений хiд методу гауса }
for i:=k+1 downto 1 do
begin
s:=b[i];
for j:=i+1 to k+1 do s:=s-a[j]*matr[i,j];
a[i]:=s/matr[i,i];
end;
writeln ('Моменти:');
for i:=1 to k+1 do
writeln ('a[',i-1,']=',a[i]:0:4);
d:=sy[2]-a[1]*sy[1]-a[2]*sxy[1]-a[3]*sxy[2]-a[4]*sxy[3];
writeln ('Похибка:');
writeln ('d = ',d:0:4);
writeln ('Enter для перегляду графiка');
repeat
chr:=readkey;
if ord(chr)=13 then break;
until false;
m:=50;v:=160;ex:=false;
repeat
gd:=detect;
initgraph(gd,gm,'');
initgrah(m);
highvideo;
setcolor(green);
for i:=1 to n do
begin
line (round(ch+abs(xn[i]*m))-3, round(cv-yn[i]*m)+3,round(ch+abs(xn[i]*m))+3, round(cv-yn[i]*m)-3);
line (round(ch+abs(xn[i]*m))+3, round(cv-yn[i]*m)+3,round(ch+abs(xn[i]*m))-3, round(cv-yn[i]*m)-3);
end;
setcolor(magenta);
{лўва частина графўка}
for i:=(-v) to 0 do
begin
x:=i/20;
y:=a[1] + a[2]*x + a[3]*x*x + a[4]*x*x*x +a[5]*x*x*x*x;
if abs(ch-abs(x)*m) <32500 then
if abs(cv-y*m)<32500 then
lineto(round(ch-abs(x)*m),round(cv-y*m));
end;
{права частина графўка}
for i:=0 to v do
begin
x:=i/20;
y:=a[1] + a[2]*x + a[3]*x*x + a[4]*x*x*x +a[5]*x*x*x*x;
if abs(ch+abs(x)*m) <32500then
if abs(cv-y*m)<32500 then
lineto(round(ch+abs(x)*m),round(cv-y*m));
end;
outtextxy(30,30,'graphic');
{маштабування графўка}
repeat
chr:=readkey;
case ord(chr) of
{збўльшення графўка}
43:begin
case m of
400:outtextxy(40,40,'no more big');
10..390:begin
m:=m+10;
v:=20*trunc(400/m);
break;
end;
end;
end;
{зменшення графўка}
45:begin
case m of
10:outtextxy(40,40,'no more small');
10..1000:begin
m:=m-10;
v:=20*trunc(400/m);
break;
end;
end;
end;
{повернення в меню}
27:begin
ex:=true;
break;
end;
end;
until false;
closegraph;
if ex=true then break;
until false;
closegraph;
end;
BEGIN
xyread;
obchysl;
END.
Список літератури
1. Крамер Гарольд. Математические методы статистики. М.: Мир, 1976.
2. Бух Арлей. Введение в теорию вероятностей и математическую статистику. М., 1951.