Полная схема исследования функции и построения ее графика Общие исследование функции y = f(x)

Полная схема исследования функции и построения ее графика

Общие исследование функции y = f(x).

• Область определения функции. Найти ее область определения D(f) . Если это не слишком сложно, то полезно найти также область значений E(f) . (Однако, во многих случаях, вопрос нахождения E(f) откладывается до нахождения экстремумов функции.)

• Особые свойства функции. Выяснить общие свойства функции: четность, нечетность, периодичность и т.п. Не любая функция обладает такими свойствами, как четность либо нечетность. Функция заведомо не является ни четной, ни нечетной, если ее область определения несимметрична относительно точки 0 на оси Ox. Точно так же, у любой периодической функции область определения состоит либо из всей вещественной оси, либо из объединения периодически повторяющихся систем промежутков.

• Вертикальные асимптоты. Выяснить, как ведёт себя функция при приближении аргумента 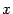к граничным точкам области определения D(f), если такие граничные точки имеются. При этом могут обнаружиться вертикальные асимптоты. Если функция имеет такие точки разрыва, в которых она не определена, то эти точки тоже проверить на наличие вертикальных асимптот функции.

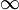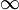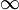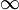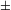
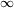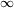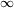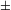
• Наклонные и горизонтальные асимптоты. Если область определения D(f) вклоючает в себя лучи вида (a;+) или (−;b), то можно попытаться найти наклонные асимптоты (или горизонтальные асимптоты) при x+ или x− соответственно, т.е. найти limxf(x). Наклонные асимптоты: y = kx + b, где k=limx+xf(x) и b=limx+(f(x)−x). Горизонтальны асимптоты: y = b, где limx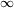f(x)=b.

• Нахождение точек пересечения графика с осями. Нахождение точки пересечения графика с осью Oy. Для этого нужно вычислить значение f(0). Найти также точки пересечения графика с осью Ox, для чего найти корни уравнения f(x) = 0 (или убедиться в отсутствии корней). Уравнение часто удается решить лишь приближунно, но уже отделение корней помогает лучше уяснить строение графика. Далее, нужно определить знак функции на промежутках между корнями и точками разрыва.

• Нахождение точек пересечения графика с асимптотой. В некоторых случаях бывает нужно найти характерные точки графика, которые не были упомянуты в предыдущих пунктах. Например, если функция имеет наклонную асимптоту, то можно попытаться выяснить, нет ли точек пересечения графика с этой асимптотой.

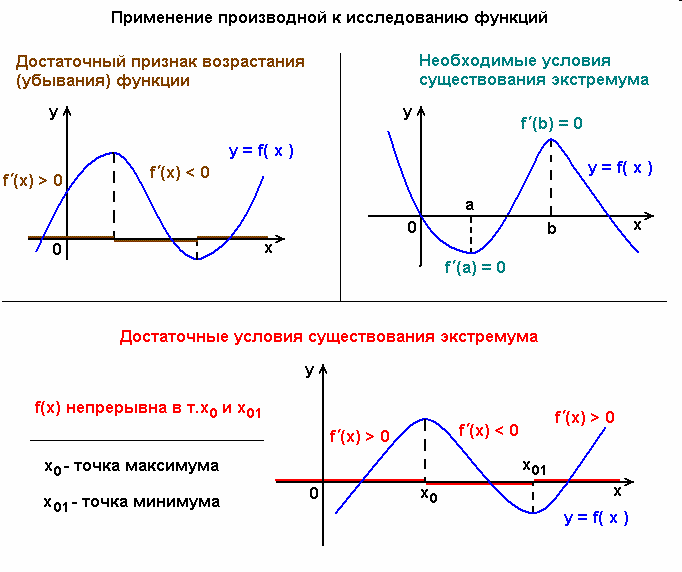
Исследования с помощью производной (продолжение)

Нахождение промежутков монотонности. Найти интервалы монотонности функции f(x) (то есть интервалы возрастания и убывания). Это делается с помощью исследования знака производной f(x). Для этого находят производную f(x) и решают неравенство f(x)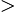0. На промежутках, где это неравенство выполнено, функция f(x) возрастает. Там, где выполнено обратное неравенство f(x)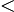0, функция f(x) убывает.

Нахождение локального экстремума. Найдя интервалы монотонности, мы можем сразу определить точки локального экстремума там, где возрастание сменяется убыванием, располагаются локальные максимумы, а там, где убывание сменяется возрастанием -- локальные минимумы. Вычислить значение функции в этих точках. Если функция имеет критические точки, не являющиеся точками локального экстремума, то полезно вычислить значение функции и в этих точках.

• Нахождение интервалов выпуклости и вогнутости. Это делается с помощью исследования знака второй производной f(x). Найти точки перегиба на стыках интервалов выпуклости и вогнутости. Вычислить значение функции в точках перегиба. Если функция имеет другие точки непрерывности (кроме точек перегиба), в которых вторая производная равна 0 либо не существует, то в этих точках также полезно вычислить значение функции. Найдя f(x) , мы решаем неравенство f(x)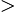0. На каждом из интервалов решения функция будет выпуклой вниз. Решая обратное неравенство f(x)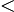0, мы находим интервалы, на которых функция выпукла вверх (то есть вогнута). Определяем точки перегиба как те точки, в которых функция меняет направление выпуклости (и непрерывна).

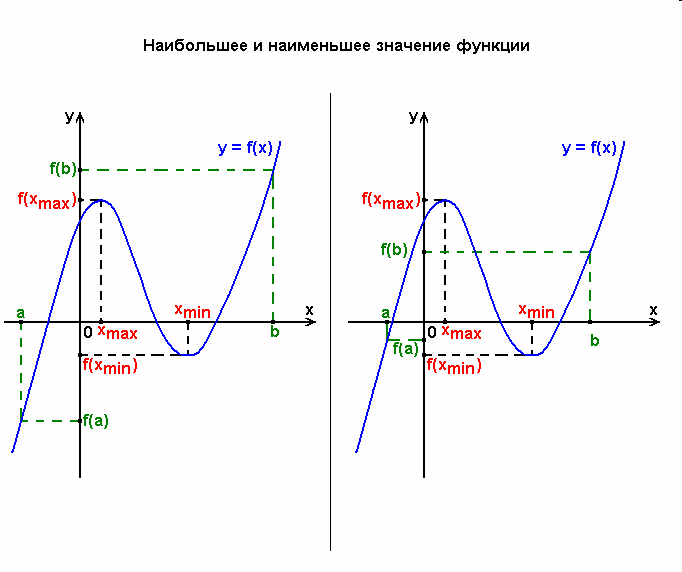
Нахождение наибольшего и наименьшего значений функции y = f(x) на отрезке [a; b] (продолжение)

1. Найти производную функции: f(x).

2. Найти точки, в которых производная равна нулю: f(x)=0 x_1, x₂,...

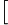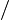
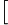3. Определить принадлежность точек х₁, х₂, … отрезку [a; b]: пусть x1a;b , а x2a;b .

4. Найти значения функции в выбранных точках и на концах отрезка: f(x₁), f(x₂),..., f(x_a), f(x_b),

5. Выбор наибольшего и наименьшего значений функции из найденных.

Замечание. Если на отрезке [a; b] имеются точки разрыва, то необходимо в них вычислить односторонние пределы, а затем их значения учесть в выборе наибольшего и наименьшего значений функции.