Урок 1 Понятие функции у = sin х. График функции у = sin х
Цели: ввести понятие функции у = sin х и выделить её основные свойства; построить в прямоугольной системе координат график функции у = sin х на основе выделенных свойств; формировать умения находить значение функции у = sin х для заданных аргументов, строить график функций вида у = sin (х + а) + b.
Ход урока
I. Организационный момент.
II. Устная работа.
1. Вычислите.
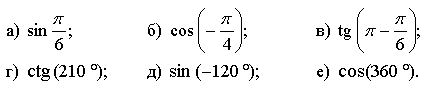
2. Сопоставьте графики функций и формулы их задающие.
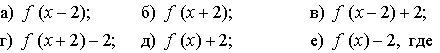
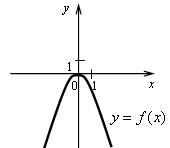
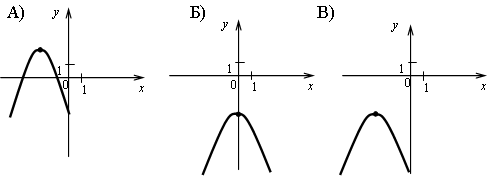
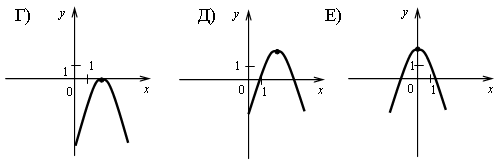
а
б
в
г
д
е
III. Объяснение нового материла.
1. Объяснение проводить согласно пункту учебника. Как и в случае изучения любой другой функции, необходимо рассмотреть у = sin х системно, с разных сторон в различных ситуациях. Для этого рассматриваем шесть направлений:
1) графическое решение уравнений;
2) отыскание наибольшего и наименьшего значений функции на заданном промежутке;
3) преобразование графиков;
4) функциональная символика;
5) кусочные функции;
6) чтение графика.
2. Замечаем, что с функцией 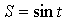 мы уже знакомы. t – числовой либо угловой коэффициент, число, соответствующее точке на числовой окружности. Нам привычнее запись
мы уже знакомы. t – числовой либо угловой коэффициент, число, соответствующее точке на числовой окружности. Нам привычнее запись  Записываем: у = sin х.
Записываем: у = sin х.
Рассматриваем пять основных свойств функции  :
:
1) ОДЗ: (–; +).
2) Нечетная функция.
3) Возрастает на 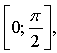 убывает на
убывает на 
4) Ограничена снизу и сверху.
5) Sнаиб = 1; Sнаим = –1.
Строим график функции у = sin х в прямоугольной системе координат. Обязательно подчеркиваем выбор единичных отрезков и отметку ключевых точек на оси 0х ( = 3). Составив таблицу значений функции у = sin х, строим точки и соединяем плавной кривой.
3. Пользуясь формулами приведения показываем, что на отрезке 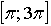 график функции у = sin х совпадает с графиком на отрезке
график функции у = sin х совпадает с графиком на отрезке 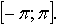 Записываем, что графиком функции у = sin х является кривая, называемая синусоидой.
Записываем, что графиком функции у = sin х является кривая, называемая синусоидой.
4. Опираясь на построенный график, отмечаем еще несколько свойств функции у = sin х:
6) Возрастает на любом отрезке вида 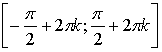 и убывает на любом отрезке вида
и убывает на любом отрезке вида 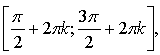 где
где 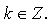
7) Непрерывная функция.
 ОЗФ: [–1; 1].
ОЗФ: [–1; 1].
IV. Формирование умений и навыков.
Упражнения, выполняемые на этом уроке, можно разбить на группы.
1-я группа. Упражнения на изучение функциональной символики: № 10.1 (а; б), № 10.2 (а; б), № 10.3 (а; б).
2-я группа. Нахождение значения функции у = sin х и функции вида у = sin (х + а) + b для заданных значений аргумента: № 10.4 (а; б), № 10.5 (а; б).
3-я группа. Отыскание наибольшего и наименьшего значения функции у = sin х на заданном промежутке: № 10.6 (а; б).
4-я группа. Построение графика функции вида у = sin (х + а) + b на основе механических преобразований графика функции у = sin х: № 10.7 (а; б), № 10.8 (а; б), № 10.9 (а), № 10.10 (а).
Решение:
№ 10.1.
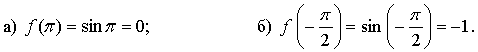
№ 10.2.
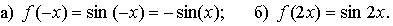
№ 10.3.
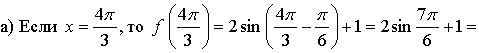
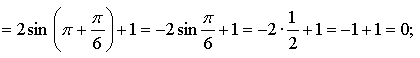
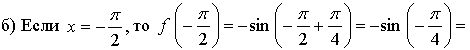
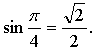
№ 10.4.
а) Если 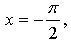 то
то 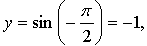 значит, точка
значит, точка 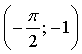 принадлежит графику функции у = sin х.
принадлежит графику функции у = sin х.
б) Если 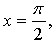 то
то 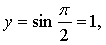 значит, точка
значит, точка 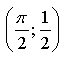 не принадлежит графику функции у = sin х.
не принадлежит графику функции у = sin х.
№ 10.5.
а) Если х = 0, то 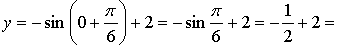
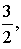 значит, точка
значит, точка 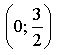 принадлежит графику данной функции.
принадлежит графику данной функции.
б) Если 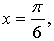 то
то 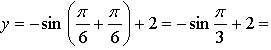
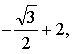 значит, точка
значит, точка 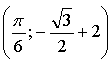 принадлежит графику данной функции.
принадлежит графику данной функции.
№ 10.6.
а) Построив график функции у = sin х и выделив его часть на отрезке 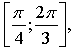 убеждаемся, что
убеждаемся, что 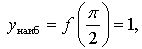 а
а 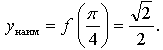
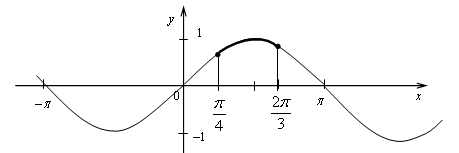
б) На луче 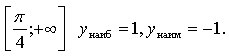
Выполняя упражнения № 10.7 – 10.10, учащиеся должны проговаривать правила «механического» преобразования графика исходной функции у = sin х.
№ 10.7.
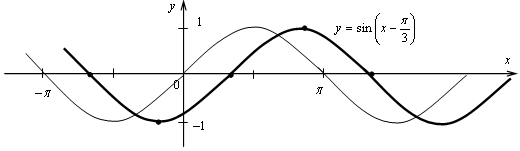
а) Сдвиг графика функции у = sin х на 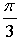 вправо.
вправо.
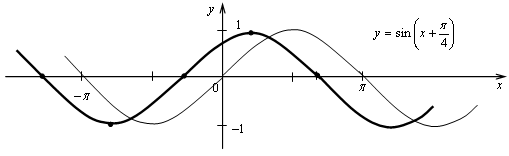
б) Сдвиг графика функции у = sin х на 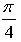 влево.
влево.
№ 10.8.
а) Сдвиг графика функции у = sin х на 2 вниз.
б) Сдвиг графика функции у = sin х на 1 вверх.
№ 10.9 (а).
Сдвиг графика функции у = sin х на 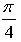 вправо и на 1 вверх.
вправо и на 1 вверх.
№ 10.10 (а).
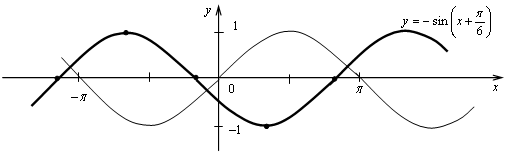
Сдвиг графика функции у = sin х на 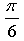 влево и зеркальное отображение относительно оси 0х.
влево и зеркальное отображение относительно оси 0х.
№ 10.7 (а).
№ 10.7 (б).
№ 10.8 (а).
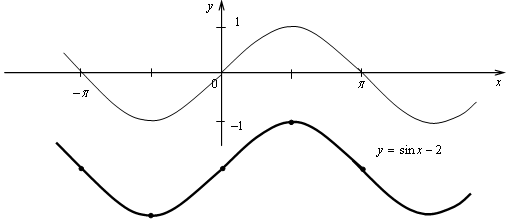
№ 10.8 (б).
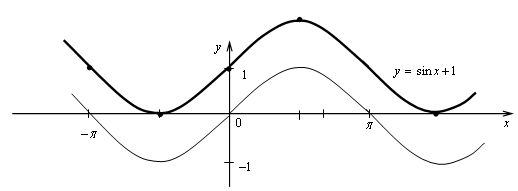
№ 10.10 (а).
V. Итоги урока.
Вопросы учащимся:
– Назовите Df и Ef функции у = sin х.
– Как называется график функции у = sin х?
– Назовите основные свойства функции у = sin х.– Принадлежат ли графику функции у = sin х точки А (0; 0); 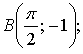

Домашнее задание: № 10.1 (в; г) – 10.8 (в; г); 10.9 (б), № 10.10 (б).