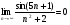Практичне заняття
1. Довести, що 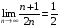 . Починаючи з якого n маємо
. Починаючи з якого n маємо 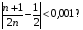
Виберемо довільне число 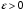 і покажемо, що існує такий номер N, що для всіх членів послідовності з номерами n > N виконується нерівність
і покажемо, що існує такий номер N, що для всіх членів послідовності з номерами n > N виконується нерівність
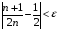 (1)
(1)
Для визначення N досить розв’язати нерівність (1) відносно n:
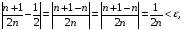
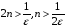 .
.
Отже, якщо 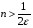 , то нерівність (1) виконується для будь-якого наперед заданого числа
, то нерівність (1) виконується для будь-якого наперед заданого числа 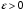 . Якщо
. Якщо 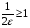 , то за N беремо цілу частину виразу
, то за N беремо цілу частину виразу 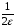 , тобто N =
, тобто N = 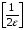 . А якщо
. А якщо 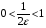 , то за N можна взяти 1 або будь-яке інше натуральне число.
, то за N можна взяти 1 або будь-яке інше натуральне число.
Зокрема, при 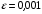 , N =
, N = 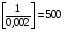 . Отже, при
. Отже, при 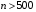 дістанемо
дістанемо 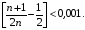
2. З’ясувати, чи має границю послідовність (xn), якщо:
а) 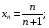 б)
б) 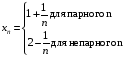
в) 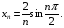
а) Оскільки 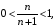 то послідовність (
то послідовність (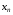 ) обмежена. Неважко бачити, що
) обмежена. Неважко бачити, що 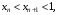 для всіх
для всіх 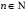 , тобто (
, тобто (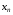 ) монотонно зростає. Отже, вона має границю.
) монотонно зростає. Отже, вона має границю.
б) Члени послідовності з парними номерами прямують до 1 при 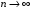 , оскільки
, оскільки 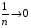 . А члени послідовності з непарними номерами прямують до 2 при
. А члени послідовності з непарними номерами прямують до 2 при 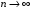 . Отже, згідно з означенням, послідовність немає границі, тобто є розбіжною.
. Отже, згідно з означенням, послідовність немає границі, тобто є розбіжною.
в) Дана послідовність є добутком нескінченно малої послідовності 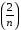 , оскільки
, оскільки 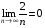 , і обмеженої послідовності
, і обмеженої послідовності 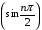 , тому що
, тому що 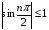 . Тоді за властивістю 2) задана послідовність має границю, що дорівнює 0.
. Тоді за властивістю 2) задана послідовність має границю, що дорівнює 0.
3. Обчислити границі:
а) 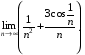 б)
б) 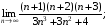
в) 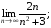 г)
г) 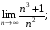
д) 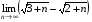 ; е)
; е) 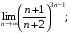
є) 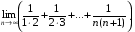
ж) 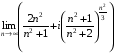
а) скористаємось теоремою про границю двох послідовностей. Неважко побачити, що границя першого доданка дорівнює 0, а другий доданок є добутком нескінченно малої послідовності 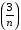 на обмежену послідовність
на обмежену послідовність 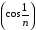 , тому його границя також дорівнює нулю. Отже, за властивістю 1( задана послідовність є нескінченно малою.
, тому його границя також дорівнює нулю. Отже, за властивістю 1( задана послідовність є нескінченно малою.
б) У даному випадку чисельник і знаменник мають нескінченні границі, тому користуватись теоремою про границю частки не можна. Перетворимо дріб, поділивши чисельник і знаменник на 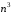 (найвищий степінь n). Дістанемо
(найвищий степінь n). Дістанемо
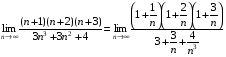
Оскільки 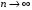 маємо
маємо 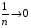 ,
, 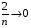 ,
, 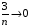 ,
, 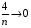 , то, застосувавши теорему про границю суми і добутку, помічаємо, що границя чисельника дорівнює 1, а знаменника 3. за теоремою про границю частки маємо
, то, застосувавши теорему про границю суми і добутку, помічаємо, що границя чисельника дорівнює 1, а знаменника 3. за теоремою про границю частки маємо
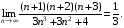
в) Поділимо чисельник на знаменник дробу на 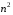 , а потім скористаємось теоремою про границю суми і частки. Дістанемо
, а потім скористаємось теоремою про границю суми і частки. Дістанемо
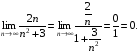
г) Аналогічно попередньому маємо
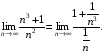
Оскільки 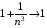 при
при 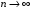 , а знаменник є нескінченно малою послідовністю, то задана послідовність є нескінченно великою, тобто
, а знаменник є нескінченно малою послідовністю, то задана послідовність є нескінченно великою, тобто 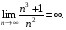
У прикладах б) - г) порівняйте старші степені чисельників і знаменників заданих дробів і зробіть висновок відносно одержаних відповідей.
д) У даному випадку маємо різницю двох нескінченно великих послідовностей. Позбавимося ірраціональності в чисельнику, вважаючи, що знаменник дорівнює 1, і застосуємо теорему про зв’язок нескінченно малої і нескінченно великої послідовностей. Матимемо.
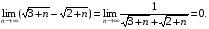
е) Поділивши чисельник і знаменник виразу, що стоїть в дужках, на n і скориставшись властивістю степеня, дістанемо
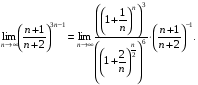
Користуючись теоремою про границю добутку, частки і формули (1), маємо
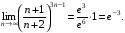
є) Оскільки 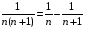 , то
, то
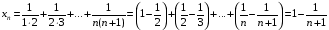 . Тоді
. Тоді 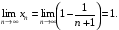
ж) Маємо границю послідовності комплексних чисел. Обчислимо границі дійсної та уявної частин цієї послідовності. Оскільки
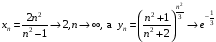 , то
, то 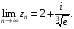
Вправи для самоперевірки
1. Довести, що:
а) 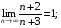 б)
б) 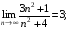 в)
в) 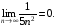
2. Обчислити 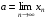 і визначити номер N (
і визначити номер N (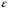 ) такий, що
) такий, що 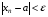 при всіх
при всіх 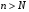 , коли:
, коли:
а) 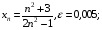 б)
б) 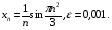
Відповідь: а) 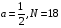 ; б)
; б) 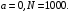
3. Зясувати, чи має границю послідовність 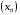 , якщо:
, якщо:
а) 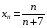 ; б)
; б) 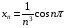 ;
;
в) 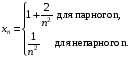
Відповідь: а) так; б) так; в) ні.
4. Обчислити границі:
1) 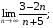 2)
2) 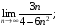 3)
3) 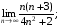
4) 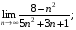 5)
5) 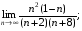
6) 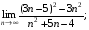 7)
7) 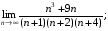

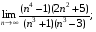 9)
9) 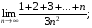
10) 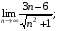 11)
11) 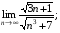
12) 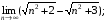 13)
13) 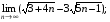
14) 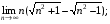 15)
15) 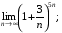
16) 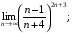 17)
17) 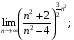
18) 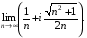
Відповідь: 1) -2; 2) 0; 3) 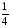 ; 4)
; 4) 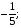 5)
5) 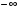 ; 6) 6; 7) 1;
; 6) 6; 7) 1;  2;
2;
9) 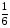 ; 10) 3; 11)
; 10) 3; 11) 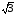 ; 12) 0; 13)
; 12) 0; 13) 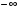 ; 14)
; 14) 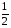 ; 15)
; 15) 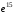 ;
;
16) 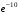 ; 17)
; 17) 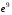 ; 18)
; 18) 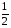 .
.
5. Обчислити суму всіх членів спадної геометричної прогресії 1, 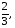
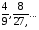
Відповідь: S=3.
1. Знайти 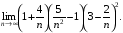
Використовуючи теорему про границю добутку маємо:
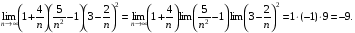
Оскільки 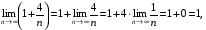
аналогічно 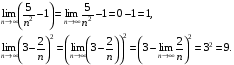
Відповідь: - 9.
2. Знайти 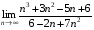
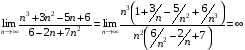 .
.
3. Знайти 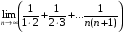
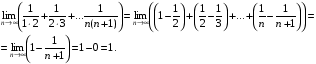
Завдання для перевірки знань
1. Довести, що при 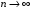 послідовність 3,
послідовність 3, 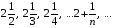 має границею число 2.
має границею число 2.
2. Довести, що при 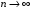 послідовність
послідовність 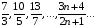 має границею число 1,5.
має границею число 1,5.