Павлюк Ирина Владиславовна
учитель математики
МБОУ гимназия №19 г. Липецка
Применение графического метода
при решении неравенств с параметром
Алгебра и начала анализа
11 класс
2012
Решение неравенств с параметром – не сама простая тема в курсе средней школы. Но содержание этой темы весьма востребовано при подготовке к ЕГЭ. Как учить решать неравенства с параметром? Когда следует начинать этим заниматься?
Мне представляется, что задания с параметрами должны быть естественным образам включены в рассмотрение всех разделов программы для класса с углубленным изучением математики или предпрофильной подготовки по математике. В частности:
7 класс: линейные уравнения с параметром;
8 класс: линейные неравенства и их системы с параметром, квадратные уравнения с параметром;
9 класс: исследование квадратного трёхчлена;
10-11 класс: решение уравнений и неравенств с параметрами при изучении тригонометрии, показательной и логарифмической функций и т.д., а главное – в рамках повторения, особенно активно – в рамках итогового повторения в 11-м классе.
Было бы нелишним введение элективного курса «Уравнения и неравенства с параметром».
Итак, какие навыки необходимы, и какие навыки или хотя бы умения желательны для обучения решению неравенств с параметром?
Минимально необходимые навыки
Желательные навыки
Желательные умения
Решение линейных неравенств, в том числе двойных.
Решение алгебраических неравенств (обобщённый метод интервалов)
Решение систем и совокупностей неравенств.
Построение графиков и знание свойств линейной и квадратичной функций.
Решение линейных уравнений параметром.
Решение линейных неравенств с параметром.
Решение квадратных уравнений с параметром.
Решение систем и совокупностей линейных неравенств с параметром. Решение квадратных уравнений с параметром.
Исследование квадратного трёхчлена графическими методами.
Решение квадратных неравенств с параметром.
Часто решение неравенств с параметром аналитическим методом приводит к большому числу так называемых «переборов», нередко с весьма громоздкими преобразованиями, а иногда – к невозможности решения вообще. При этом хорошие результаты даёт графический метод решения, в том числе и там, где «аналитика» просто не проходит.
В качестве пропедевтики изучения графического метода решения неравенств, можно рекомендовать рассмотрение темы «Исследование квадратного трёхчлена». Эта дидактическая единица, разумеется, не включена в базовый программный минимум основной общеобразовательной школы. Тем не менее, приёмы графического исследования, вводимые при рассмотрении данной темы, являются необходимым инструментом в использовании графического метода при решении неравенств с параметром в старшей школе. В любом случае при модификации программ для профильных (математических, политехнических и экономических) классов придётся изыскать возможность включения в планирование соответственно либо повторения, либо изучения в качестве нового материала темы «Исследование квадратного трёхчлена».
Данный материал не привязан к конкретному учебнику, однако целесообразнее его внедрен в учебный процесс следующим образом:
Методическая разработка №1 − в 10 классе при изучении темы «Числовые функции. Свойства квадратичной функции»;
Методическая разработка №2 − в 11 классе при изучении темы «Уравнения и неравенства. Задачи с параметрами».
Методическая разработка №1
Тема урока*. Решение задач по исследованию квадратного трехчлена с использованием свойств квадратичной функции.
Цели урока:
Выработка творческого подхода к использованию теоретического материала вообще и свойств квадратичной функции в частности для решения задач.
Овладение новым методом решения задач по исследованию квадратного трехчлена.
Развитие навыков решения задач с параметром.
Программно-методическое обеспечение: Задания для проведения письменного экзамена по математике в 9 классе: Пособие для учителя / Л. И. Звавич и др. – М.: Просвещение, 1994 и последующие. - [1].
План урока:
Постановка цели урока и домашнее задание.
Анализ домашней работы.
Решение задач из домашней работы новым способом.
Систематизация новых методов решения.
Решение задач:
на доске,
самостоятельно.
Итоги урока.
Ход урока.
Постановка цели урока и домашнее задание.
В классе (записать на доске):
К пункту 3:
При каких значениях параметра уравнение 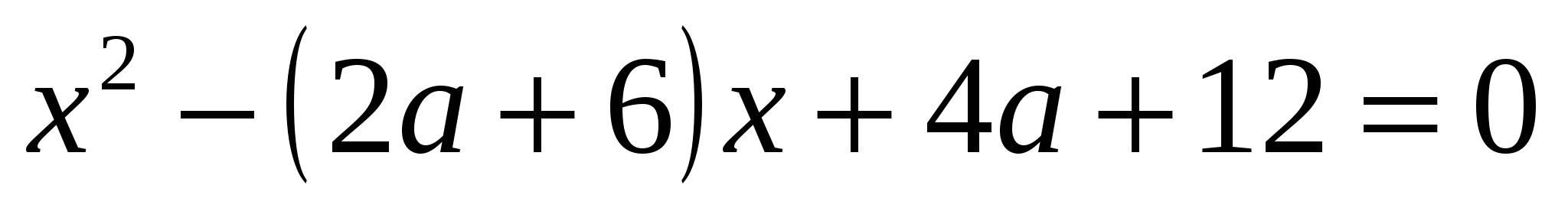 имеет два различных корня одного знака?
имеет два различных корня одного знака?
К пункту 5а:
Найдите все значения параметра, при которых уравнение 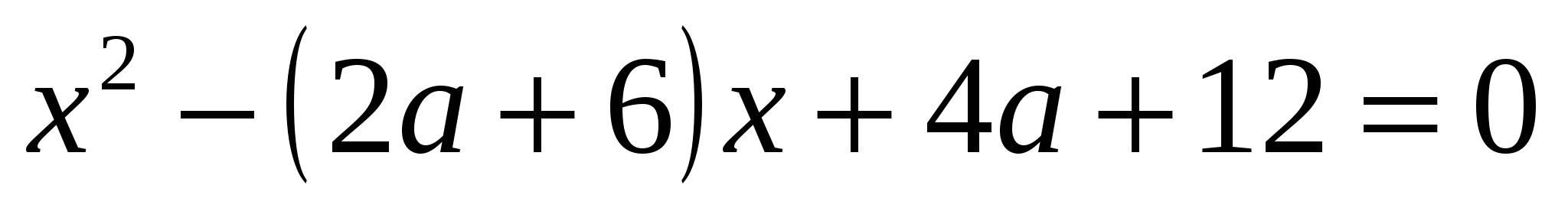 имеет хотя бы один корень и каждый корень меньше 1 ([1], №2.536(а)).
имеет хотя бы один корень и каждый корень меньше 1 ([1], №2.536(а)).
Найдите все значения параметра при которых корни квадратного трехчлена 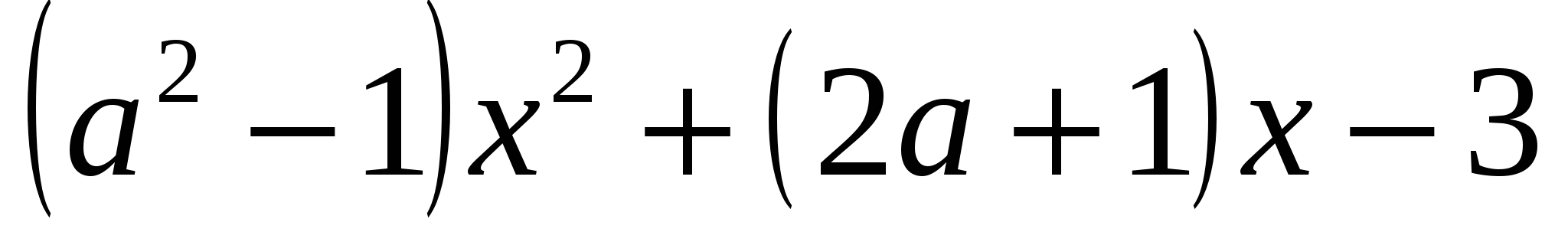 лежат по разные стороны от точки
лежат по разные стороны от точки 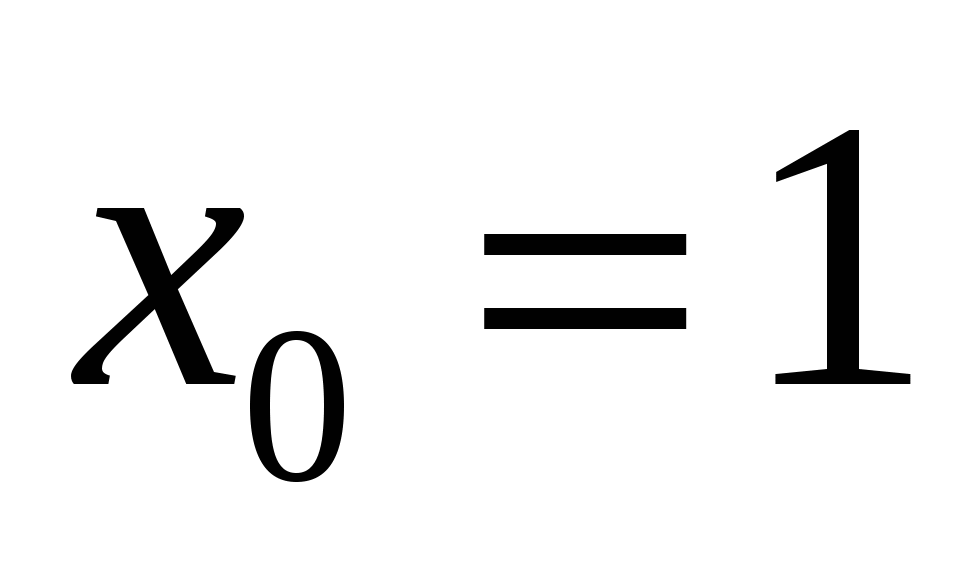 ([1], №2.534(а))
([1], №2.534(а))
К пункту 5б:
Найдите все значения параметра при которых квадратный трехчлен 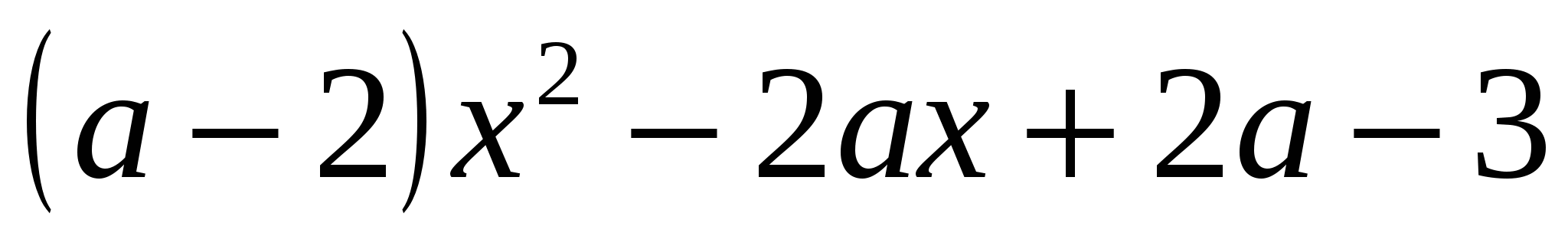 имеет два различных корня одного знака ([1], №2.535(а))
имеет два различных корня одного знака ([1], №2.535(а))
Домашнее задание:
Найдите все значения параметра при которых два корня уравнения 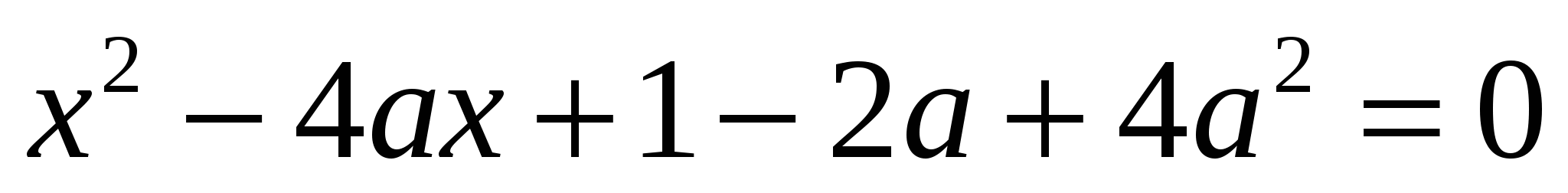 различны и каждый из них больше 1 ([1], №2.536(б)).
различны и каждый из них больше 1 ([1], №2.536(б)).
Найдите все значения параметра при которых корни квадратного трехчлена 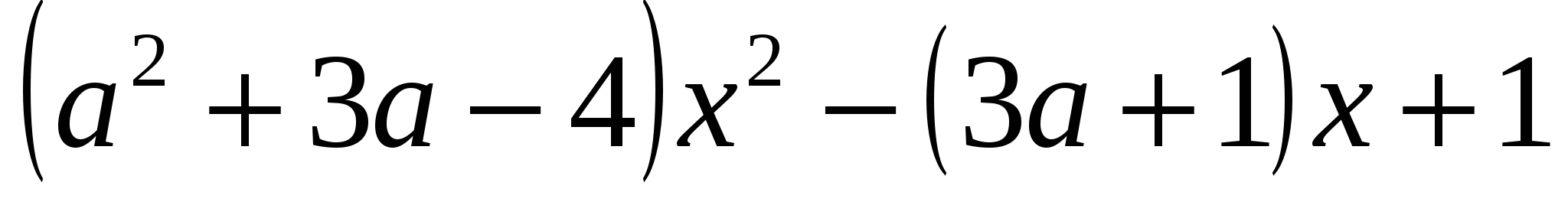 имеют разные знаки и расположены по разные стороны от числа 1 ([1], №2.535(б)).
имеют разные знаки и расположены по разные стороны от числа 1 ([1], №2.535(б)).
Анализ домашней работы
На дом была задана задача: выясните, при каких значениях параметра уравнение 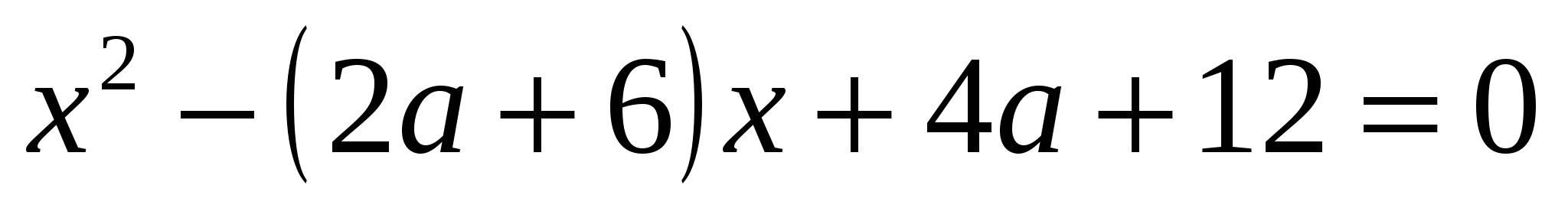 имеет два различных корня одного знака.
имеет два различных корня одного знака.
Дома учащиеся пытались решить эту задачу стандартным методом. Квадратное уравнение имеет два различных (действительных) корня, если его дискриминант положителен.
Найдем дискриминант данного уравнения:
 .
.
Итак, заданное уравнение имеет два различных корня, если  . Найдем корни заданного уравнения:
. Найдем корни заданного уравнения:
 ,
, .
.
Для того чтобы уравнение имело два различных корня одного знака необходимо выполнение совокупности условий:
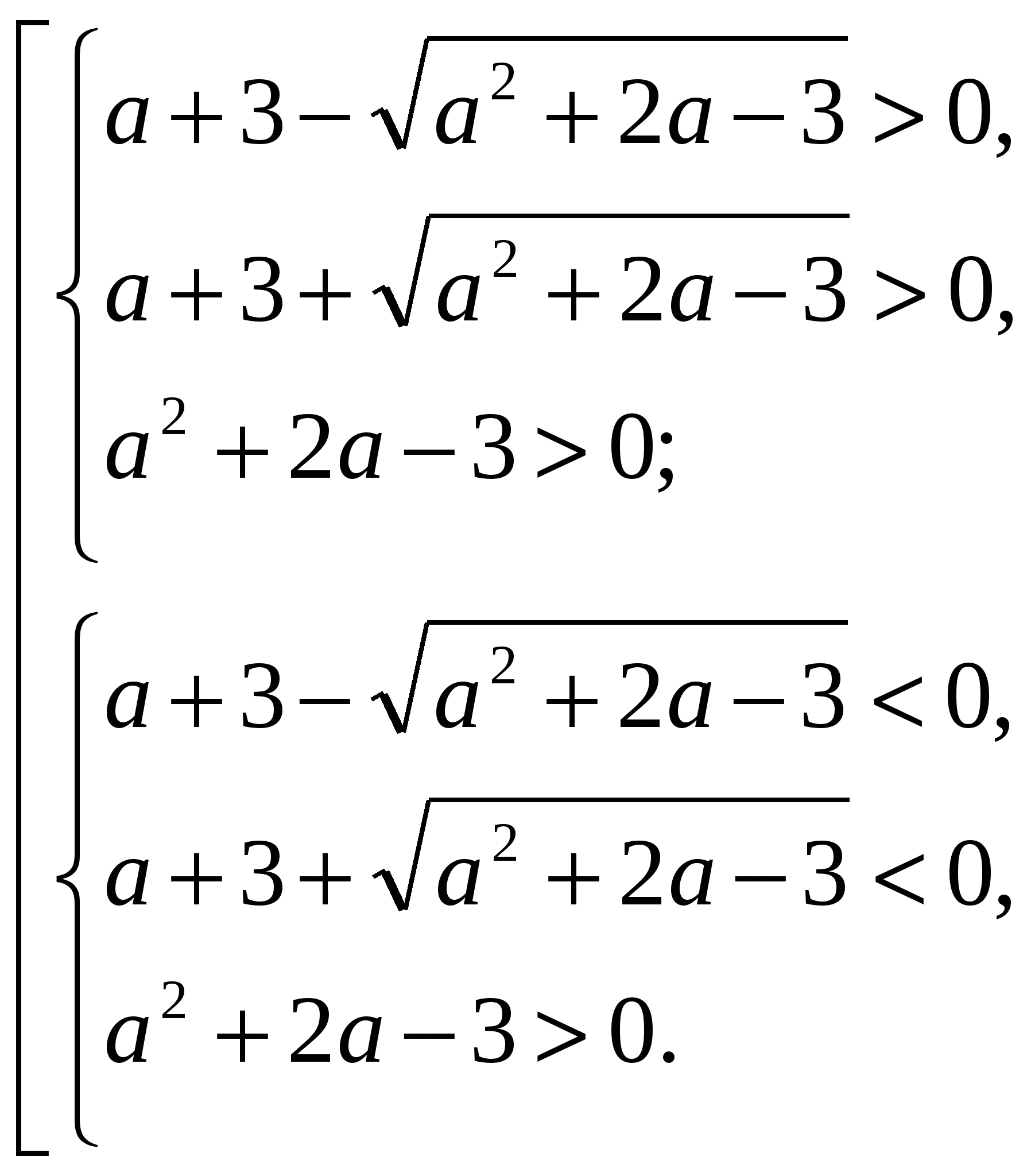
Полученная совокупность неравенств содержит иррациональные неравенства. Если методы решения таких уравнений еще не изучены, то решение в принципе невозможно. Если изучены − то оно оказывается весьма громоздким. В любом случае, возникает необходимость поиска другого способа решения.
Решение задач из домашней работы новым способом.
Учащимся предлагается рассмотреть функцию 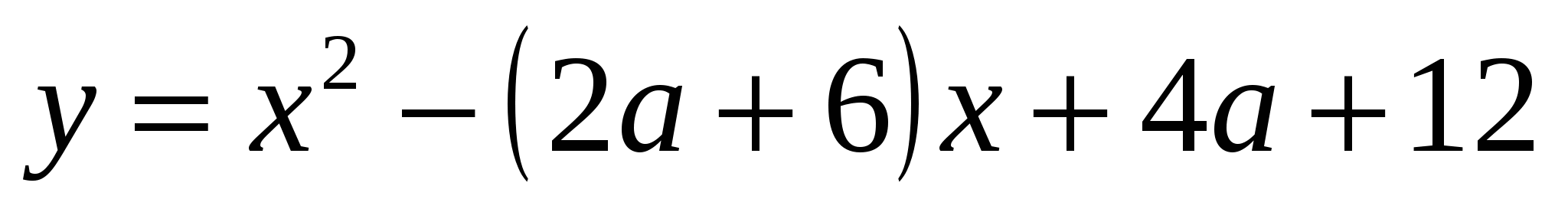 и последовательно ответить на ряд вопросов.
и последовательно ответить на ряд вопросов.
Вопросы учителя
Ответы учащихся
1. Какой график имеет рассматриваемая функция?
1. Графиком этой функции является парабола с ветвями, направленными вверх и вершиной 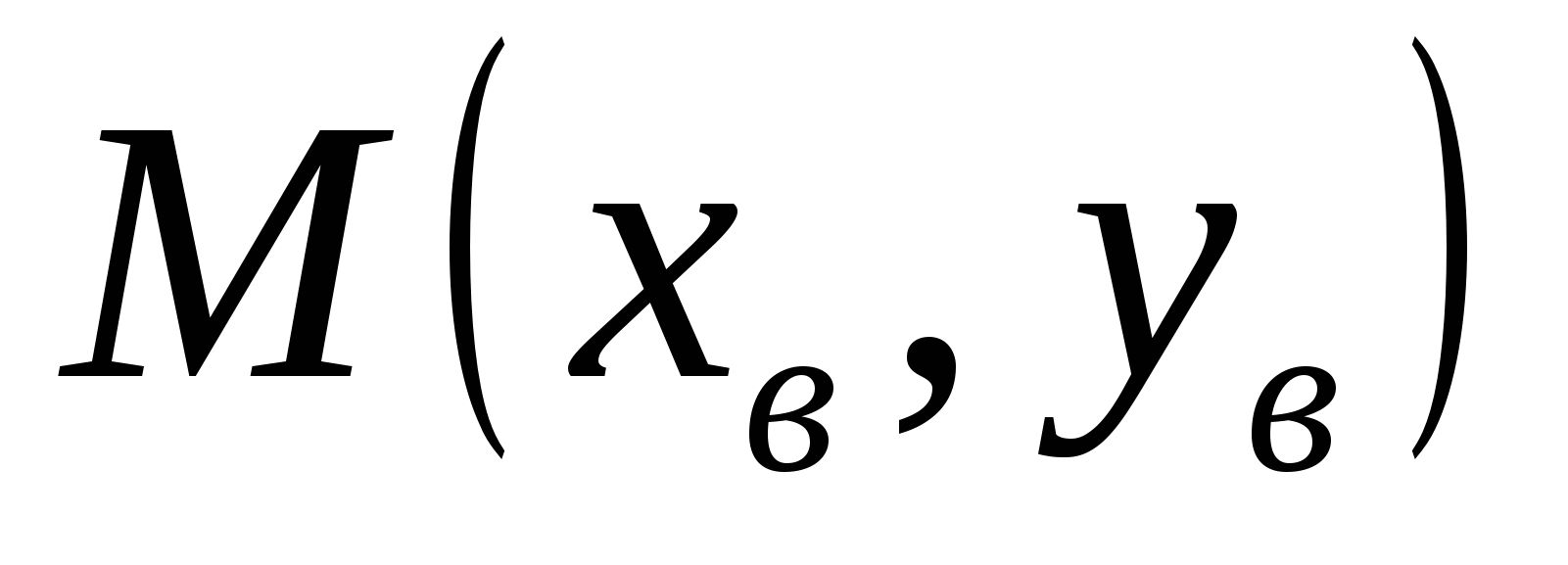 , где
, где 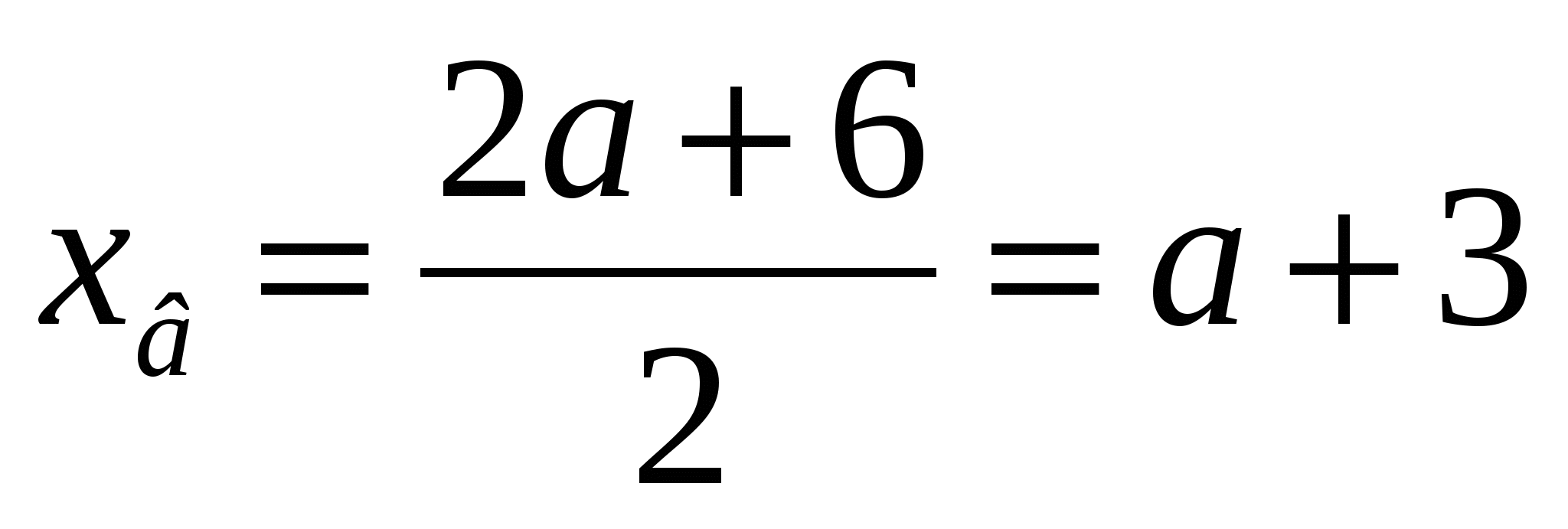 ,
, 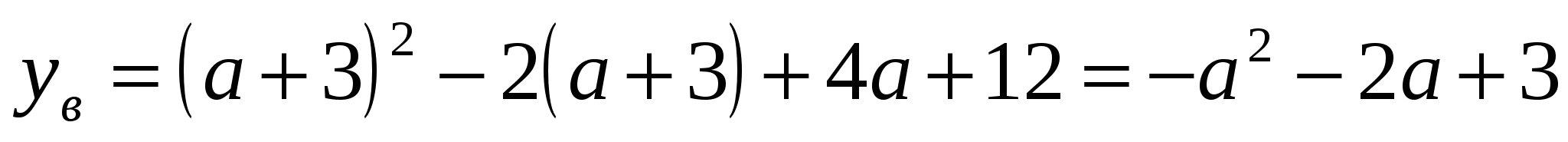
2а. При каком расположении графика функции заданное уравнение имеет два различных корня?
2а. Уравнение имеет два различных корня, если график функции пересекает ось 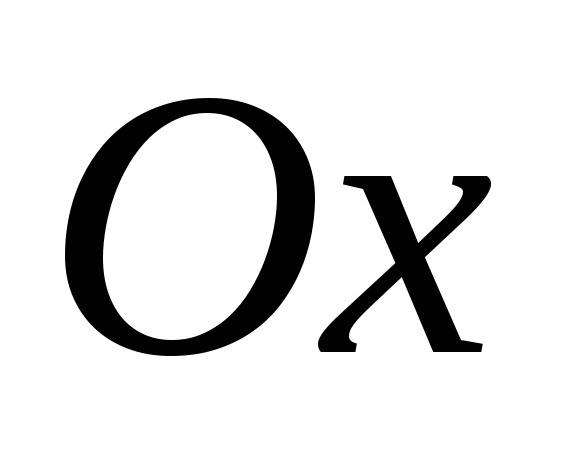 в двух точках, и вершина параболы расположена ниже оси
в двух точках, и вершина параболы расположена ниже оси 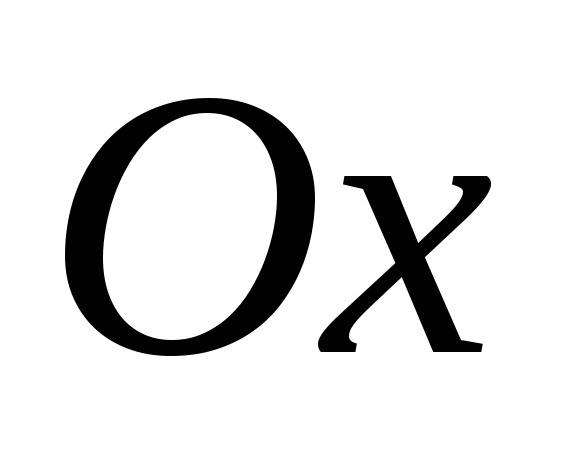 ( Рис. 1).
( Рис. 1).
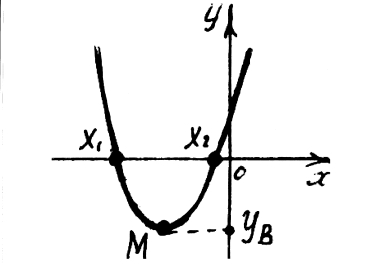
Рис. 1
2б. Сформулируйте условие, при котором данное расположение имеет место.
2б. Вершина параболы расположена ниже оси 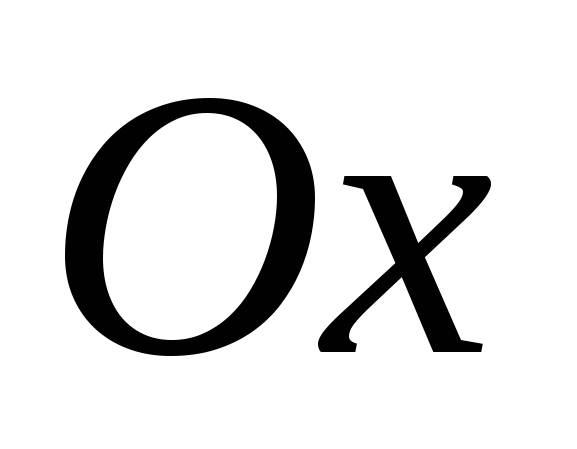 , если
, если 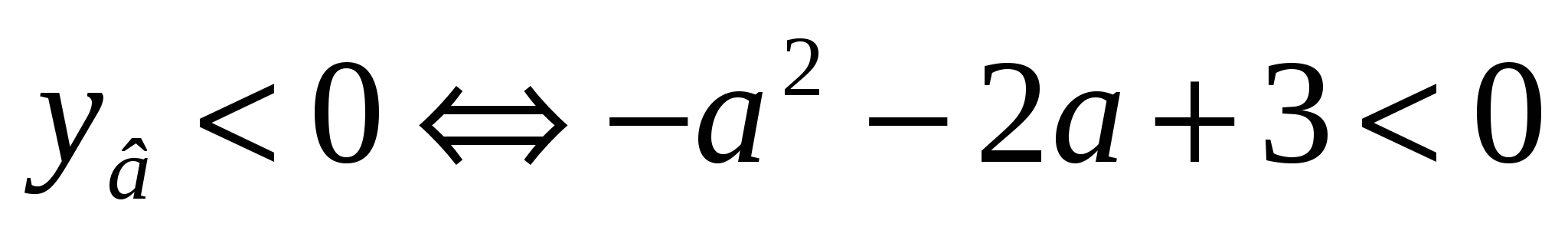 (это соответствует условию
(это соответствует условию 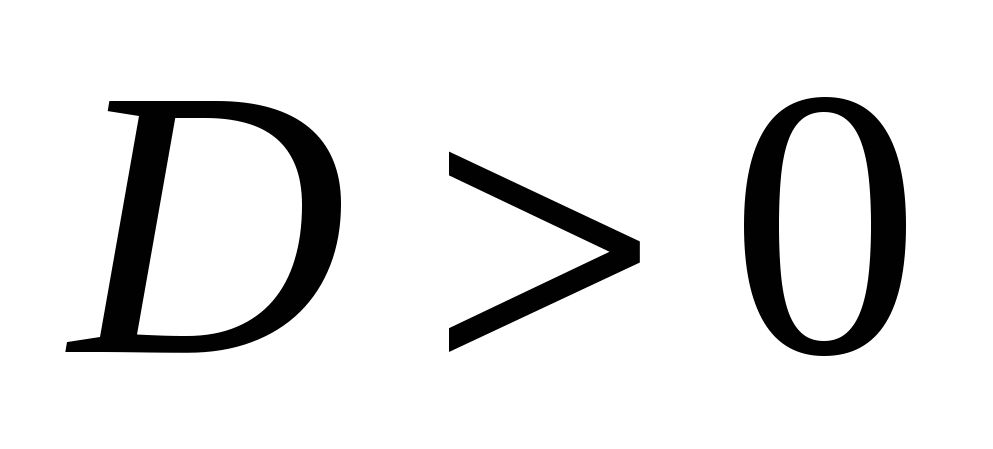 ) .
) .
3а. Изобразите все возможные варианты расположения графика рассматриваемой функции с тем, чтобы заданное уравнение имело два различных корня одного знака.
3а.
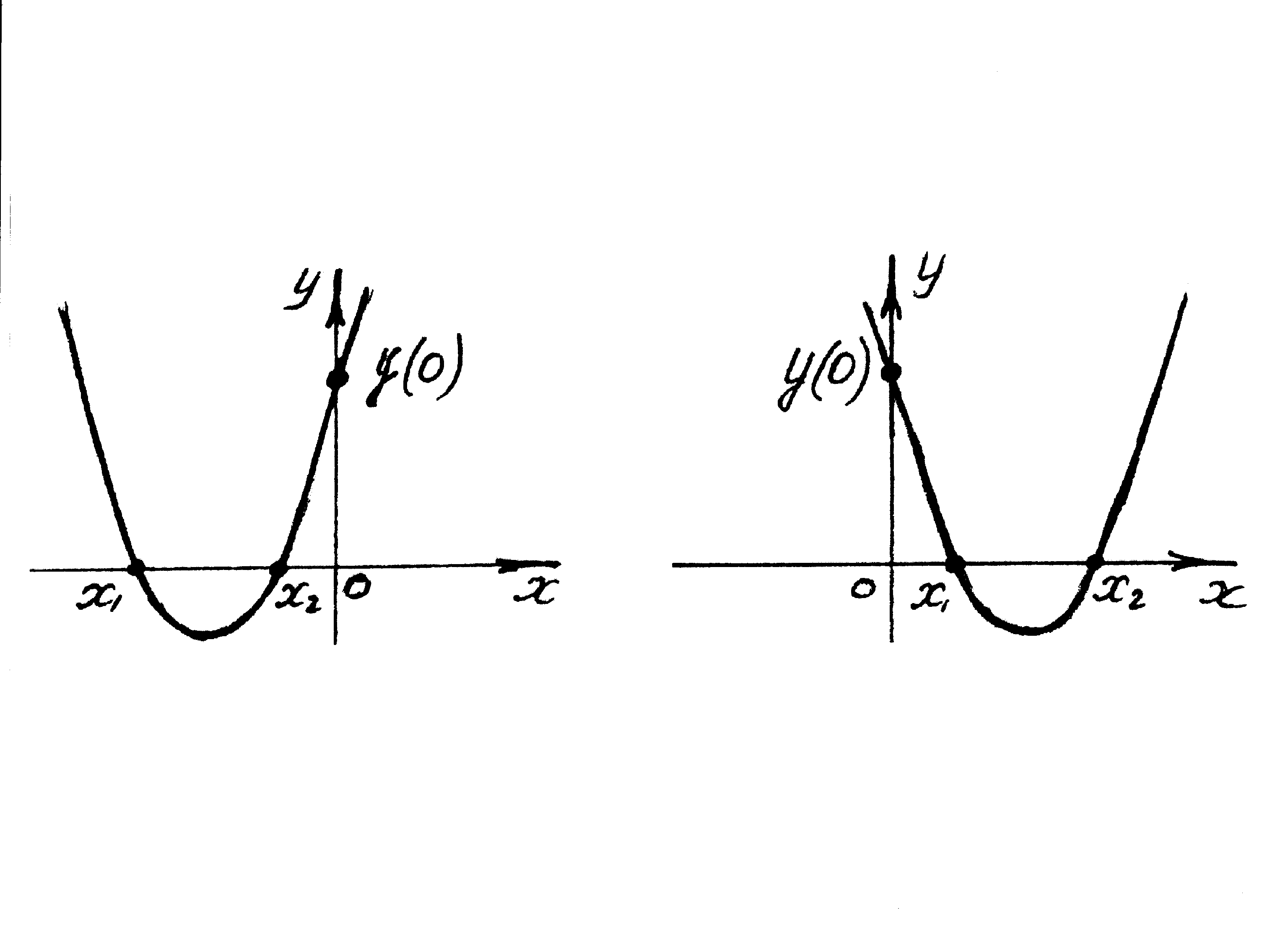
Рис. 2
Здесь 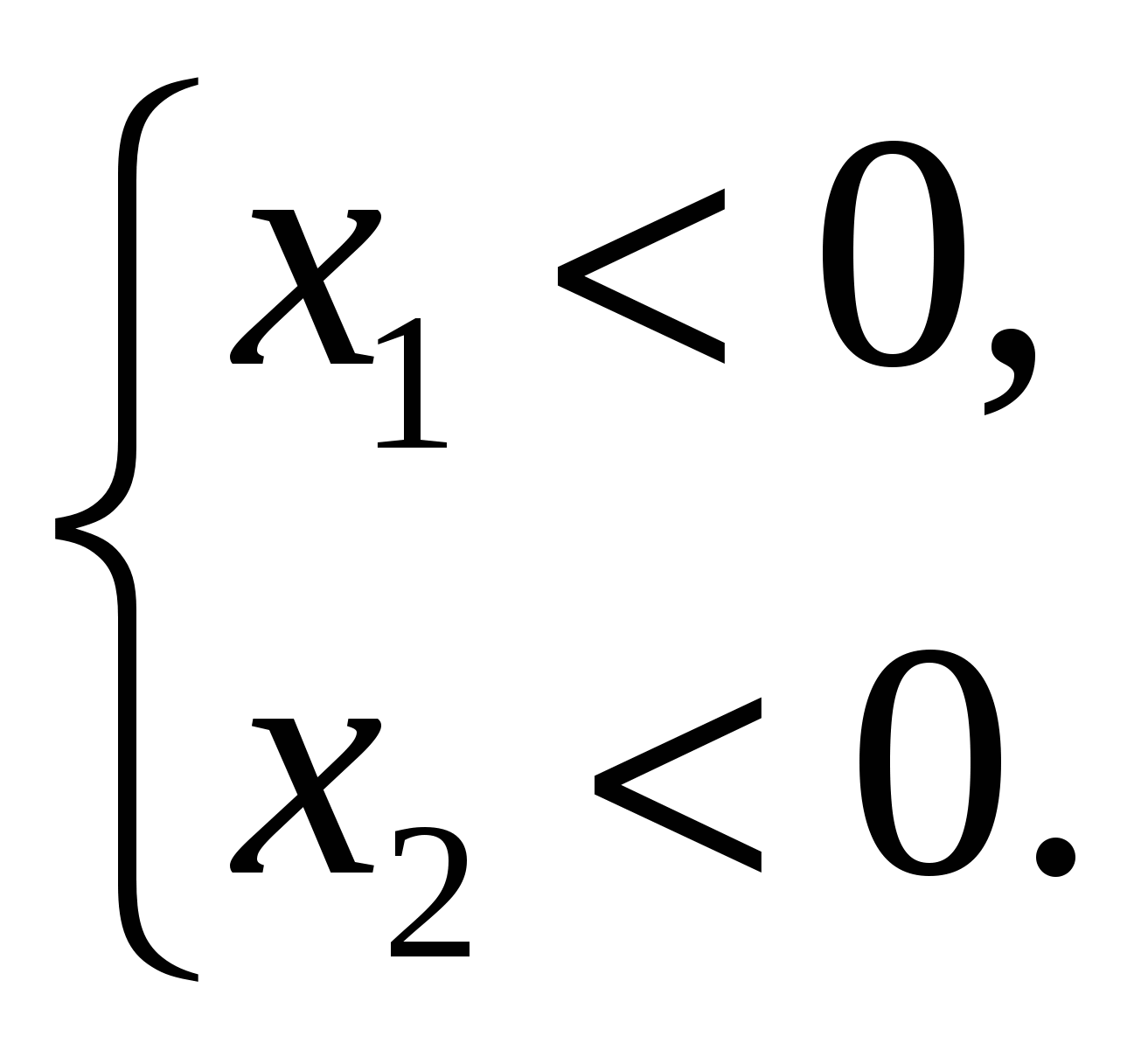
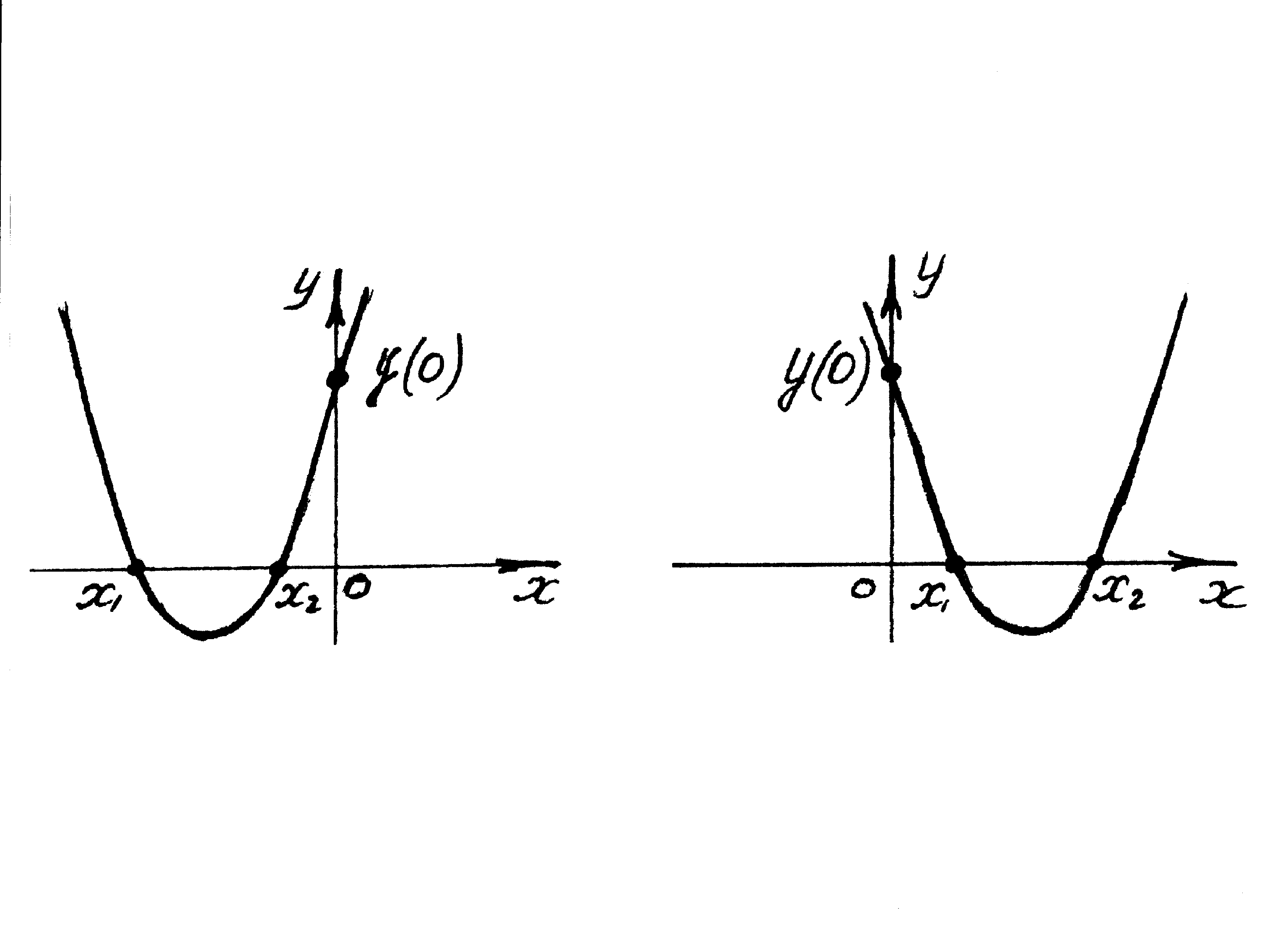
Рис. 3
Здесь 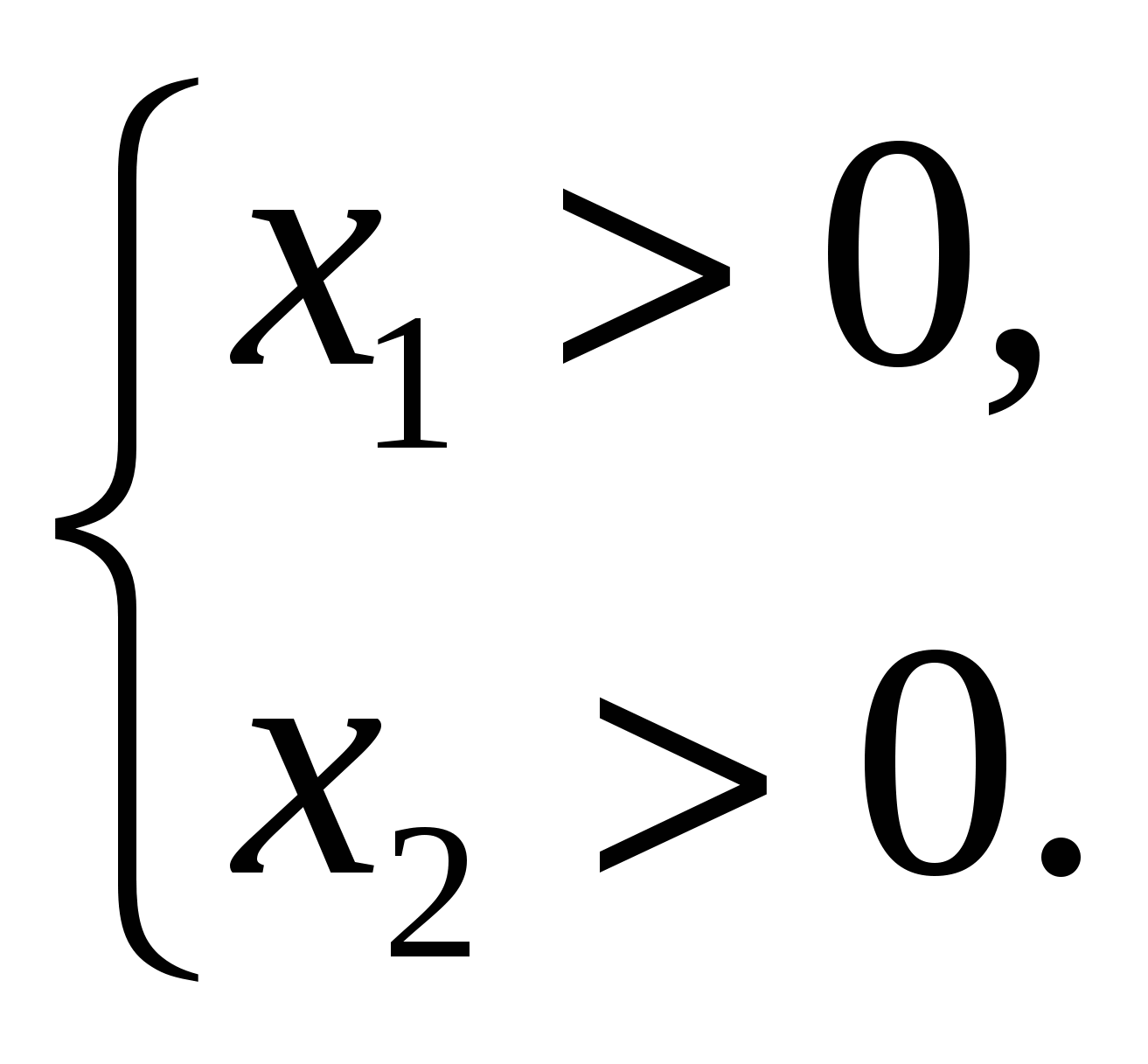
3б. Найдите условие необходимое и достаточное для того, чтобы корни данного уравнения имели разные знаки.
Обратите внимание на точку пересечения графика функции с осью OY. Сравните рисунки 2, 3 и рисунки 4,5,6.
3б. Для того чтобы заданное уравнение имело два различных корня одного знака необходимо и достаточно выполнения системы условий:
1) вершина параболы-графика рассматриваемой функции расположена ниже оси ох, при этом 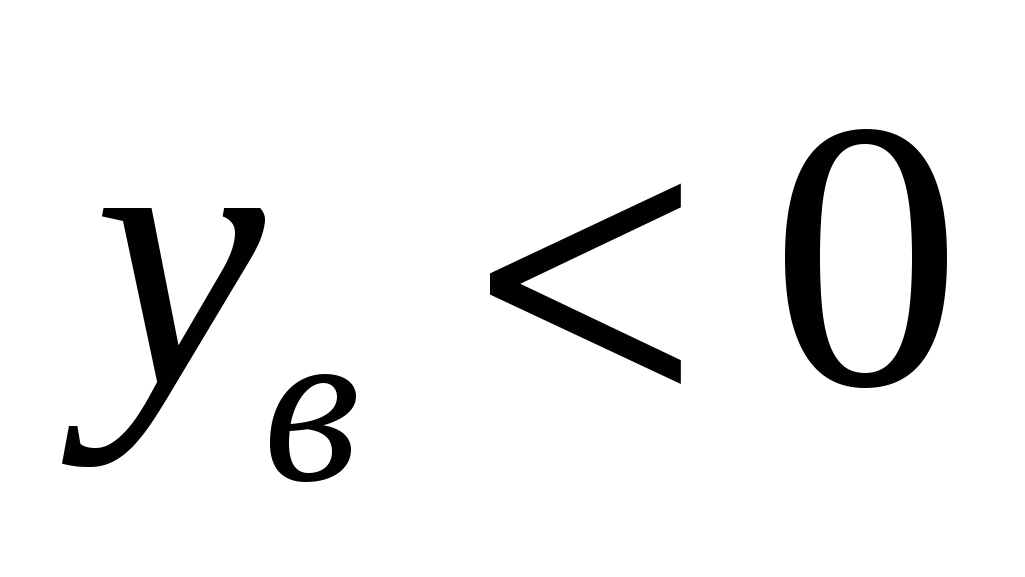 ;
;
2) график рассматриваемой функции пересекает ось ординат в верхней полуплоскости, при этом 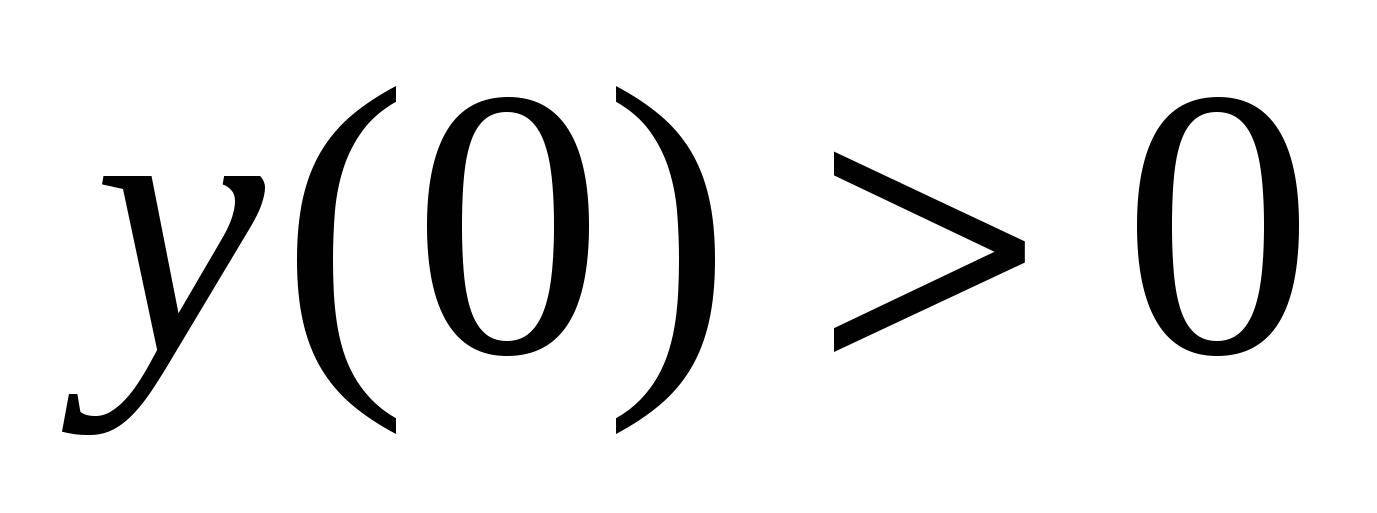 ; то есть
; то есть 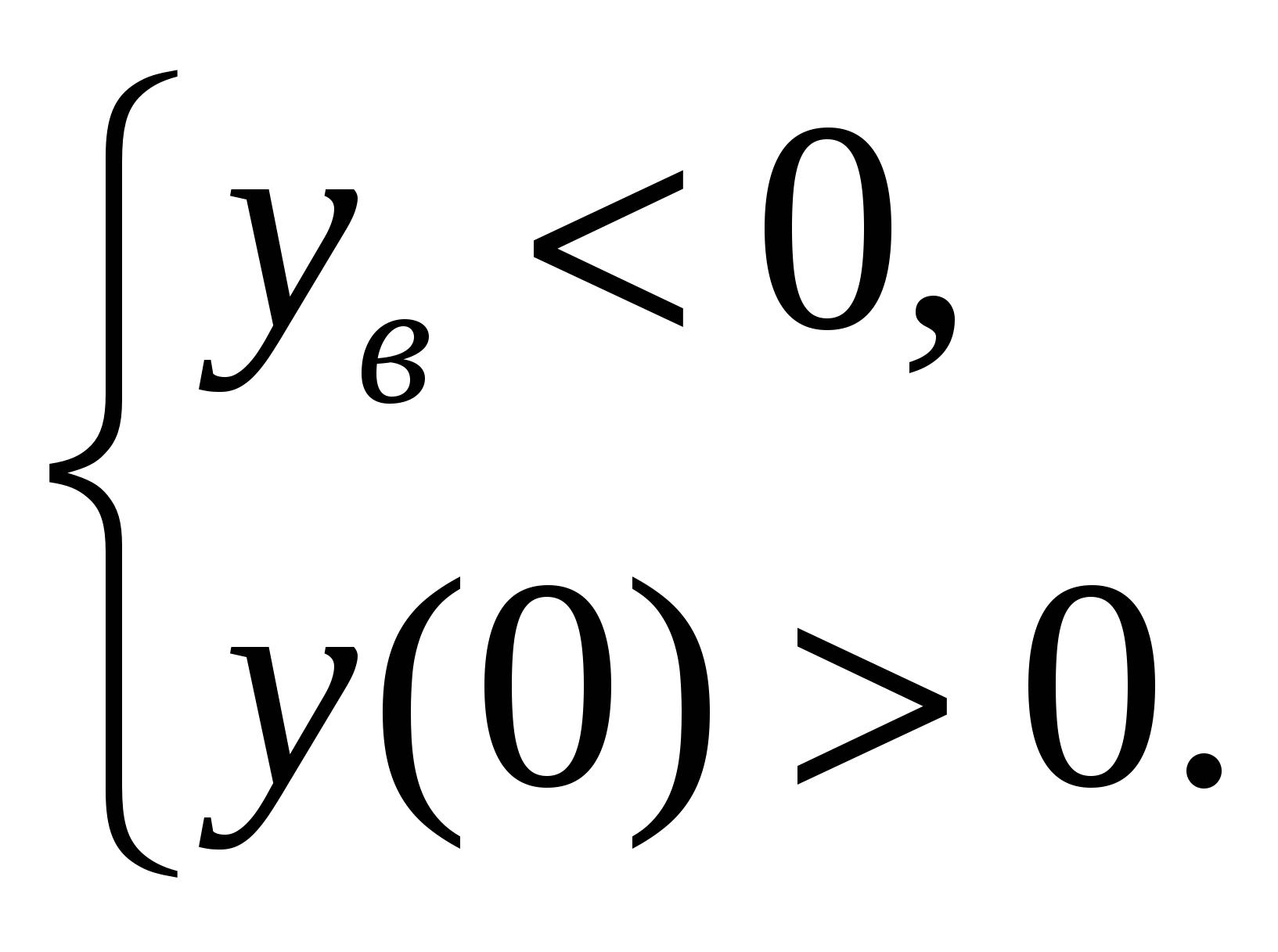
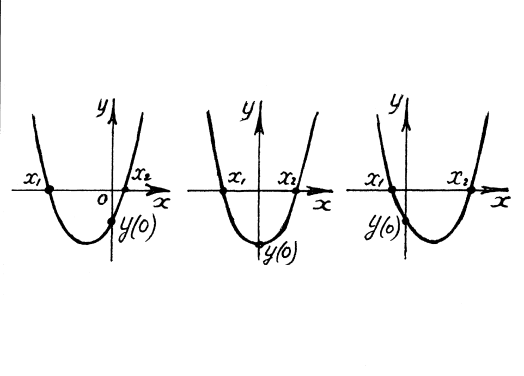
Рис. 4
Здесь
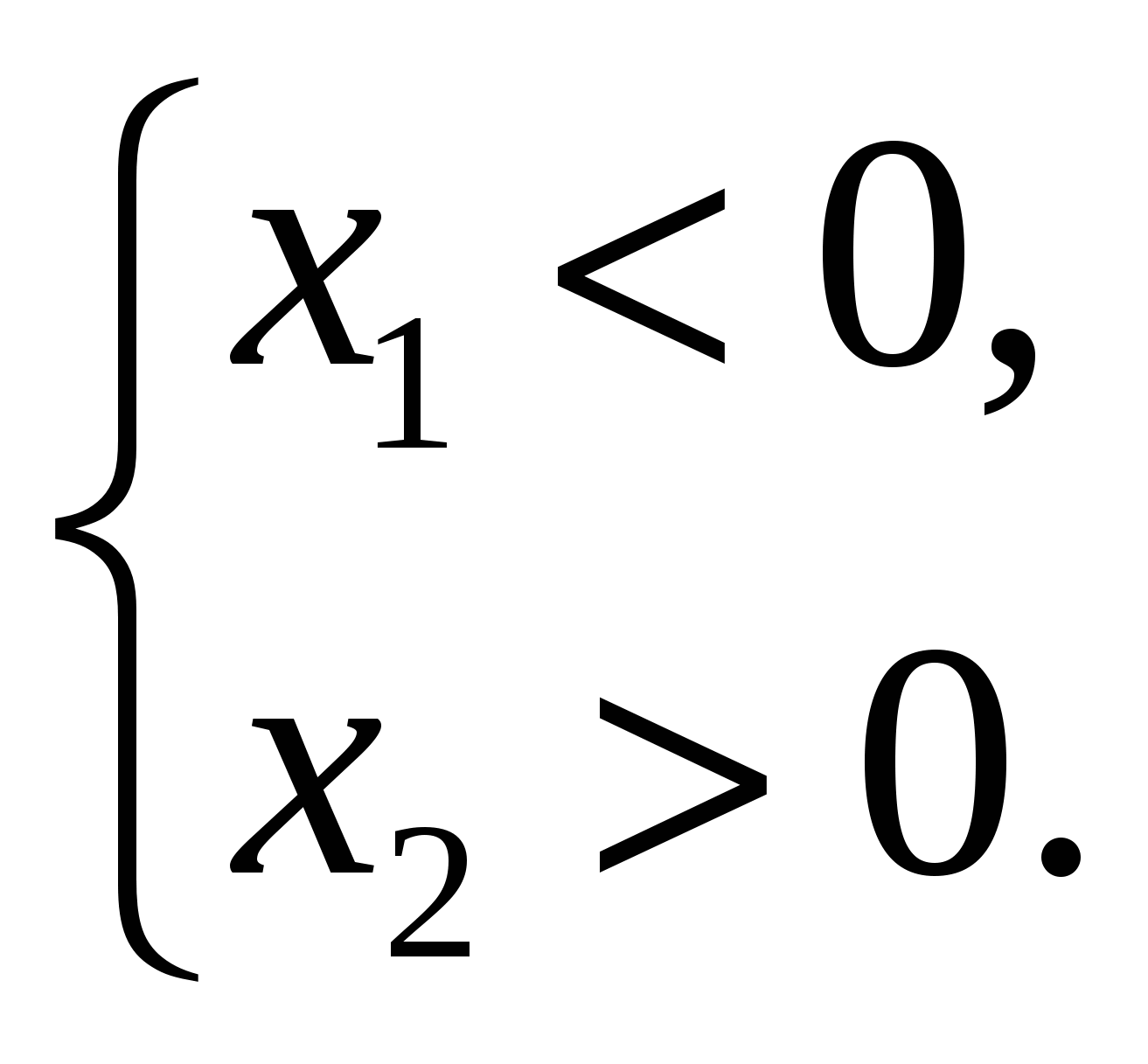
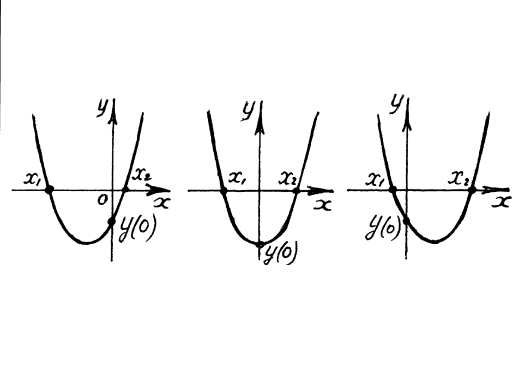
Рис. 5
Здесь
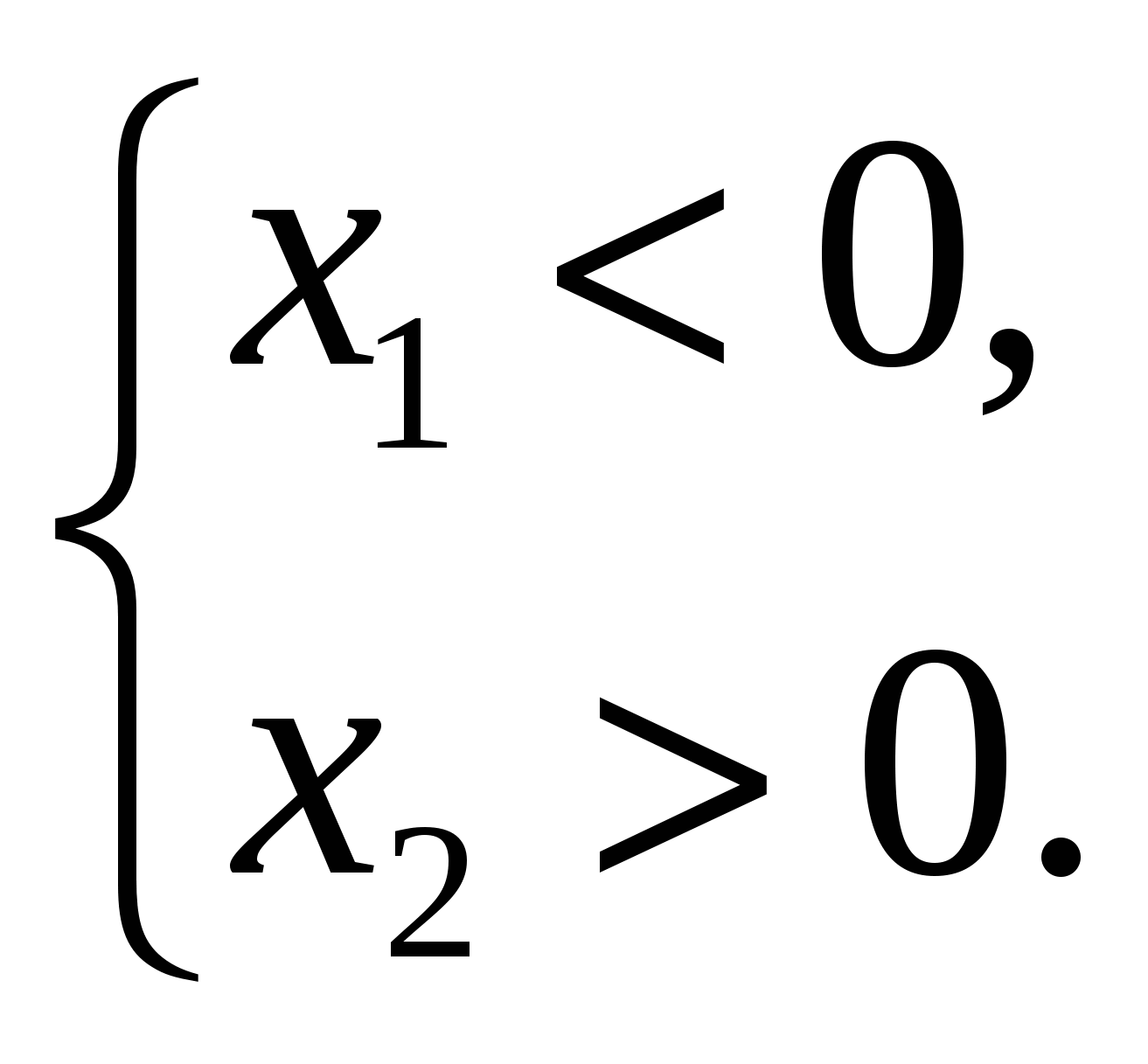
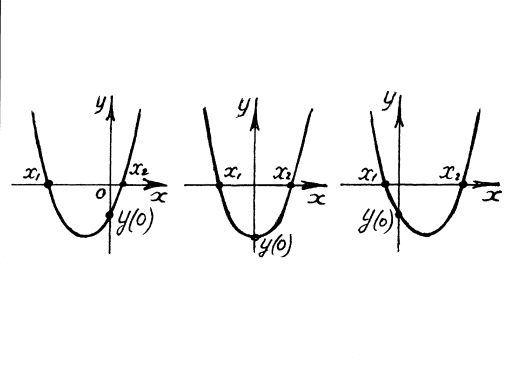
Рис. 6
Здесь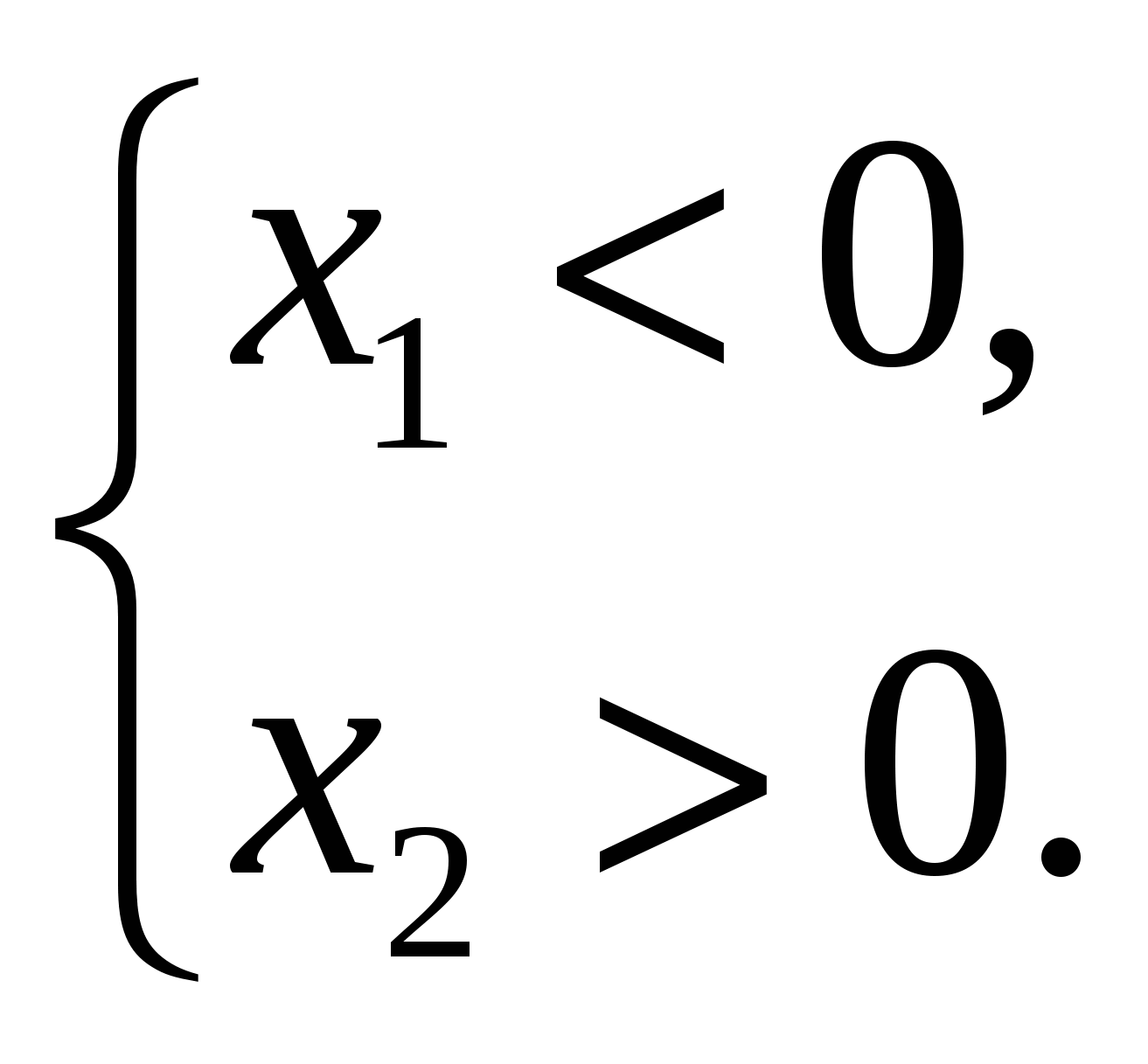
4. Решите полученную систему.
4.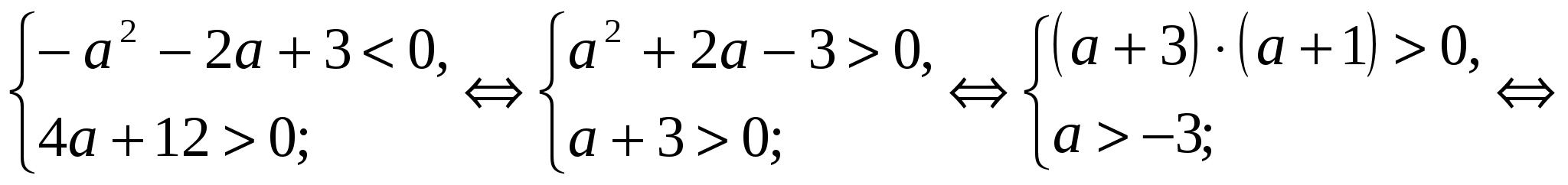
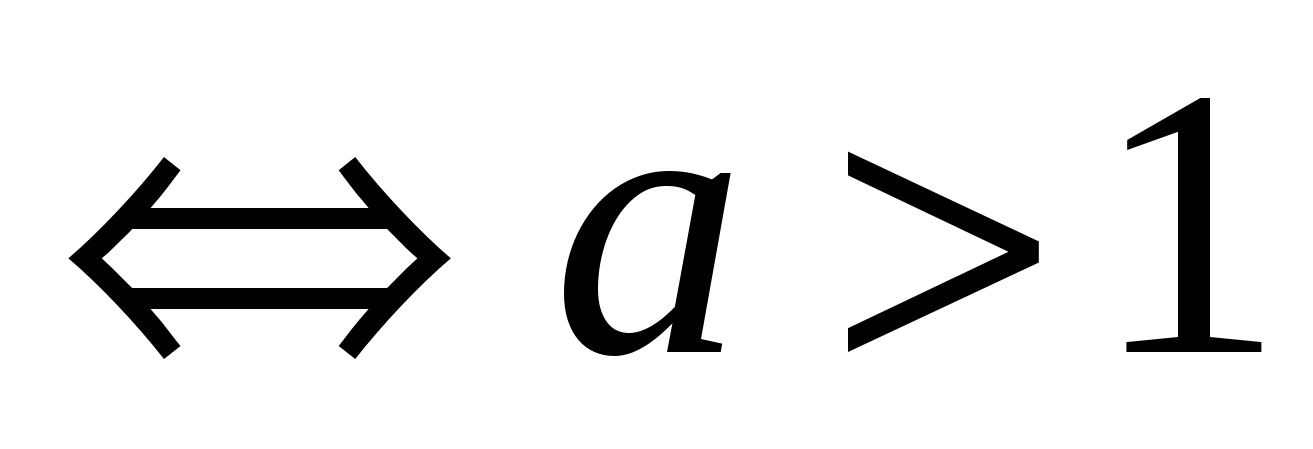 .
.
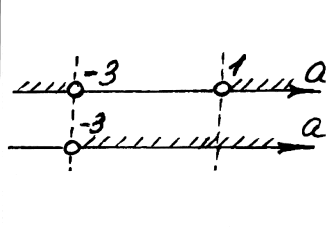
Рис. 7
5.Сформулируйте ответ на вопрос задачи.
5. Уравнение 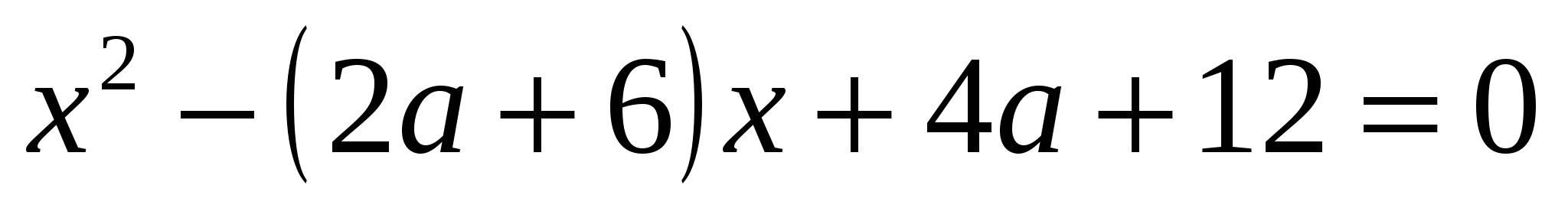 имеет два различных корня одного знака при
имеет два различных корня одного знака при 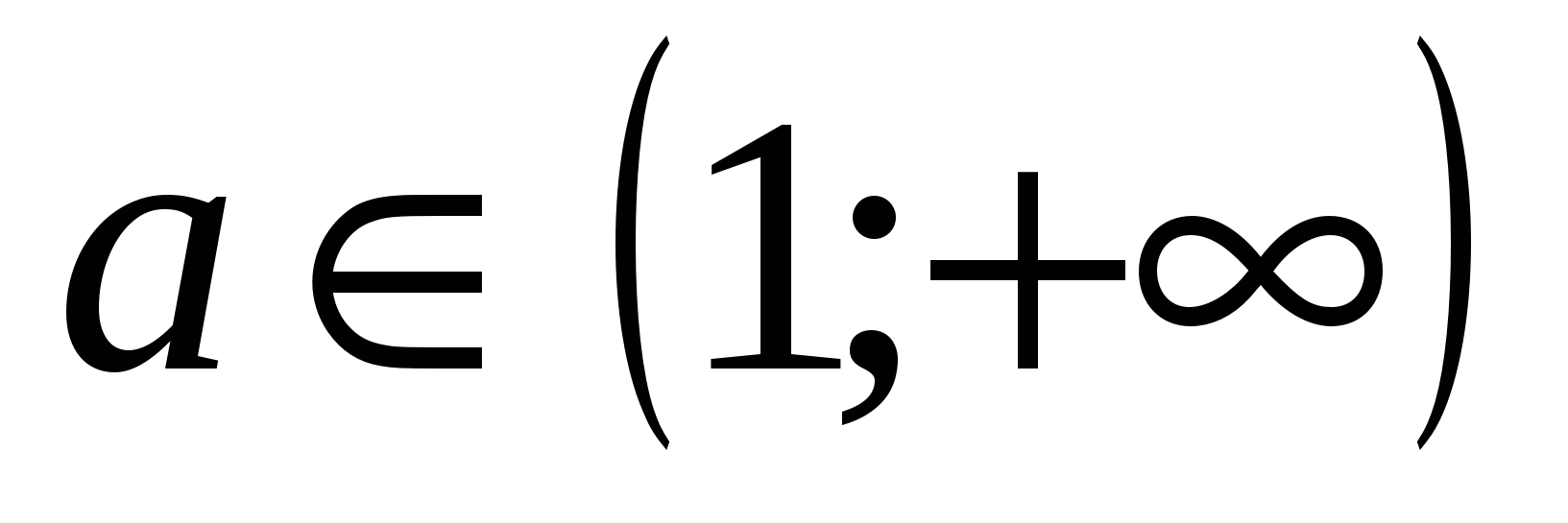 .
.
Систематизация новых методов решения.
Полученный способ решения задачи оказался очень удобным. Разработаем теоретическое обоснование для решения трех основных задач на исследование квадратного трехчлена.
Задача 1: выяснить, при каких значениях параметра корни квадратного трехчлена различны и оба корня меньше  .
.
Задача 2: выяснить, при каких значениях параметра корни квадратного трехчлена различны и оба корня больше  .
.
Задача 3: выяснить, при каких значениях параметра корни квадратного трехчлена расположены по разные стороны от точки 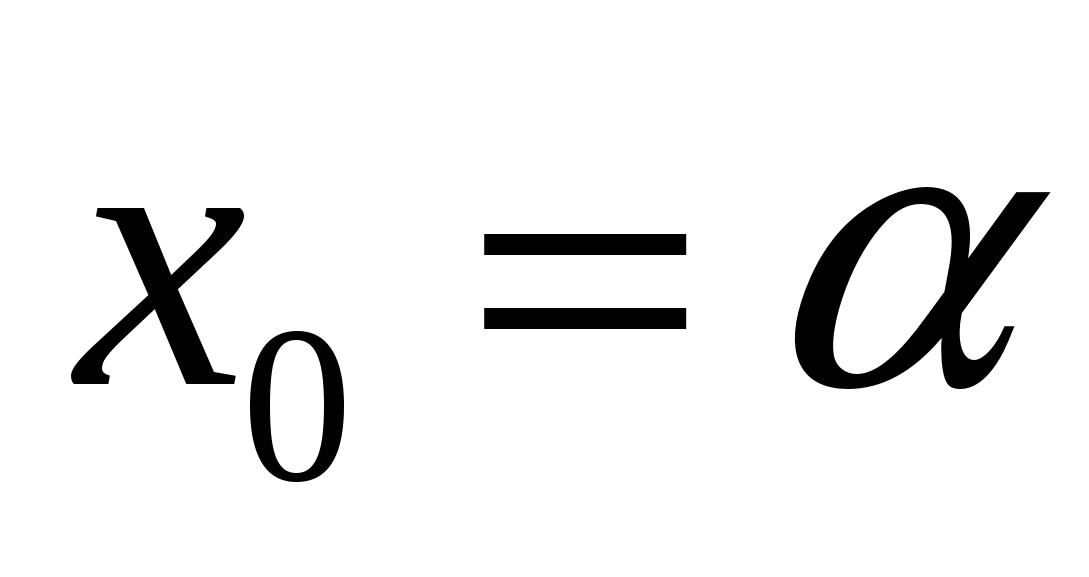 .
.
Пусть задан квадратный трехчлен вида 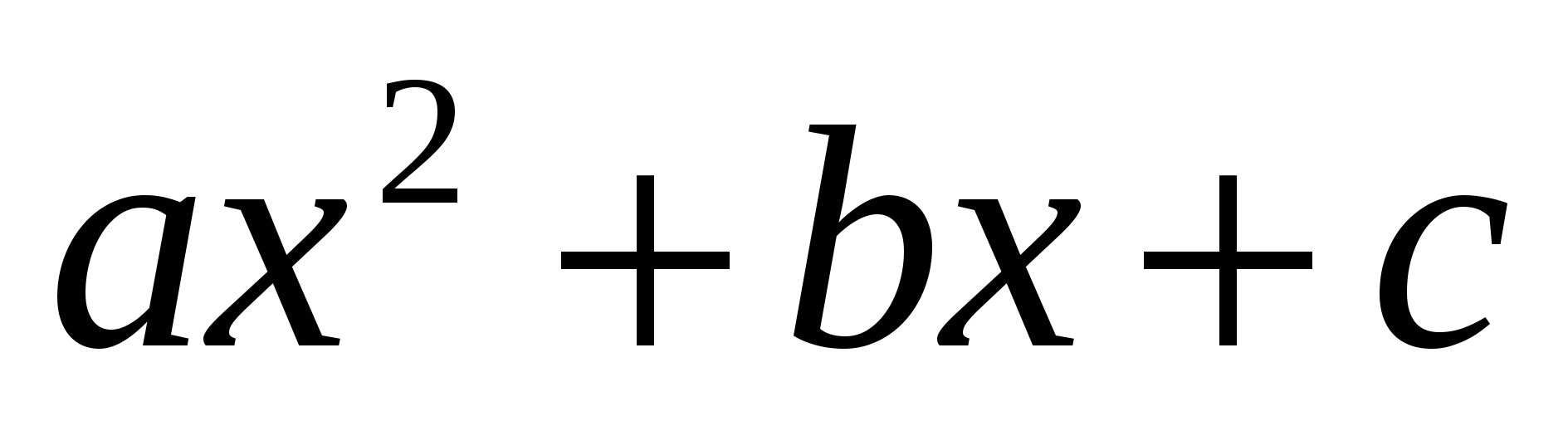 ,
, 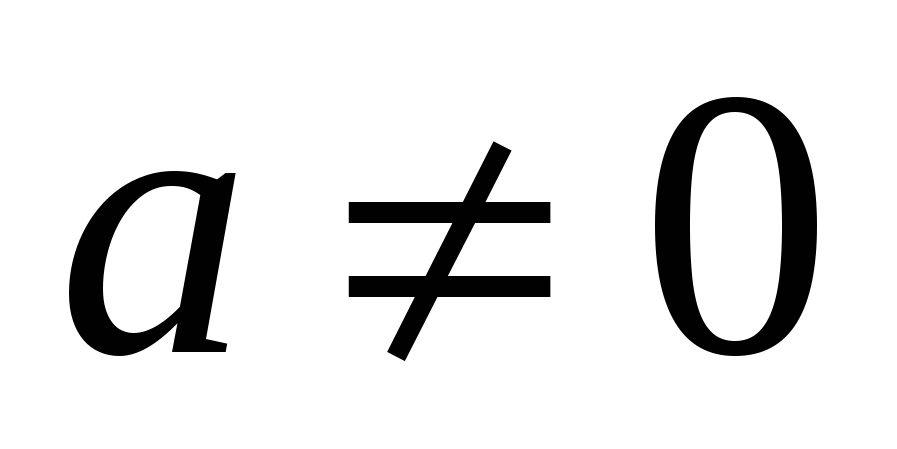 . Пусть
. Пусть 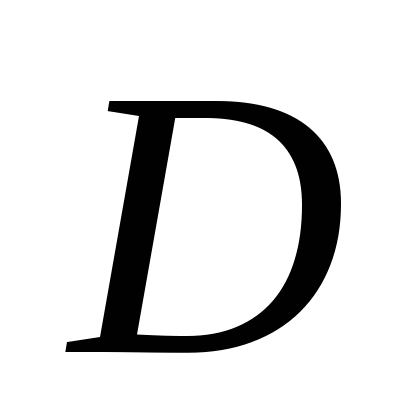 − дискриминант этого трехчлена, а
− дискриминант этого трехчлена, а 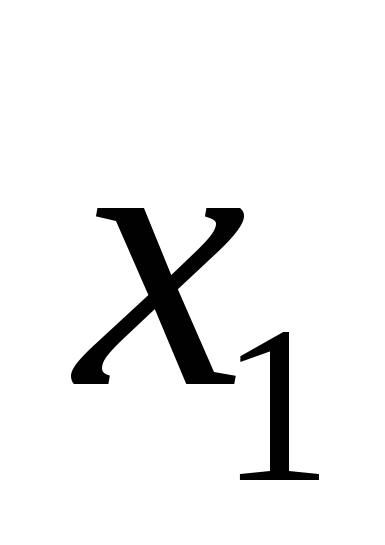 и
и 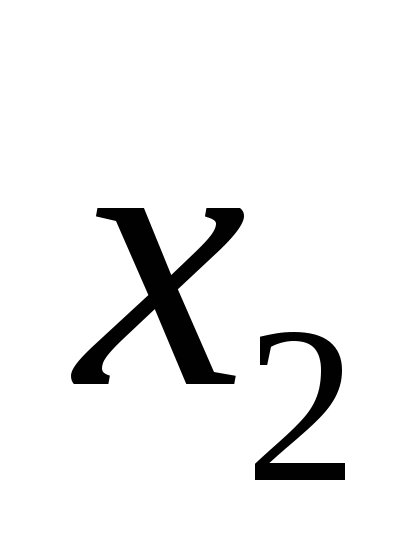 − его корни, причем
− его корни, причем 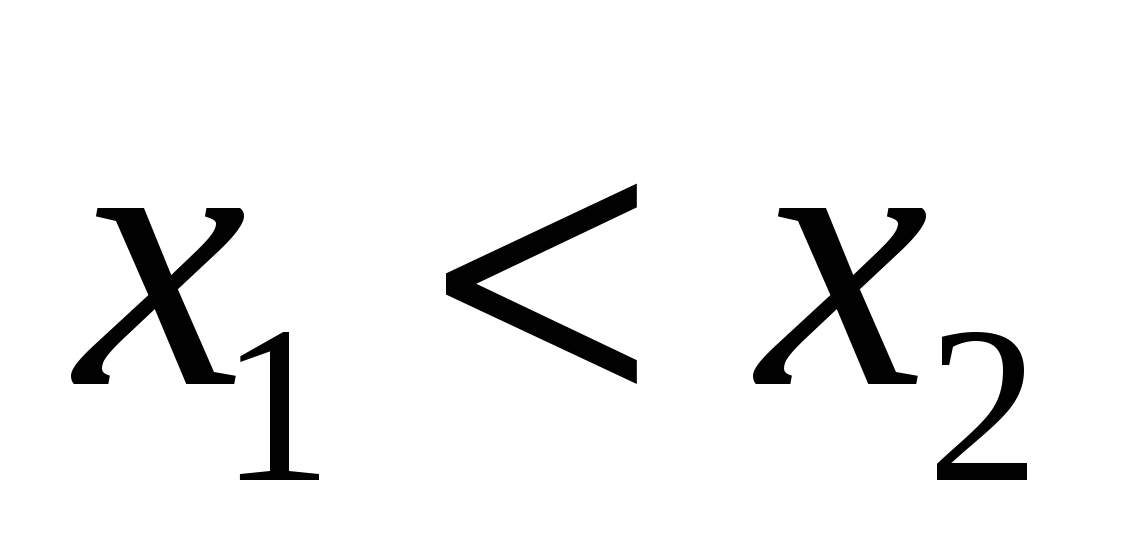 .
.
Если заведомо 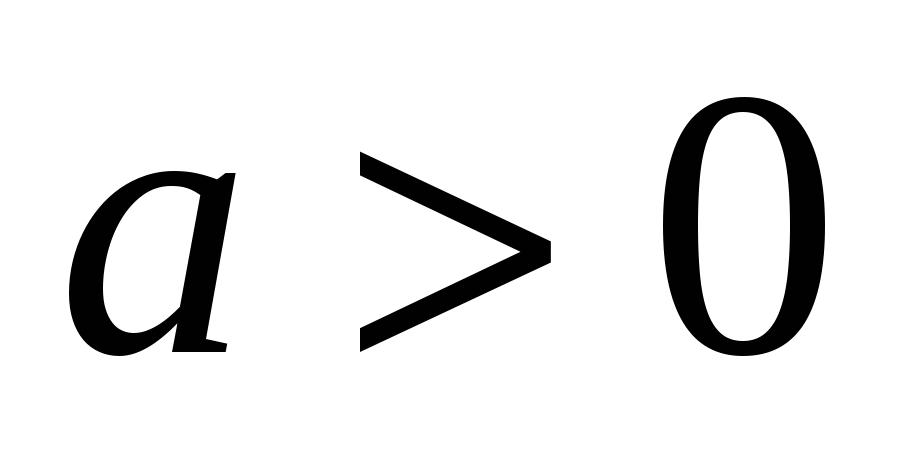 , то следует рассмотреть функцию
, то следует рассмотреть функцию 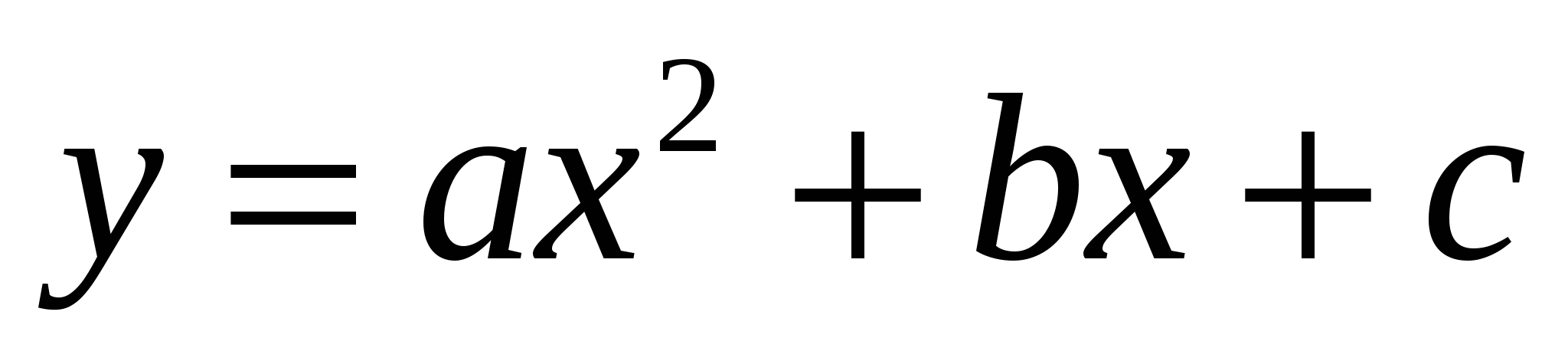 . Графиком этой квадратичной функции является парабола, ветви которой направлены вверх.
. Графиком этой квадратичной функции является парабола, ветви которой направлены вверх.
Задача 1.Для того чтобы  (Рис. 8) необходимо и достаточно выполнение системы условий:
(Рис. 8) необходимо и достаточно выполнение системы условий: 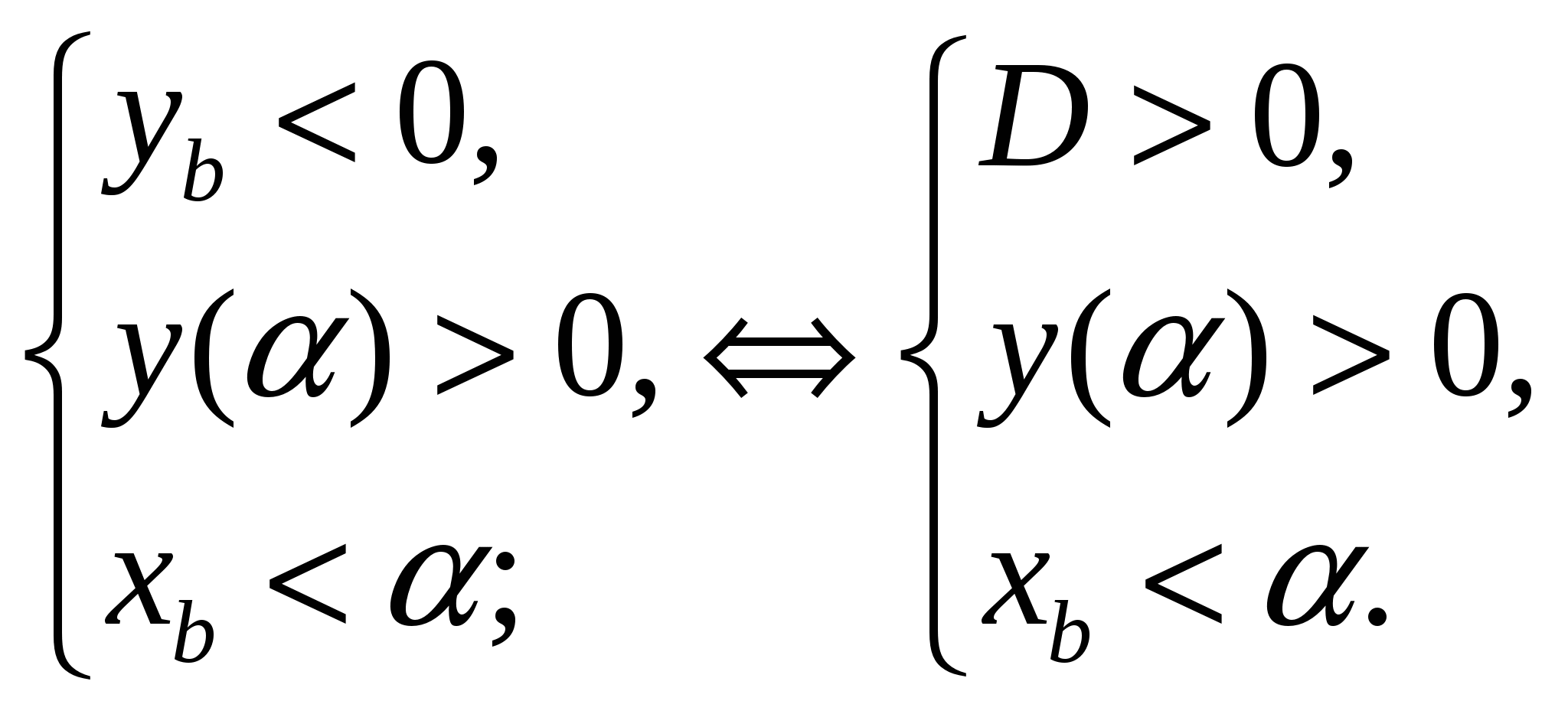
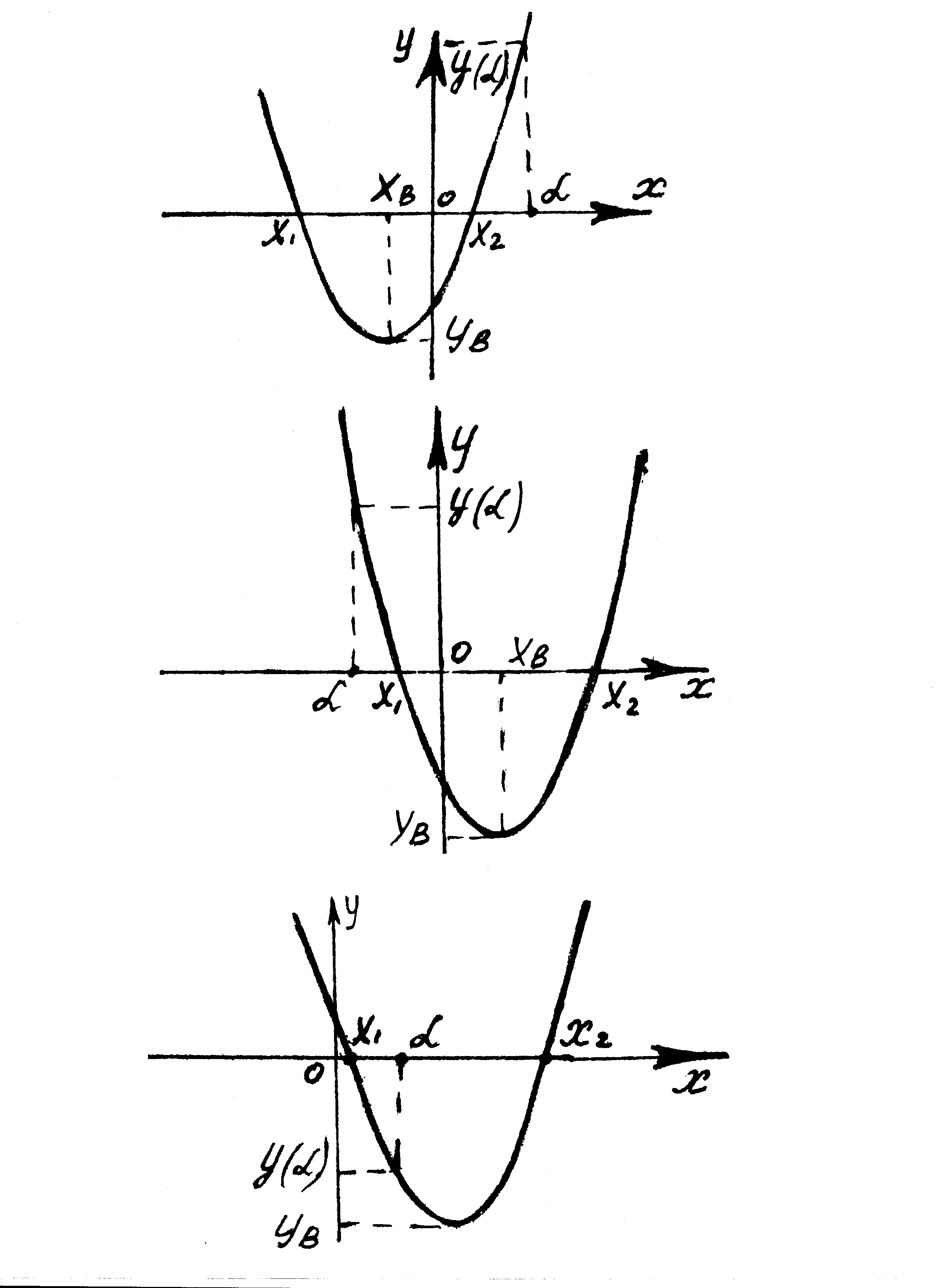
Рис. 8
Задача 2. Для того чтобы 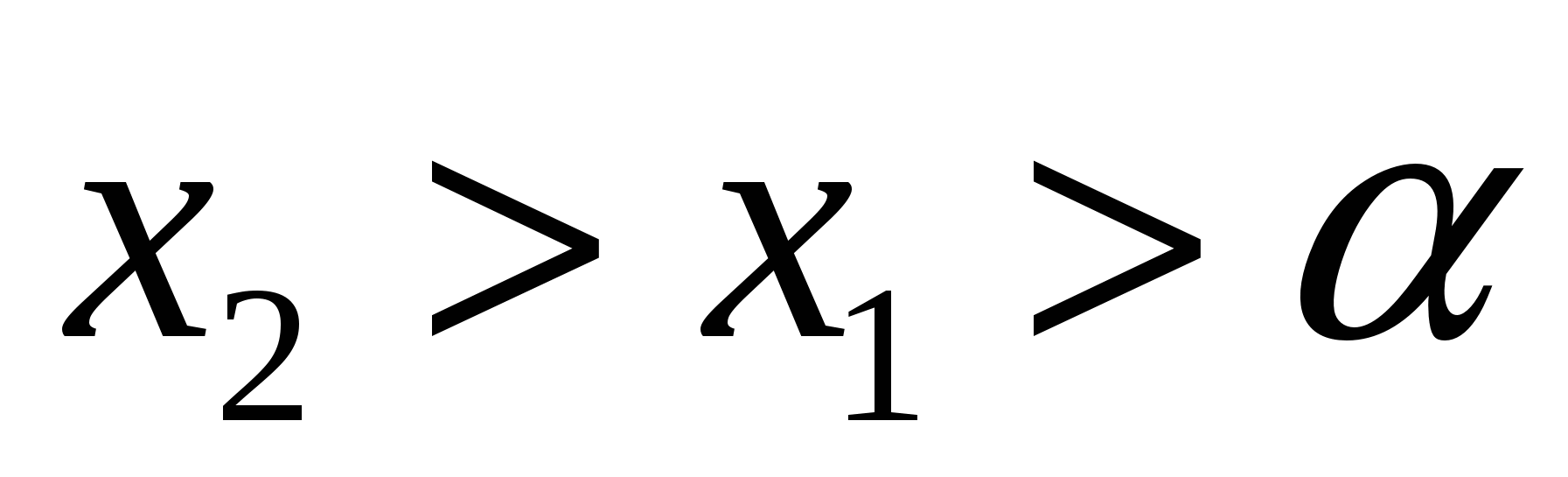 (Рис. 9) необходимо и достаточно выполнение системы условий:
(Рис. 9) необходимо и достаточно выполнение системы условий: 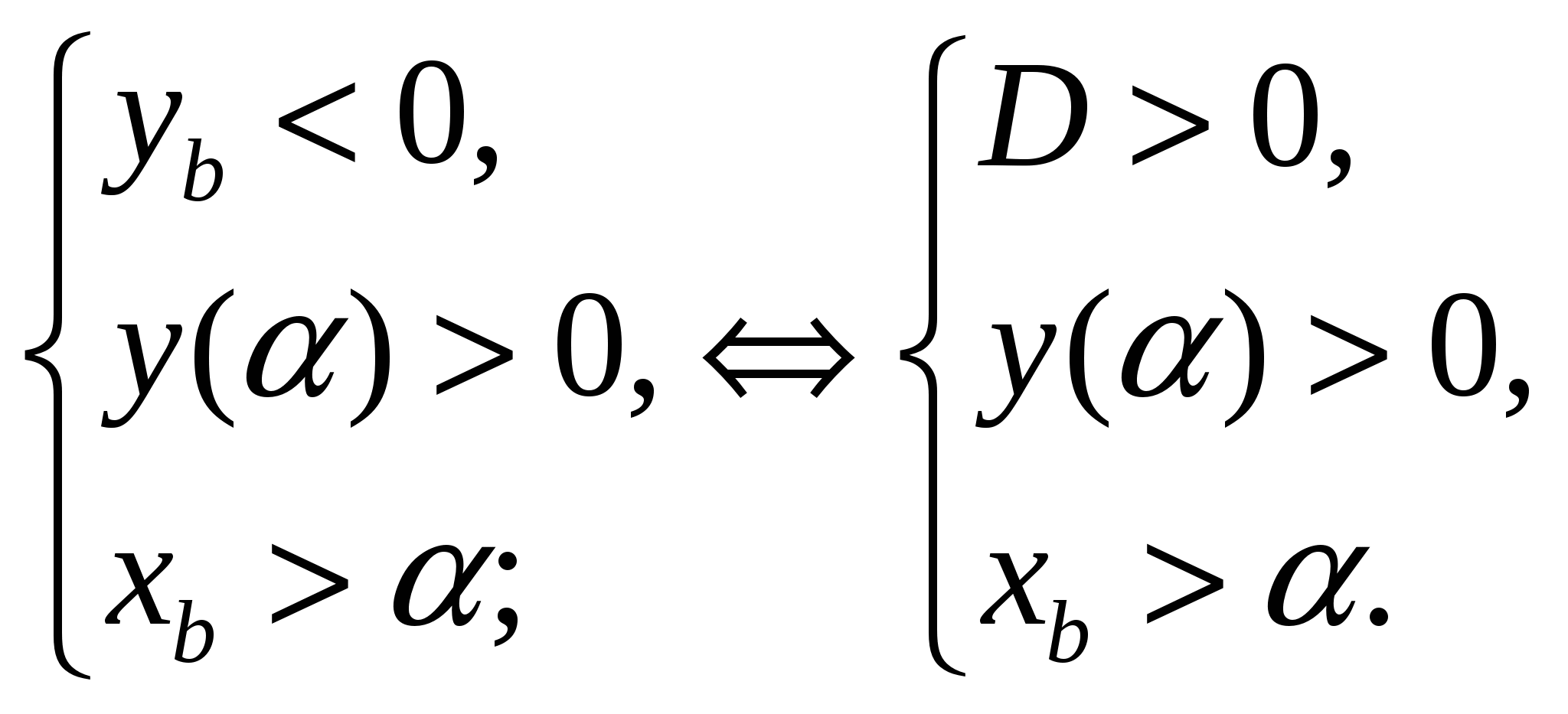
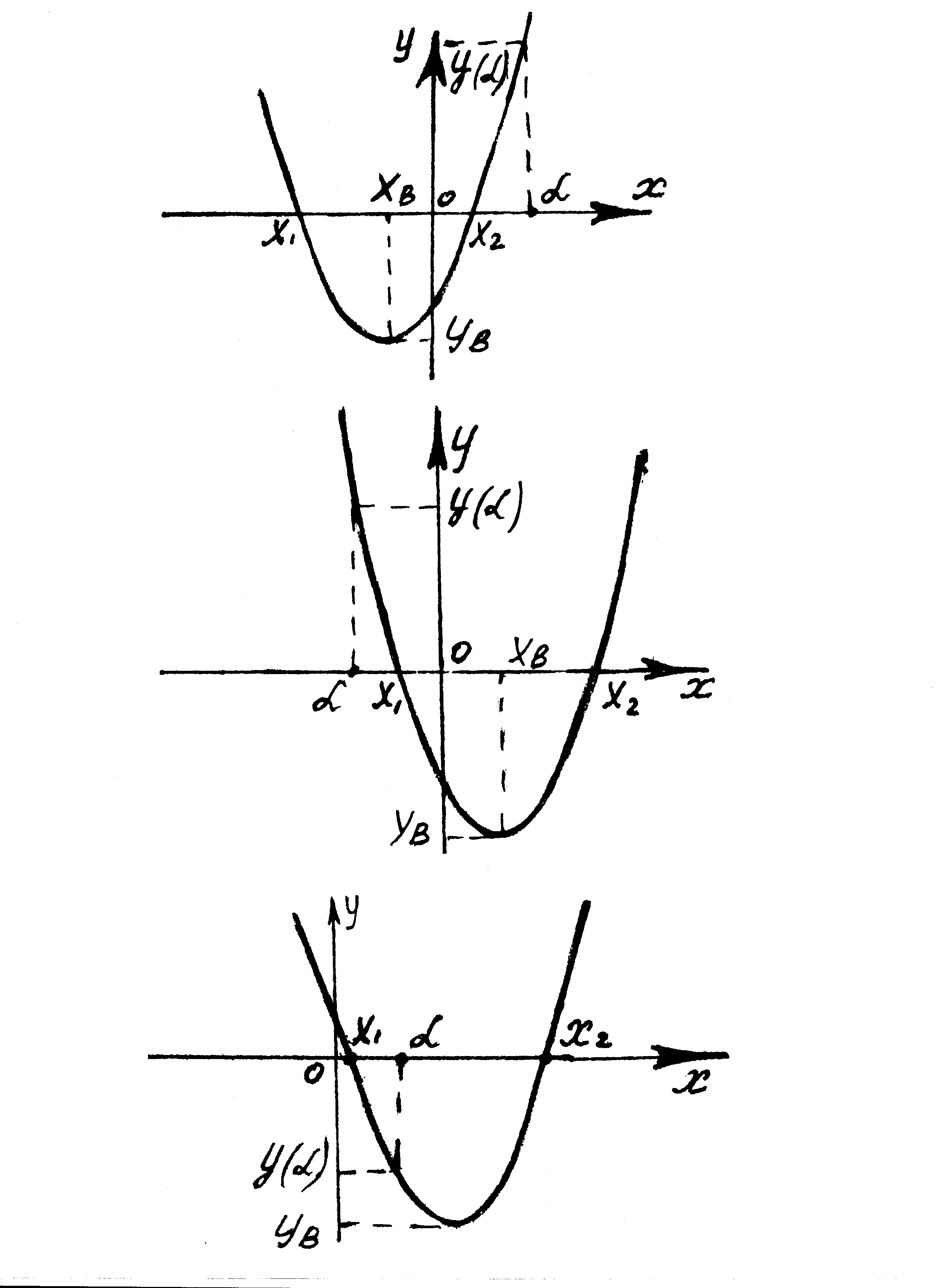
Рис. 9
Задача 3. Так как здесь 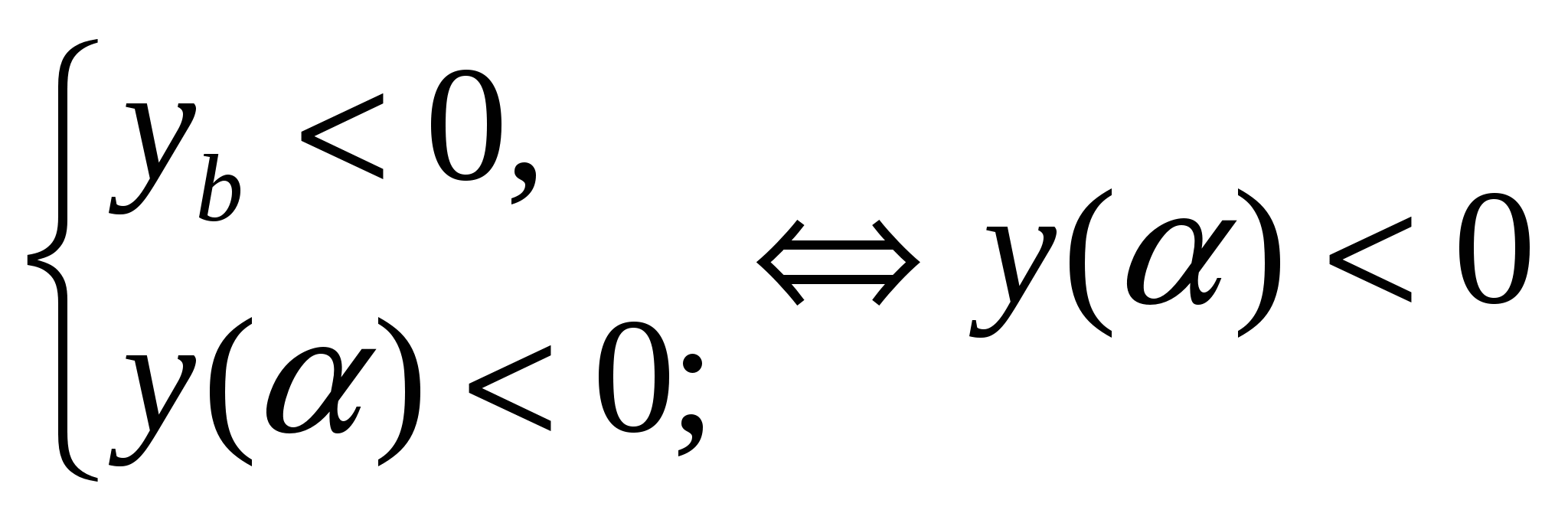 , то для того, чтобы
, то для того, чтобы 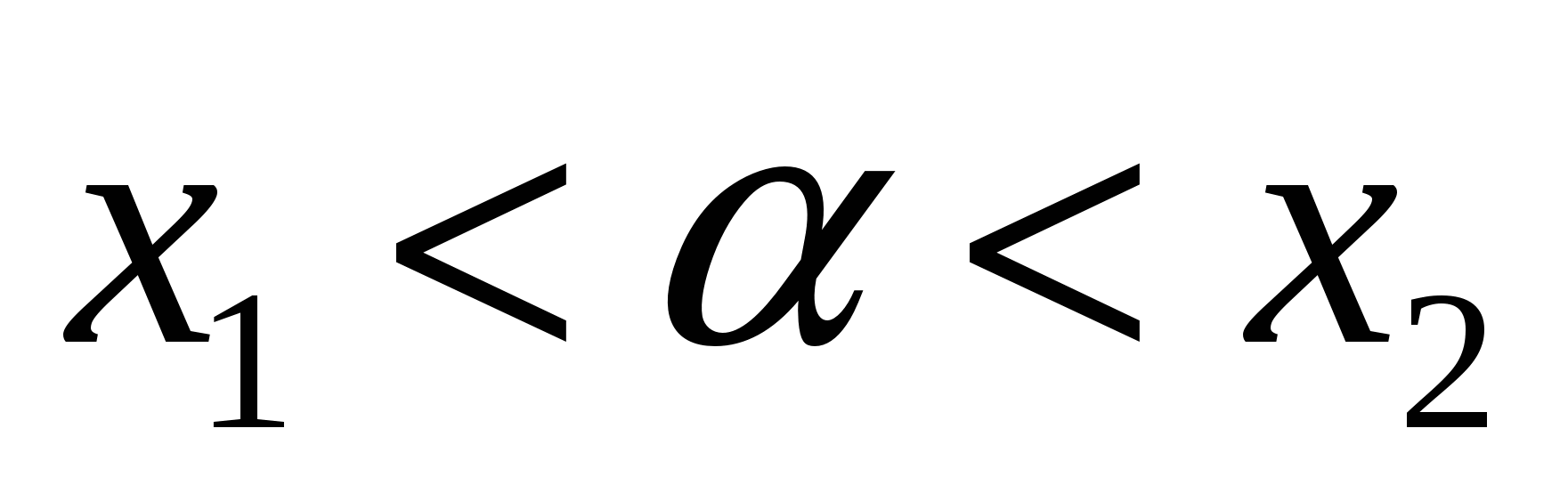 (Рис. 10) необходимо и достаточно выполнение условия:
(Рис. 10) необходимо и достаточно выполнение условия: 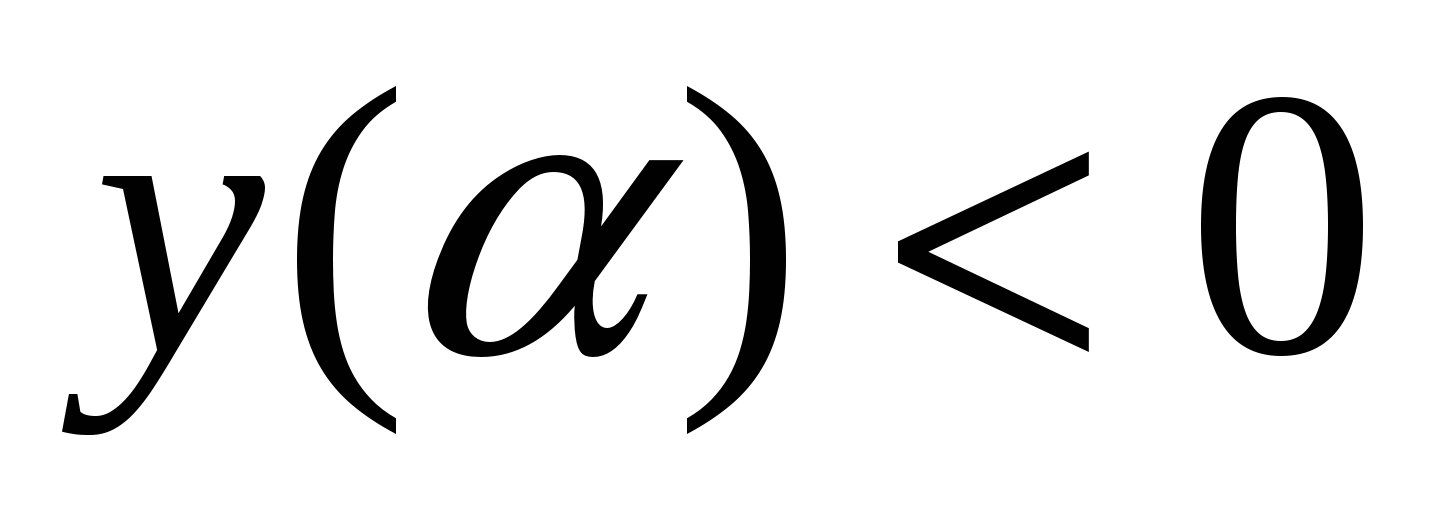 .
.
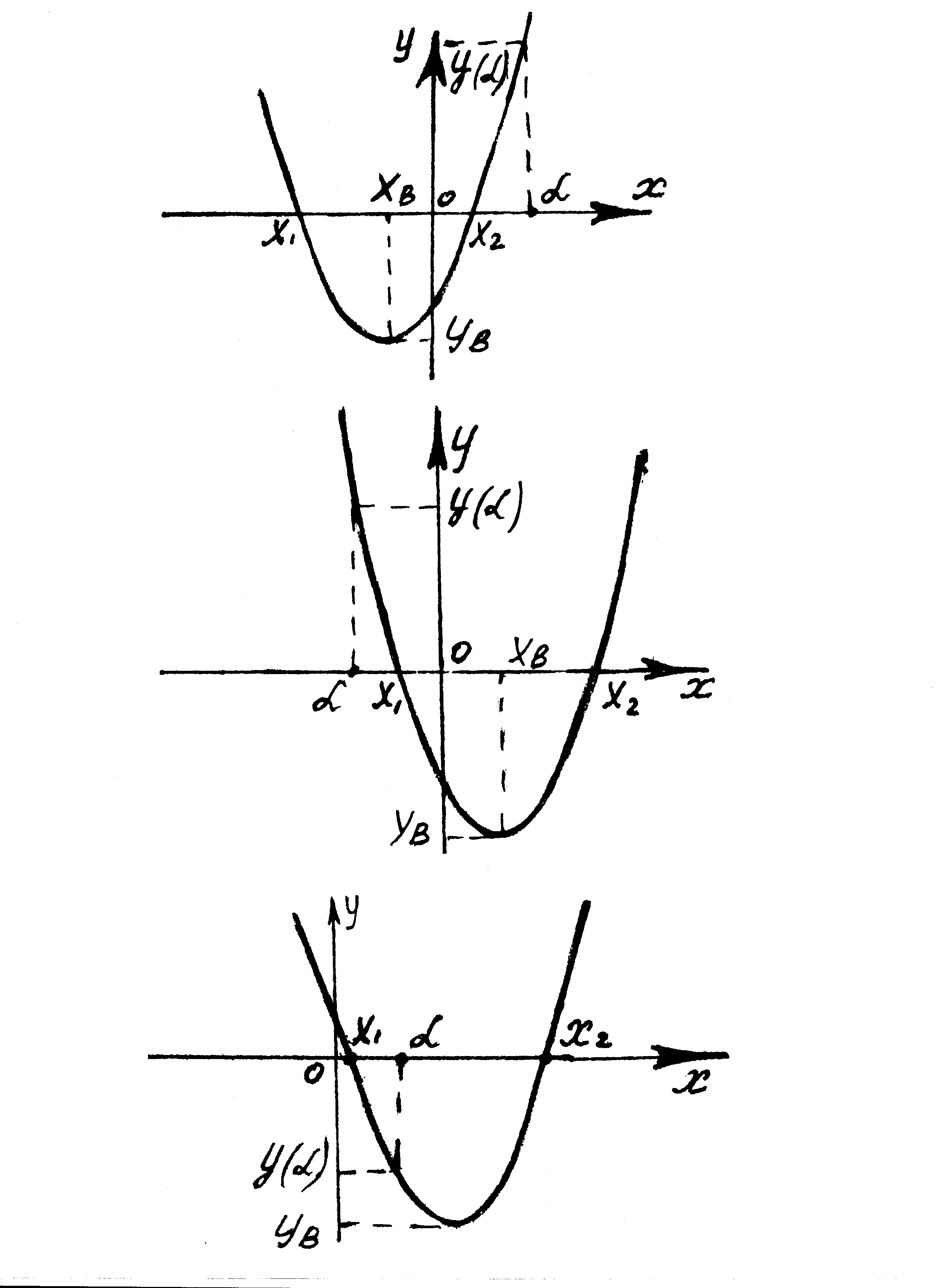
Рис. 10
Если заведомо 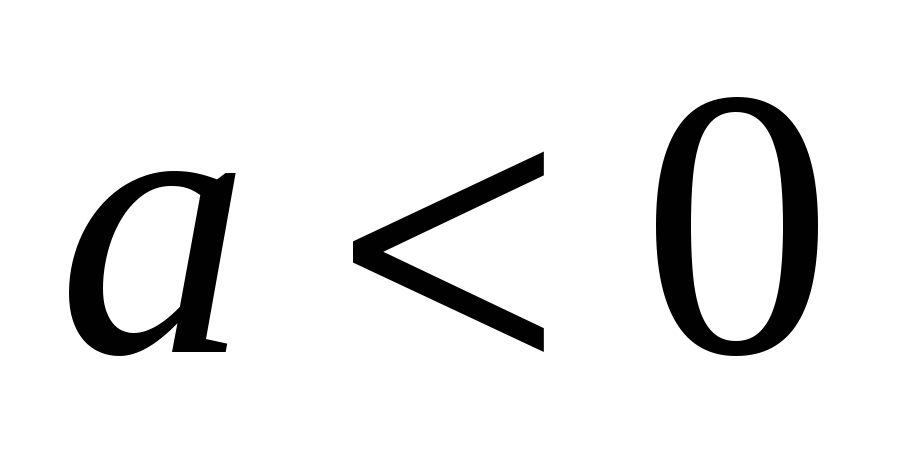 , то следует рассмотреть функцию
, то следует рассмотреть функцию 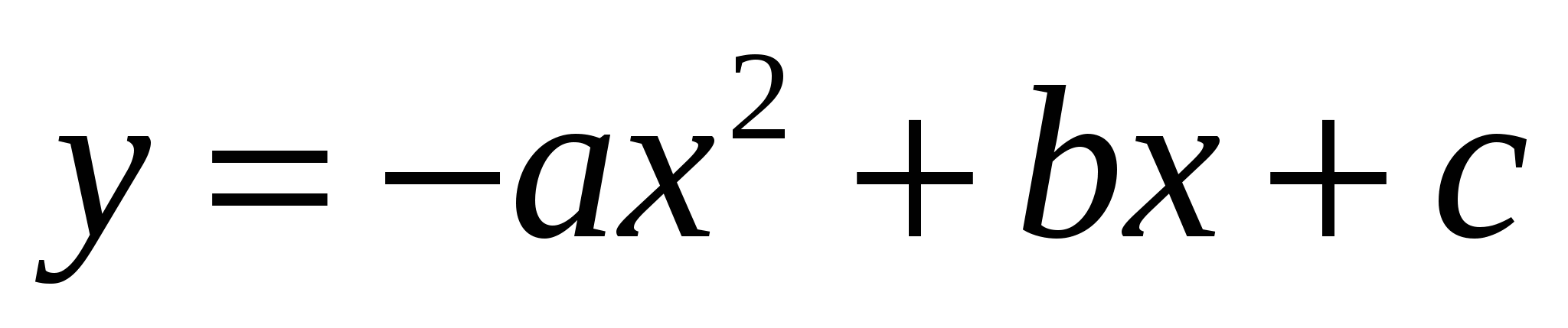 .
.
Если же знак  заранее не известен, то рассматривается функция
заранее не известен, то рассматривается функция  . Графиком и этой квадратичной функции является парабола, ветви которой направлены вверх.
. Графиком и этой квадратичной функции является парабола, ветви которой направлены вверх.
В двух последних случаях решения трех основных задач идентичны их решениям для первого случая (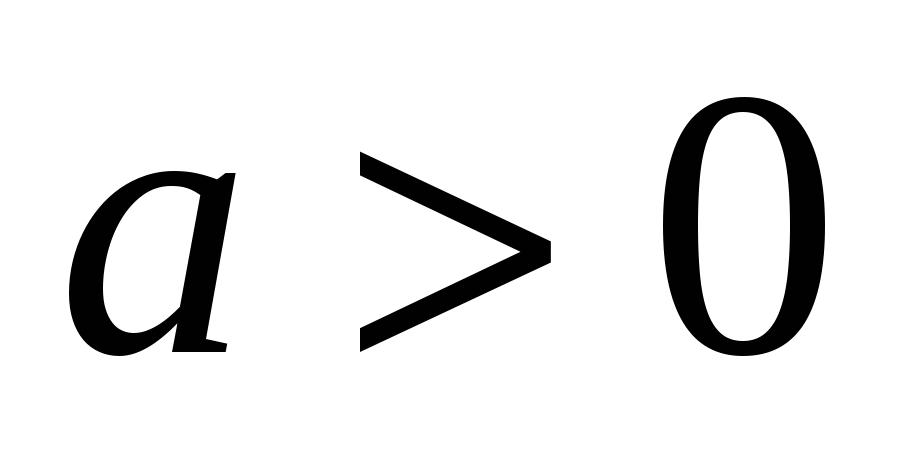 ). Составим таблицу.
). Составим таблицу.
Условия, налагаемые на корни
Необходимые и достаточные условия для параметра
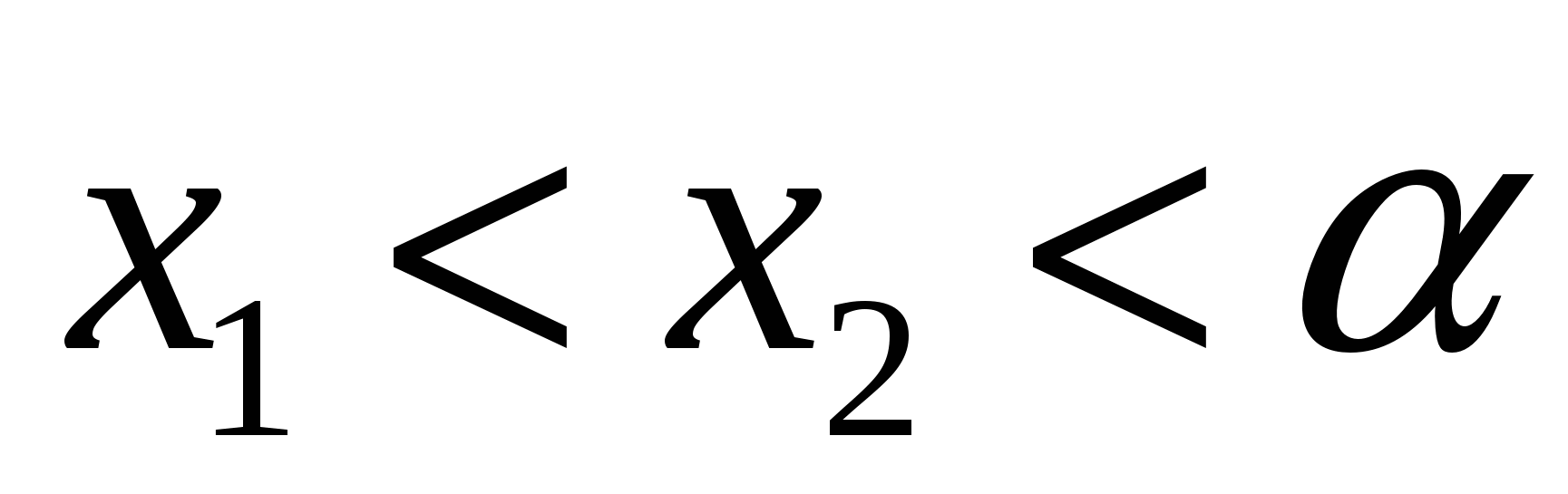
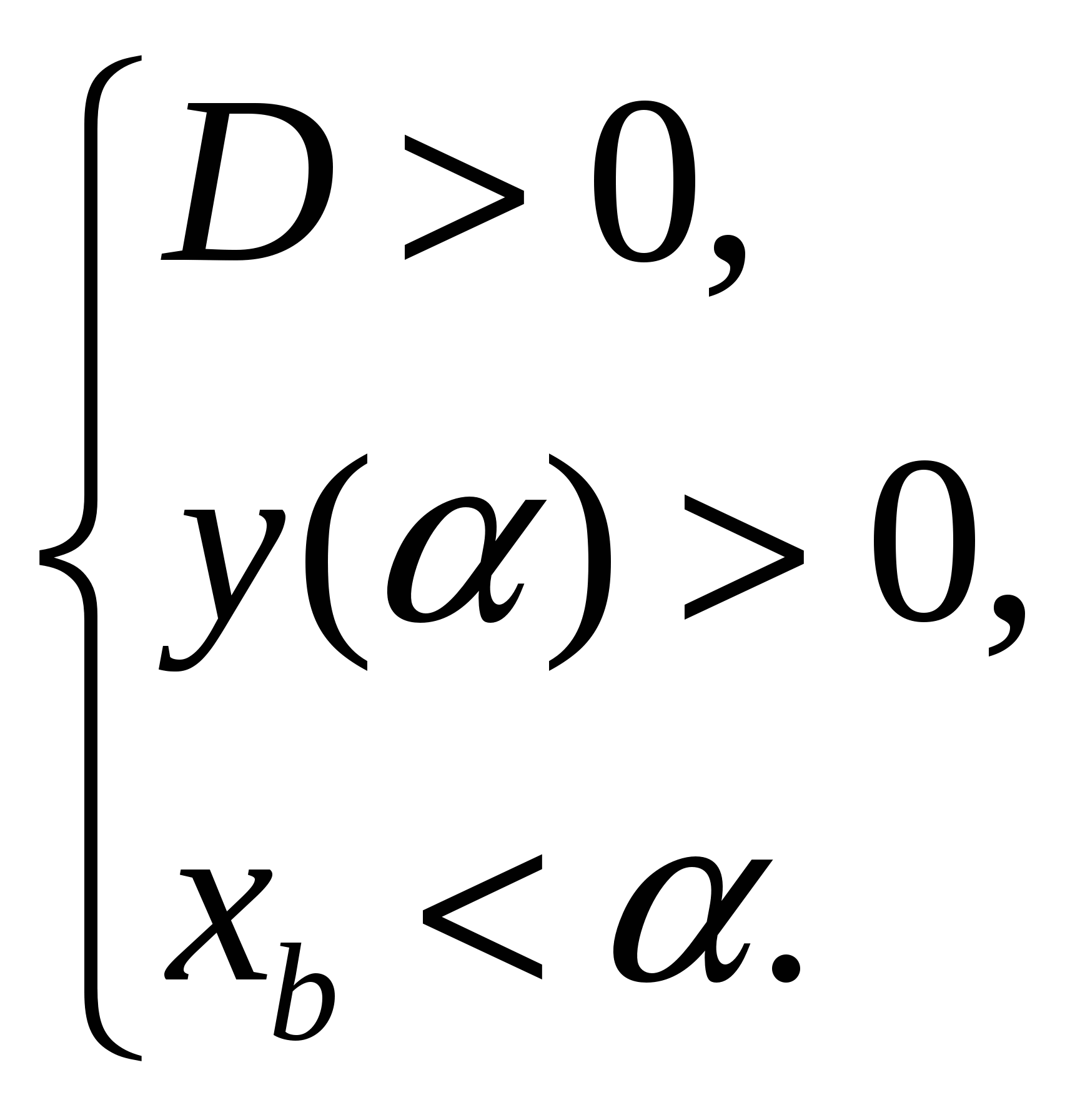
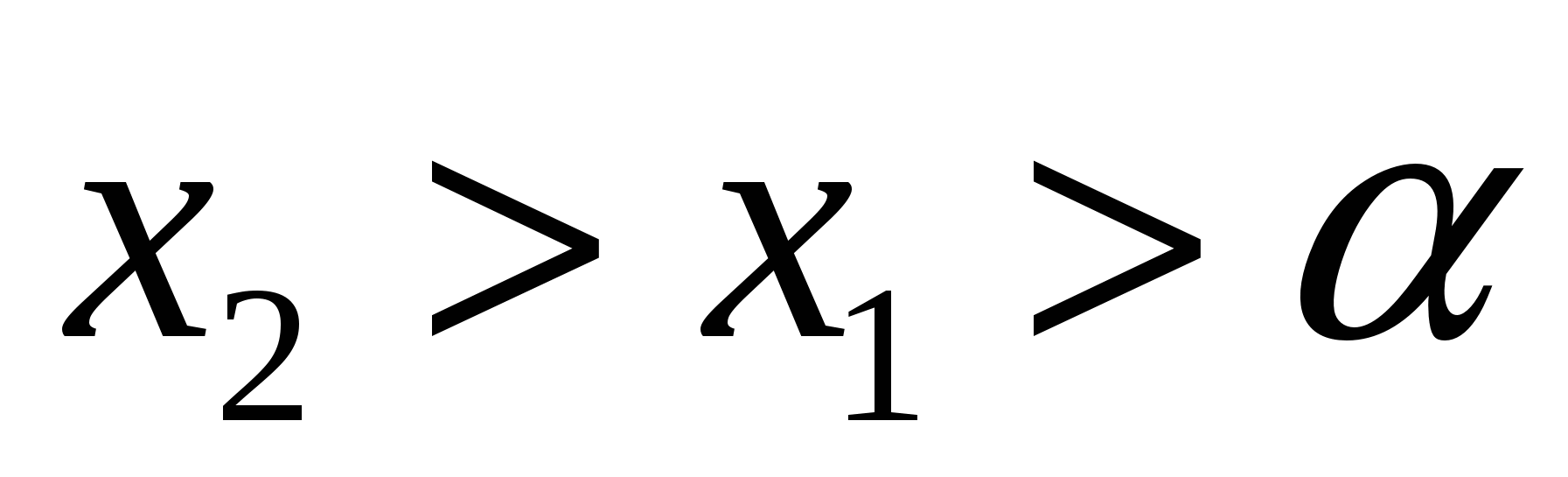
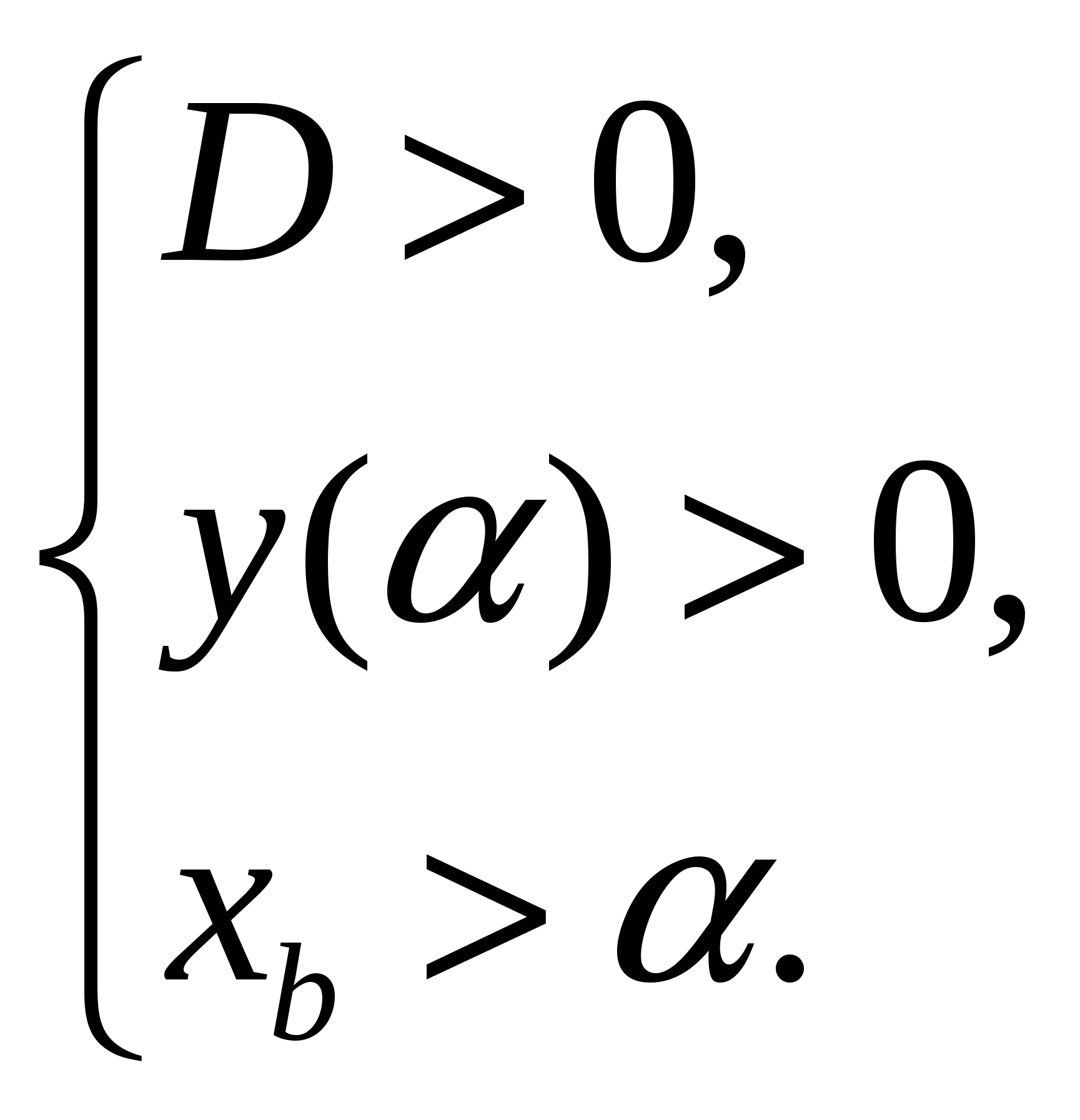
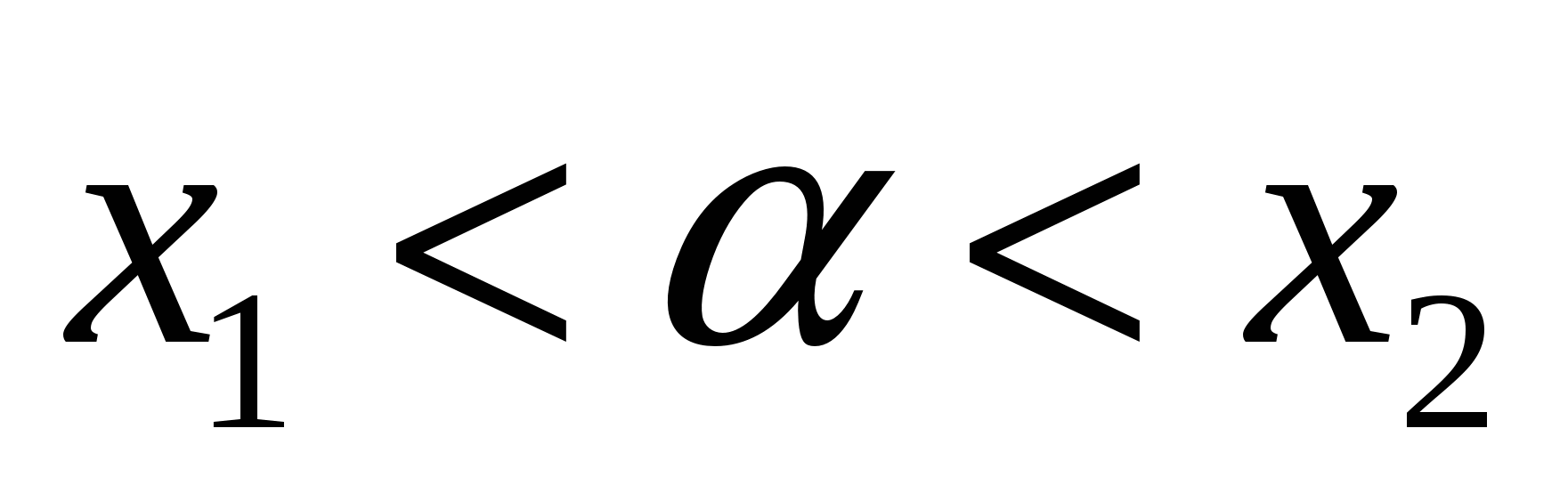
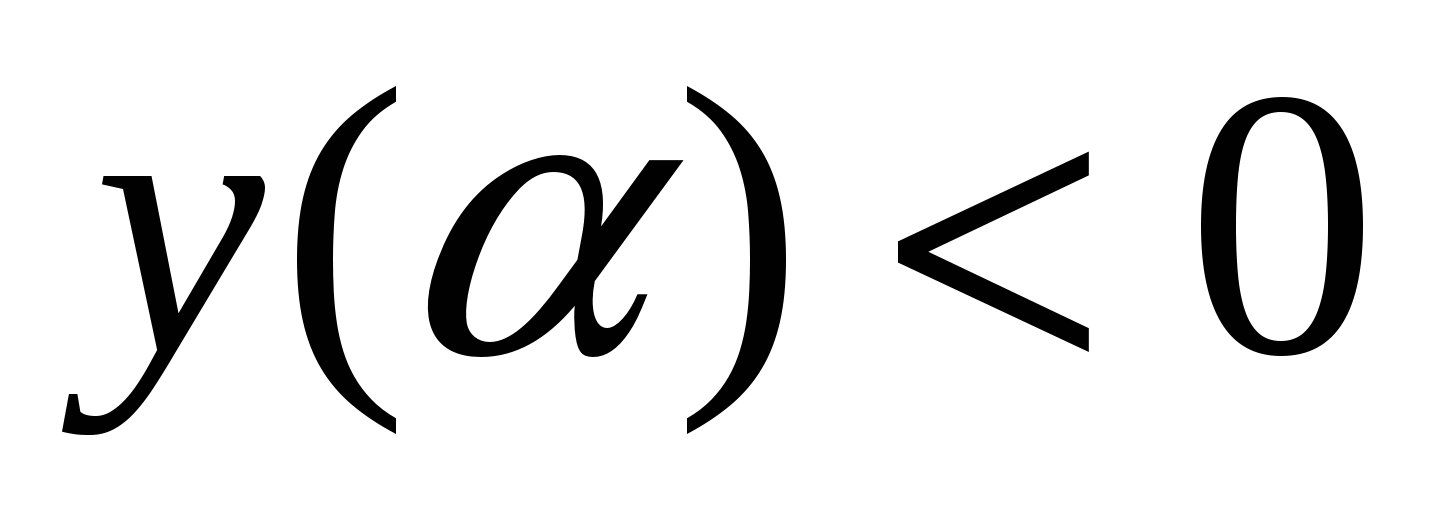
Решение задач.
5а.
Задача 1. Найдите значение параметра  , при которых уравнение
, при которых уравнение 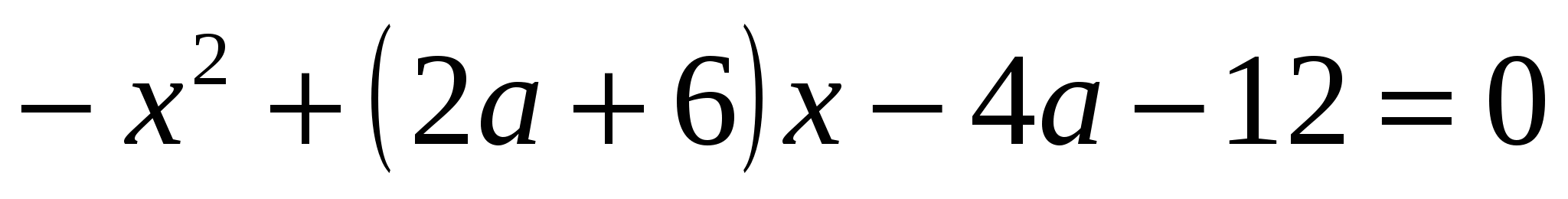 имеет по крайней мере один корень и каждый корень уравнения меньше 1.
имеет по крайней мере один корень и каждый корень уравнения меньше 1.
Решение. Преобразуем исходное уравнение
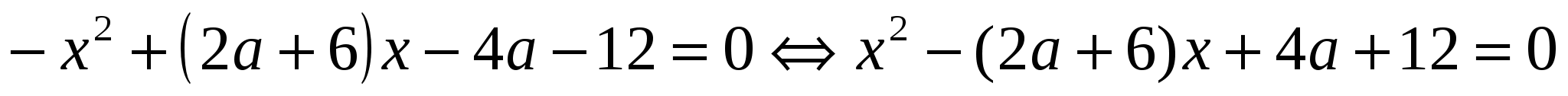
и найдем его дискриминант
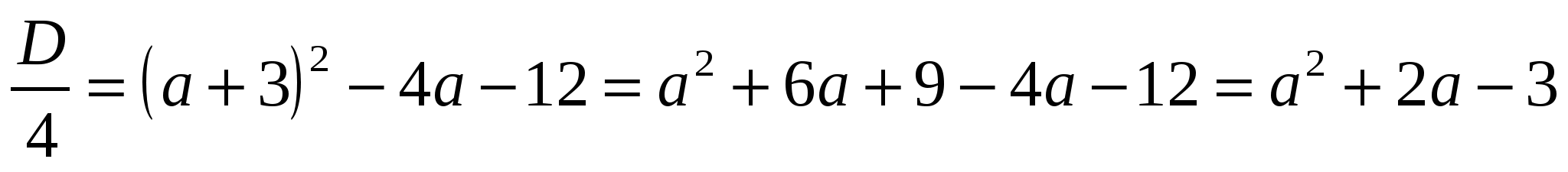 .
.
Рассмотрим функцию
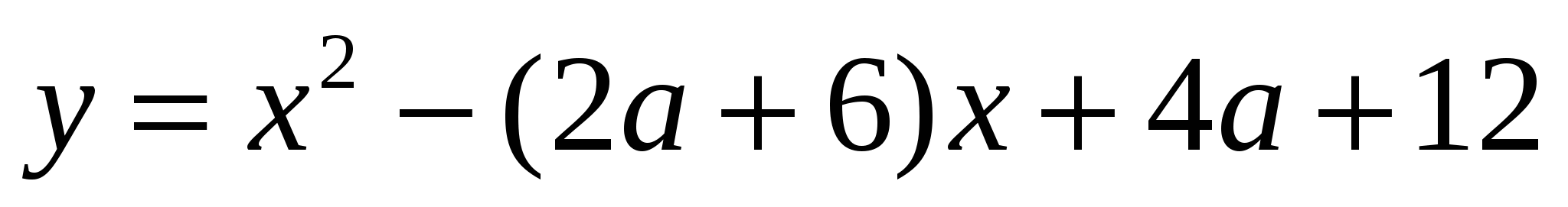 .
.
Для того, чтобы заданное уравнение имело хотя бы один корень и оба корня были меньше 1, необходимо и достаточно выполнения системы уравнений:
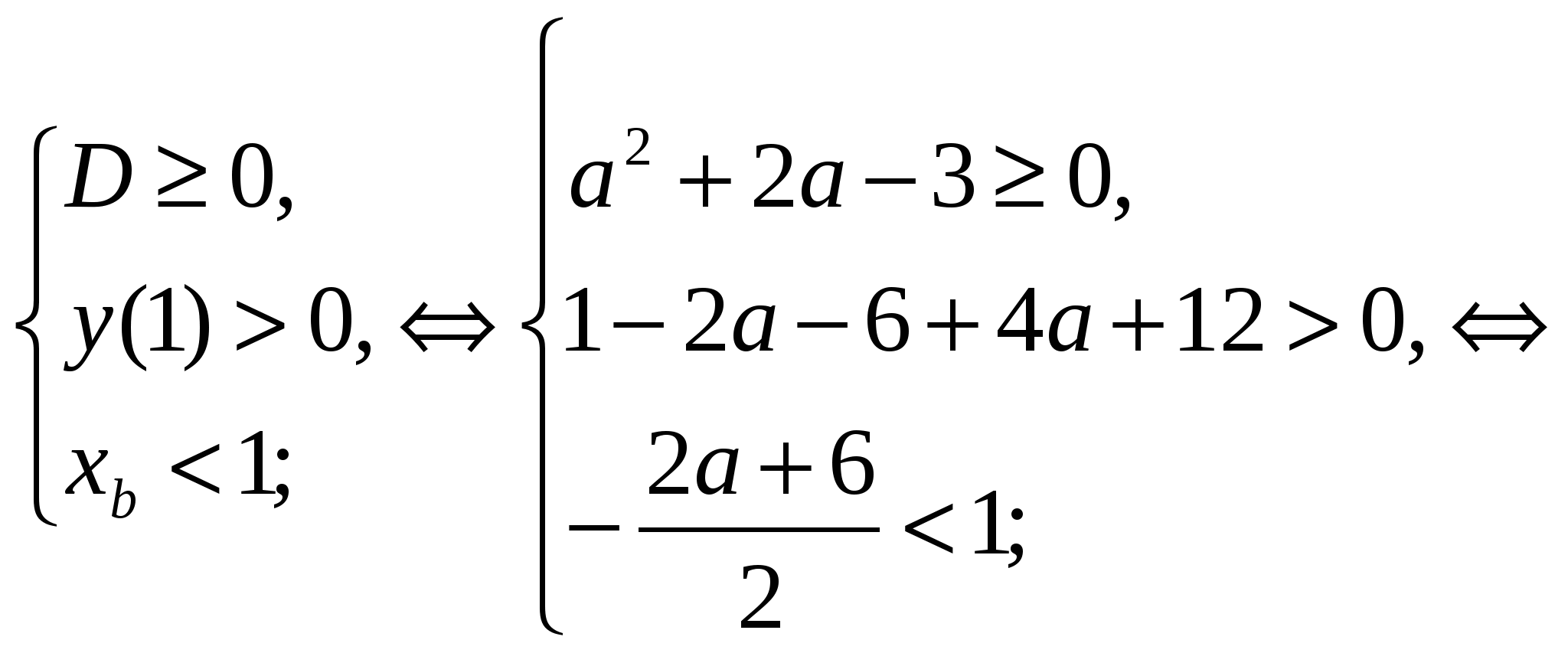
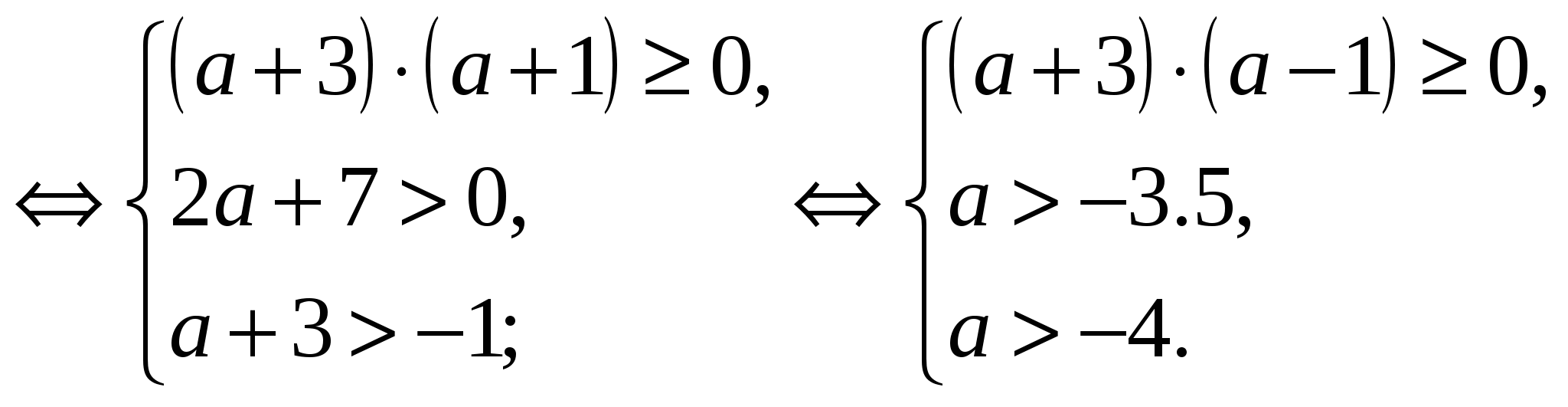

Рис. 11
Итак, решение системы 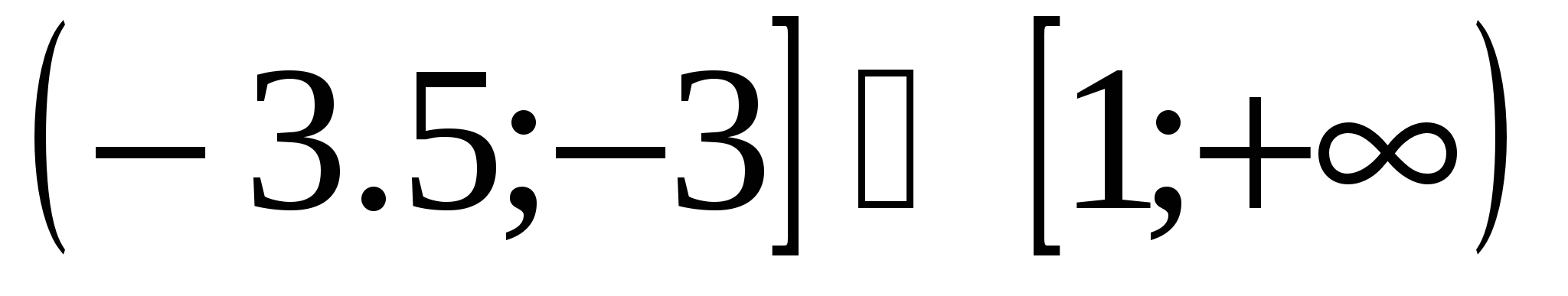 (Рис. 11).
(Рис. 11).
Ответ: 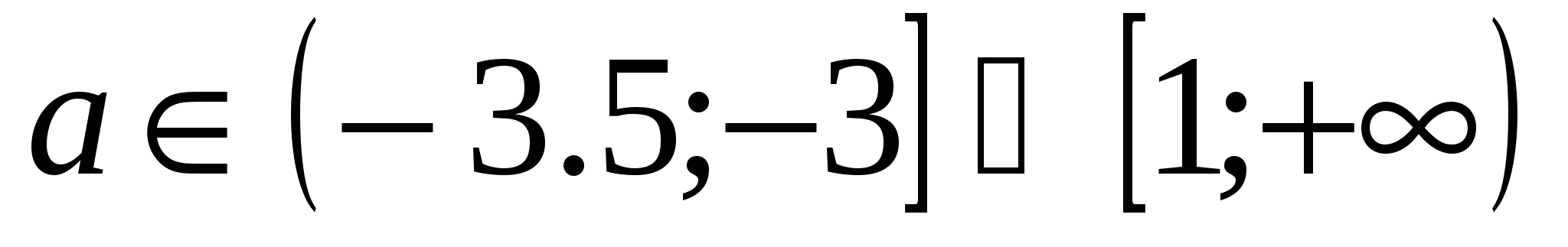 .
.
Задание 2. Найдите все значения параметра  при которых корни квадратного трехчлена
при которых корни квадратного трехчлена 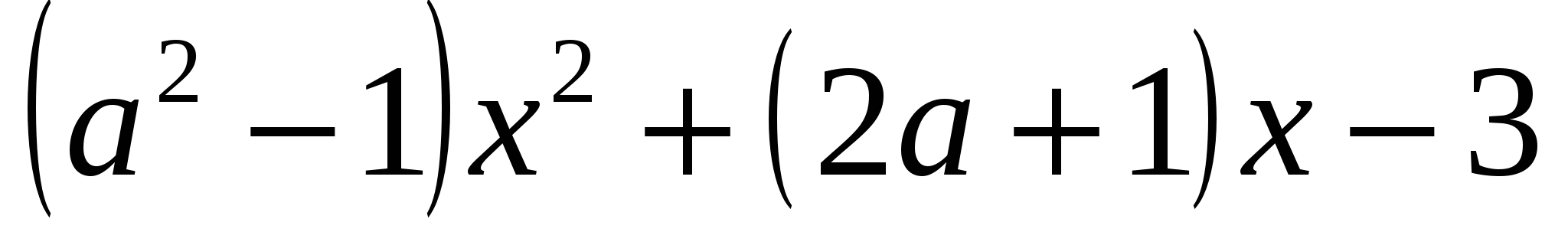 лежат по разные стороны от точки
лежат по разные стороны от точки 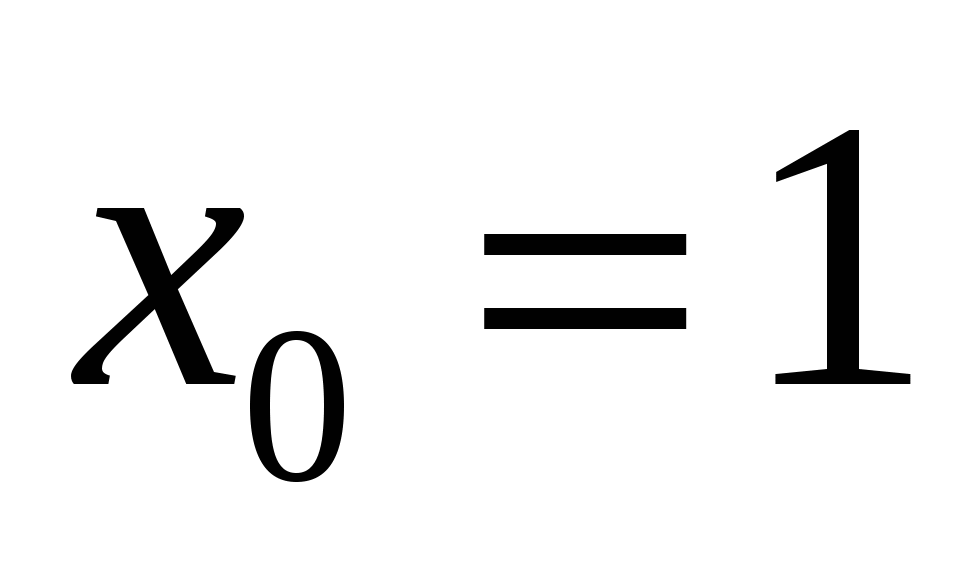 ([1], 2.534(а)).
([1], 2.534(а)).
Решение. Рассмотрим функцию:
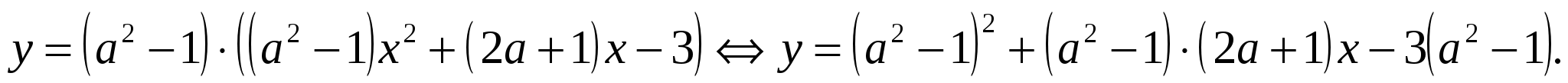 .
.
При 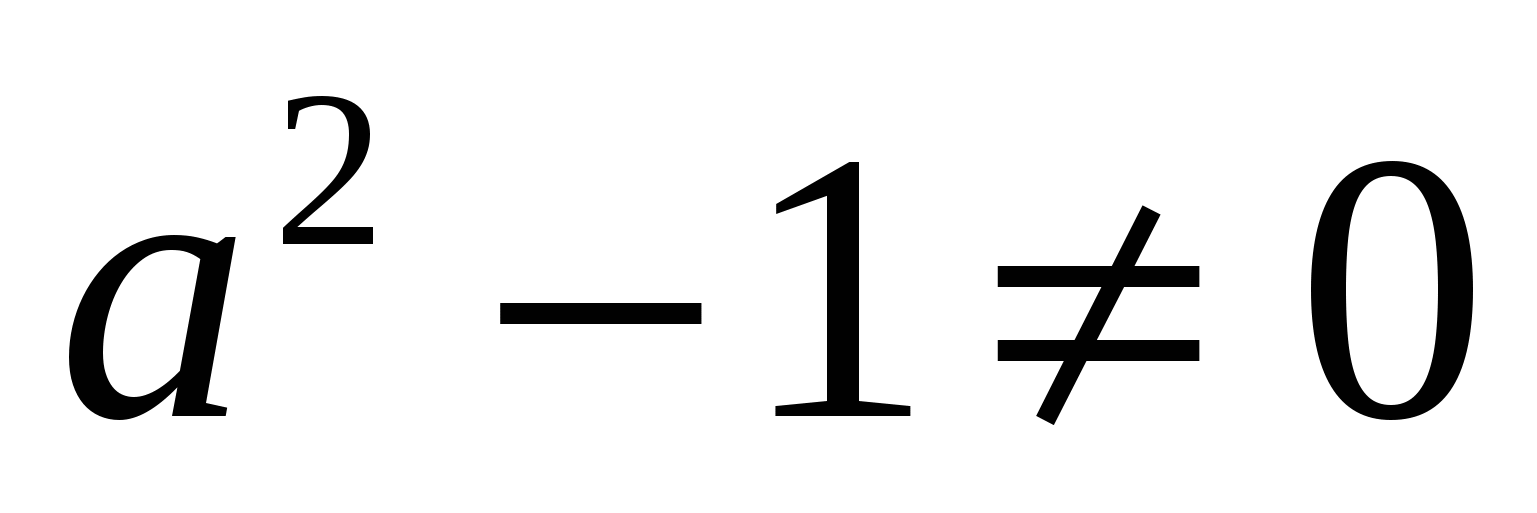 эта функция является квадратичной. Её график – парабола, ветви которой направлены вверх.
эта функция является квадратичной. Её график – парабола, ветви которой направлены вверх.
Корни заданного уравнения расположены по разные стороны от точки 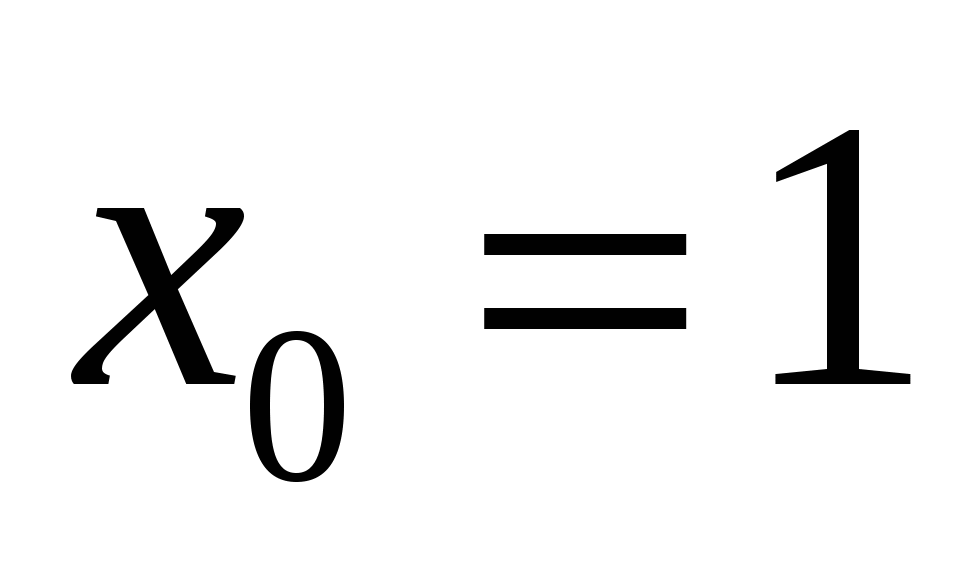 тогда и только тогда, когда
тогда и только тогда, когда
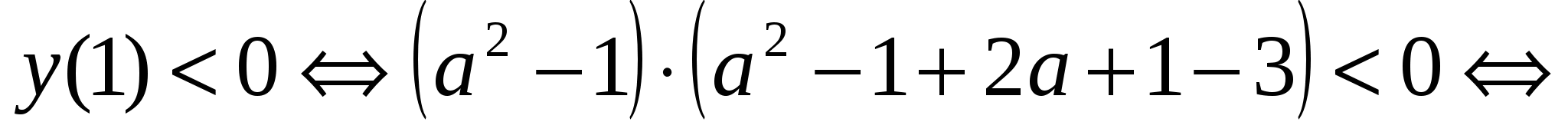
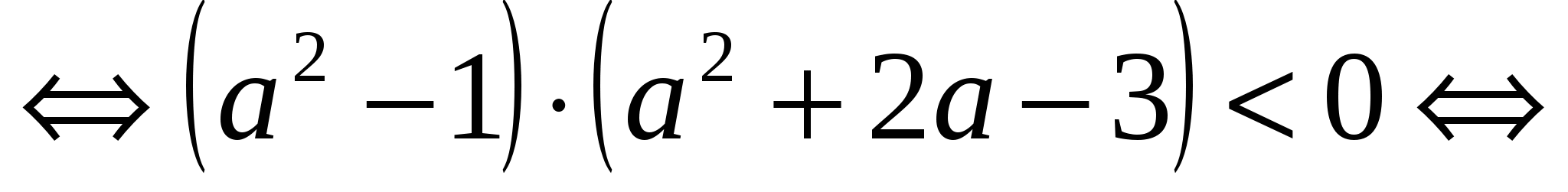
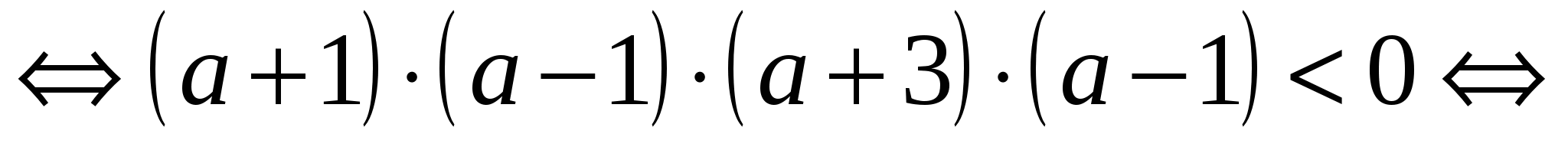
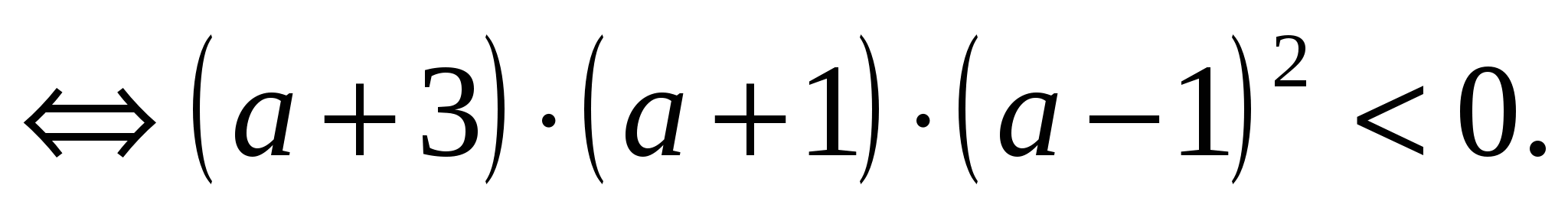
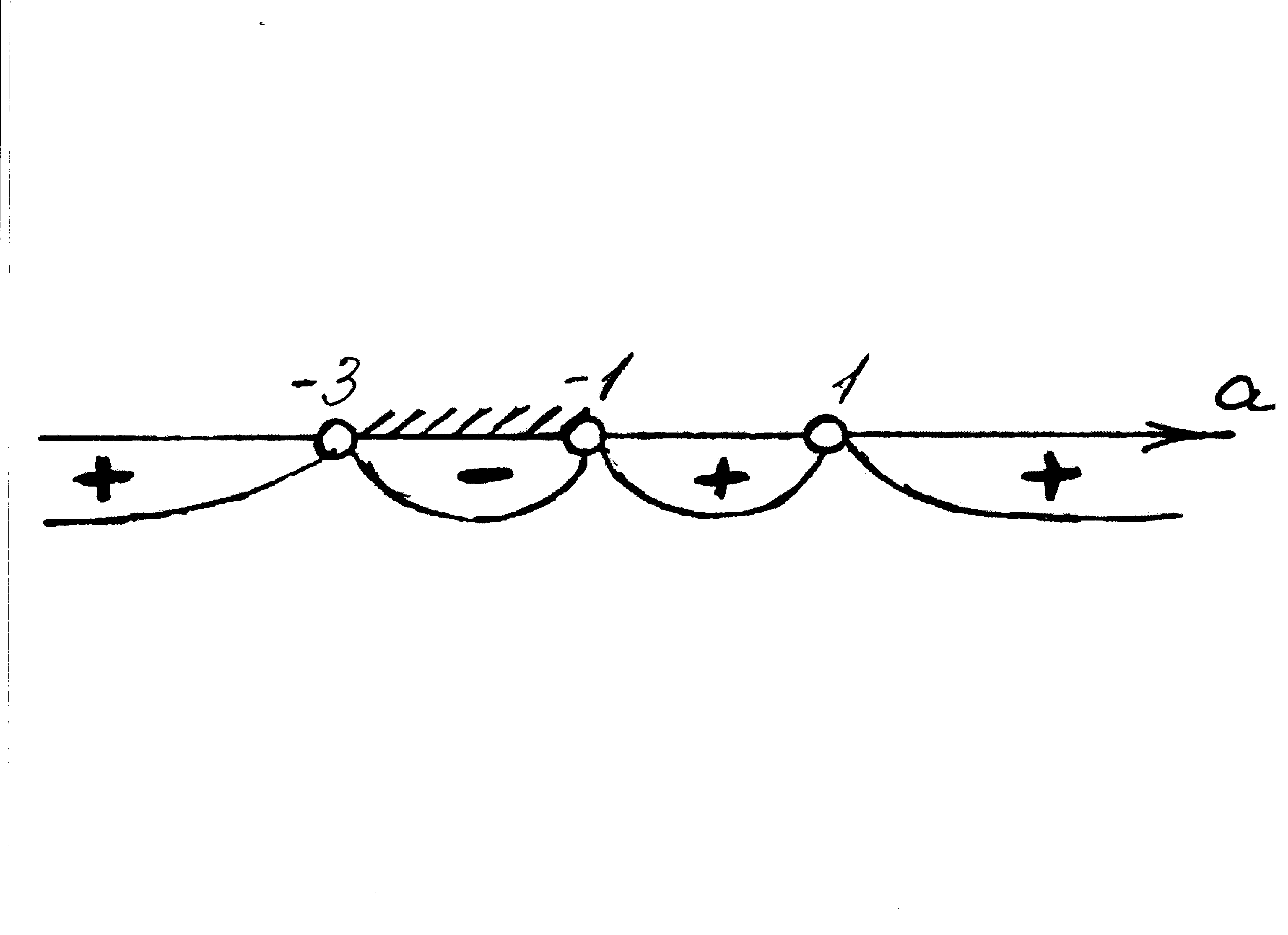
Рис. 12
Используем для решения последнего неравенства метод интервалов (рис. 12). Итак, решение неравенства:  . При
. При 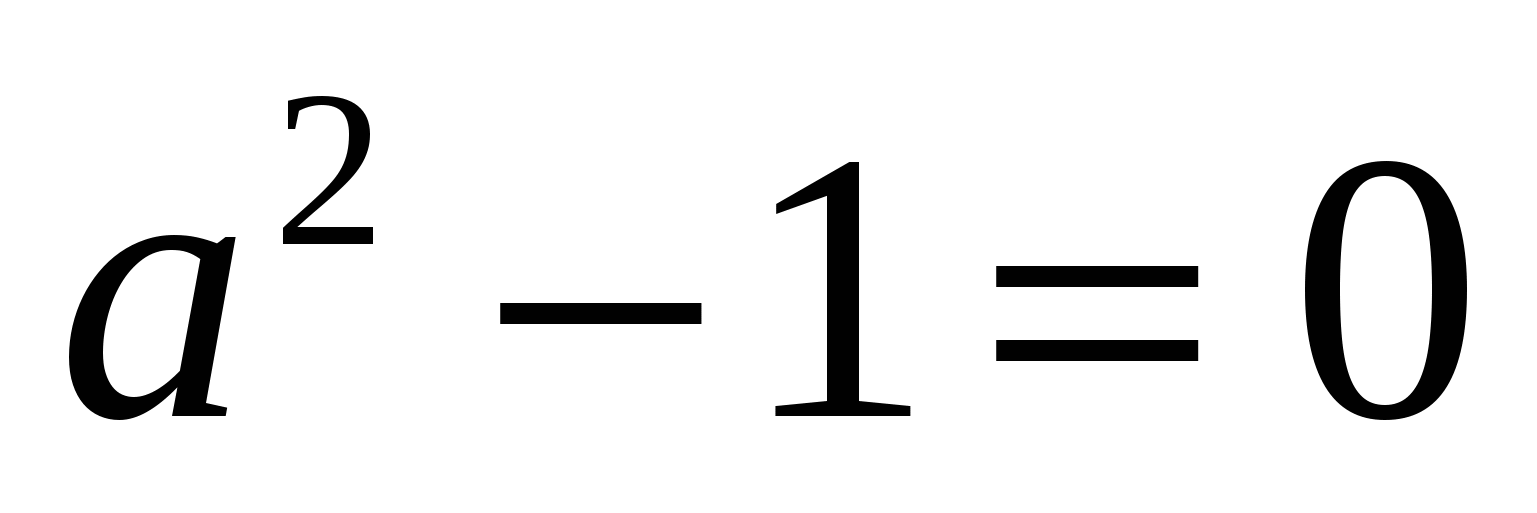 заданное уравнение является линейным и имеет не более одного корня.
заданное уравнение является линейным и имеет не более одного корня.
Ответ:  .
.
5б.
Задание 3. При каких значениях параметра  квадратный трехчлен
квадратный трехчлен 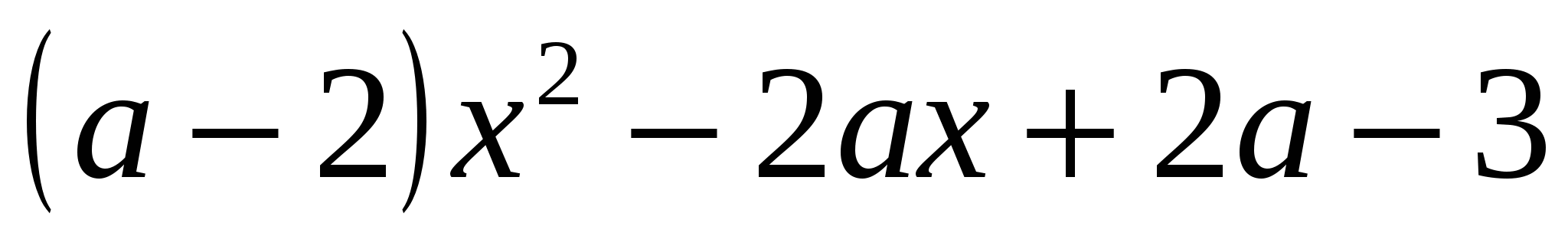 имеет два различных корня одного знака. ([1], 2.535(а)).
имеет два различных корня одного знака. ([1], 2.535(а)).
Решение. Дискриминант соответствующего квадратного уравнения:
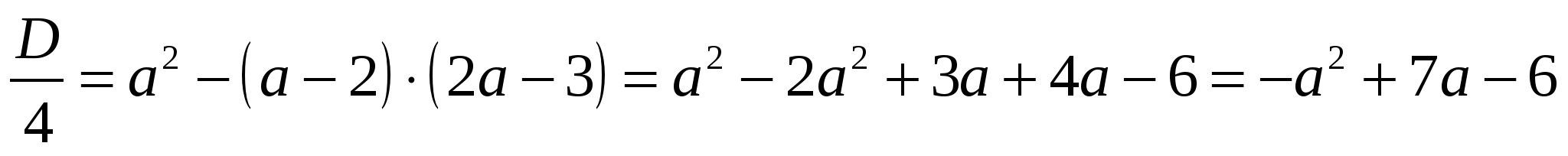 .
.
Рассмотрим функцию
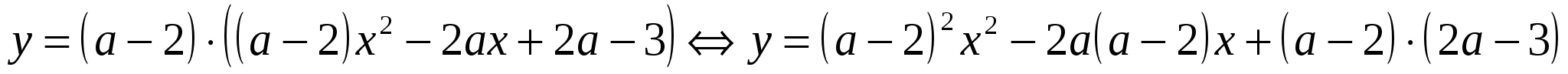
При 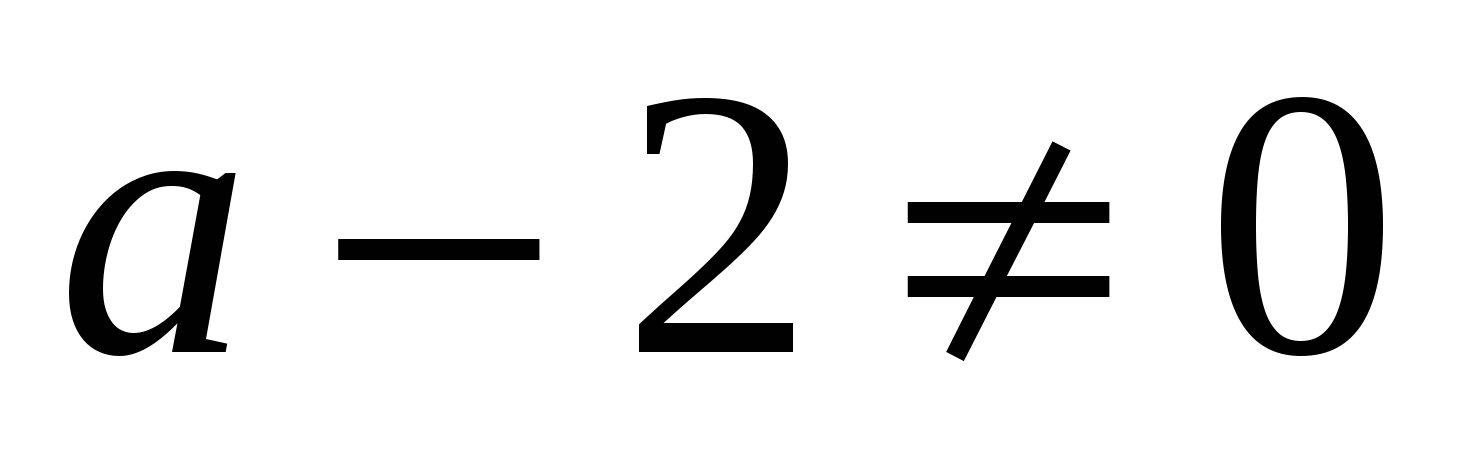 - это квадратичная функция, график которой – парабола с ветвями, направленными вверх.
- это квадратичная функция, график которой – парабола с ветвями, направленными вверх.
Заданный квадратный трехчлен имеет два различных корня одного знака, то есть
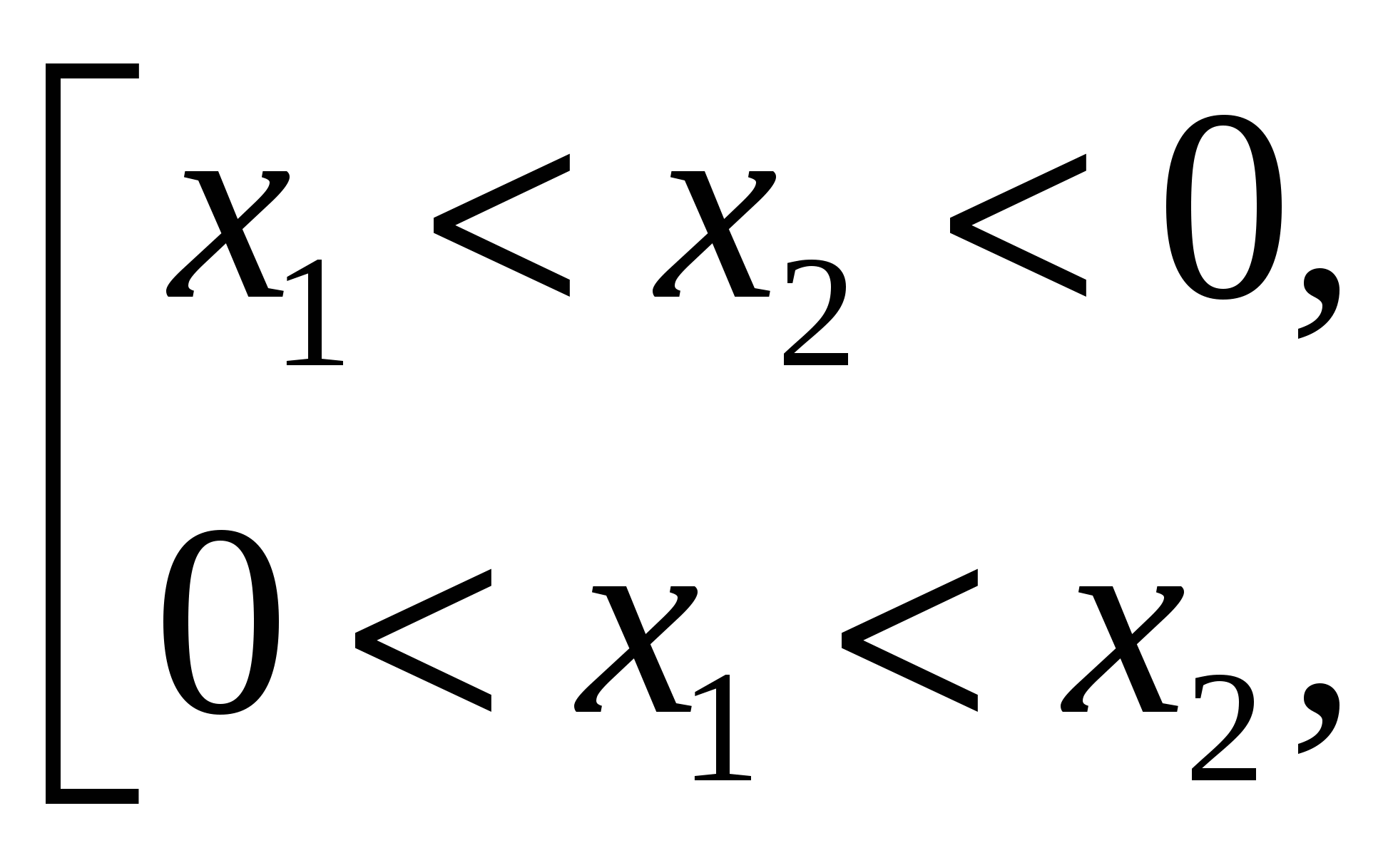
тогда и только тогда, когда выполняется система условий:
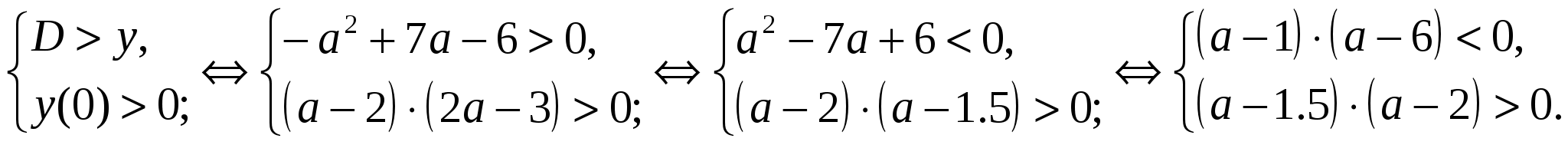
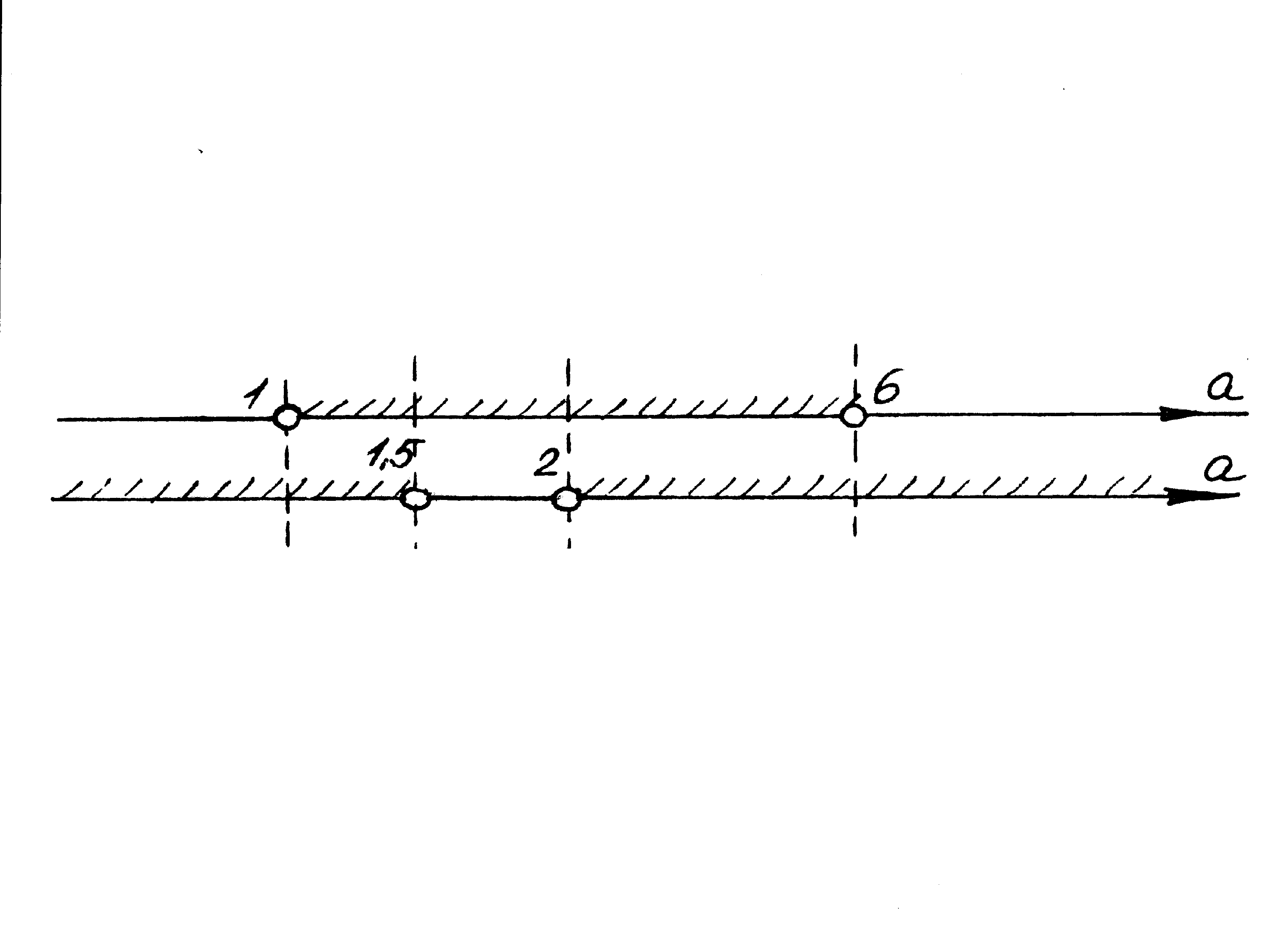
Рис. 13
При 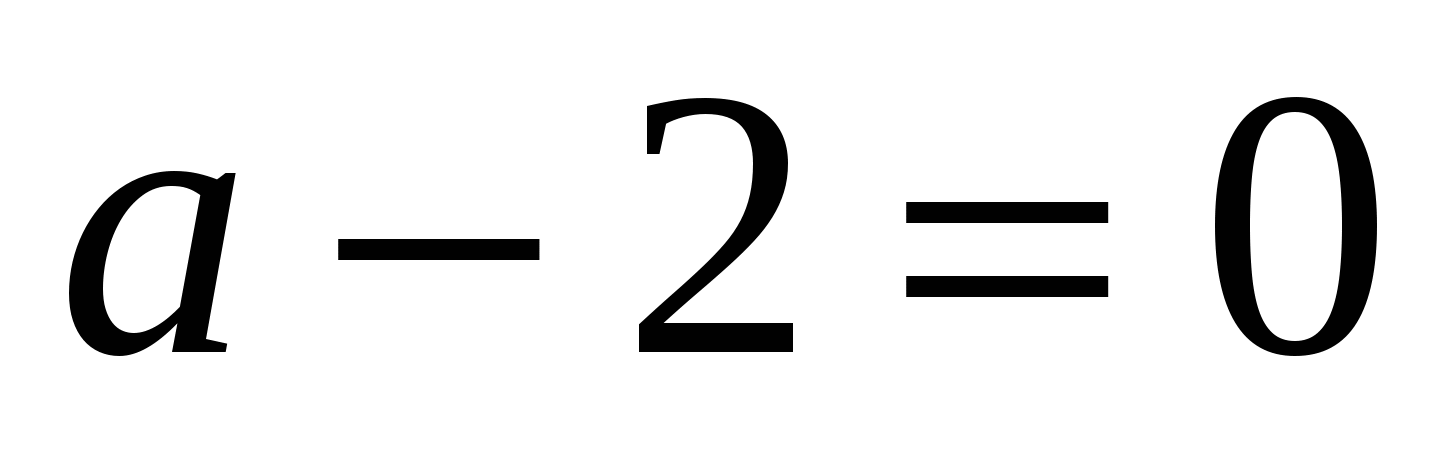 заданный трехчлен превращается в двучлен
заданный трехчлен превращается в двучлен 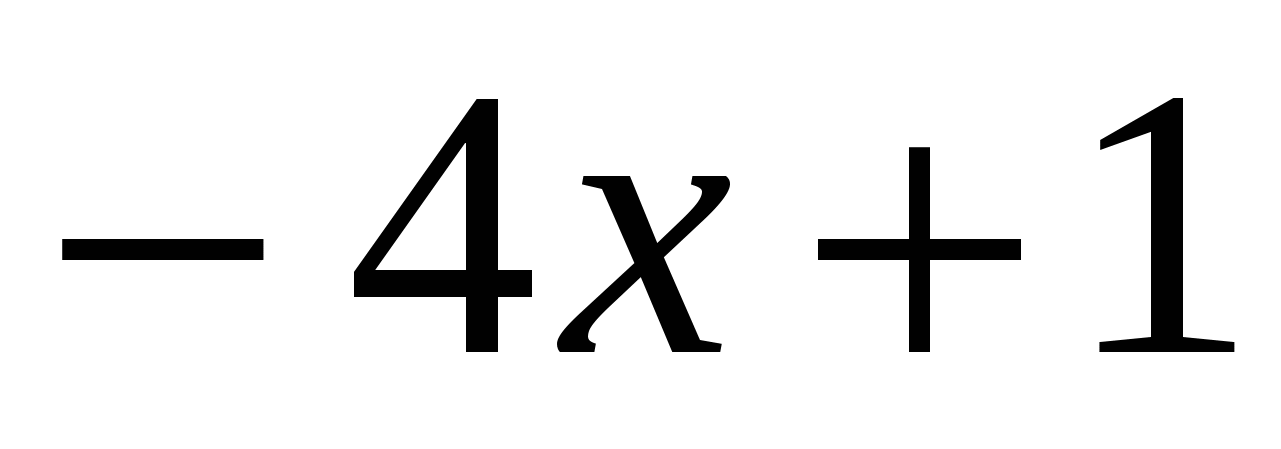 и имеет только один корень.
и имеет только один корень.
Ответ: 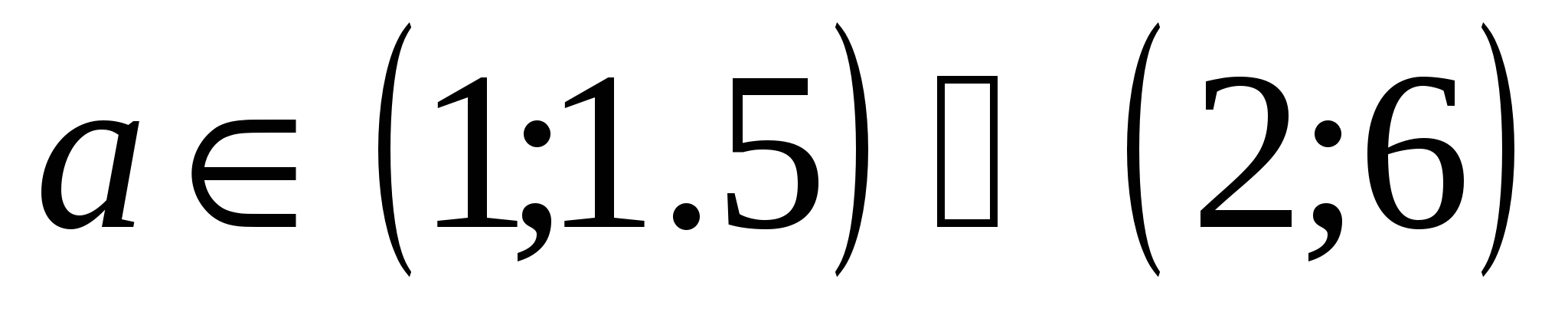 .
.
Итоги урока
Методическая разработка №2
Тема урока*. Решение неравенств с параметрами.
Цели урока:
Актуализация и систематизация знаний по темам «Исследования квадратного трёхчлена» и «Неравенства с параметром»
Овладение графическим методом решения задач по исследованию неравенств с параметром.
Развитие навыков решения задач с параметром.
Программно-методическое обеспечение: Математика. ЕГЭ-2008. Вступительные испытания / Под редакцией Лысенко Ф.Ф.– Ростов-на-Дону: Легион, 2007 - [1]; Математика. ЕГЭ-2008. Тесты для подготовки / Под редакцией Лысенко Ф.Ф.– Ростов-на-Дону: Легион, 2008 - [2];
План урока:
Постановка цели урока
Актуализация и систематизация знаний по теме «Неравенства с параметром»:
создание математической модели для решения задачи по исследованию неравенства с параметром;
решение неравенства с параметром аналитическим методом.
Актуализация знаний по теме «Исследование квадратного трёхчлена» (на основе самостоятельного домашнего повторения по материалам 9-го класса).
Решение задач по исследованию неравенств с параметром графическим методом.
Итоги урока.
Ход урока.
1. Постановка цели урока
Необходимым условием решений неравенств с параметром является правильная, конкретная и простая переформулировка условия задачи, то есть создание математической модели. Прежде всего систематизируем знания по этому вопросу.
Отдельно стоит остановиться на выборе между аналитическим и графическим способами решений рассматриваемых задач. Не следует думать, что графический метод всегда предпочтительнее: в ряде случаев лучше остановить свой выбор на аналитическом способе. В качестве примера можно рассмотрим задание С3 − вариант 7 [1].
Но, тем не менее, при решении многих задач графический метод позволяет получить более короткое и «красивое» решение, а иногда и единственно возможное решение. Для успешного освоения графического метода актуализируем умение исследовать квадратный трёхчлен. Этот материал будет востребован при решении задач по исследованию неравенств с параметрами, а именно: задание С3 – вариант5 [1], задание С3 − вариант 28 [1], задание С3 − вариант 3 [2], задание С3 − вариант 18 [1], задание С3 − вариант 23 [1].
Домашнее задание: задание С3 – вариант 6 [1], задание С3 − вариант 27 [1], задание С3 − вариант 4 [2], задание С3 − вариант 17 [1], задание С3 − вариант 24 [1].
2. Актуализация и систематизация знаний по теме «Неравенства с параметром»
а)Создание математической модели для решения задачи по исследованию неравенства с параметром.
Пусть задано одно из неравенств:
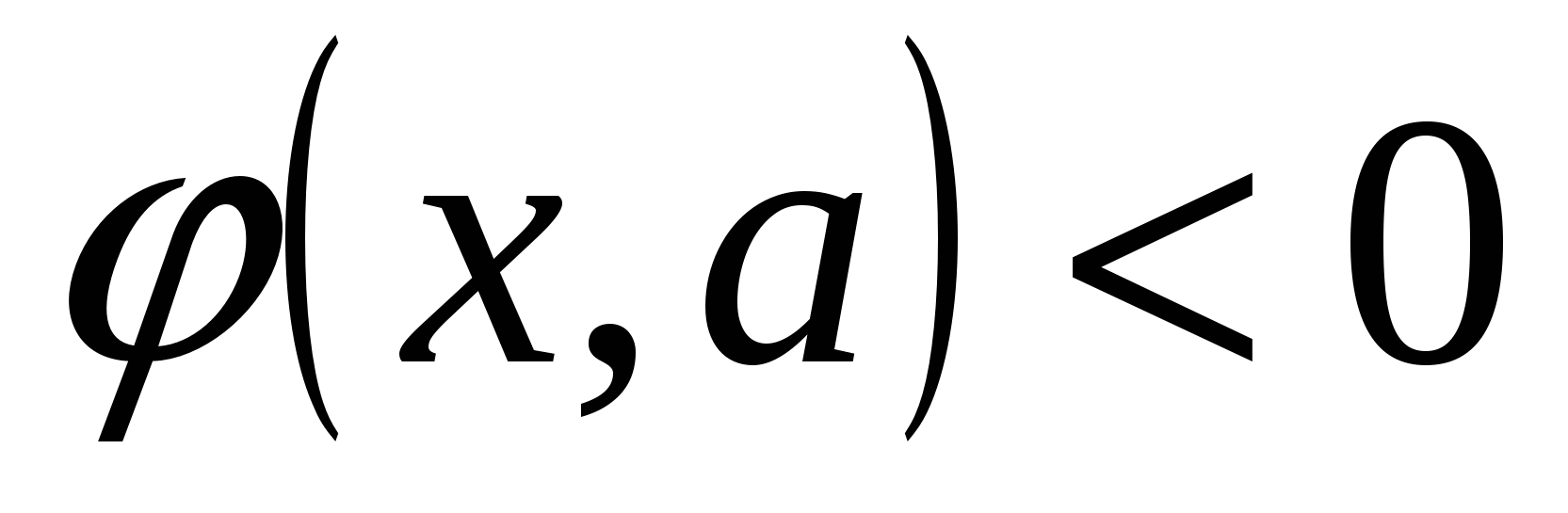 ,
, 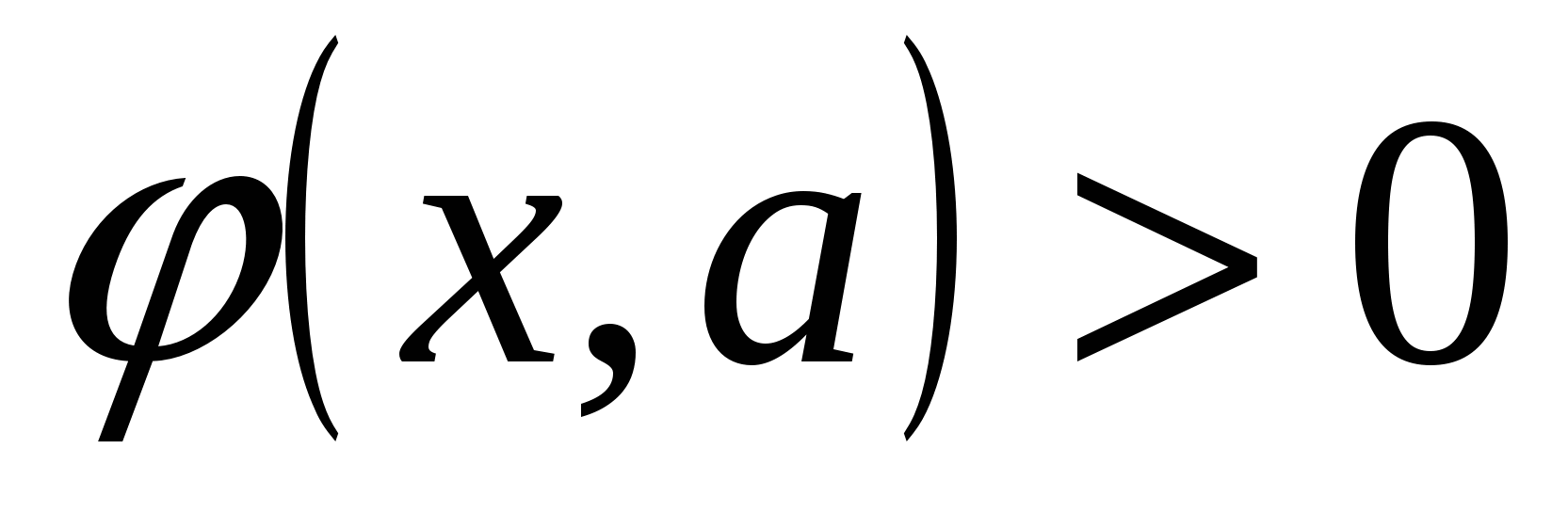 или
или 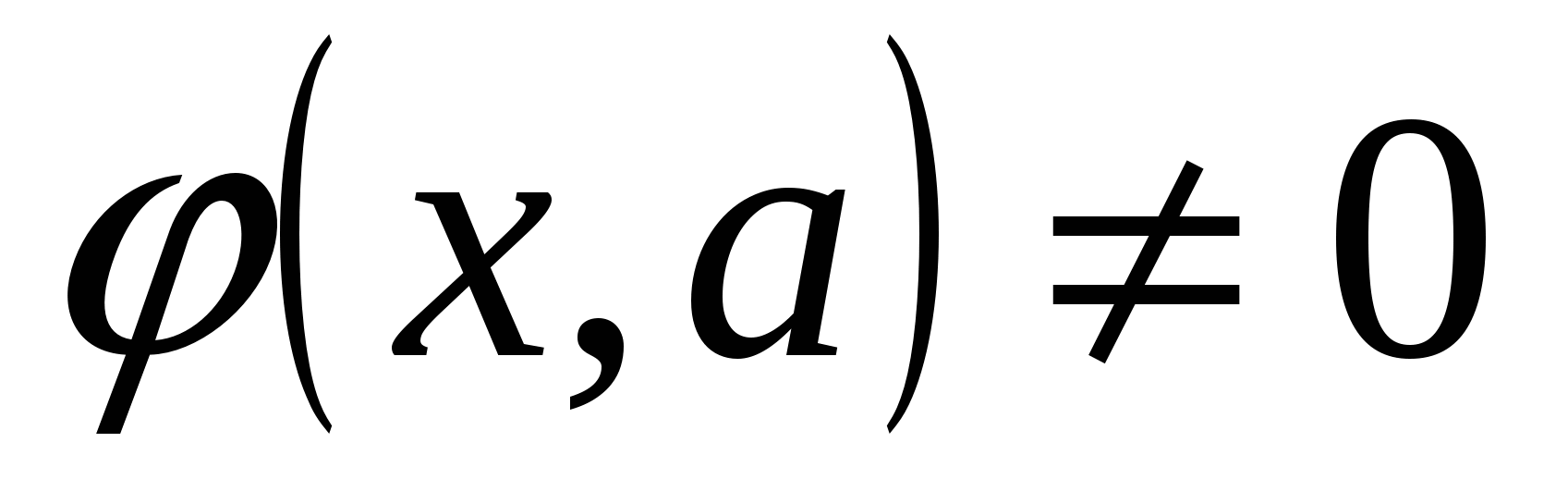 .
.
(*)
Прежде всего нужно определиться какую из неизвестных х и а удобно рассматривать как параметр, а какую – как, собственно, переменную.
Условие
Найдите все значения а, при которых для неравенства (*) выполняется некоторое условие, заданное по х.
Найдите все значения х, при которых для неравенства (*) выполняется некоторое условие, заданное по а.
Решение
Удобно рассматривать а как параметр, а х – как переменную и неравенство (*) решать относительно х.
Удобно рассматривать х как параметр, а а – как переменную и неравенство (*) решать относительно а.
Затем следует переформулировать условие задачи. Для этого удобно использовать лексику и символику теории множеств.
Условие
Переформулировка
Найти все значения  , для которых при каждом
, для которых при каждом  из промежутка
из промежутка 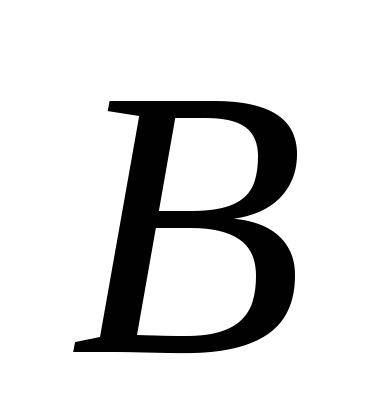 выполняется неравенство (*).
выполняется неравенство (*).
Найти все значения а, при которых 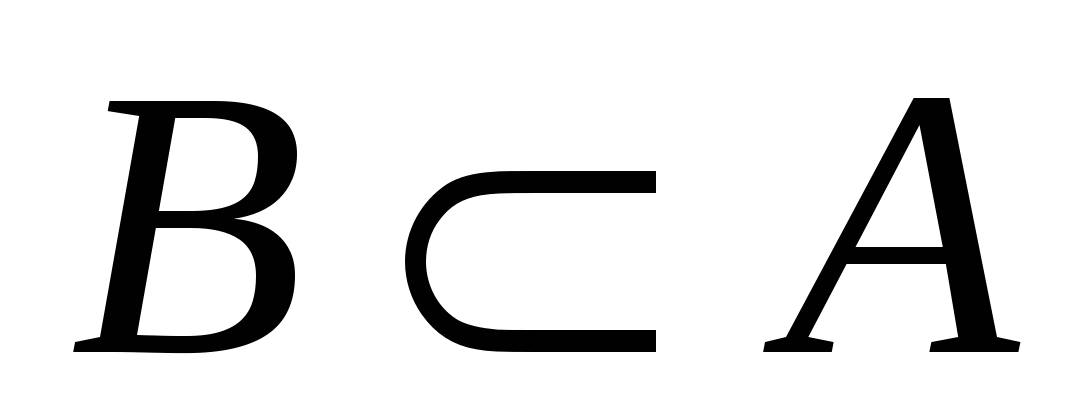 , где
, где  – множество решений неравенства (*) относительно
– множество решений неравенства (*) относительно  .
.
Найти все значения  , которые удовлетворяют неравенству (*) при любом значении параметра
, которые удовлетворяют неравенству (*) при любом значении параметра  , принадлежащего промежутку
, принадлежащего промежутку 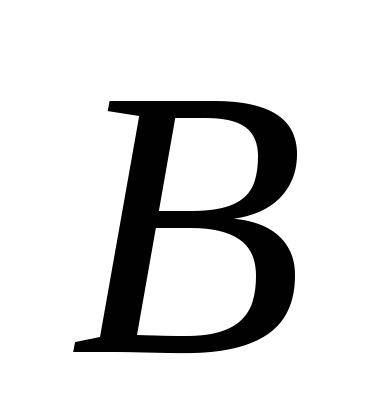 .
.
Найти все значения  , при которых
, при которых 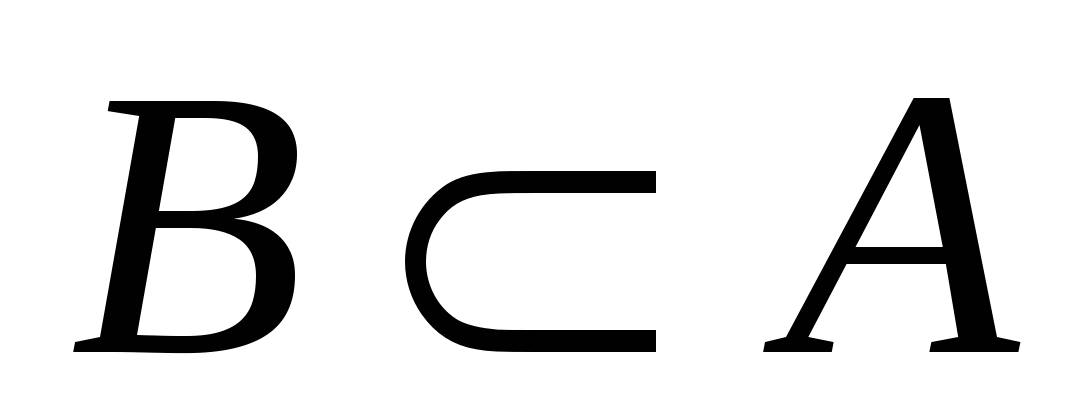 , где
, где  – множество решений неравенства (*) относительно
– множество решений неравенства (*) относительно  .
.
Найдите при каких значениях  неравенство (*) выполняется хотя бы при одном
неравенство (*) выполняется хотя бы при одном  из промежутка
из промежутка 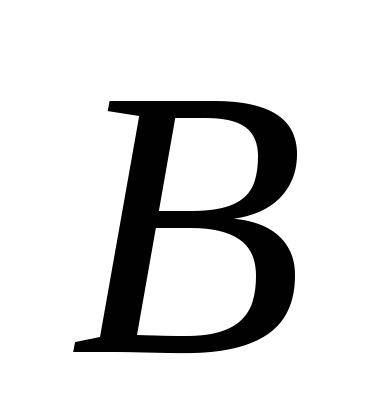 .
.
Найти все значения  , при которых
, при которых 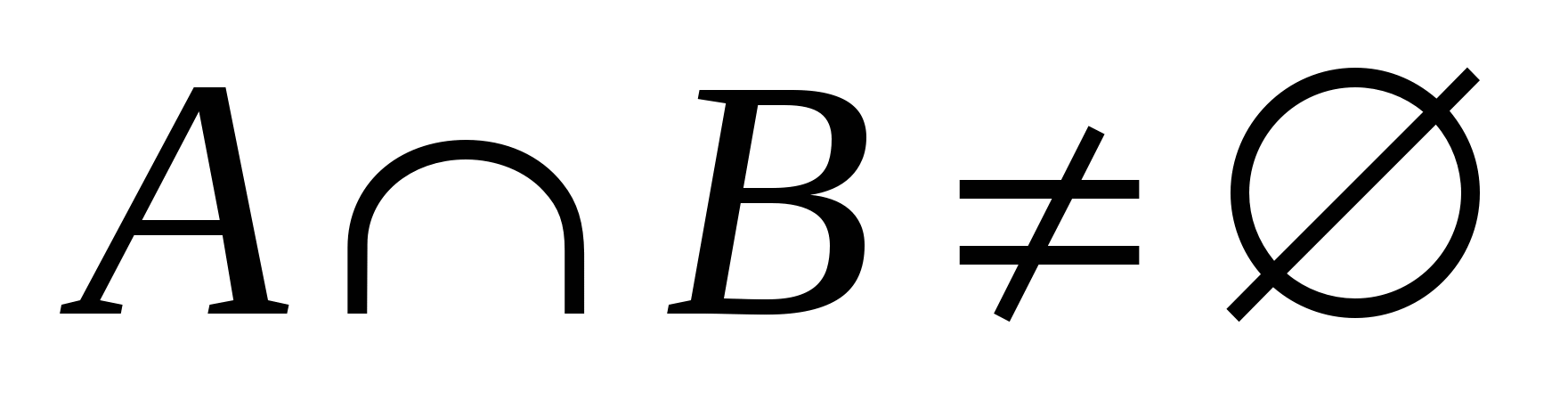 , где
, где  – множество решений неравенства (*) относительно
– множество решений неравенства (*) относительно  .
.
Найдите все значения  , при которых неравенство (*) справедливо хотя бы для одного
, при которых неравенство (*) справедливо хотя бы для одного  из промежутка
из промежутка 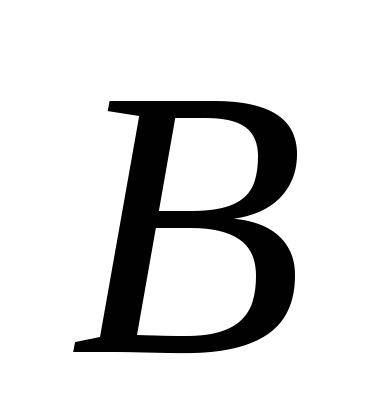 .
.
Найти все значения  , при которых
, при которых 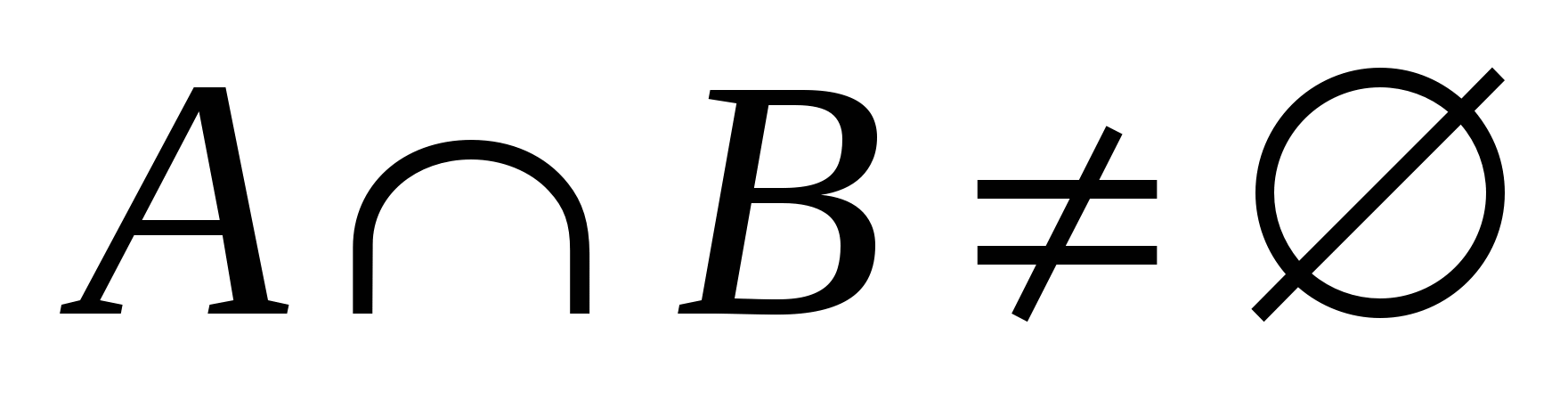 , где
, где  – множество решений неравенства (*) относительно
– множество решений неравенства (*) относительно  .
.
Найдите все значения  , при которых каждое решение неравенства (*) являлось бы также решением неравенства (*).
, при которых каждое решение неравенства (*) являлось бы также решением неравенства (*).
Найти все значения параметра  , при которых
, при которых 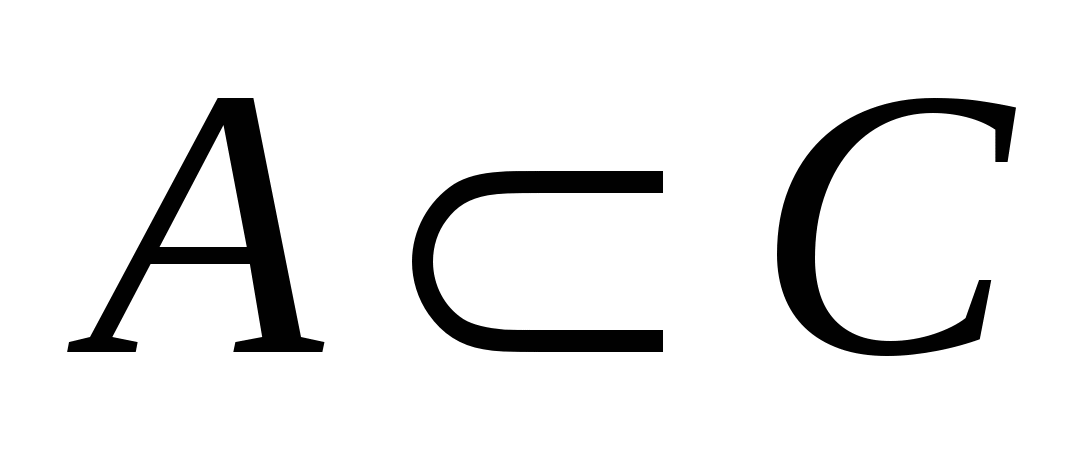 , где
, где  – множество решений неравенства (*) и где
– множество решений неравенства (*) и где 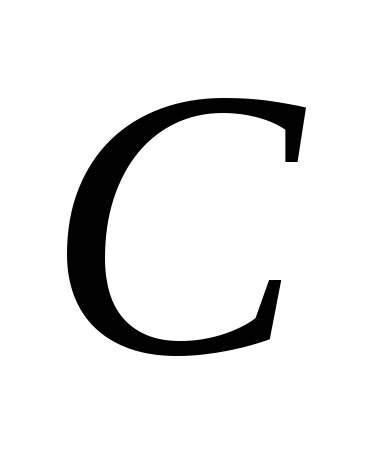 – множество решений неравенства (*) относительно
– множество решений неравенства (*) относительно  .
.
Далее учащимся предлагается самостоятельно переформулировать условия следующих задач.
Условие
Переформулировка
Найти все значения  , для которых при каждом
, для которых при каждом  из промежутка
из промежутка 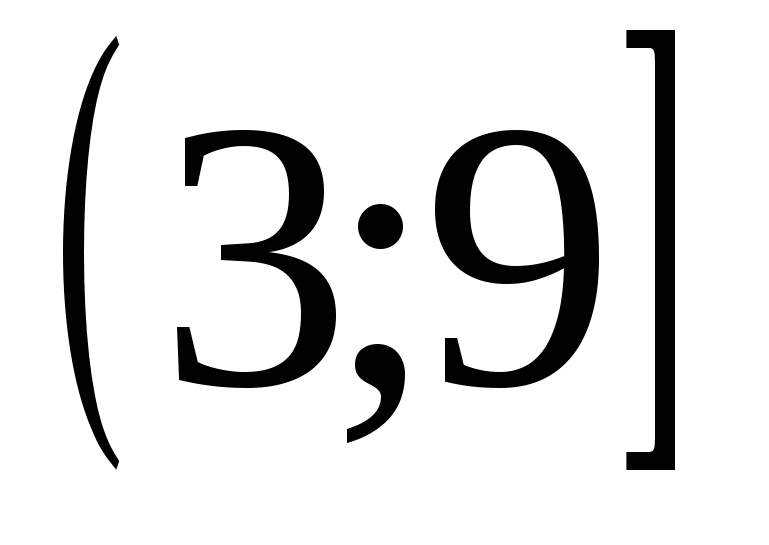 значение выражения
значение выражения 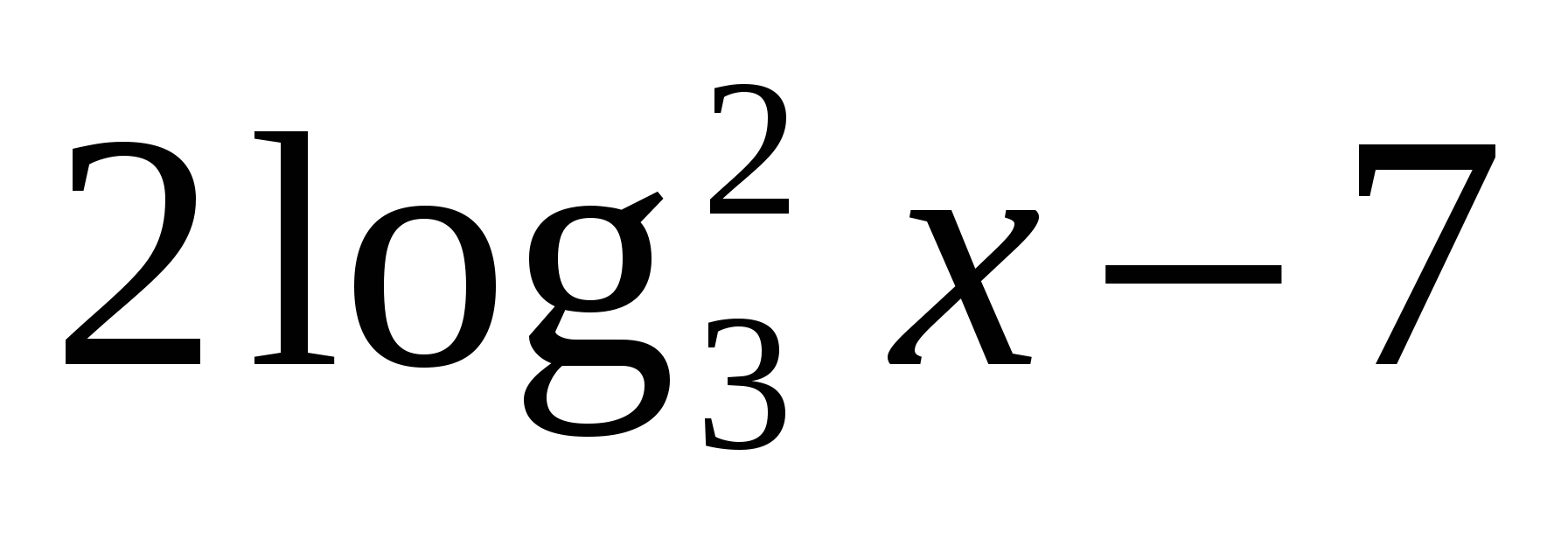 не равно значению выражения
не равно значению выражения 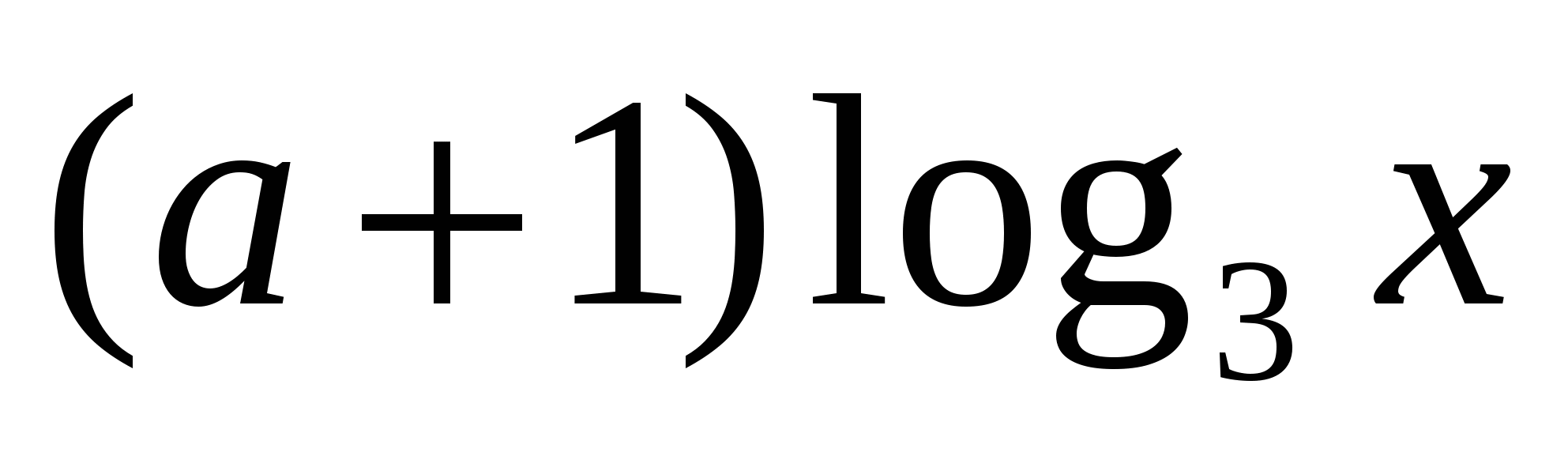 .
.
Пусть 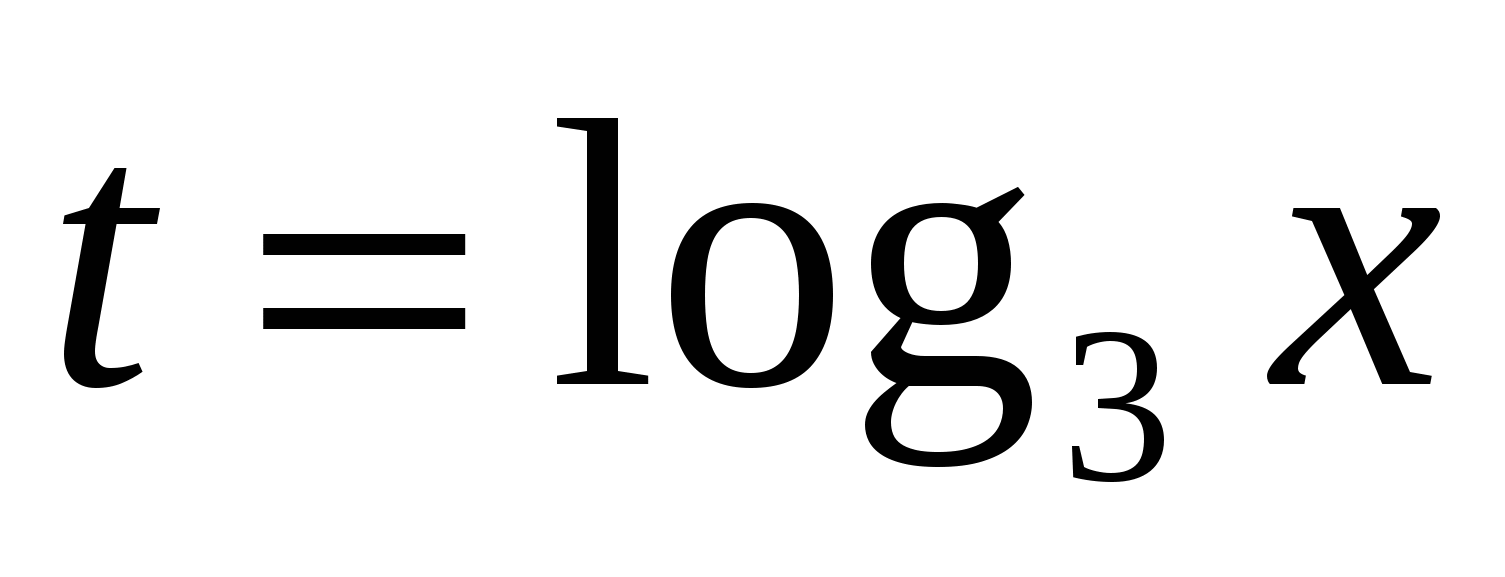 . Выясним при каком а
. Выясним при каком а 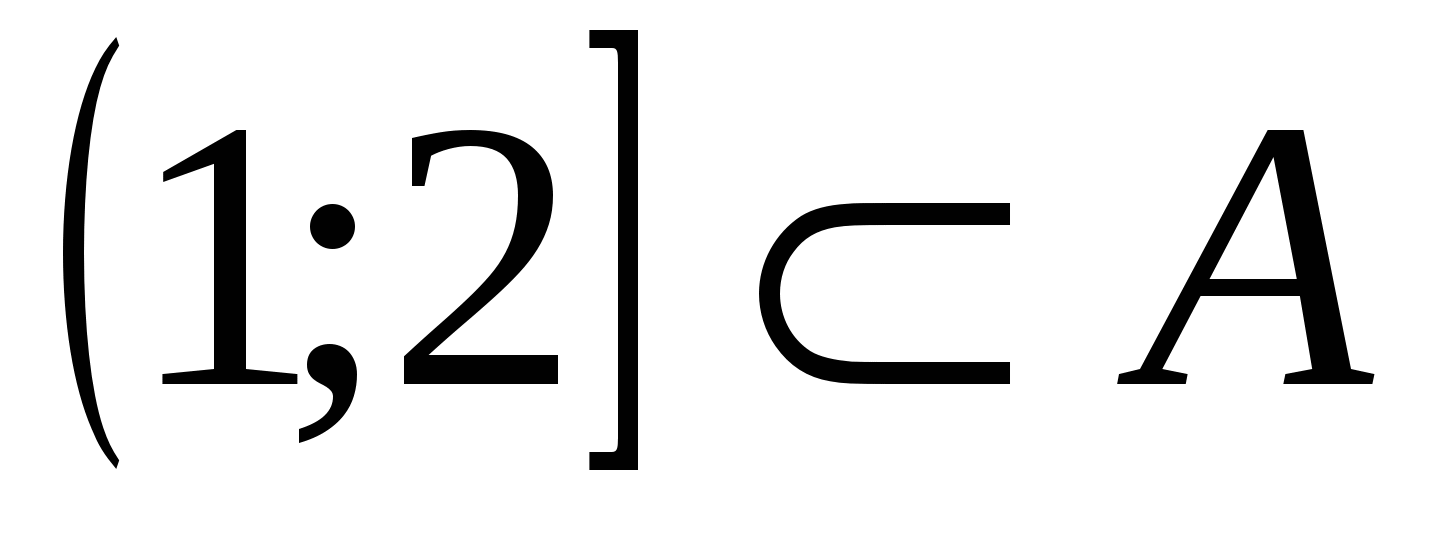 , где
, где  – множество решений неравенства
– множество решений неравенства 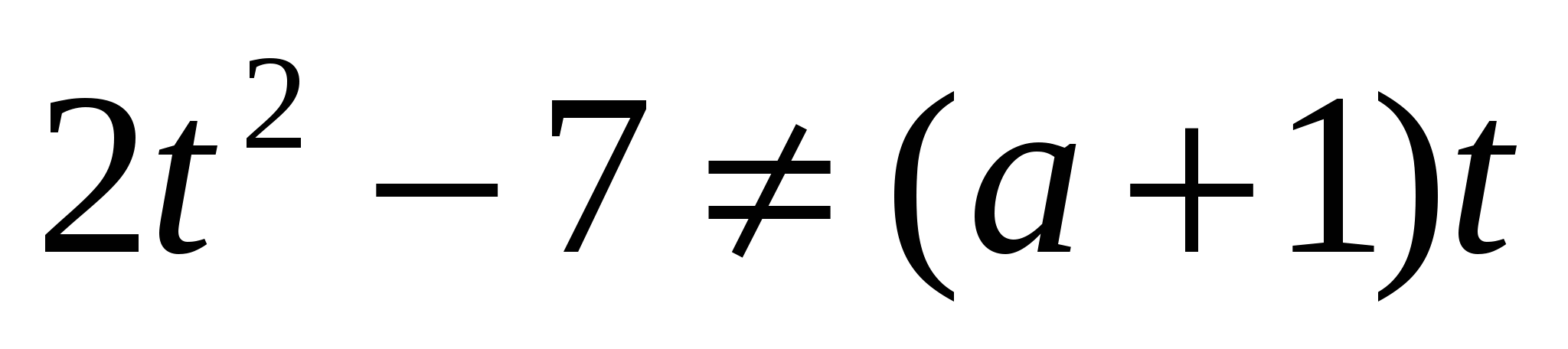 относительно t.
относительно t.
Найти все значения параметра  , при которых неравенство
, при которых неравенство 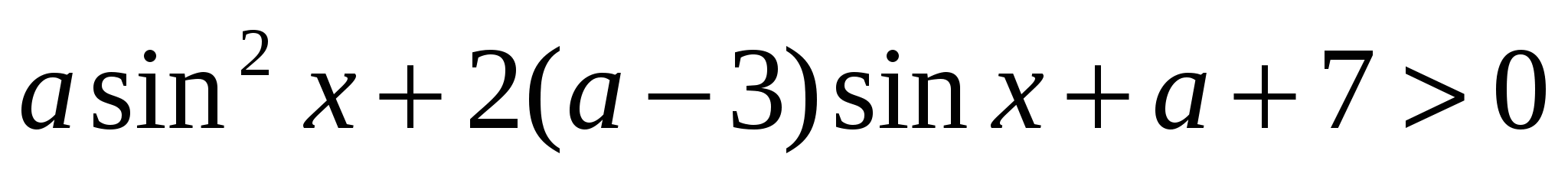 выполняется для любых значений
выполняется для любых значений  .
.
Пусть 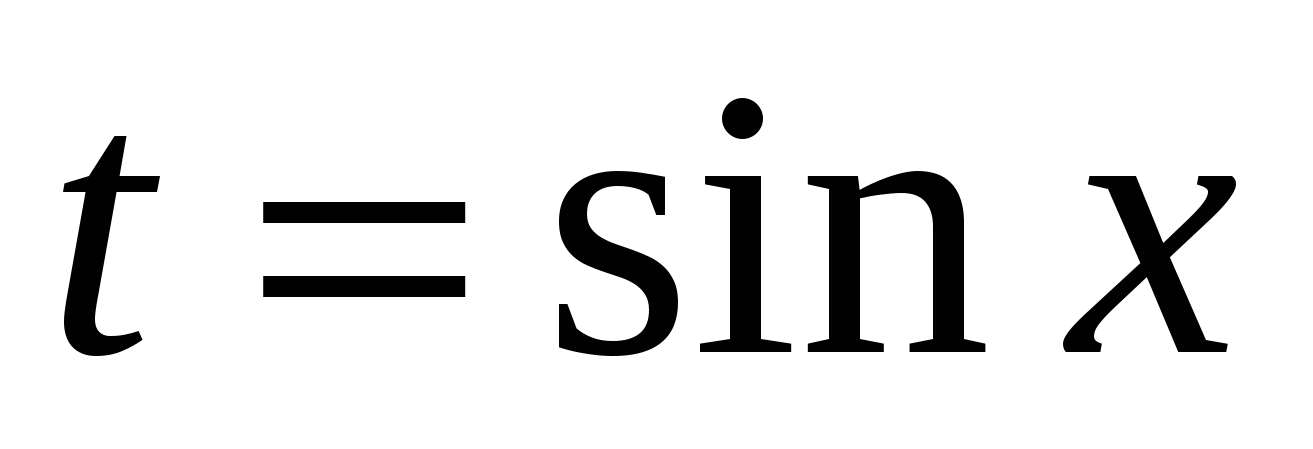 , причем
, причем 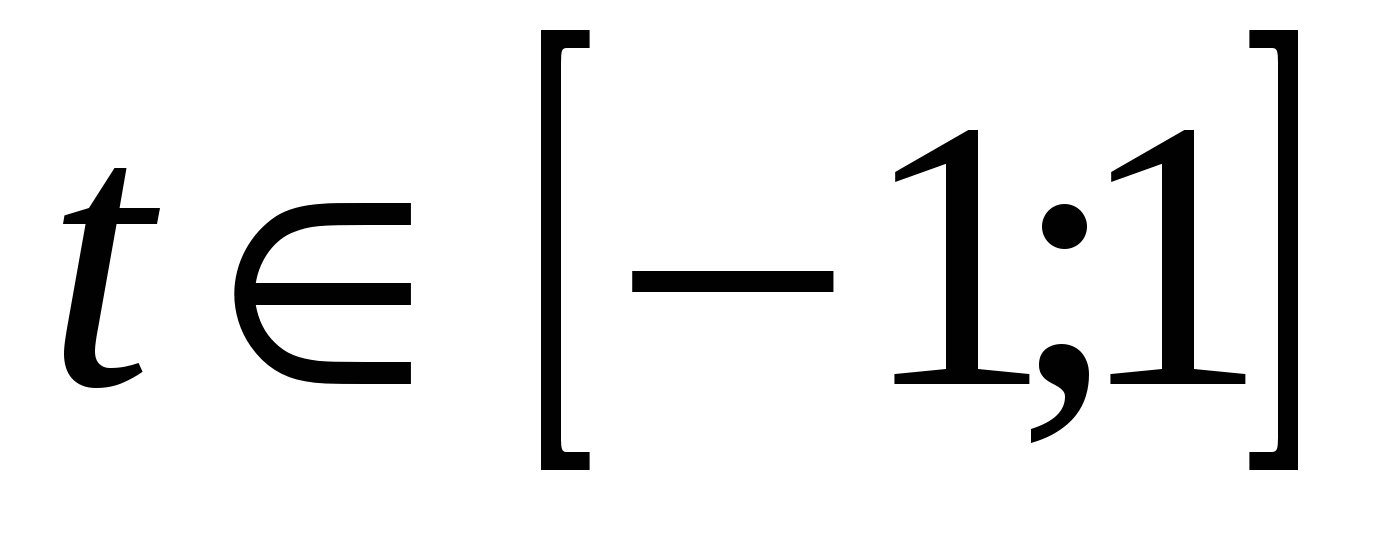 . Выясним при каких а,
. Выясним при каких а,  , где
, где  – множество решений неравенства
– множество решений неравенства 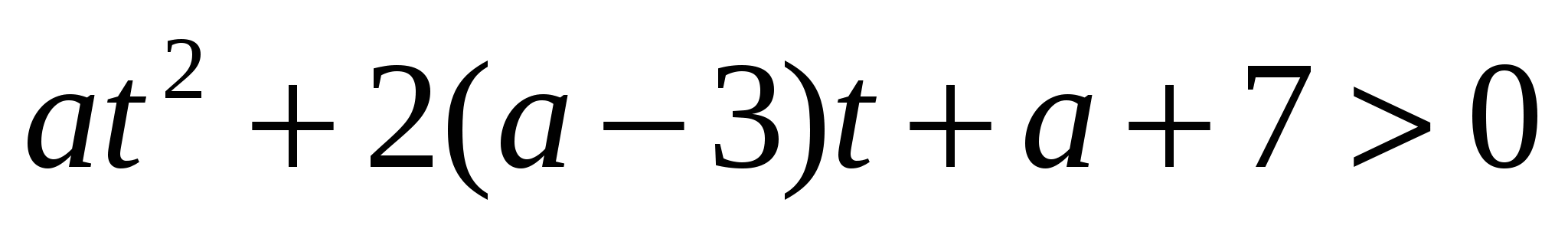 относительно
относительно 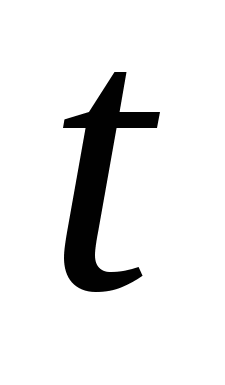 .
.
Найти все значения  , которые удовлетворяют неравенству
, которые удовлетворяют неравенству 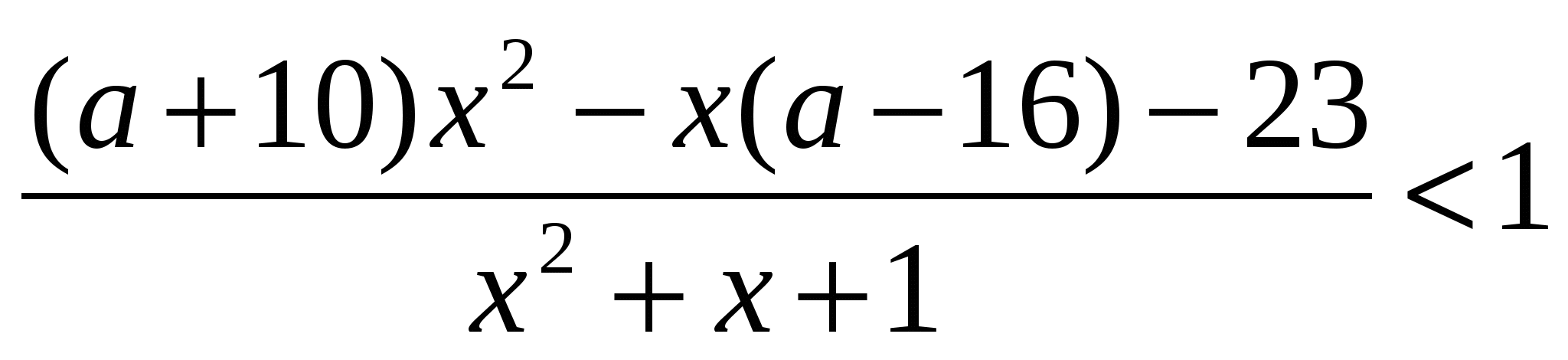 при любом значении параметра
при любом значении параметра  , принадлежащего промежутку (-1;3).
, принадлежащего промежутку (-1;3).
Выясним при каком  ,
, 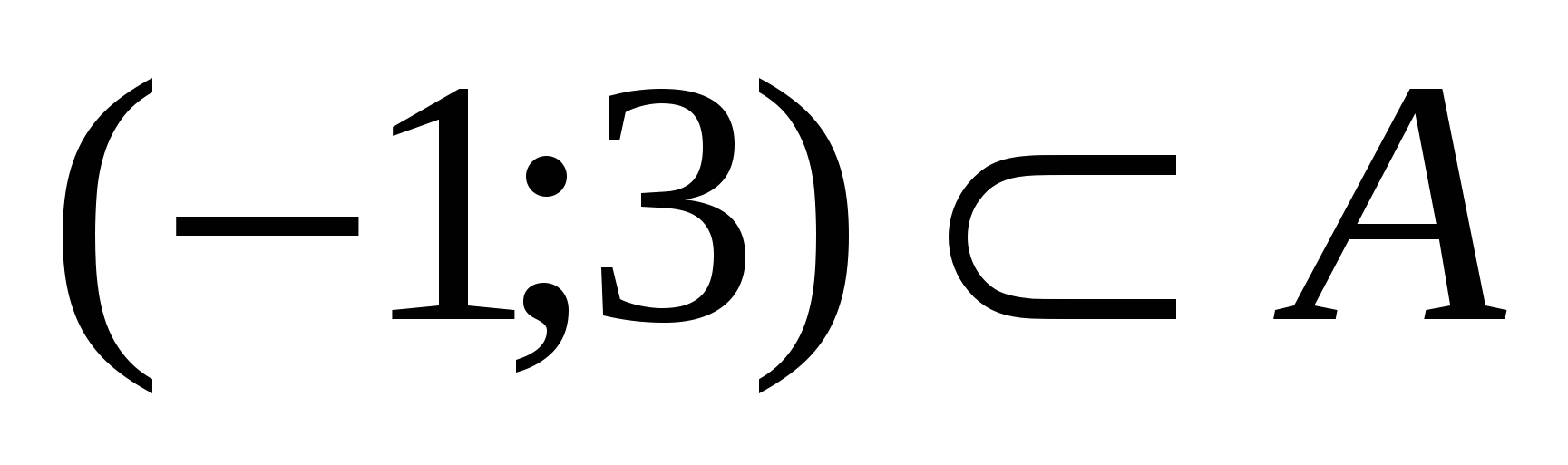 , где
, где  – множество решений неравенства
– множество решений неравенства 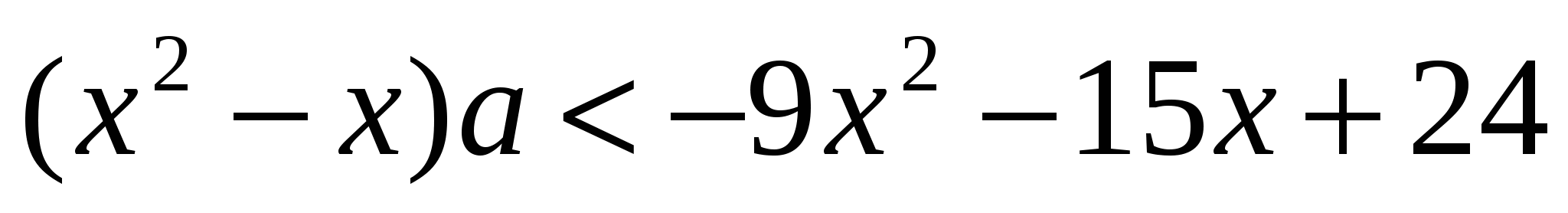 относительно
относительно  .
.
Найдите при каких значениях  неравенство
неравенство 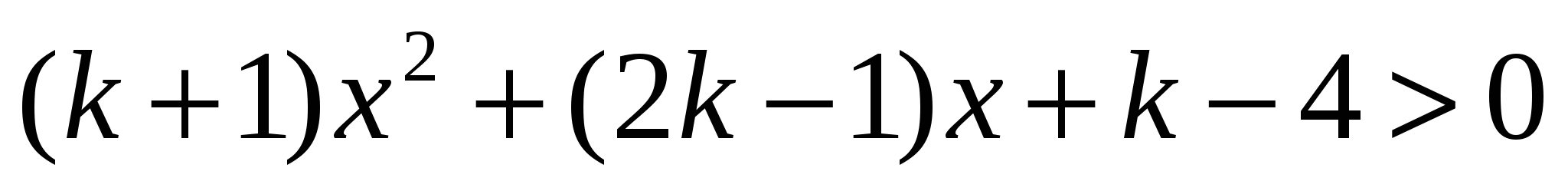 выполняется хотя бы при одном
выполняется хотя бы при одном 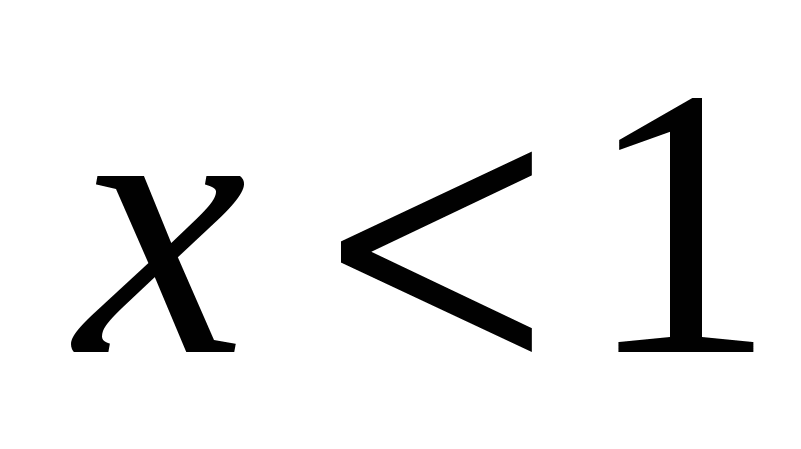 .
.
Найти все значения а, при которых 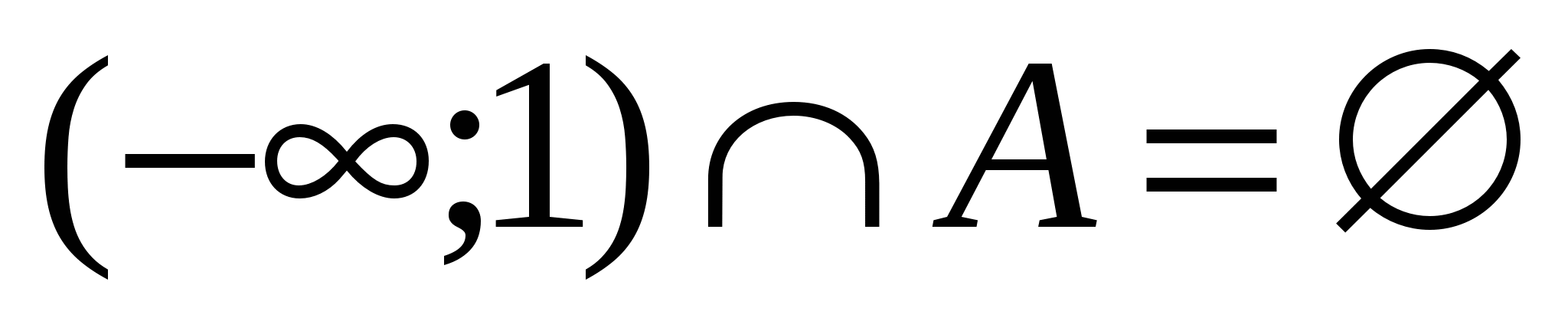 , где
, где  – множество решений заданного неравенства относительно
– множество решений заданного неравенства относительно  .
.
Найдите все значения  , при которых неравенство
, при которых неравенство 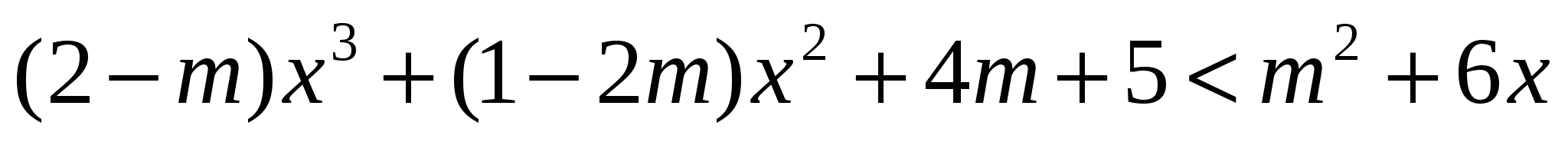 справедливо хотя бы для одного
справедливо хотя бы для одного  из промежутка
из промежутка 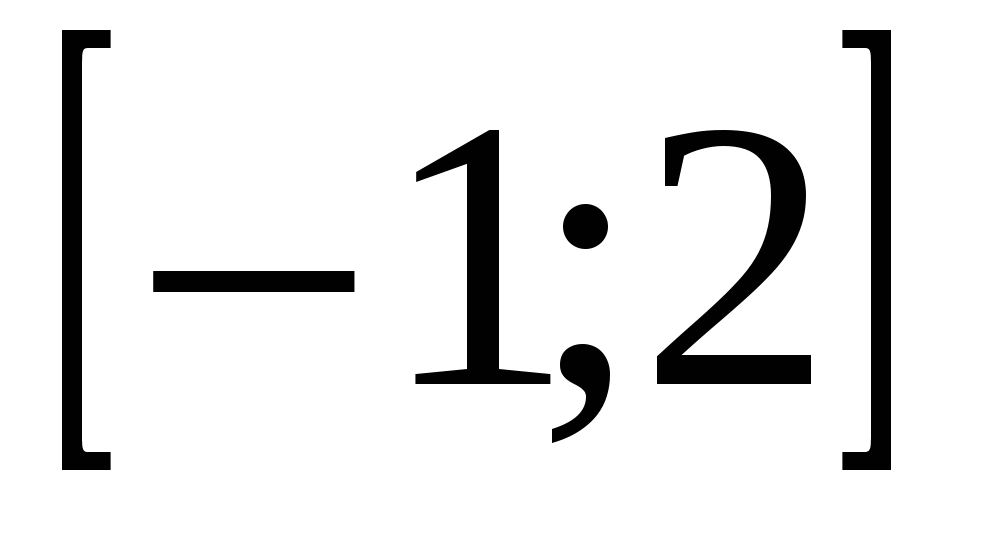 .
.
Найти все значения  , при которых
, при которых 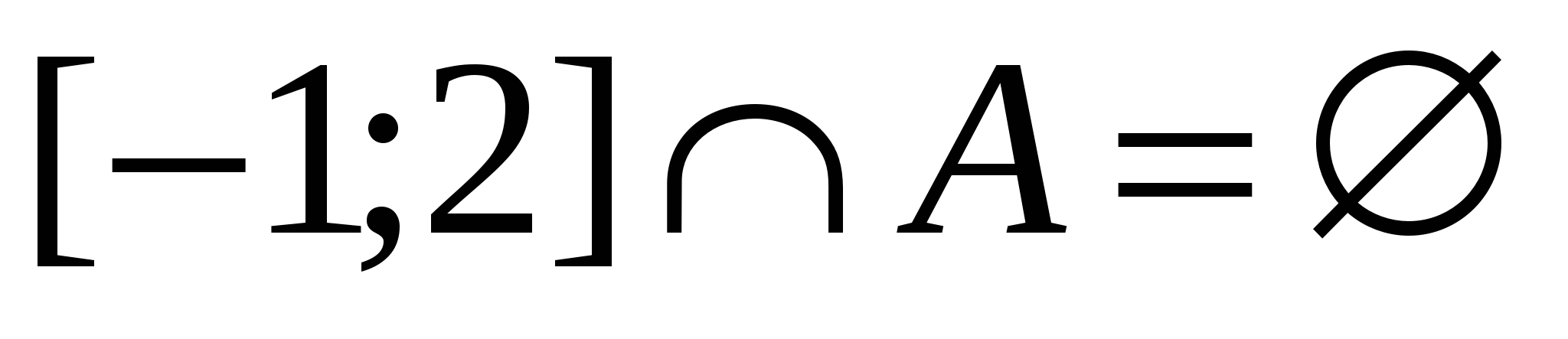 , где
, где  – множество решений заданного неравенства относительно
– множество решений заданного неравенства относительно  .
.
Найдите все значения  , при которых каждое решение неравенства
, при которых каждое решение неравенства 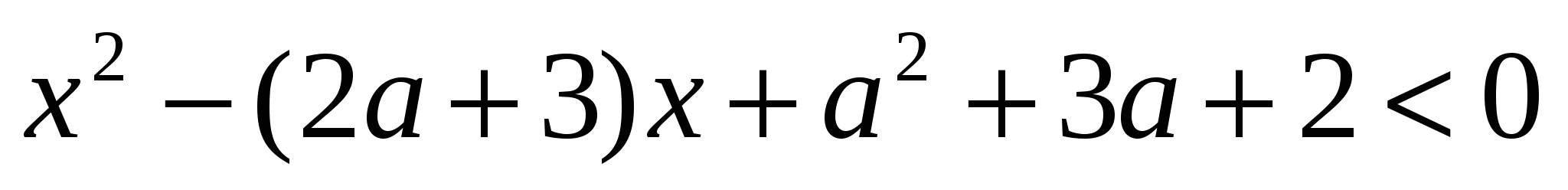 являлось бы также решением неравенства
являлось бы также решением неравенства 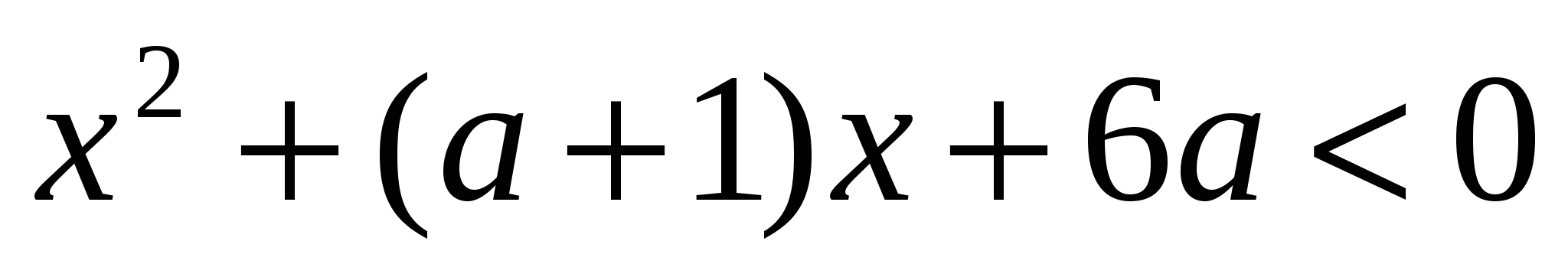 .
.
Найти все значения параметра  , при которых
, при которых  , где
, где  – множество решений неравенства
– множество решений неравенства 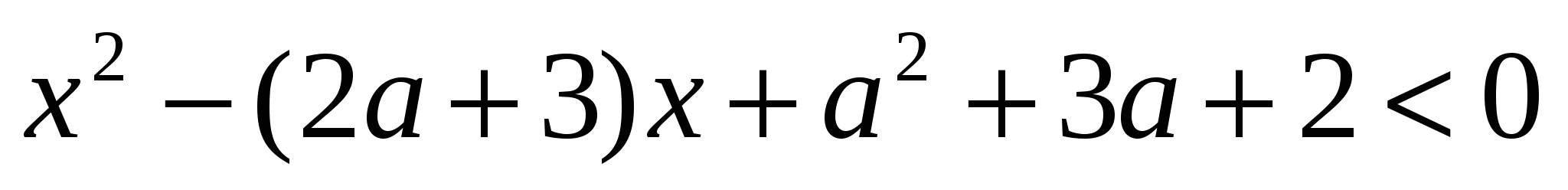 и где
и где 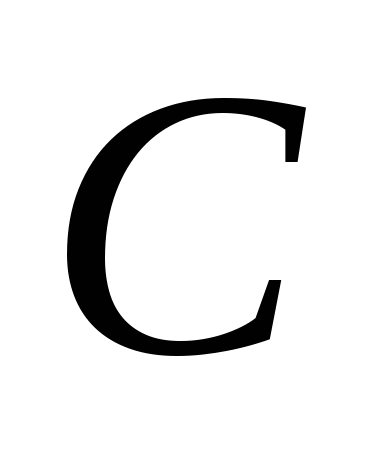 – множество решений неравенства
– множество решений неравенства 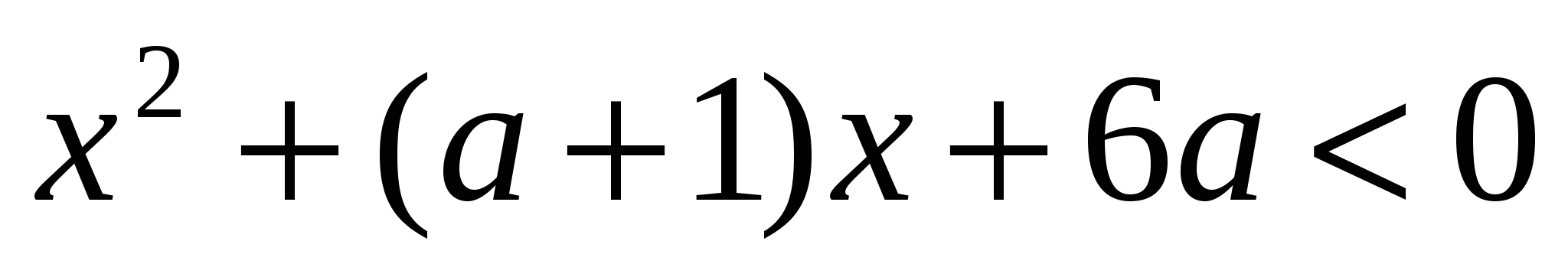 относительно х.
относительно х.
Найдите все значения параметра  , при которых неравенство
, при которых неравенство 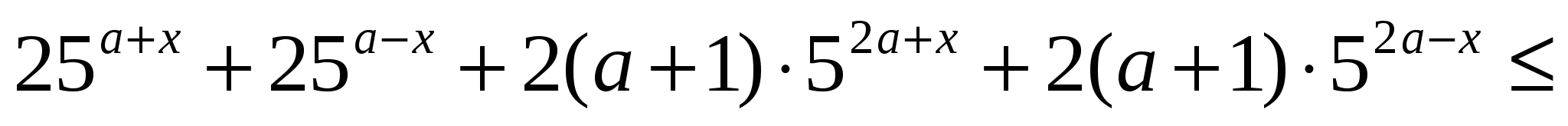
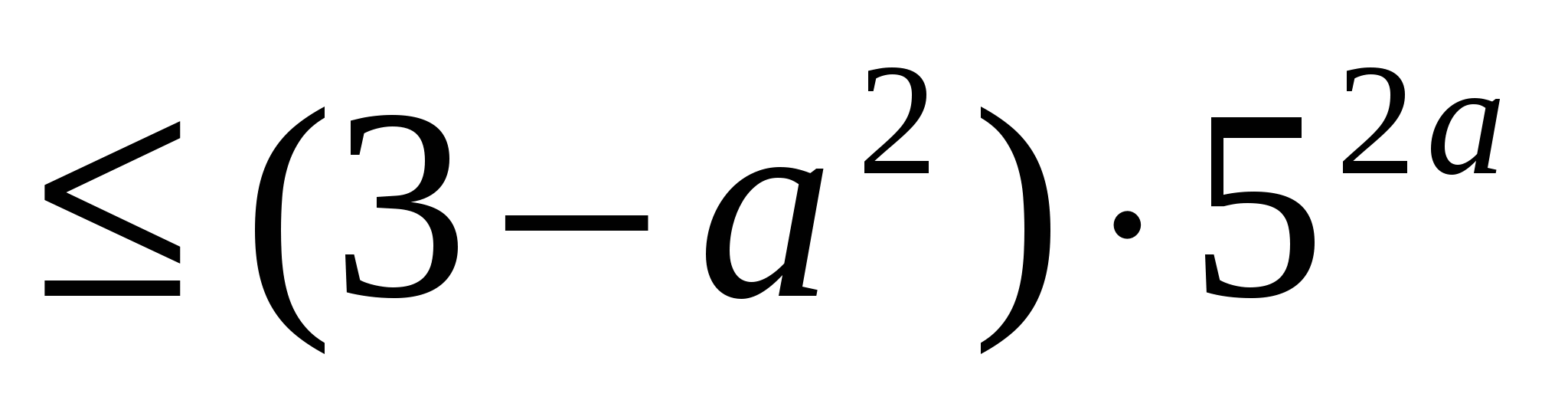 не имеет решений.
не имеет решений.
Пусть 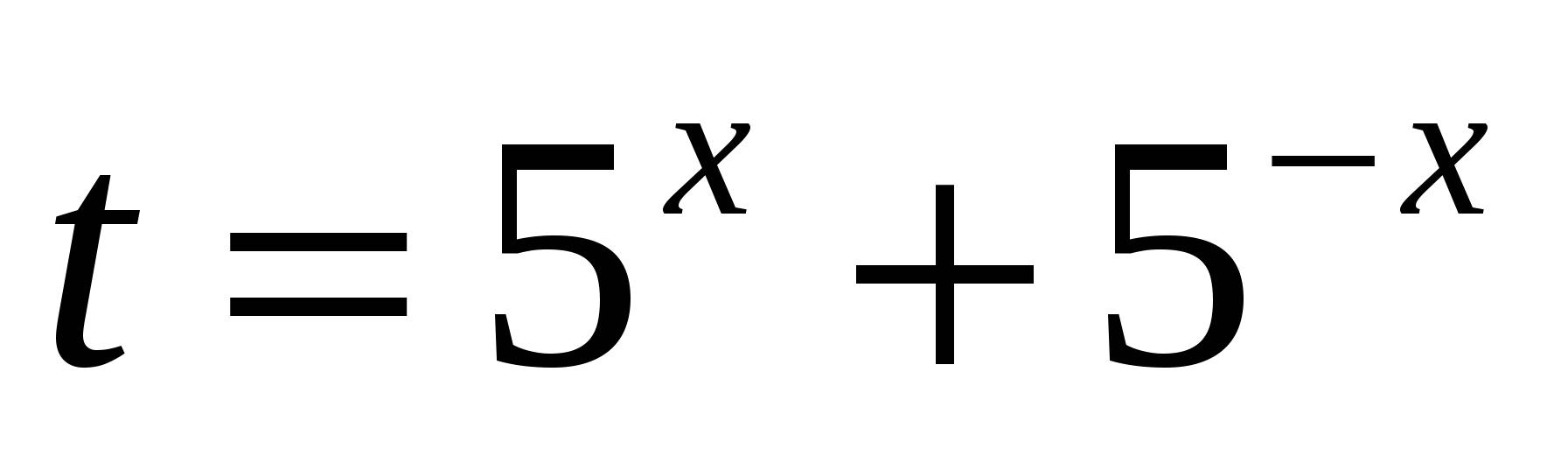 , причём
, причём 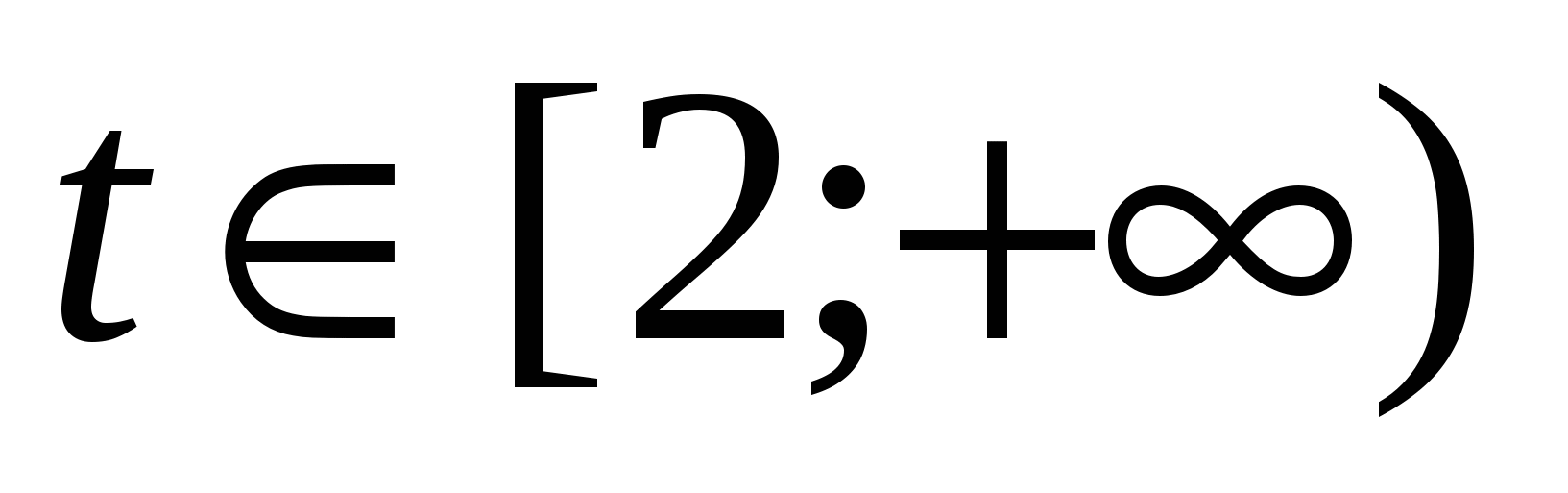 . Сначала для того, чтобы выяснить при каких
. Сначала для того, чтобы выяснить при каких  заданное неравенство имеет хотя бы одно решение, найдём при каких а
заданное неравенство имеет хотя бы одно решение, найдём при каких а 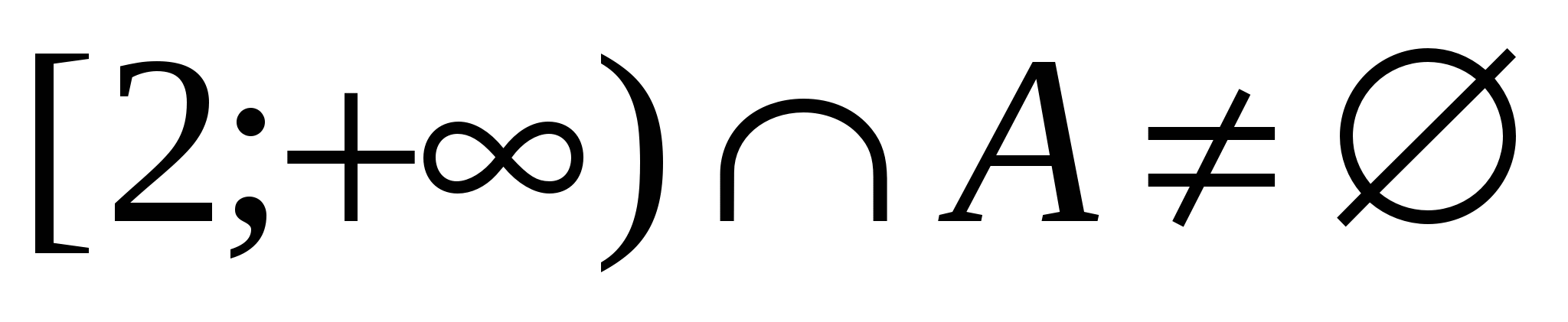 , где
, где  – множество решений неравенства
– множество решений неравенства 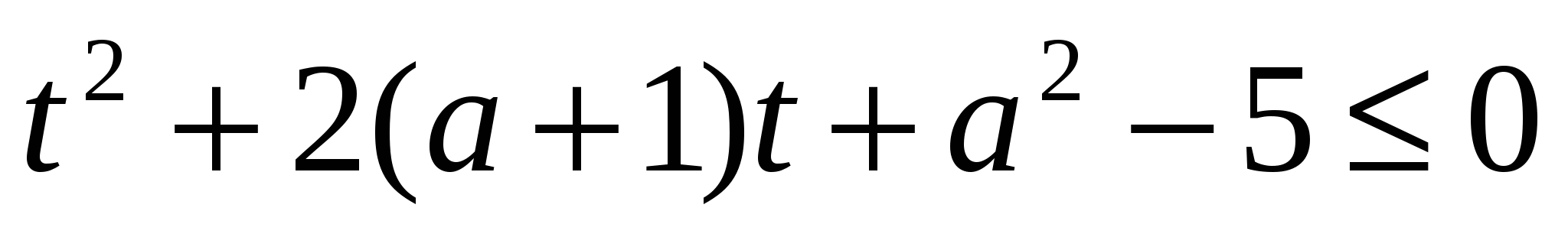 относительно
относительно 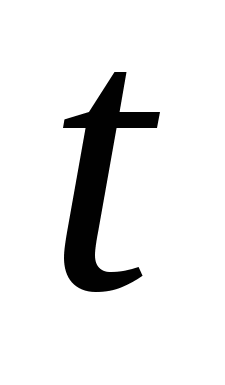 . А затем для того, чтобы выяснить при каких
. А затем для того, чтобы выяснить при каких  заданное неравенство не имеет решений, найдем дополнение полученного множества значений
заданное неравенство не имеет решений, найдем дополнение полученного множества значений  до множества
до множества 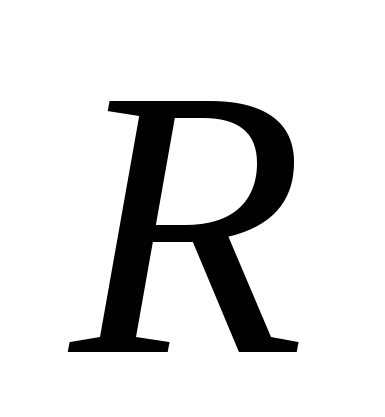 .
.
б) Решение задачи по исследованию неравенства с параметром аналитическим методом.
Пример 1. (задание С3 − вариант 7 [1]). Найдите все значения параметра  , при которых неравенство
, при которых неравенство 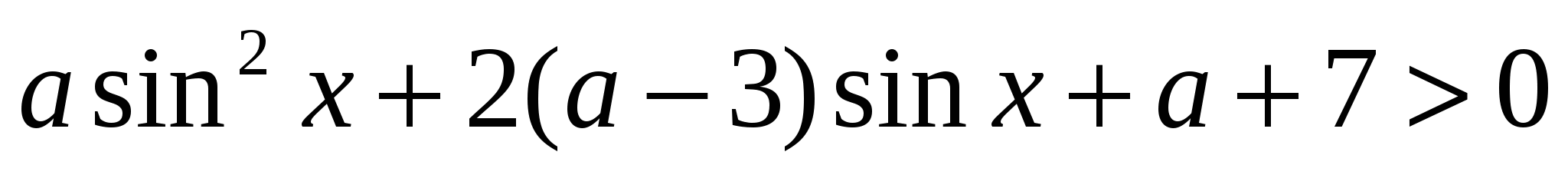 выполняется для любых значений
выполняется для любых значений  .
.
Решение. Пусть 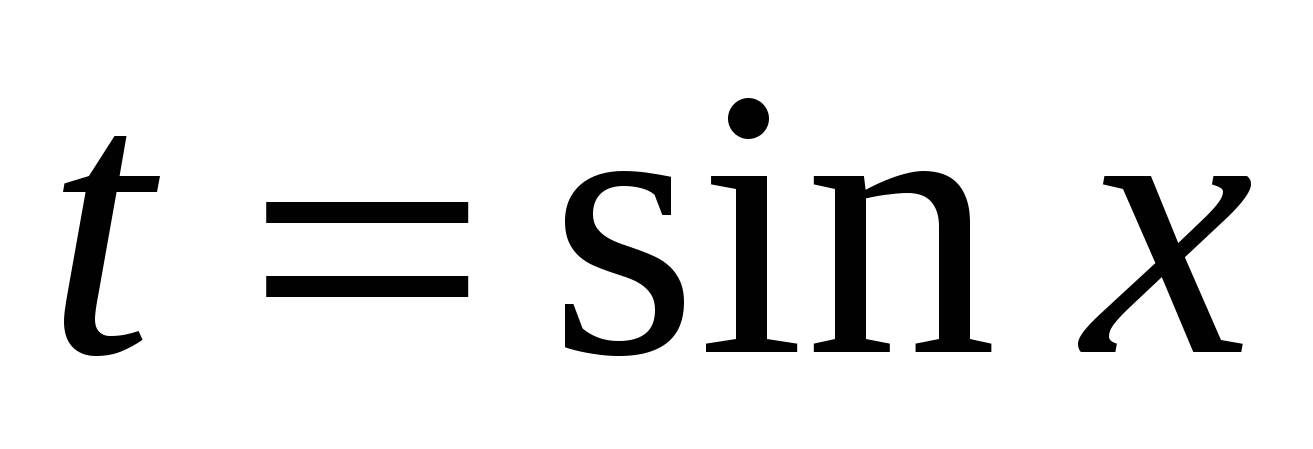 , причем
, причем 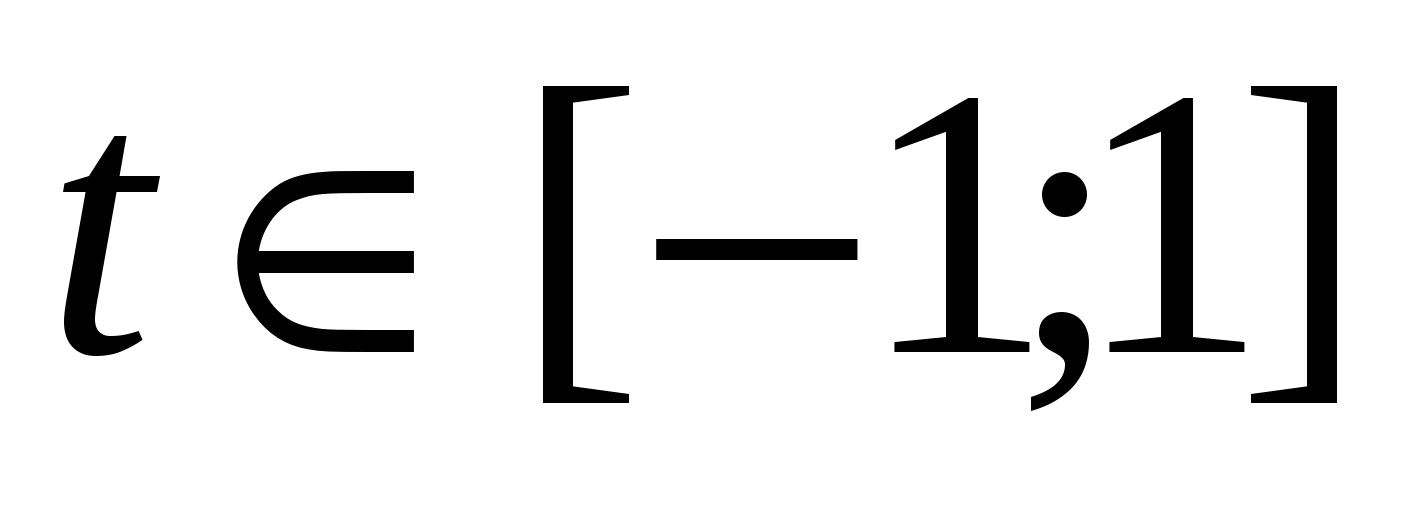 , тогда
, тогда
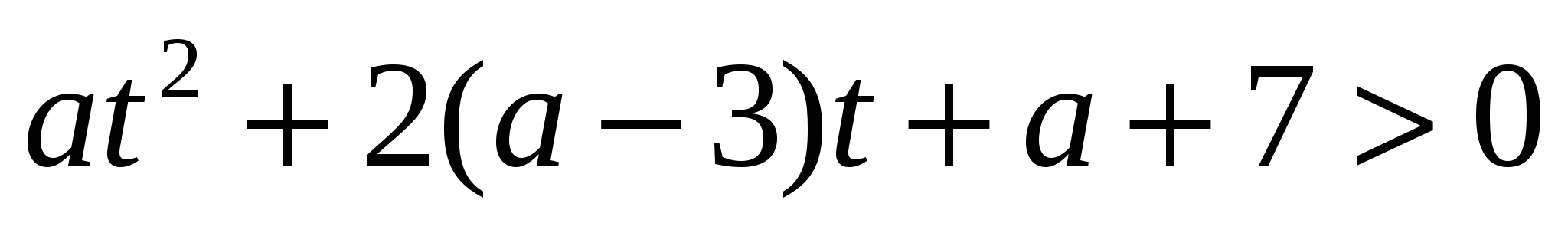 .
.
(*)
Выясним, при каких  выполняется
выполняется
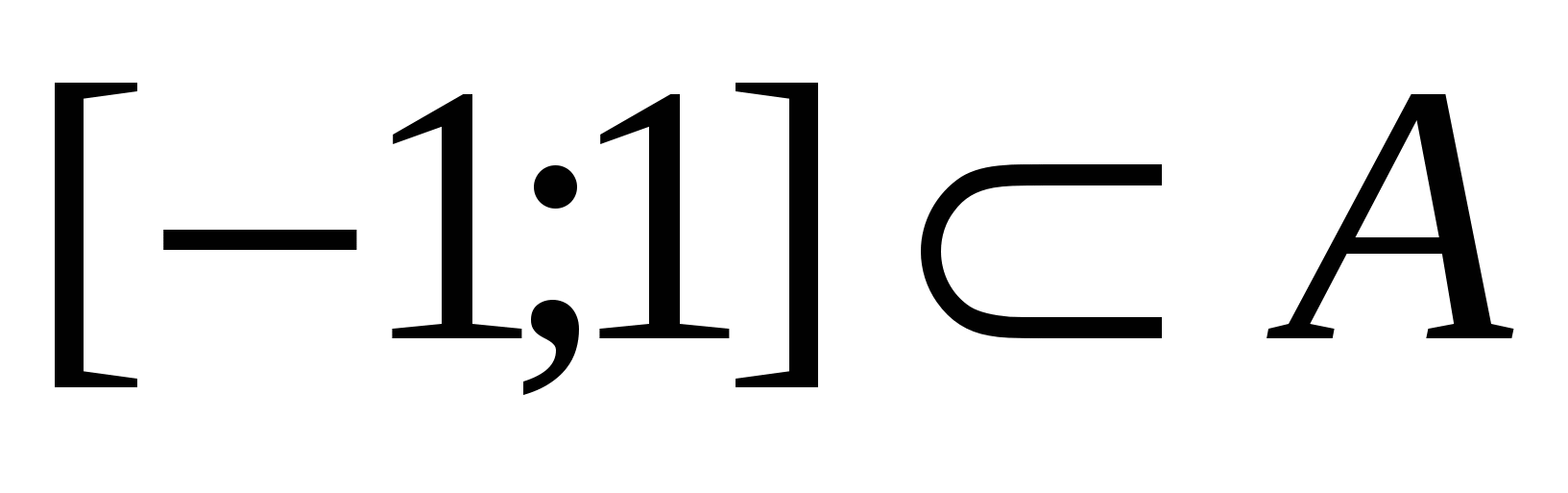 ,
,
(**)
где  – множество решений (*) относительно
– множество решений (*) относительно 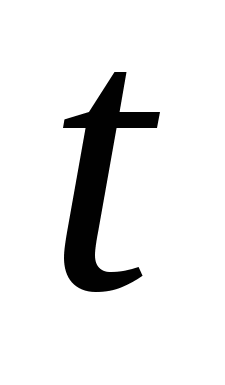 .
.
Если 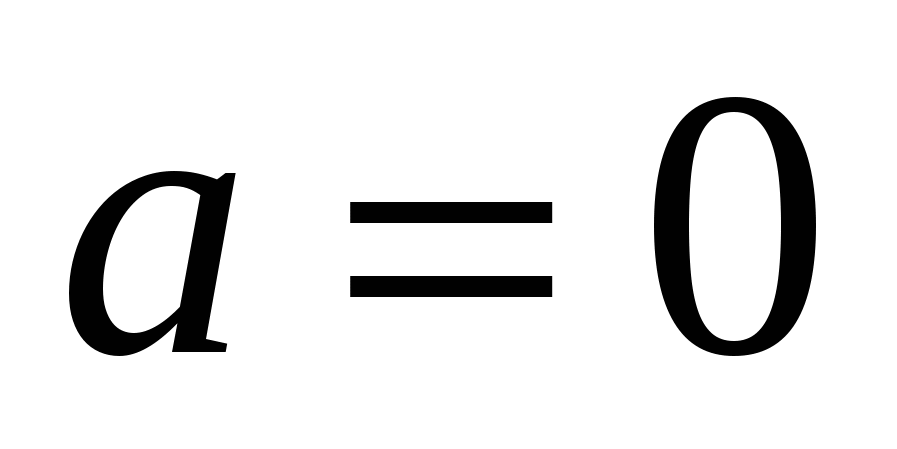 , то (*) – линейное неравенство:
, то (*) – линейное неравенство:
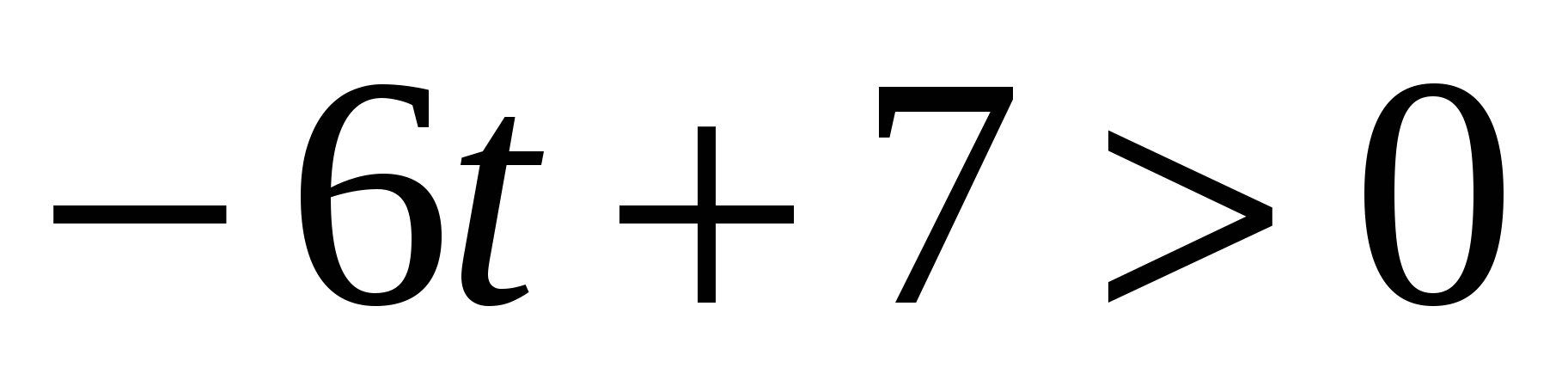 ,
, 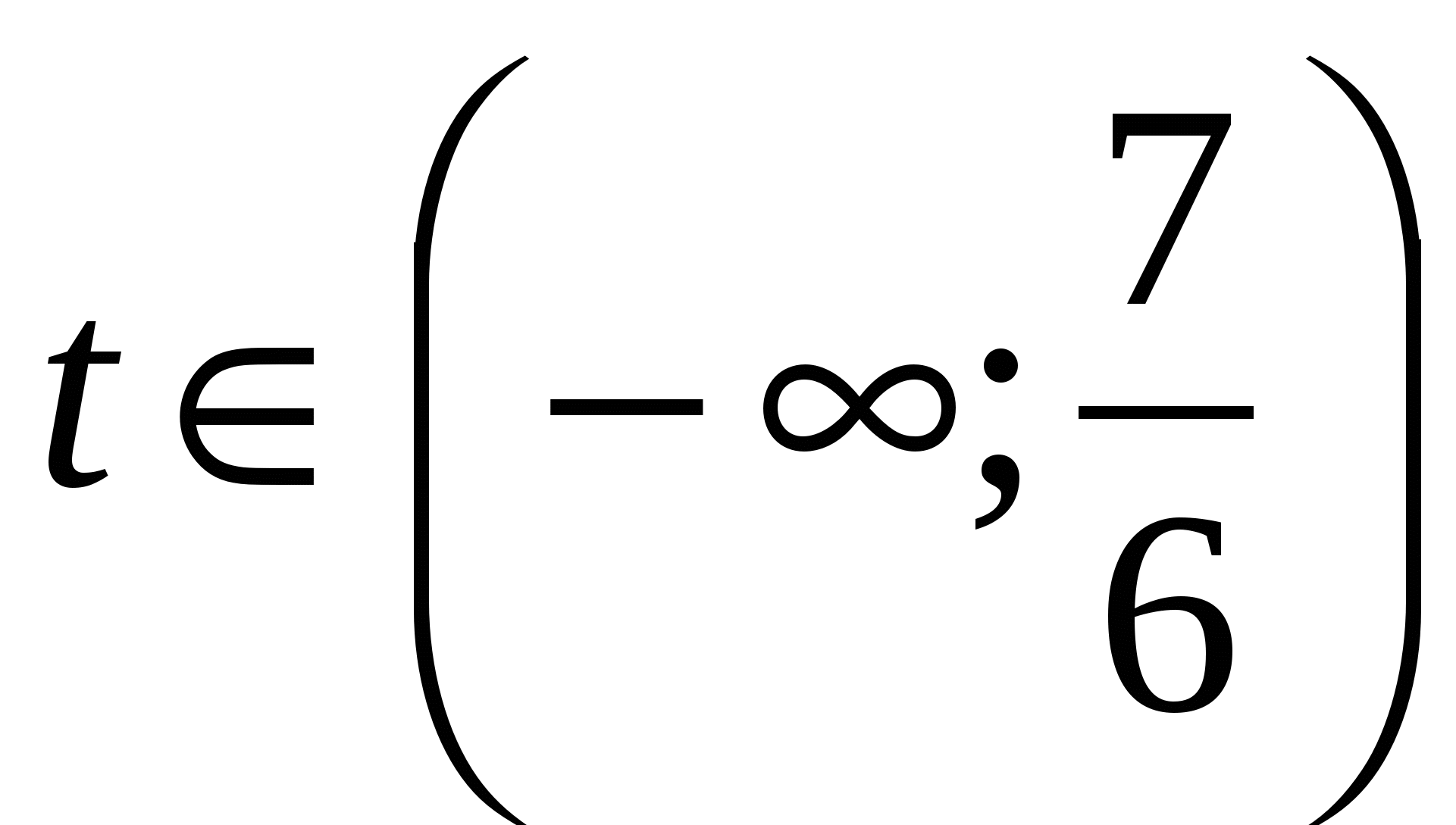 ,
,
что удовлетворяет условию задачи (**), значит 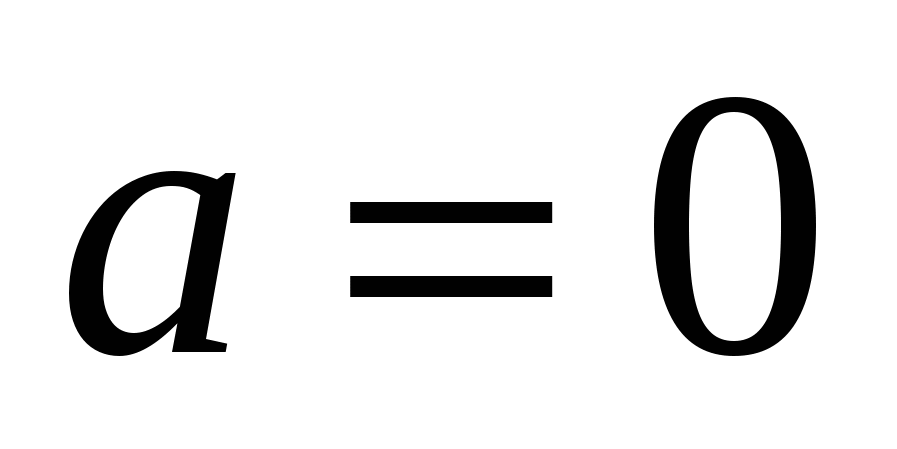 − одно из решений.
− одно из решений.
Если 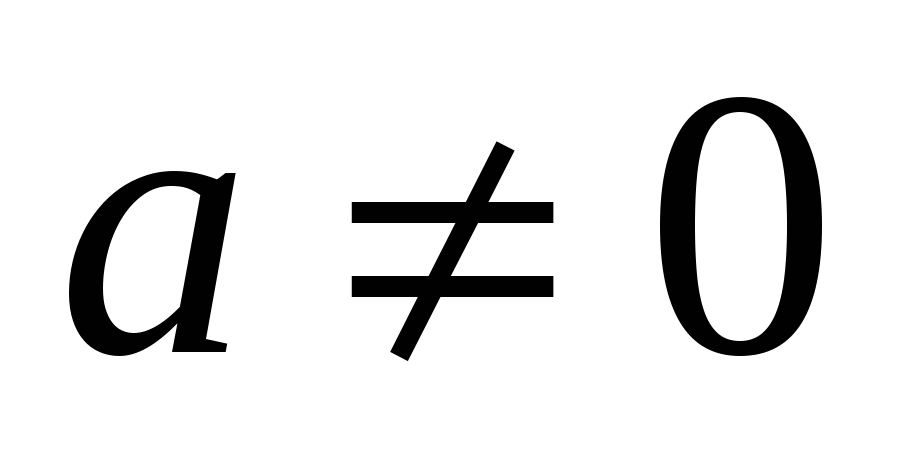 , то (*) – квадратное неравенство.
, то (*) – квадратное неравенство.
Рассмотрим уравнение 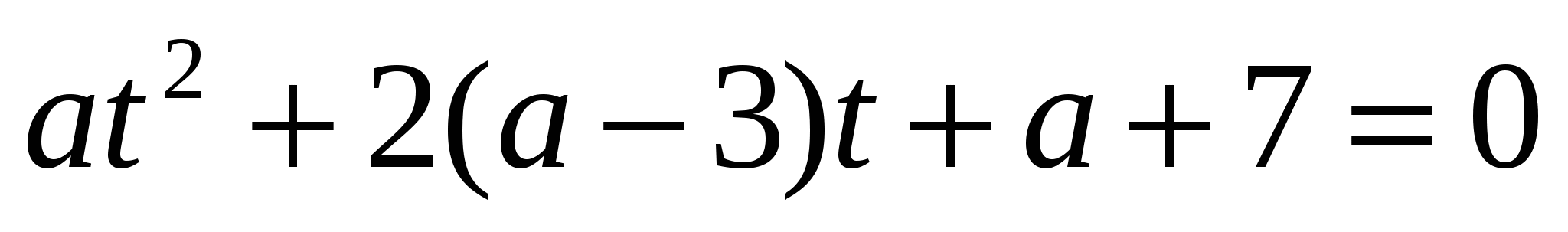 ;
;
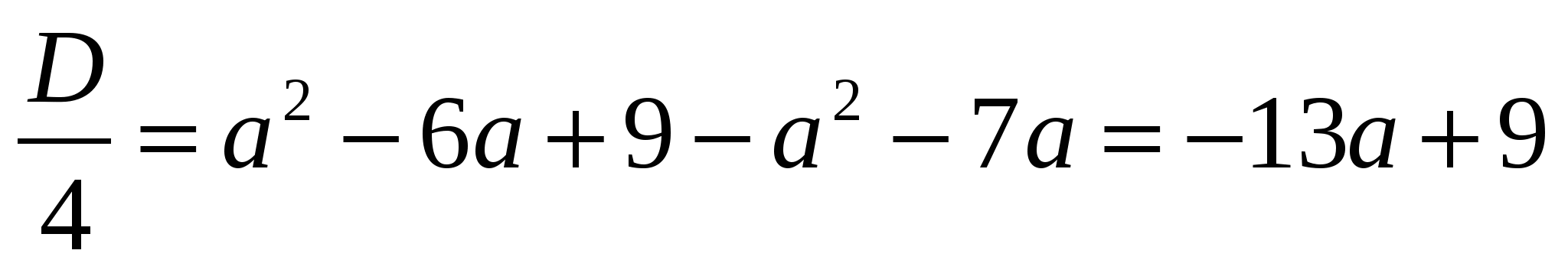 ;
; 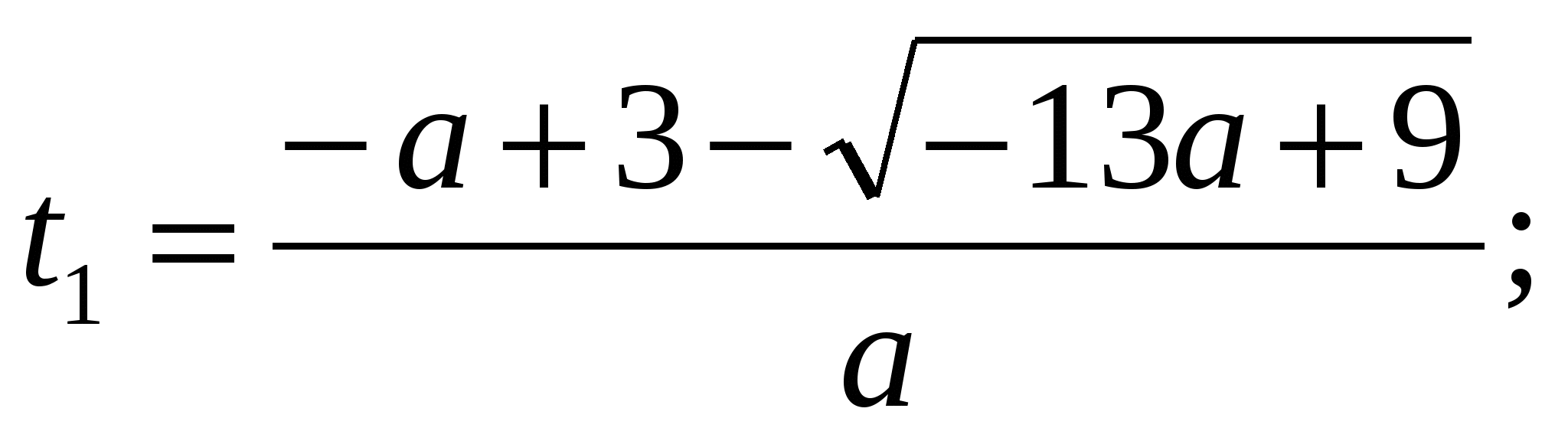
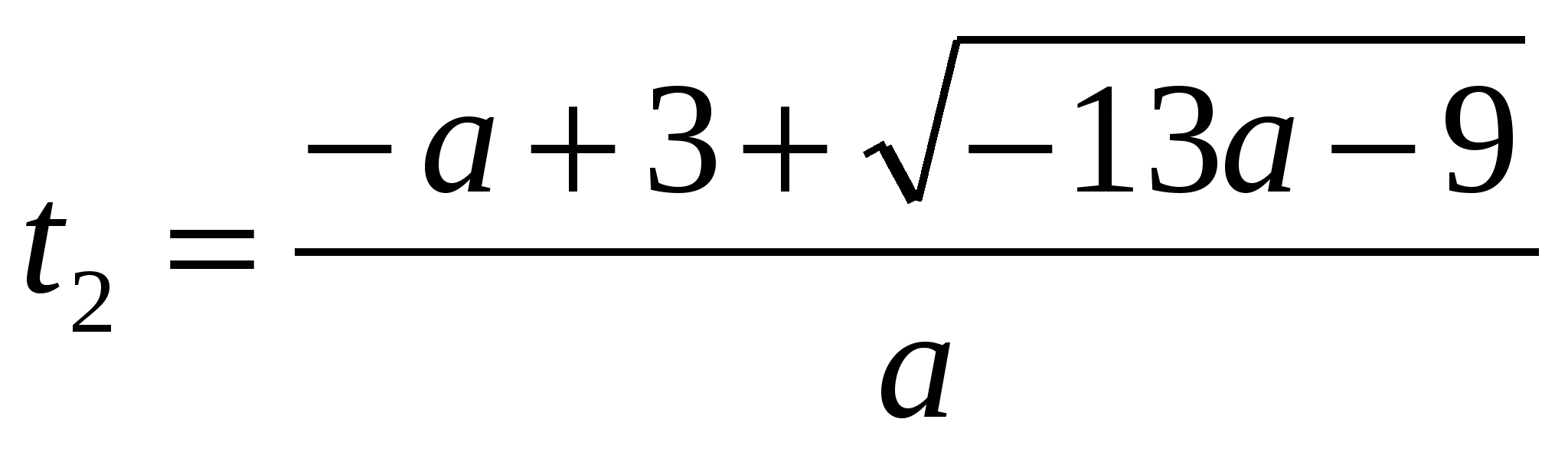 .
.
В зависимости от знака 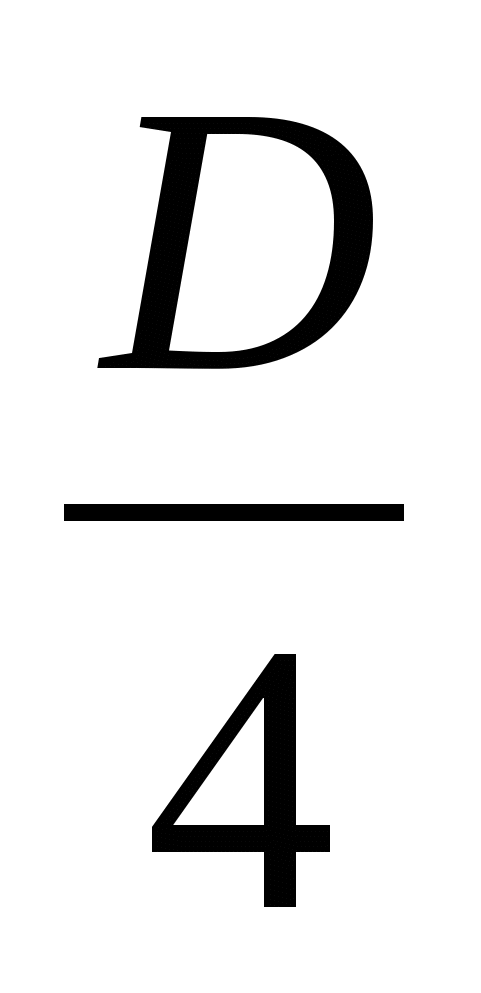 и
и  , получаем четыре случая:
, получаем четыре случая:
а) 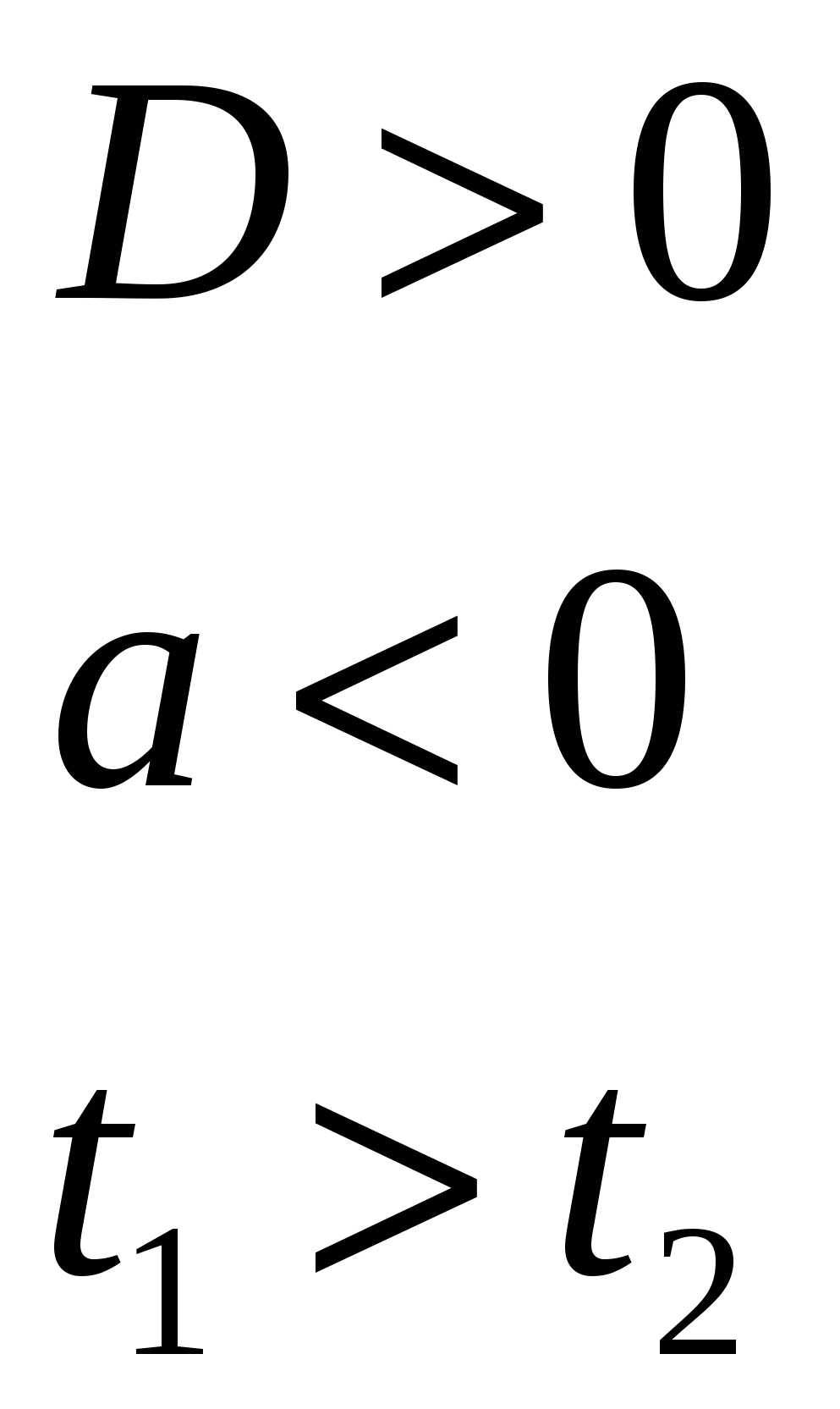
т. е. 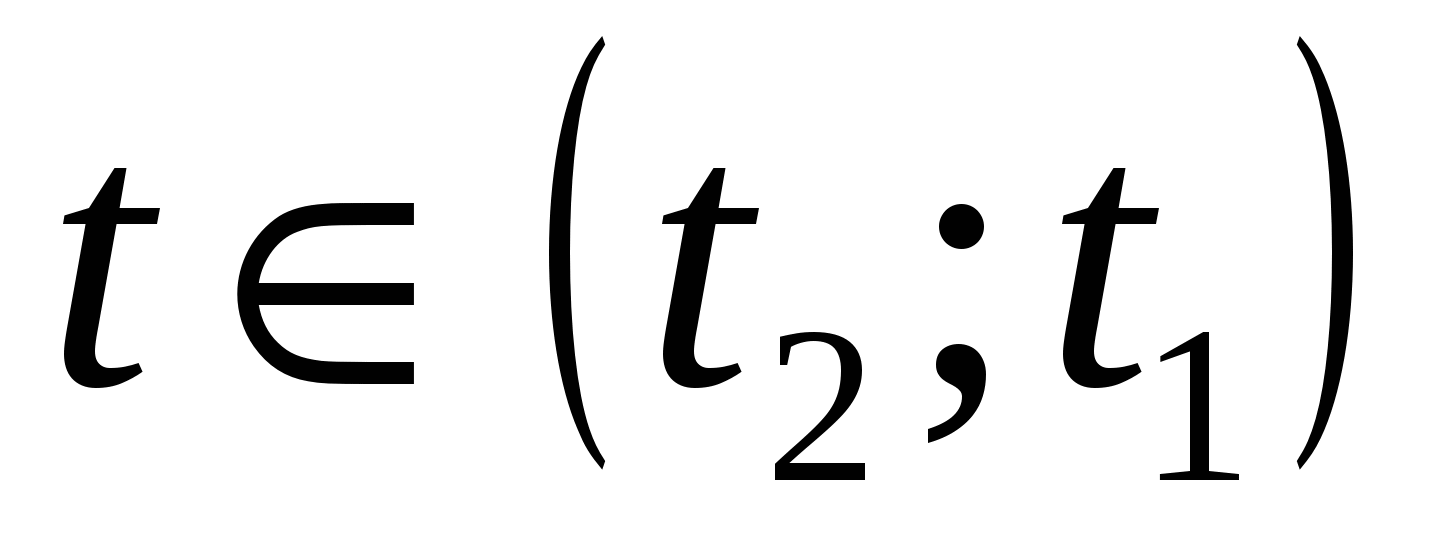 .
.
б) 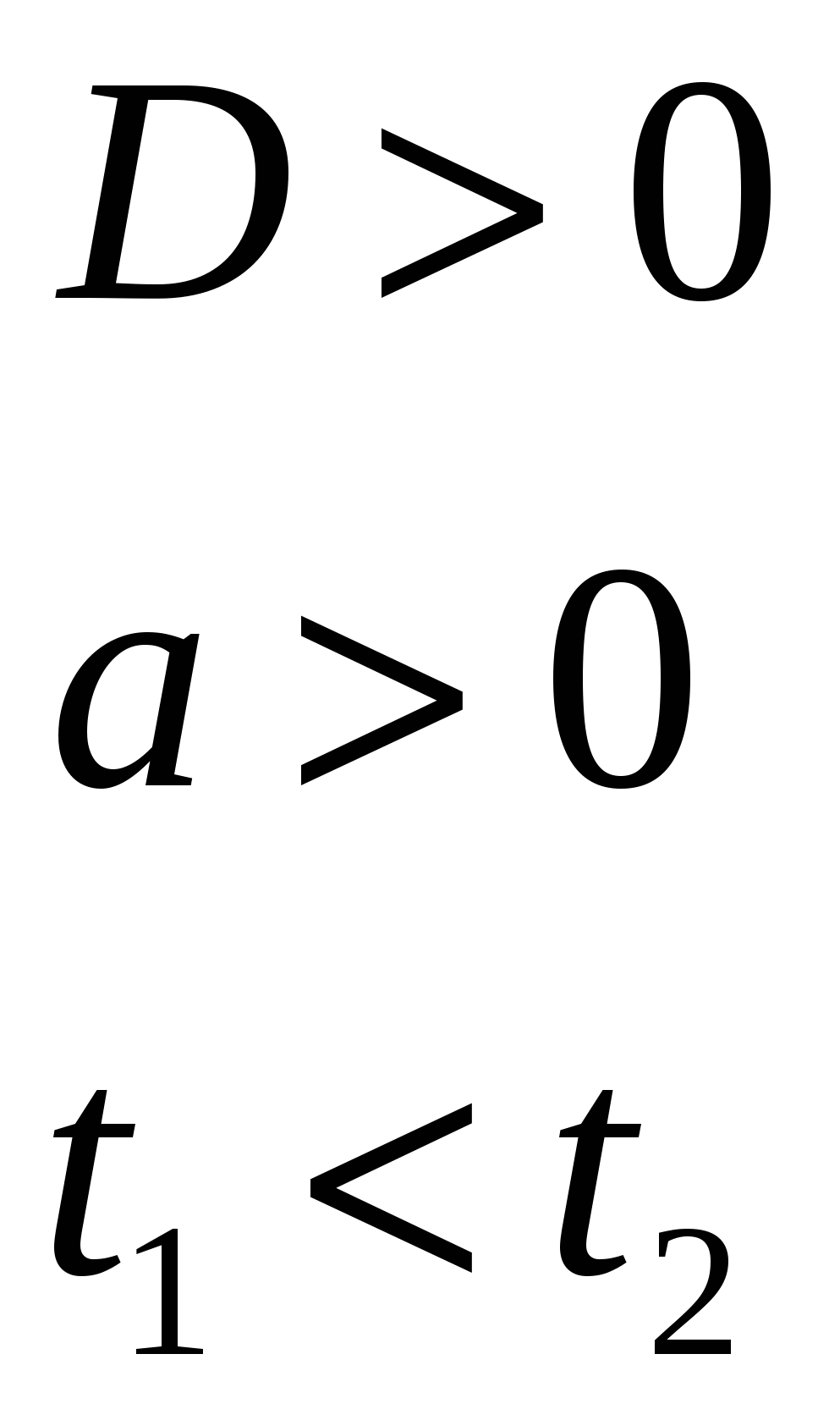
т. е. 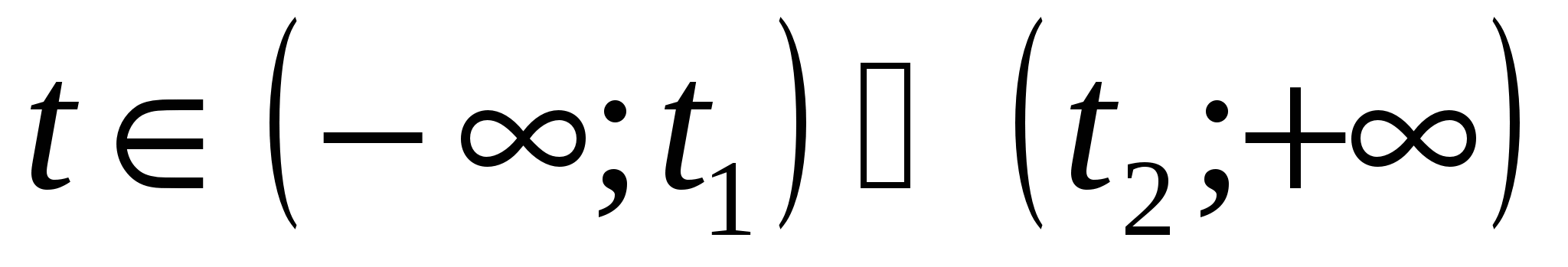 .
.
в) 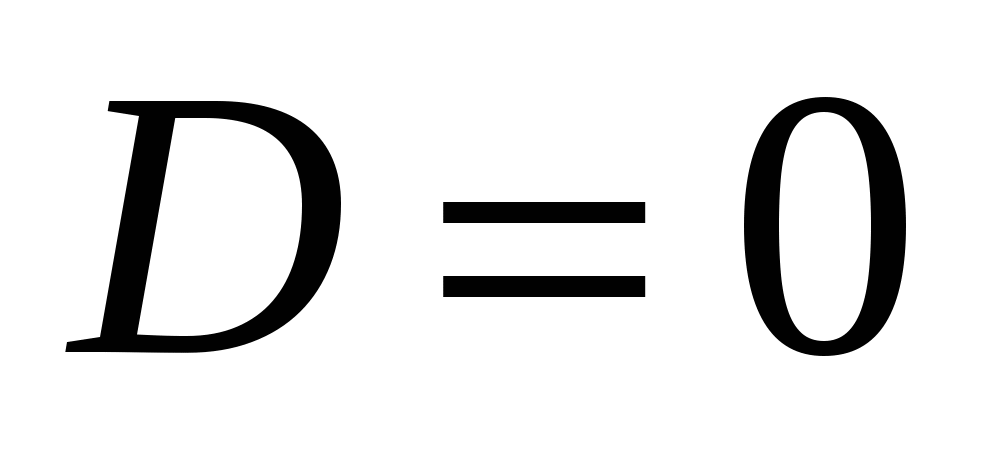 .
.
г) 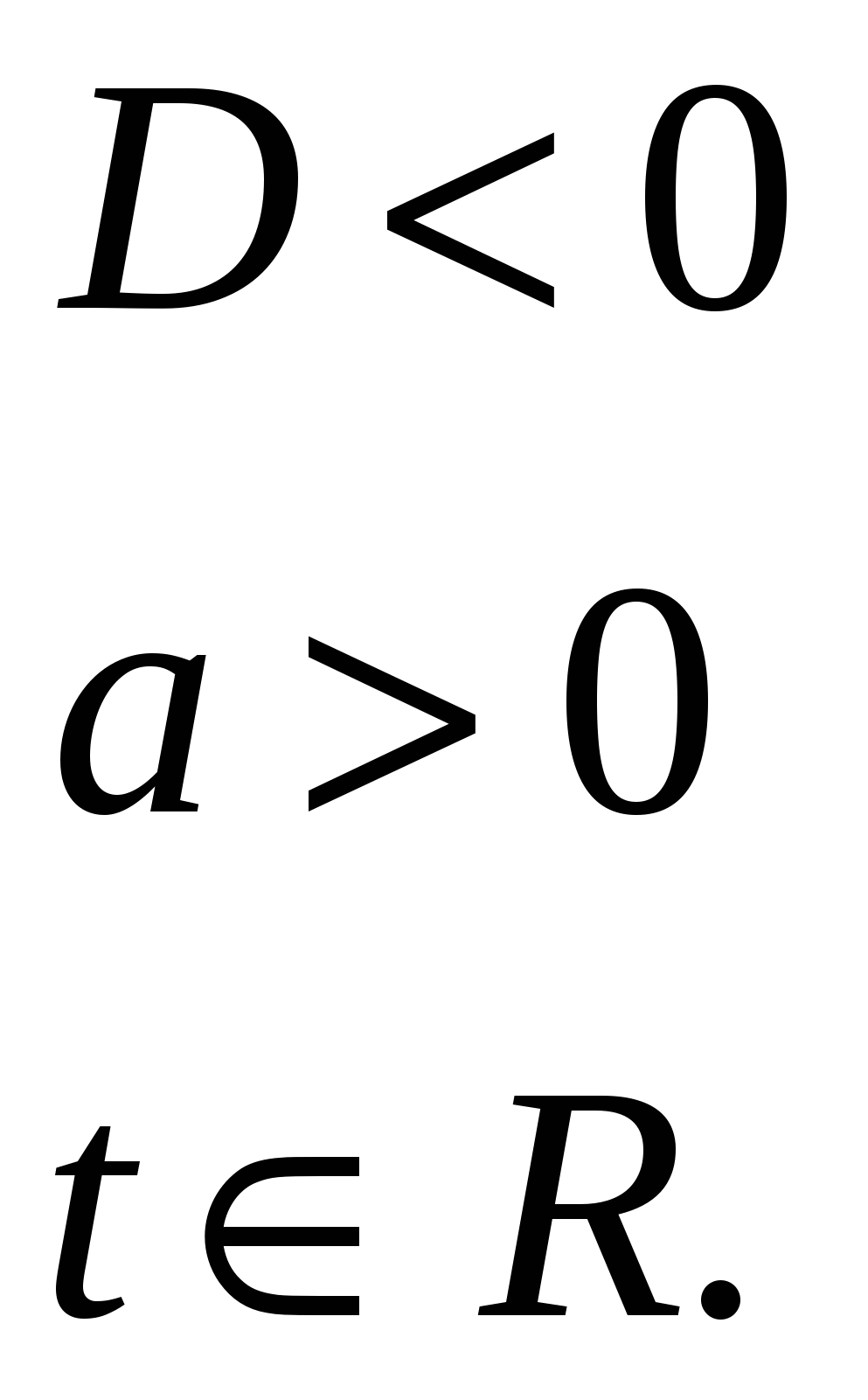
Рассмотрим случай а)
Если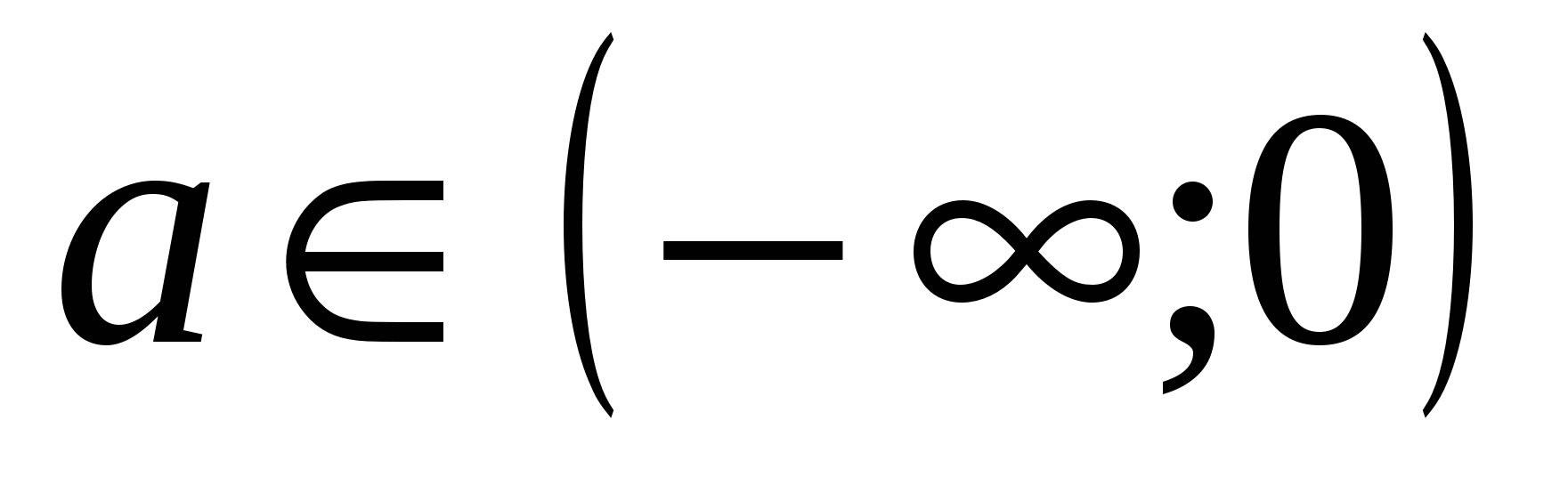 , то (*):
, то (*): 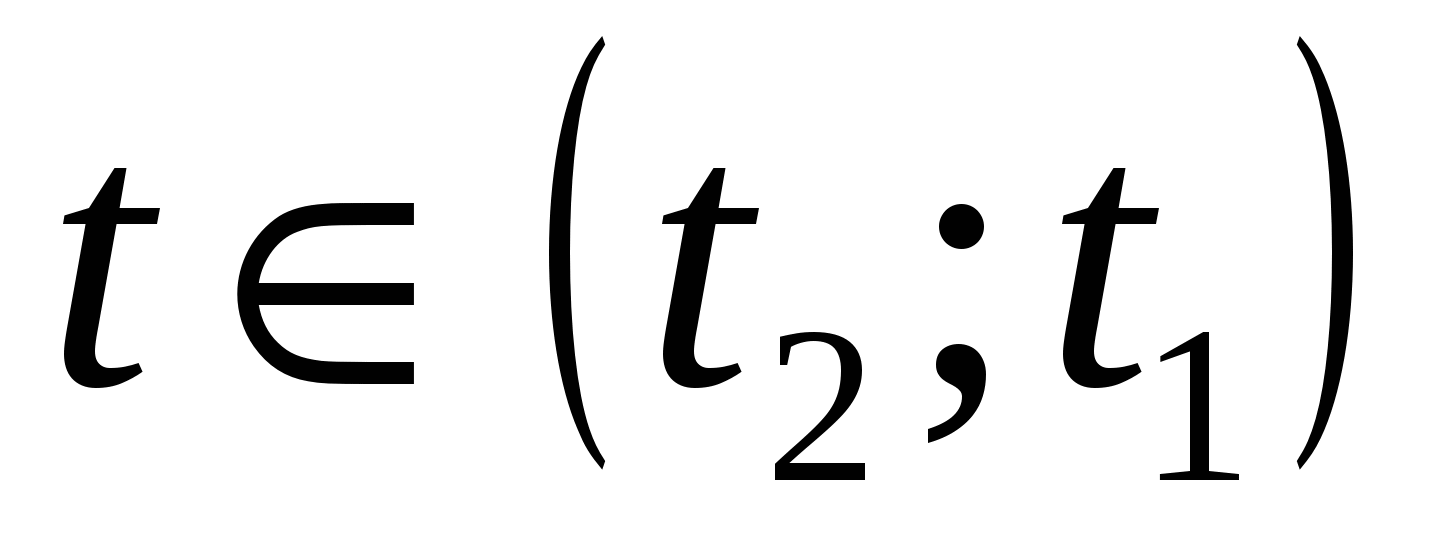 . По условию задачи (**) Рис. 1:
. По условию задачи (**) Рис. 1:
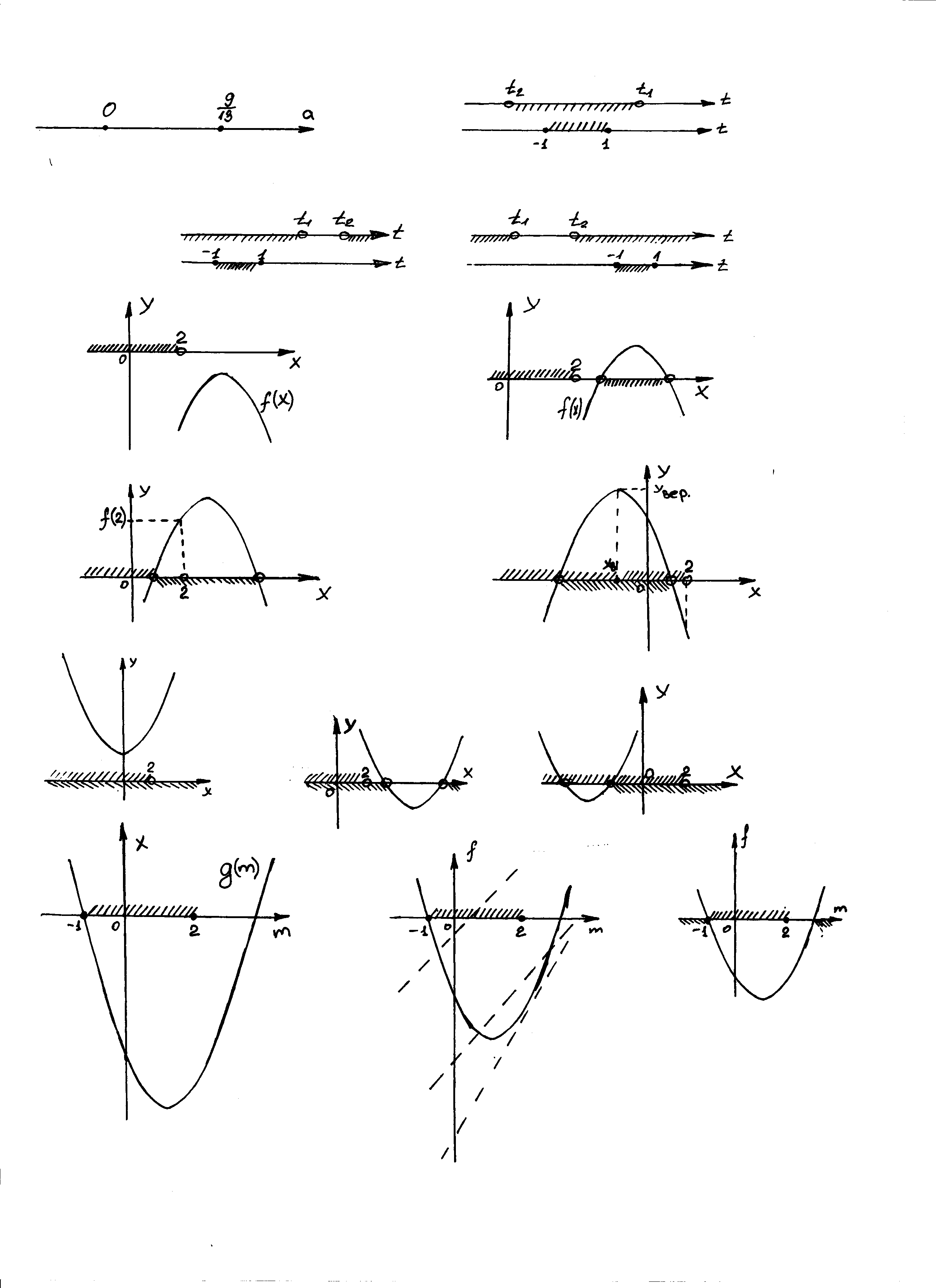
Рис. 1

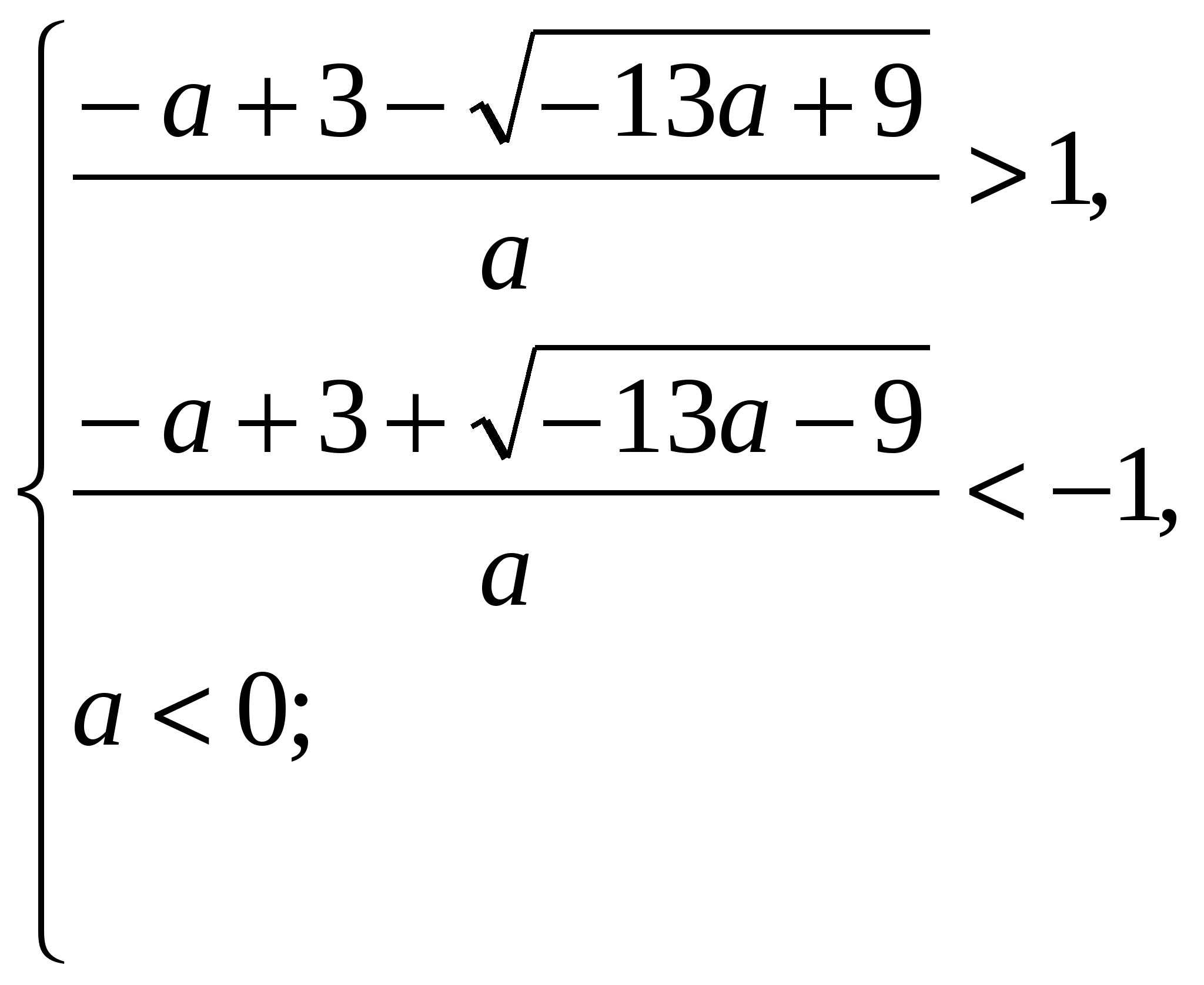
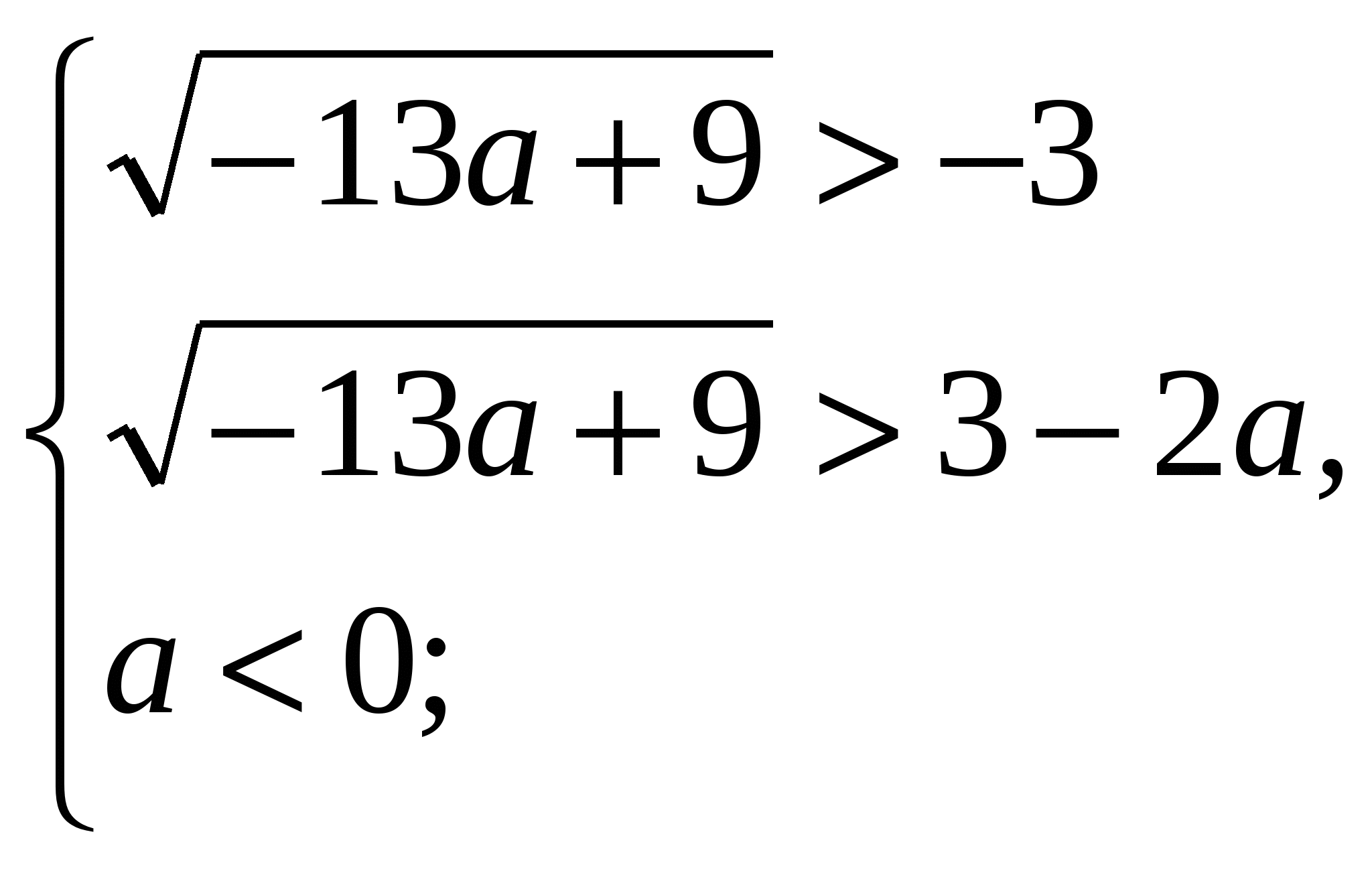
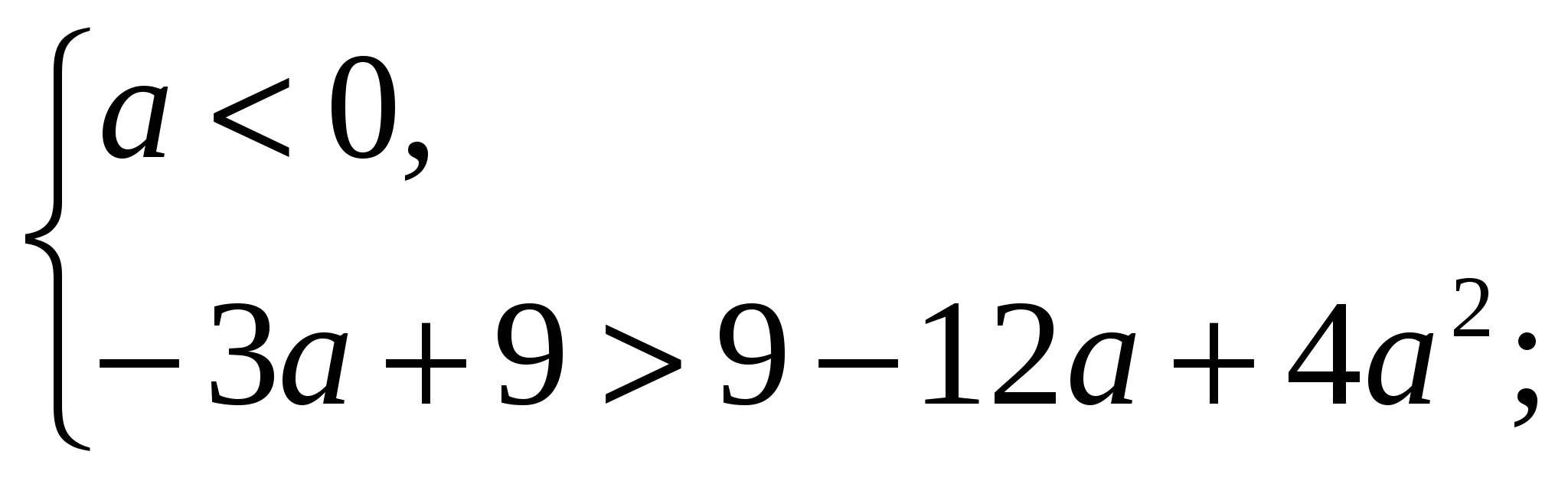
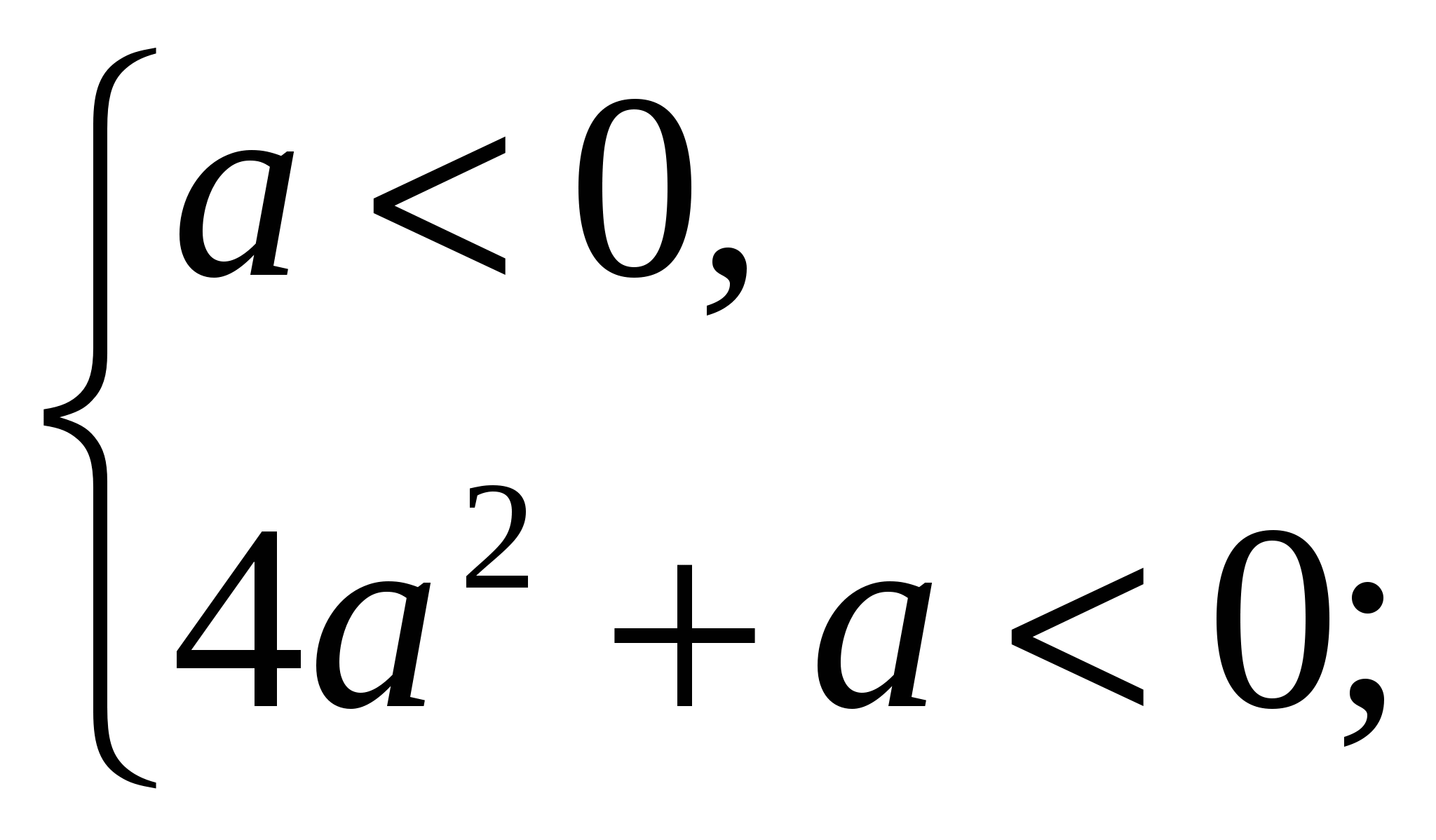
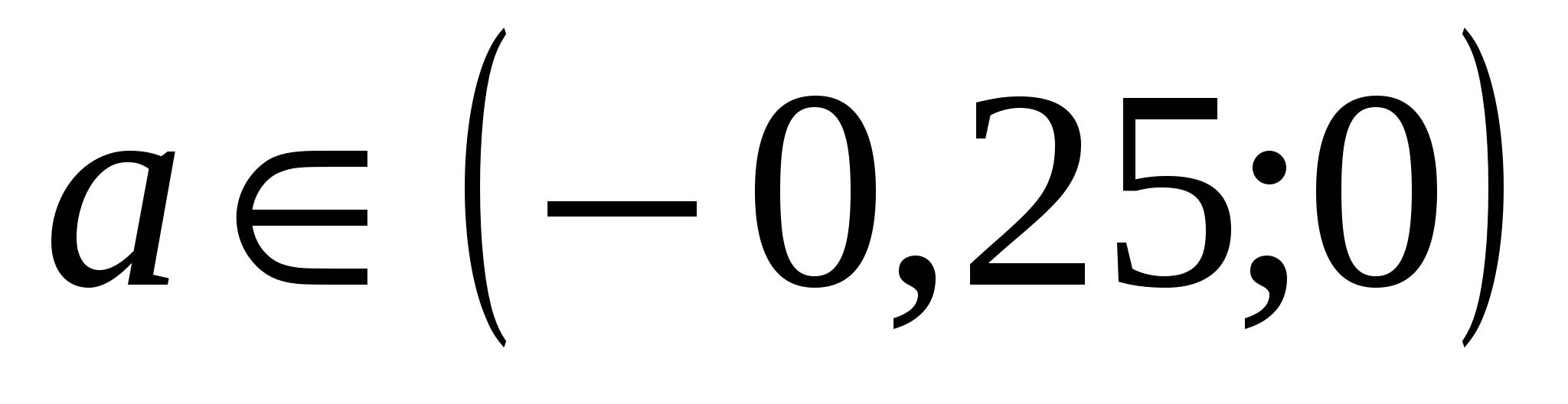 .
.
Рассмотрим случай б)
Если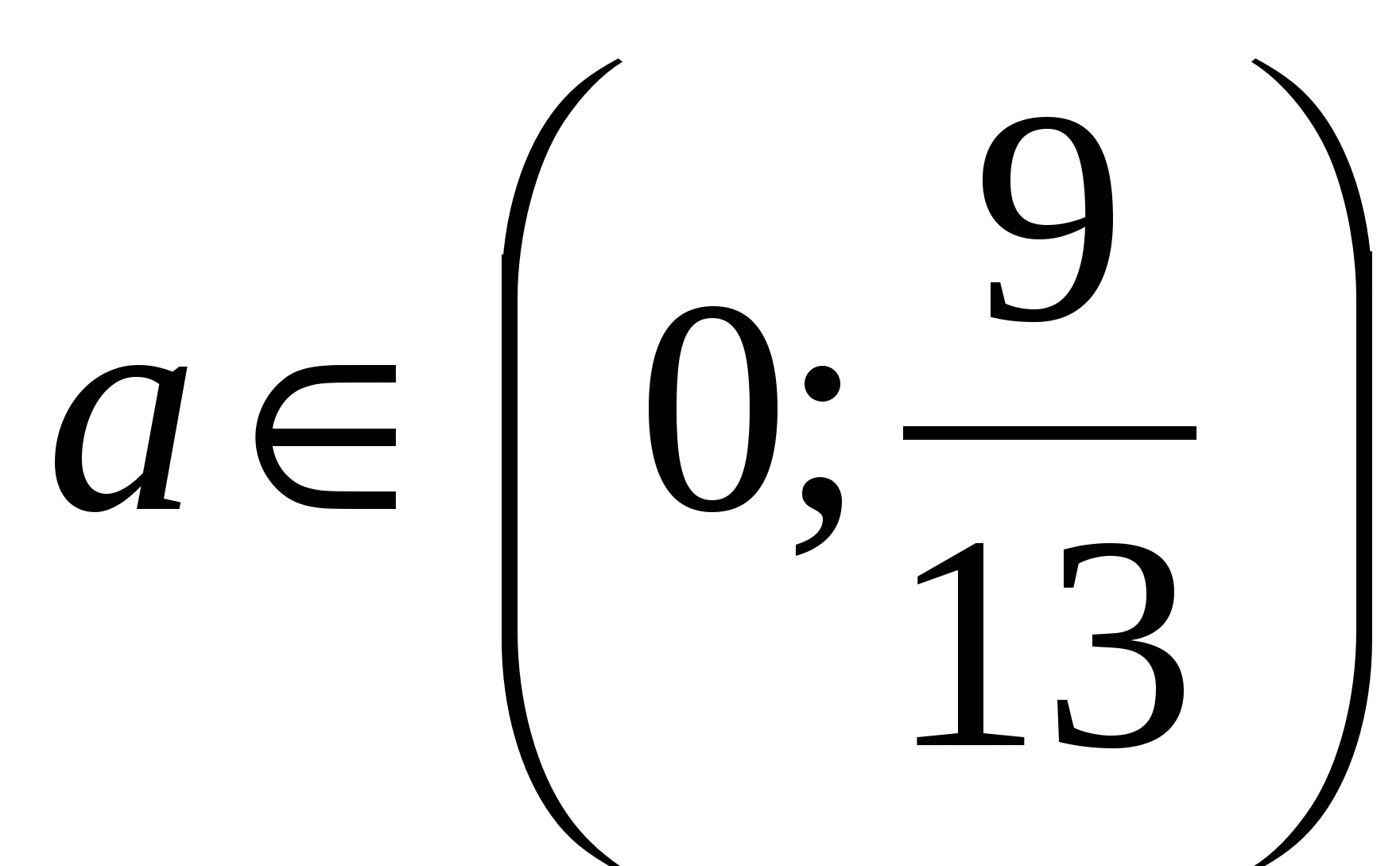 , то (*):
, то (*):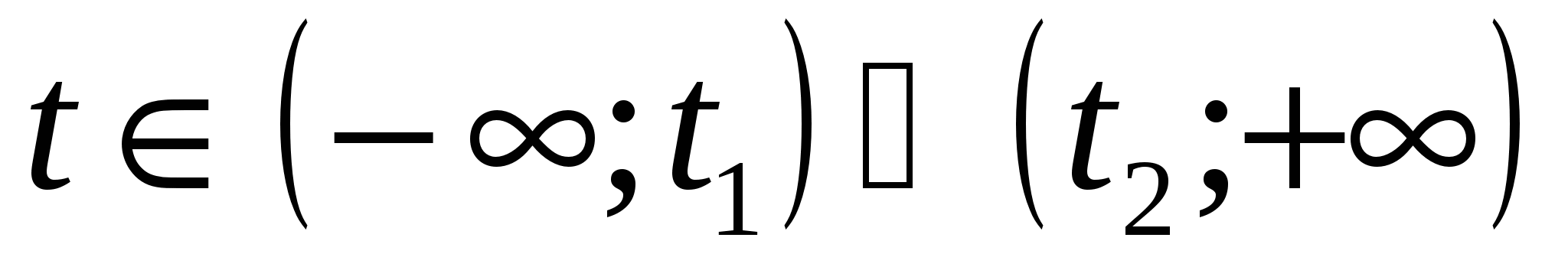 .
.
По условию задачи (**) Рис. 2 и Рис. 3:

Рис. 2
или

Рис. 3
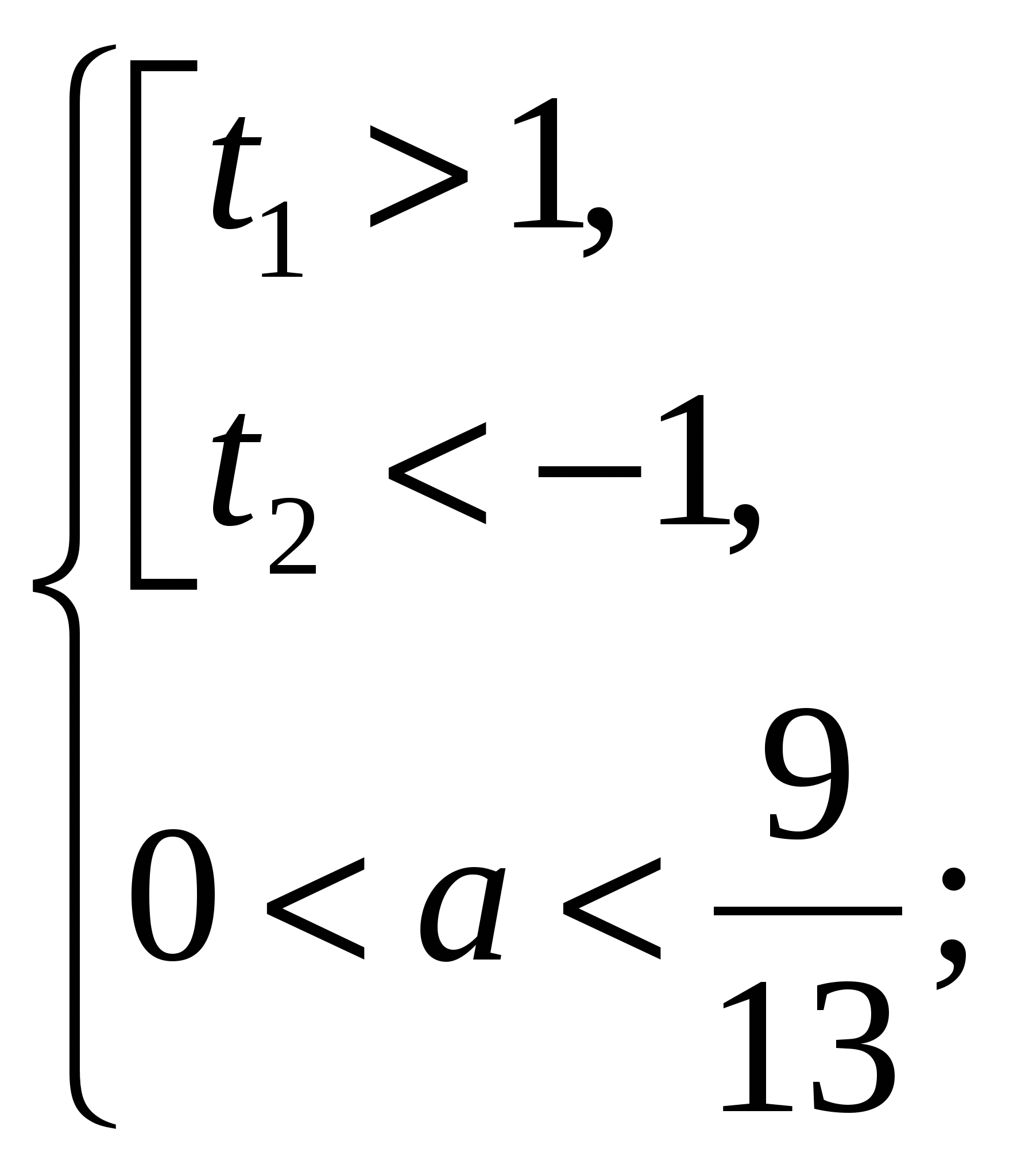
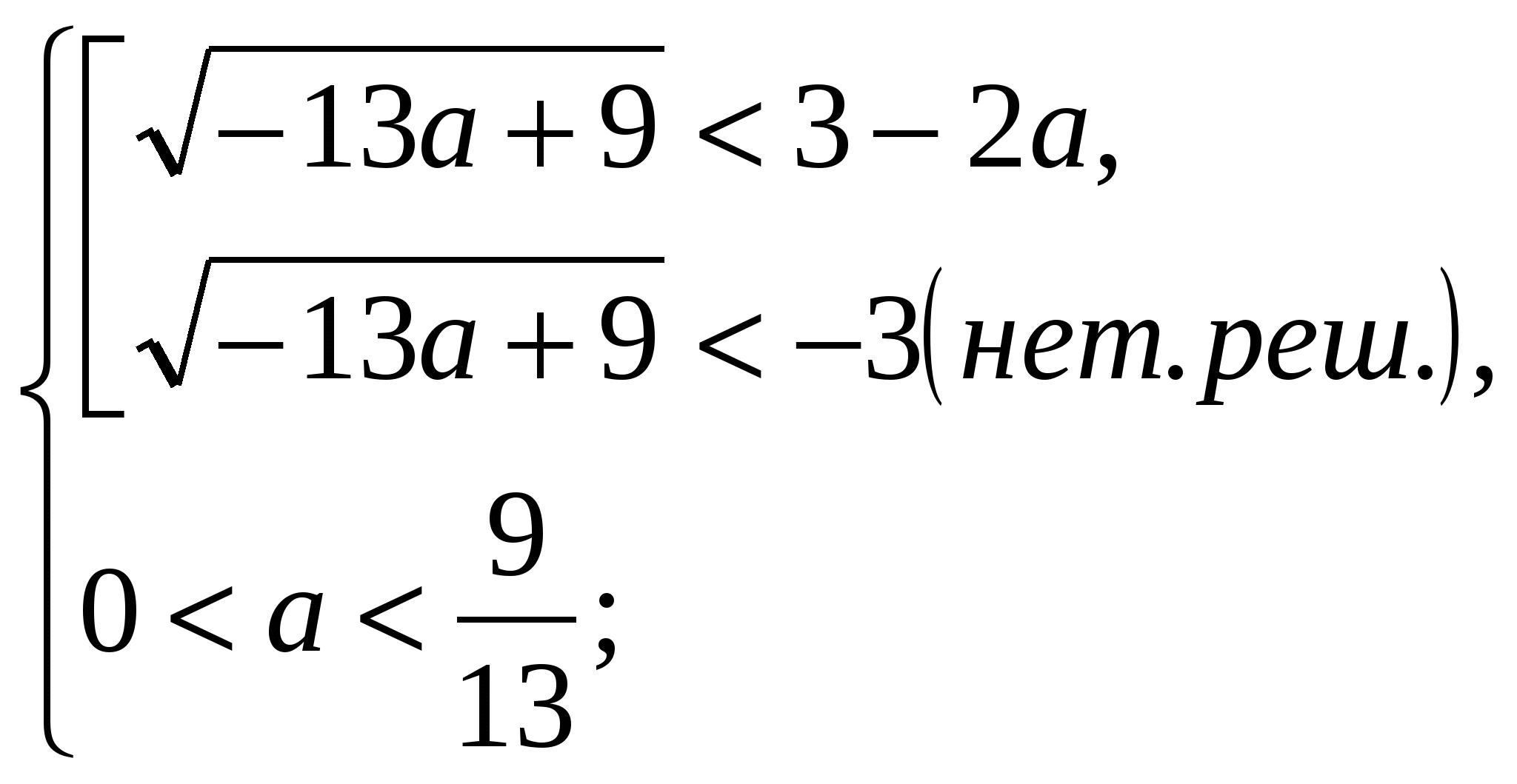
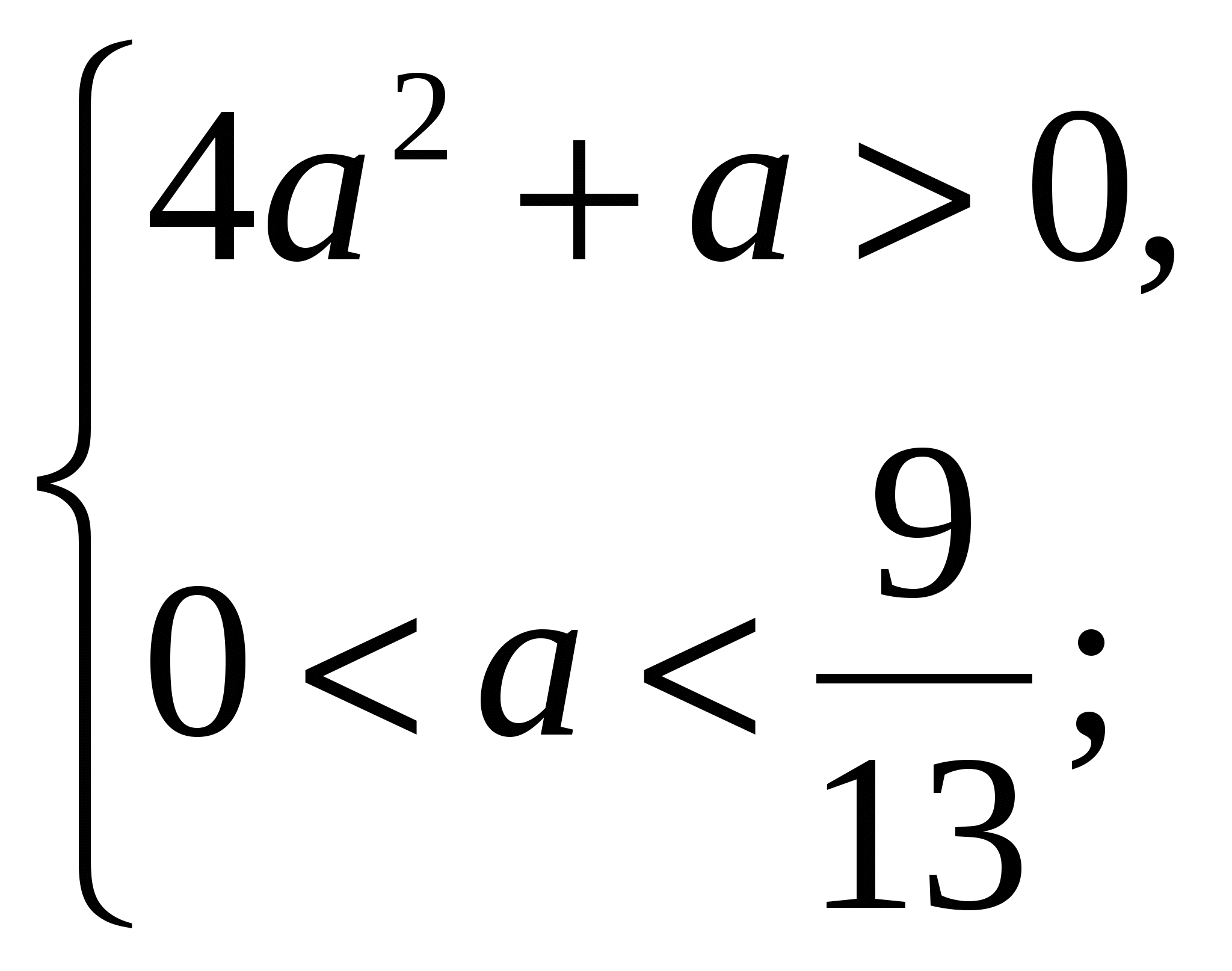
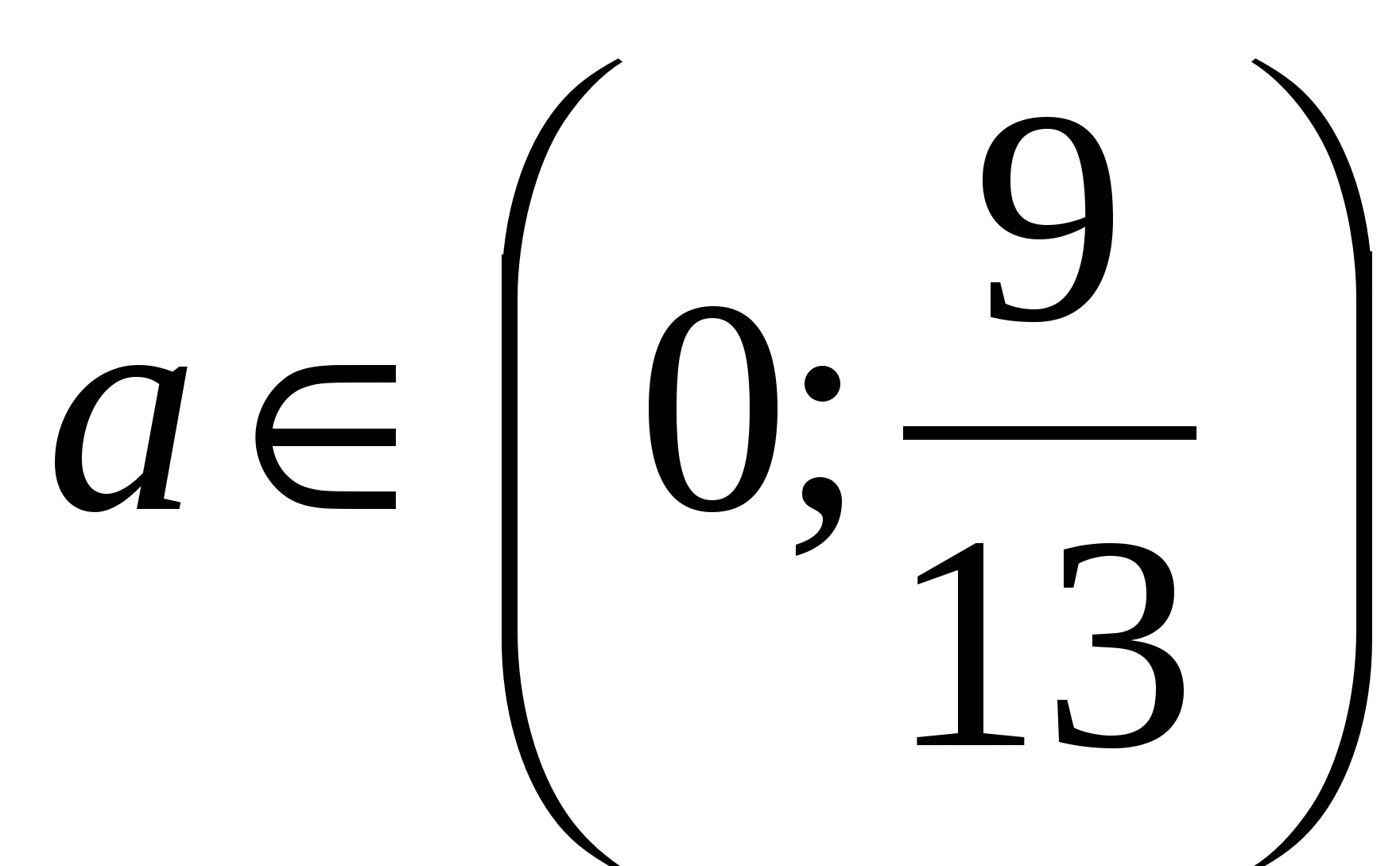 .
.
Рассмотрим случай в)
Если 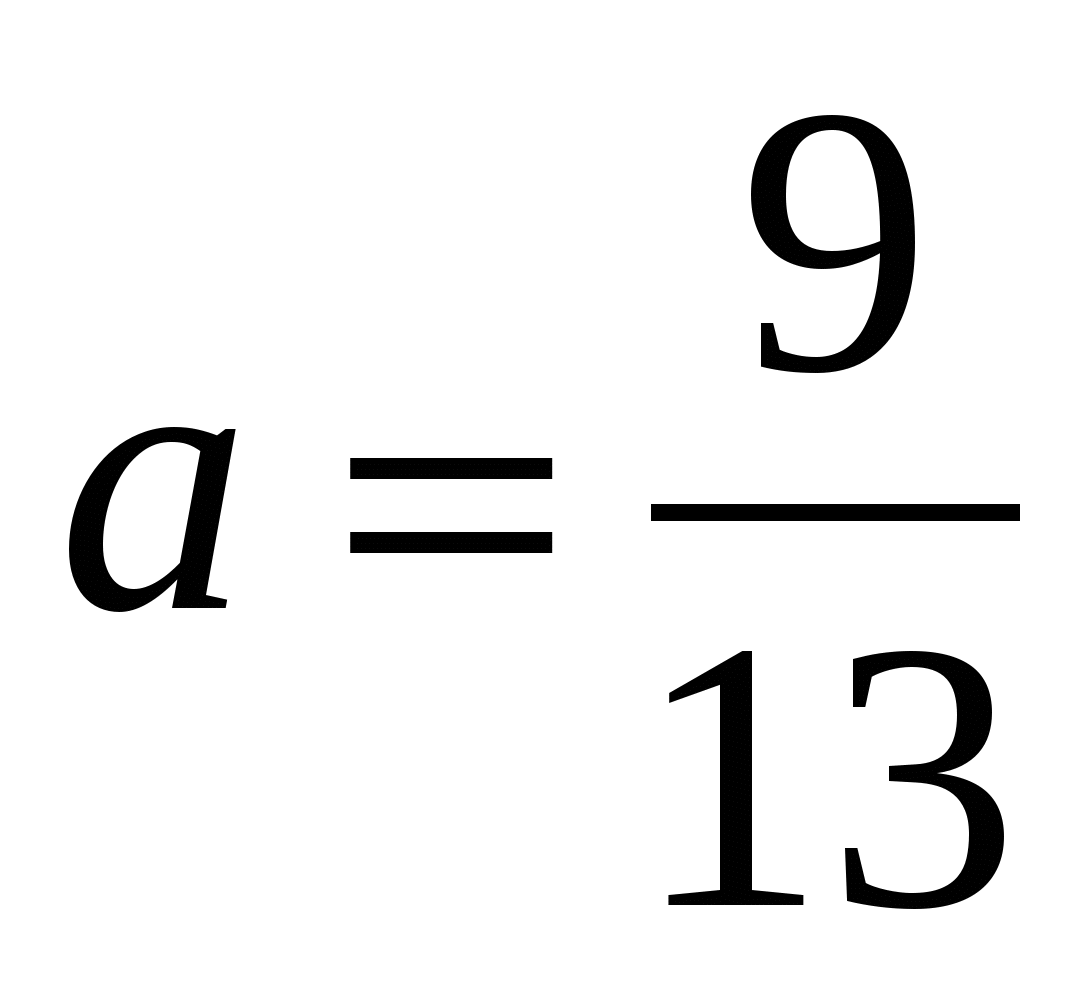 , то (*):
, то (*): 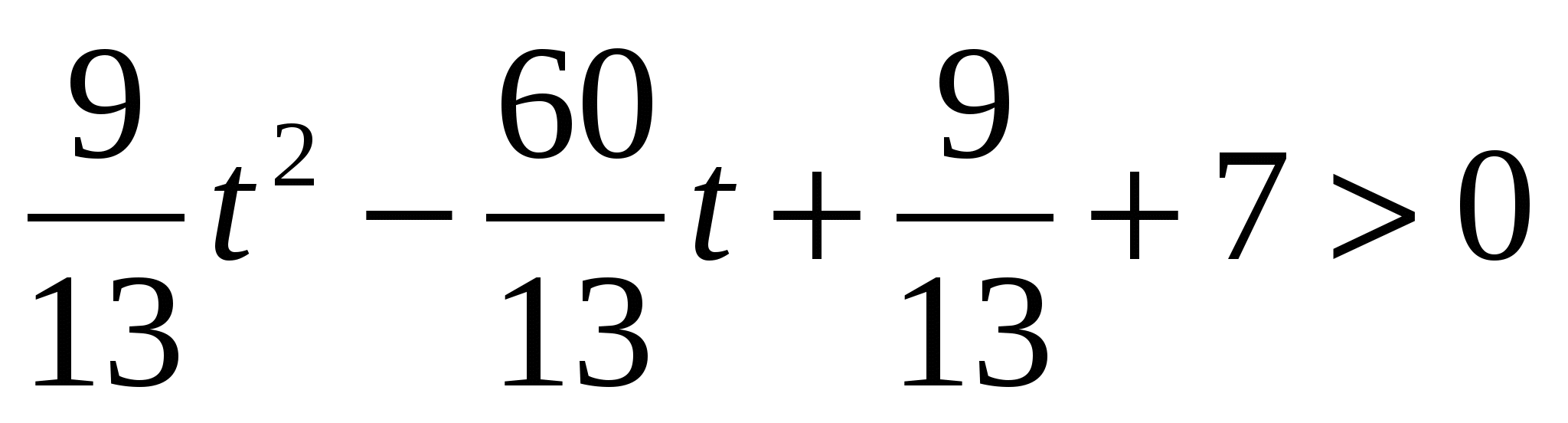 ;
; 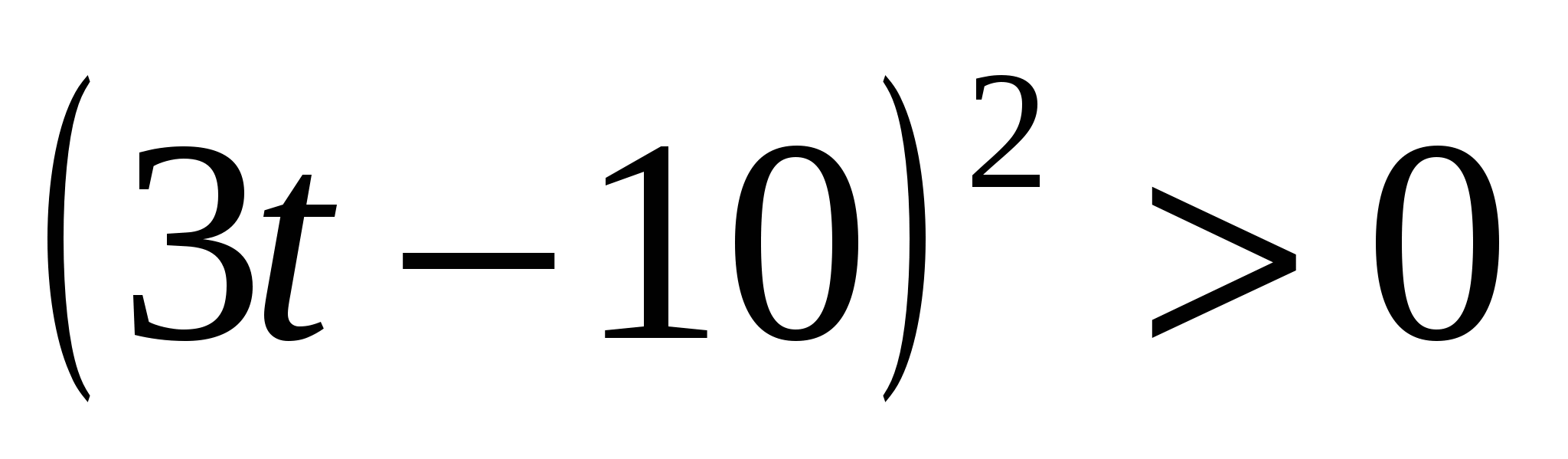 ;
; 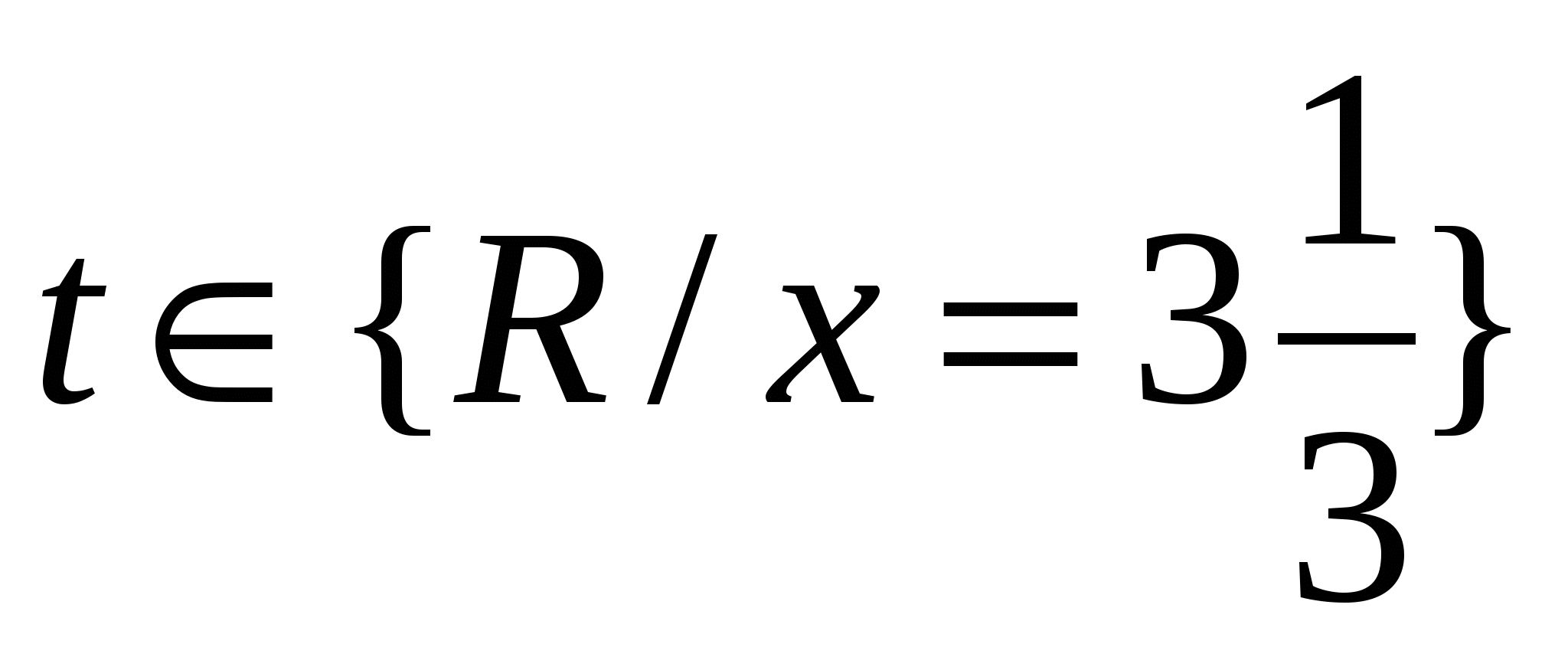 , что удовлетворяет условию задачи (**), значит
, что удовлетворяет условию задачи (**), значит 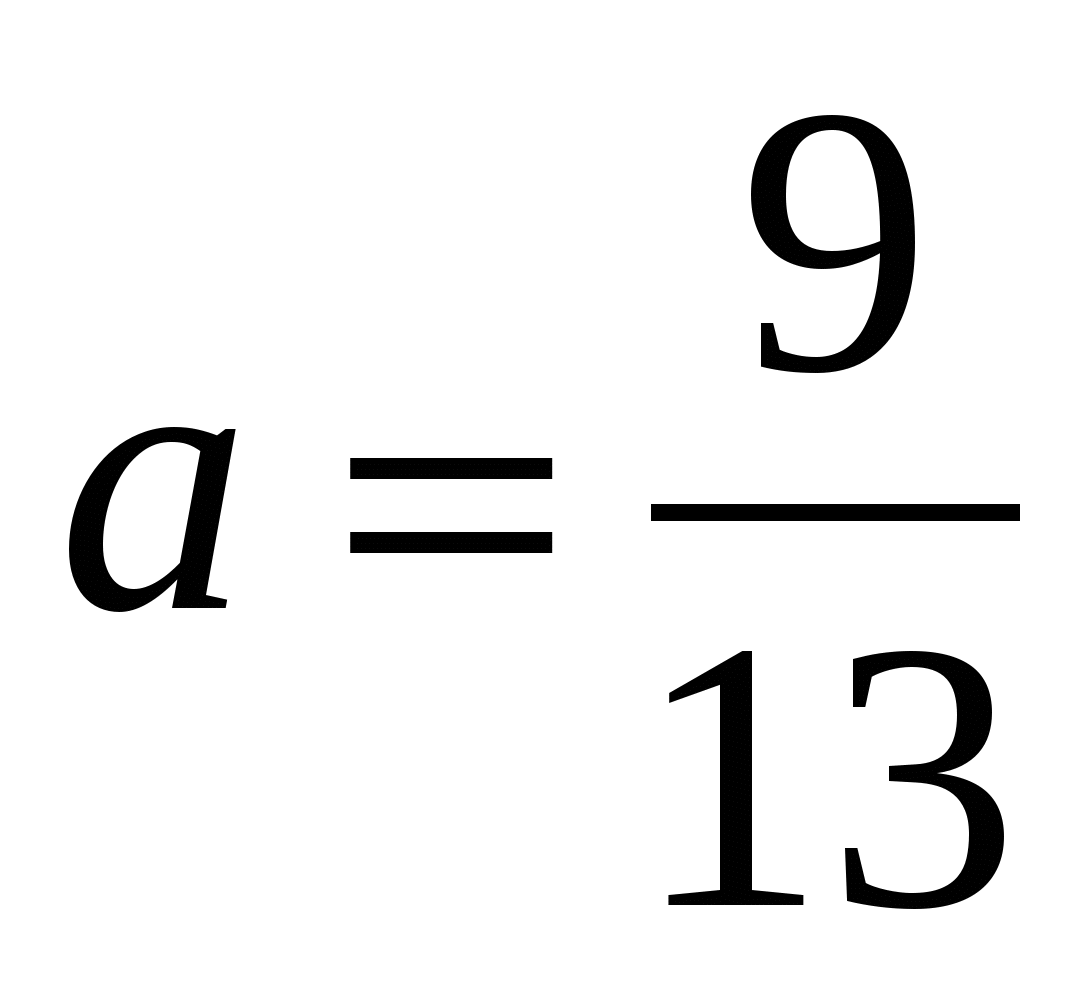 - одно из решений.
- одно из решений.
Рассмотрим случай г)
Если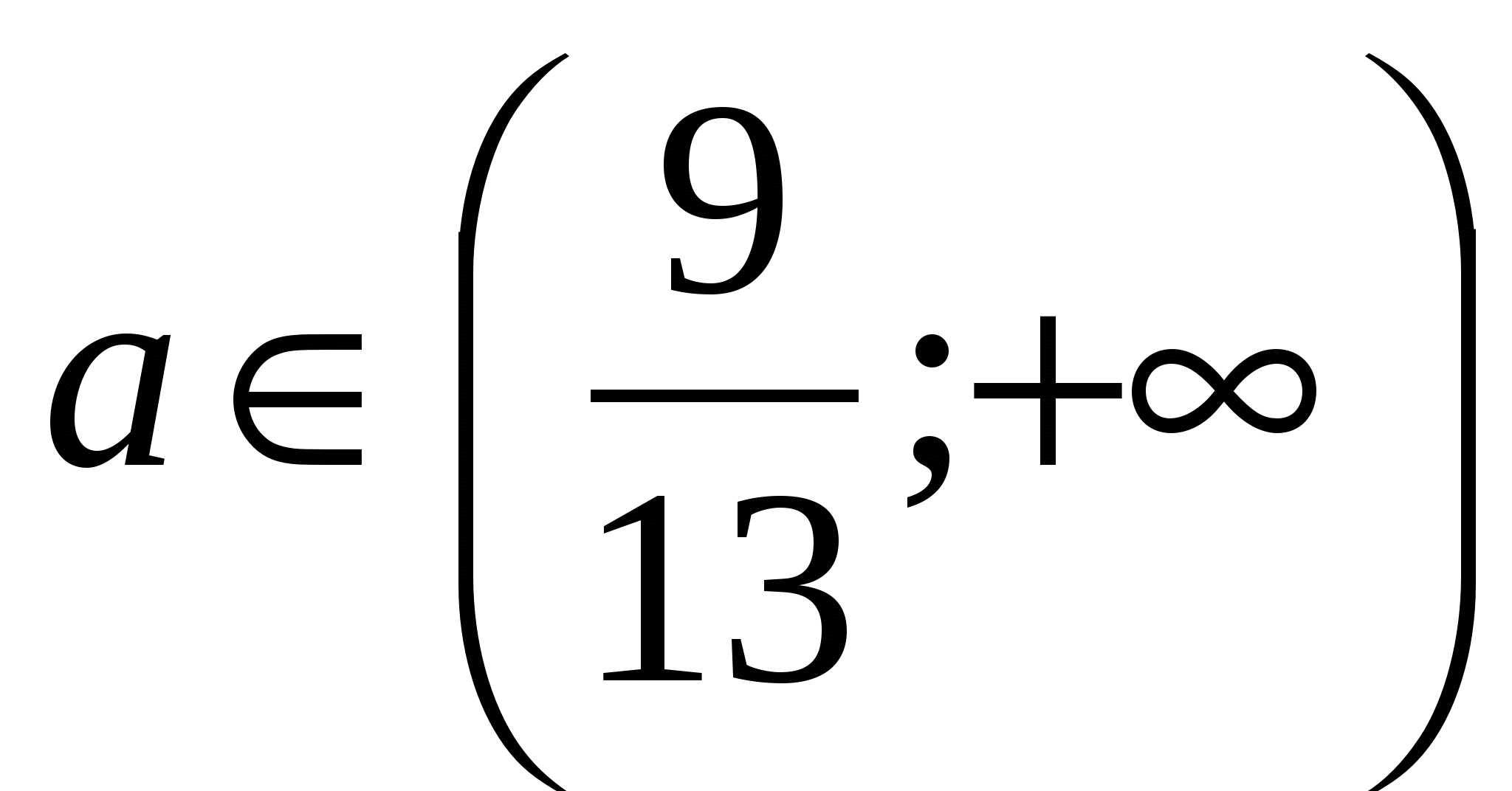 , то (*):
, то (*): 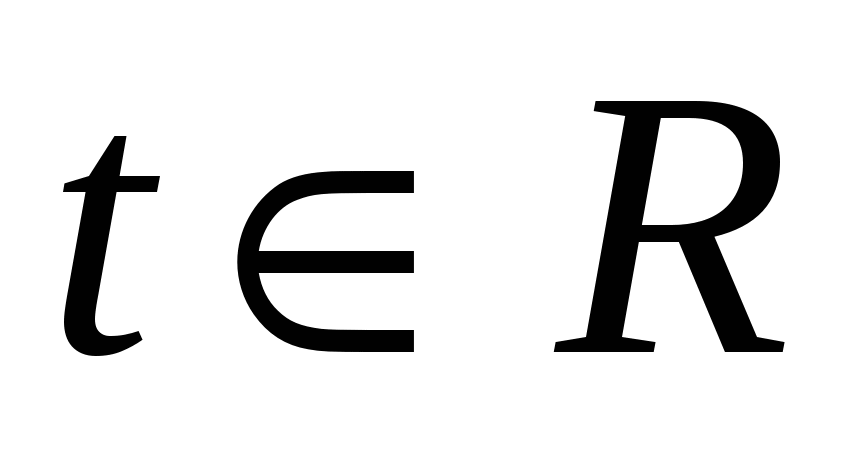 , что удовлетворяет условию задачи (**), значит
, что удовлетворяет условию задачи (**), значит 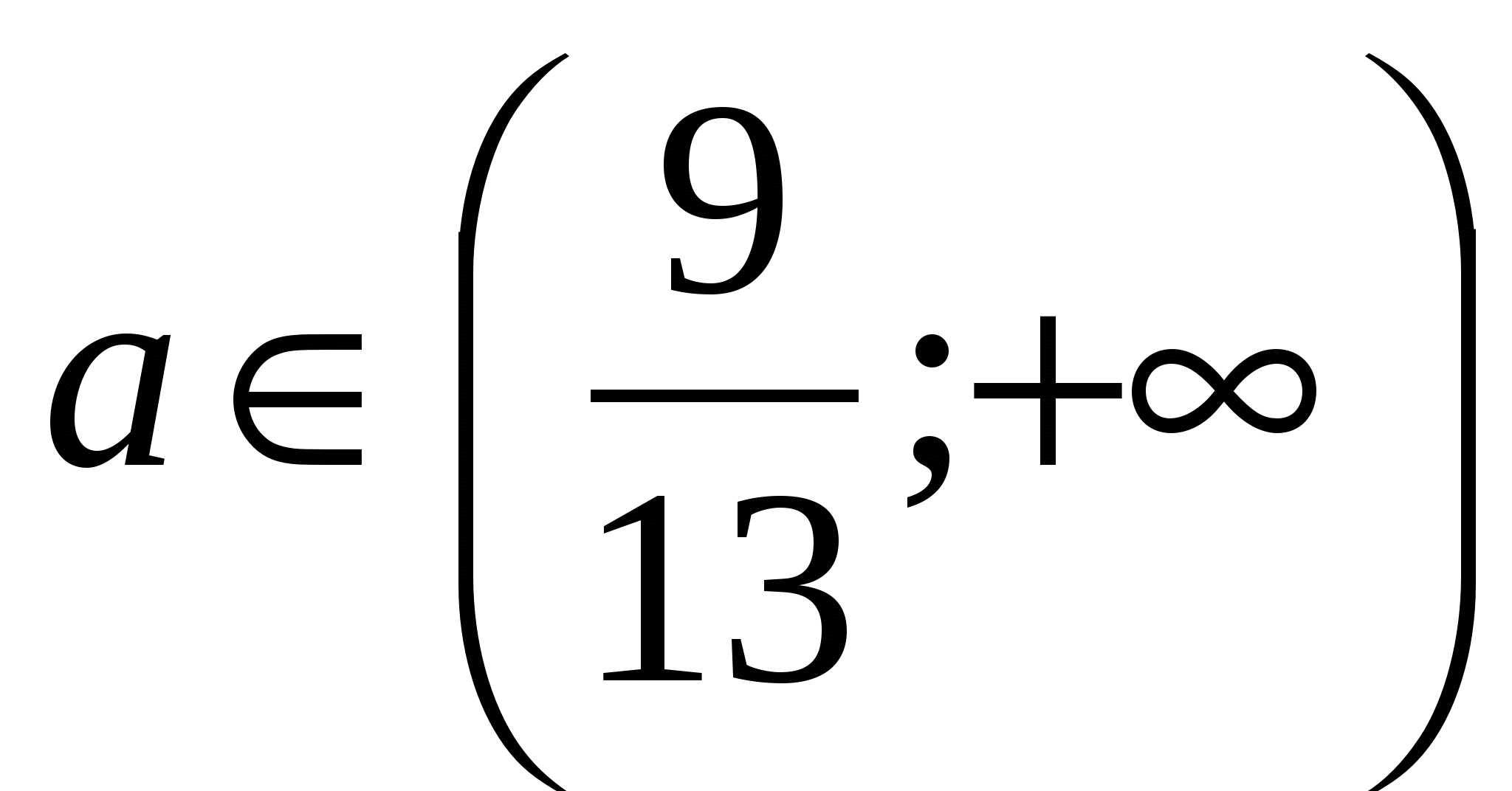 - промежуток содержащий решение.
- промежуток содержащий решение.
Ответ: 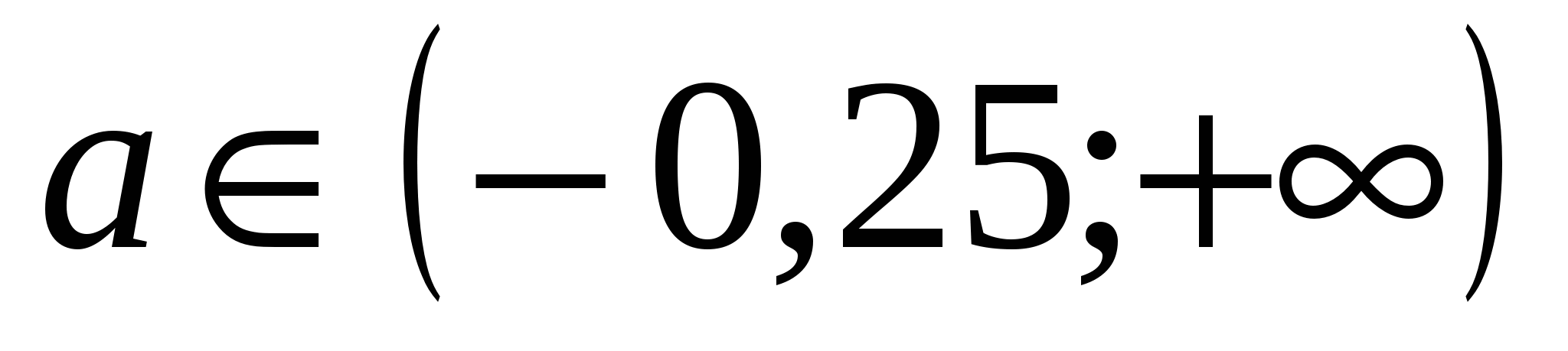
3. Актуализация знаний по теме «Исследование квадратного трёхчлена»
Пусть задан квадратный трехчлен вида 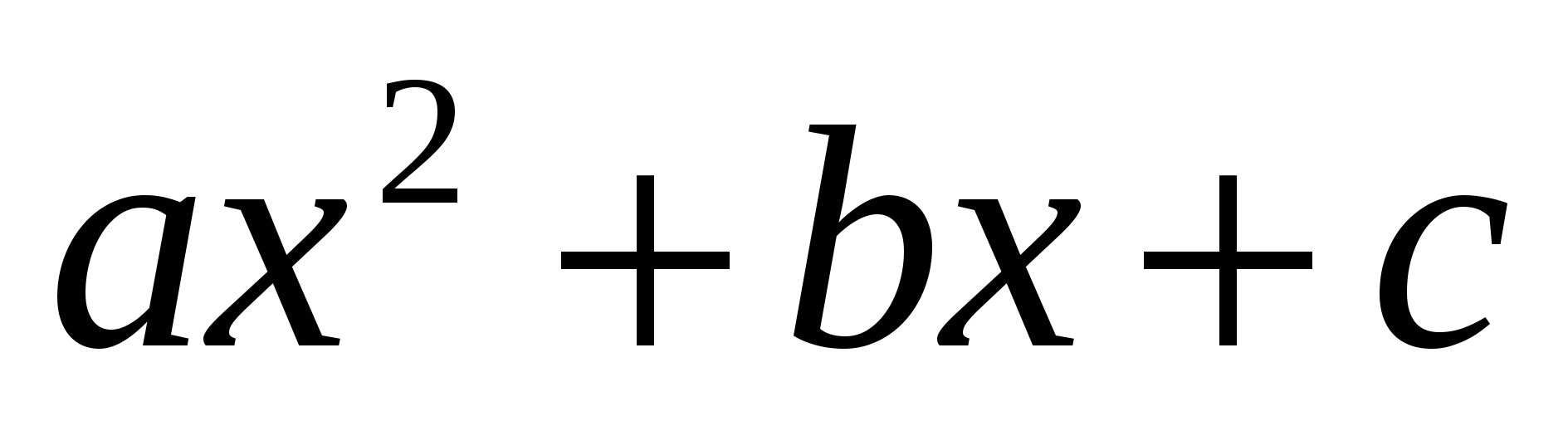 ,
, 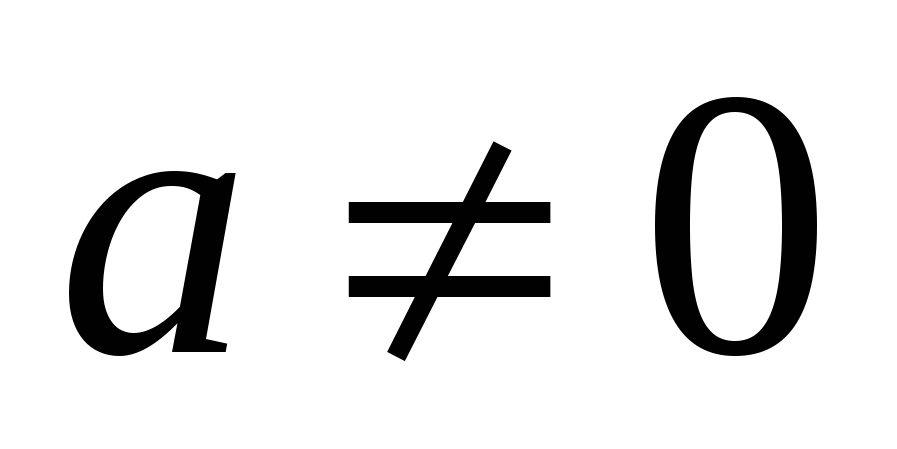 . Пусть
. Пусть 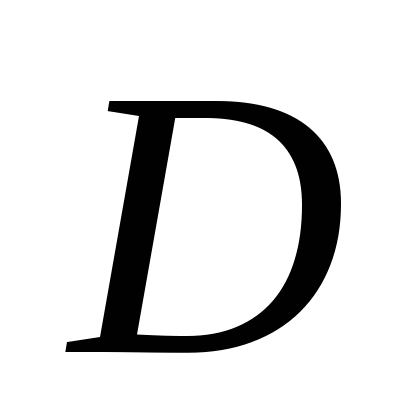 − дискриминант этого трехчлена, а
− дискриминант этого трехчлена, а 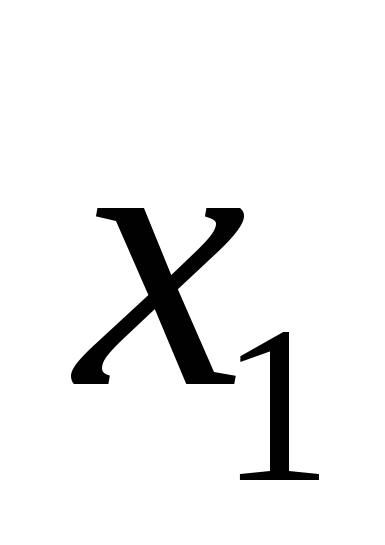 и
и 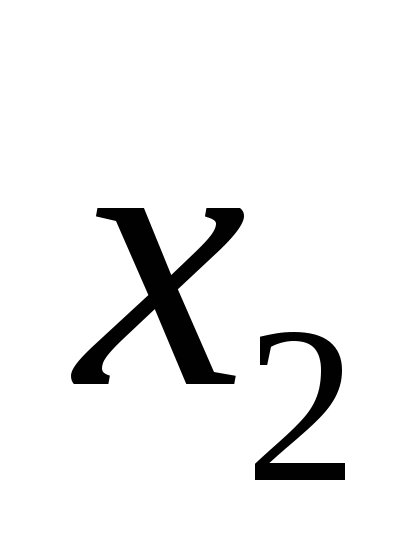 − его корни, причем
− его корни, причем 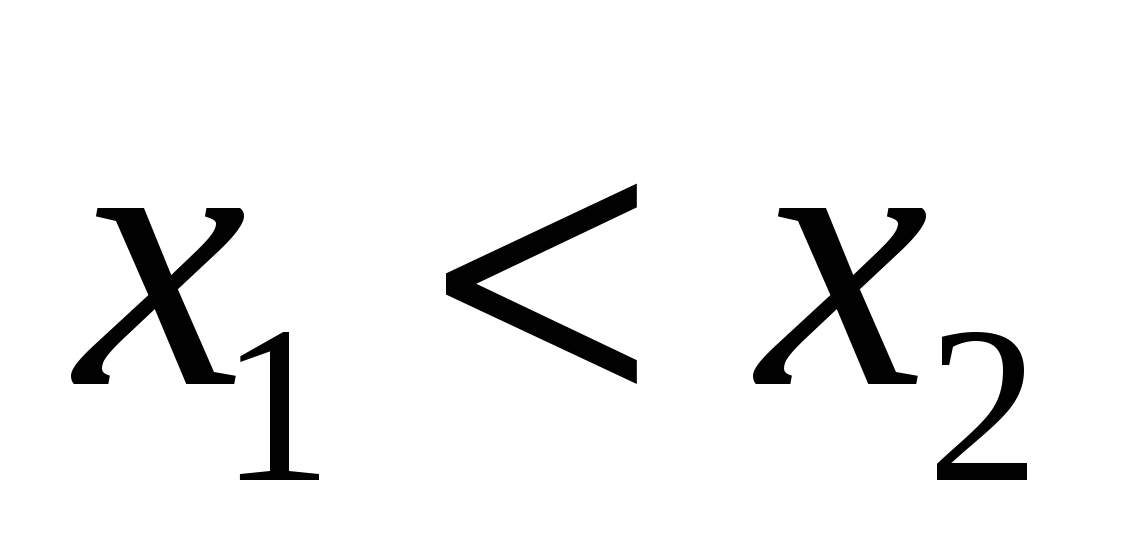 .
.
Рассмотрим квадратичную функцию 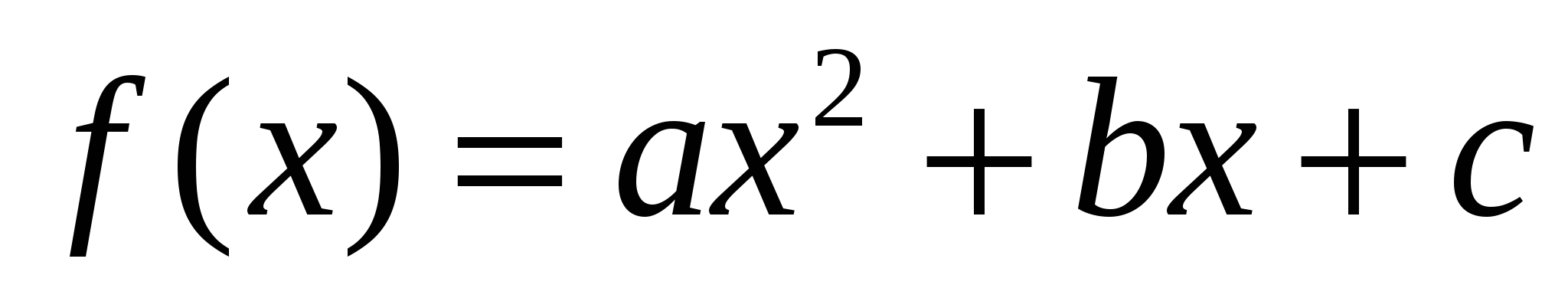
Для 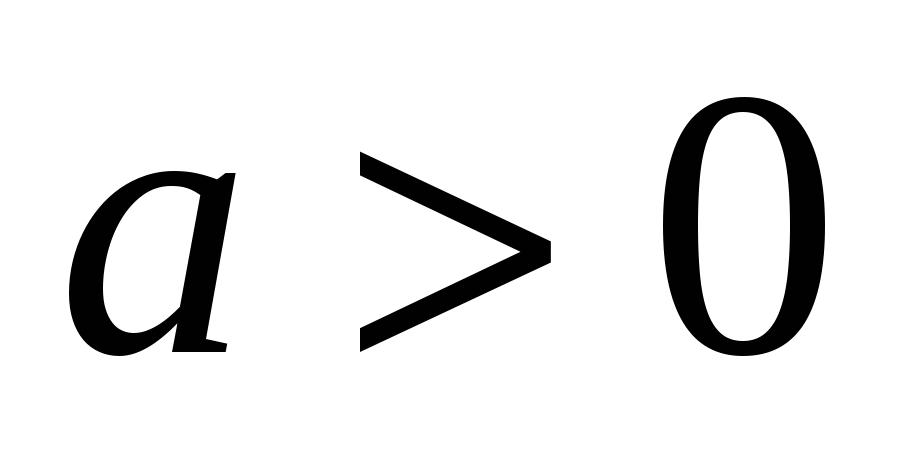 :
:
Задача по исследованию квадратного трёхчлена
Рисунок
Задача по исследованию неравенства
Для того чтобы  (Рис. 8) необходимо и достаточно выполнение системы условий:
(Рис. 8) необходимо и достаточно выполнение системы условий: 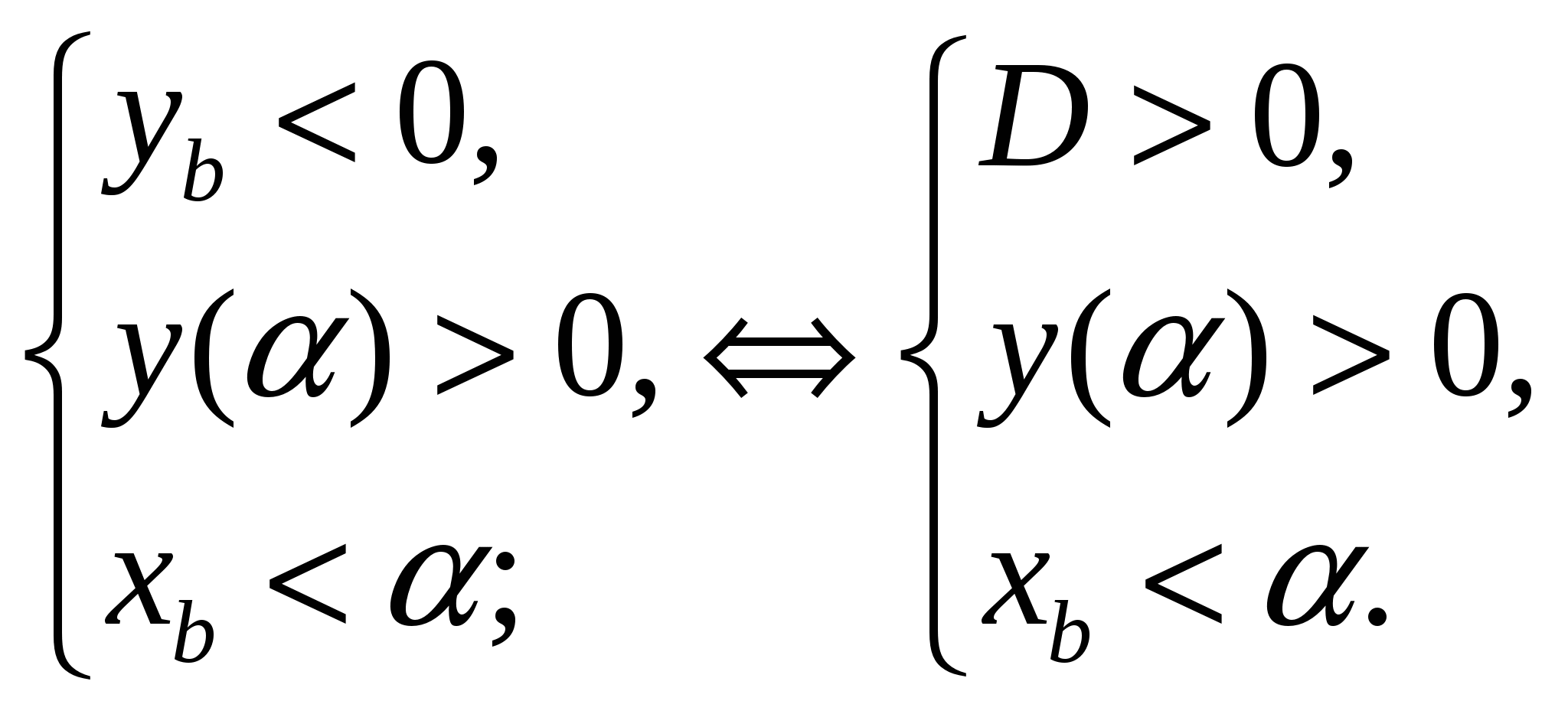
Рис.4
Для того чтобы множество 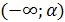 являлось подмножеством множества решений неравенства
являлось подмножеством множества решений неравенства 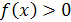
необходимо и достаточно выполнение системы условий: 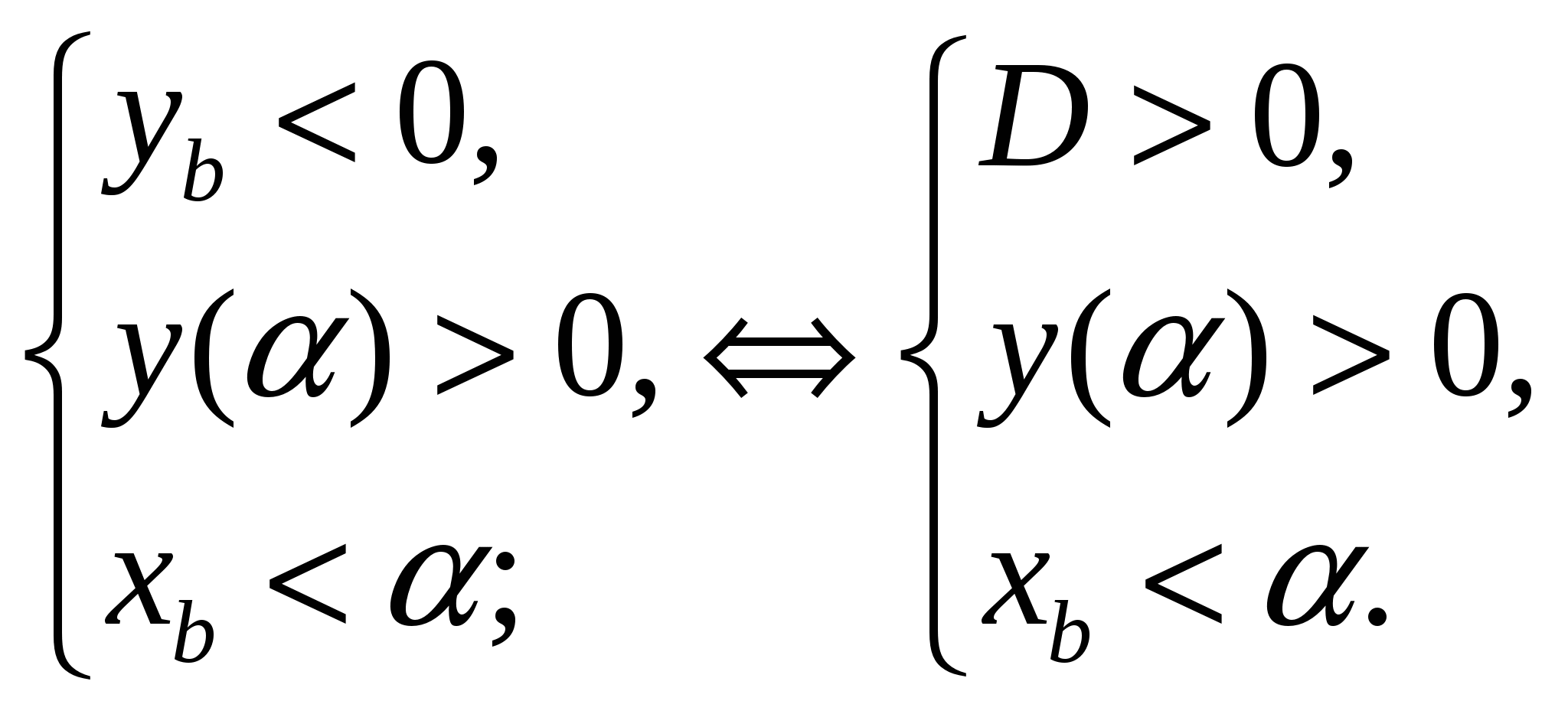
Для того чтобы 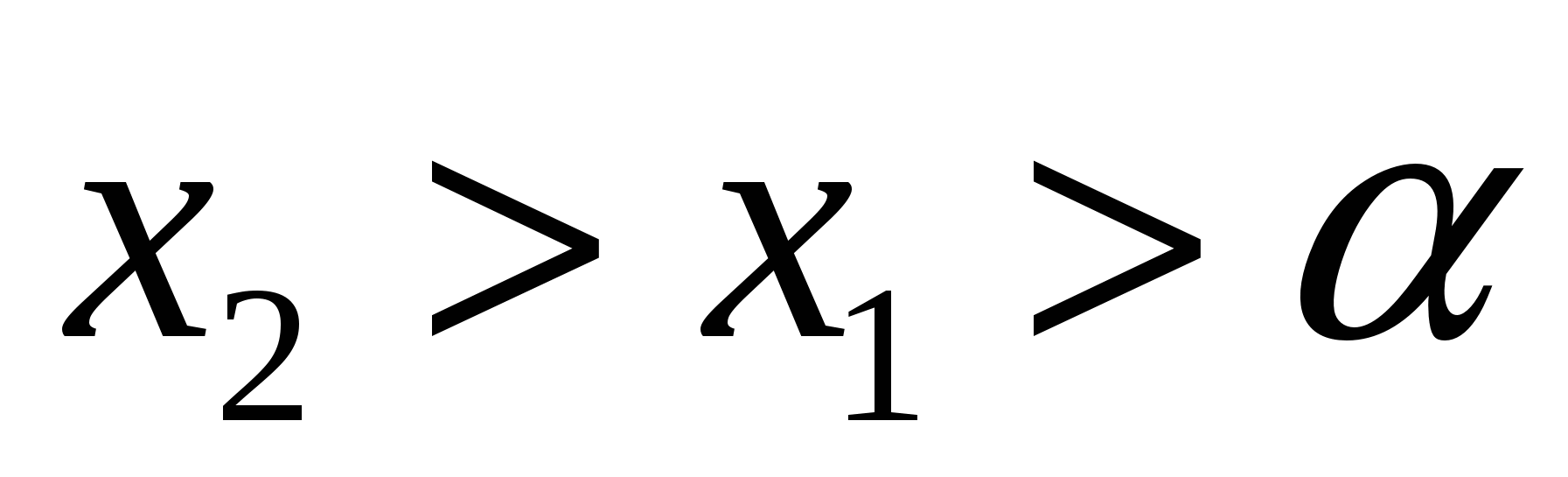 (Рис. 9) необходимо и достаточно выполнение системы условий:
(Рис. 9) необходимо и достаточно выполнение системы условий: 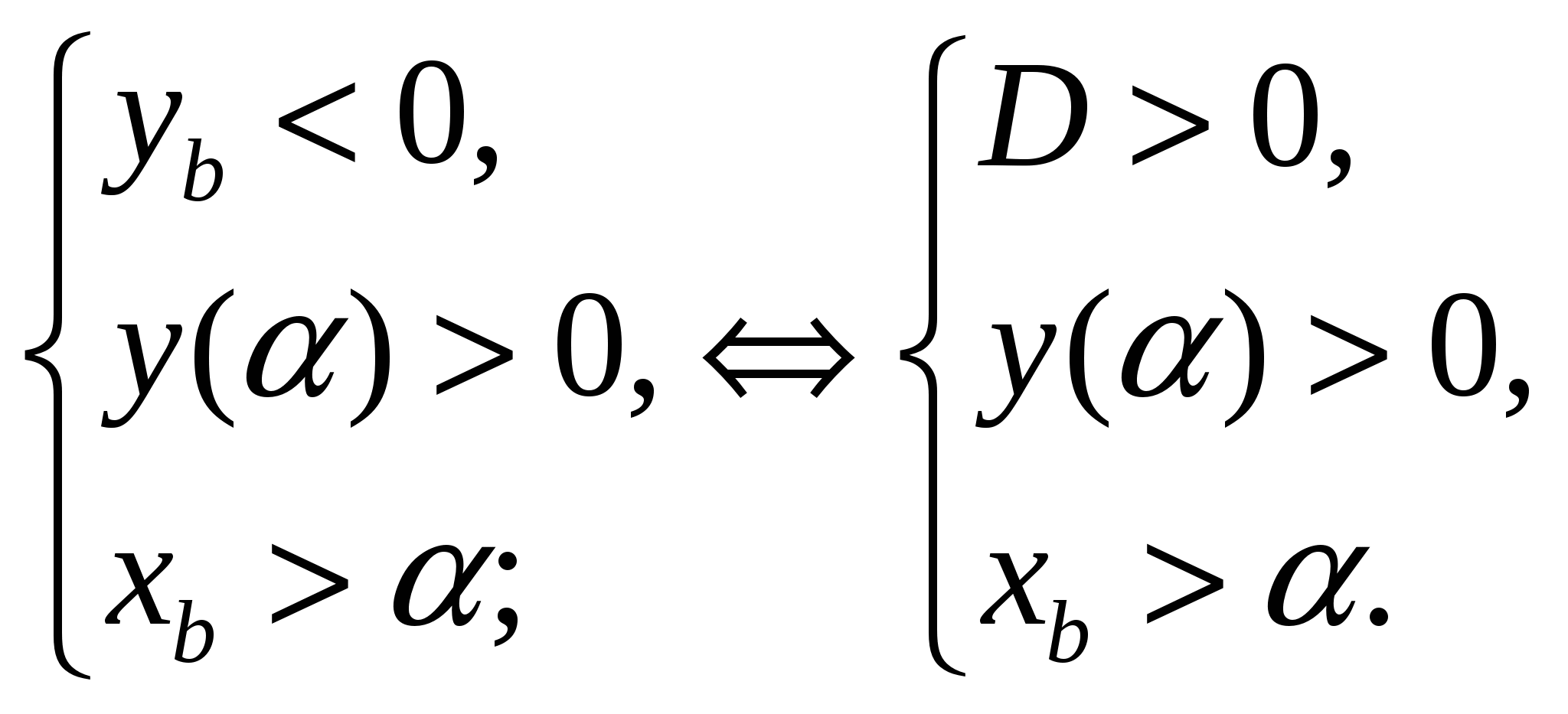
Рис.5
Для того чтобы множество 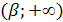 являлось подмножеством множества решений неравенства
являлось подмножеством множества решений неравенства 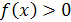 необходимо и достаточно выполнение системы условий:
необходимо и достаточно выполнение системы условий: 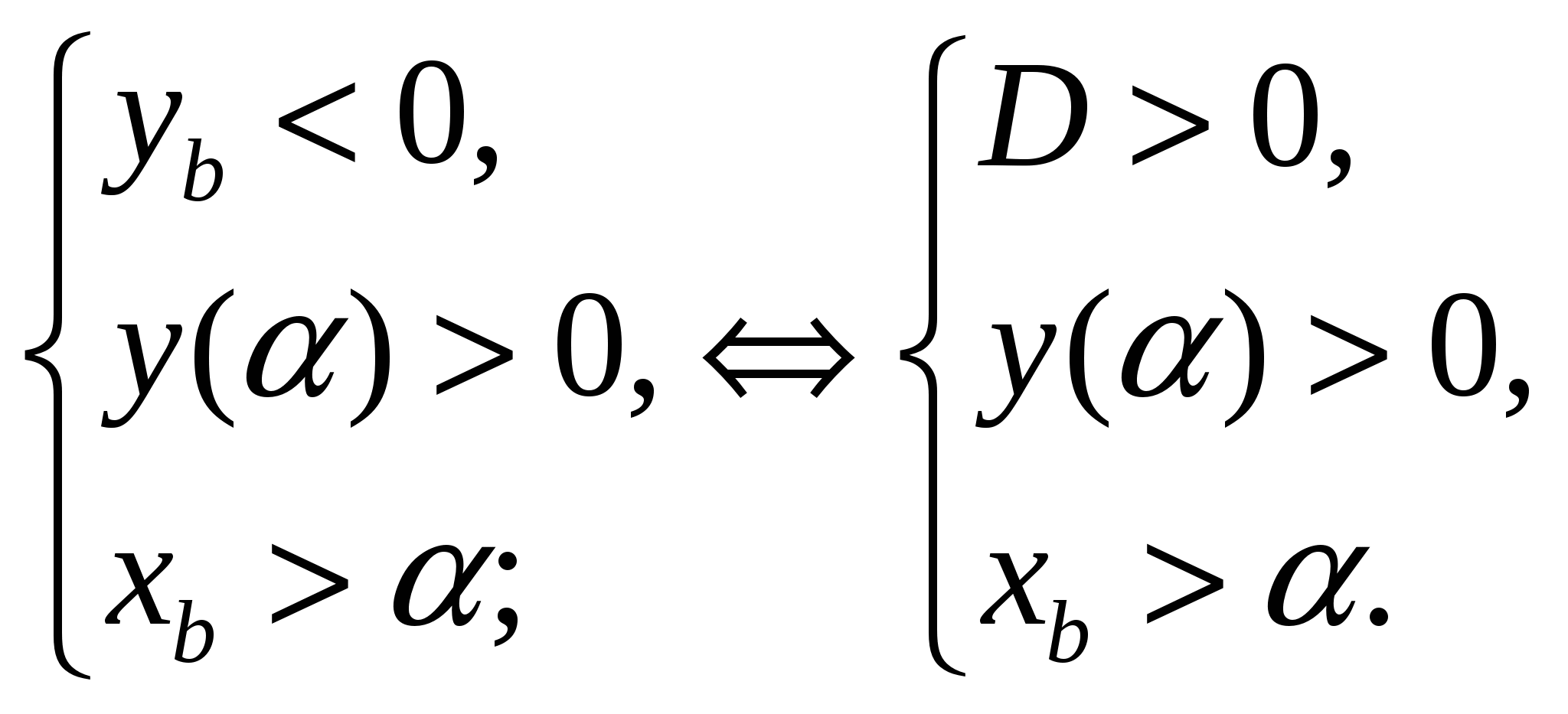
Для того, чтобы 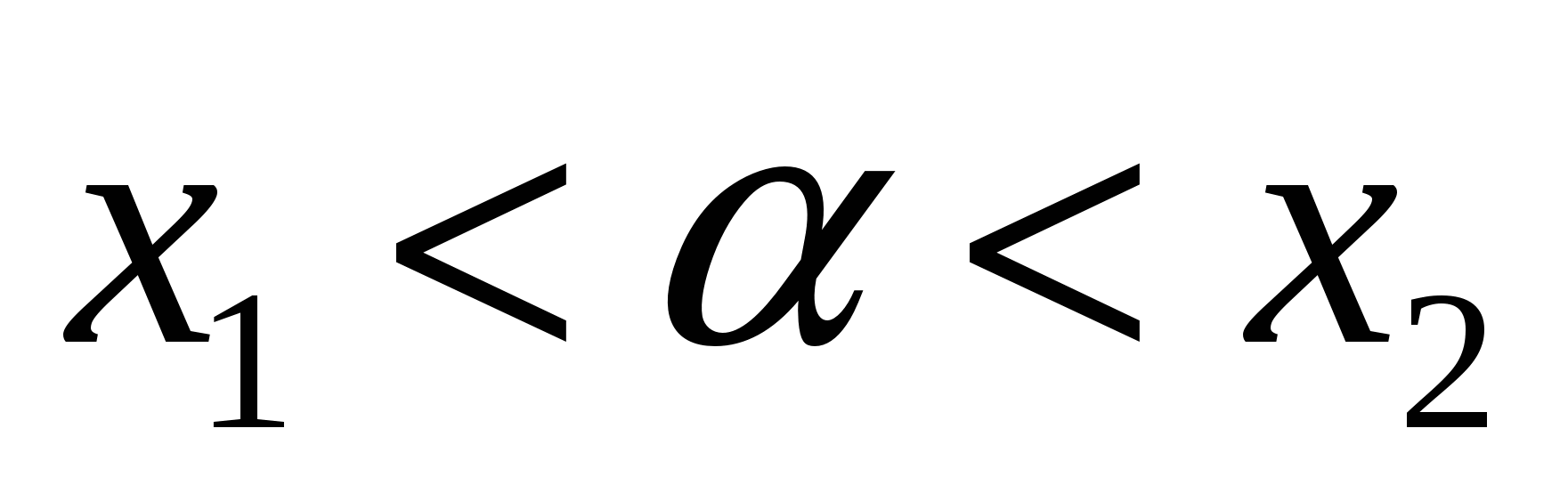 (Рис. 10) необходимо и достаточно выполнение условия:
(Рис. 10) необходимо и достаточно выполнение условия: 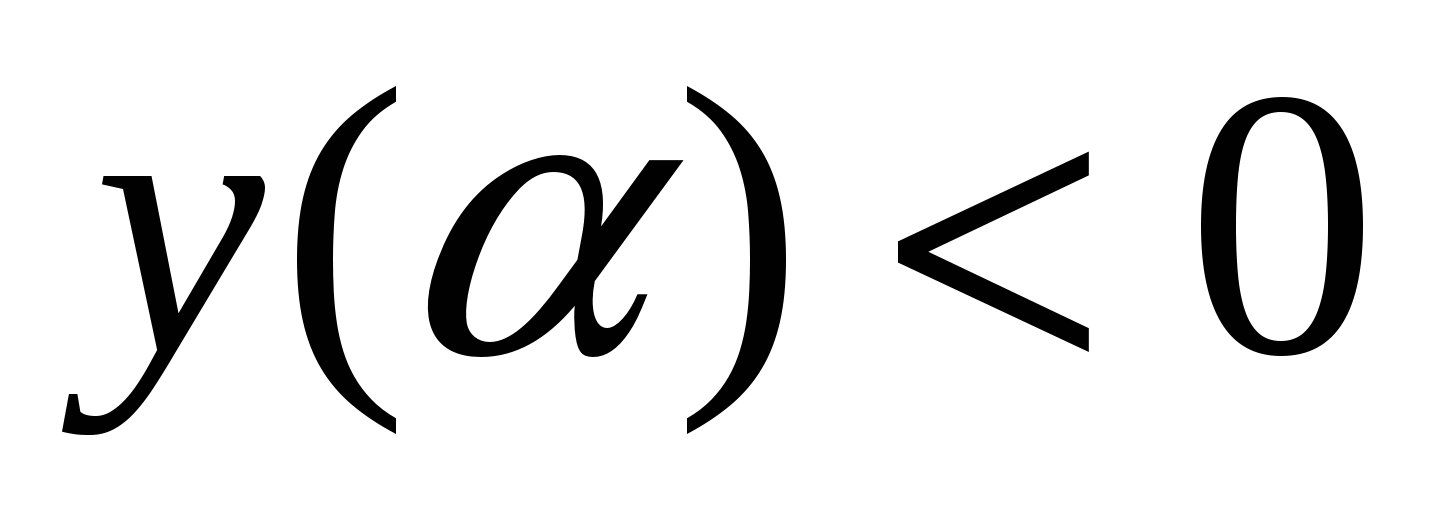 .
.
Рис.6
Для того чтобы множество 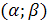 являлось подмножеством множества решений неравенства
являлось подмножеством множества решений неравенства 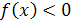 необходимо и достаточно выполнение условия:
необходимо и достаточно выполнение условия: 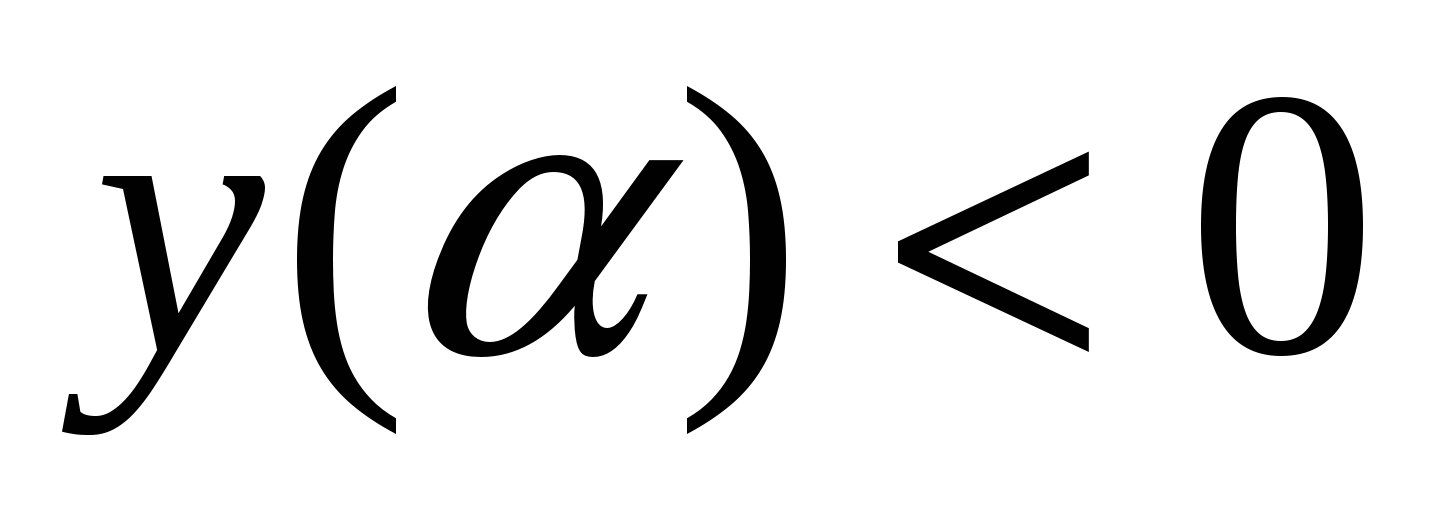 .
.
Для 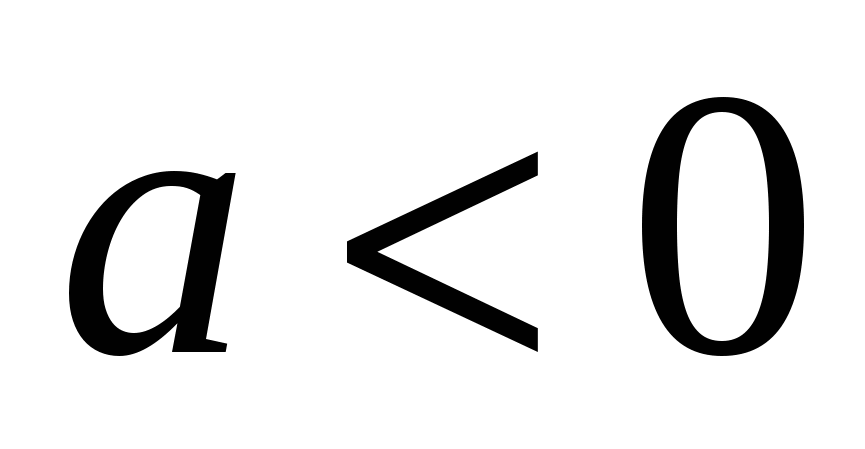 :
:
Задача по исследованию квадратного трёхчлена
Рисунок
Задача по исследованию неравенства
Для того чтобы  (Рис. 8) необходимо и достаточно выполнение системы условий:
(Рис. 8) необходимо и достаточно выполнение системы условий: 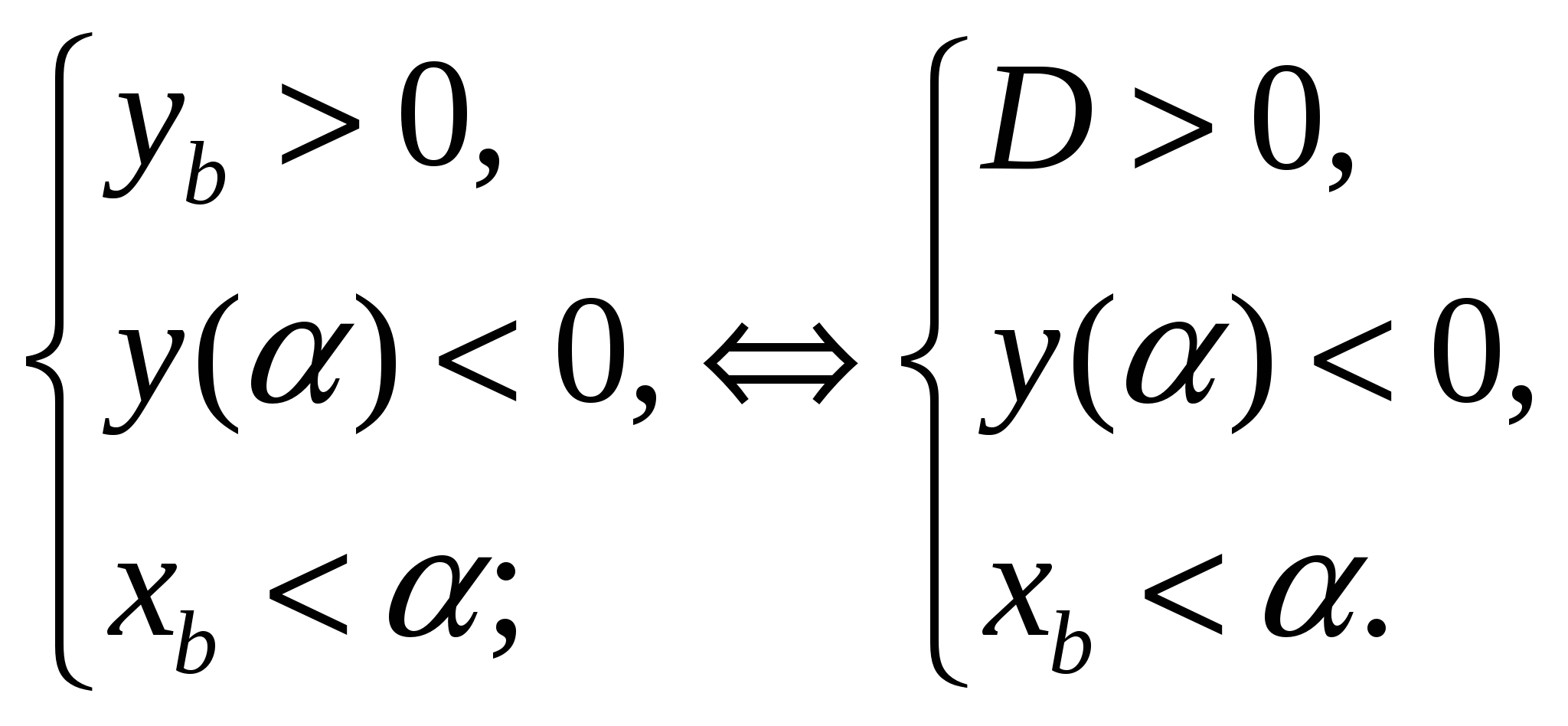
Рис.7
Для того чтобы множество 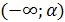 являлось подмножеством множества решений неравенства
являлось подмножеством множества решений неравенства 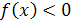 необходимо и достаточно выполнение системы условий:
необходимо и достаточно выполнение системы условий: 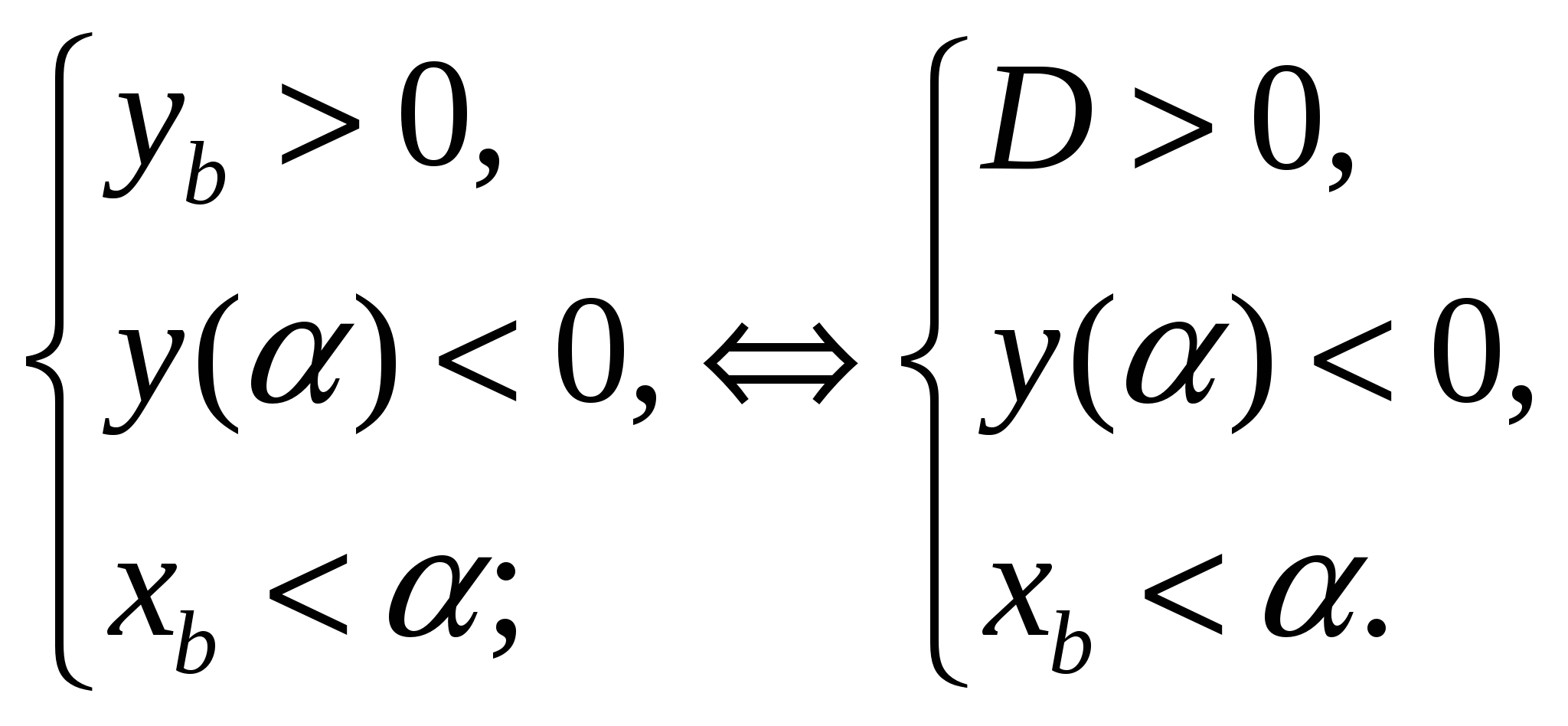
Для того чтобы 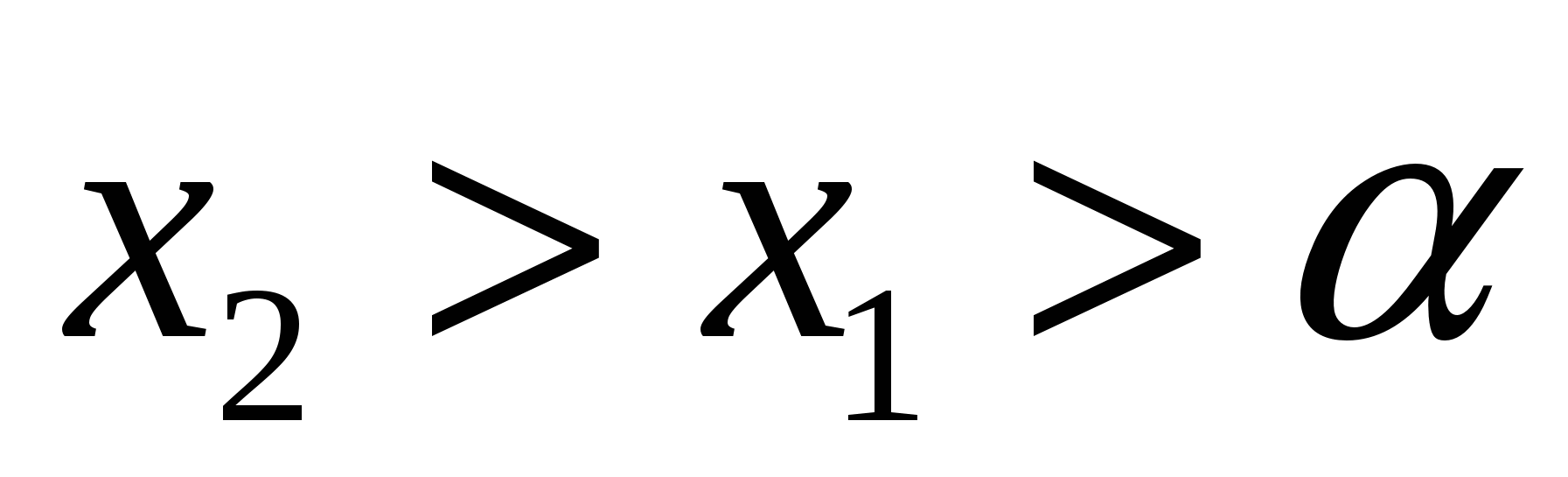 (Рис. 9) необходимо и достаточно выполнение системы условий:
(Рис. 9) необходимо и достаточно выполнение системы условий: 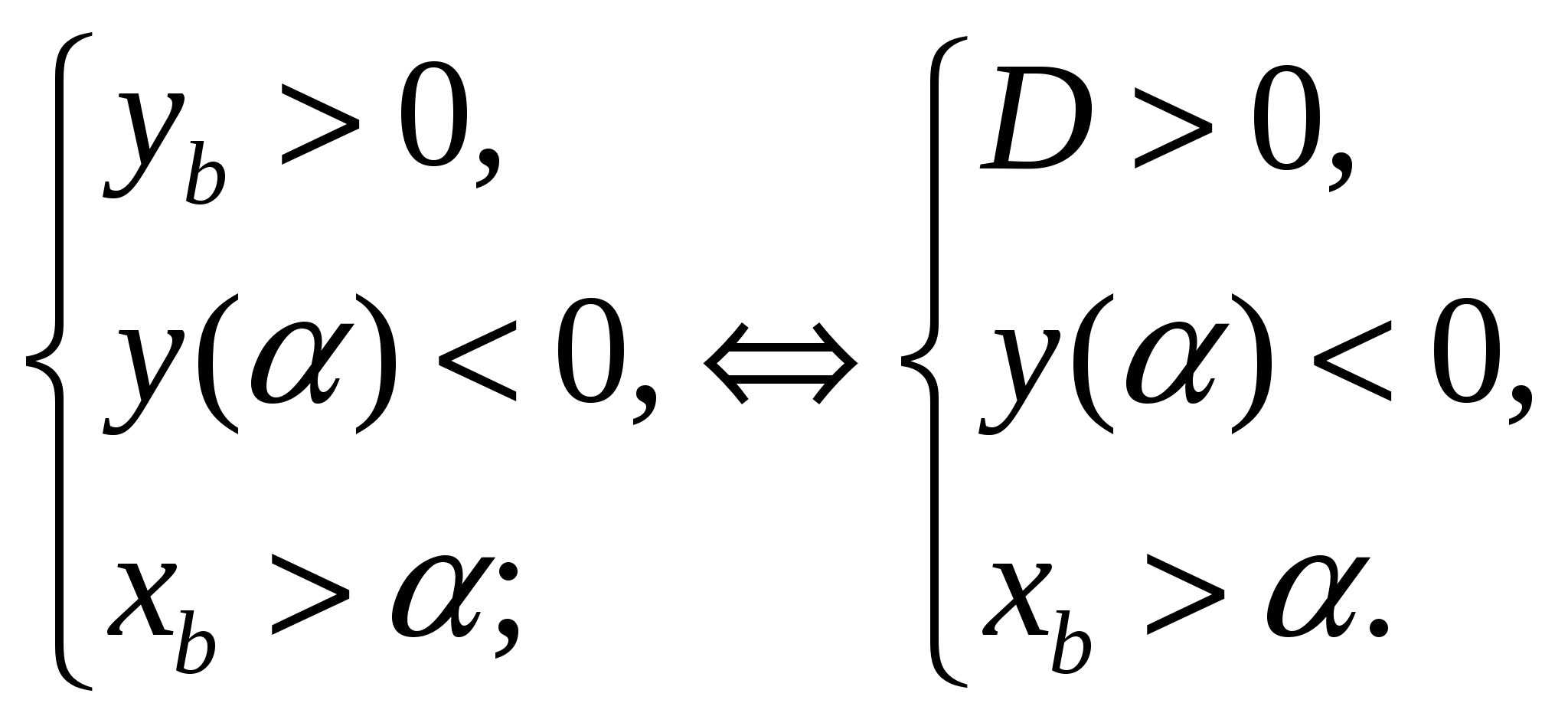
Рис.8
Для того чтобы множество 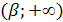 являлось подмножеством множества решений неравенства
являлось подмножеством множества решений неравенства 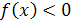 необходимо и достаточно выполнение системы условий:
необходимо и достаточно выполнение системы условий: 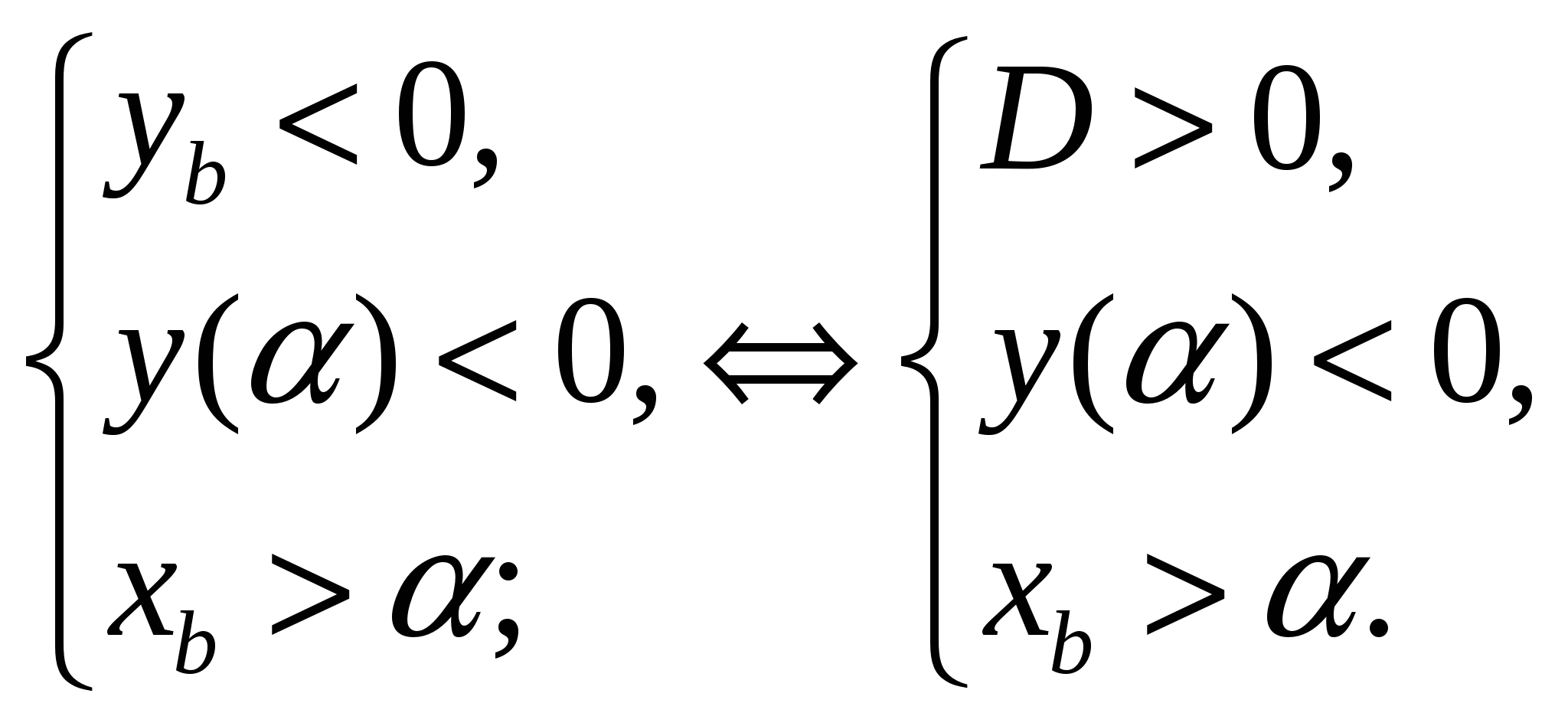
Для того, чтобы 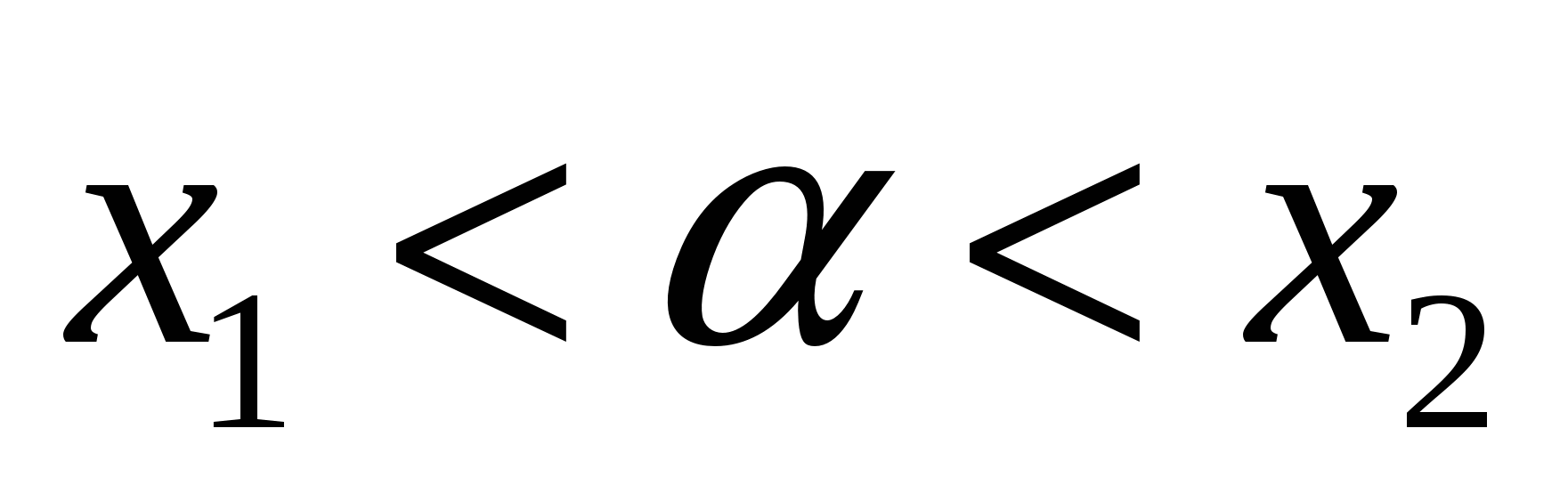 (Рис. 10) необходимо и достаточно выполнение условия:
(Рис. 10) необходимо и достаточно выполнение условия:  .
.
Рис.9
Для того чтобы множество 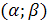 являлось подмножеством множества решений неравенства
являлось подмножеством множества решений неравенства 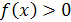 необходимо и достаточно выполнение условия:
необходимо и достаточно выполнение условия:  .
.
Упражнения.
Задание
Рисунок
Решение
а) Пусть заданы функции  , причём
, причём 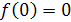 , и
, и 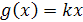 .
.
Запишите условия для ситуации: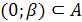 , где А – множество решений неравенства
, где А – множество решений неравенства 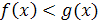 .
.
Рис.10
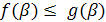
б) Пусть заданы функции 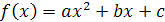 , причём
, причём 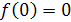 , и
, и 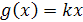 .
.
Запишите условия для ситуации: 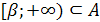 , где А – множество решений неравенства
, где А – множество решений неравенства 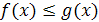 .
.
Рис.11
Рис.12
Рис.11: при 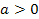 нет решений;
нет решений;
Рис.12: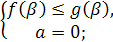
Рис.13:
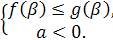
Итак, 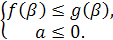
Рис.13
в) Пусть заданы функции  , причём
, причём 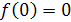 , и
, и 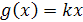 .
.
Запишите условия для ситуации: 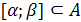 , где А – множество решений неравенства
, где А – множество решений неравенства 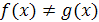 .
.
Рис.14
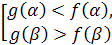
г) Пусть заданы функции  и
и 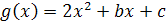 .
.
Запишите условия для ситуации: 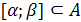 , где А – множество решений неравенства
, где А – множество решений неравенства 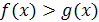 .
.
Рис.15
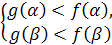
4. Решение задач по исследованию неравенств с параметром графическим методом.
Пример 2. (задание С3 − вариант 5 [1]). Найти все значения  , для которых при каждом
, для которых при каждом  из промежутка
из промежутка 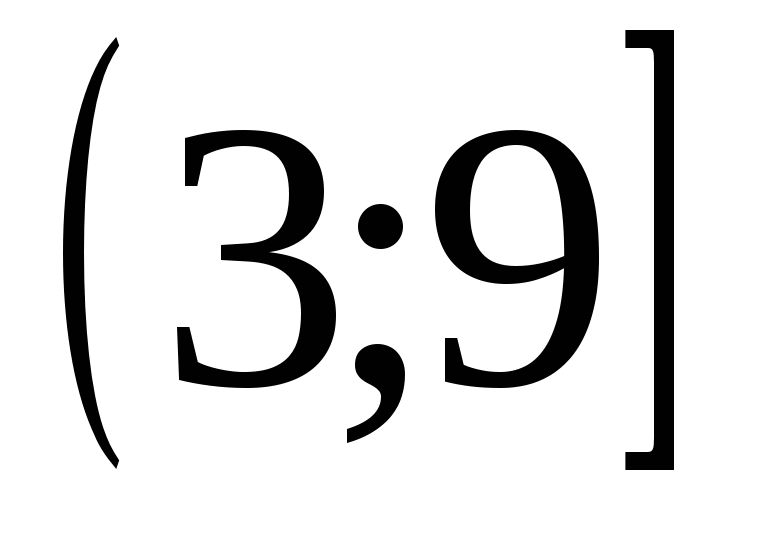 значение выражения
значение выражения 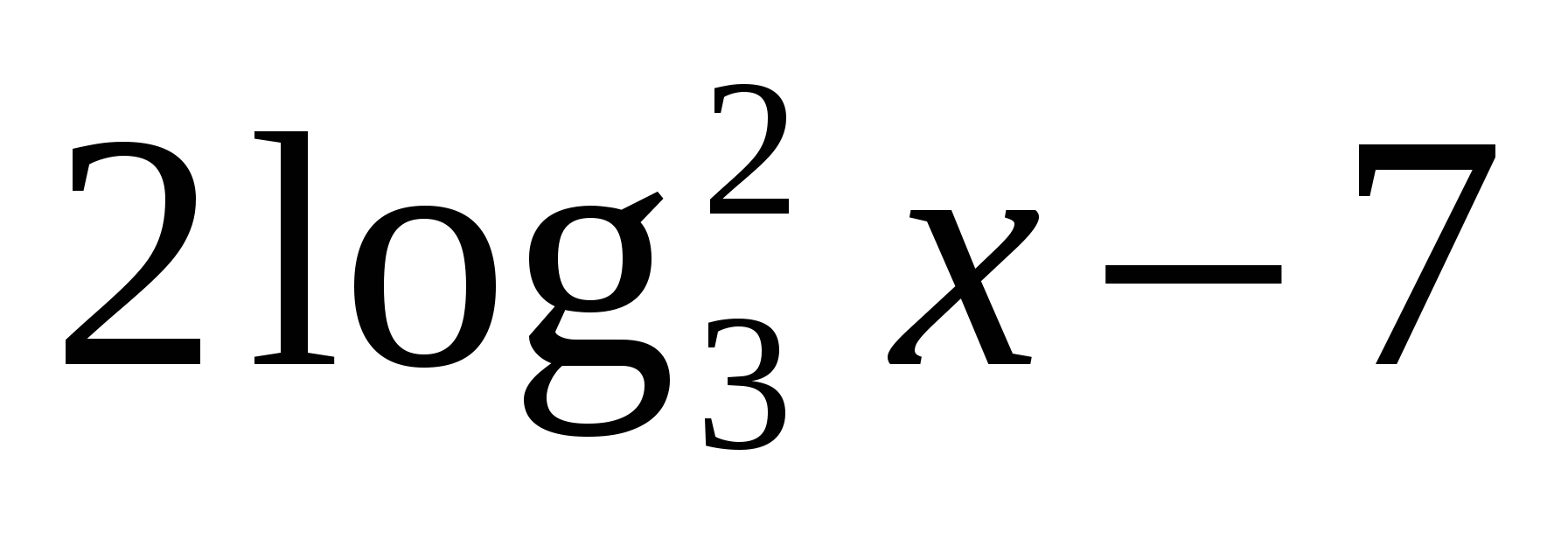 не равно значению выражения
не равно значению выражения 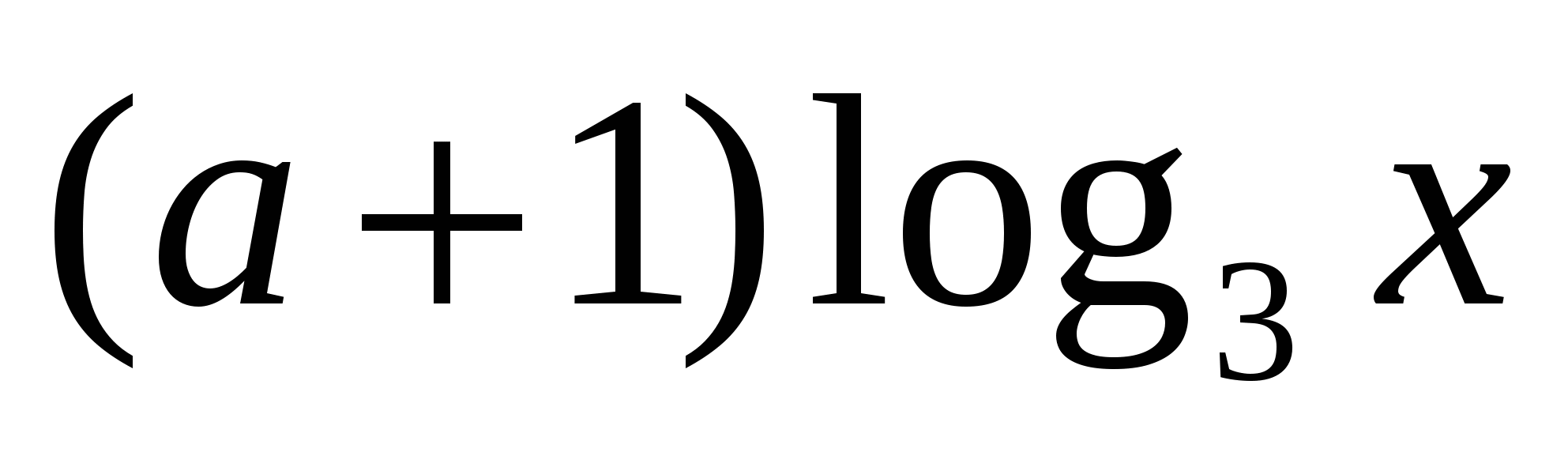 .
.
Решение.
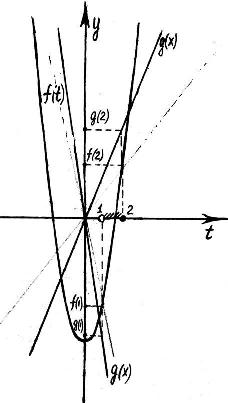
Рис. 16
Пусть 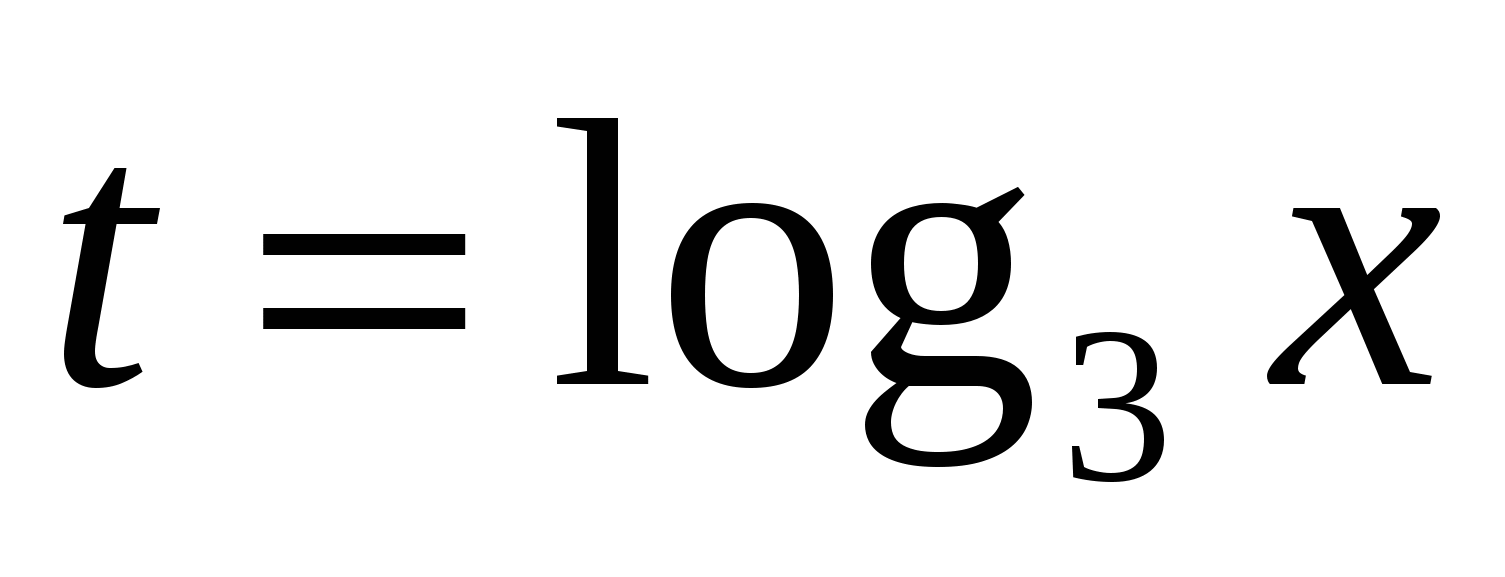 .
.
Выясним, при каком  выполняется
выполняется 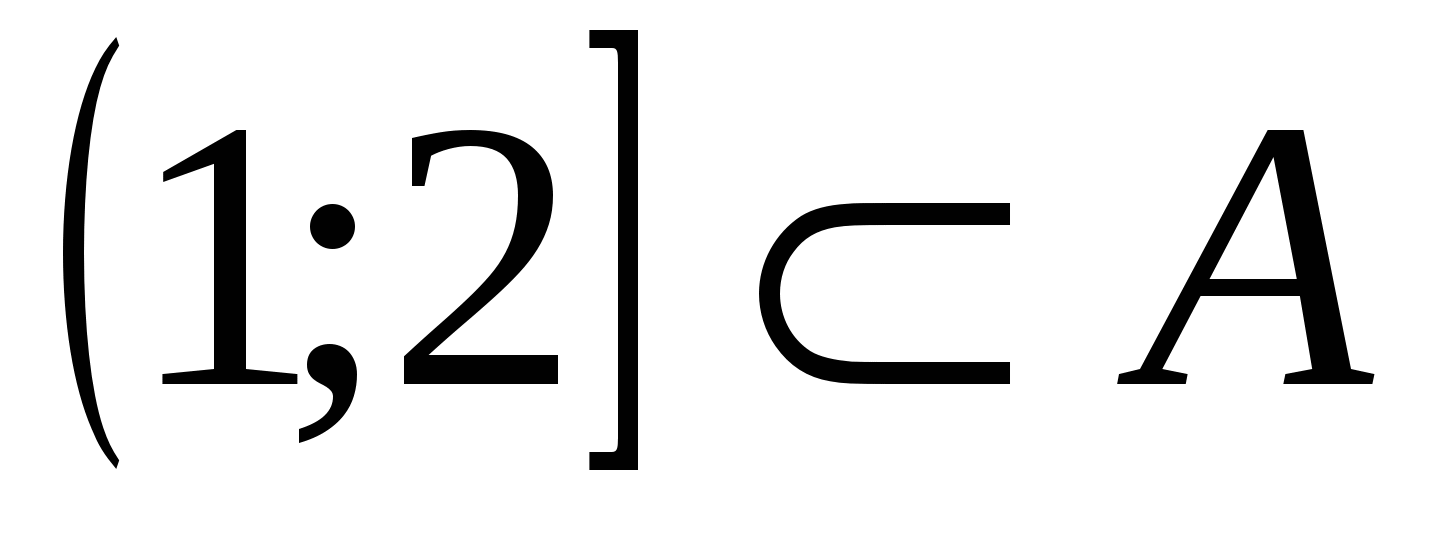 , где
, где  – множество решений неравенства
– множество решений неравенства 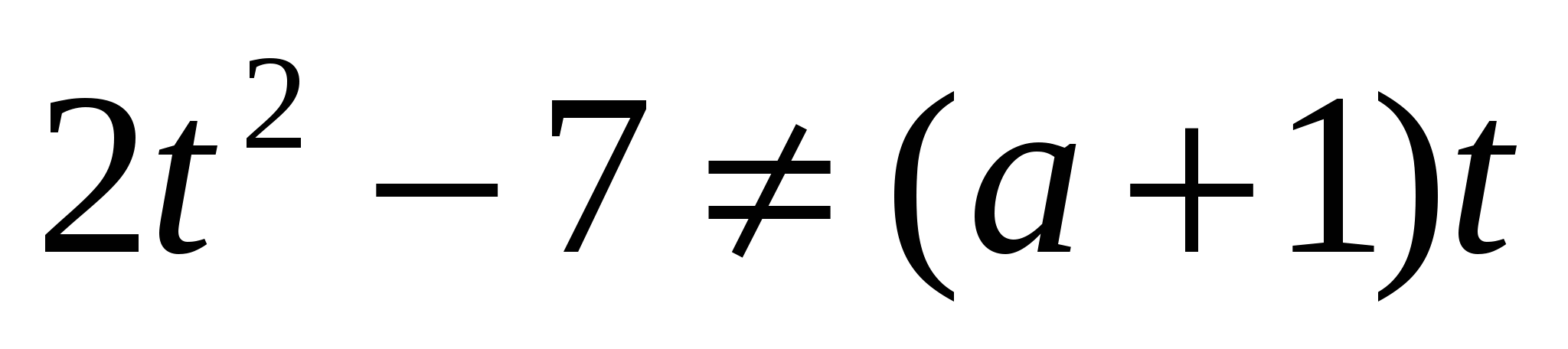 относительно t.
относительно t.
Пусть 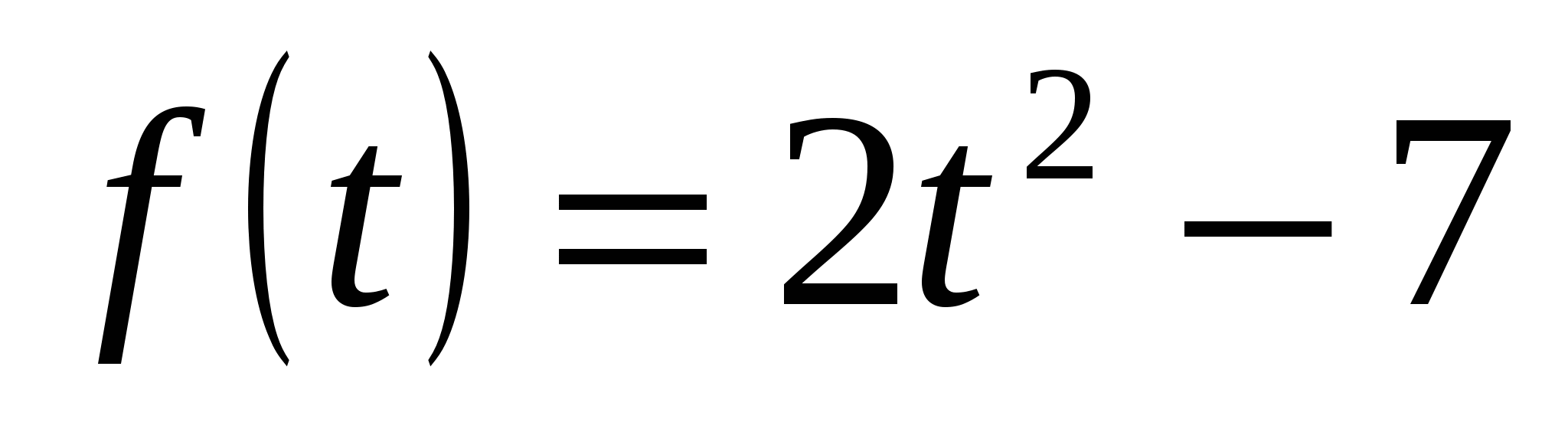 ж
ж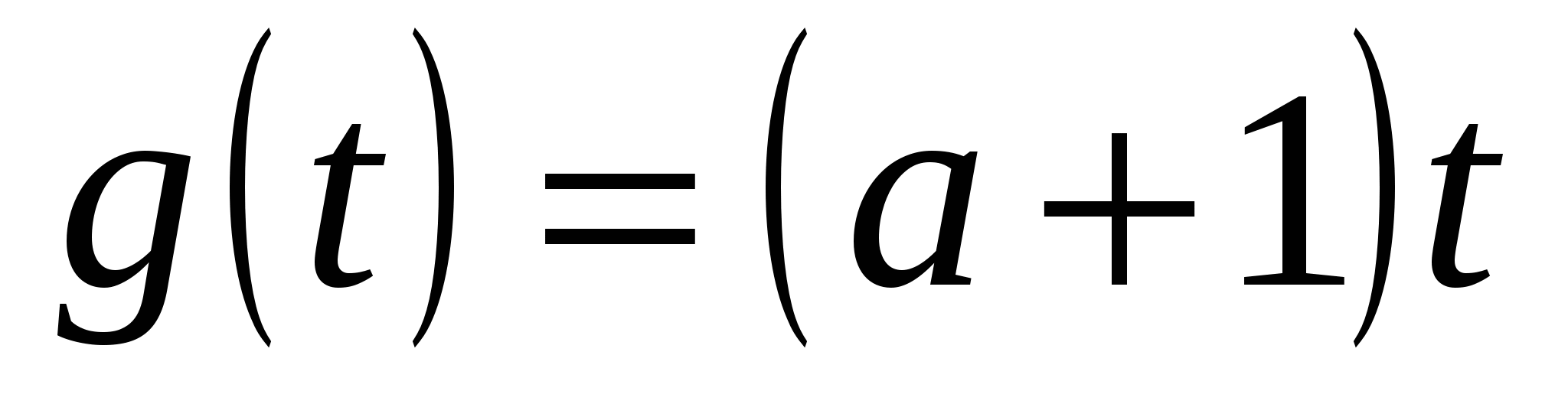 .
.
По условию задачи и Рис. 16:
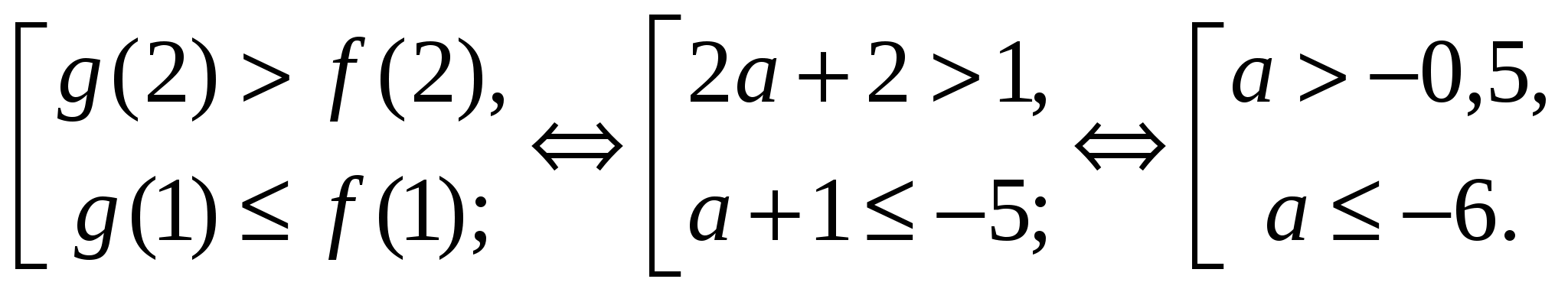
 .
.
Ответ: 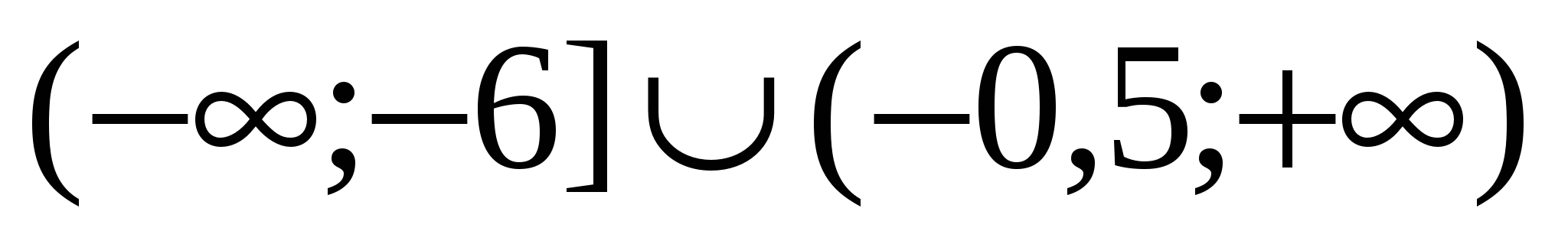
Пример 3. (задание С3 − вариант 28 [1]). Найдите все значения  , при которых каждое решение неравенства
, при которых каждое решение неравенства 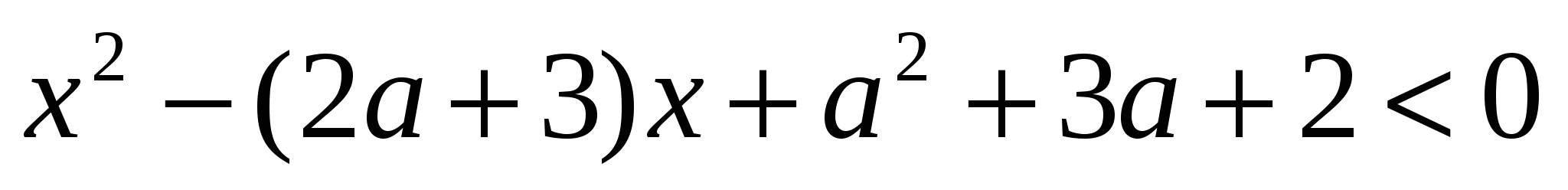 являлось бы также решением неравенства
являлось бы также решением неравенства 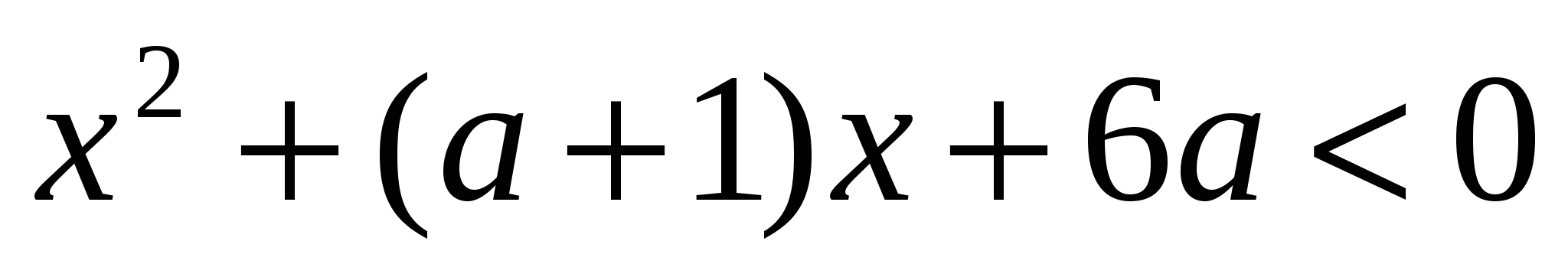 .
.
Решение. Выясним, при каких значениях параметра  :
:  , где
, где  – множество решений неравенства
– множество решений неравенства 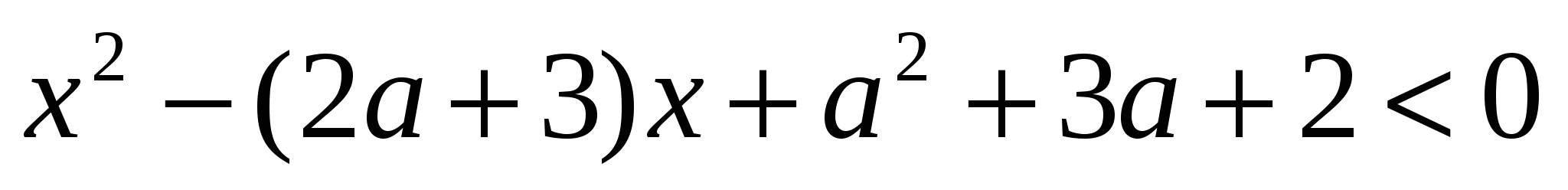 и где
и где  – множество решений неравенства
– множество решений неравенства 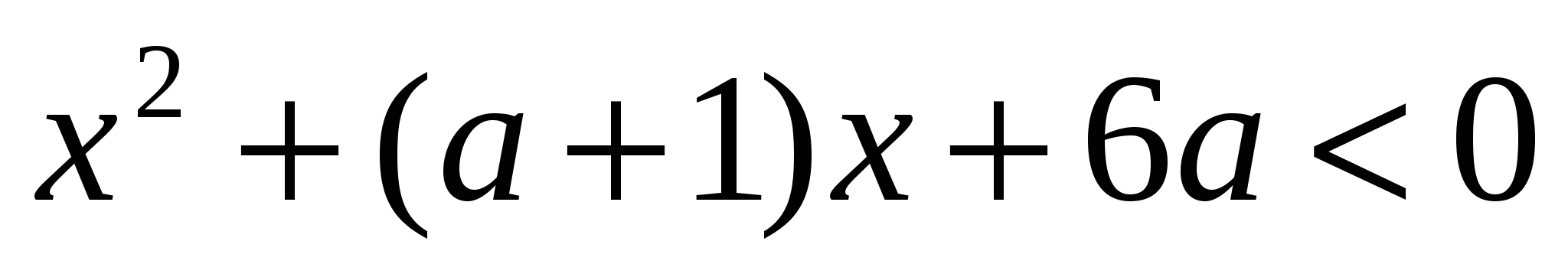 относительно
относительно  .
.
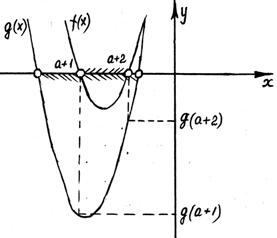
Рис. 17
Пусть 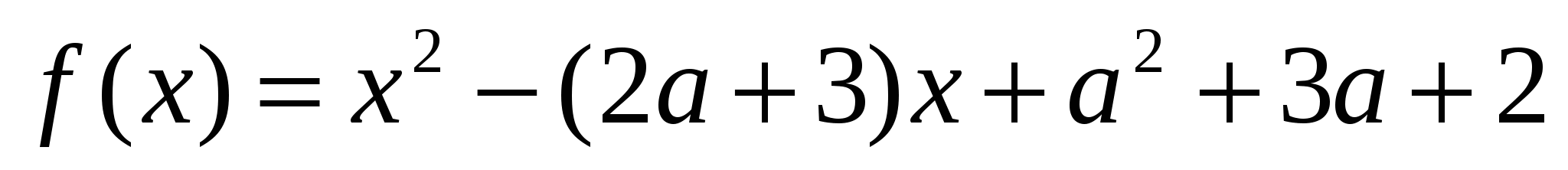 ,
, 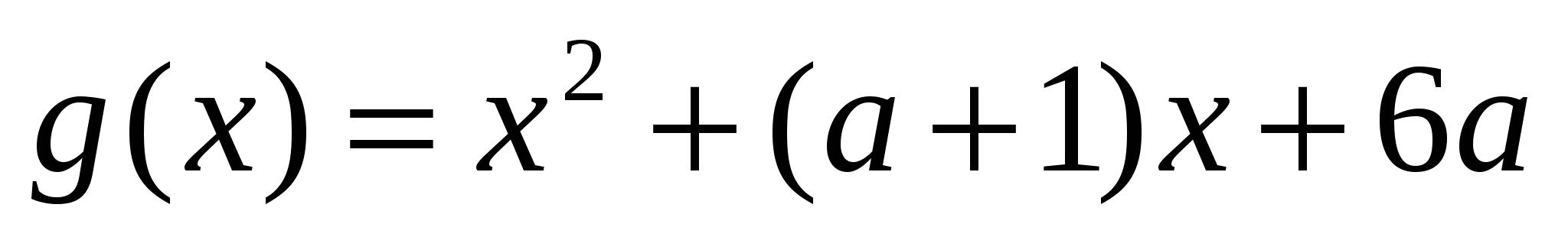 .
.
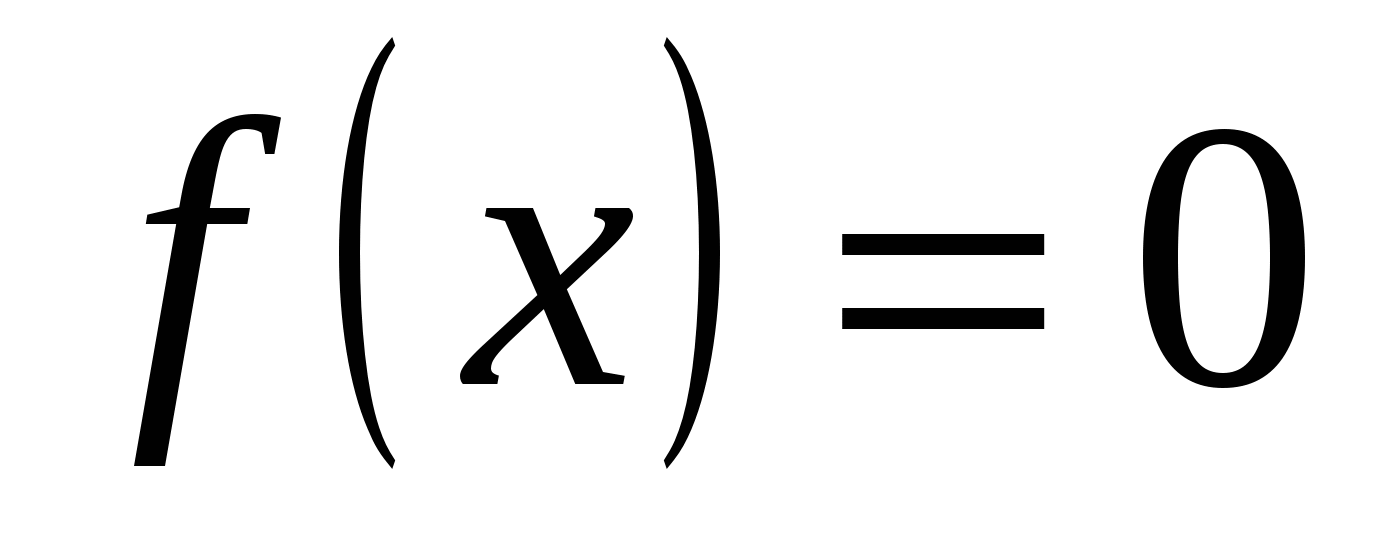 , если
, если 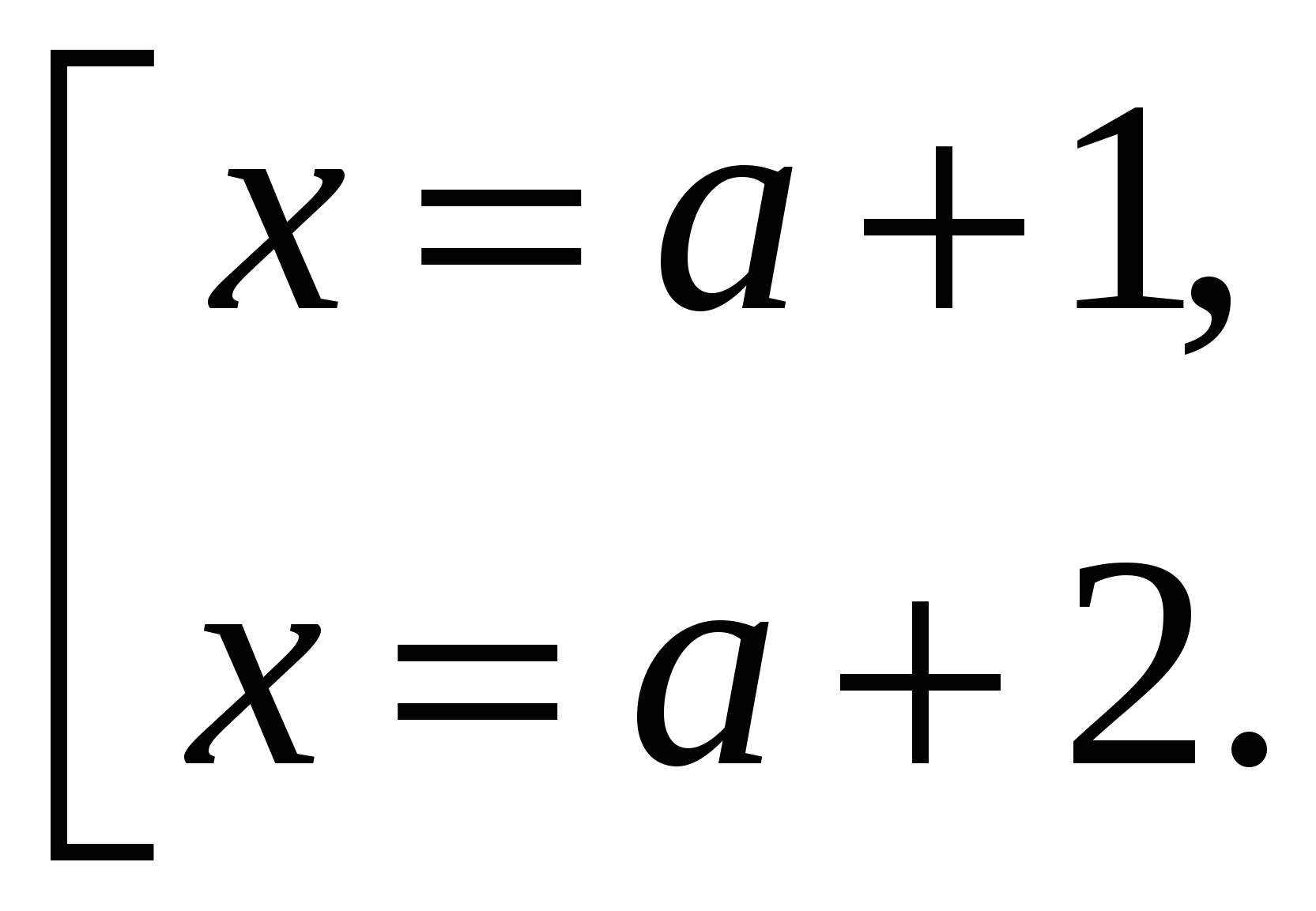
По условию задачи и Рис. 17:
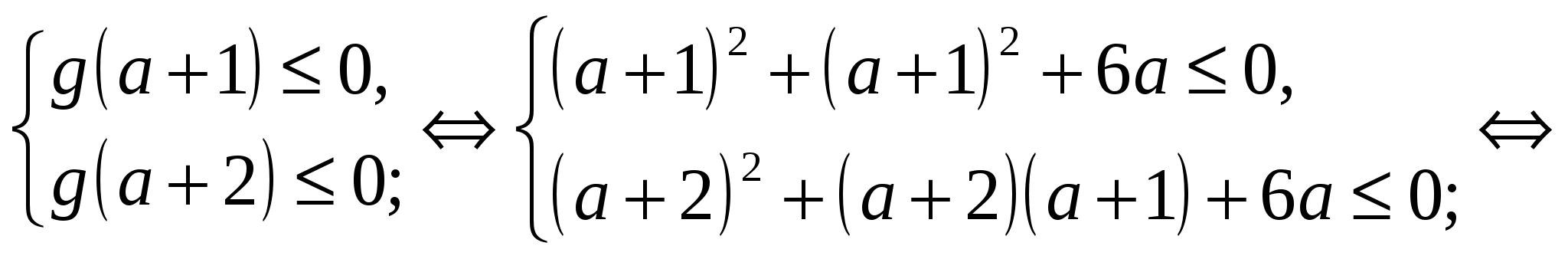
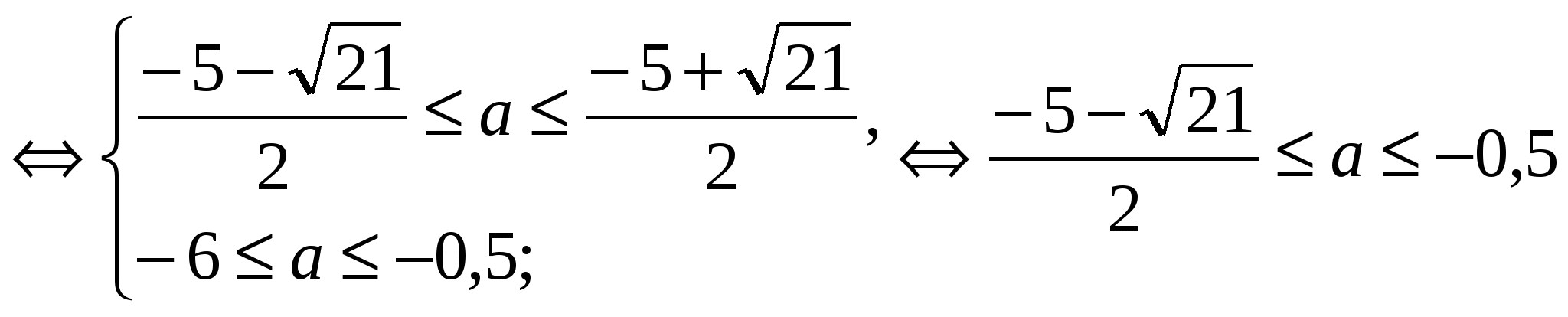
Ответ: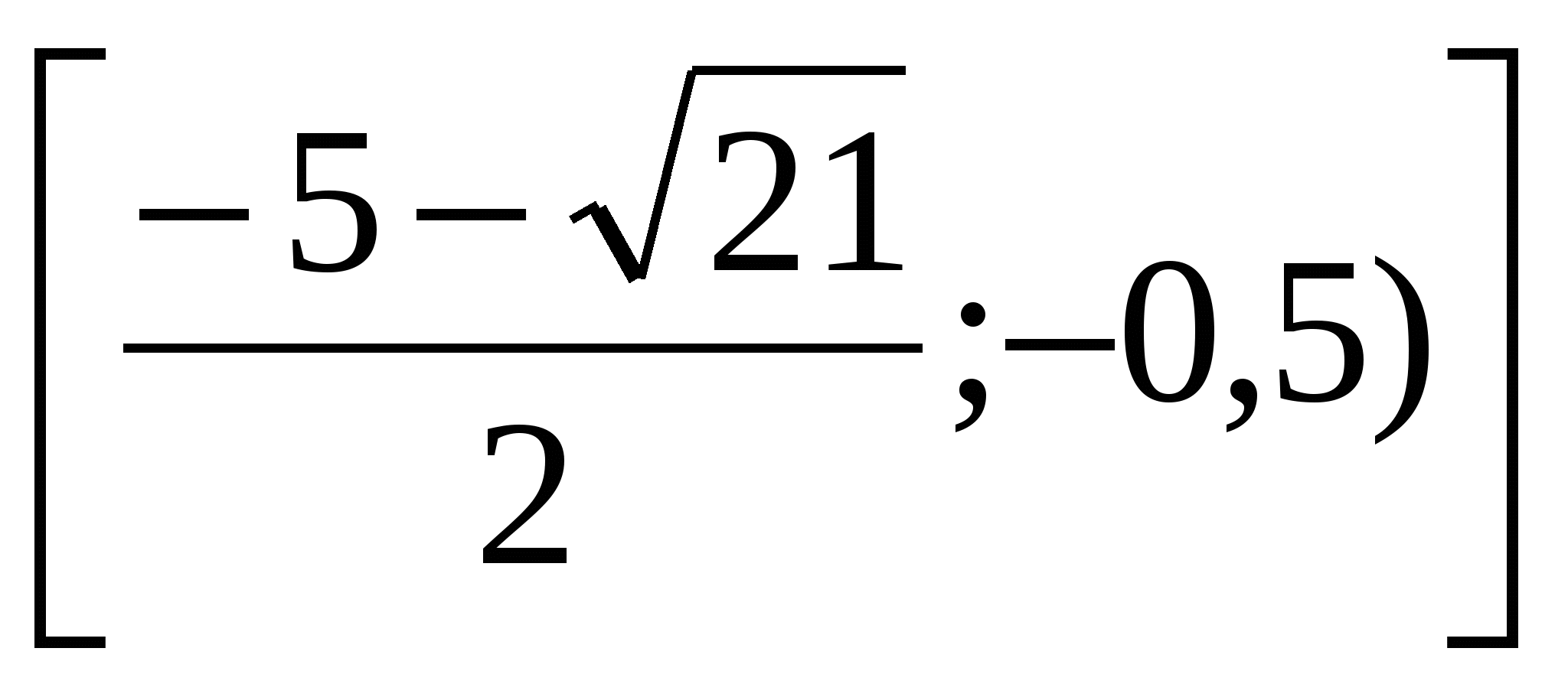 .
.
Пример 4. (задание С3 − вариант 3 [2]). Найдите все значения параметра а, при которых неравенство 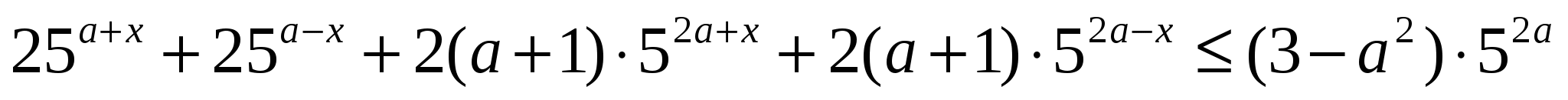 не имеет решений.
не имеет решений.
Решение. Пусть  , причём
, причём 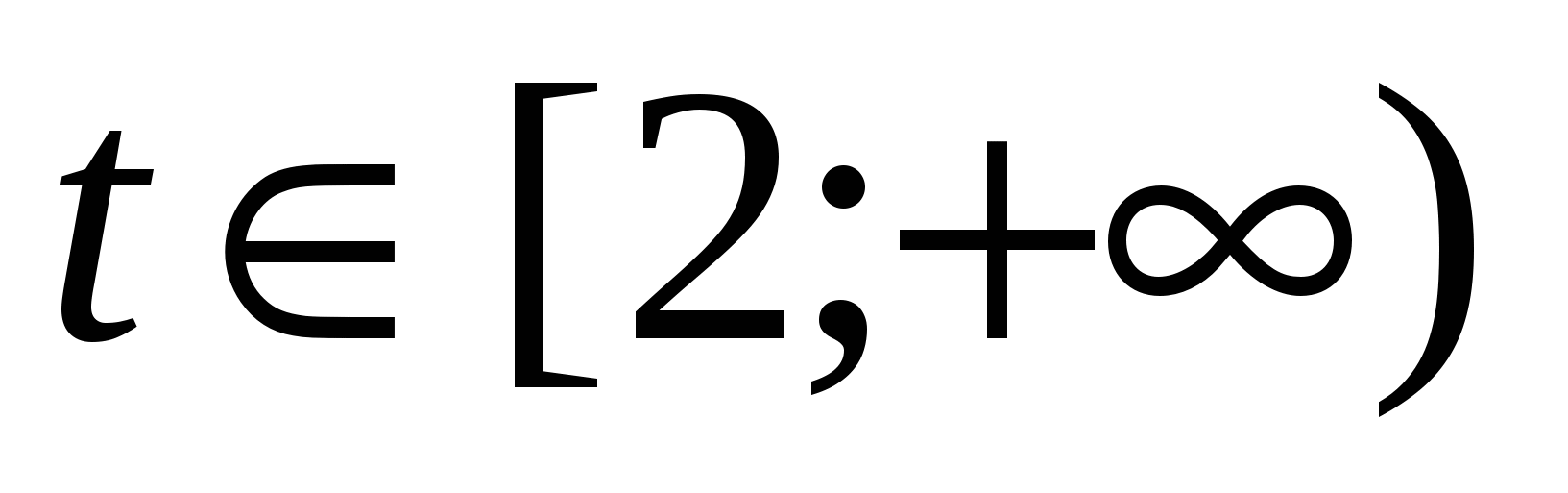 . Сначала для того, чтобы выяснить при каких
. Сначала для того, чтобы выяснить при каких  заданное неравенство имеет хотя бы одно решение, найдём при каких а
заданное неравенство имеет хотя бы одно решение, найдём при каких а 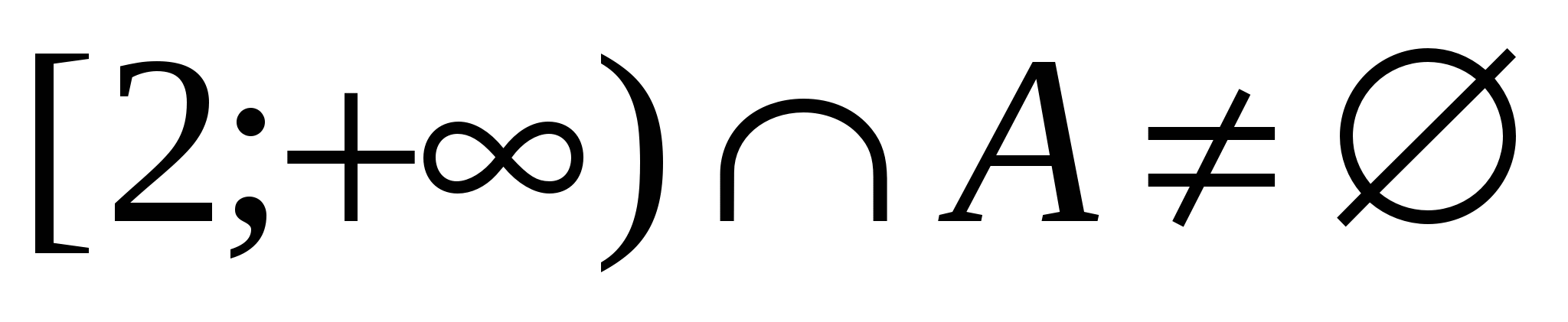 , где
, где  – множество решений неравенства
– множество решений неравенства 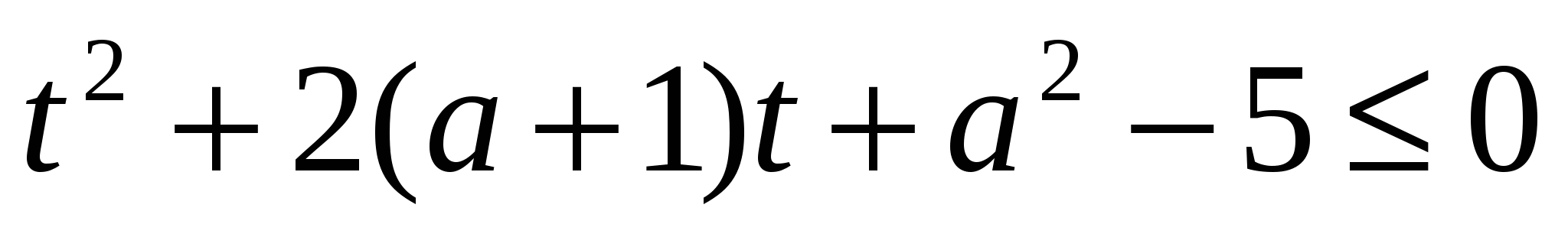 относительно
относительно 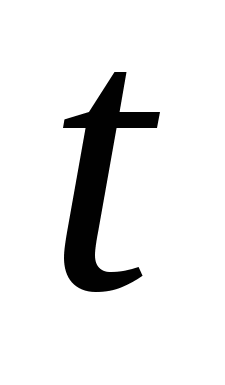 . А затем для того, чтобы выяснить при каких
. А затем для того, чтобы выяснить при каких  заданное неравенство не имеет решений, найдем дополнение полученного множества значений
заданное неравенство не имеет решений, найдем дополнение полученного множества значений  до множества
до множества 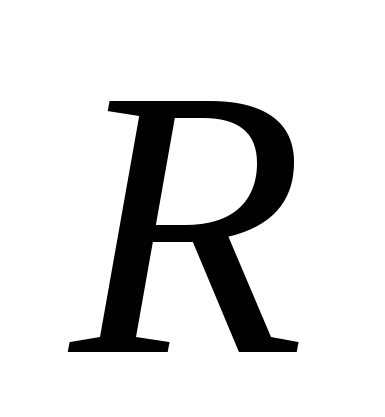 .
.
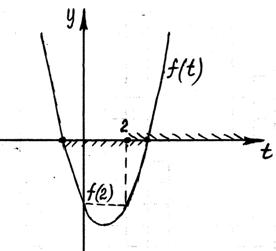
Рис. 18
Пусть 
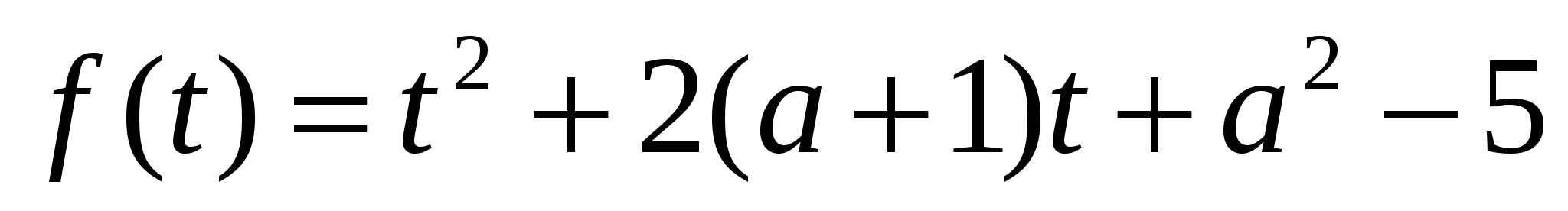
Заданное неравенство имеет хотя бы одно решение (Рис. 18), если 
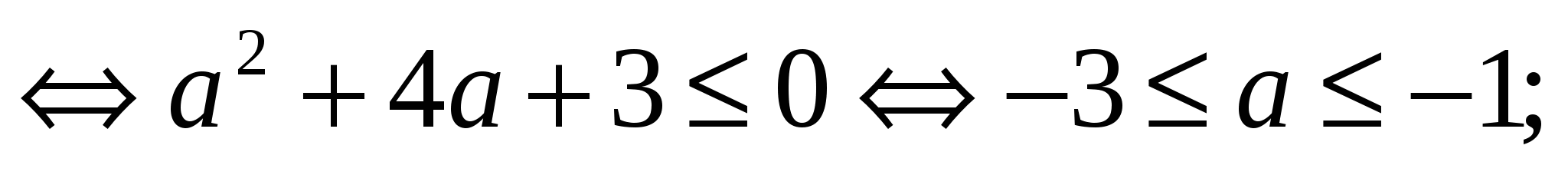
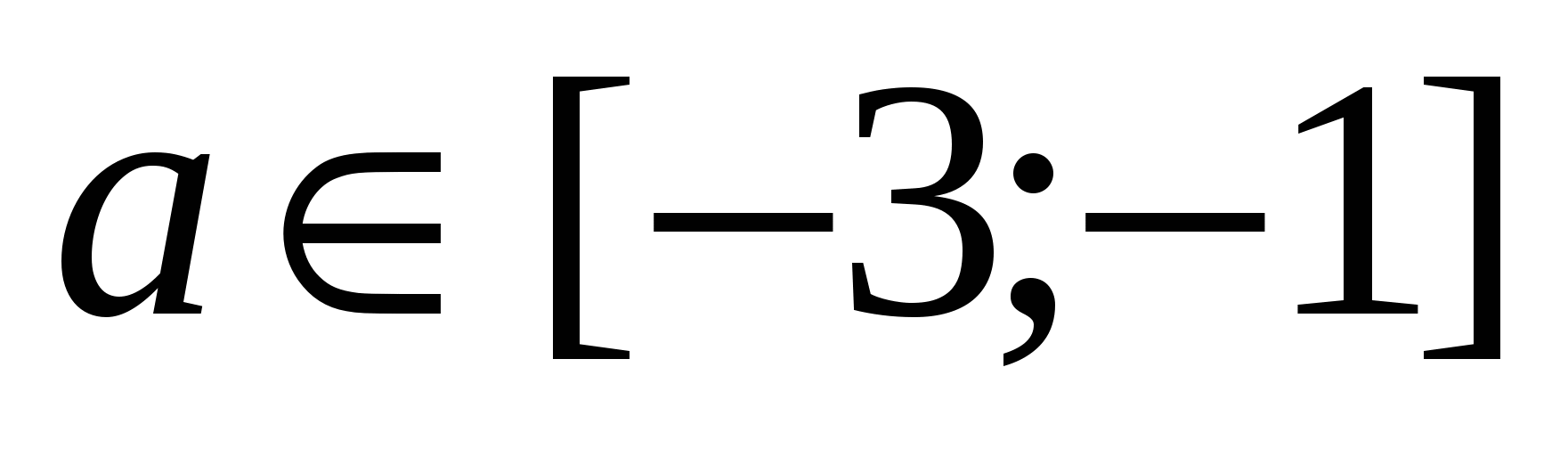 .
.
Заданное неравенство не имеет решений при 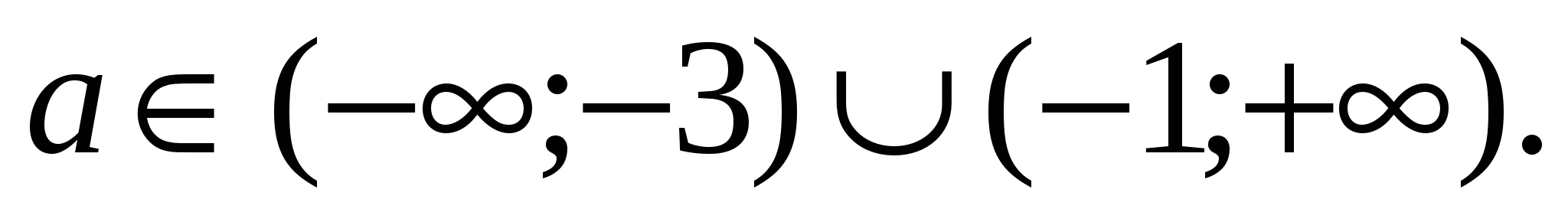
Ответ: 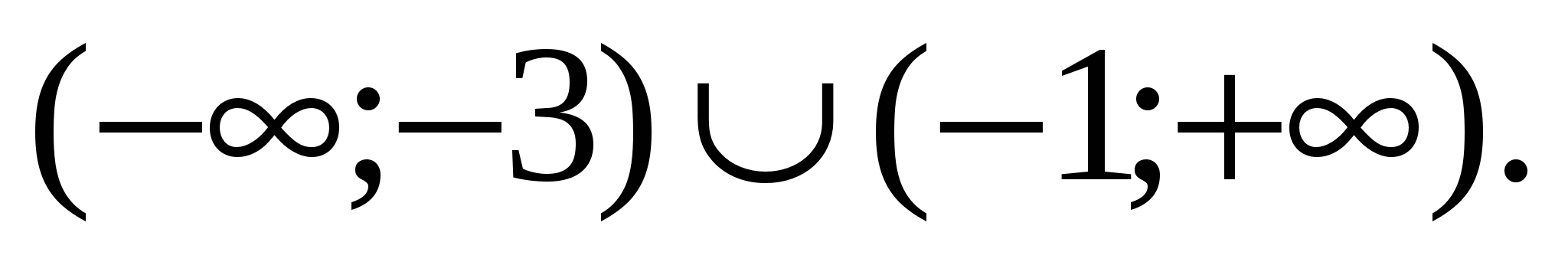
Пример 5. (задание С3 − вариант 18 [1]). Найдите, при каких значениях параметра 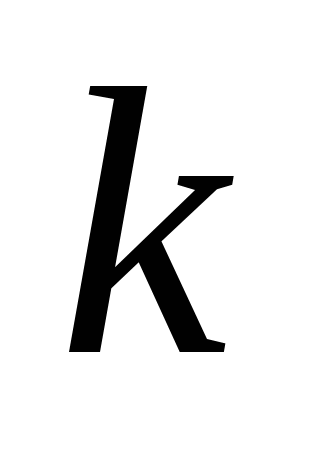 неравенство
неравенство 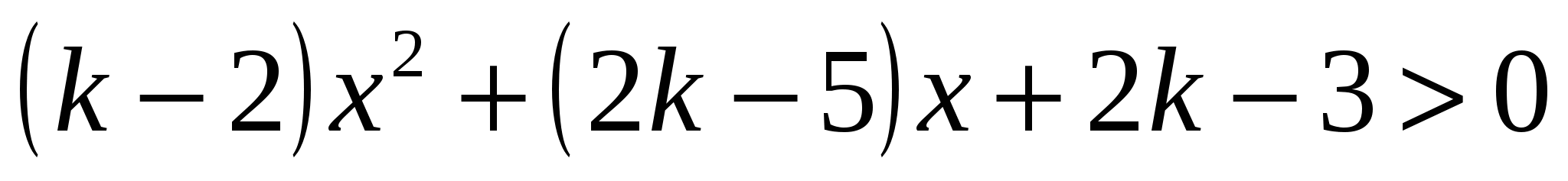 выполняется хотя бы при одном
выполняется хотя бы при одном 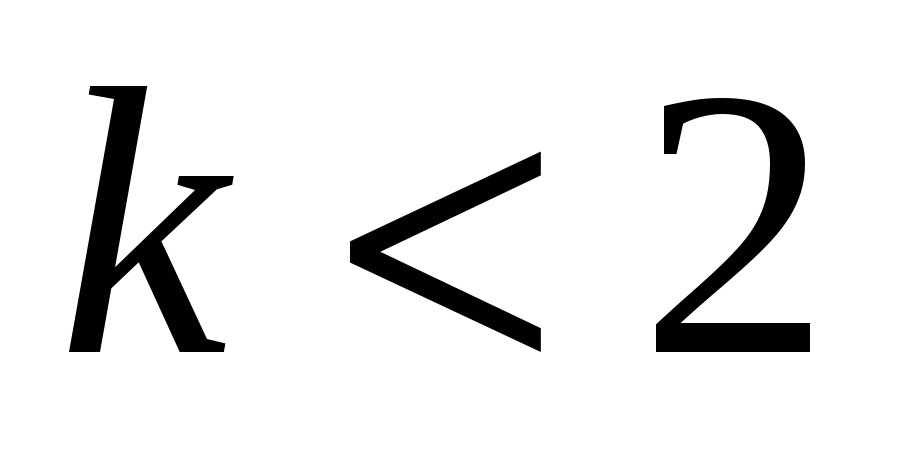 .
.
Решение. Обозначим исходное неравенство
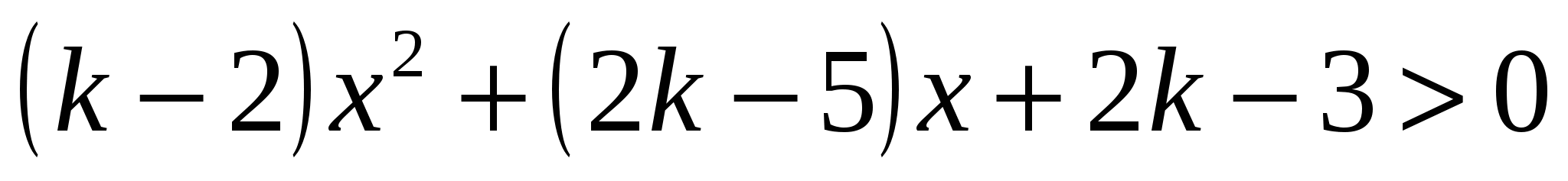 ,
,
(*)
и выясним при каком 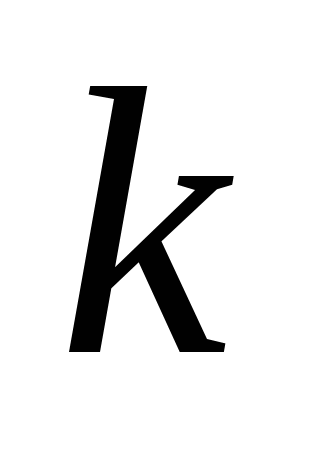
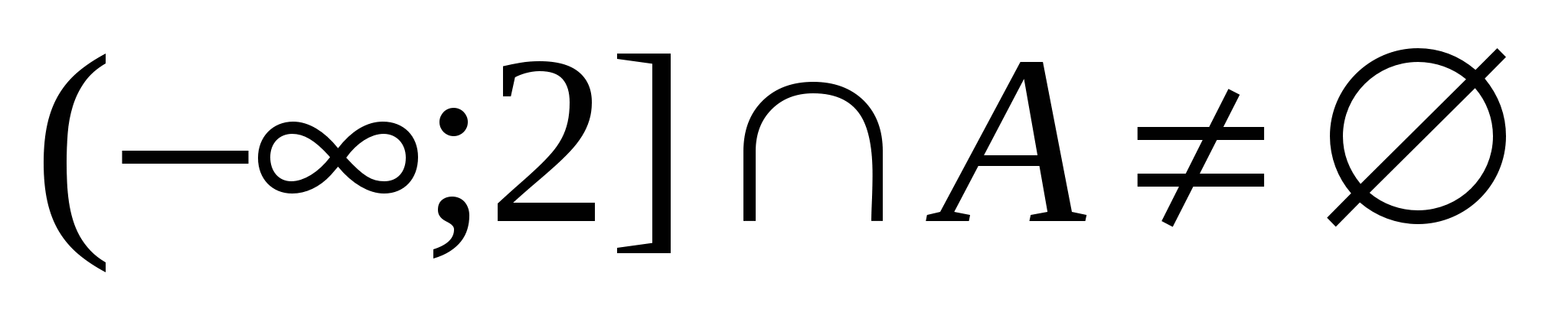 ,
,
(**)
где  – множество решений (*) относительно
– множество решений (*) относительно  .
.
Если 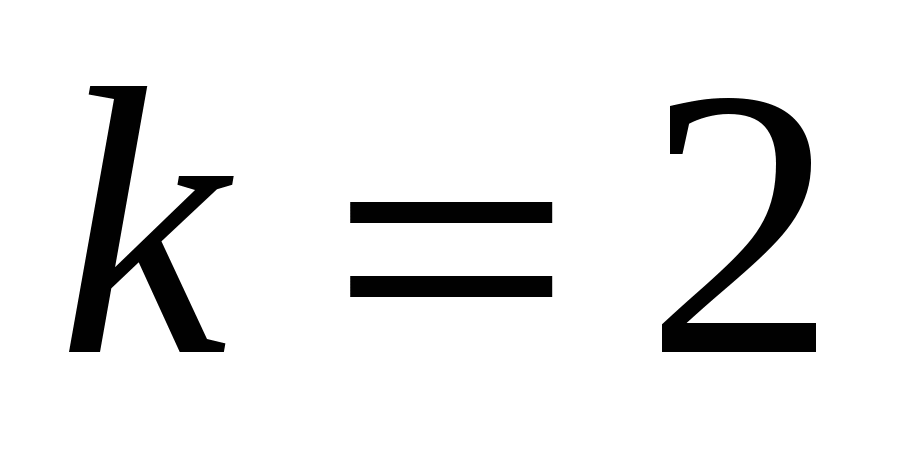 , то (*) примет вид:
, то (*) примет вид:
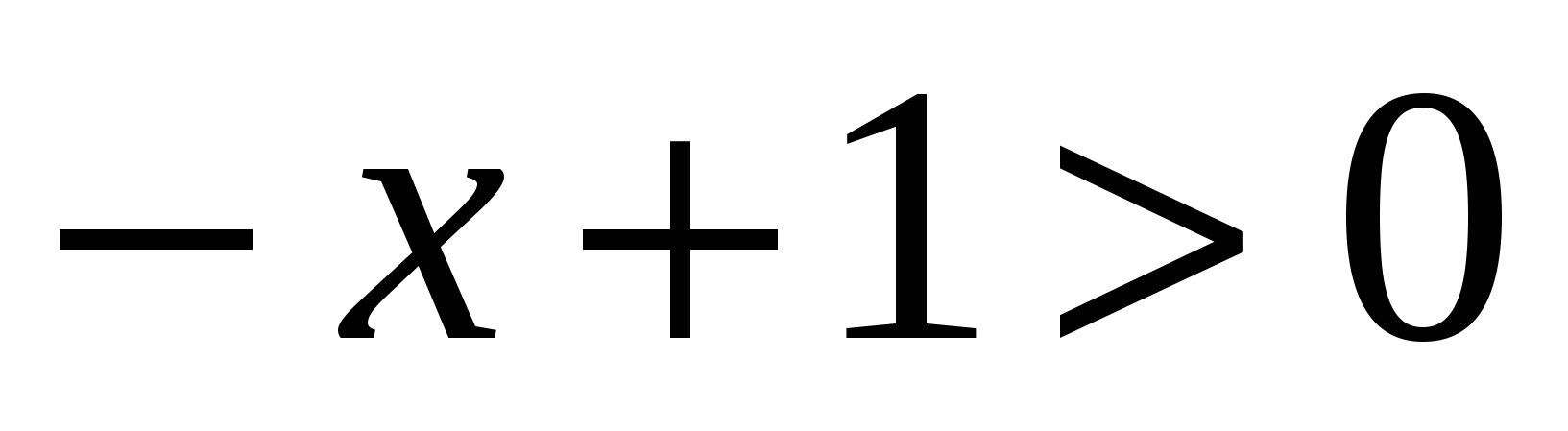 ;
; 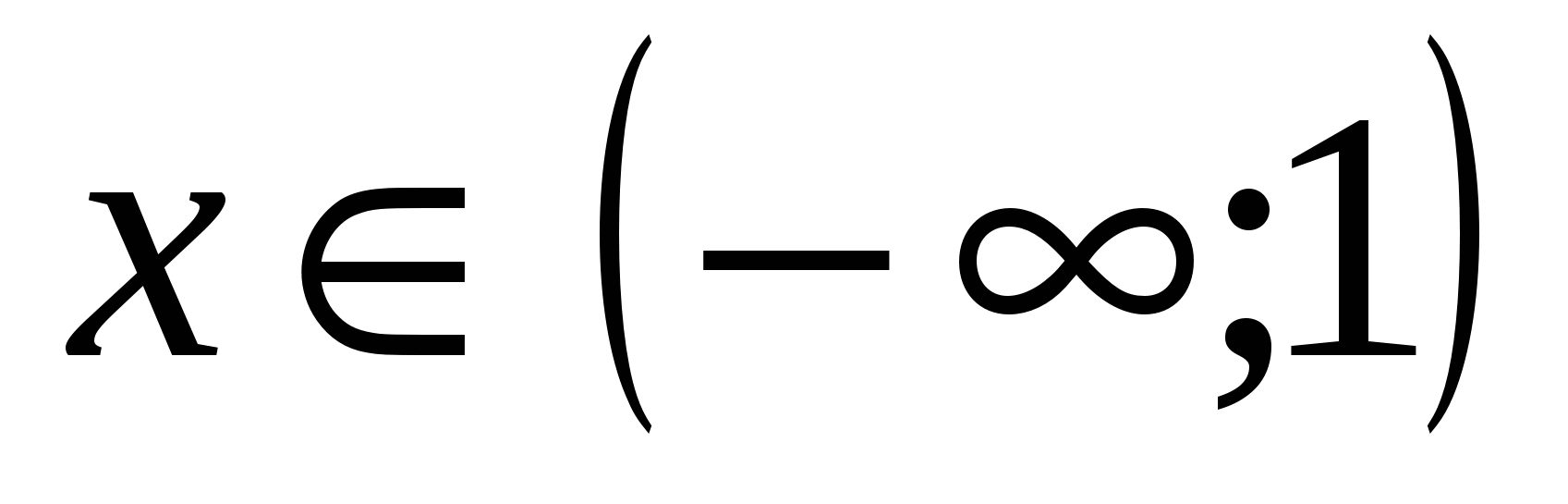 ,
,
что удовлетворяет условию задачи (**), значит 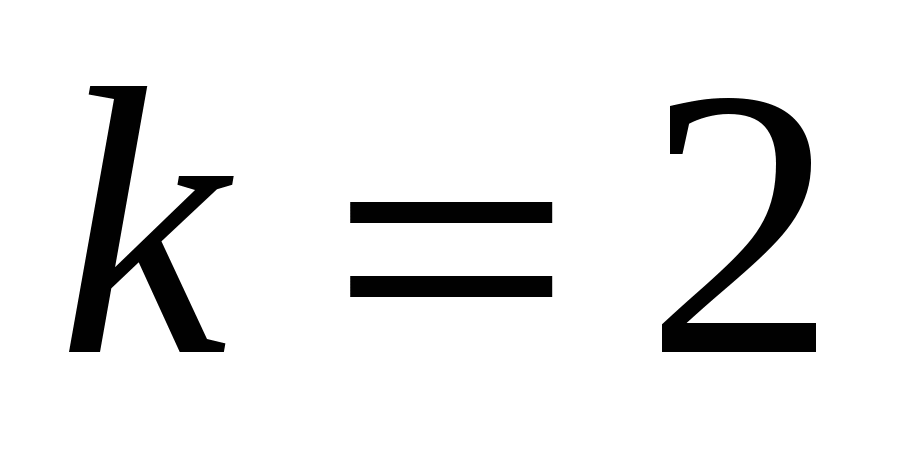 − одно из решений.
− одно из решений.
Пусть 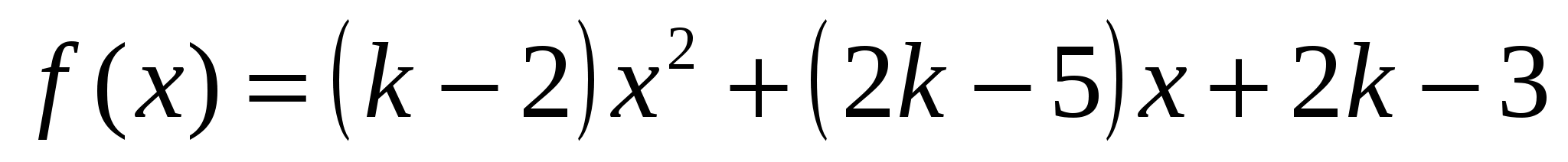 , тогда (*) имеет вид :
, тогда (*) имеет вид :
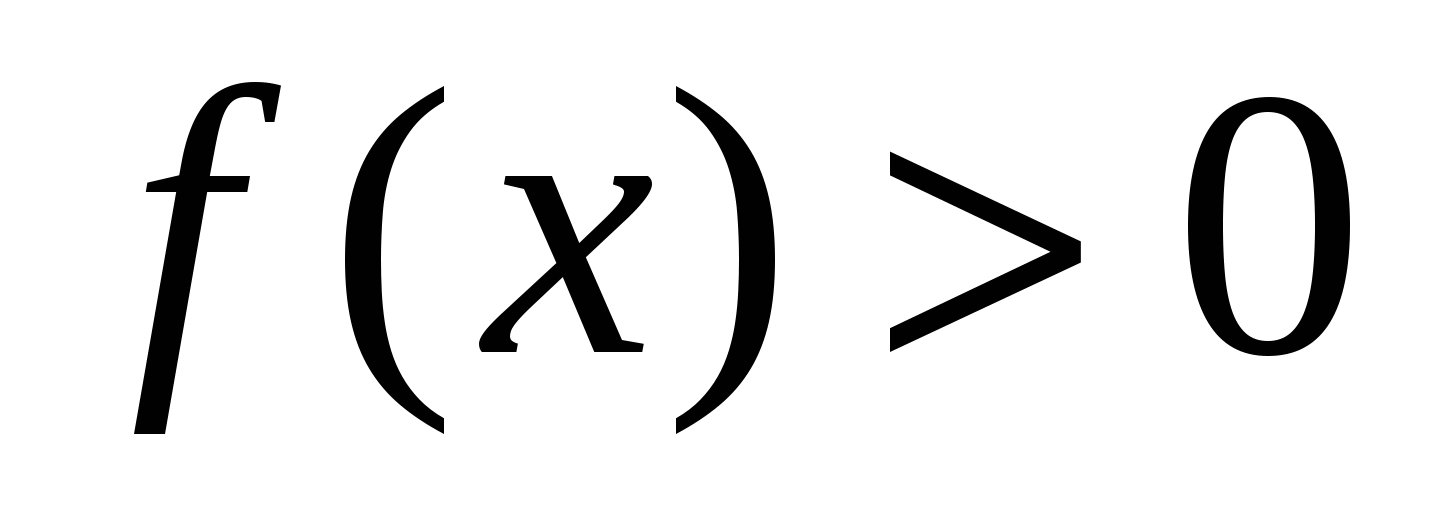 .
.
Если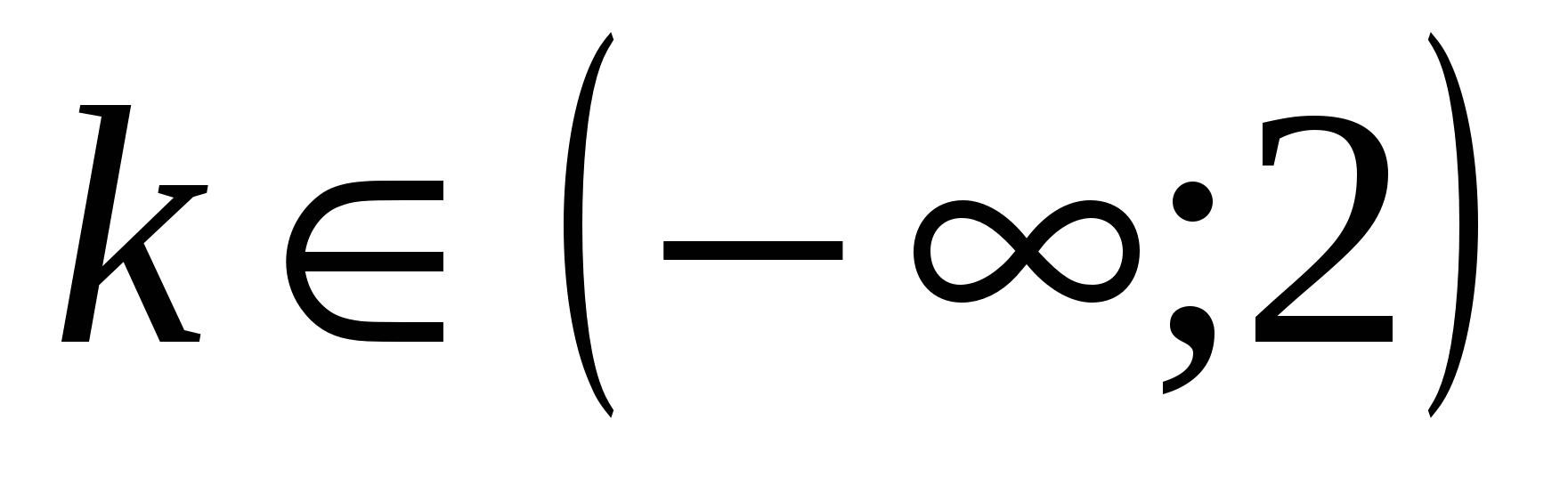 , то возможны 4 случая:
, то возможны 4 случая:
а) Рис. 19: (*) не имеет решений , что не соответствует условию задачи (**).

Рис. 19
б) Рис. 20: 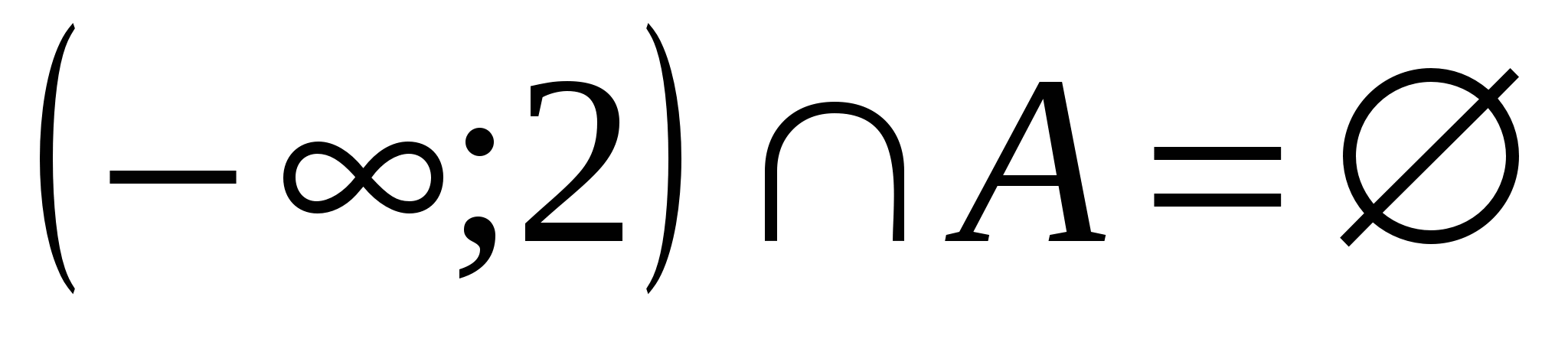 , что не соответствует условию задачи (**).
, что не соответствует условию задачи (**).

Рис. 20
в) По условию задачи (**) и Рис. 21: 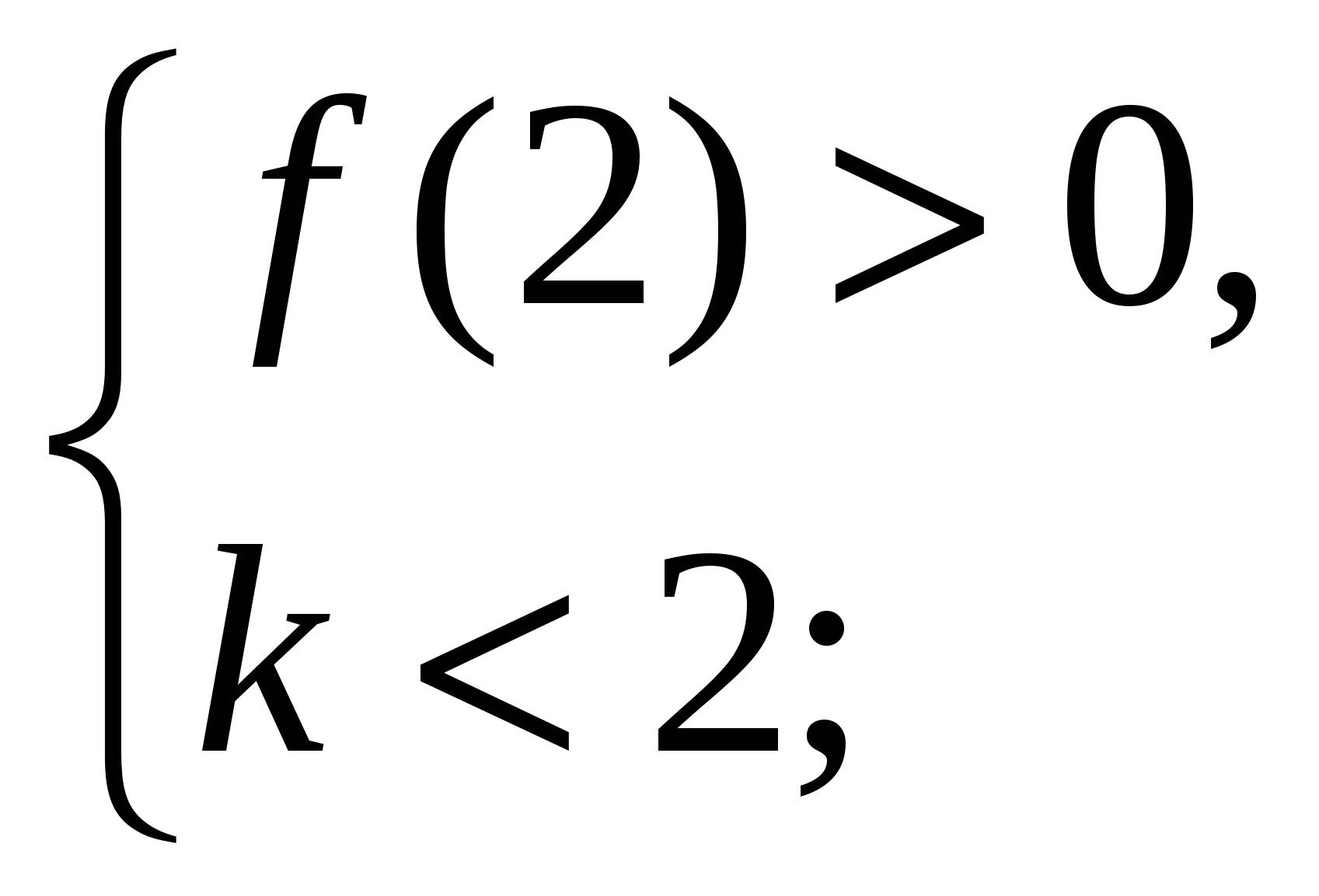
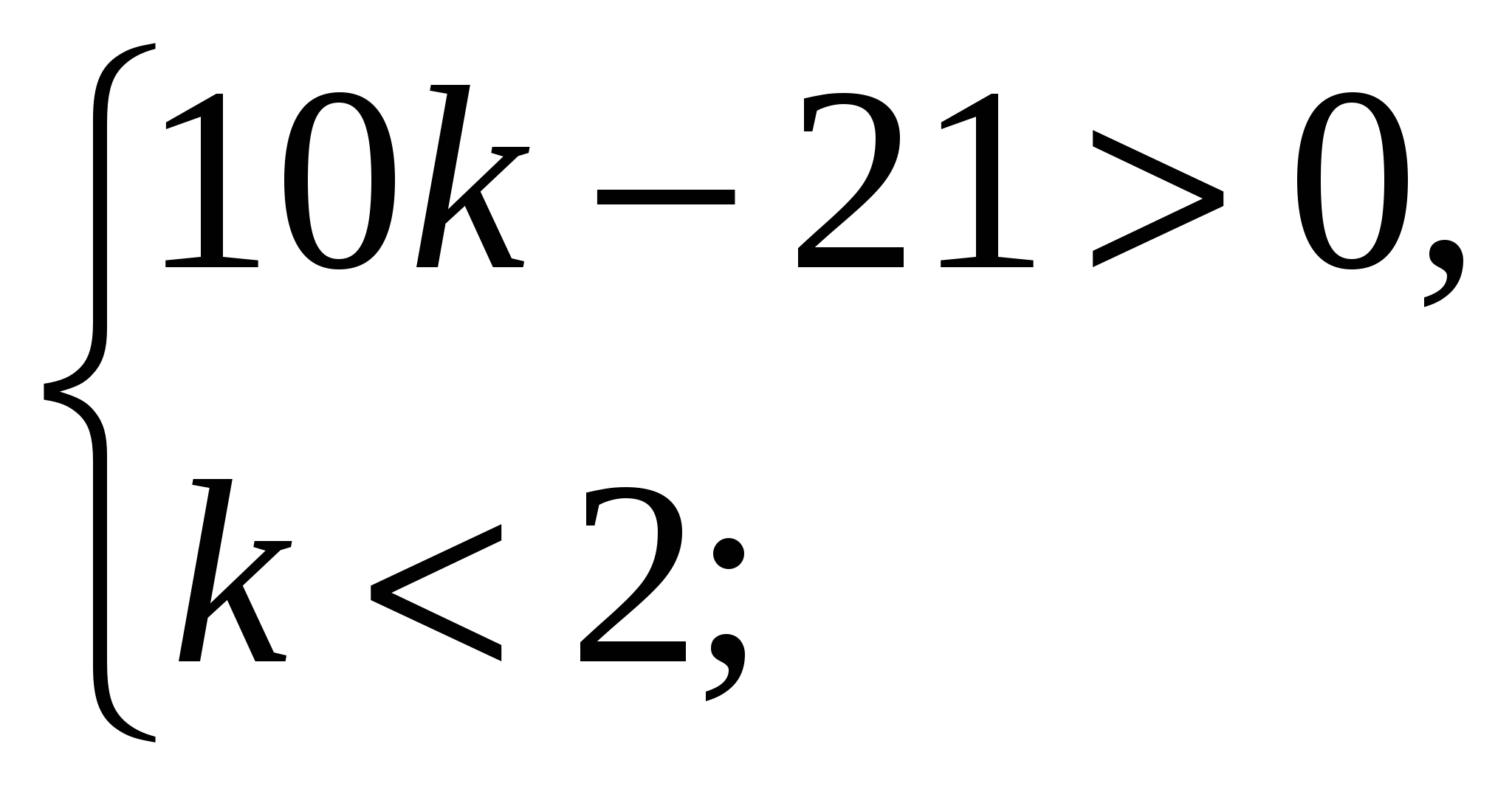
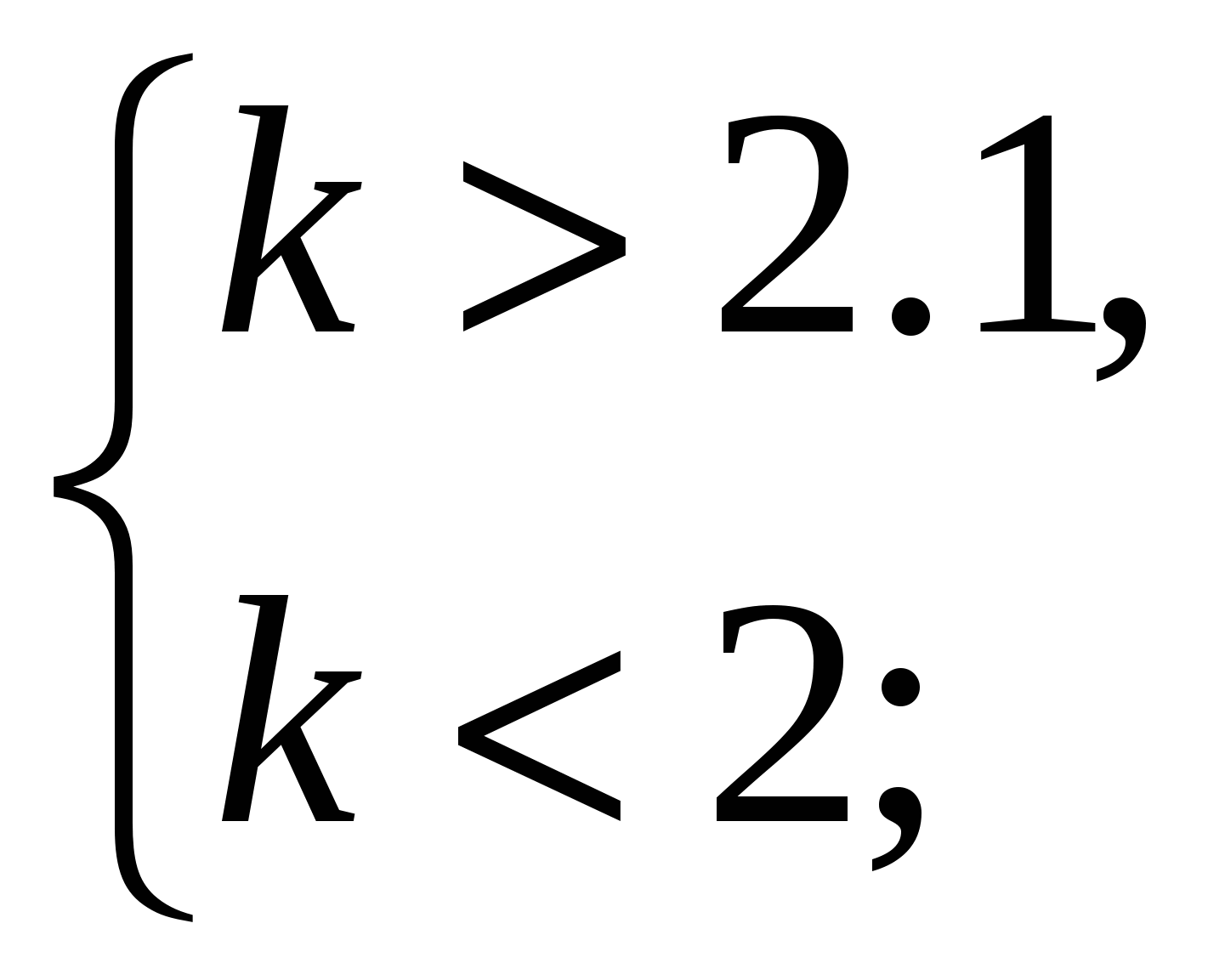
нет решений.

Рис. 21
г) По условию задачи и Рис. 23 (**):
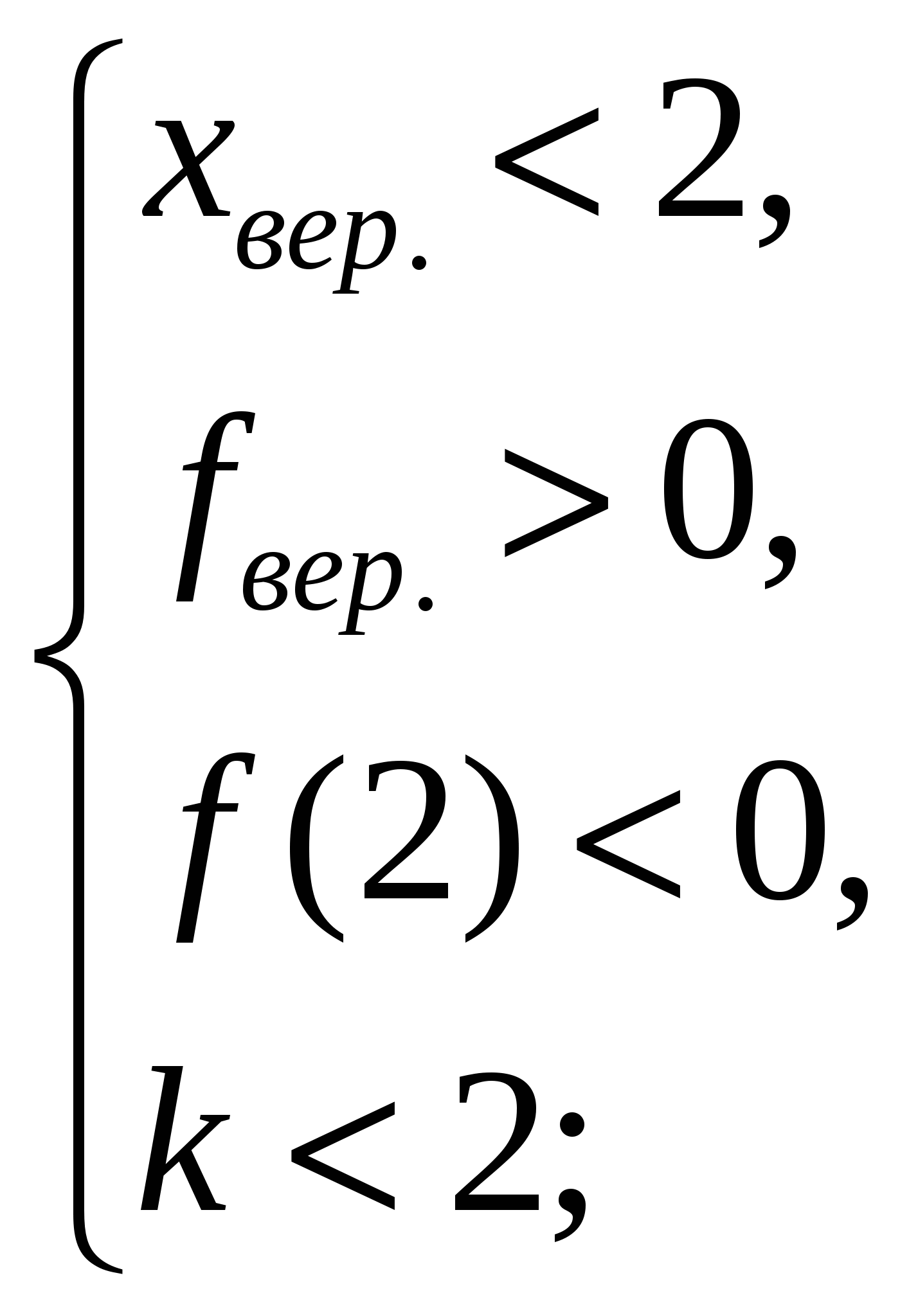

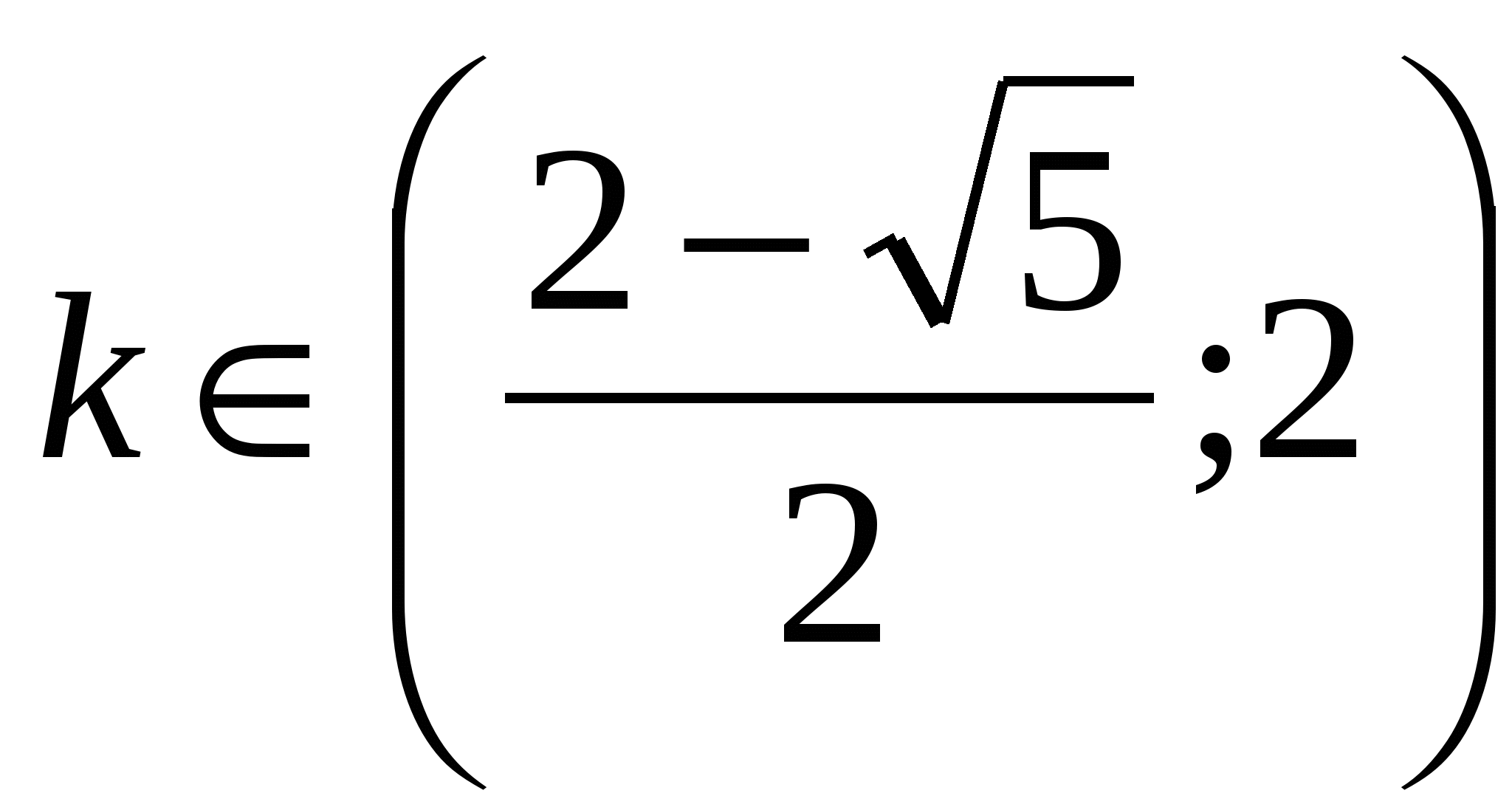 .
.
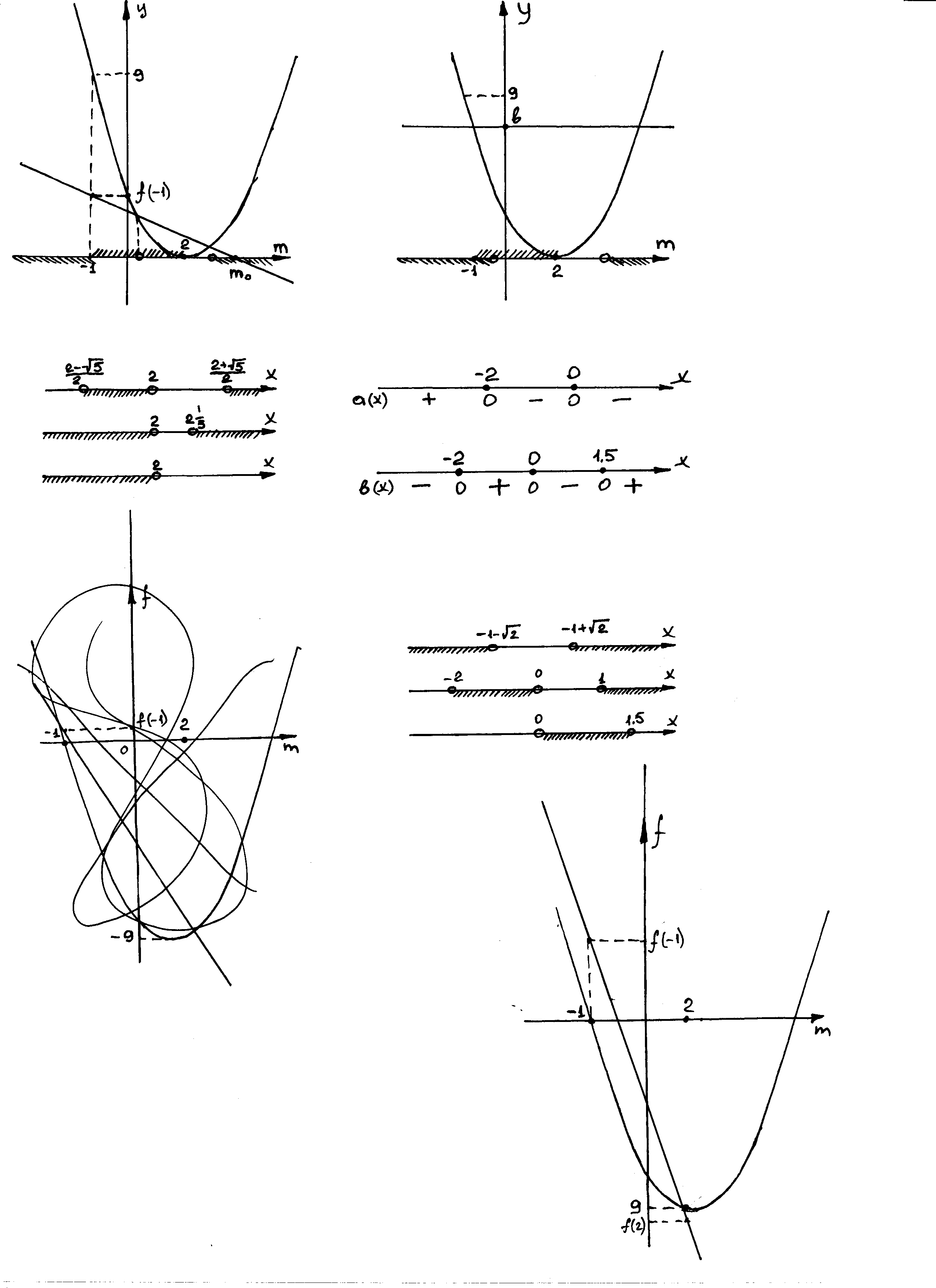
Рис. 22

Рис. 23
Если 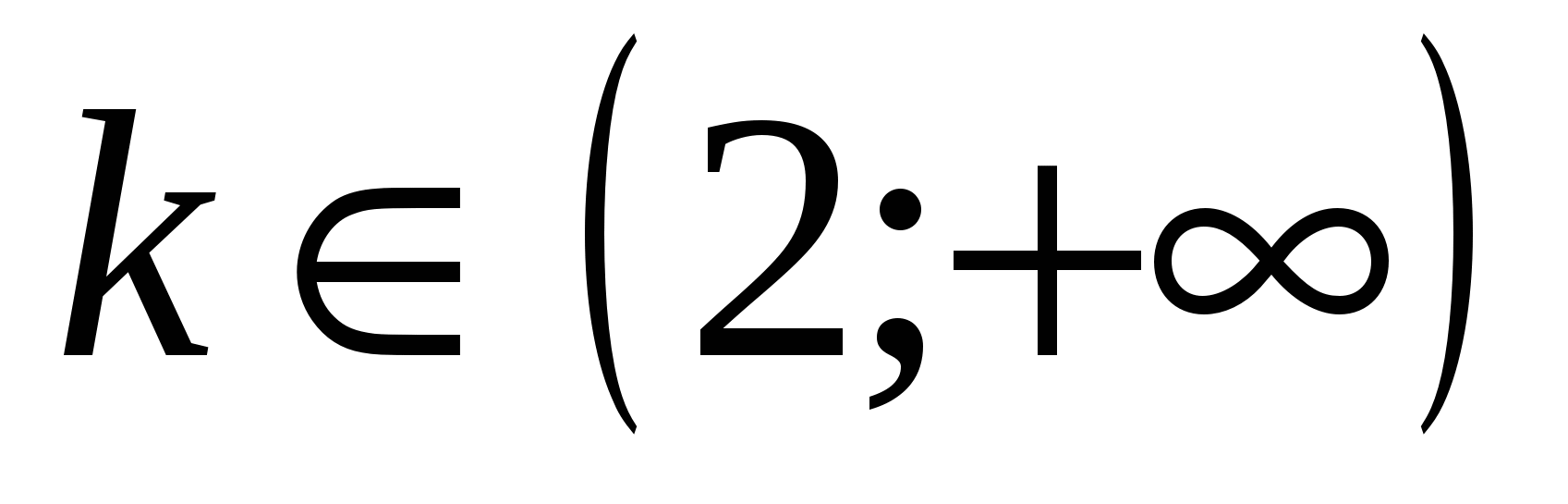 , то условие задачи (**) выполняется (Рис. 24, Рис. 25 и Рис.26).
, то условие задачи (**) выполняется (Рис. 24, Рис. 25 и Рис.26).



Рис. 24
Рис. 25
Рис. 26
Значит, 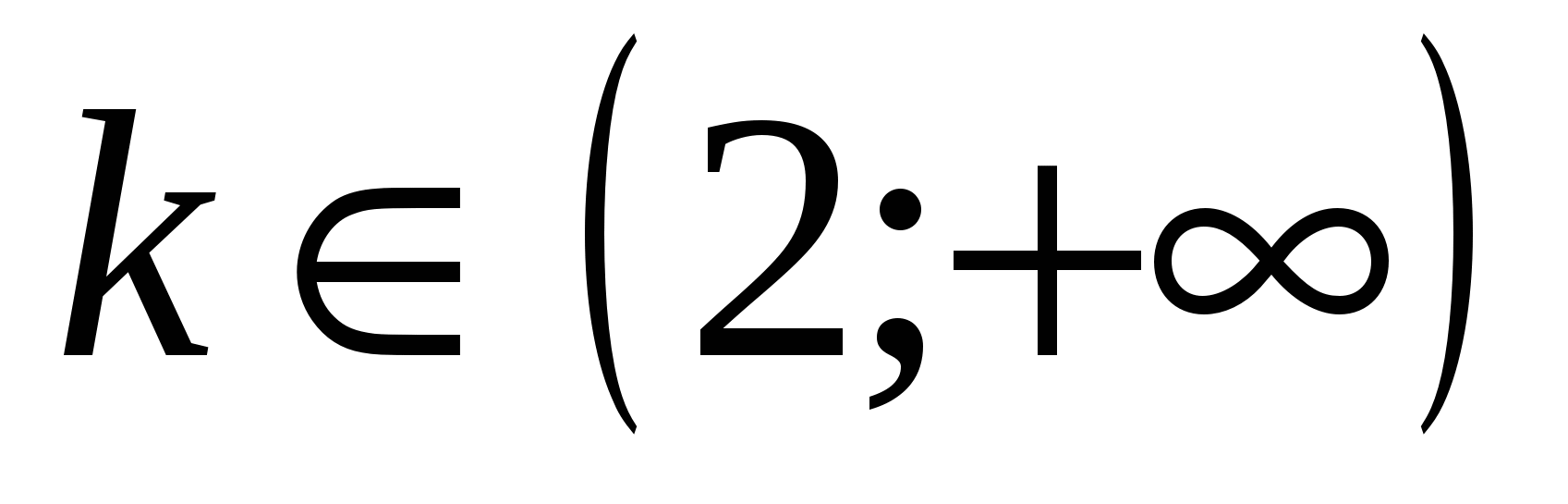 - промежуток, содержащий решение задачи.
- промежуток, содержащий решение задачи.
Ответ: 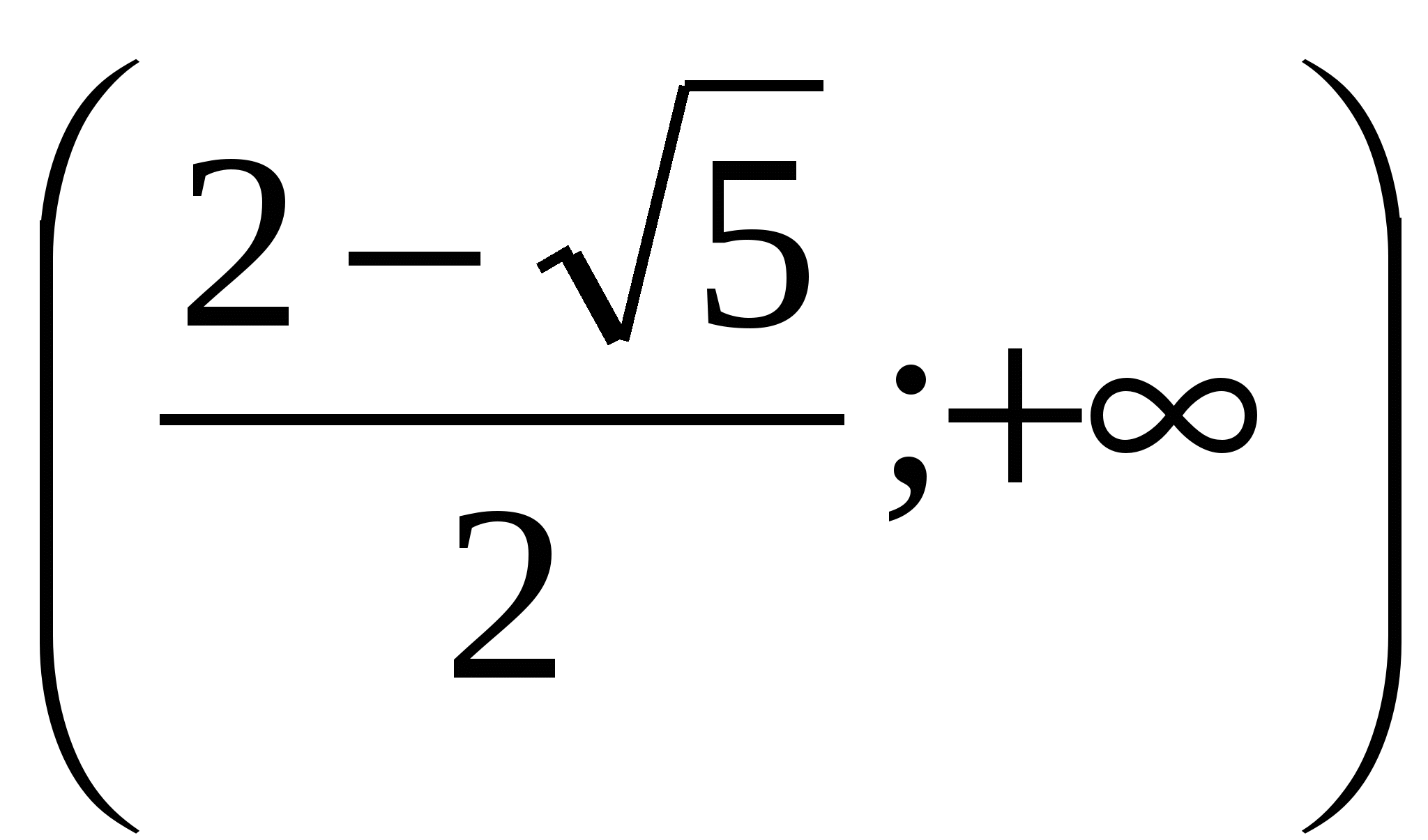 .
.
Пример 6. (задание С3 − вариант 23 [1]). Найдите все значения  , при которых неравенство
, при которых неравенство 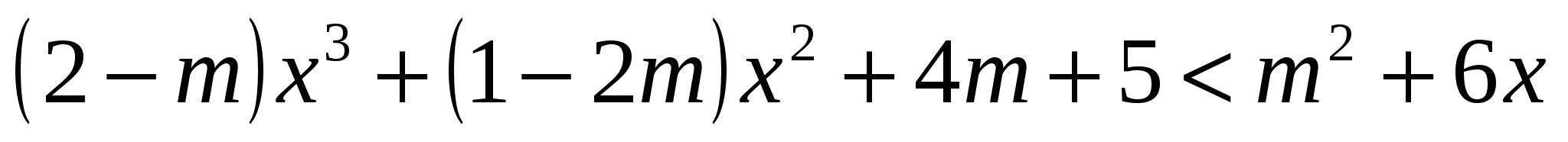 справедливо хотя бы для одного значения
справедливо хотя бы для одного значения 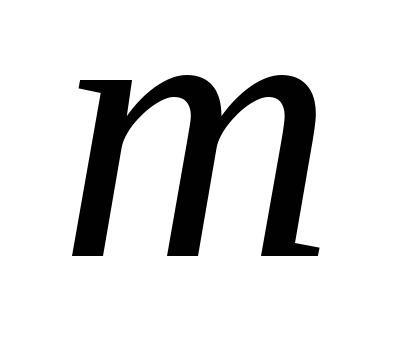 из
из 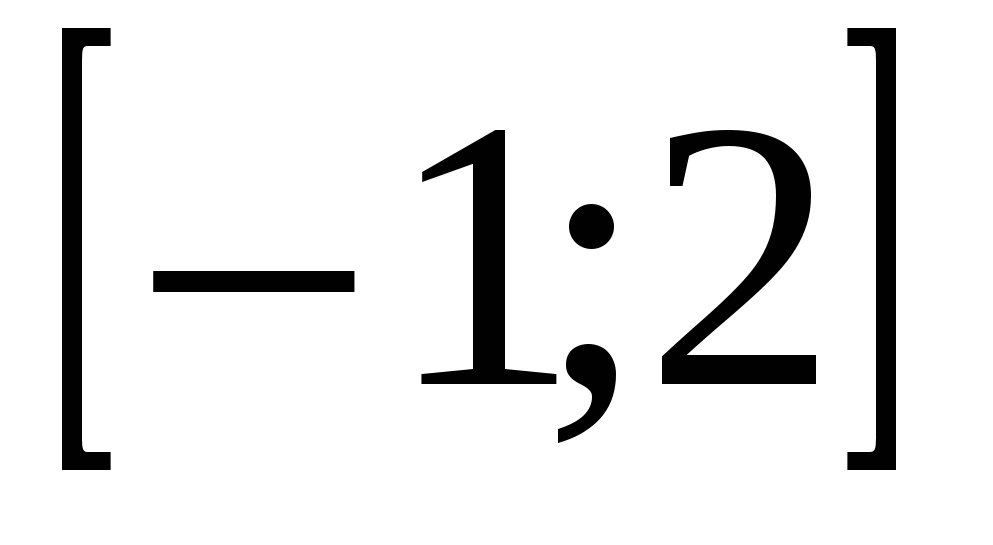 .
.
Преобразуем неравенство:
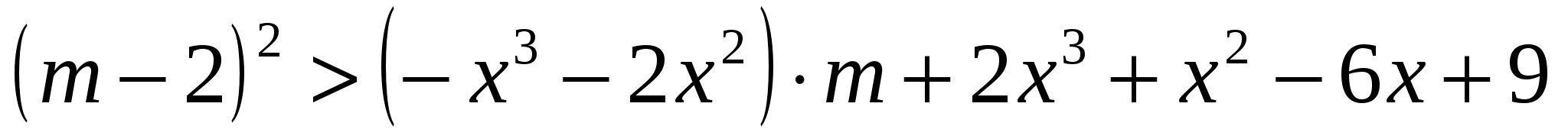 .
.
Рассмотрим функции: 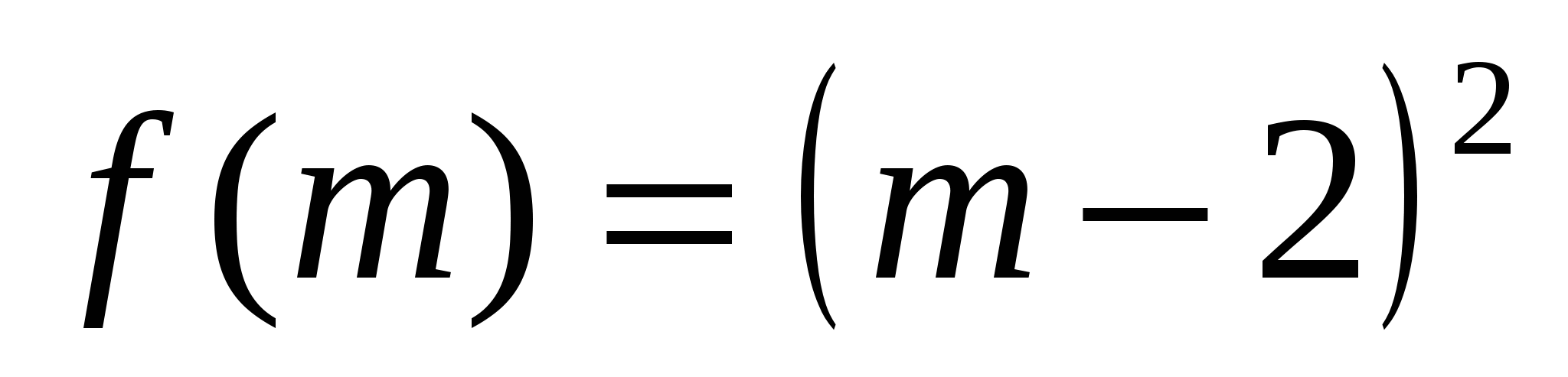 и
и 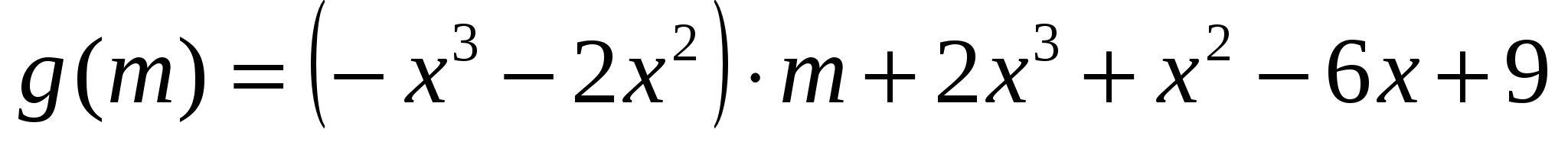 . Выясним при каких
. Выясним при каких  выполняется
выполняется 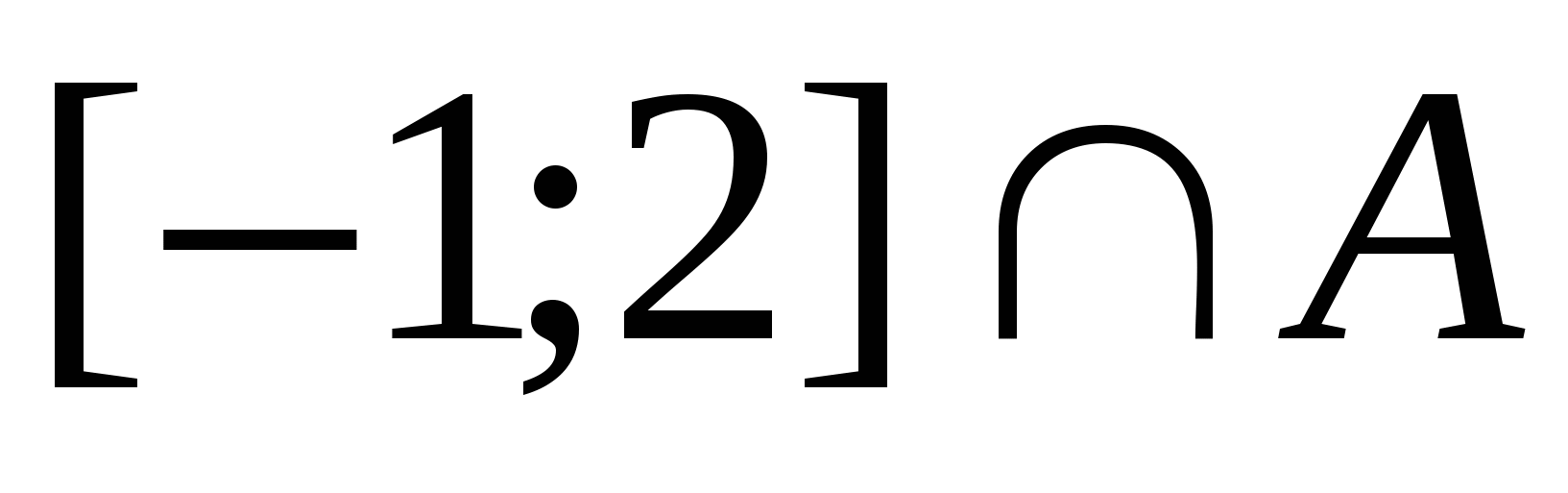 - непустое множество, где
- непустое множество, где  – множество решений заданного неравенства
– множество решений заданного неравенства 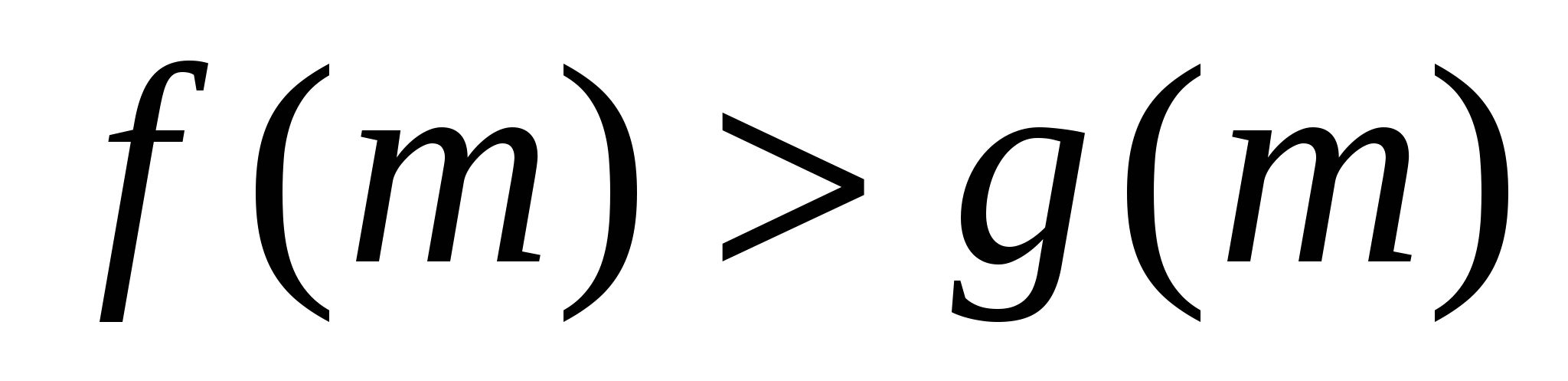 .
.
Условие задачи выполняется в 5 случаях.
а) Рис. 27: 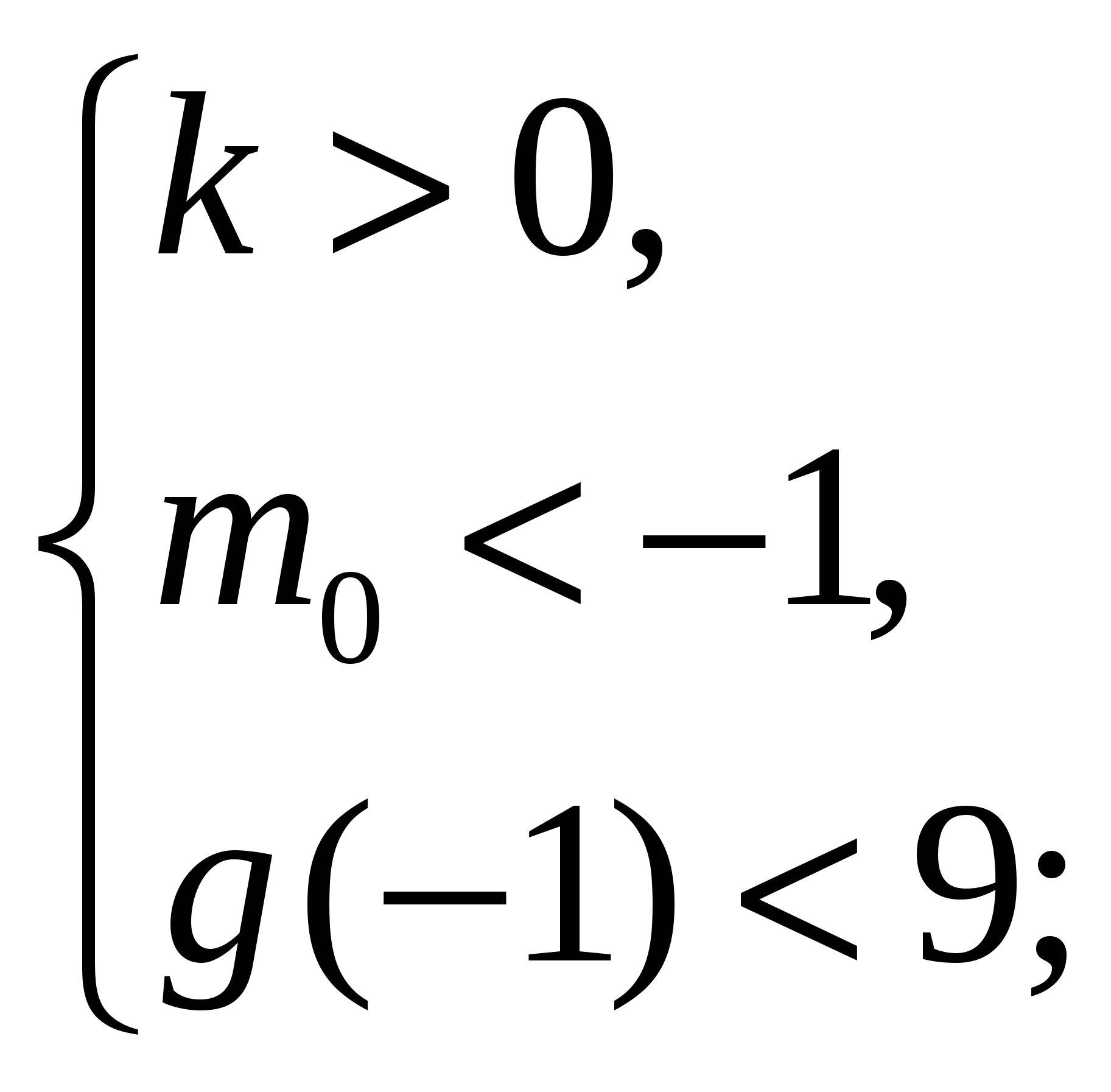
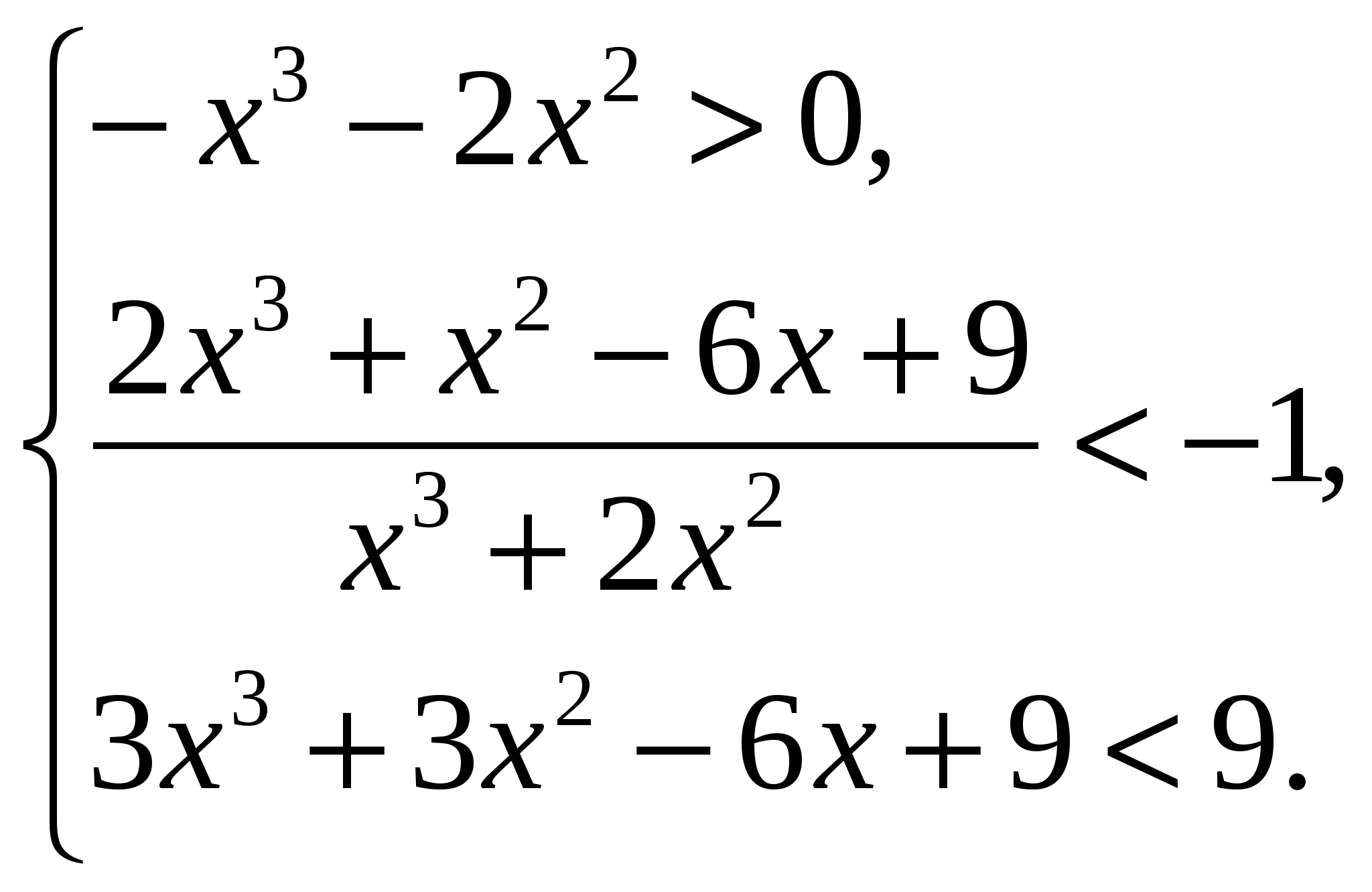
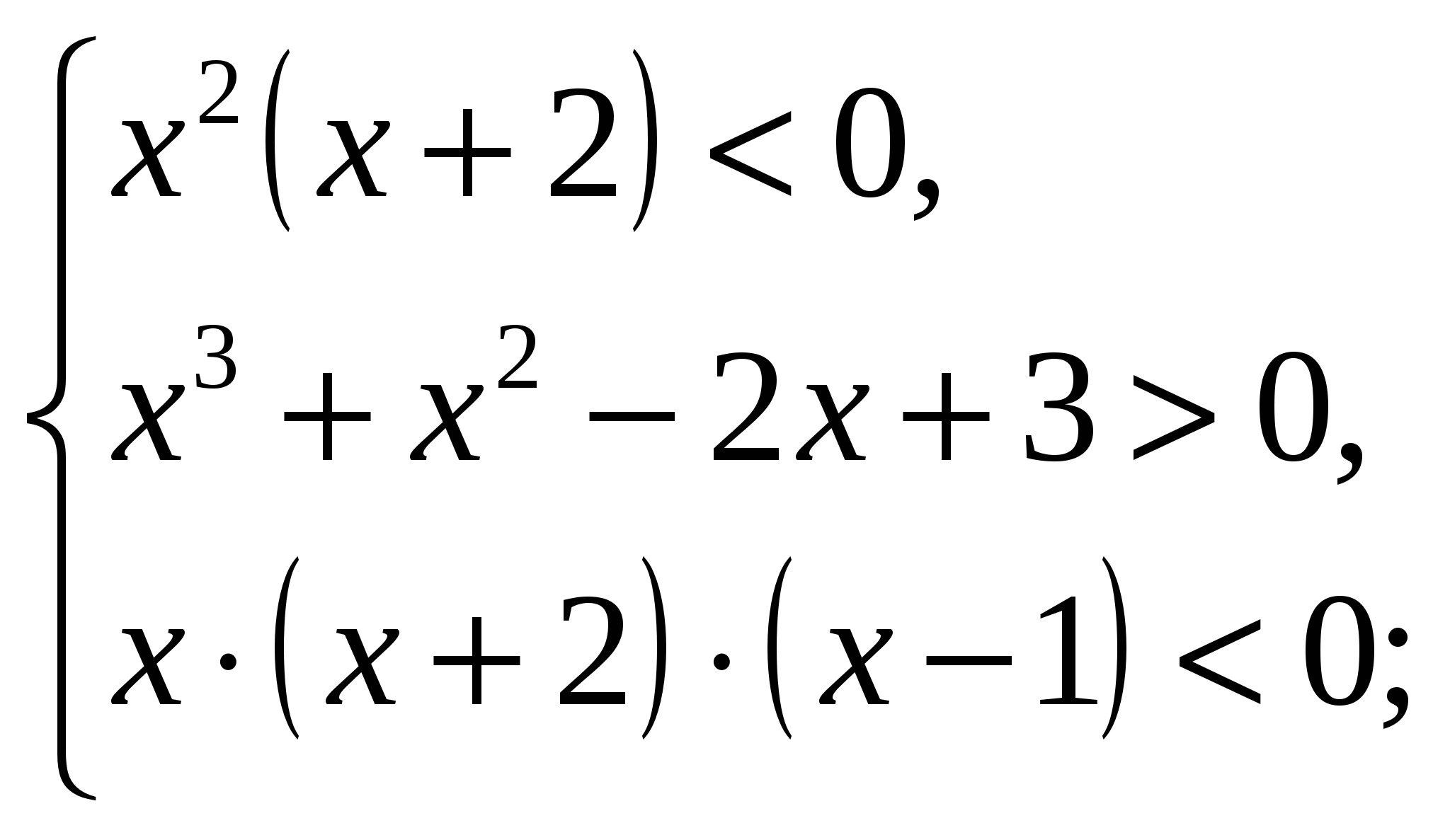
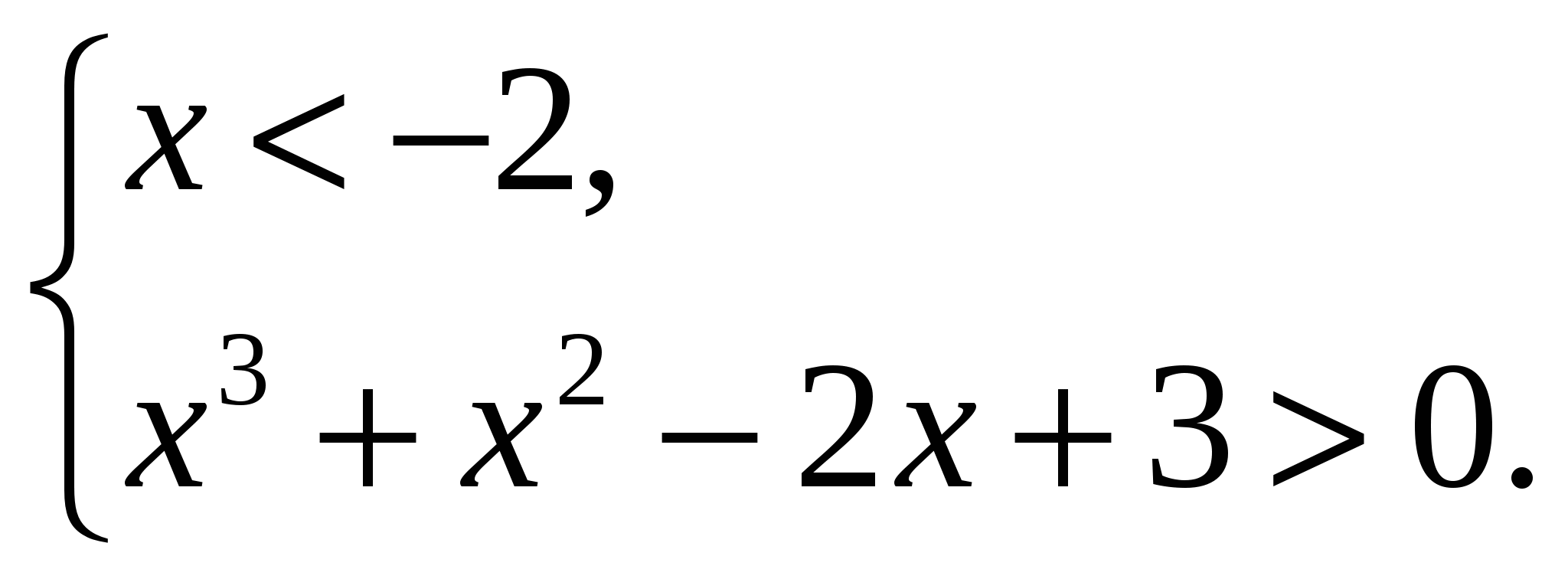 (1)
(1)
б) Рис. 28: 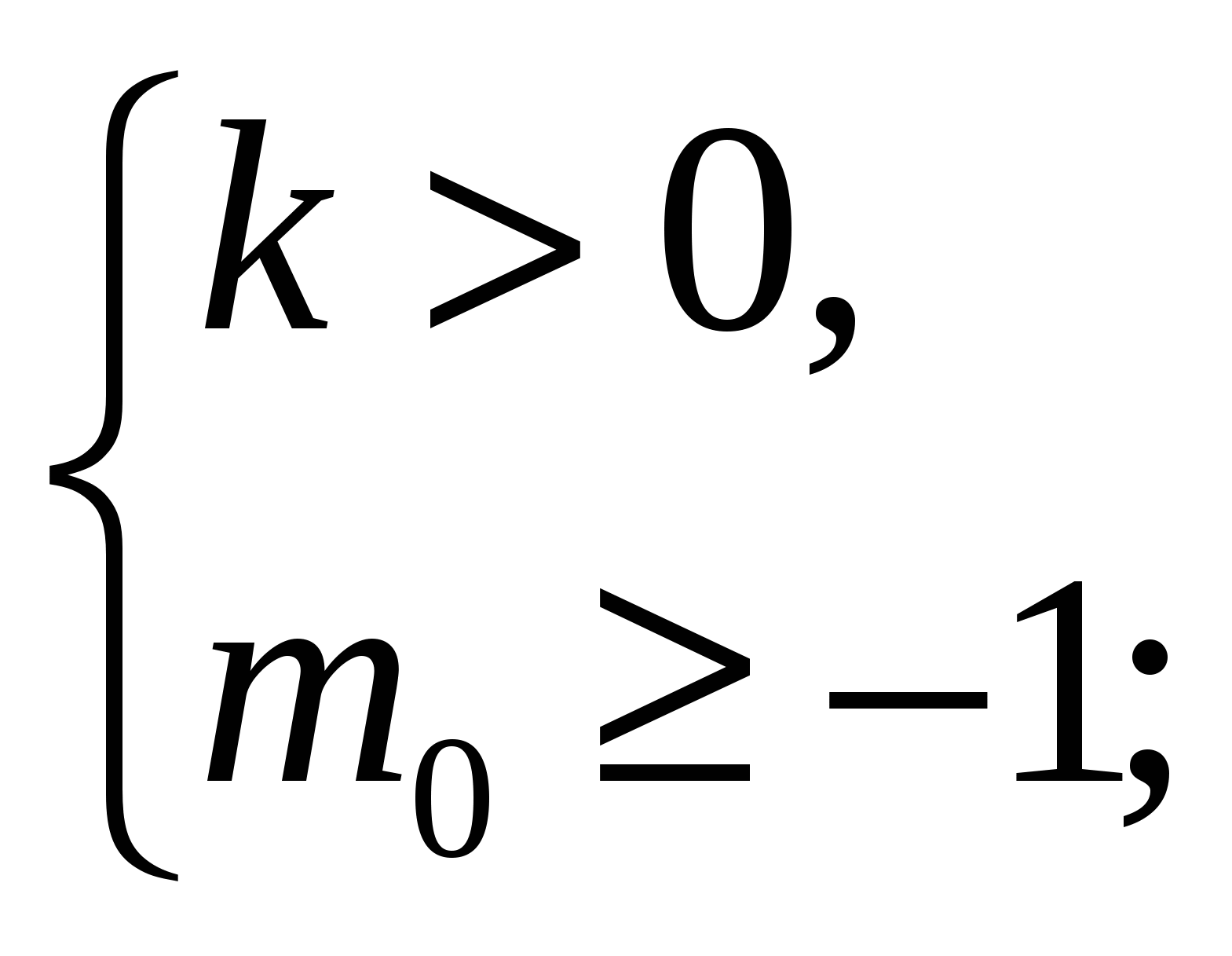
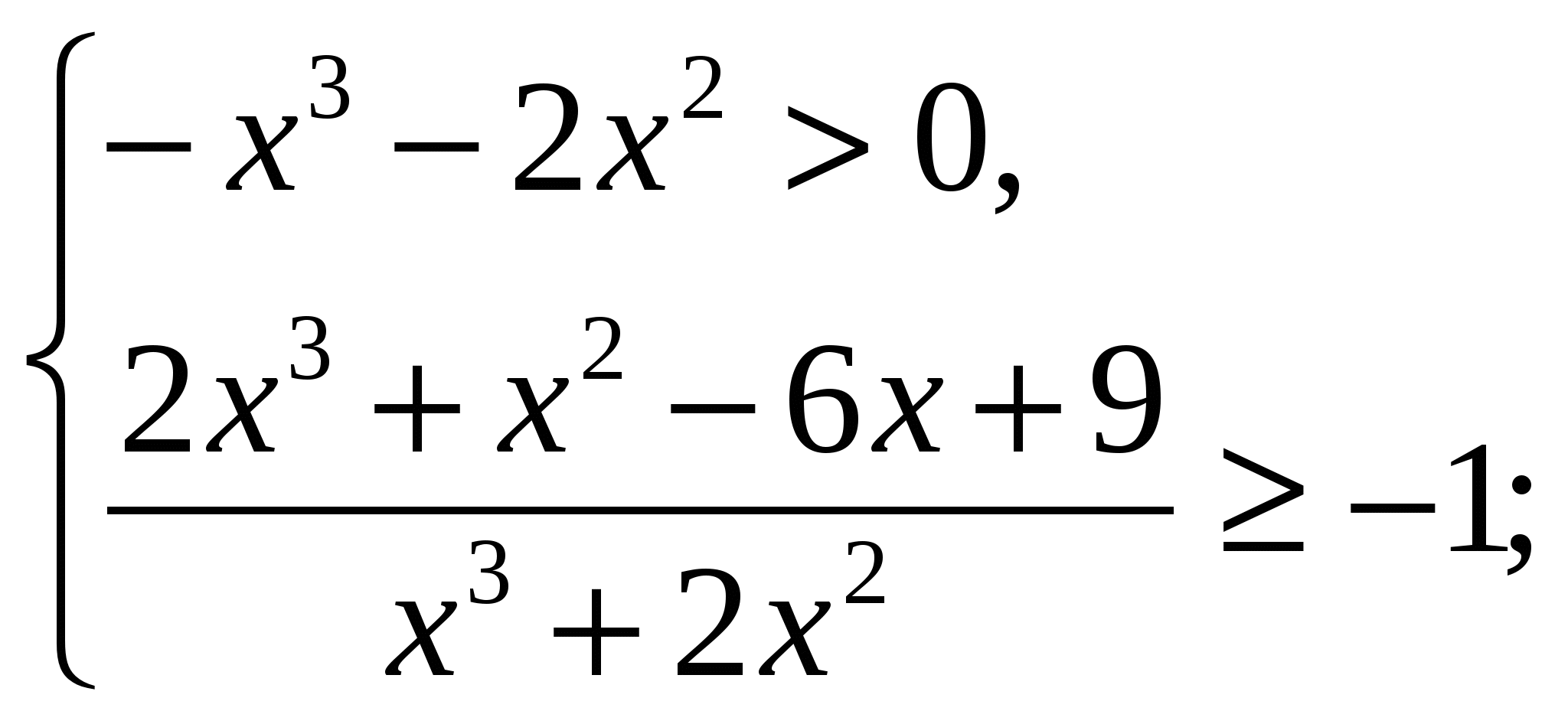
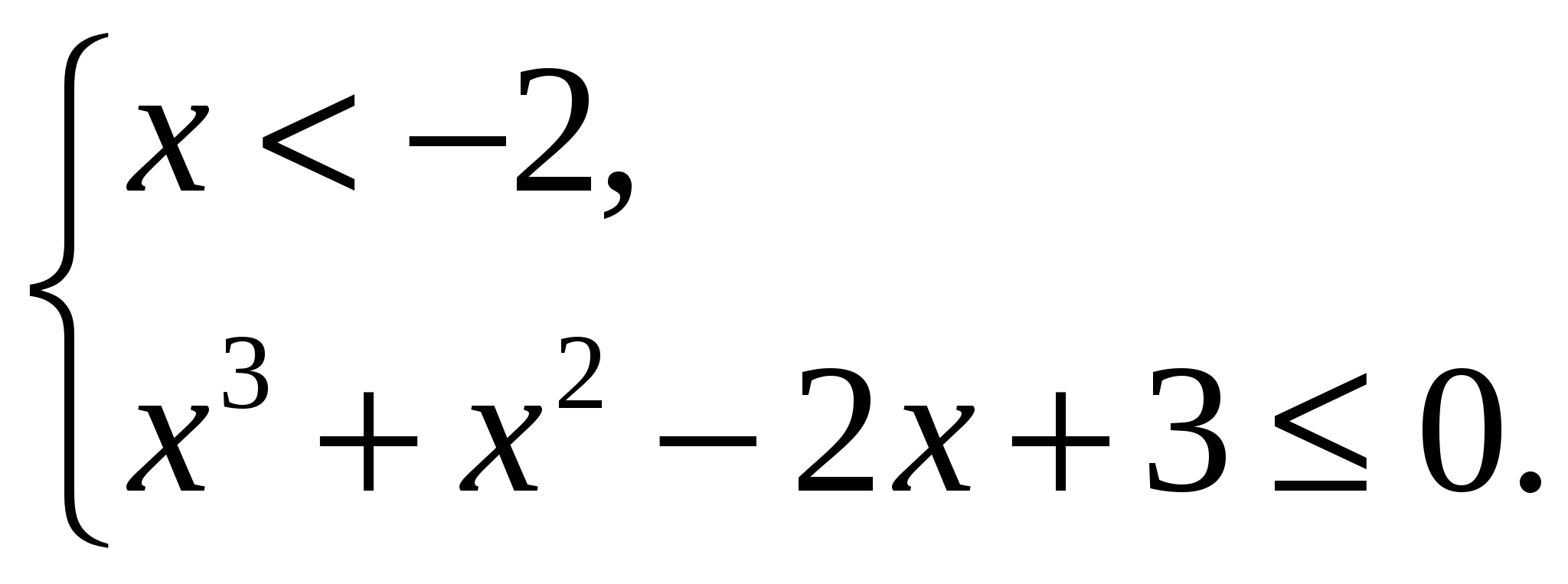 (2)
(2)
Из (1) и (2) получим 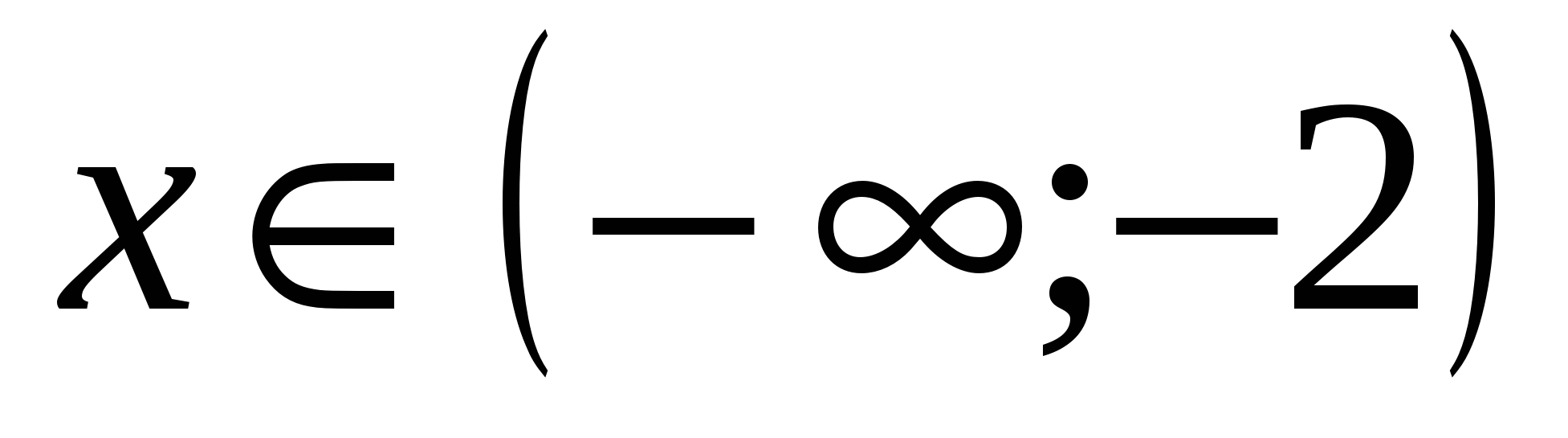
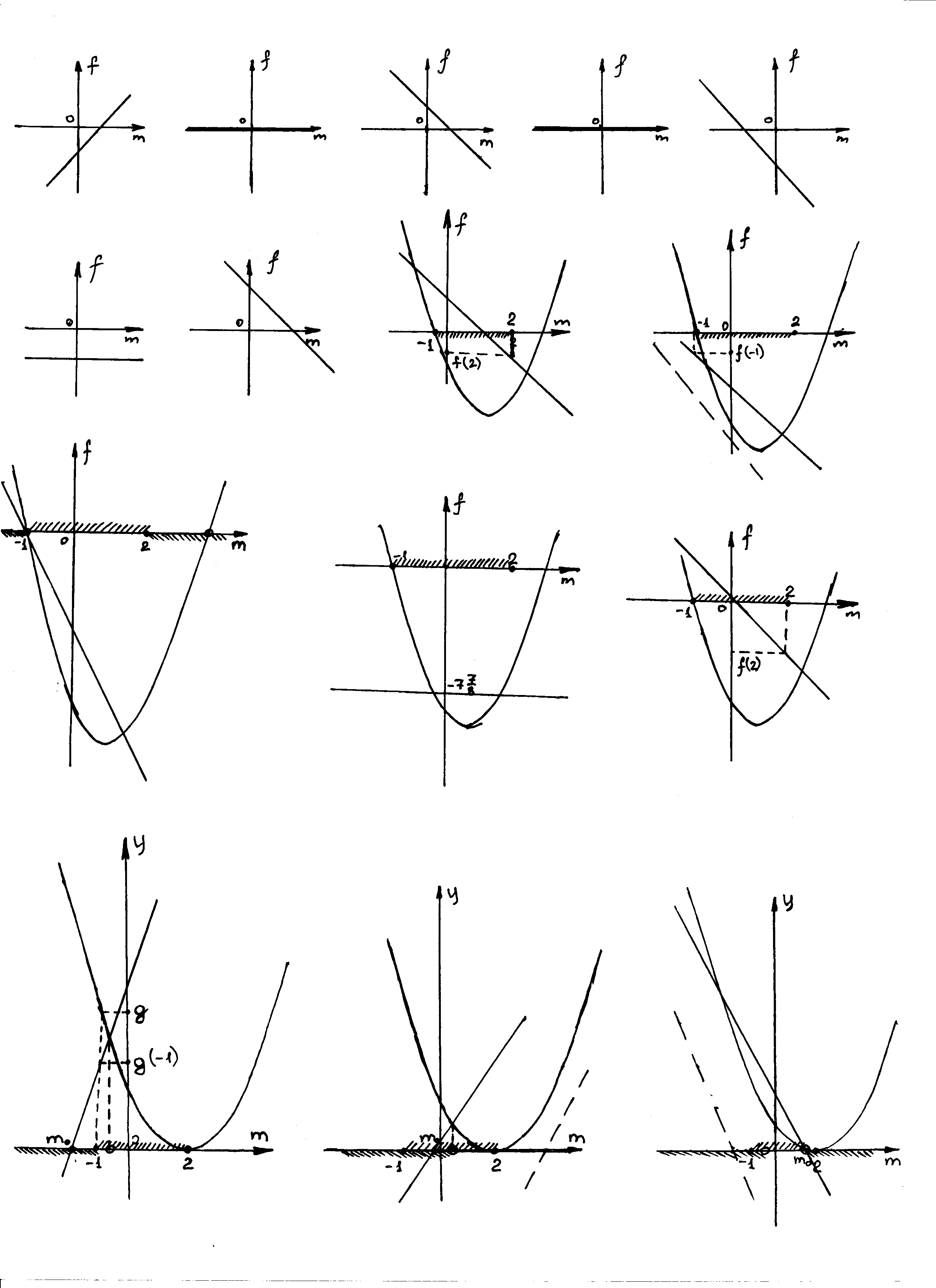
Рис. 27
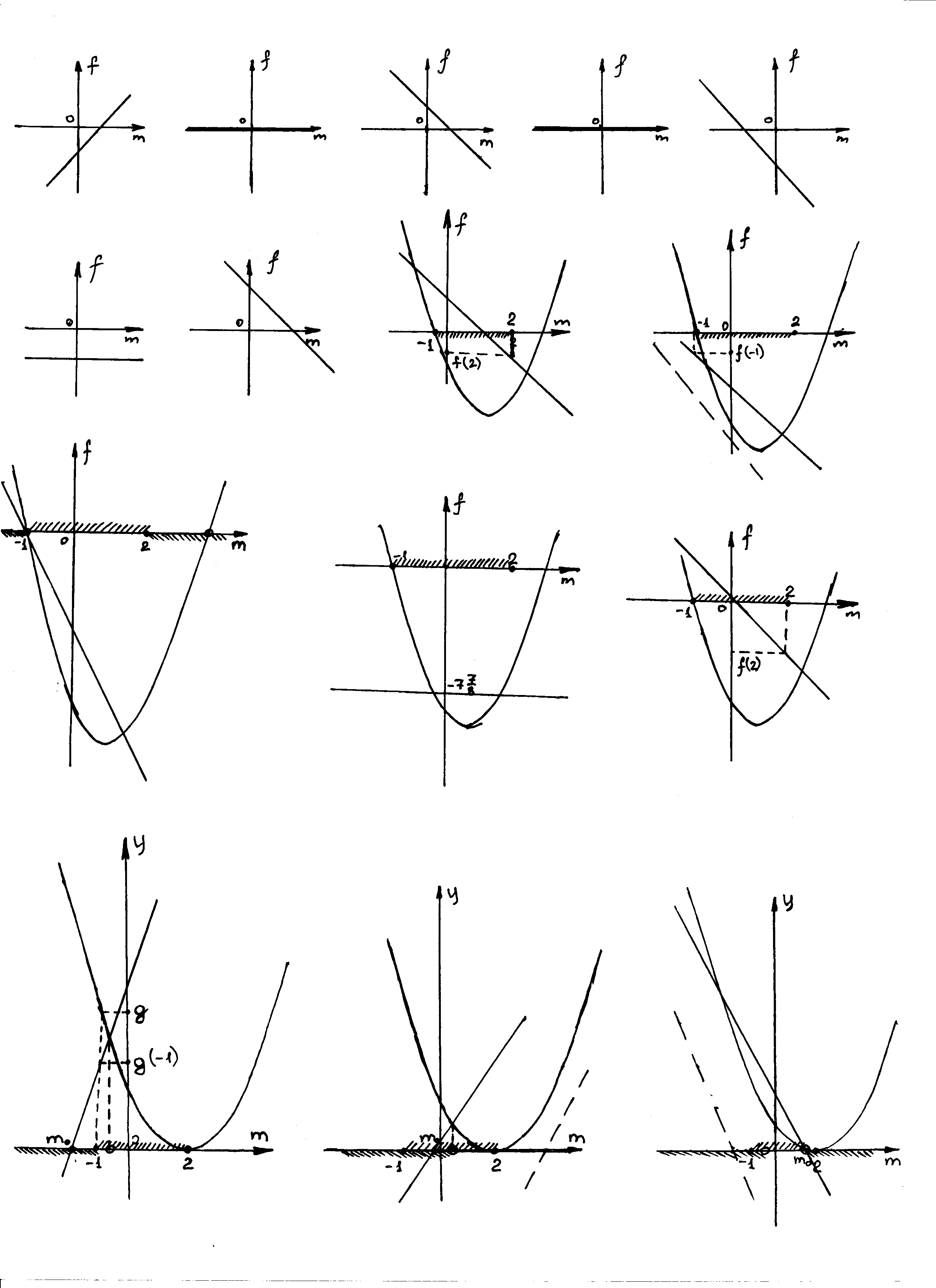
Рис. 28
в) Рис. 29: 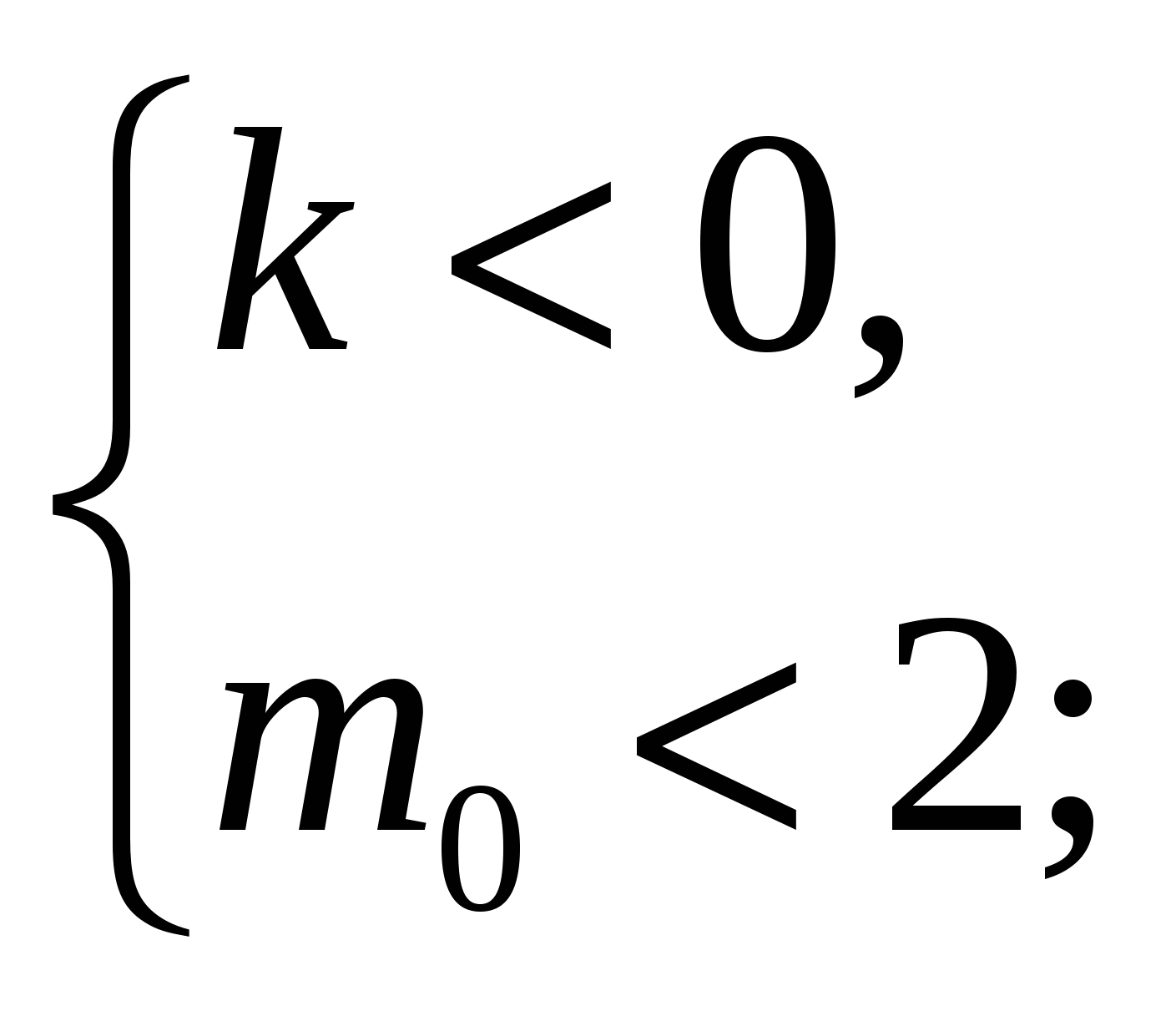
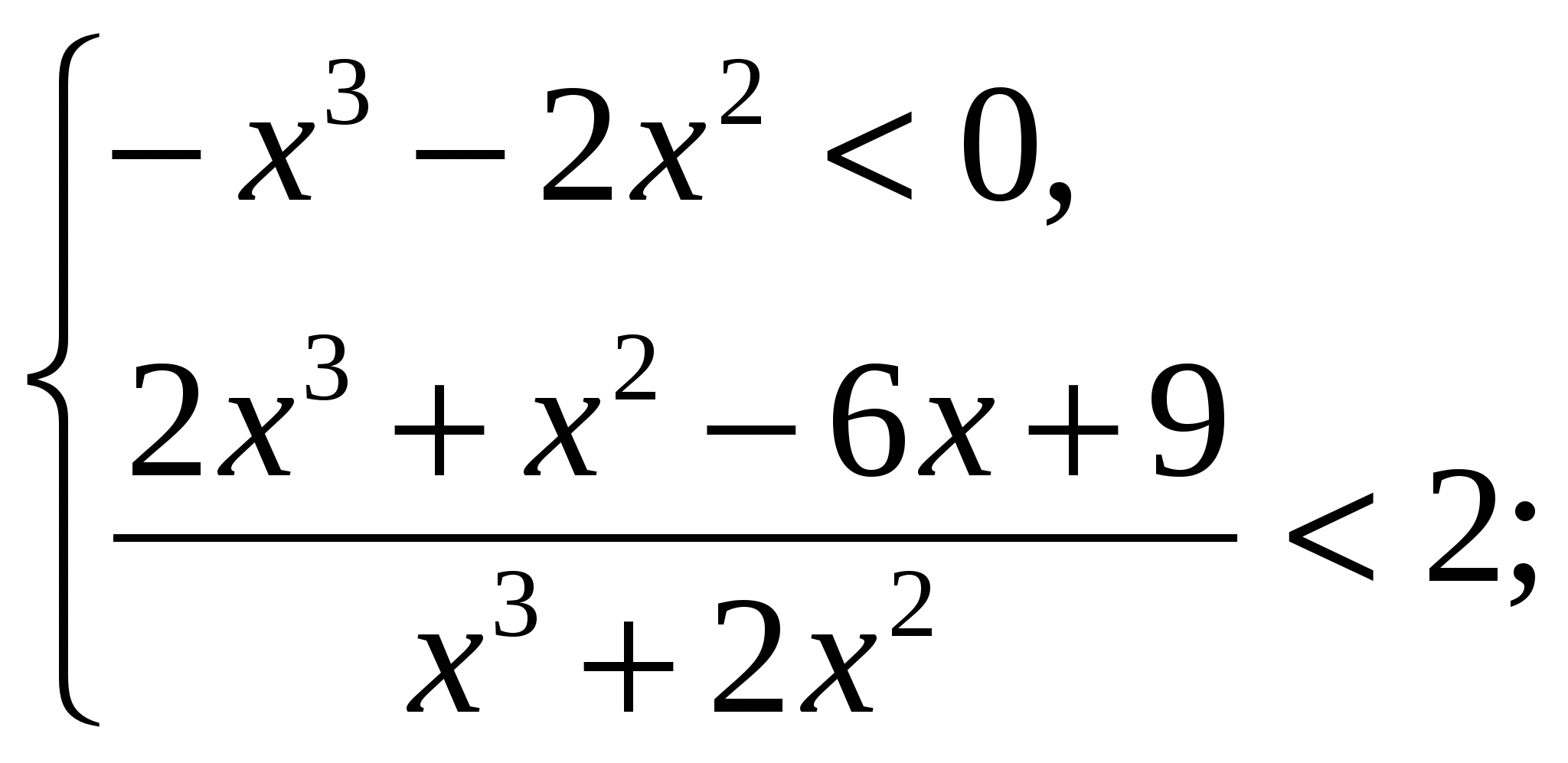
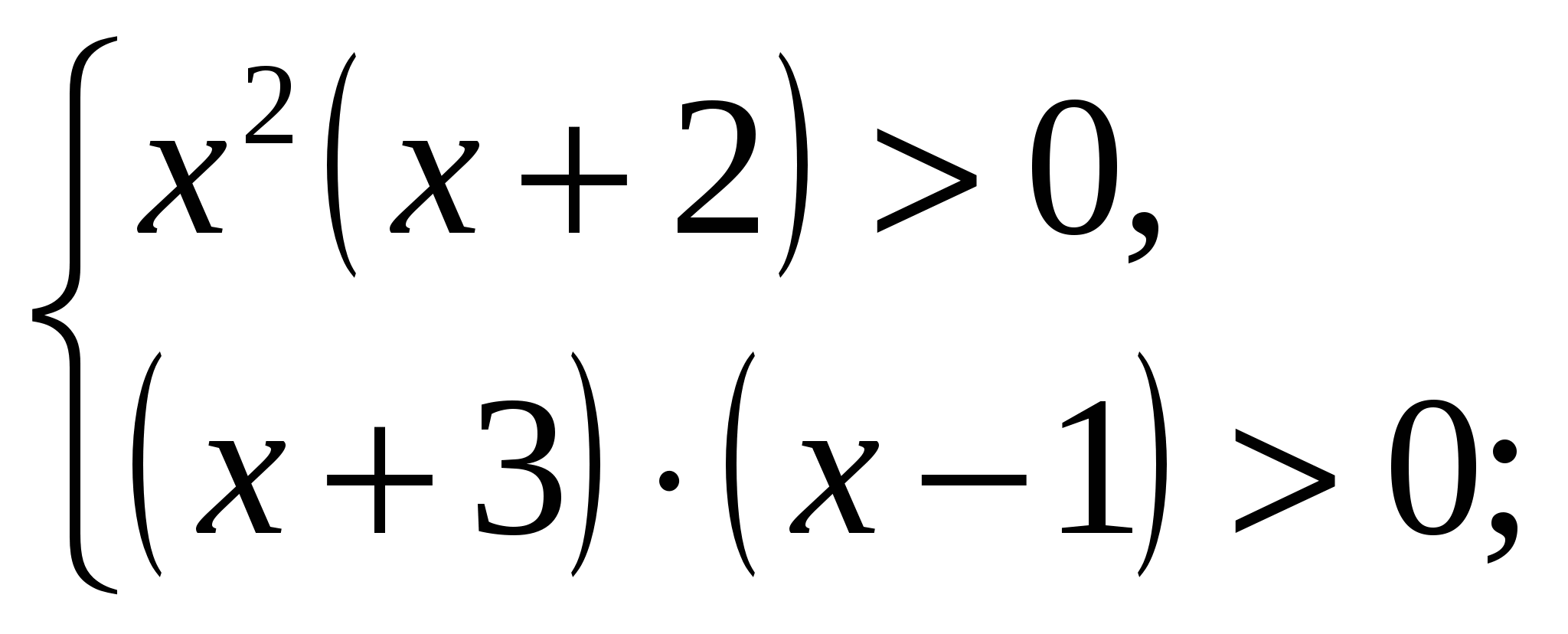
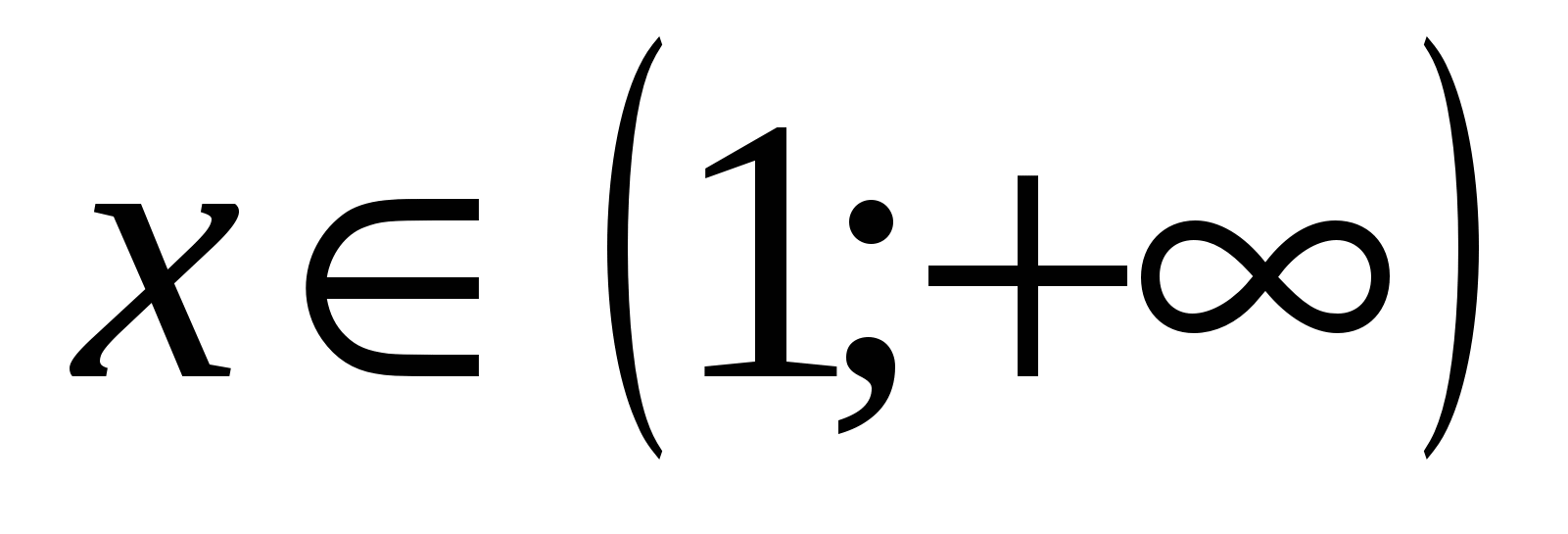 .
.
г) Рис. 30: 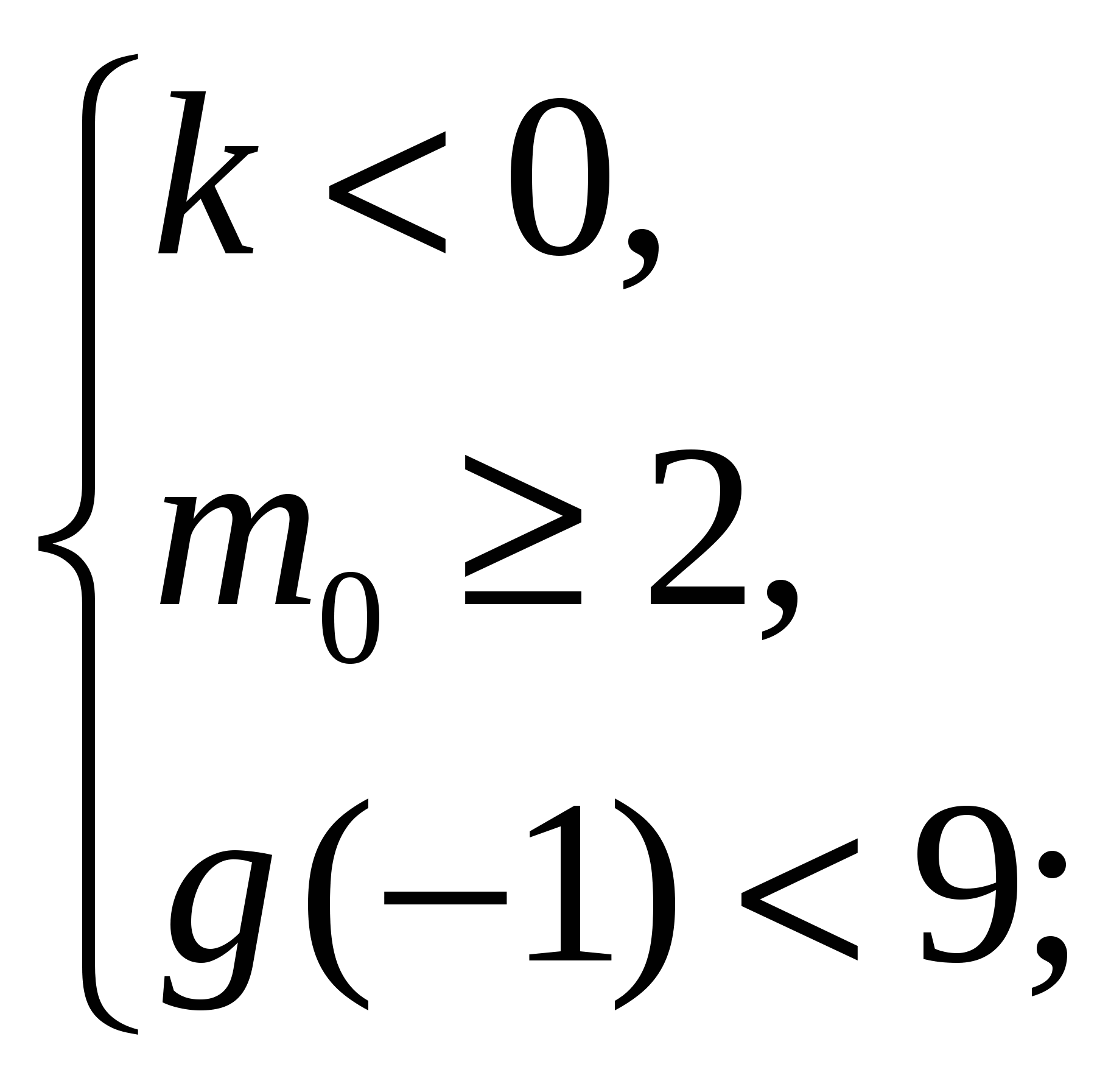
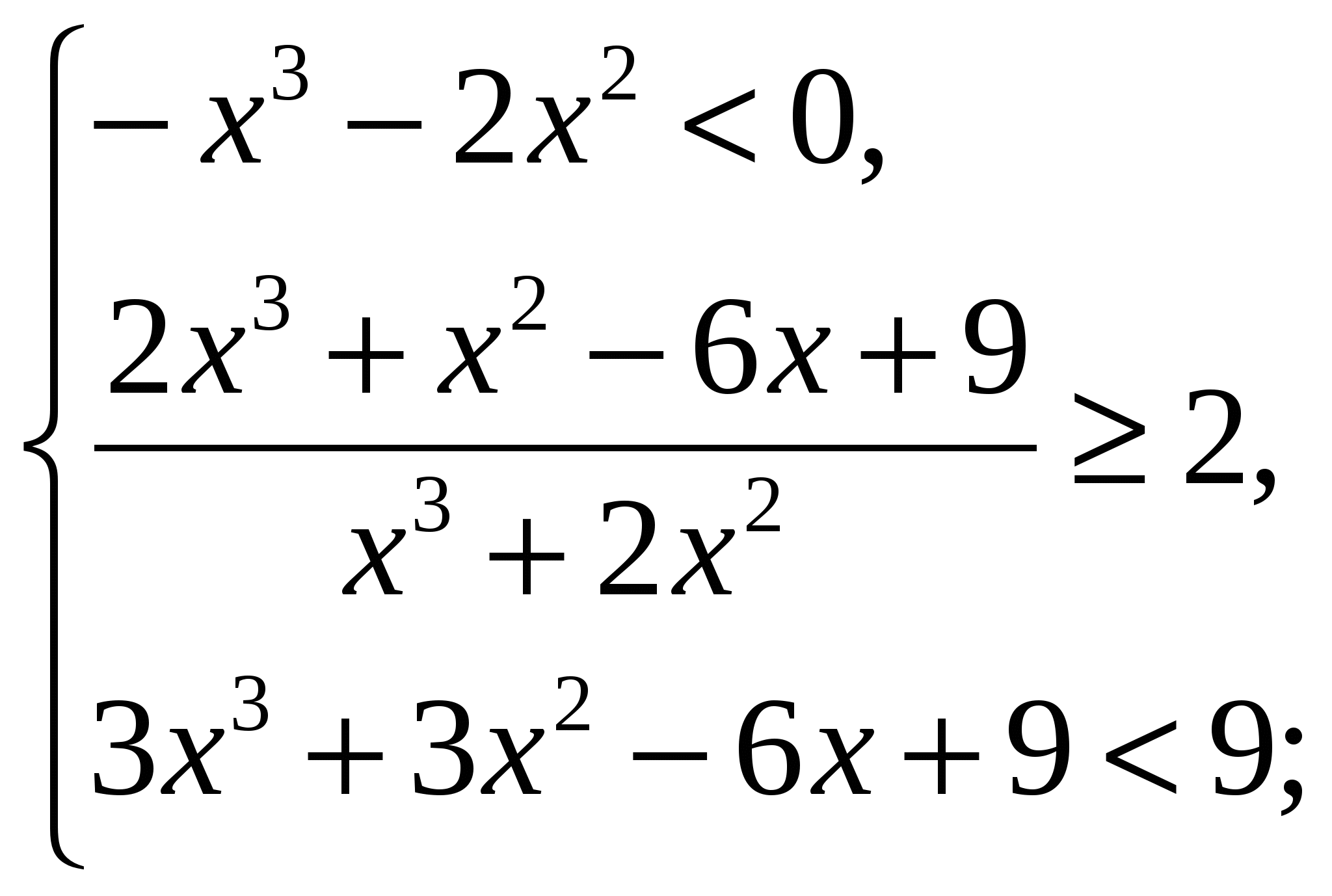
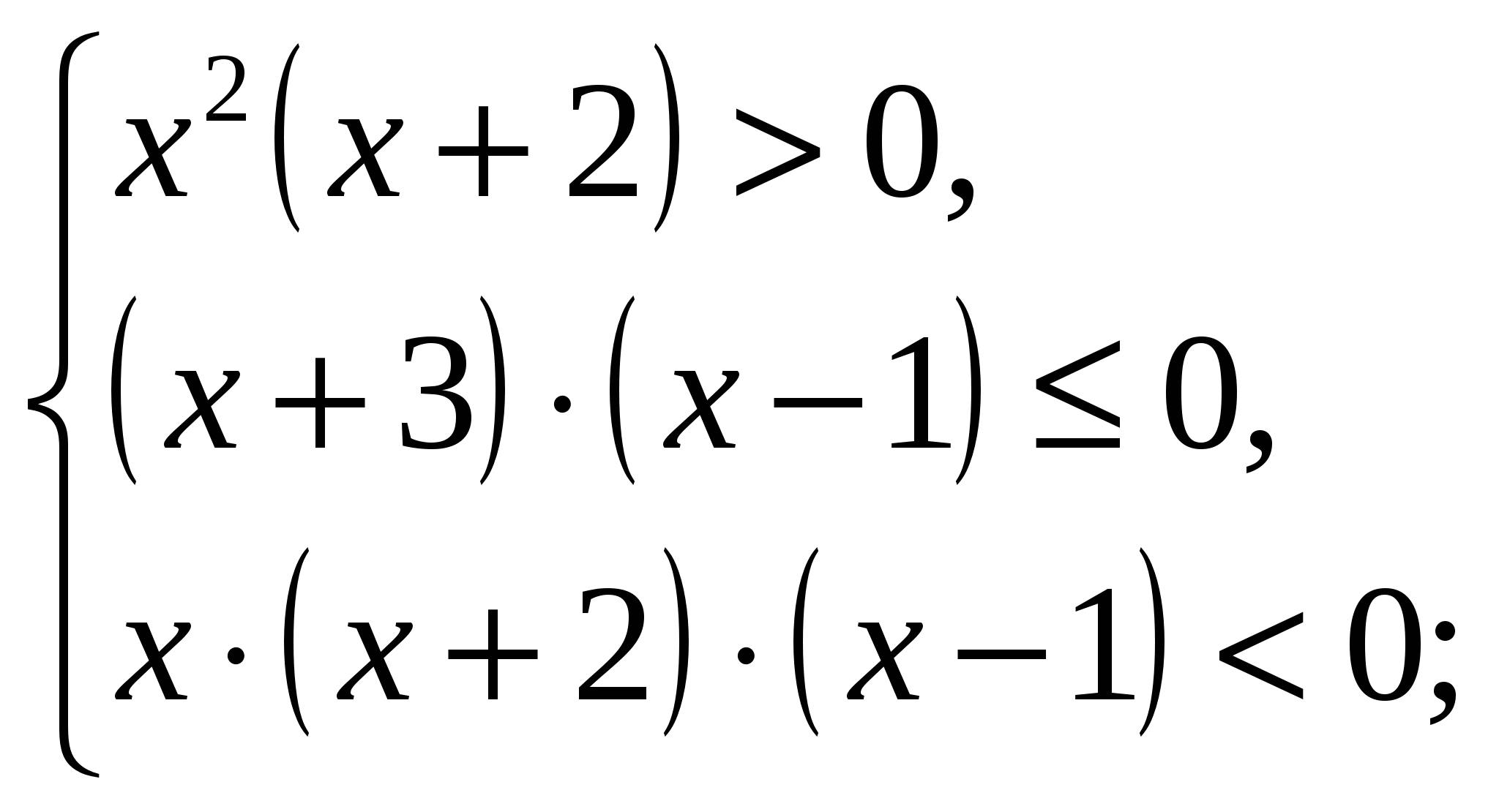
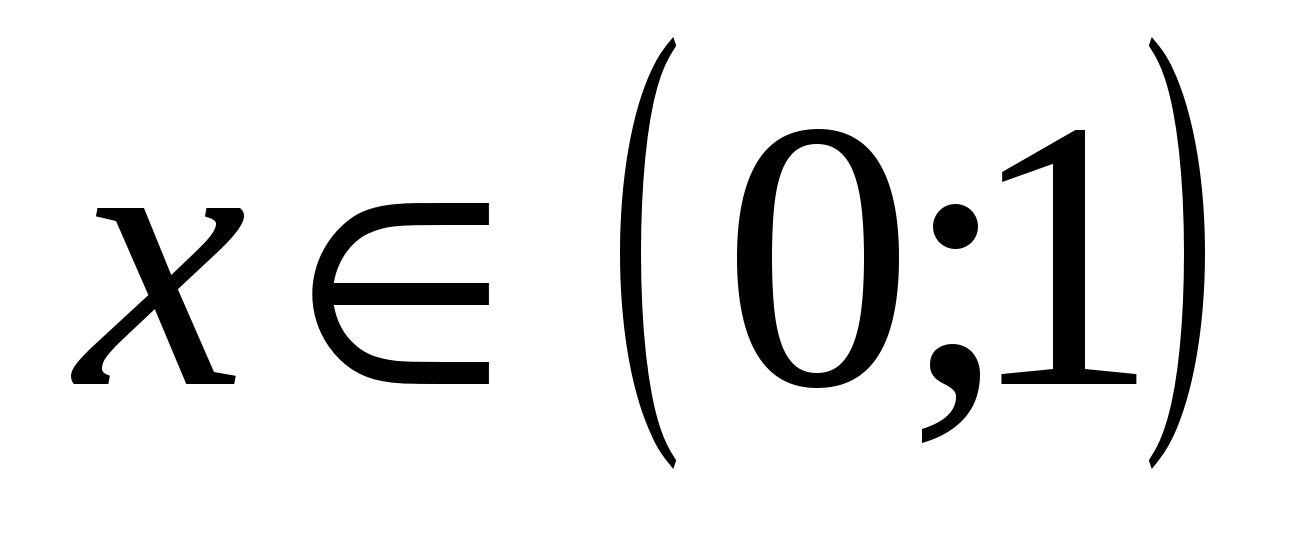
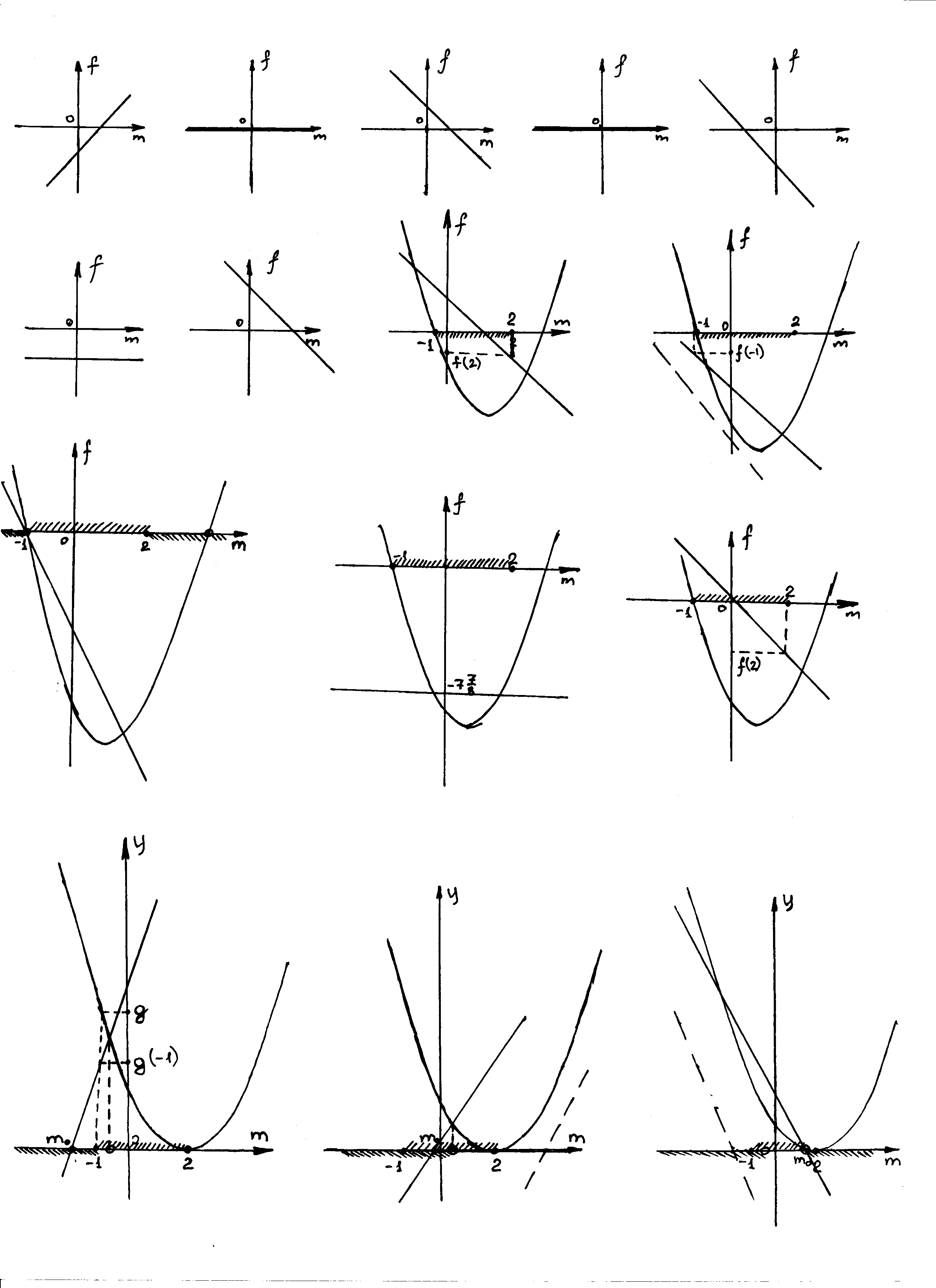
Рис. 29

Рис. 30
д) Рис. 31: 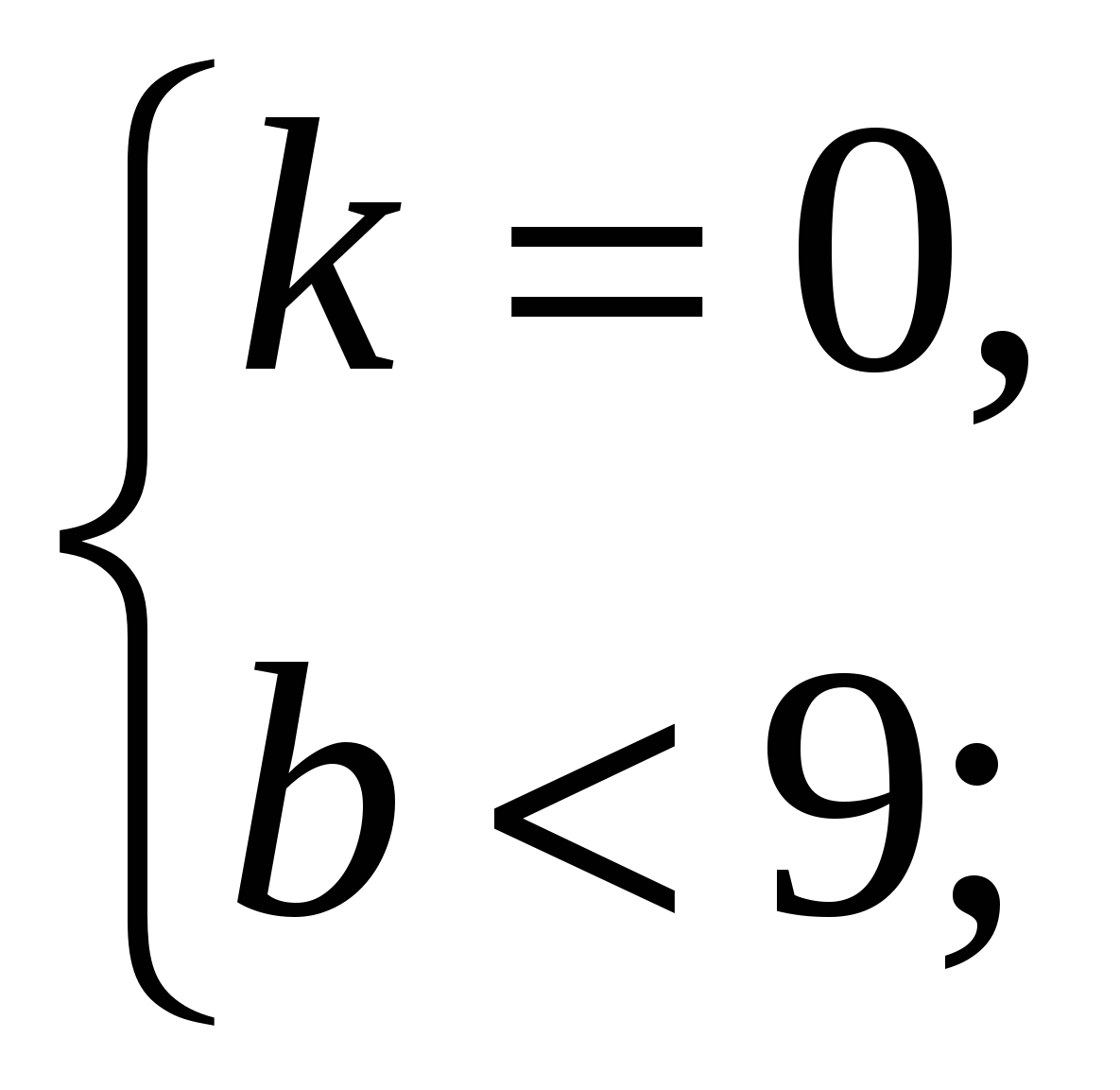
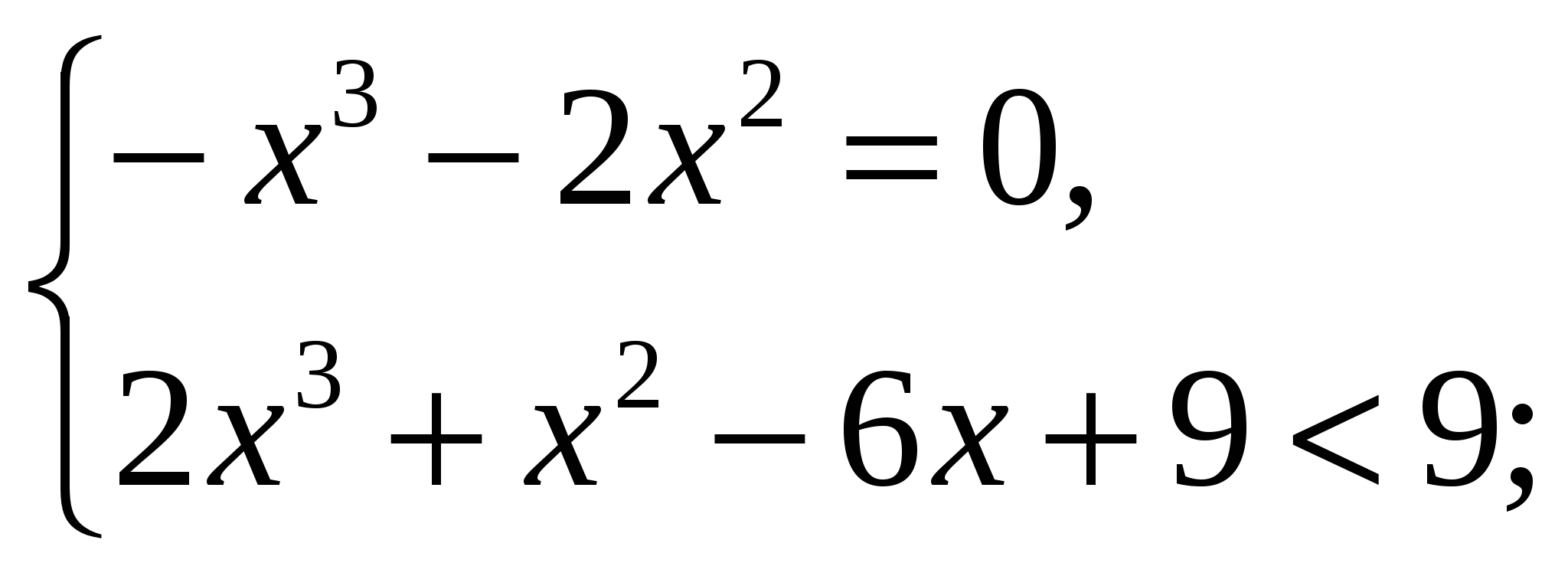

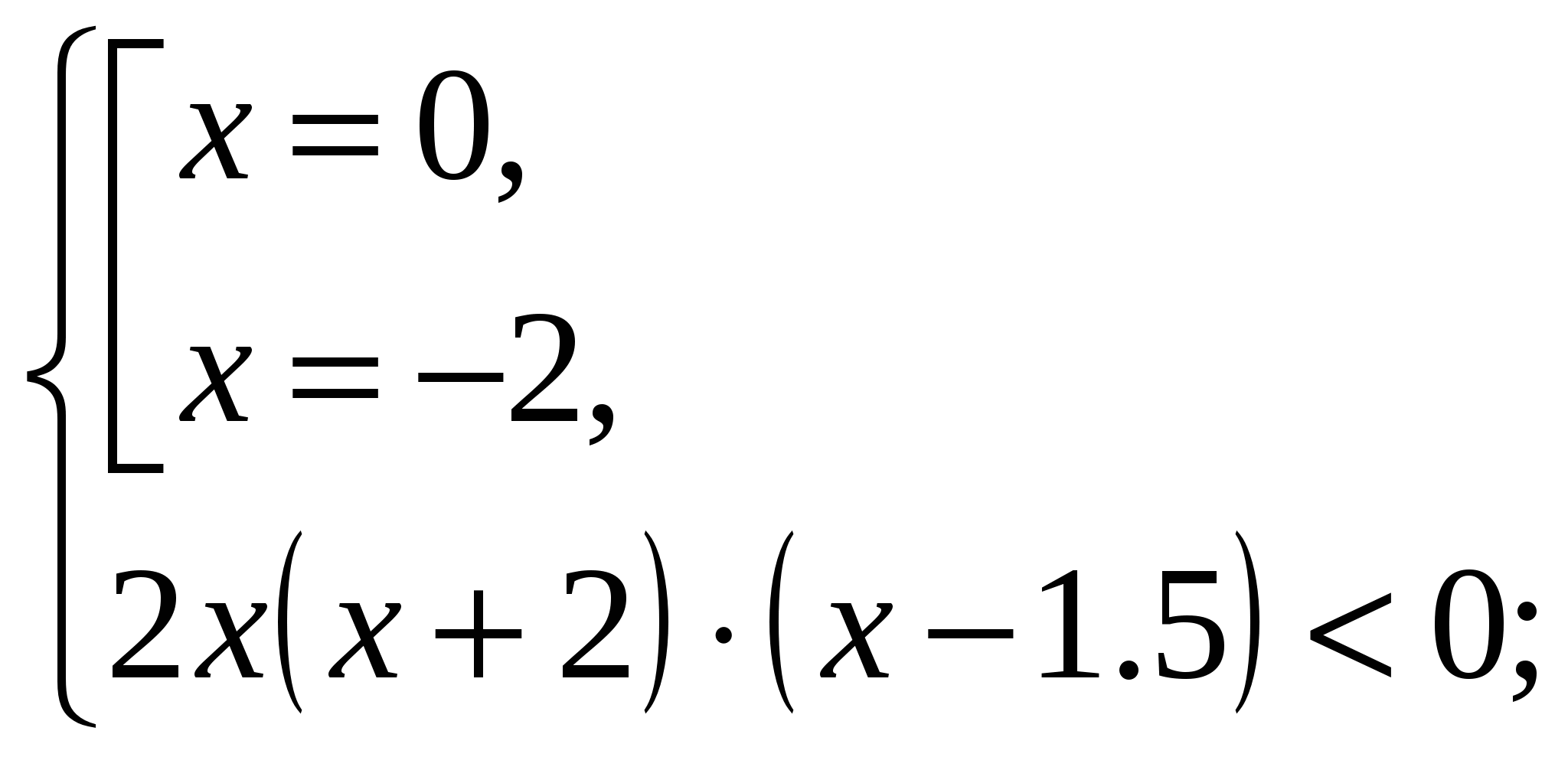 решений нет.
решений нет.
Итак, 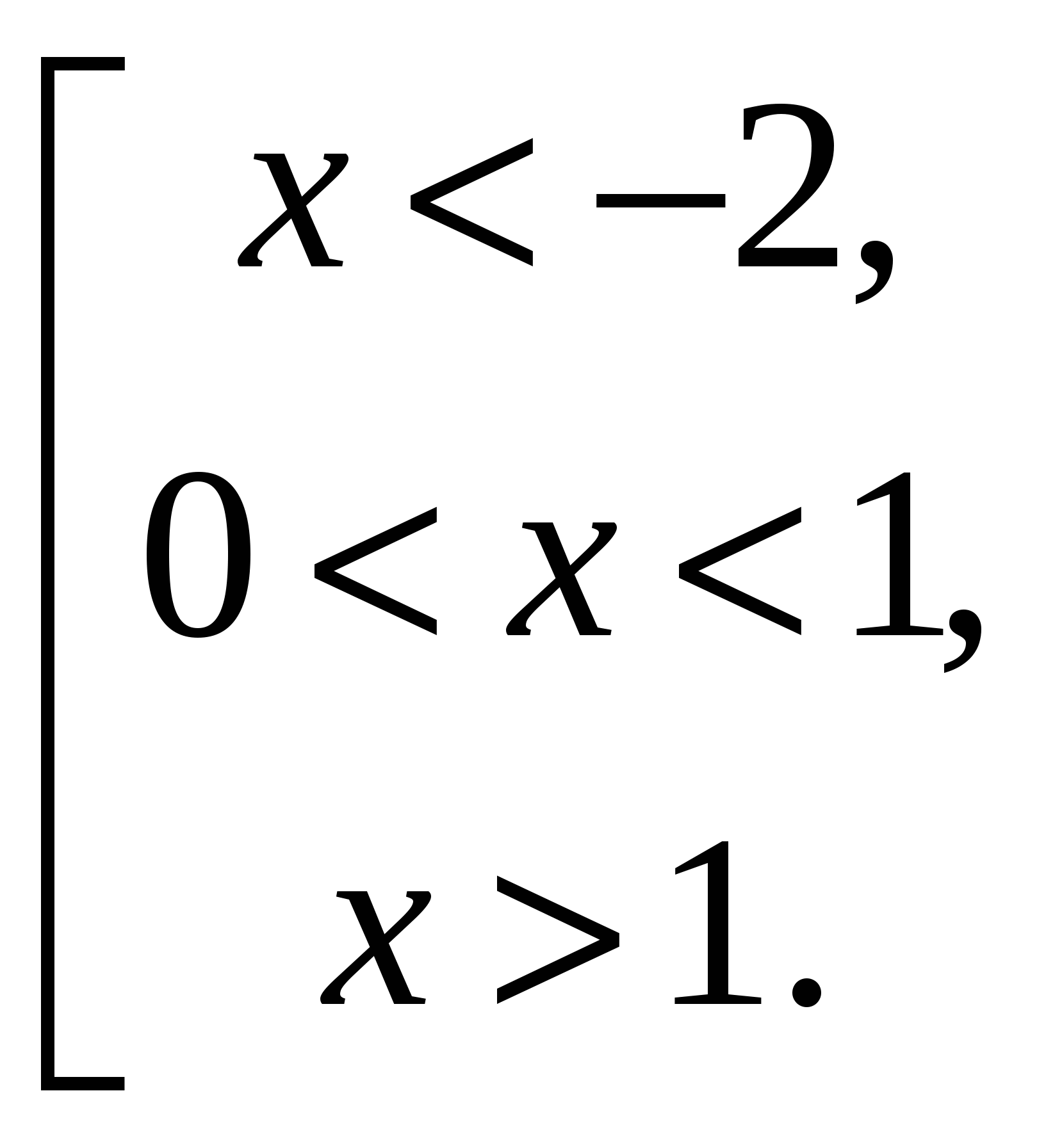

Рис. 31
Ответ: 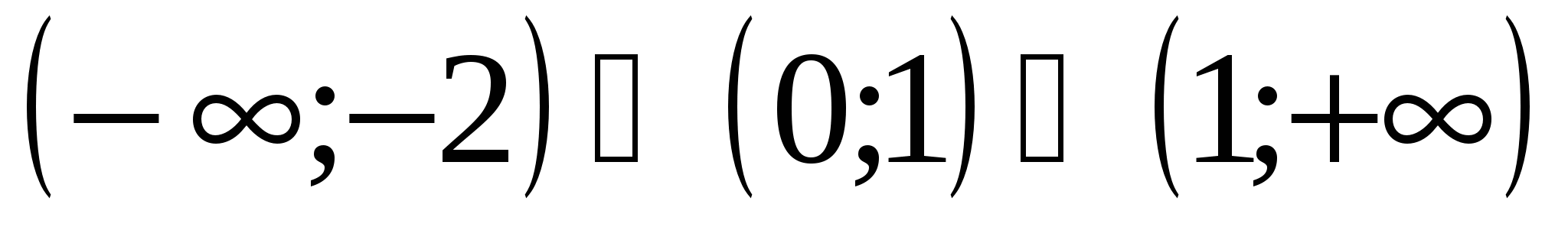
Программно-методическое обеспечение:
Математика. ЕГЭ-2006. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2005. - [1],
Математика. ЕГЭ-2009. Часть II. Вступительные экзамены. / Под редакцией Ф.Ф.Лысенко. – Ростов на Дону: Легион, 2009. - [2].
* Материал рассчитан на 2 часа (сдвоенный урок)
* Материал рассчитан на 2 часа (сдвоенный урок), но может возникнуть необходимость в дополнительном времени