Муниципальное общеобразовательное учреждение
средняя общеобразовательная школа № 31
города Мурманска
конспект урока
«Применение производной
для решения задач экономического
содержания»
10класс
Автор: Иванова Татьяна Ивановна
учитель математики МОУ СОШ № 31
Вступление
Тема нашего урока «Применение производной для решения задач экономического содержания». Математика и экономика - две, на первый взгляд разные науки, одна абстрактна другая практична, однако важность применения математических методов и моделей для анализа экономических процессов отмечали учёные, как математики, так и экономисты ещё в 17 веке.
Отсюда и цель нашего урока:
научиться анализировать реальные ситуации с помощью доступного нам математического аппарата.
Почему именно экономика выбрана нами для демонстрации прикладного значения математики.
Все мы участвуем в экономических отношениях, иногда в роли производителя или продавца, иногда в роли потребителя, или покупателя. Но в независимости от нашего места в экономических отношениях мы все преследуем одну цель: получить как можно большую прибыль, а она всегда связана с определёнными затратами.
Какие же затраты несёт предприятие при производстве продукции?
Это: налоги, электроэнергия, зарплата, аренда и т.д. Все эти затраты измеряются в разных единицах измерения ( рубль, киловатт-час, тонны, метры и т.д.), что не удобно. Поэтому для удобства ведения бухгалтерской и экономической отчетности все издержки производства измерять принято в их стоимостном выражении, то есть в рублях.
А функцию, выражающую зависимость между стоимостью выпускаемой продукции и стоимостью суммарных затрат на её производство, называют производственной функцией.
Но мы всё пока говорим об экономике. Какое отношение это имеет к теме нашего урока?
Для ответа на этот вопрос рассмотрим следующую ситуацию:
Пусть предприятие «А» производит Х единиц продукции.
К - суммарные затраты или издержки производства.
Производственная функция, описывающая зависимость затрат от объёма производства имеет вид: К=f(х).
Увеличим производство на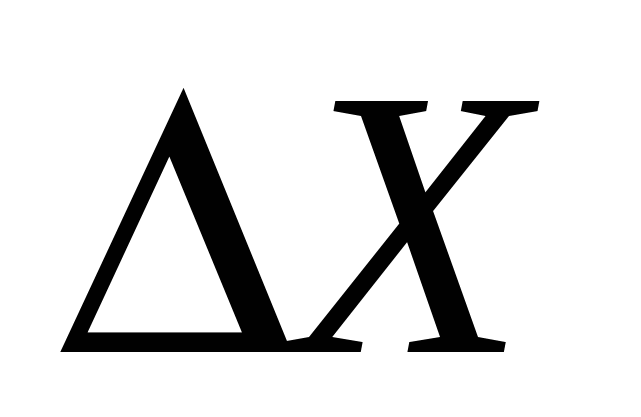 
,тогда затраты вырастут на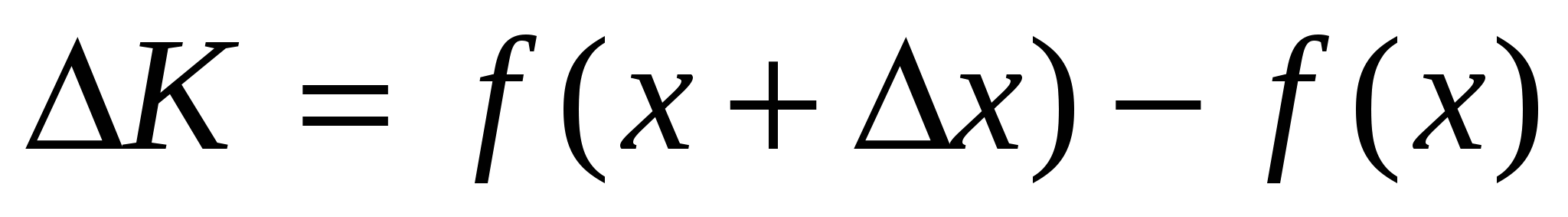 
Среднее приращение затрат будет равно
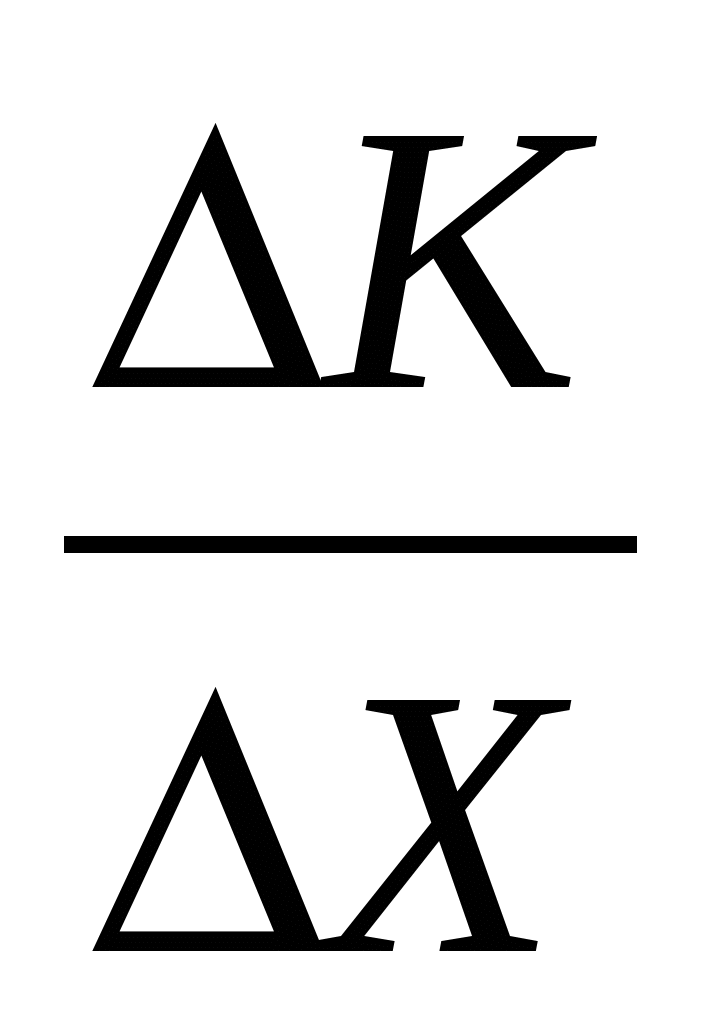
Теперь рассмотрим понятие предельных издержек производства:
Предельные издержки производства – это дополнительные затраты, которые несёт предприятие при увеличении объёма производства на бесконечно малую величину.
А это не что иное, как предел среднего приращения затрат при стремлении 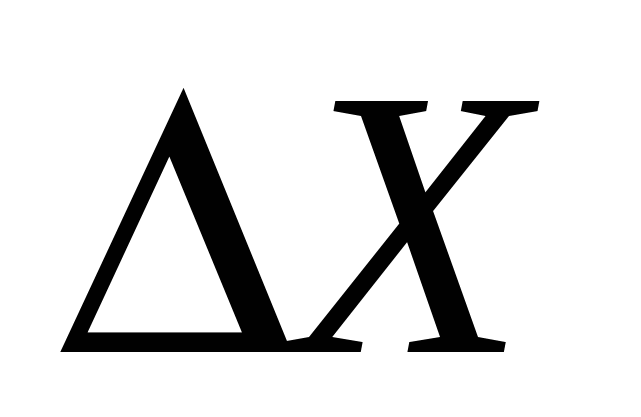к нулю.
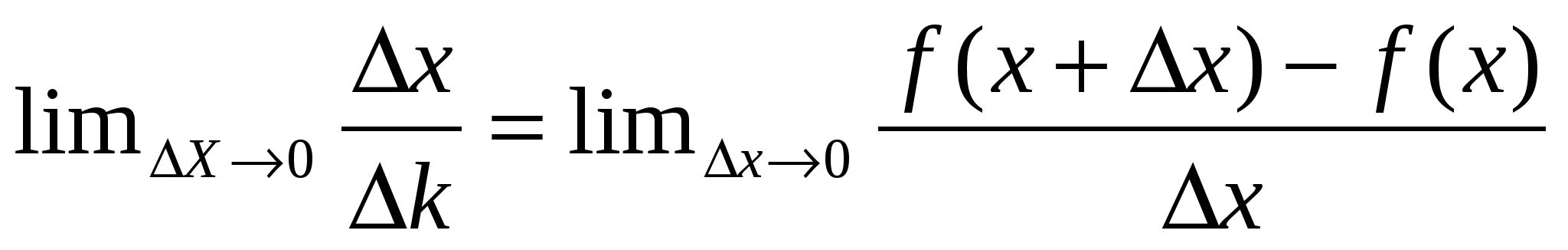Вопрос: что напоминает вам эта формула?
Ответ: так вычисляется значение производной функции в точке.
Да! А мы с вами получили не что иное, как ещё одно понятие производной, а точнее её экономический смысл.
экономический смысл производной.
Значение производной функции в данной точке есть предельные издержки производства при данном его объёме.
Таким образом у нас появилась ещё одна трактовка понятия производной к уже имеющимся.
механический смысл производной.
Значение производной функции в данной точке есть мгновенная скорость изменения функции в этой точке.
геометрический смысл производной.
Значение производной функции в данной точке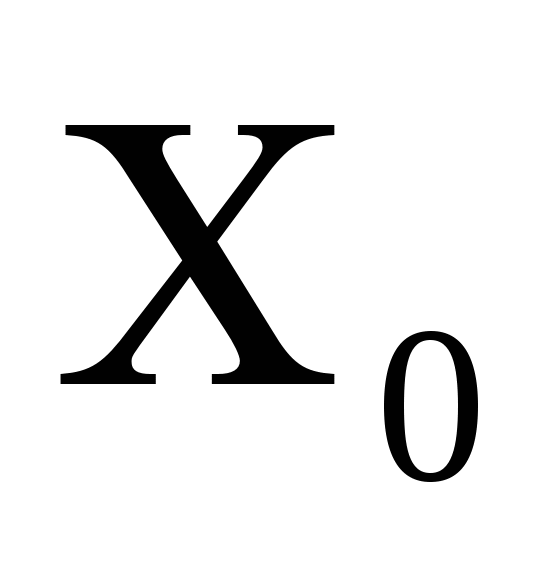 
есть тангенс угла наклона касательной, проведённой к графику данной функции в точке с абсциссой .
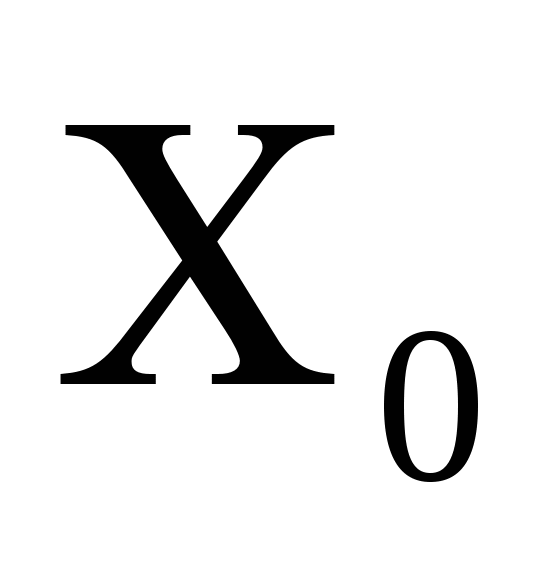Рассмотрим несколько задач, где рассмотренные нами понятия могут нам понадобиться.
Задача № 1.
Пусть функция затрат при производстве апатитового концентрата имеет вид:
К(Х)=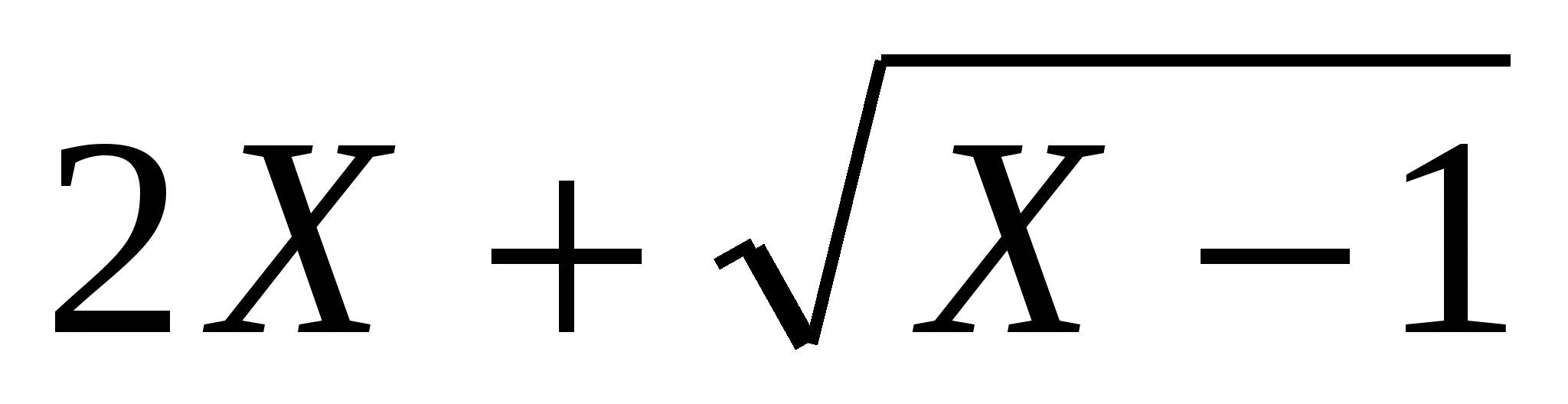
. Определить предельные издержки производства при увеличении объёма выпуска на 
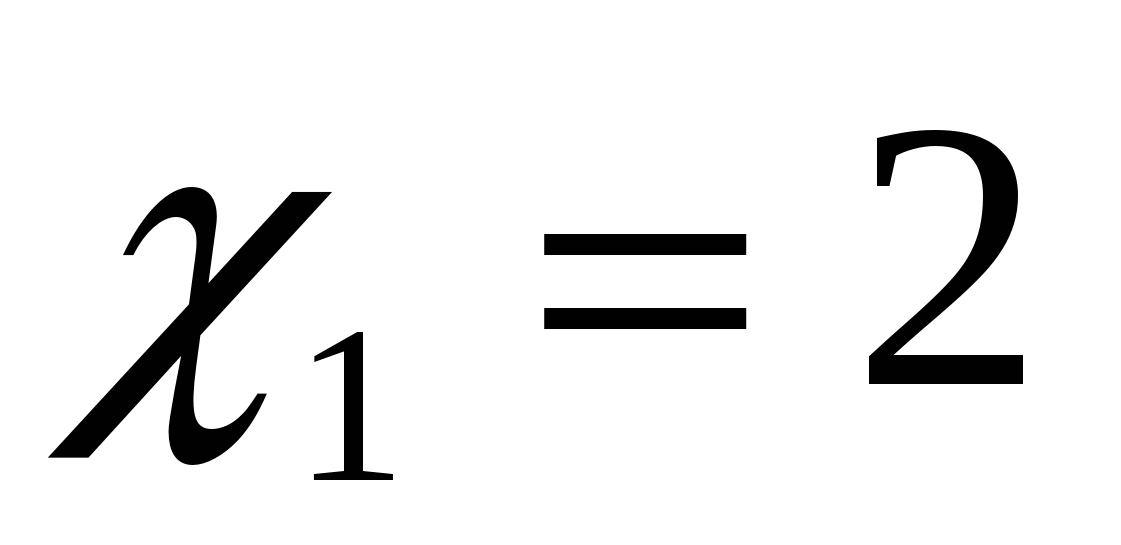ед. и на 
ед.
Решение:
Предельные издержки это рост затрат при увеличении объёма производства на 2 ед. и на 10 ед.
Но предельные издержки это ещё и значение производной функции в точке.
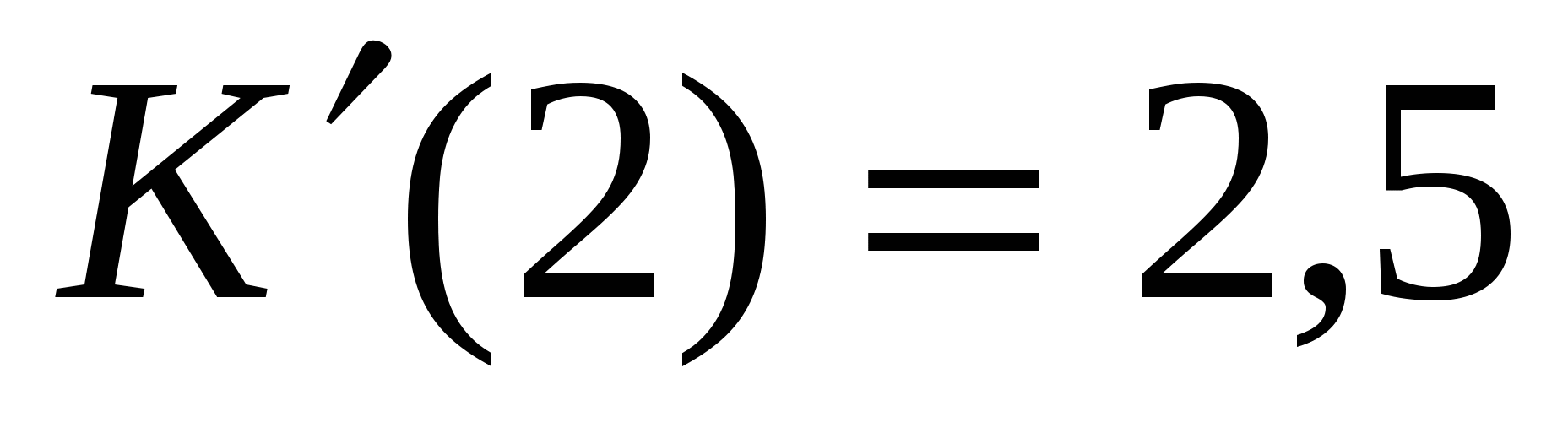
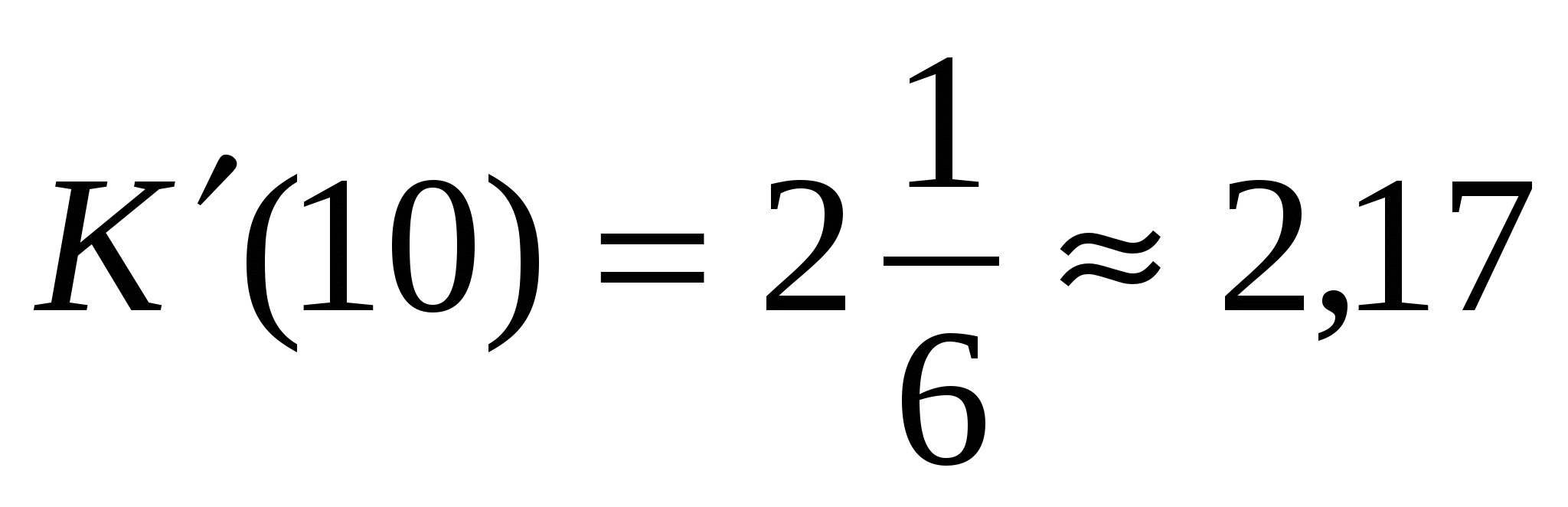
предельные издержки производства составляют 2,5 ден.ед. при росте объёма производства на 2 ед. и 2,17 при росте объёмов производства на 10 ед.
Вопрос: выгодно ли данному предприятию наращивать производство, если уровень затрат не изменится?
Вывод: с ростом производства затраты на каждую следующую единицу продукции уменьшаются, следовательно, в данном случае увеличивать объём производства выгодно.
Задача № 2.
Предприятие производит Х единиц продукции.
Установлено, что зависимость финансовых накоплений от объёма выпуска задаётся формулой: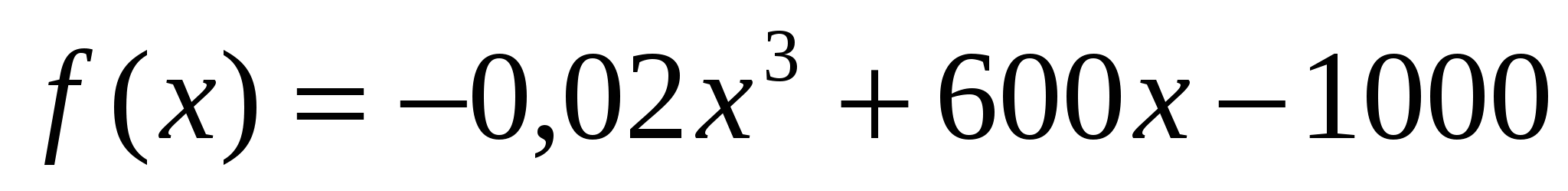 
.
Определить максимально возможную величину финансовых накоплений.
Вопрос: переведите экономический вопрос задачи на математический язык, или др. словами составьте математическую модель данной задачи.
Ответ: необходимо найти наибольшее и наименьшее значение функции.
Решение:
1) Из экономического смысла переменной определяем, что она должна быть неотрицательной, т.е.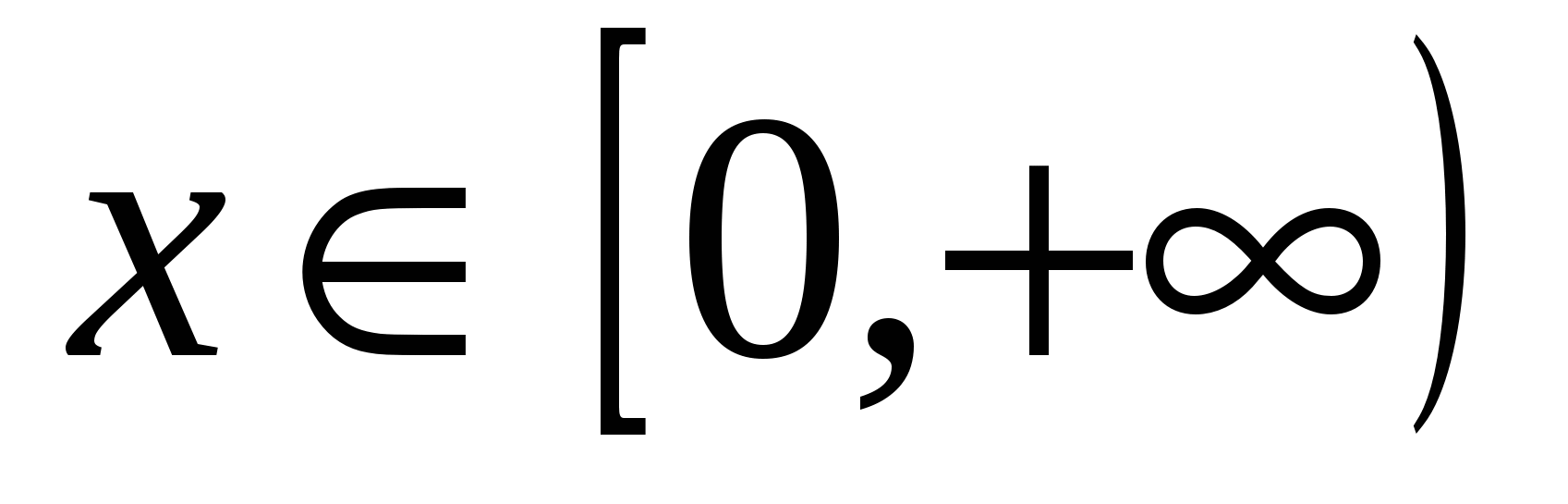 
2) 
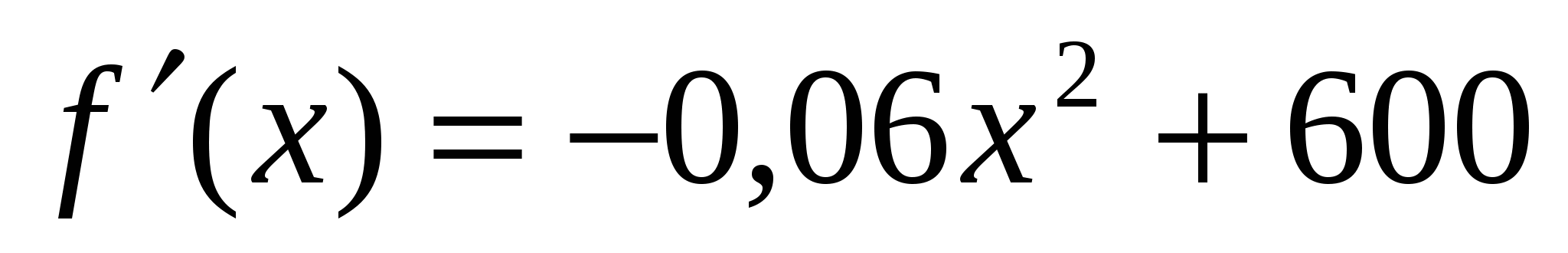
3) 
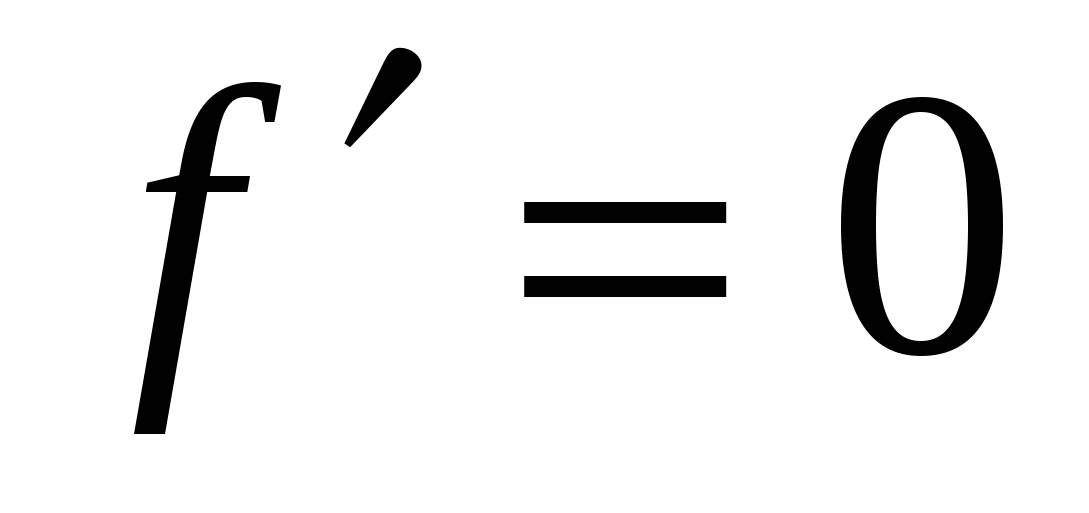при х =100 и х= -100, критическая точка х = - 100 не удовлетворяет экономическому смыслу задачи, и в дальнейшем рассматриваться не будет.
4)
5) 
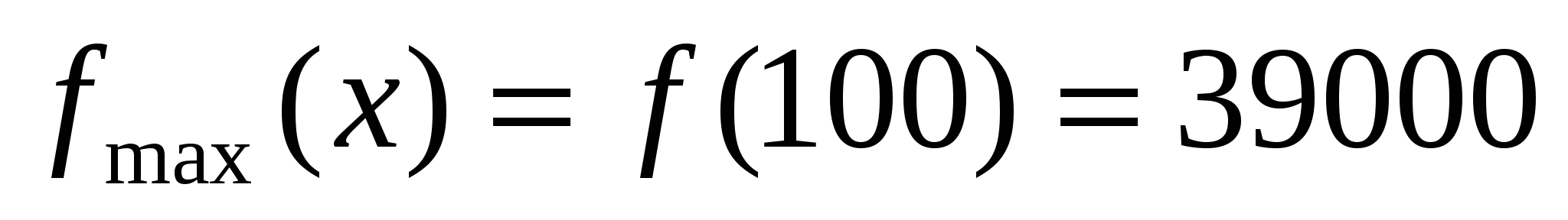
Вывод: финансовые накопления предприятия растут при увеличении объёма производства до100 единиц, достигая суммы 39000 ден. единиц.
Вопрос: выгодно ли наращивать объёмы производства при неизменных прочих условиях?
Ответ: дальнейший рост производства нецелесообразен, т.к. он приведёт к сокращению финансовых накоплений.
Задача № 3.
Цементный завод производит X тонн цемента в день. По договору н должен ежедневно поставлять строительной фирме не менее 20 тонн цемента. Производственные мощности завода таковы, что выпуск не может превышать 90 тонн в день.
Определить: 1) при каком объёме производства удельные затраты производства будут наибольшими ( наименьшими);
2) выгодно ли строительной фирме быть единственным партнёром завода.
Функция суммарных затрат имеет вид: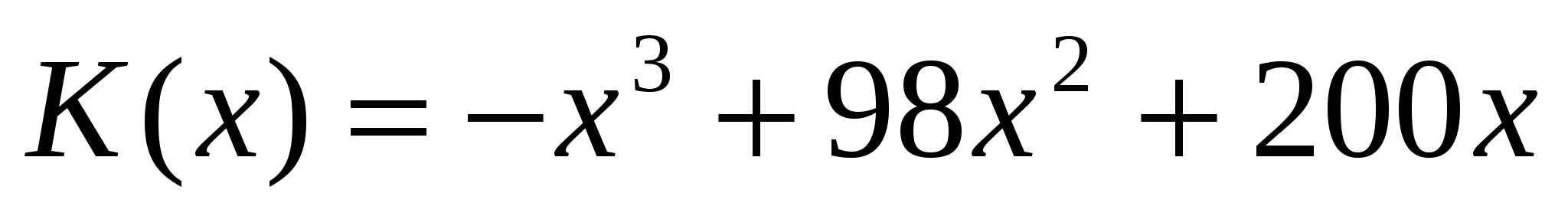 
.
Решение:
Приданном объёме производства удельные затраты составят:
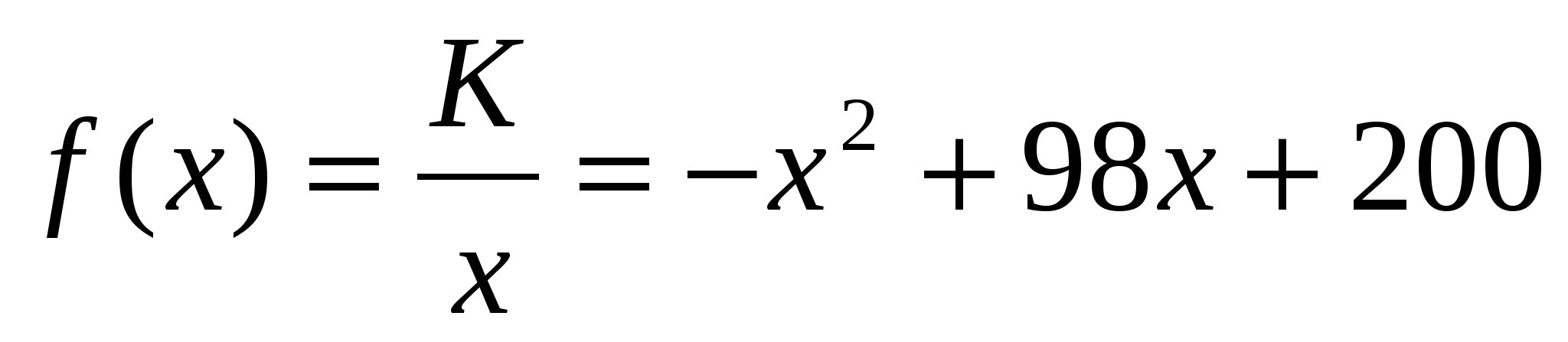
Наша задача сводится к отысканию наибольшего и наименьшего значений функции на промежутке
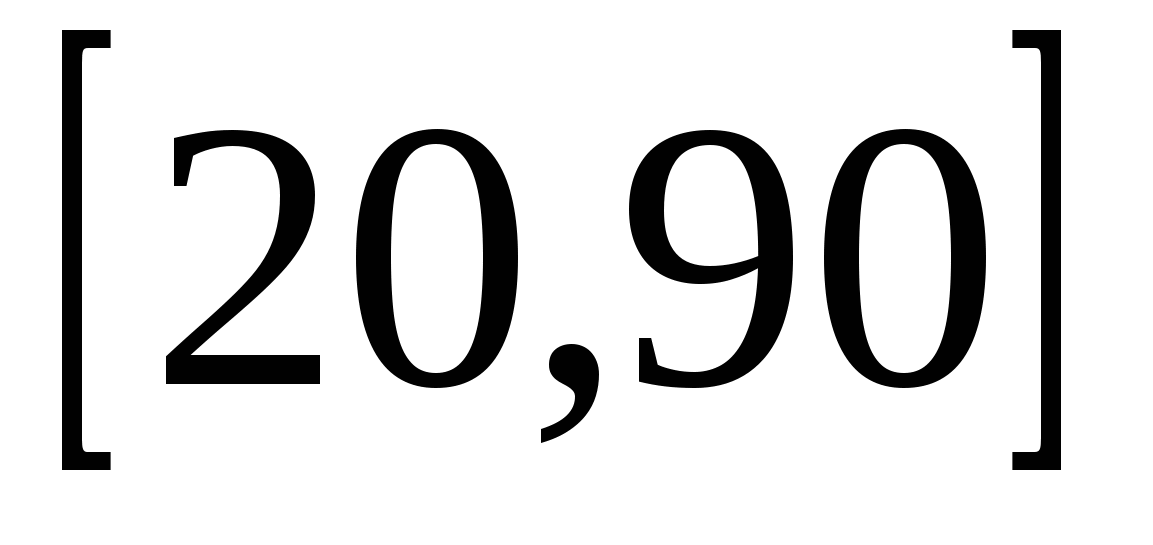
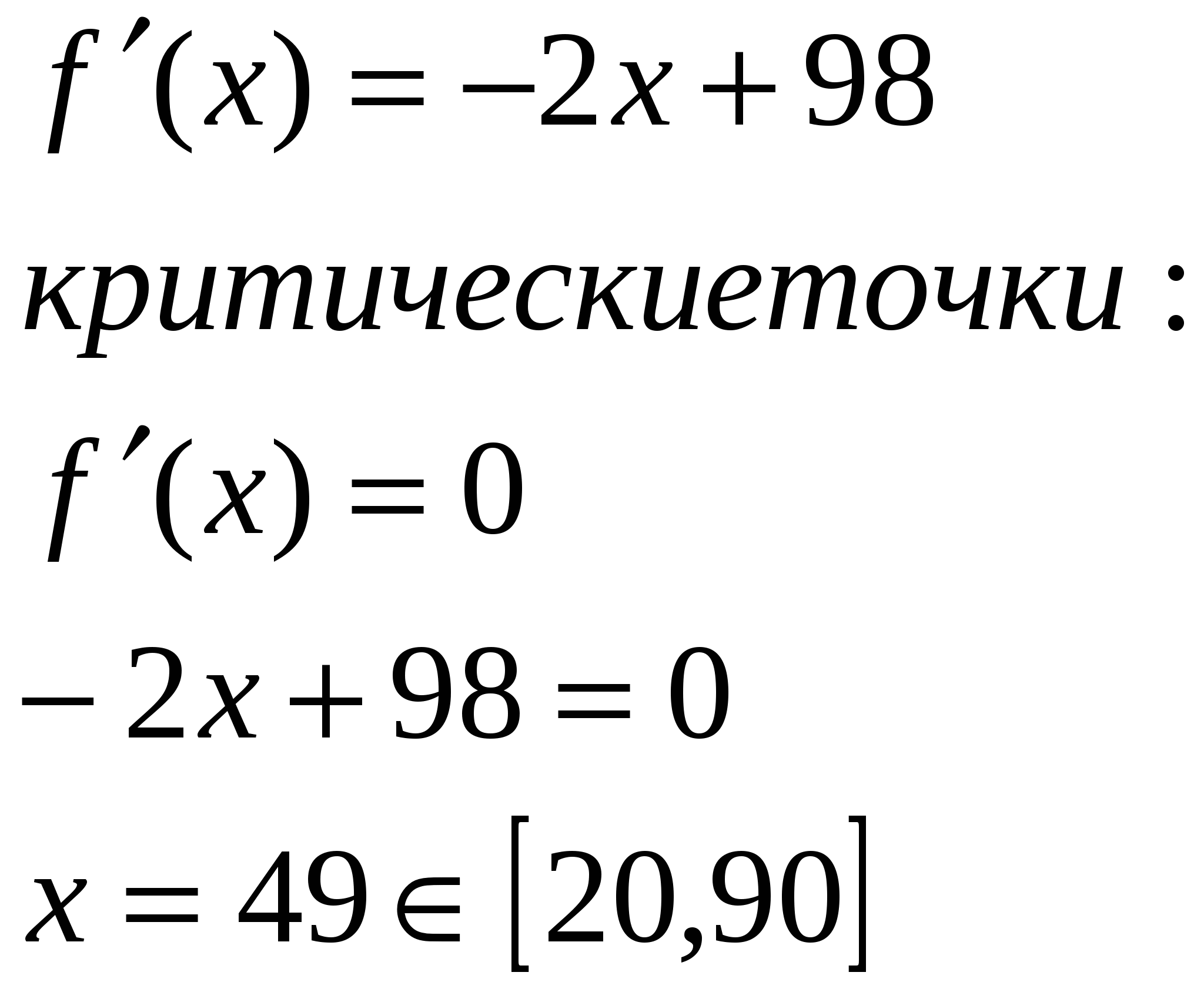
f(20)=1760
f(49)=2601
f(90)=920
Вывод: 1) наибольшая величина затрат на единицу продукции составит 2601ден.единицу при выпуске 49 тонн цемента в день , а наименьшая 920 ден. единиц при выпуске 90 тонн цемента в день.
2) фирме не выгодно быть единственным потребителем цемента, т.к. она переплачивает за товар.
Вопрос: каковы должны быть ближайшие шаги руководства заводом?
Ответ: срочный поиск новых потребителей, иначе завод рискует потерять и тех клиентов, которых имеет.
Задача № 4.
К задаче снят видеофильм, и первоначально условие задачи
учащиеся просматривают, как кино.
Я хотел подзаработать на продаже газет. На соседнем углу дневной спрос- прямая линия. При этом если цена газеты 12,5 рублей, то газеты не берут вовсе, а больше 50 газет продать не удаётся никогда. Тётя Клава, которая работает в типографии, сказала, что даст мне столько газет, сколько надо за коробку конфет, а Витька, мой конкурент из параллельного класса, сказал, что даст мне 30 рублей, если я вовсе не появлюсь на том углу со своими газетами.
Стоит ли мне начинать продажу газет, если да, то, сколько газет просить, и по какой цене продавать?
Решение.
Определим функцию спроса, т.е. определим,по какому закону продаются газеты.
График уравнения, описывающего закон продаж должен проходить через точки (12,5 ; 0)
и (0 ; 50), значит это будет линейная зависимость.
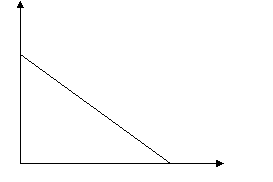
Q(P)= kP+b
а) при Р = 0 , а Q = 50 получаем, что k*0+b= 50, значит b=50.
б) при P = 12,5, а Q= 0 получаем, что 12,5 k+ 50 = 0, значит k = -4
в) объём продаж будет выражаться формулой: Q(P) = - 4P+ 50
По условию задачи бизнес следует начинать если прибыль будет наибольшей, значит нам следует найти наибольшую величину прибыли ( выручки).
Обозначим прибыль через R(P).
R = P*Q 
R(P) =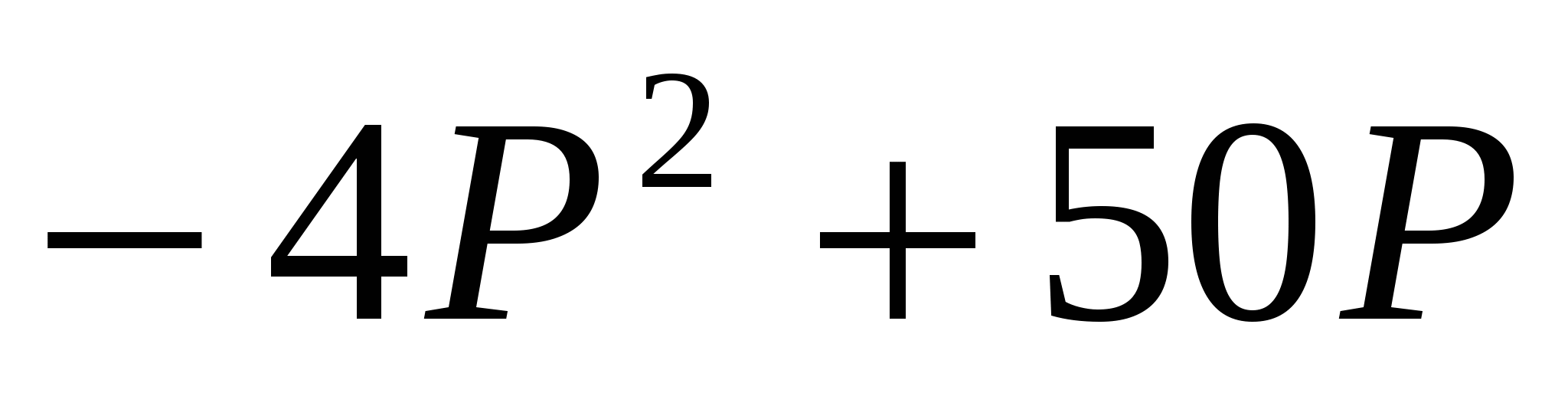 
4) Найдём наибольшее значение выручки на промежутке (0, 12,5)
+ -
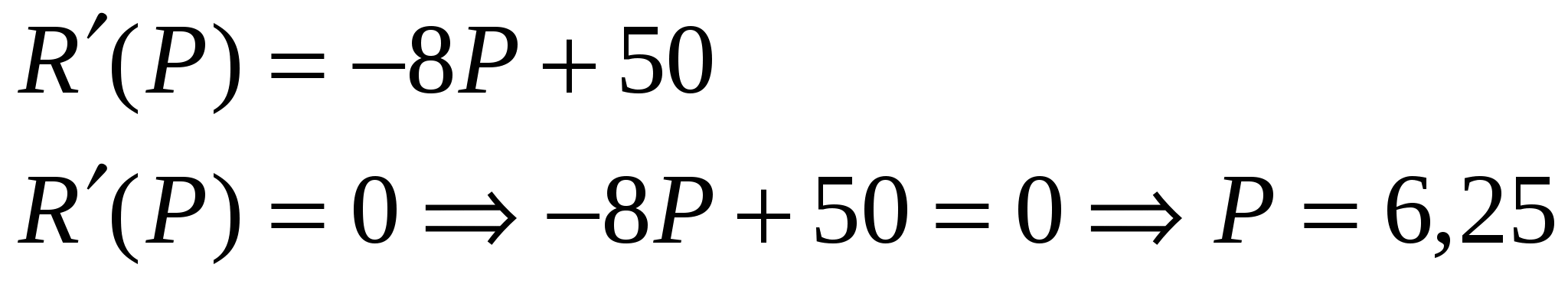
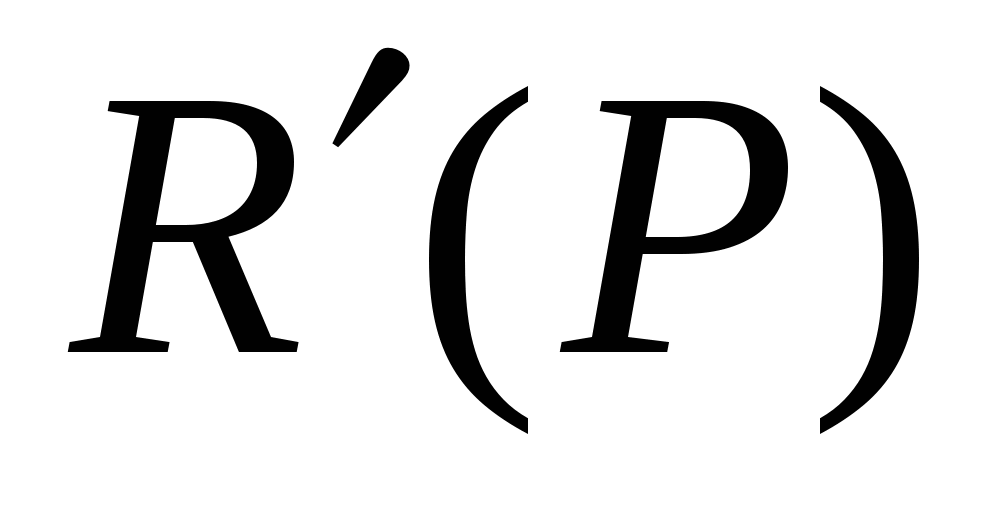R(P) 6,25
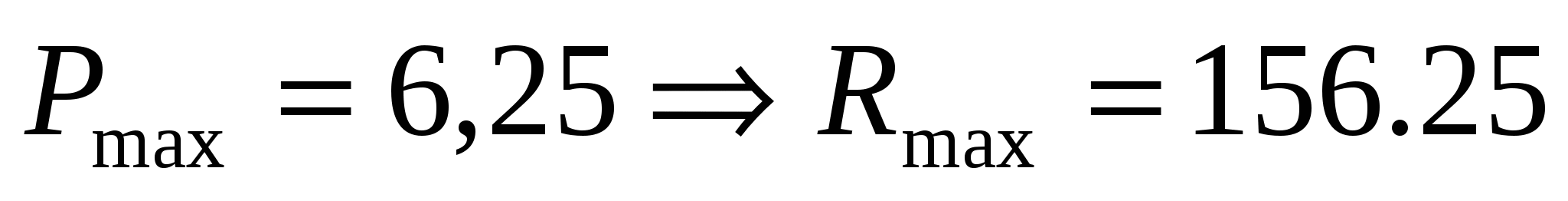, значит, при такой цене и выручке следует просить
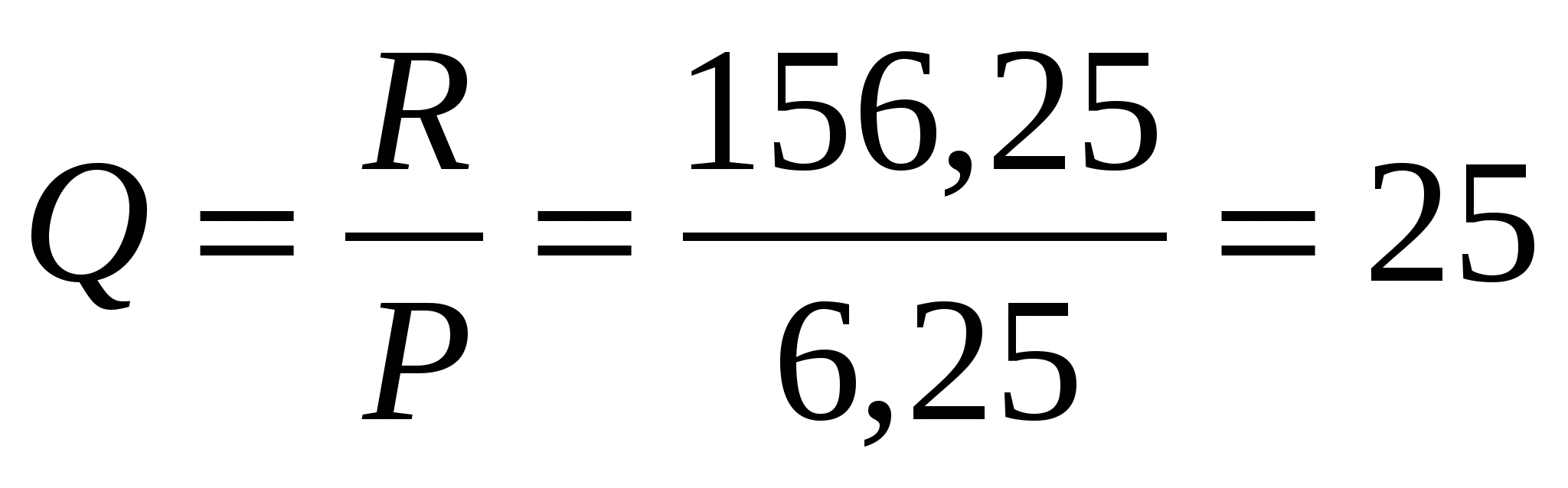газет.
Вопрос: мы ответили на вопрос задачи о прибыли от бизнеса?
Ответ: нет, т.к. мы не приняли в расчёт тётю Клаву с её коробкой конфет, а это величина наших затрат, которая повлияет на прибыль.
Итак: начинать бизнес следует, если прибыль от него будет выше суммы предложенной Витькой (альтернативный доход), с учётом купленной коробки конфет.
Если цена конфет будет выше 156.25-30=126,25 рублей, то дело не будет выгодно.
Вывод: бизнес следует начинать, если цена коробки конфет будет меньше 126, 25 р., брать25 газет и продавать по 6,25р.
Итог урока:
Целью нашего сегодняшнего урока было научиться анализировать реальные ситуации с помощью доступного нам математического аппарата. Мы рассмотрели, как методами математики, а если точнее, то мат. анализа, а если точнее, то его разделом «Дифференциальное исчисление», можно решать экономические задачи, т.е. задачи, на первый взгляд, далёкие от математики.
Очень часто, решая задачу на математики, особенно, если она даётся нам не легко, мы думаем: « А зачем нам всё это надо?»
- А вот затем и надо, чтобы суметь применить полученные знания для решения, на первый взгляд, совсем нематематической задачи, я уж не говорю о таких науках, как физика и химия.
Ведь недаром Лейбниц сказал, что если наши открытия не подтверждены математически, то и нет никакой уверенности в их достоверности.
Используемая литература:
Симонов А.С.«Экономика на уроках математики» Школа- Пресс,М,1999
Мицкевич А.А.«Экономика в задачах и тестах»
Задачи олимпиады по экономике. 1997г.
учебник «Алгебра и начала анализа 10 класс» под редакцией А.Г,Мордкович,изд. Мнемозина, 2007 год