Муниципальное образовательное учреждение

средняя общеобразовательная школа № 33

с углубленным изучением отдельных предметов

Дзержинского района города Волгограда

Программа элективного курса по алгебре для 9 класса

Десятая проблема Гильберта, или уравнения Диофанта

Составитель:

Кулик Татьяна Анатольевна,

учитель математики

МОУ СОШ № 33

Волгоград, 2013

Данное практическое занятие является обобщающим занятием. Перед решением задачи необходимо повторить теоретический материал, опираясь на вопросы домашнего задания занятия № 7. Целесообразно суть выбранного способа решения задачи повторить непосредственно перед его применением к решению поставленной задачи. В целях самоконтроля за выполнением задания учащимся предлагается решить одну задачу разными способами и сравнить полученные ответы, поэтому условно данное занятие можно назвать «уроком одной задачи. Форма работы с учащимися — фронтальная. Но учащимся, которые достаточно хорошо усвоили материал, можно предложить нестандартные задания № 17, 23 из списка задач (Приложение 1). 39

Занятия 11—12. Решение задач с использованием различных диофантовых уравнений или их систем 40

Заключение 45

Введение элективного курса «Десятая проблема Гильберта или уравнения Диофанта» необходимо учащимся как при подготовке к ГИА, ЕГЭ, так и к вступительным экзаменам в вузы. Владение различными приемами решения уравнений можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления. 45

Решение задач и уравнений открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях и на любом другом математическом материале. Именно такие задания играют большую роль в формировании логического мышления и математической культуры у школьников. Поэтому учащиеся, владеющие методами решения задач с помощью уравнений, успешно справляются и с другими задачами. 45

Приложение 1 46

Литература 49

Введение

Актуальность курса

Элективный курс по предпрофильной подготовке учащихся девятых классов посвящен одной из важных тем «Решение уравнений». В предложенном курсе освещаются вопросы, связанные с проблемой решения неопределенных уравнений первой степени в целых (натуральных) числах и с рассмотрением данных уравнений в качестве математических моделей реальных ситуаций, позволяющих продемонстрировать интересные приложения математических методов. Работа с учащимися на занятиях данного курса опирается на базовый уровень знаний и умений по теме «Линейные уравнения с двумя переменными и их системы», а также на умения выполнять операции над числами, особое внимание уделяется использованию знаний, связанных с вопросами делимости во множестве целых чисел.

В базовом школьном курсе при изучении линейного уравнения с двумя переменными рассматриваются только самые общие вопросы: определение линейного уравнения с двумя переменными, определение решения данного уравнения, график линейного уравнения. Вопрос о нахождении целых (натуральных) решений линейного уравнения с двумя переменными, о возможных методах его решения остается за рамками школьного учебника. Однако многие практические задачи сводятся к решению линейного уравнения с двумя переменными, эти задачи часто встречаются в вариантах математических олимпиад, вступительных экзаменов в вузы. Знание общих методов решения таких уравнений, названных в математике диофантовыми, существенно расширяет математический кругозор учащихся, позволяет им осознать необходимость изучения математики, способствует повышению интереса к предмету «математика», а как следствие ориентирует их на выбор математического (или естественно-научного) профиля в старших классах средней школы.

Классы: 8—9.

Количество часов: 12.

Основная цель курса: развивать способность к самоопределению в выборе профиля обучения на старшей ступени.

Цель изучения курса: углубление и расширение знаний по теме «Решение диофантовых уравнений», развитие логического мышления, навыков исследовательской работы, формирование познавательного интереса к предмету.

Основные задачи курса:

— познакомить учащихся с понятием диофантова уравнения, историей его появления в математической науке;

— научить решать диофантовы уравнения первой степени с двумя переменными различными способами;

— научить решать текстовые задачи, описывающие реальные (практические) ситуации, математической моделью которых являются диофантовы уравнения первой степени с двумя переменными или их системы;

— расширить представления учащихся в области истории математики;

— продемонстрировать значимость математических методов в решении разнообразных задач науки и практики;

— развивать логическое мышление, алгоритмическую культуру, интуицию;

— формировать навыки самообразования, критического мышления, самоорганизации и самоконтроля, работы в команде, умения ставить, формулировать и решать проблемы.

Планируемые результаты.

В результате изучения курса учащиеся должны знать:

- определение диофантовых уравнений первой степени с двумя переменными;

- владеть математическими знаниями и умениями, необходимыми для решения диофантовых уравнений первой степени с двумя переменными и их систем;

уметь:

- решать диофантовы уравнения и их системы различными методами,

- составлять математические модели реальных ситуаций с помощью диофантовых уравнений и их систем,

- решать практические задачи с помощью уравнений Диофанта и их систем.

Организация изучения курса. Целесообразно включать предлагаемый элективный курс в учебный процесс после изучения необходимого материала в базовом курсе. В целях проведения профессиональной ориентации школьников наиболее удачным будет постановка этого курса в 9 классе.

Основные организационные формы реализации предлагаемой программы — лекционные, практические и семинарские занятия. Методы обучения, применяемые в процессе проведения занятий — школьная лекция, рассказ, беседа, метод упражнений и др. Формы обучения имеют как фронтальный, так и групповой, и индивидуальный характер. В ходе изучения курса используются и современные информационные технологии. Учащимся предлагается тематика учебно-исследовательских заданий, результаты выполнения которых школьники представляют в форме доклада (реферата), сопровождая свое выступление на семинарских занятиях презентацией.

Система оценки достижений учащихся. В технологии проведения занятий присутствуют элементы групповой работы, взаимопроверки и самопроверки, что позволяет учащимся самим проверить, как усвоен ими изученный материал. Также оценивается и самостоятельно подготовленный школьниками образовательный продукт в форме доклада (реферата) и компьютерной презентации.

Содержание курса

1. Введение.1 час. Цели и задачи курса, его организация. 10-я проблема Гильберта: история математического открытия. Диофант и его уравнения (исторический экскурс).

2. Решение диофантовых уравнений способом перебора вариантов. 1 час. Актуализация знаний по теме «Линейное уравнение с двумя переменными» (определение уравнения, решения уравнения, график уравнения). Определение диофантова уравнения первой степени с двумя неизвестными. Способ перебора вариантов — метод решения диофантовых уравнений. Решение текстовых задач.

3. Решение диофантовых уравнений с использованием алгоритма Евклида. 2 часа. Актуализация знаний по теме «Наибольший общий делитель. Алгоритм Евклида». Вывод формул для целых решений диофантова уравнения первой степени с двумя переменными на основе применения алгоритма Евклида. Решение уравнений с использованием алгоритма Евклида. Решение текстовых задач.

4. Решение диофантовых уравнений с использованием цепной дроби. 2 часа. Введение понятия цепной дроби. Алгоритм получения цепной дроби. Формулы целых решений диофантова уравнения первой степени с двумя переменными на основе применения цепных дробей. Решение уравнений с использованием цепной дроби. Решение текстовых задач.

5. Метод рассеивания (измельчения) в решении диофантовых уравнений. 2 часа. Алгоритм решения диофантова уравнения методом измельчения коэффициентов. Решение уравнений. Решение текстовых задач.

6. Решение диофантовых уравнений различными способами. 2 часа.

7. Решение задач, сводимых к диофантовым уравнениям или их системам. Решение диофантовых уравнений и их систем с использованием других приемов и методов.2 часа.

Учебно-тематический план

№

п/п

Тема занятия

Количество часов

Вводное занятие

Решение диофантовых уравнений способом перебора вариантов

Решение диофантовых уравнений с использованием алгоритма Евклида

Решение диофантовых уравнений с использованием цепной дроби

Метод рассеивания (измельчения) в решении диофантовых уравнений

Решение диофантовых уравнений различными способами

Решение задач, с использованием различных диофантовых уравнений или их систем

Итого:

Методическое обеспечение

Занятие 1. Вводное

План занятия:

Цели и задачи элективного курса «Десятая проблема Гильберта, или уравнения Диофанта». Организация занятий курса.
10 проблема Гильберта: история математического открытия.
Диофант и его уравнения (исторический экскурс).
Распределение заданий к занятиям для групповой и индивидуальной работы учащихся.

Оборудование: портреты (слайды) Гильберта, Диофанта, Д. Робинсон, Н. Воробьева, Ю. Матиясевича; плакаты (слайды) с текстом надписи на гробнице Диофанта (компьютерная презентация, иллюстрирующая рассказ учителя о Диофанте и его уравнениях).

Вступительное слово учителя.

На первом вводном занятии слушателям сообщаются цели проведения данного элективного курса, обращается внимание на необходимость выбора учащимися профиля класса на старшей ступени, задается ориентация на математический (естественно-научный) профиль, подчеркивается значимость математических методов для решения различных задач, отражающих реальные ситуации.

Раскрывая суть названия курса, первое занятие следует начать с истории.

В 1900 году на Втором международном конгрессе математиков, проходившем в Париже, великий немецкий математик Давид Гильберт огласил список из 23 самых важных, по его мнению, нерешенных математических проблем, которые уходящий 19-ый век оставлял в наследие наступающему 20-му веку. История показала, что проблемы Гильберта оказали значительное влияние на дальнейшее развитие математики. Проблема под номером десять касалась так называемых диофантовых уравнений. Эти уравнения имеют простую структуру в виде равенства нулю многочлена от многих неизвестных. Трудность в решении таких уравнений состоит в ограничении на допустимые значения неизвестных, которые должны быть числами целыми или натуральными, то есть целыми положительными. Такое условие естественно возникает как в чисто теоретических математических задачах, так и в прикладных. Примером может служить расчет зубчатой передачи - количество зубьев у шестеренок

обязательно должно быть натуральным числом. Уравнения названы в честь греческого математика Диофанта, который жил в третьем веке нашей эры. За период, прошедшей от этого времени до конца 19-го века, специалисты по теории чисел нашли решения у большого количества диофантовых уравнений, и про многие другие диофантовы уравнения доказали, что решений у них нет. Почему же Гильберт все еще рассматривал диофантовы уравнения как открытую проблему? Дело в том, что для решения отдельных классов диофантовых уравнений, а иногда и для конкретных уравнений, математикам приходилось изобретать все новые и новые методы. Ярким примером здесь может служить Великая теорема Ферма, утверждающая, что конкретная серия диофантовых уравнений с тремя неизвестными не имеет решений. Более трех столетий прошло с момента, когда Пьер Ферма сформулировал эту теорему, до ее доказательства в 20-ом веке английским математиком Эндрю Уайлсом.

В 10-ой проблеме Гильберт просил решить не конкретные диофантовы уравнения, а найти общий, универсальный метод - алгоритм - который будучи применен к конкретному диофантову уравнению за конечное число шагов давал ответ на вопрос, имеет ли это уравнение решения или нет. По этой причине 10-ую проблему Гильберта можно рассматривать не только как математическую проблему, но и проблему теоретической информатики, которая в 1900 году еще не существовала как самостоятельная дисциплина. Сегодня мы знаем, что 10-ая проблема Гильберта неразрешима - требуемого в ней алгоритма не существует. Однако в 1900 году это утверждение нельзя было даже сформулировать строго математически. Общее понятие алгоритма было выработано много позднее, в 30-ые годы 20-го века. В наши дни алгоритм можно отождествить с программой на любом языке программирования. Таким образом, полученное "отрицательное решение" 10-ой проблемы Гильберта состояло в доказательстве невозможности написать программу, которая про любое диофантово уравнение говорила бы нам, имеет ли это уравнение решения или нет. Какая же может быть польза от этого доказательства невозможности? В чем-то ситуация здесь схожа с законом сохранения энергии, который делает невозможным построение "вечного двигателя", избавляя тем самым изобретателей от заведомо бесполезной траты времени на его построения. Аналогично доказанная неразрешимость 10-ой проблемы Гильберта дает математикам "моральное право" больше не тратить свое время на бывшие всегда бесплодными попытки найти универсальный метод решения диофантовых уравнений. Не следует думать, что с установлением неразрешимости 10-ой проблемы Гильберта закрыты все алгоритмические проблемы про диофантовы уравнения. Напротив, здесь имеется много открытых проблем, которые 21-ый век унаследовал от 20-го. Это направление продолжает активно развиваться, публикуется много новых исследований и регулярно проводятся международные конференции.

2. Рассказ учителя об известном ученом-математике Диофанте и его уравнениях.

Алгебраические уравнения с целыми коэффициентами, решаемые во множестве целых (реже рациональных) чисел, вошли в историю математики как диофантовы. Наиболее интересными являются неопределенные уравнения или их системы, т. е. такие, в которых количество переменных больше числа уравнений. Наиболее изучены диофантовы уравнения первой и второй степени. В содержание нашего элективного курса включены задачи, которые сводятся к решению уравнения первой степени с двумя неизвестными

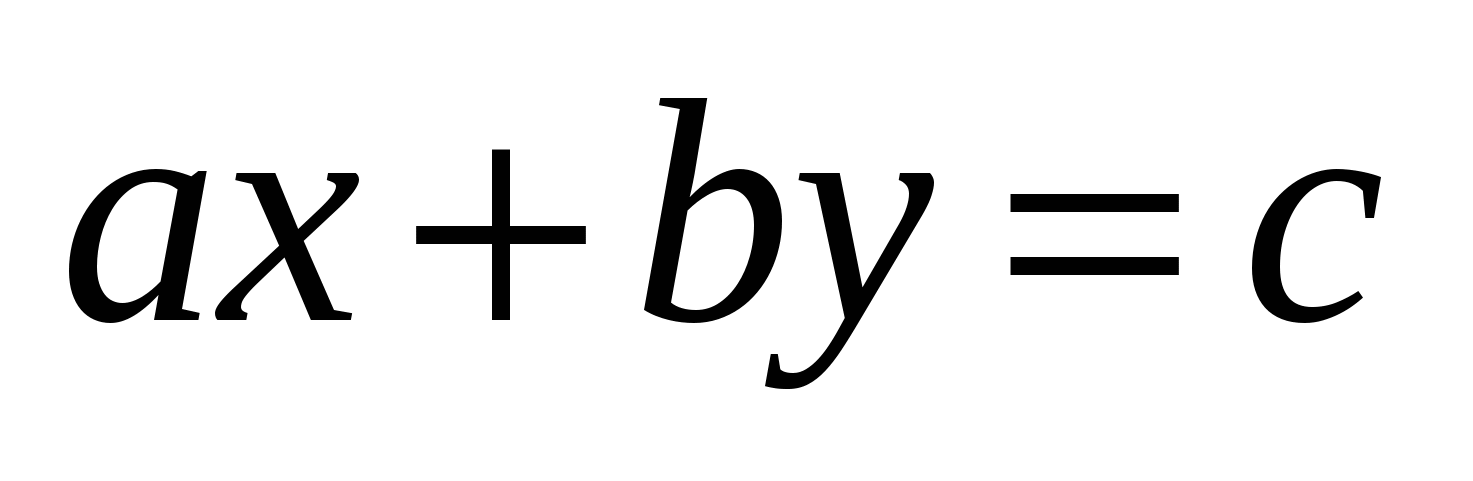. (1)

Существует несколько способов решения уравнения (1). Мы рассмотрим их на следующих занятиях.

Отметим, что в первый раз сочинения Диофанта были изданы в латинском переводе, в 1575 году; затем в 1621 году Bachet de Méziriac издал греческий текст Диофанта с переводом на латинский язык и собственными примечаниями; тот же перевод был переиздан в 1670 году с замечательными примечаниями Ферма; кроме того, имеются переводы на французский и немецкий.

3. Распределение заданий для подготовки к следующим занятиям проводится в соответствии с Приложением 2. Учащимся предлагается как групповая форма для подготовки заданий, так и по желанию — индивидуальная. Учитель раздает карточки с заданиями, в которых указаны тема, список литературы. Предлагается для поиска тематической информации использовать и ресурсы сети Интернет. Обращается внимание, что задание может быть выполнено в форме презентации или реферата. Учитель определяет дату выступления учащихся на занятии, график консультаций.

Занятие 2. Решение диофантовых уравнений способом перебора вариантов

План занятия

Актуализация знаний учащихся по теме «Линейное уравнение с двумя переменными».
Изучение нового материала. Определение диофантова уравнения, диофантова уравнения первой степени с двумя переменными. Способ перебора вариантов как один из методов нахождения целых (натуральных) решений диофантовых уравнений.
Решение задач способом перебора вариантов.
Постановка домашнего задания.

Оборудование: компьютер, слайды с заданиями, карточки с заданиями.

Ход занятия.

1. Актуализация знаний

Рассмотрим задачу.

В клетке находится x фазанов и у кроликов. Сколько в клетке фазанов и кроликов, если общее количество ног равно 62.

Общее число ног можно записать с помощью уравнения

2х + 4у = 62. (*)

Это равенство, которое мы составили по условию задачи, как вы знаете, называют уравнением с двумя переменными. Более того, данное уравнение мы называли линейным уравнением. Линейные уравнения играют важную роль при решении различных задач. Далее следует напомнить основные положения, связанные с этим понятием: определения линейного уравнения с двумя переменными и его решения, определения графика уравнения, равносильных уравнений, свойств равносильности.

2. Изучение нового материала

Алгебраические уравнения с целыми коэффициентами, решаемые во множестве целых (реже рациональных) чисел, вошли в историю математики как диофантовы. Учитель обращает внимание на то, что различные текстовые задачи часто можно решать с помощью некоторого уравнения или системы уравнений. При этом стремимся составить по условиям задачи столько независимых уравнений, сколько имеется неизвестных. Но иногда это сделать невозможно: число независимых уравнений, которые можно составить по условию задачи, меньше числа неизвестных. Однако достаточно часто условие задачи накладывает какие-то другие дополнительные ограничения на неизвестные, которые вместе с полученными уравнениями позволяют найти значения неизвестных. Так, из условия может быть ясно, что искомые числа — целые или натуральные или заключенные в заданных пределах. Как, например, в задаче про кроликов и фазанов.

Таким образом, учитель подводит учащихся к определению диофантовых уравнений вообще и диофантовых уравнений первой степени с двумя переменными в частности. Обращается внимание учащихся на то, что фактически данное уравнение является линейным с двумя переменными, с которым они знакомились в курсе алгебры. Мы будем рассматривать задачи, которые сводятся к решению диофантова уравнения первой степени с двумя неизвестными: 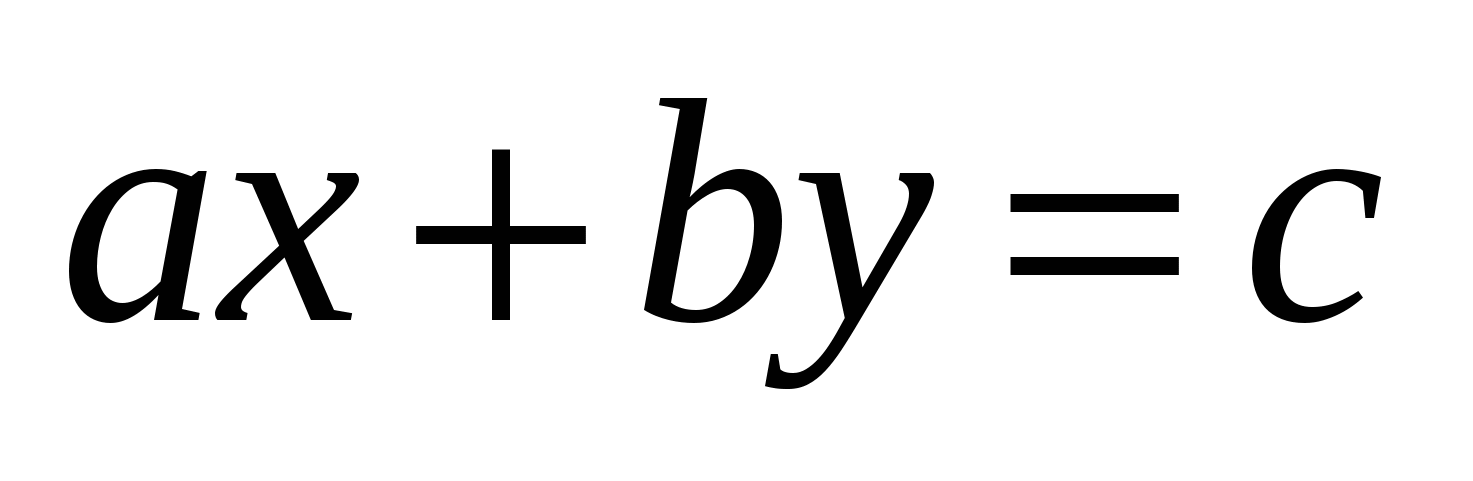(1), где a, b, c — целые коэффициенты.

Существует несколько способов решения уравнения (1). На этом занятии рассмотрим способ перебора вариантов.

Рассматривая способ перебора вариантов, необходимо учитывать количество возможных решений уравнения. Целесообразно использовать задачи, у которых количество решений не превышает 5. Рассмотрим данный способ при решении следующей задачи.

Пример 1.

Андрей работает летом в кафе. За каждый час ему платят 10 р. И высчитывают 2 р. за каждую разбитую тарелку. На прошедшей неделе он заработал 180 р. Определите, сколько часов он работал и сколько разбил тарелок, если известно, что он работает не более 3 ч в день.

Решение.

Пусть x часов он всего работал в неделю, тогда 10х р. ему заплатили, но он разбил у тарелок, и с него вычли 2у р. Имеем уравнение 10х – 2у = 180, причем x меньше или равен 21. Получим: 5х – у = 90, 5х = 90 + у, х = 18 + у : 5.

Так как x — целое число, то у должно нацело делится на 5, чтобы в правой части получилось целое число. Возможны четыре случая:

у = 0, х = 18, т. е. решением является пара — (18; 0);
у = 5, х = 19, (19; 5);
у = 10, х = 20, (20; 10);
у = 15, х = 21, (21; 15).

3. Решение задач

Для решения на занятии можно предложить задачи № 1(а), 2, 5 из Приложения 1. Приведем решение задачи № 5.

Задача № 5. Из двухрублевых и пятирублевых монет составлена сумма в 23 р. Сколько среди этих монет двухрублевых?

Решение. Пусть x — количество двухрублевых монет, у — количество пятирублевых монет. Составим и решим уравнение: 2х + 5у = 23; 2х = 23 – 5у; x = (23 – 5у) : 2; x = (22 + 1 – 5у) : 2, почленно поделим 22 на 2 и (1 – 5у) на 2, получим: x = 11 + (1 – 5у) : 2.

Так как x и y — натуральные числа по условию задачи, то левая часть уравнения есть натуральное число, значит, и правая часть должна быть натуральным числом. К тому же, чтобы получить в правой части число натуральное, нужно чтобы выражение (1 – 5у) нацело делилось на 2. Осуществим перебор вариантов.

y = 1, х = 9, то есть двухрублевых монет может быть 9;
у = 2, при этом выражение (1 – 5у) не делится нацело на 2;
у = 3, х = 4, то есть двухрублевых монет может быть 4;
при у больше или равном 4 значение x не является числом натуральным.

Таким образом, ответ в задаче: среди монет 9 или 4 двухрублевых.

4. Домашнее задание (в домашнее задание включаются упражнения, аналогичные, рассмотренным заданиям в классе).

Выучить определение диофантова уравнения первой степени, повторить основные сведения по теме «Линейные уравнения с двумя переменными», знать суть способа перебора вариантов для решения диофантовых уравнений.
Решить № 1(б), 3, 4 из Приложения 1.
Составить задачу, математической моделью которой является уравнение из № 1(б).

Занятие 3. Решение диофантовых уравнений с использованием алгоритма Евклида

План занятия

Применение алгоритма Евклида для нахождения наибольшего общего делителя двух чисел (повторение).
Вывод формул для решения диофантовых уравнений с использованием алгоритма Евклида.
Примеры решения диофантовых уравнений с использованием алгоритма Евклида.

Оборудование: конспект лекции на доске (интерактивной доске) и индивидуальные заготовки для каждого ученика.

Ход занятия

Применение алгоритма Евклида для нахождения наибольшего общего делителя двух чисел (повторение)

Существует довольно простой прием, позволяющий находить наибольший делитель двух натуральных чисел. Этот прием называется алгоритмом Евклида. Вы с ним познакомились еще при изучении курса математики в 6 классе. Евклид, великий ученый, живший около 2000 лет назад, занимался не только геометрией, которая носит его имя. Ему принадлежит решение ряда важных задач арифметики и, в частности, тот способ нахождения наибольшего общего делителя, который мы сегодня будем использовать при изучении нового материала. А сейчас повторим суть алгоритма Евклида. Чтобы найти наибольший общий делитель двух чисел:

1) надо большее из двух чисел разделить на меньшее;

2) потом меньшее из чисел на остаток при первом делении;

3) затем остаток при первом делении на остаток при втором делении и вести этот процесс до тех пор, пока не произойдет деление без остатка. Последний отличный от нуля остаток и есть искомый НОД двух данных чисел.

Рассмотрим пример.

Найти НОД (645; 381).

Решение.

Разделим с остатком 645 на 381. Мы получим: 645 = 381 · 1 + 264.

Далее разделим с остатком 381 на 264, получим: 381 = 264 · 1 + 117.

Теперь разделим с остатком 264 на 117, получим: 264 = 117 · 2 + 30.

Продолжим процесс деления, разделим с остатком 117 на 30, получим: 117 = 30 · 3 + 27. Далее, 30 = 27 · 1 + 3. Следующий шаг — делим 27 на 3, получаем, что 27 = 3 · 9 + 0, т. е. 27 делится на 3 без остатка. Значит, наибольший общий делитель чисел 27 и 3 равен 3, следовательно, и наибольший общий делитель чисел 645 и 381 равен 3, т. е. последнему отличному от нуля остатку. Таким образом, НОД (645; 381) = 3.

Прием разыскания наибольшего общего делителя, примененный в этом примере, и представляет собой алгоритм Евклида.

2. Вывод формул для решения диофантовых уравнений с использованием алгоритма Евклида.

3. Примеры решения диофантовых уравнений с использованием алгоритма Евклида

Рассмотрим решение заданий № 6(а), 7 из Приложения 1.

Задание № 6. Решить уравнение на множестве целых чисел

а) 7х + 11у = 69.

НОД (7; 11) = 1, Найдем значение х₀ и у₀ для получения решений уравнения по формулам (3). Применим алгоритм Евклида к числам 11 и 7:

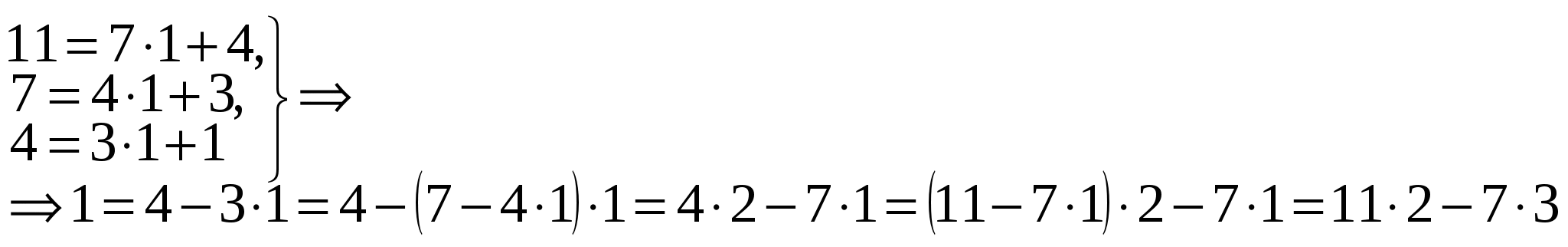
Таким образом, получаем: 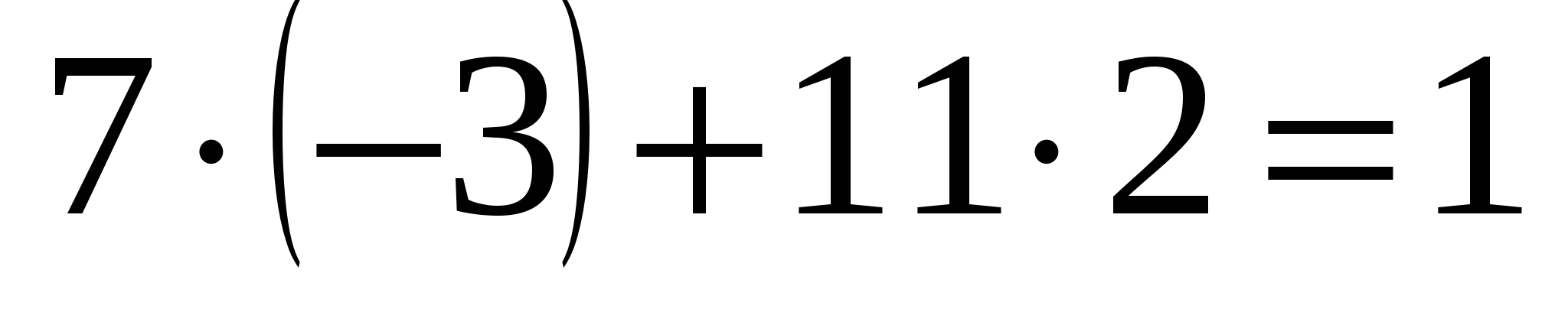, следовательно, х₀ = –3, у₀ = 2.

Запишем общее решение уравнения на множестве целых чисел согласно формулам (3):

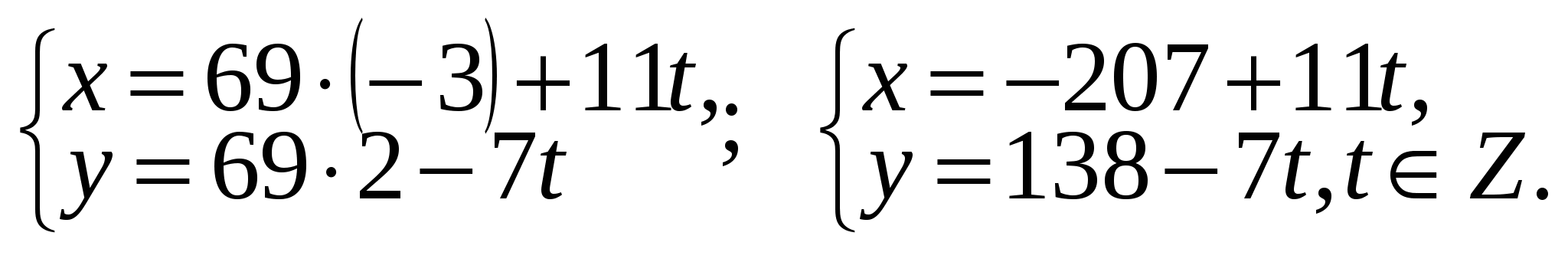
Придавая конкретные целые значения t, можно получить частные решения уравнения. Например, при t = 1, имеем x = –196, у = 131.

Задача № 7. Для газификации жилого дома требуется проложить газопровод протяженностью 150 м. Имеются трубы длиной 13 м и 9 м. Сколько требуется труб, чтобы не приходилось их разрезать при прокладке газопровода.

Решение.

Пусть требуется x труб по 9 м, и у труб по 13 м. Составим и решим уравнение: 9х + 13у = 150.

НОД (9; 13) = 1, уравнение разрешимо во множестве целых чисел.

Найдем значения х₀ и у₀ для получения решений уравнения по формулам (3). Применим алгоритм Евклида к числам 13 и 9:

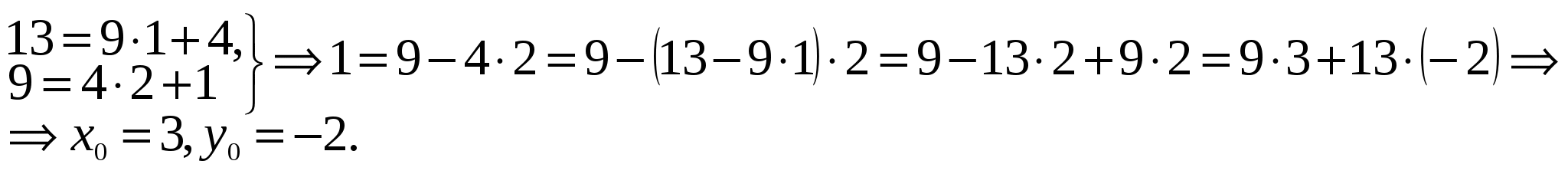
Запишем общее решение уравнения согласно формулам (3).

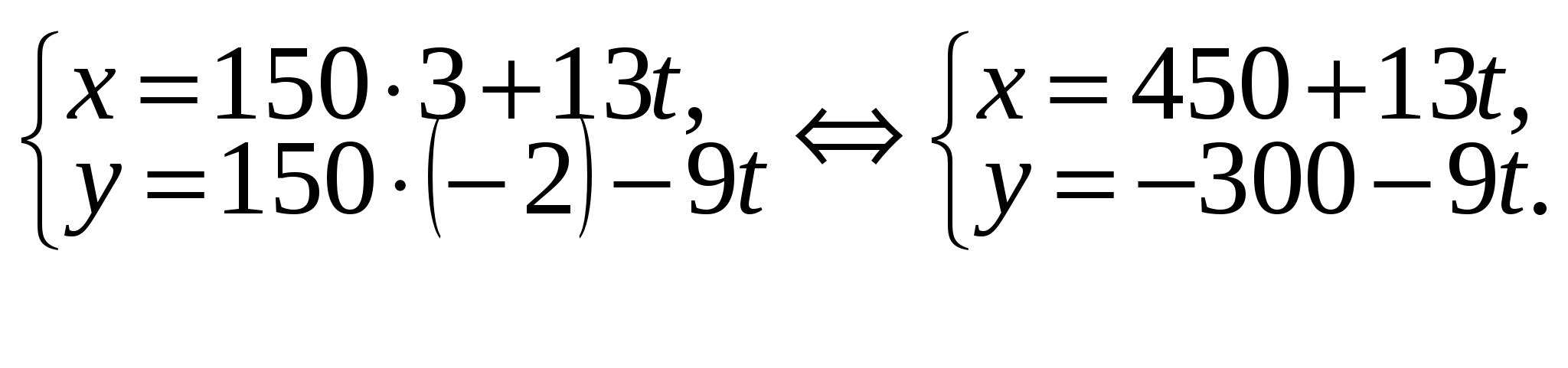
Так как x и y — неотрицательные целые числа, то чтобы найти значение t, решим систему неравенств:

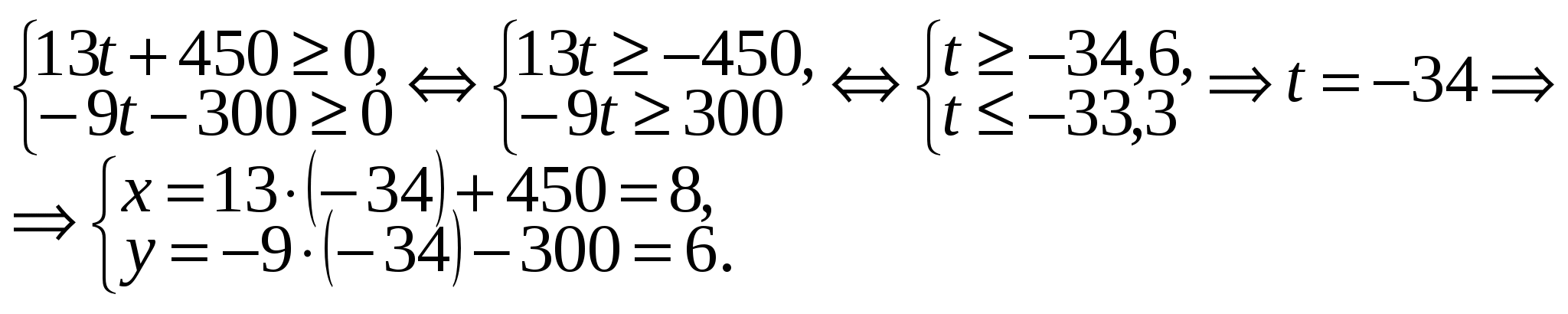
Ответ. Для прокладывания газопровода потребуется 8 труб длиной по 9 м и 6 труб по 13 м.

4. Домашнее задание:

Решить № 6(б), 8 из Приложения 1, составить сюжетную задачу, решение которой сводится к уравнению из № 6(б) на множестве целых неотрицательных или натуральных чисел. Найти ее решения.

Занятие 4. Решение диофантовых уравнений с использованием алгоритма ЕвклидаПлан занятия:

Актуализация знаний (проверка знания теории и выполнения практических заданий).
Решение задач с использованием алгоритма Евклида.
Постановка домашнего задания.

Оборудование: опорные конспекты предыдущей лекции, карточки с заданиями для фронтальной и групповой работы.

Ход занятия

Актуализация знаний

Проведение первого этапа занятия-практикума — учитель может спланировать по своему усмотрению. Необходимо организовать проверку выполнения домашнего задания, включающего как теоретические вопросы, так и практические задания.

Решение задач с использованием алгоритма Евклида

Задания для решения выбираются по принципу: от простого к сложному. Для овладения методом решения диофантовых уравнений с использованием алгоритма Евклида можно предложить вначале решить уравнения, не связанные с какой-либо реальной ситуацией. Например, № 6(в, г). Затем можно предложить решение текстовых задач на составление линейных диофантовых уравнений: например № 9, 10 (все задания указаны из Приложения 1). Задания можно выполнить в группах, а затем проверить полученные ответы. Ниже приведем решение задачи № 9.

Неотъемлемой частью занятия-практикума является решение нестандартных задач, заданий повышенной трудности. В процессе их выполнения можно использовать прием разбиения на подзадачи. К таким заданиям можно отнести и задачу № 11, которую мы далее рассмотрим.

Заметим, что в ходе решения задач, учащиеся могут опираться на заполненный опорный конспект предыдущей лекции, в котором выделен способ решения диофантовых уравнений с использованием алгоритма Евклида.

Задача № 9. Транспортные организации имеют в наличие машины вместимостью 3,5 т и 4,5 т. Следует перевезти груз весом 53 т. Сколько машин нужно выделить для одного рейса?

Решение.

Пусть x машин по 3,5 т, у — машин по 4,5 т. Составим и решим уравнение: 3,5х + 4,5у = 53. Перейдем к уравнению с целыми коэффициентами, например, умножим обе части уравнения на 2. Получим: 7х + 9у = 106.

НОД (7; 9) = 1, уравнение имеет целые решения.

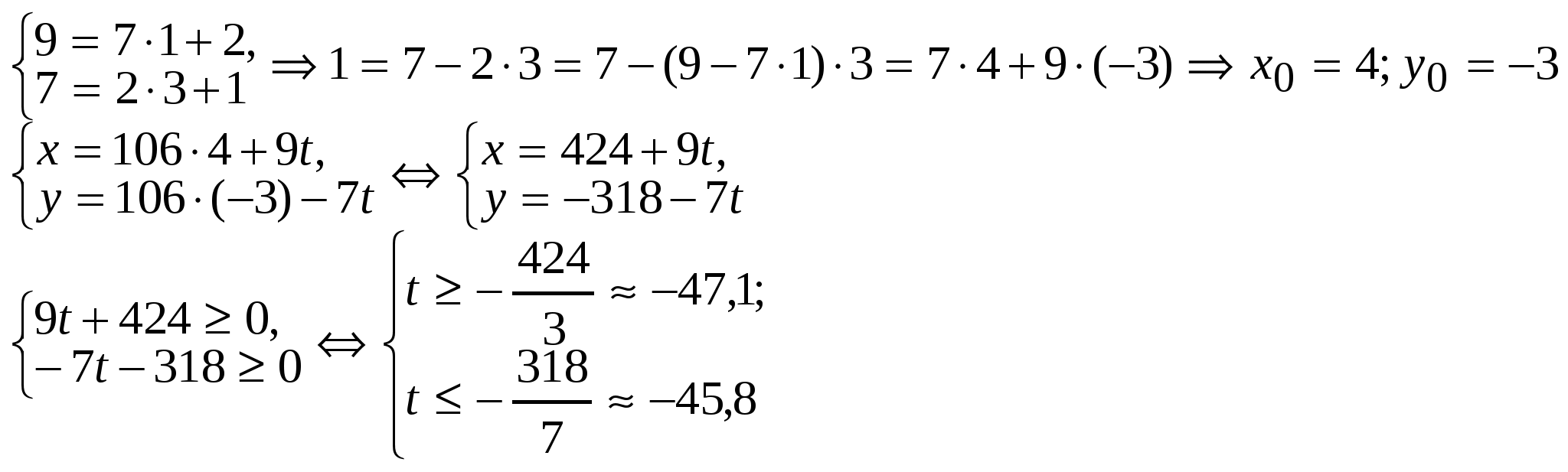
Так как t — принимает целые значения, то системе неравенств удовлетворяют значения t = –47 и t = –46. Получим решение диофантова уравнения в натуральных числах:

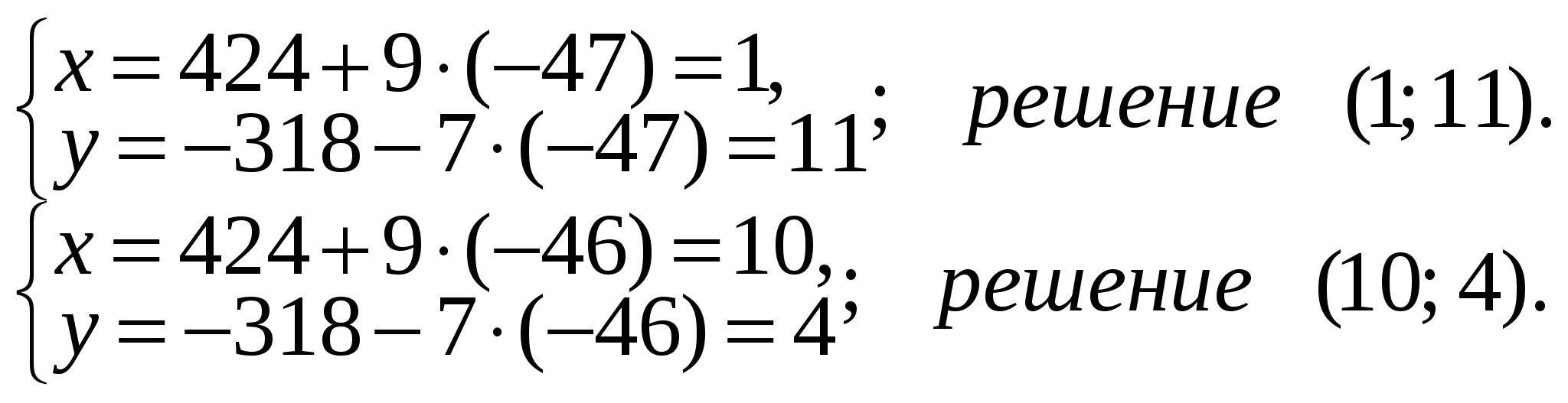
Таким образом, для одного рейса можно взять:

а) 1 машину вместимостью 3,5 т и 11 машин вместимостью 4,5 т;

б) 10 машин вместимостью 3,5 т и 4 машины вместимостью 4,5 т.

Полезно обратить внимание на то, какой из возможных вариантов будет наиболее эффективным для работы предприятия с экономической точки зрения (экономия бензина, средств на оплату труда водителям и т. д.).

Задача № 11. Школа получила 1 млн р. на приобретение 100 единиц учебного оборудования (на всю сумму без сдачи). Администрации школы предложили оборудование стоимостью 3 000, 8 000 и 12 000 р. за единицу. Сколькими способами школа может закупить это оборудование. Укажите один из способов.

Решение.

В ходе обсуждения идеи решения данной задачи, необходимо выяснить: что дано, что неизвестно в условии, как связаны между собой данные и искомые. Затем переходить к составлению математической модели задачи.

1) Составление системы уравнений.

Пусть приобретено x единиц оборудования по 12 000 р., y единиц оборудования по 8 000 р., z единиц оборудования по 3 000 р.

Всего приобретено 100 единиц оборудования, т. е. x + y + z = 100, причем на приобретение 100 единиц оборудования затрачено 1 млн р., т. е.

12 000 x + 8 000 y + 3 000 z = 1 000 000,

12x + 8y + 3z = 1 000.

Таким образом, получаем систему двух уравнений с тремя неизвестными:

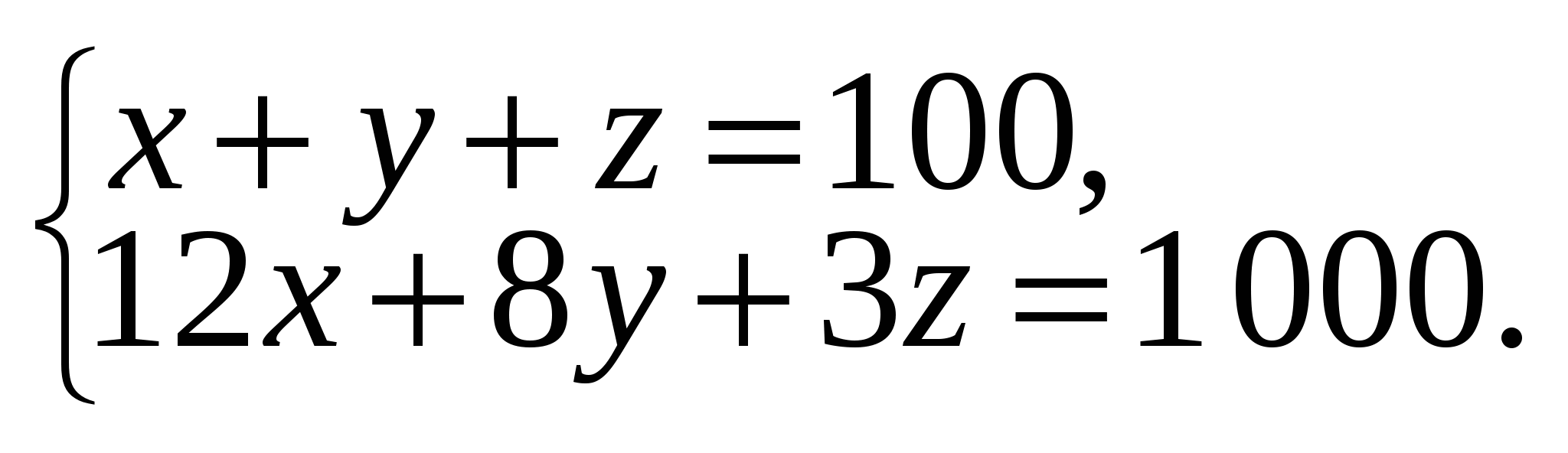
Вопрос учителя: всегда ли задача будет иметь решение? Иначе: какими должны быть x, y, z ?

(Ответ: x > 0, y > 0, z > 0.)

2) Обсуждение решения системы.

Во-первых, исключим z путем вычитания из второго уравнения первого, умноженного на 3. Следовательно, получаем диофантово уравнение первой степени с двумя неизвестными 9 x+ 5 y = 700.

Во-вторых, его можно решить способом с использованием алгоритма Евклида.

3) Оформление решения задачи.

Так как уже получили уравнение, которое решается известным способом, то оформление решения можно предложить выполнить учащимся дома. В результате решения получается, что приобрести оборудование библиотека может шестью способами. Укажем одно из частных решений задачи: x = 65, y = 23, z = 12, т. е. школа на 1 млн р. может приобрести 65 единиц оборудования по 12 000 р., 23 единицы оборудования по 8 000 р., 12 единиц оборудования по 3 000 р.

3. Постановка домашнего задания

В качестве домашнего задания можно предложить учащимся решить задачи № 2, 3, 5 из Приложения 1 с использованием алгоритма Евклида.

Занятие 5. Решение диофантовых уравнений с использованием цепной дроби

План занятия:

Понятие цепной дроби. Представление рациональных чисел в виде цепной дроби.
Формулы для решения диофантовых уравнений с использованием цепной дроби.
Примеры решения диофантовых уравнений с использованием цепной дроби.

Оборудование: конспект лекции на доске и индивидуальные заготовки для каждого ученика.

Ход занятия

Занятие 5 по своей структуре аналогично занятию 3. В качестве примеров решения диофантовых уравнений с использованием цепной дроби предлагается рассмотреть задания из Приложения 1. Заметим, что можно взять уже ранее решенные задачи и выполнить их решение новым способом.

Понятие цепной дроби. Представление рациональных чисел в виде цепной дроби.

Обратимся вновь к алгоритму Евклида. Из первого равенства системы (2) вытекает, что дробь a/b можно записать в виде суммы целой части и правильной дроби: 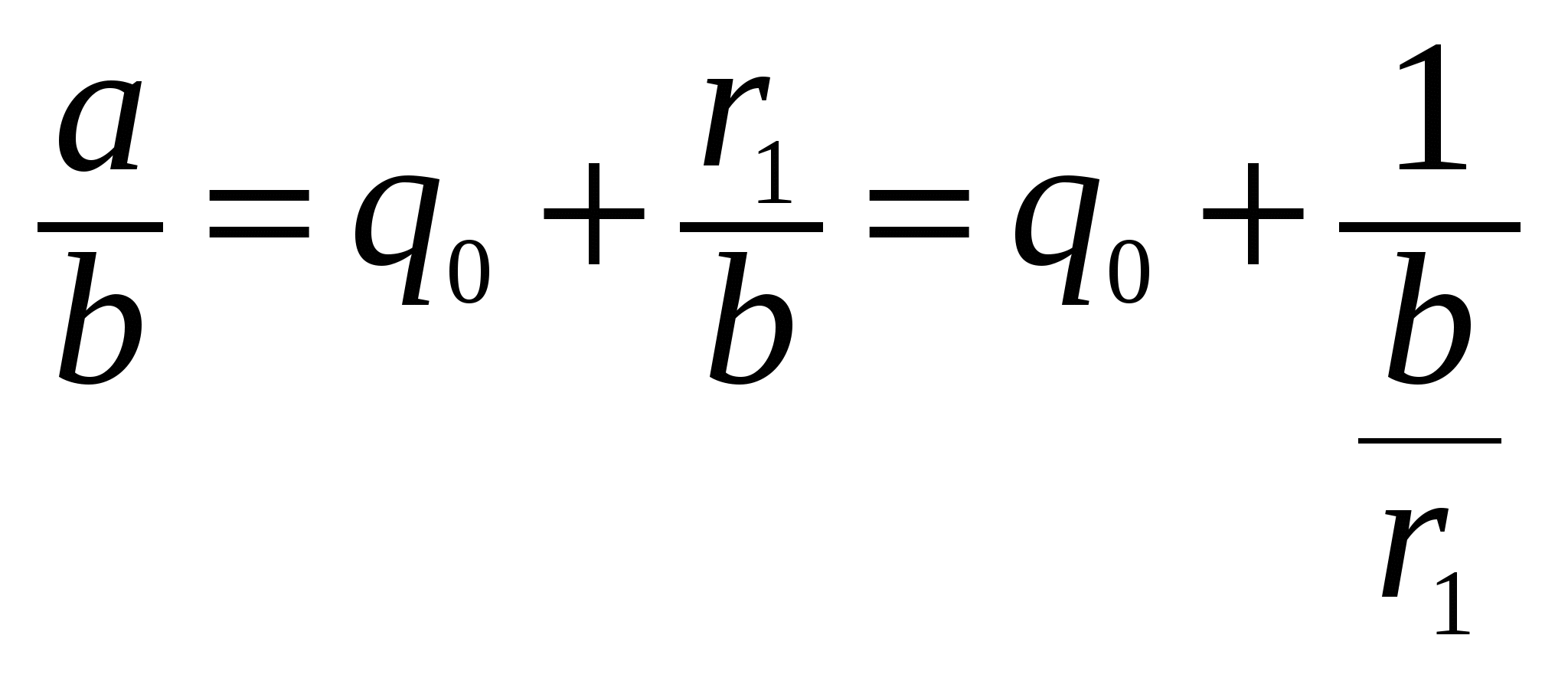. Из второго равенства той же системы имеем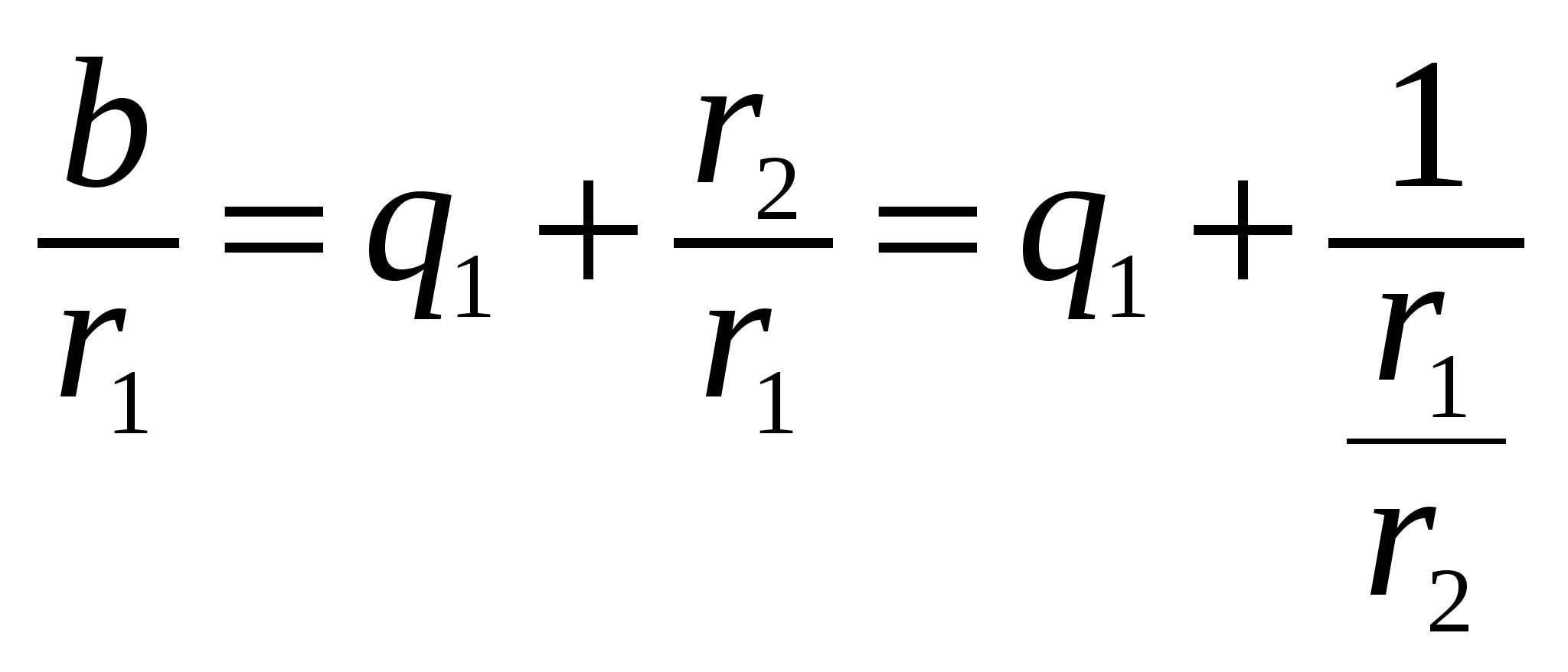. Значит, .

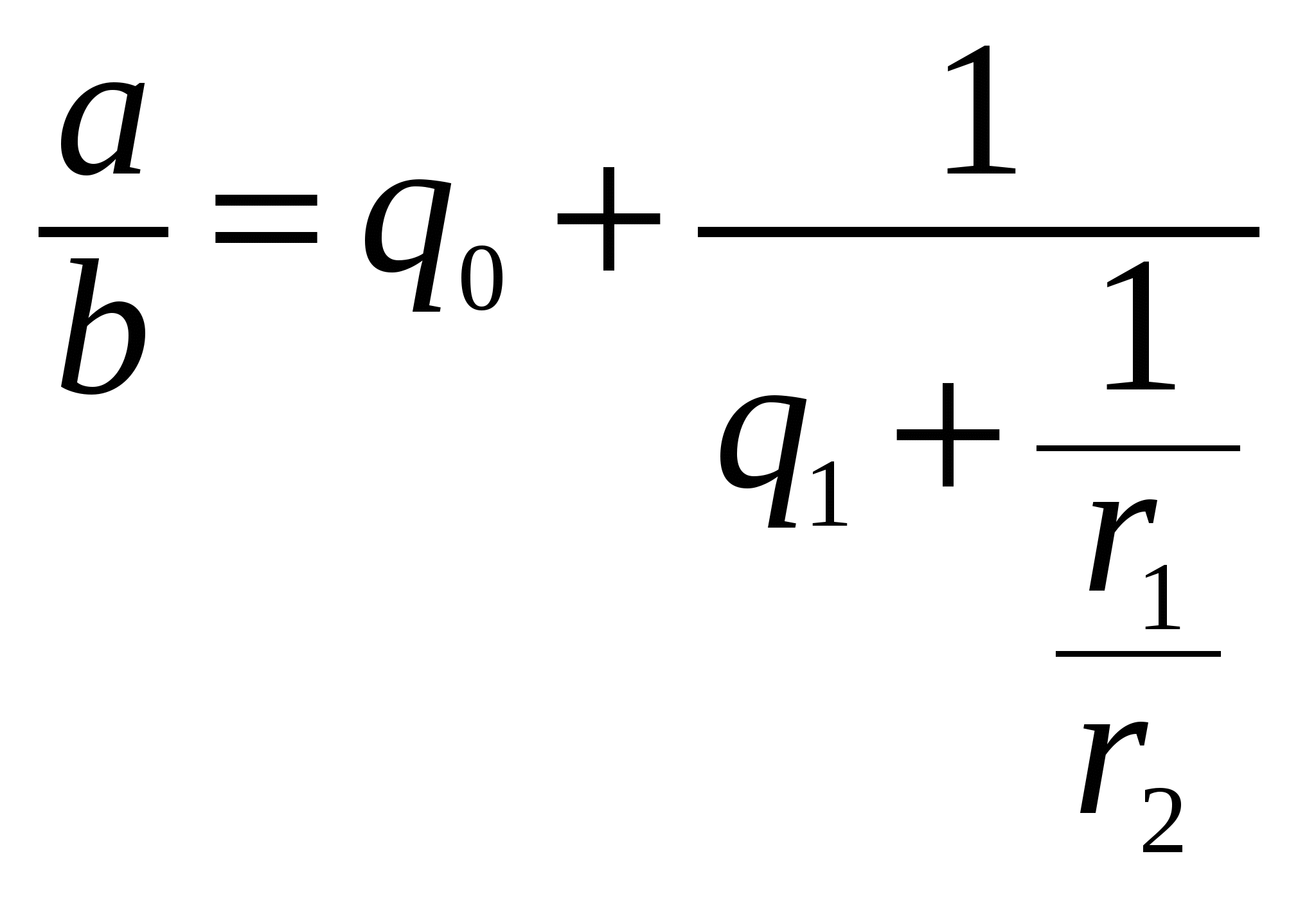Продолжим этот процесс до тех пор, пока не придем к знаменателю q_п.

В результате мы представим обыкновенную дробь a/b в следующем виде: 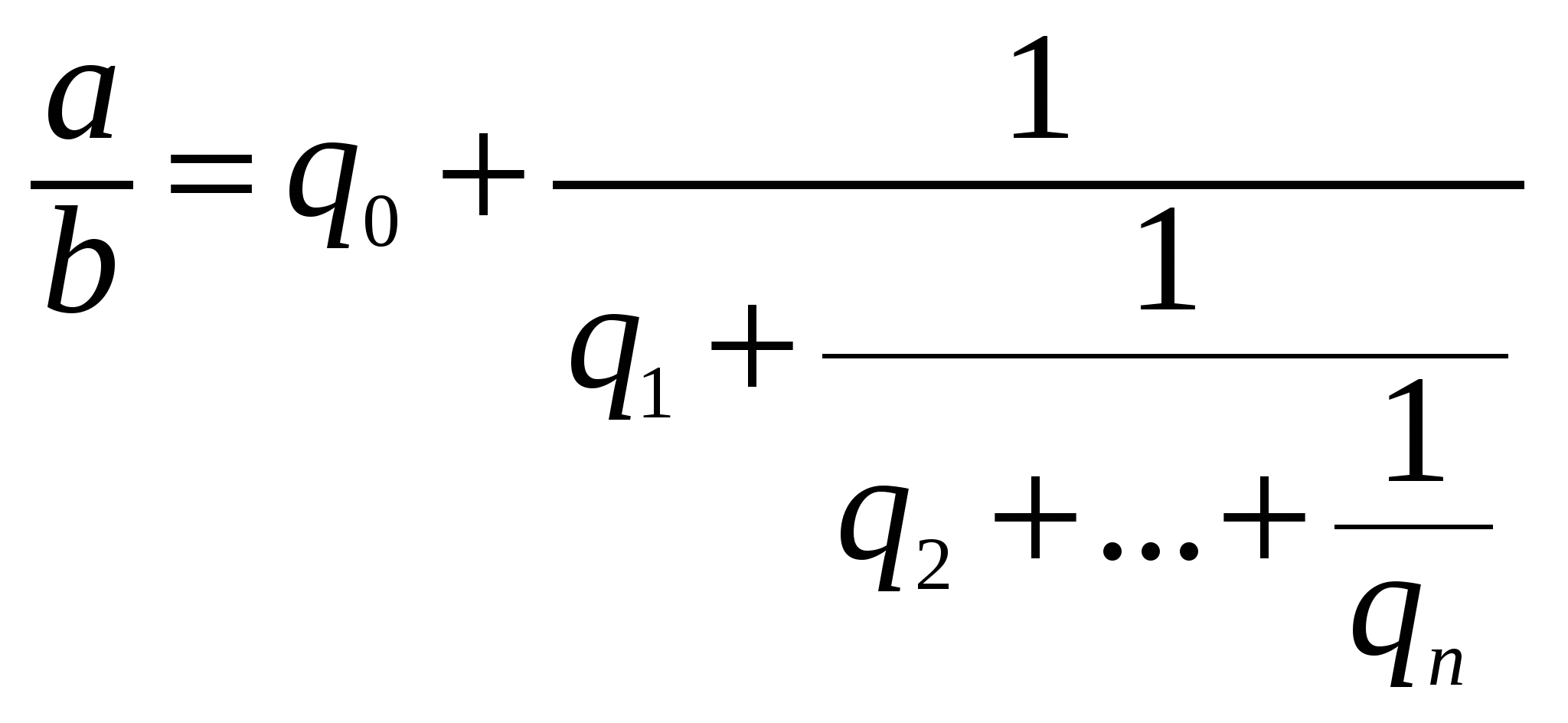. Эйлер назвал дробь, стоящую в правой части равенства непрерывной. Приблизительно в то же время в Германии появился другой термин — цепная дробь. Так за этими дробями и сохранились оба названия. Ввиду громоздкости развернутой записи цепной дроби применяют компактную запись

a/b = [q₀; q₁, q₂, …, q_п].

Пример 1.

Представить рациональное число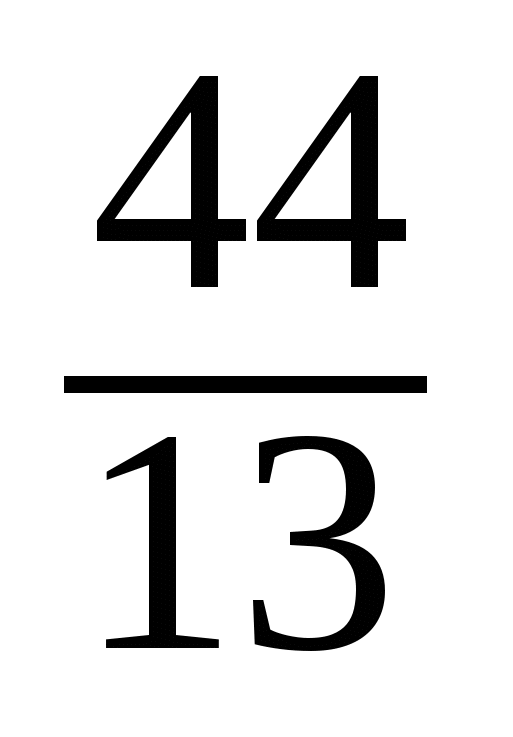 в виде цепной дроби.

Решение.

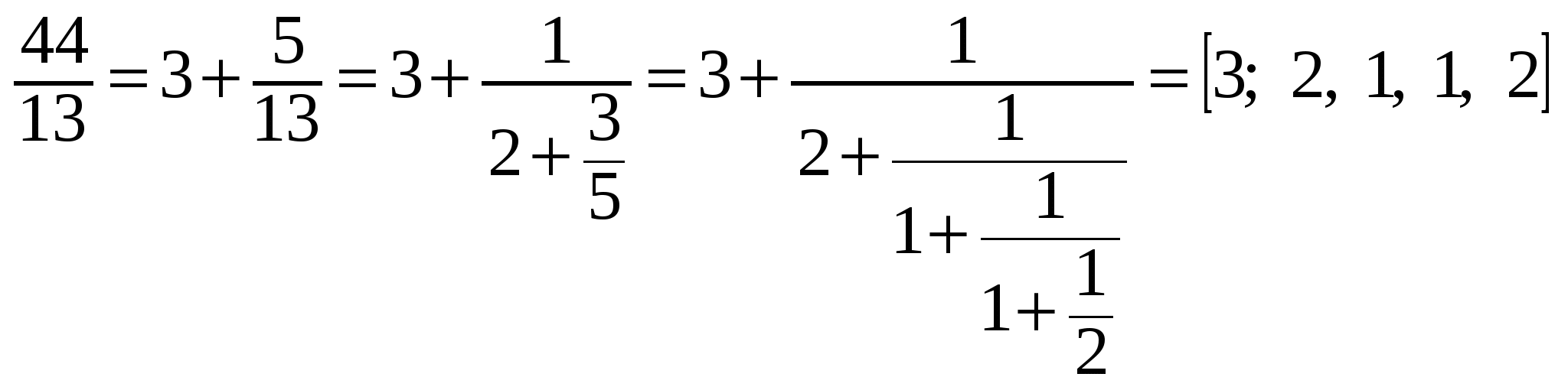Очевидно, что любое рациональное число, и только оно, записывается в виде конечной цепной дроби. Иррациональным числам соответствуют бесконечные цепные дроби.

Если при построении цепной дроби остановиться на знаменателе q_k, то получится дробь [q₀; q₁, q₂, …, q_к], которую называют к-й подходящей дробью для искомой и обозначают 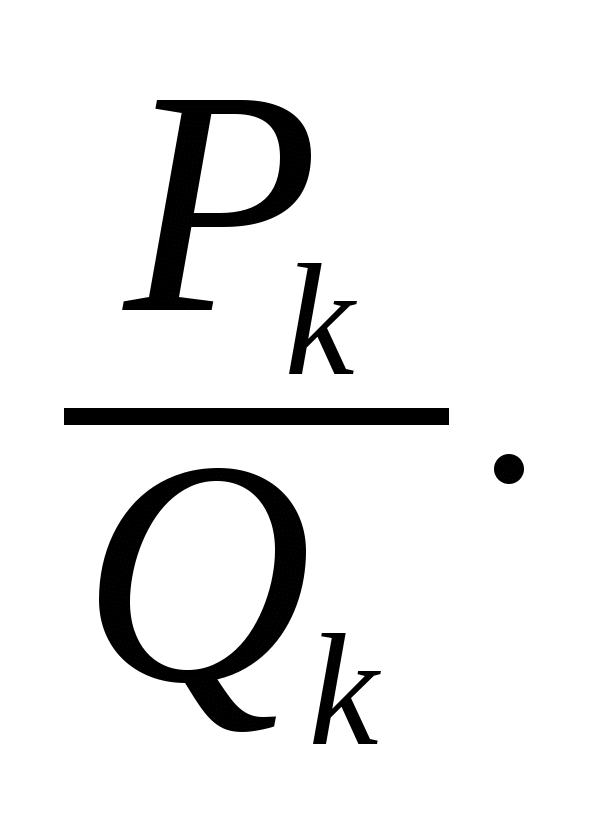Найдем вид некоторых подходящих дробей:

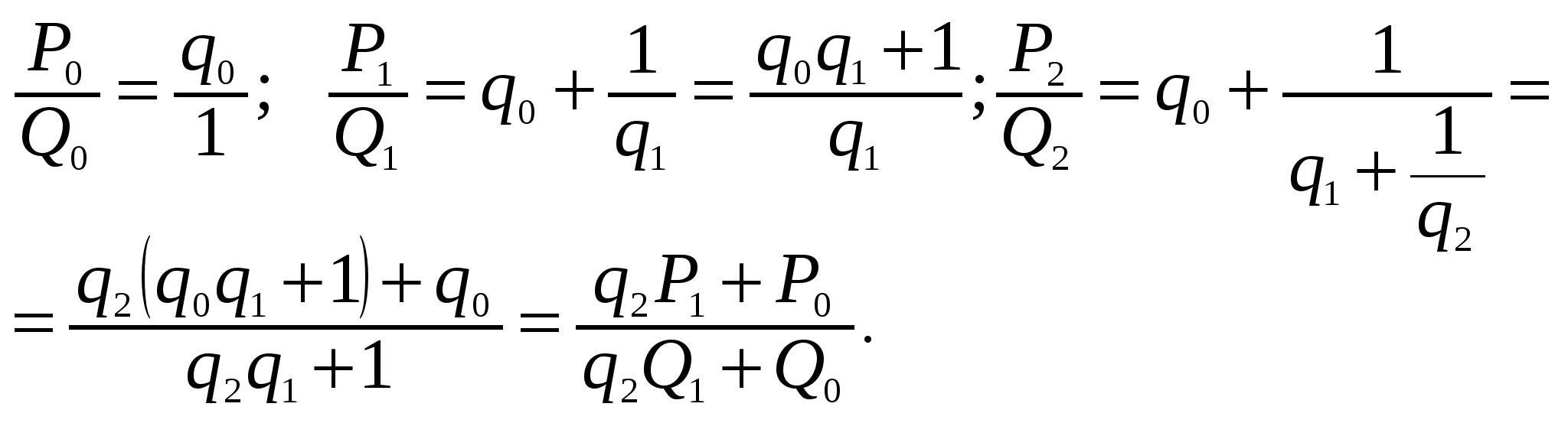
Для рационального числа a/b последовательность подходящих дробей конечна, и ее последний элемент 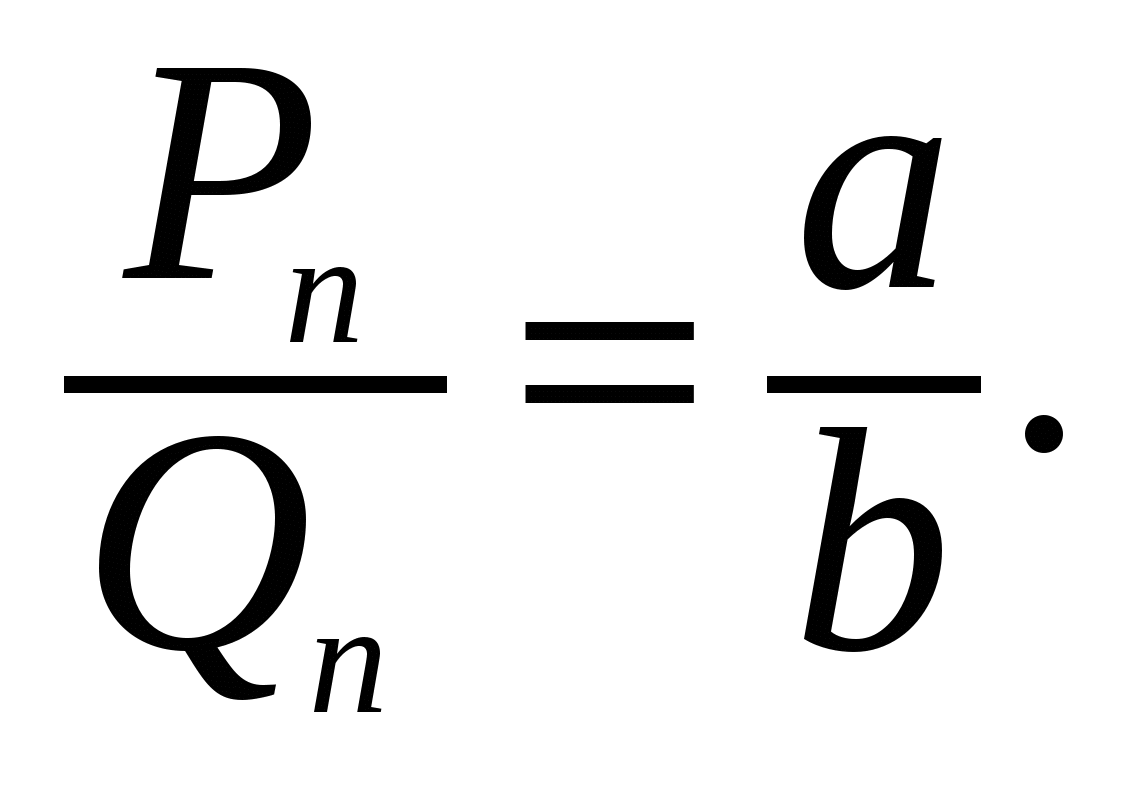Не Нетрудно заметить, что имеют место следующие рекуррентные соотношения:

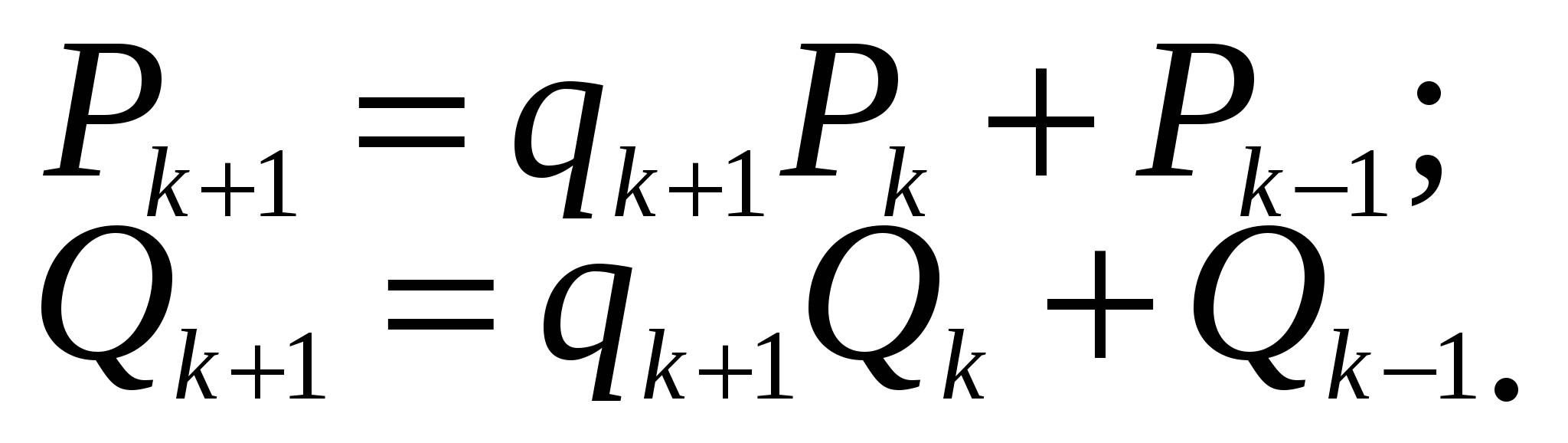(4)

Формулы для решения диофантовых уравнений с использованием цепной дроби

Вернемся к уравнению: ax + by = c (1). Напомним, что в нем a и b взаимно просты. Решение этого уравнения «способом цепной дроби» завершается применением готовых формул (доказательство которых можно найти в специальных пособиях), представляющих общее решение данного уравнения.

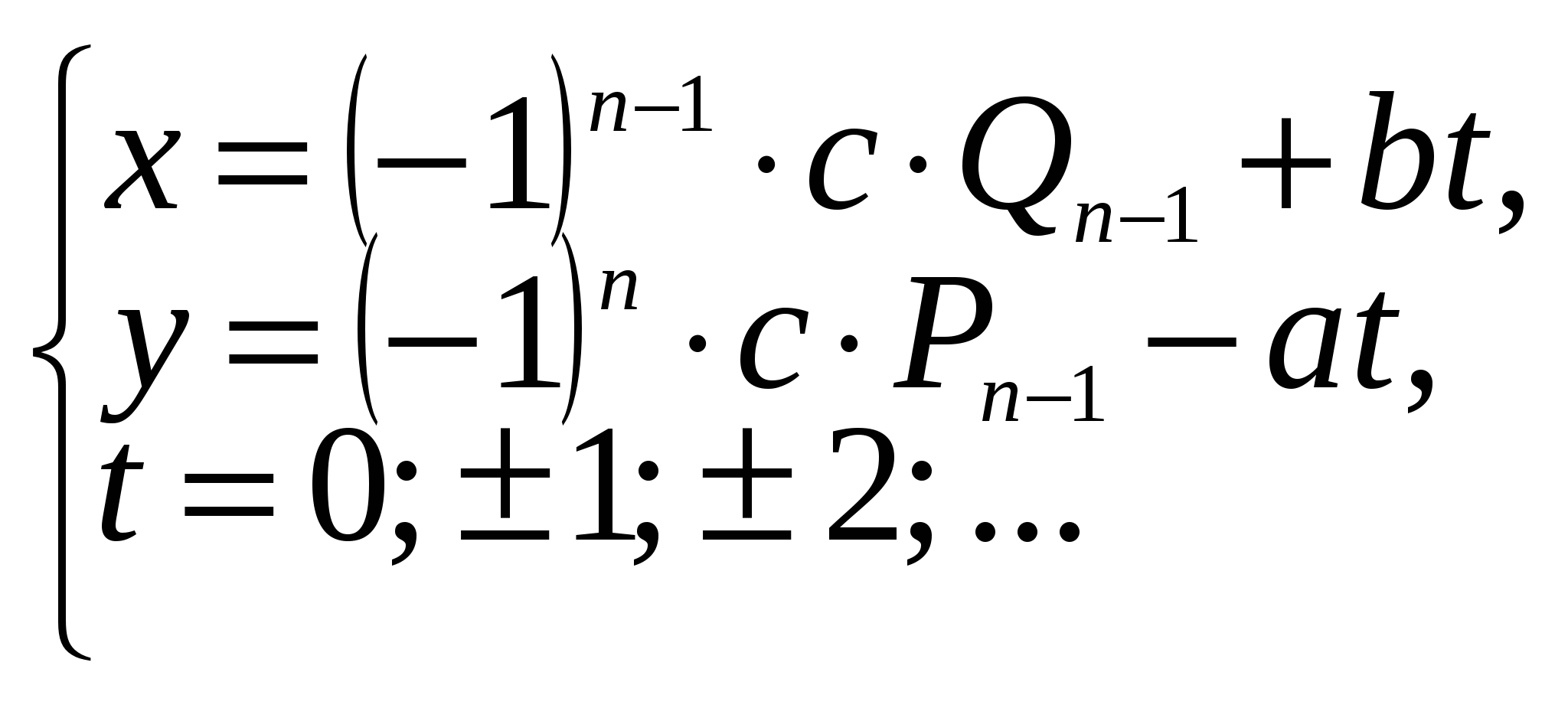(5)

Решим этим способом диофантово уравнение.

Пример 2.

Решить уравнение 44х + 13у = 5.

Решение.

Так как 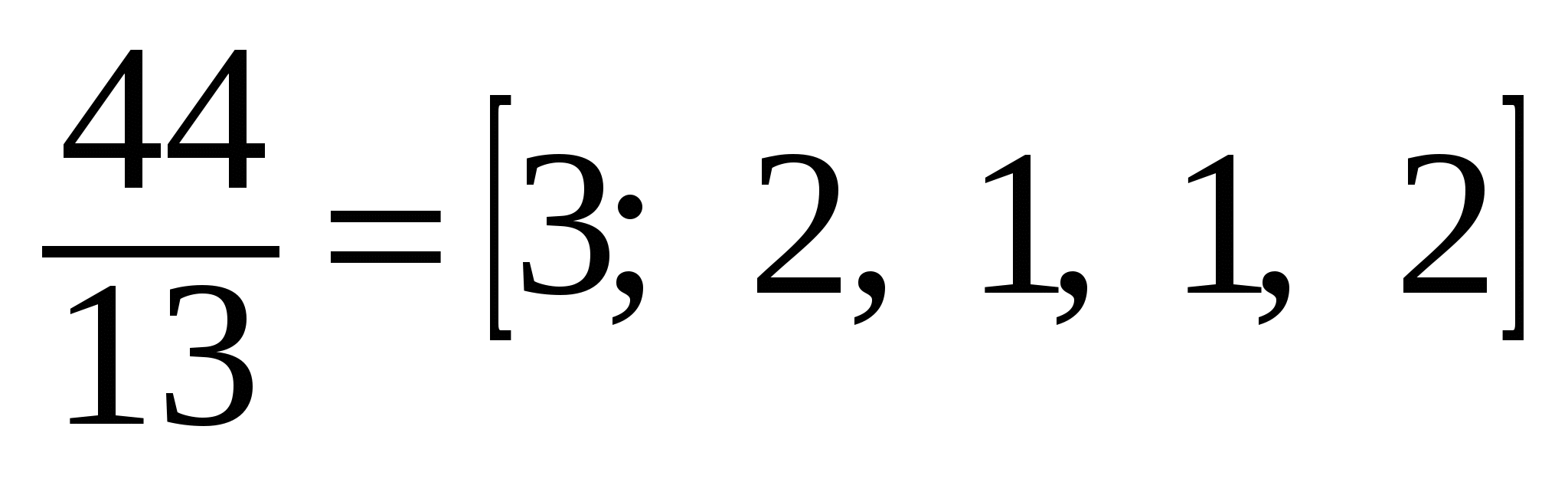, то n = 4. Составим «подходящие дроби».

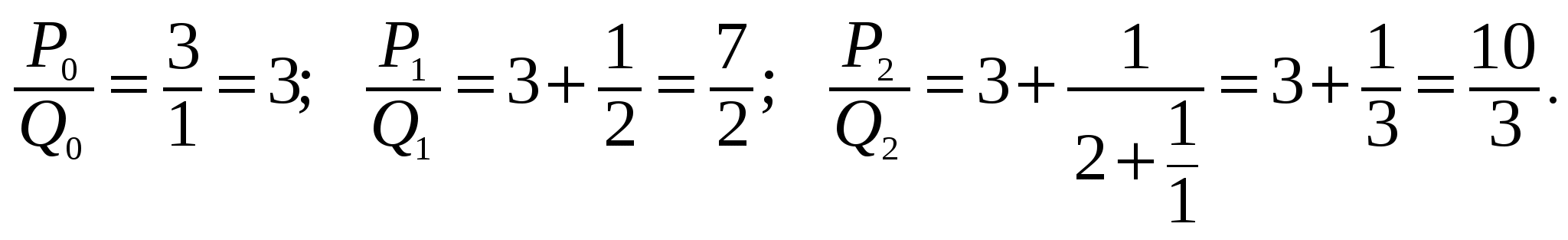
Найдем P₃ и Q₃ используя формулы (4): P₃= 10 + 7 = 17, Q₃= 3 + 2 = 5.

Все готово к применению формул (5). Общее решение уравнения будет иметь вид: х = –25 + 13t, y = 85 – 44t, где t — целое число.

После введения нового материала в конспекте-заготовке лекции необходимо выделить алгоритм решения диофантова уравнения с использованием цепной дроби. Этот алгоритм можно представить в следующем виде.

Для решения уравнения 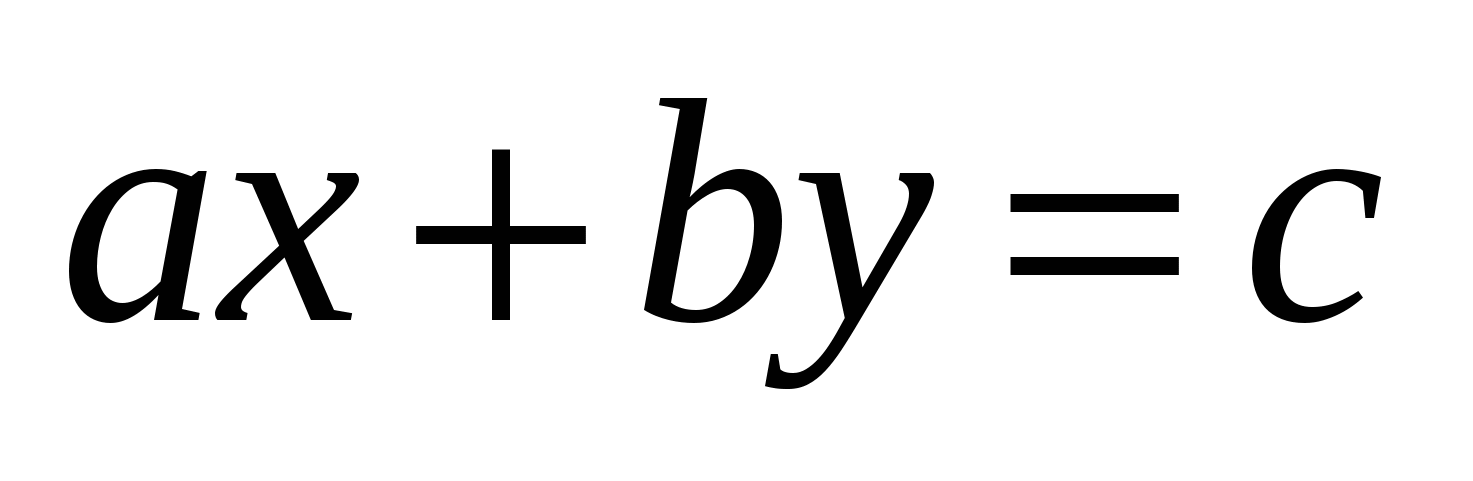(1), где a, b, c — целые коэффициенты, способом цепной дроби нужно:

Представить дробь a/b в виде конечной цепной дроби.
Записать дробь a/b= [q_0; q_1,q_2,... ,q_n].
Составить таблицу для нахождения значений числителя и знаменателя подходящих дробей 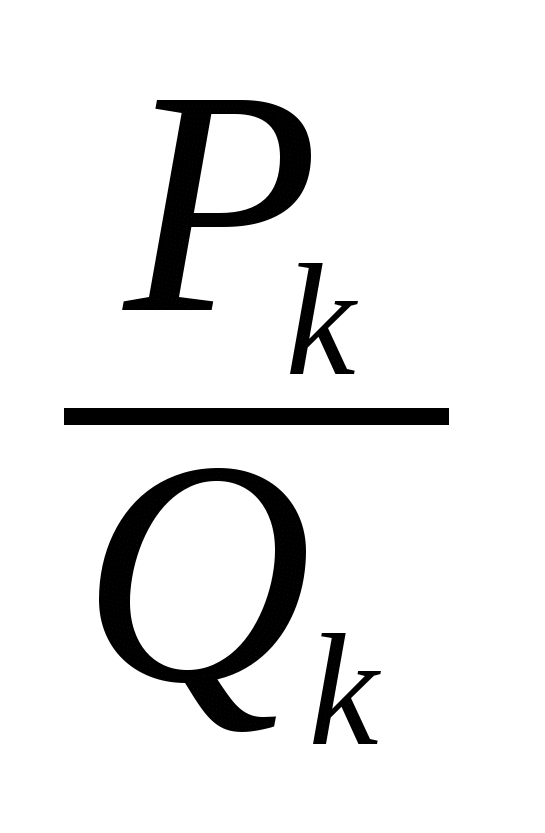для полученной цепной дроби, последняя подходящая дробь .

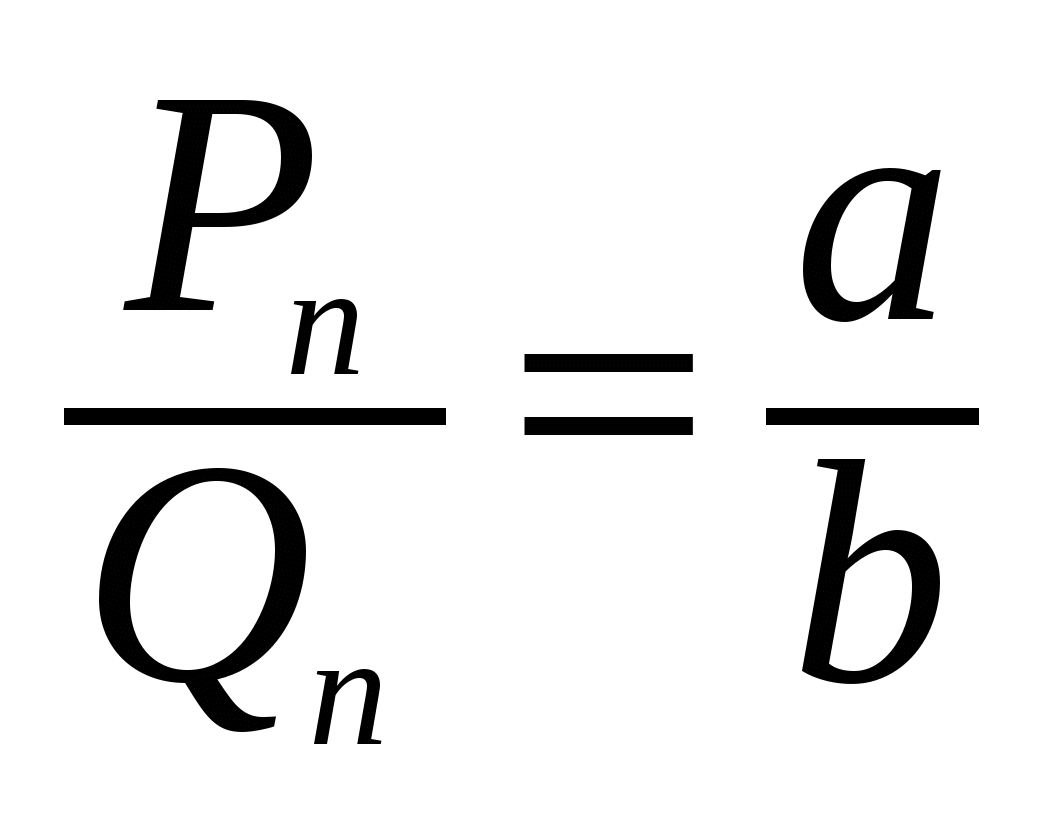Начальные условия

q₀

q₁

q₂

...

q_n

P_i

q₀

q₀ q₁+ 1

(q₀ q₁+1) q₂+ q₀

Q_i

q₁

q₂ q₁+ 1

Найдем решение уравнения по следующим формулам:

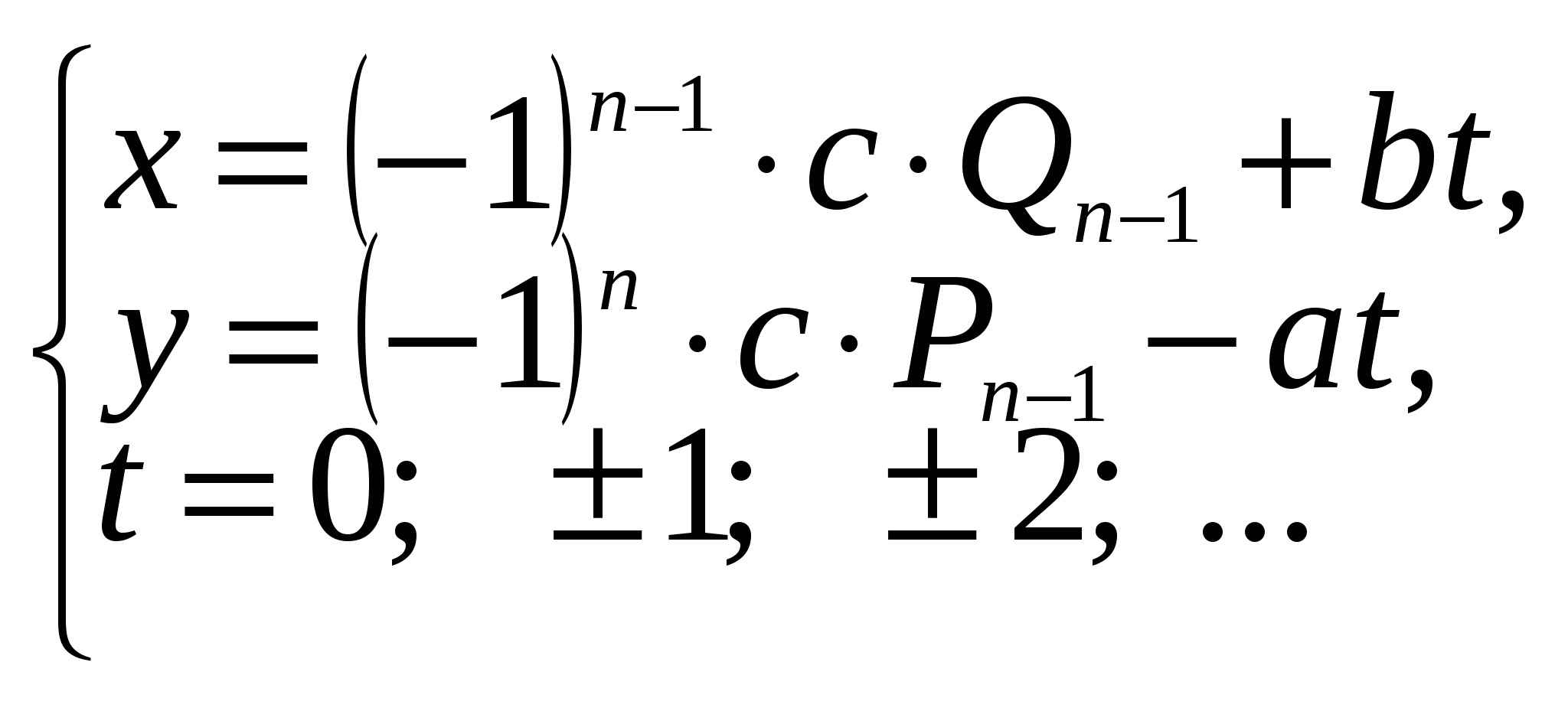
Решим задачу № 7 из Приложения 1 способом цепной дроби. Для ответа на вопрос задачи требуется решить диофантово уравнение: 9х + 13у = 150.

Решение.

Представим дробь 9/13 в виде конечной цепной дроби.

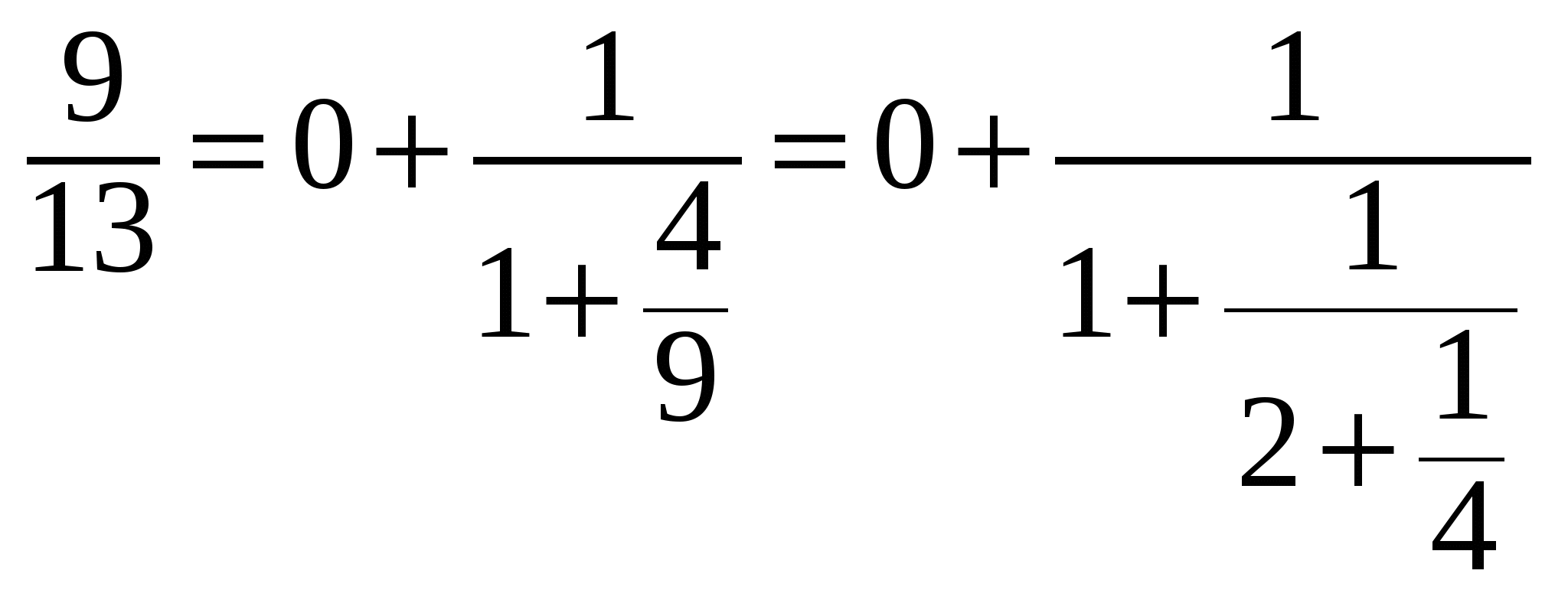Запишем дробь в виде цепной дроби 9/13 = [0; 1, 2, 4].
Составим таблицу

Начальные условия

q₀= 0

q₁= 1

q₂= 2

q₃= 4

P_i

Q_i

4. Запишем общее решение уравнения:

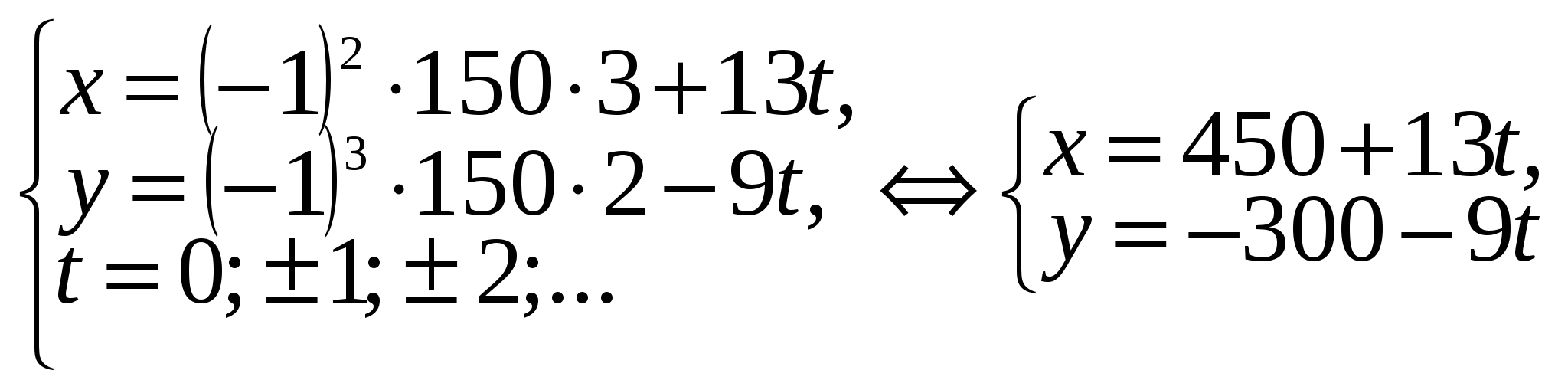
Как и в решении способом с использованием алгоритма Евклида, мы получили такой же вид общего решения. А решение задачи выражается той же парой чисел: (8; 6).

3. Домашнее задание должно включать как вопросы по теоретическому материалу, так и практические задания.

Занятие 6. Решение диофантовых уравнений с использованием цепной дробиПлан занятия

Актуализация знаний (проверка знания теории и выполнения практических заданий).
Решение задач с использованием цепной дроби.
Постановка домашнего задания.

Ход занятия

Основная цель занятия — овладение учащимися способом решения уравнений с использованием цепной дроби. Необходимо провести проверку усвоения теоретического материала: основных понятий, алгоритма решения. Целесообразно, чтобы формулы для решения уравнения были «перед глазами учащихся» в процессе проведения занятия. Можно записать их на доске, а также использовать заполненные опорные конспекты предыдущей лекции.

На занятии нужно рассмотреть задачи, для которых сразу ясна идея решения (№ 12(а, б), 13, 14 из Приложения 1), а также задачи, требующие обдумывания и смекалки (№ 15, 16 из Приложения 1). Задачи № 15, 16 можно предложить учащимся для решения в группах, а затем проверить решение фронтально. Можно до оформления решения обсудить его идею, наметив основные шаги, и предложить учащимся выполнить решение самостоятельно. Затем проверить полученный ответ. Часть из предлагаемых заданий можно дать на дом учащимся.

Рассмотрим решение задач № 15 и 16.

Задача № 15. Сколько можно купить на 100 монет петухов, кур и цыплят, если всего надо купить 100 птиц, причем петух стоит 5 монет, курица — 4, а 4 цыпленка — одну монету?

Решение.

Пусть x — искомое число петухов, у — кур, а 4z — цыплят. Составим систему уравнений, которую надо решить в целых неотрицательных числах.

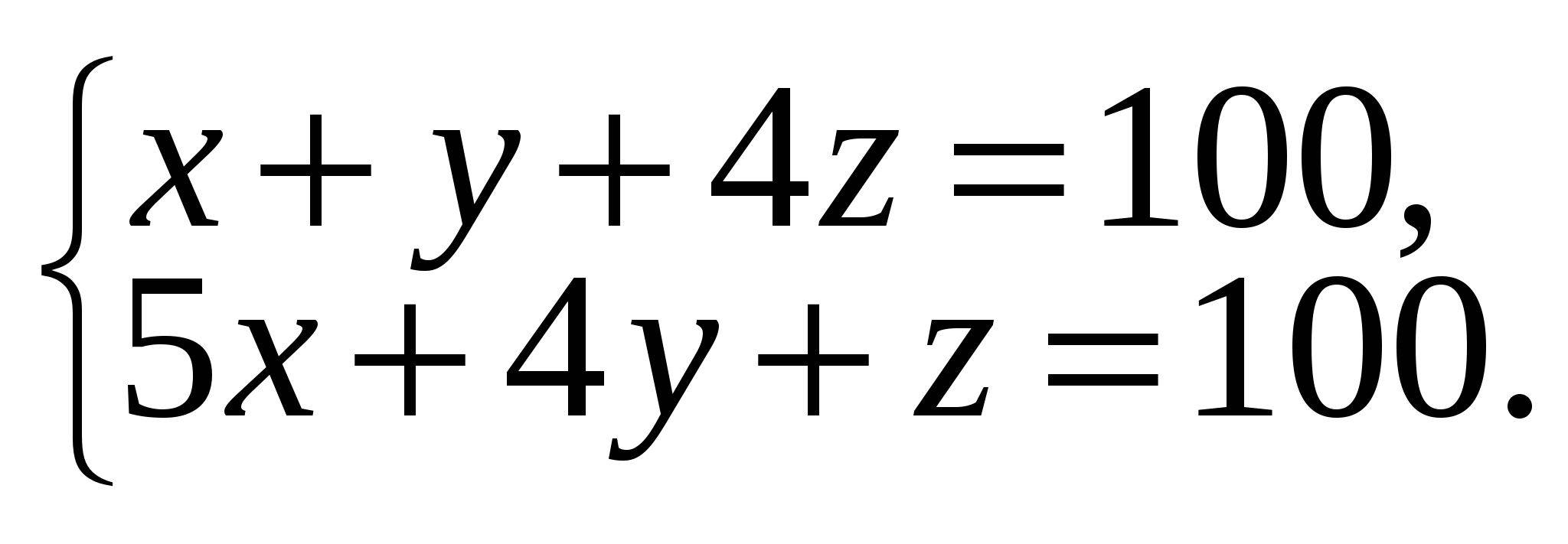
Умножив первое уравнение системы на 4, а второе на (–1) и сложив результаты, придем к уравнению –x + 15z = 300 с целочисленными решениями x = –300 + 15t, z = t. Подставляя эти значения в первое уравнение, получим y = 400 – 19t. Значит, целочисленные решения системы имеют вид

x = –300 + 15t, y = 400 – 19t, z = t.

Из условия задачи вытекает, что

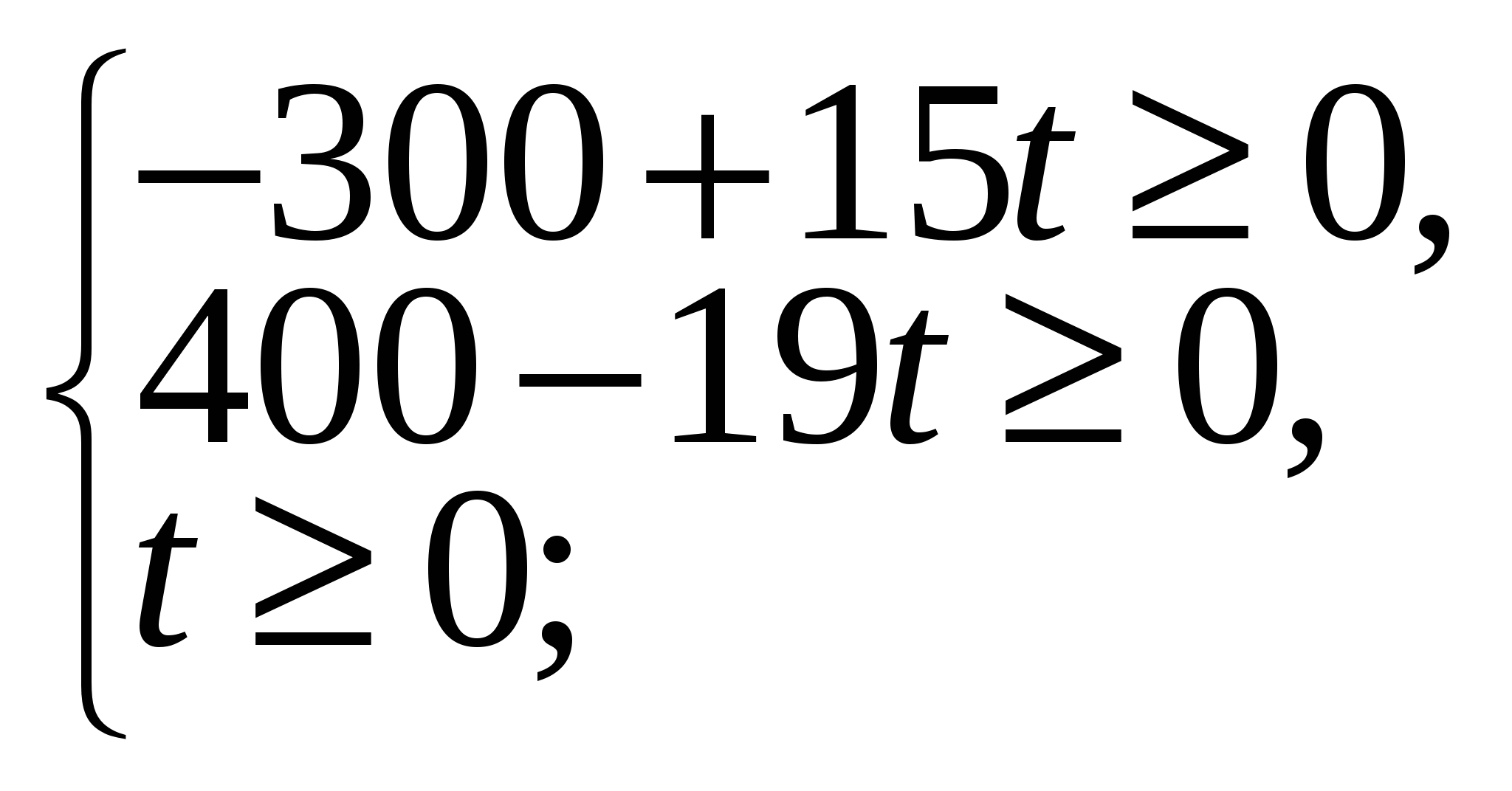откуда 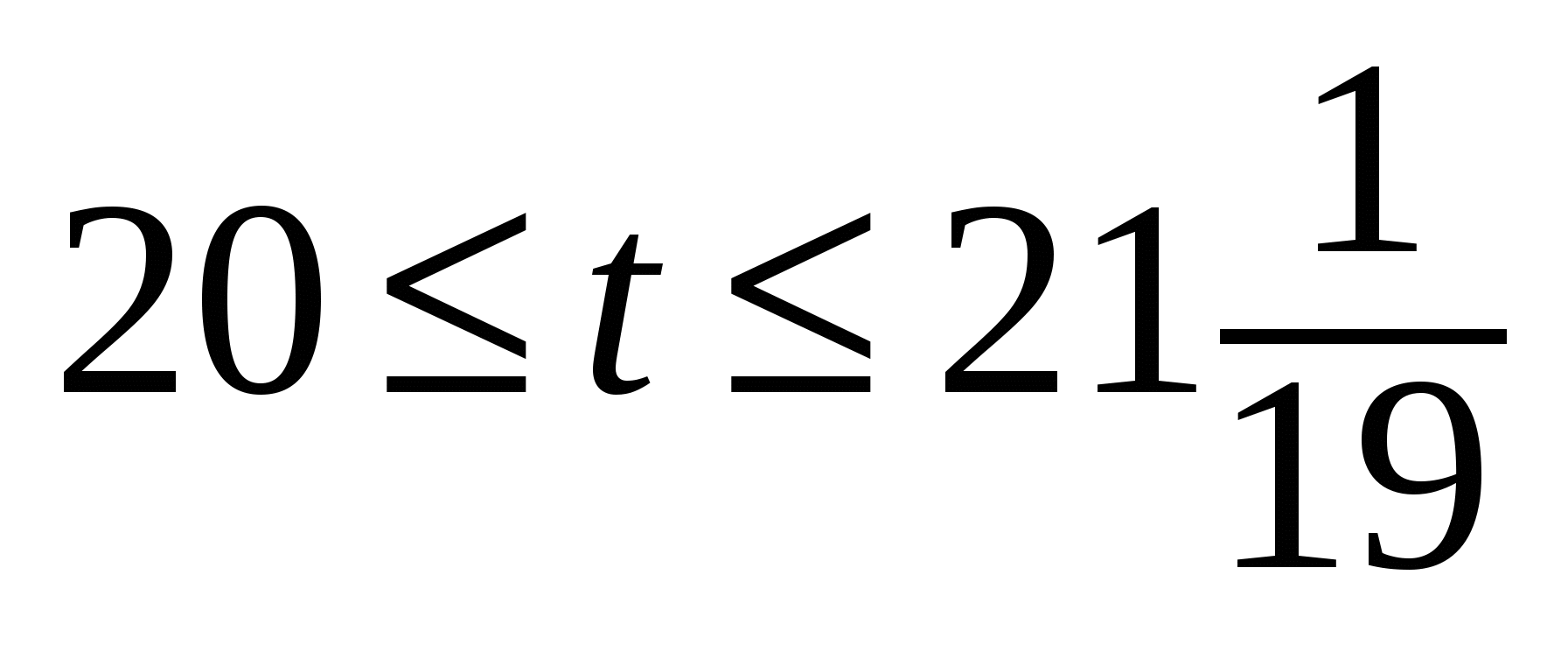, т. е. t = 20 или t = 21.

Ответ. На 100 монет можно купить 20 кур и 80 цыплят или 15 петухов, 1 курицу и 84 цыпленка.

Задача № 16. Крестьянка несла на базар корзину яиц. Неосторожный всадник, обгоняя женщину, задел корзину, и все яйца разбились. Желая возместить ущерб, он спросил у крестьянки, сколько яиц было в корзине. Она ответила, что число яиц не знает, но когда она раскладывала их по 2, по 3, по 4, по 5 и по 6, то каждый раз одно яйцо оставалось лишним, а когда она разложила по 7, лишних яиц не осталось. Сколько яиц несла крестьянка на базар?

Решение.

Пусть x — число яиц. Так как (x – 1) делится на 2, на 3, на 4, на 5, на 6, то оно делится на их НОК, равное 60. Значит, x имеет вид 60у + 1.

Поэтому для ответа на вопрос задачи надо решить в натуральных числах уравнение 60у + 1 = 7z или 7z – 60у = 1.

С помощью способа с использованием цепной дроби получаем, что целочисленные решения уравнения имеют вид у = –2 + 7t, z = –17 + 60t, где t — любое целое число.

Наименьшее положительное решение получаем при t = 1. В этом случае у = 5, z = 43. Итак, крестьянка несла на базар 301 яйцо.

Ответ. Крестьянка несла на базар 301 яйцо.

В домашнее задание обязательно включить повторение способов решения диофантовых уравнений с использованием алгоритма Евклида и цепной дроби, а также ряд задач, которые нужно решить этими способами.

Занятия 7-8. Метод рассеивания (измельчения) в решении диофантовых уравнений

План занятия

Проверка домашнего задания (форму проверки выбирает учитель, в данном случае можно провести самостоятельную работу на 10 мин по материалу предыдущих занятий).
Изучение нового материала. Способ измельчения коэффициентов как один из методов нахождения целых (натуральных) решений диофантовых уравнений.
Решение задач способом измельчения коэффициентов.
Постановка домашнего задания.

Оборудование: компьютер, проектор, слайды с заданиями, карточки с заданиями.

Ход занятия

Проверка домашнего задания (в форме самостоятельной работы)

Решить уравнение двумя способами: с использованием алгоритма Евклида и цепной дроби:

1 вариант: 2x + 5y = 17. Ответ: (1; 3), (6; 1).

2 вариант: 5х + 8у = 39. Ответ: (3; 3)

Можно предложить учащимся текстовую задачу, сводимую к диофантову уравнению. Так как уравнение нужно решить двумя способами, то ученик имеет возможность контролировать себя сам, а как следствие — искать и устранять ошибки, если таковые имеются.

Изучение нового материала

На этом этапе необходимо ознакомить учащихся с методом рассеивания (измельчения) для решения диофантовых уравнений: разъяснить суть данного метода, привести некоторые исторические сведения, показать на примере использование данного метода для решения задач.

Способ рассеивания (размельчения) впервые применил в начале VI века индийский математик Ариабхатта. Метод заключается в сведении данного уравнения к последовательности других уравнений с убывающими по абсолютной величине коэффициентами перед неизвестными.

Продемонстрируем его на примере решения следующей задачи.

Задача. Найти два числа, если разность произведений первого на 19 и второго на 8 равна 13.

Решение.

Требуется решить уравнение 19х – 8у = 13.

Перепишем его иначе: 8y =19x – 13; 8y = 16x + 3x – 13; у = 2х +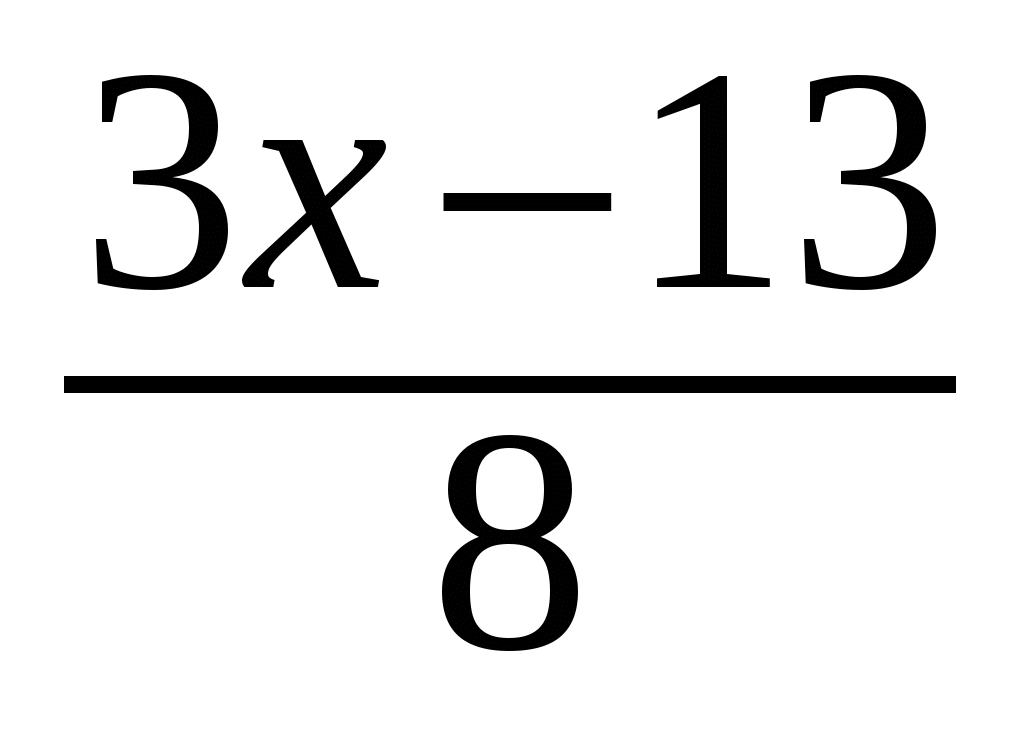

и обозначим y₁ = у – 2х.

В результате уравнение примет вид 8у₁ = 3x – 13 или x = 2y₁_.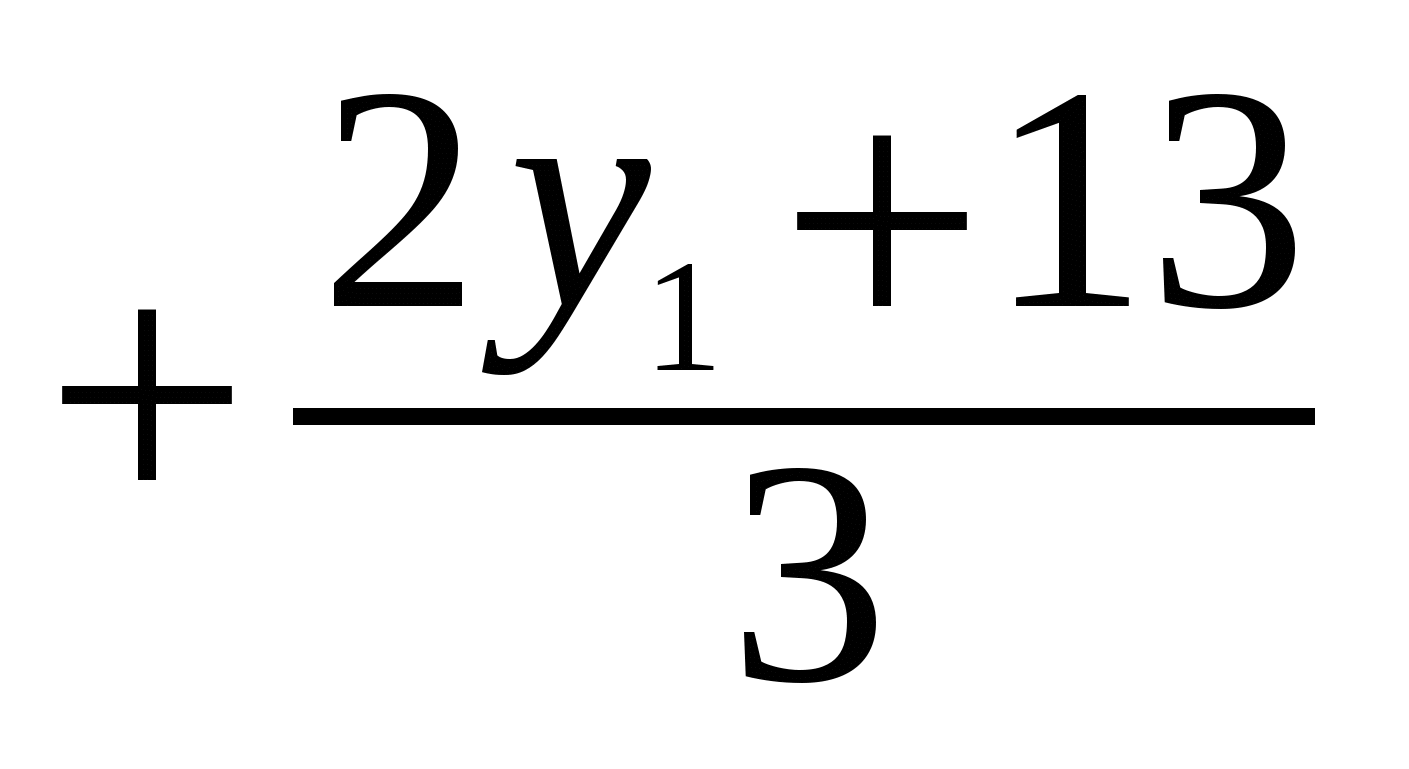

Если вновь произвести замену х₁ = x – 2у₁, то придем к уравнению 3x_l – 2у₁ = 13.

Заметим, что коэффициенты при неизвестных уменьшились — измельчились. Продолжим дальнейшее их уменьшение: так как y₁ = x_l +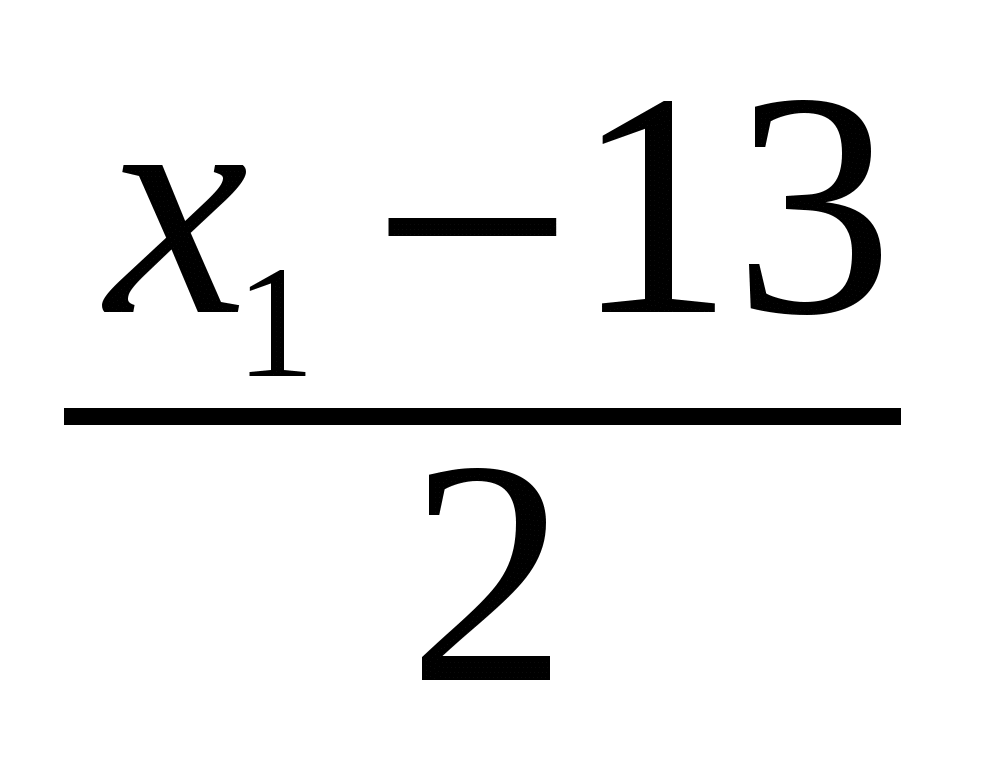, то положим у₂ = у₁ –х₁.

В результате последнее уравнение преобразуется к виду х₁ – 2у₂= 13. Здесь коэффициент при х₁, равен 1, а поэтому при любом целом у₂ = t число х₁ тоже целое.

Остается выразить исходные переменные через t: вначале выразим х₁= 2t + 13, y₁ = 3t + 13; а затем x = 8t + 39, y = 19t + 91.

Итак, получаем бесконечную последовательность (39 + 8t, 91 + 19t) целочисленных решений.

Нетрудно заметить, что методы цепных дробей и рассеивания являются лишь другой формой применения алгоритма Евклида.

3. Решение задач способом измельчения коэффициентов

Для решения можно предложить учащимся как новые задания, так и уже ранее решенные, но потребовать применить способ измельчения. Данный способ еще называют «методом спуска».

Задача № 18(а).

Решить способом измельчения в целых числах уравнение 5x + 8y = 39.

Решение:

1. Выберем неизвестное, имеющее наименьший коэффициент, и выразим его через другое неизвестное: x = (39 – 8y) : 5.

Выделим целую часть: x = 7 – y + (4 – 3y) : 5.

Все число будет целым, если целым окажется значение (4 – 3y) : 5.

Это возможно тогда, когда число (4 – 3y) без остатка делится на 5. Вводя дополнительную целочисленную переменную z, последнее уравнение запишем в виде: 4 – 3y = 5z.

Мы пришли к уравнению такого же типа, как и исходное уравнение, но уже с меньшими коэффициентами. Решать его уже нужно относительно переменных y и z.

2. y = (4 – 5z) : 3 = 1 – z + (1 – 2z) : 3.

Аналогично рассуждая, запишем (1 – 2z) через новую целочисленную переменную и: 1 – 2z = 3u.

4. z = (1 – 3u) : 2 = (1 – u):2 – u; 1 – u = 2v.

3. u = 1 – 2v — дробей больше нет, спуск закончен.

5. Теперь необходимо «подняться вверх». Выразим через переменную v сначала z, потом y и затем x.

z = (1 – u) : 2 – u = (1 – 1 + 2v) : 2 – 1 + 2v = 3v – 1,

z = 3v – 1.

y = (4 – 5z) : 3 = (4 – 5(3v – 1)) : 3 = 3 – 5v,

y = 3 – 5v.

x = (39 – 8y) : 5 = (39 – 8(3 – 5v)) : 5 = 3 + 8v,

x = 3 + 8v.

6. Формулы x = 3 + 8v, y = 3 – 5v представляют общее решение исходного уравнения в целых числах.

7. Если необходимо получить только натуральные числа, то среди всех целых решений нужно выбрать такие, для которых x > 0, y > 0, то есть 3 + 8v > 0, 3 – 5v > 0. Совместно эти неравенства могут выполняться лишь при v = 0. В этом случае x = 3, y = 3.

8. Ответ. (3; 3).

С учащимися можно рассмотреть и более сложные задания, решая их именно «методом спуска».

Задача № 19.

Решить в целых числах 29х + 13у + 56 z = 17. (1)

Выразим неизвестное, коэффициент при котором наименьший, через остальные неизвестные.

y = (17 – 29 х – 56 z) : 13 = (1 – 2x – 4z) + (4 – 3x – 4z) : 13. (2)

Обозначим (4 – 3x – 4z) : 13 = t₁. (3)

Из (2) следует, что t₁ может принимать только целые значения. Из (3) имеем 13t₁ + 3x + 4z = 4. (4)

Получим новое диофантово уравнение, но с меньшими, чем в (1) коэффициентами. Применим к (4) те же соображения:

x = (4 – 13t₁– 4z) : 3 = (1 – 4t₁ – z) + (1 – t₁ – z) : 3;

(1 – t₁– z) : 3 = t₂, t₂ — целое, 3t₂+ t₁+ z = 1. (5)

В (5) коэффициент при z — неизвестном исходного уравнения равен 1 — это конечный пункт «спуска». Теперь последовательно выражаем z, x, y через t₁ и t₂.

z = –t₁ – 3t₂ + 1,

x = 1 – 4t₁ + t₁ + 3t₂ – 1 + t₂ = –3t₁ + 4t₂,

y = 1 + 6t₁ – 8t₂ + 4t₁ + 12t₂ – 4 + t₁= 11t₁ + 4t₂ – 3.

Итак, x = –3t₁ + 4t₂,

y = 11t₁ + 4t₂ – 3,

z = –t₁ – 3t₂ + 1.

t₁, t₂ — любые целые числа, определяющие все целые решения уравнения исходного уравнения.

Можно предложить учащимся найти частные решения данного уравнения и проверить их.

Например, пусть t₁= 1, t₂ = 2. Имеем х = 5, у = 16, z = –6.

Подставим найденные решения в уравнение 29х + 13у + 56z = 17, получим 145 + 208 – 336 = 17;

353 – 336 = 17;

17 = 17.

В домашнее задание можно включить практические задания из Приложения 1 (или решенные ранее другими способами), в процессе решения которых будет усваиваться метод рассеивания (метод спуска). Целесообразно предложить учащимся составить задачу, сводимую к диофантову уравнению, и решить ее одним из изученных способов.

Также для подготовки к практическому занятию № 8, которое является занятием обобщения и систематизации изученного материала, учащимся необходимо повторить:

— понятие диофантова уравнения, линейного диофантова уравнения с двумя переменными, условия существования целых решений уравнения;

— методы решения уравнения: способ перебора вариантов, с использованием алгоритма Евклида, с использованием цепной дроби.

Для повторения полезно использовать опорные конспекты лекционных занятий и конспекты практических занятий.

Занятия 9 - 10. Решение диофантовых уравнений разными способами

Данное практическое занятие является обобщающим занятием. Перед решением задачи необходимо повторить теоретический материал, опираясь на вопросы домашнего задания занятия № 7. Целесообразно суть выбранного способа решения задачи повторить непосредственно перед его применением к решению поставленной задачи. В целях самоконтроля за выполнением задания учащимся предлагается решить одну задачу разными способами и сравнить полученные ответы, поэтому условно данное занятие можно назвать «уроком одной задачи. Форма работы с учащимися — фронтальная. Но учащимся, которые достаточно хорошо усвоили материал, можно предложить нестандартные задания № 17, 23 из списка задач (Приложение 1).

Домашнее задание. Из Приложения 1 для домашней работы можно указать задания № 21, 22, а также предложить и задачи учеников, которые не были решены на занятии.

Учащимся необходимо напомнить, что следующее занятие — семинарское, назвать тех, кто будет на нем выступать, назначить день «последней» контрольной проверки выполненных учащимися индивидуальных и групповых заданий к семинару.

В целях эффективной работы на семинарском занятии, необходимо заранее подготовить соответствующее оборудование для демонстрации выполненных учащимися материалов с использованием информационных технологий, проверить совместимость электронных носителей учащихся с записанными презентациями выступлений и компьютера в классе и т. п.

Занятия 11—12. Решение задач с использованием различных диофантовых уравнений или их систем

Данные занятия относятся к категории практических.

Основная цель: рассмотреть вместе с учащимися задачи повышенной трудности на составление диофантовых уравнений или их систем, продемонстрировать различные способы их решения, в том числе и нестандартные.

Мы приведем решение некоторых задач из Приложения 1, которые можно разобрать как на занятии, так и предложить для самостоятельной работы учащимся.

Задача № 24. Решите в натуральных числах x² – 4xy – 5y² = 1 996.

Решение.

Перепишем уравнение в виде

(x²– 4ху + 4y²) – 9y²= 1 996, (х – 2у)²– 9y²= 1 996.

Разложим левую часть на множители (x – 5y)(x + у) = 1 996.

Разложим число 1996 на целые множители:

1 996 = 1 · 1 996 = 2 · 998 = 4 · 499 = –1 · (–1 996) = –2 · (–998) = –4 · (–499).

Так как x  N, y N, то (x + у)  N, причем (x + у) > 1.

Если (x + у) N и (x + у)(x – 5у) = 1 996, то (x – 5у)  N.

Тогда решение получившегося уравнения сводится к решению следующих систем:

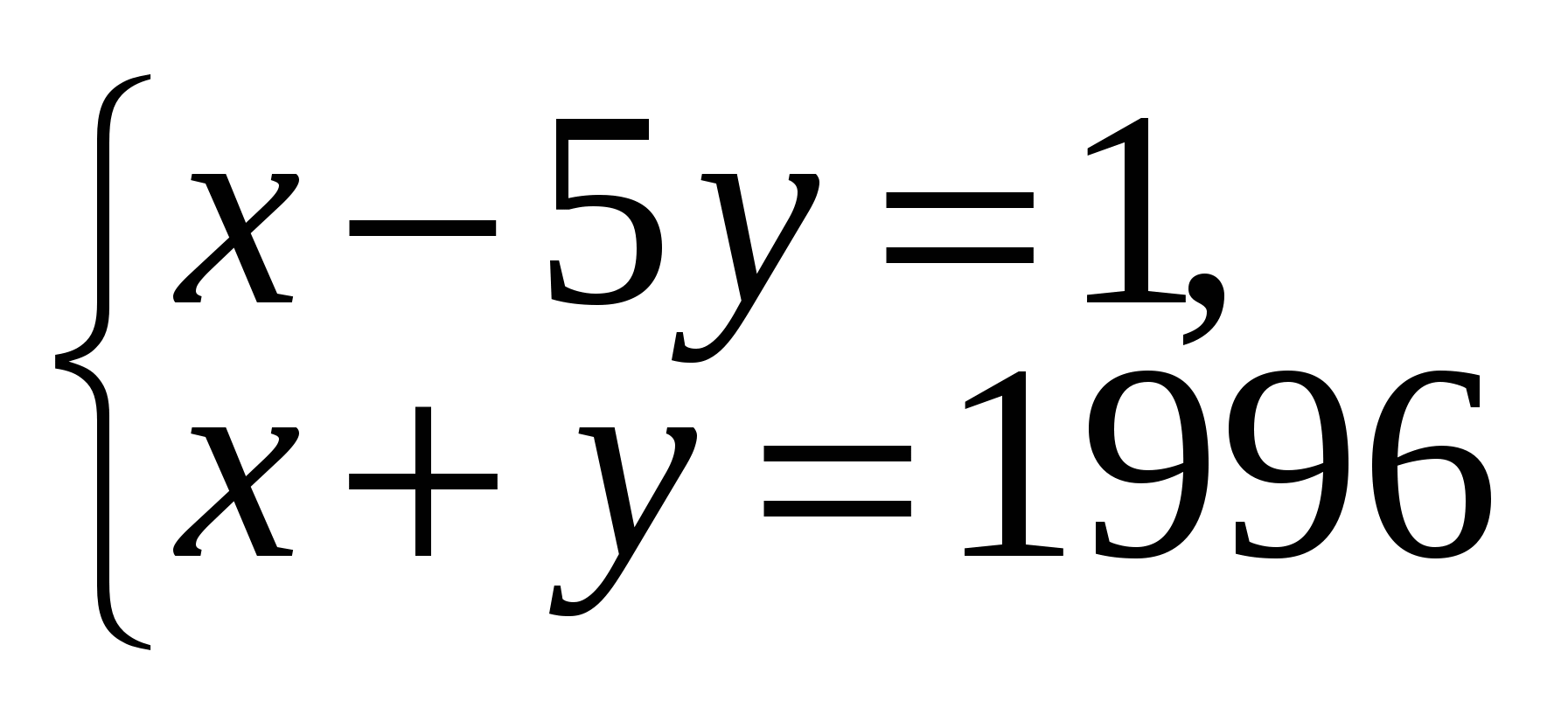
решений в натуральных числах нет

2) 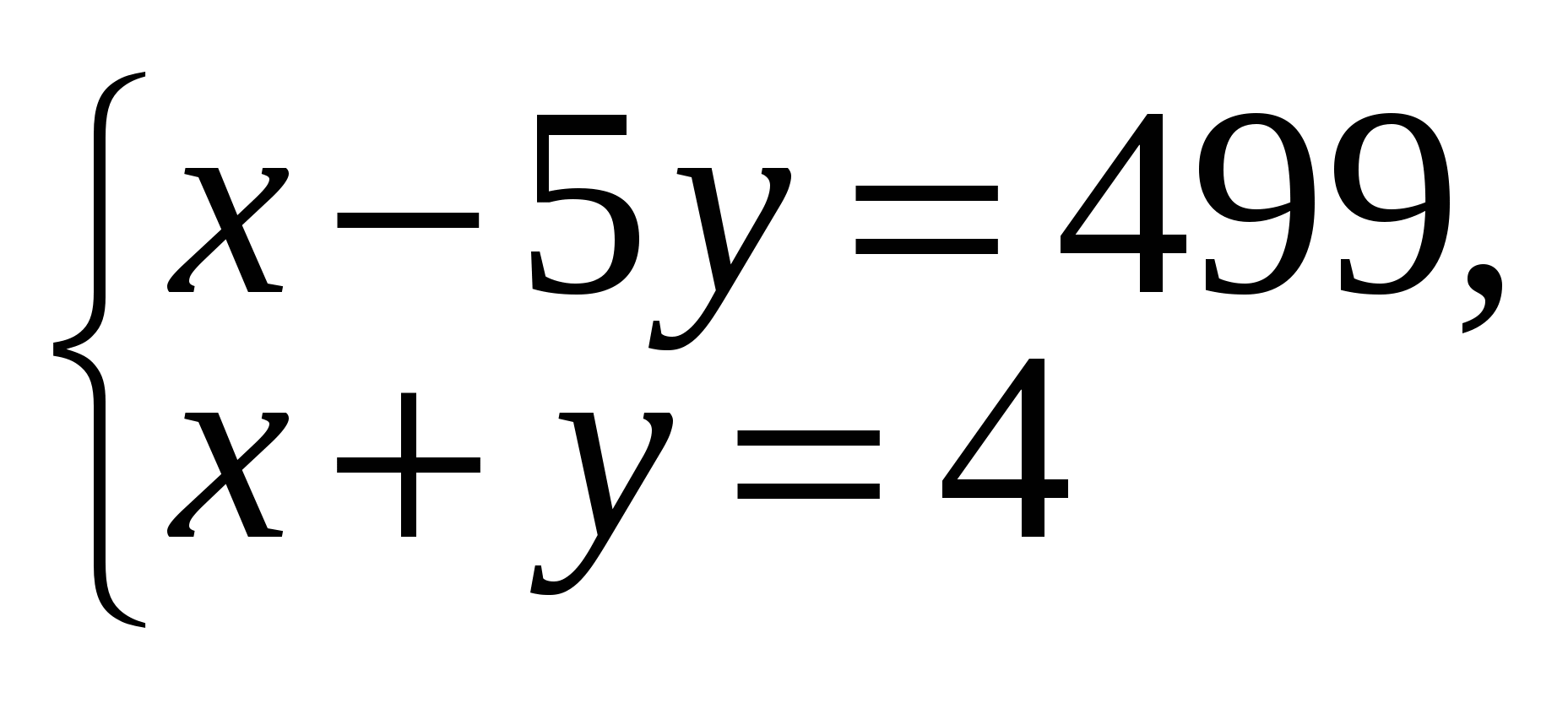или

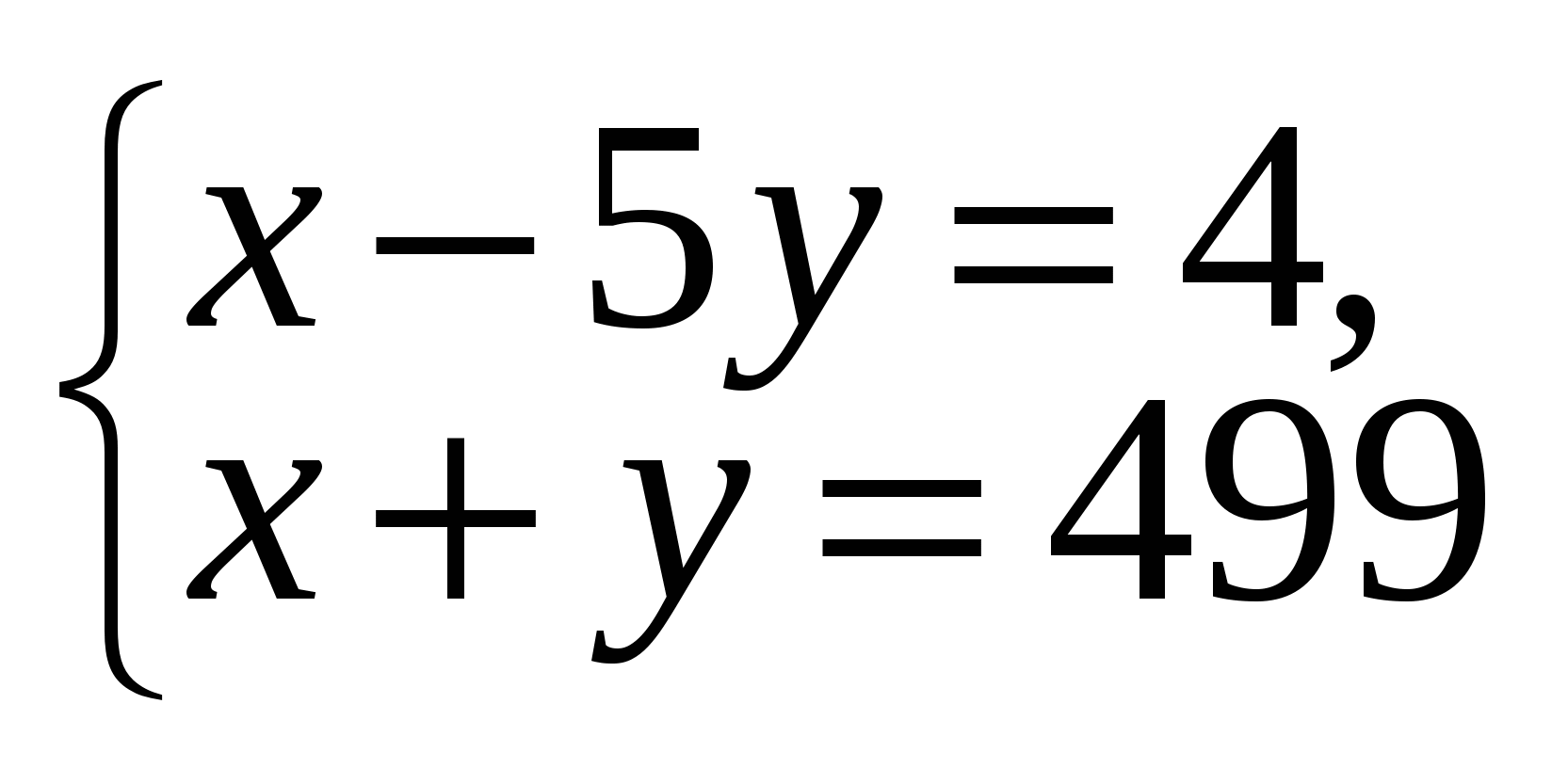
системы решений в натуральных числах не имеют

3) 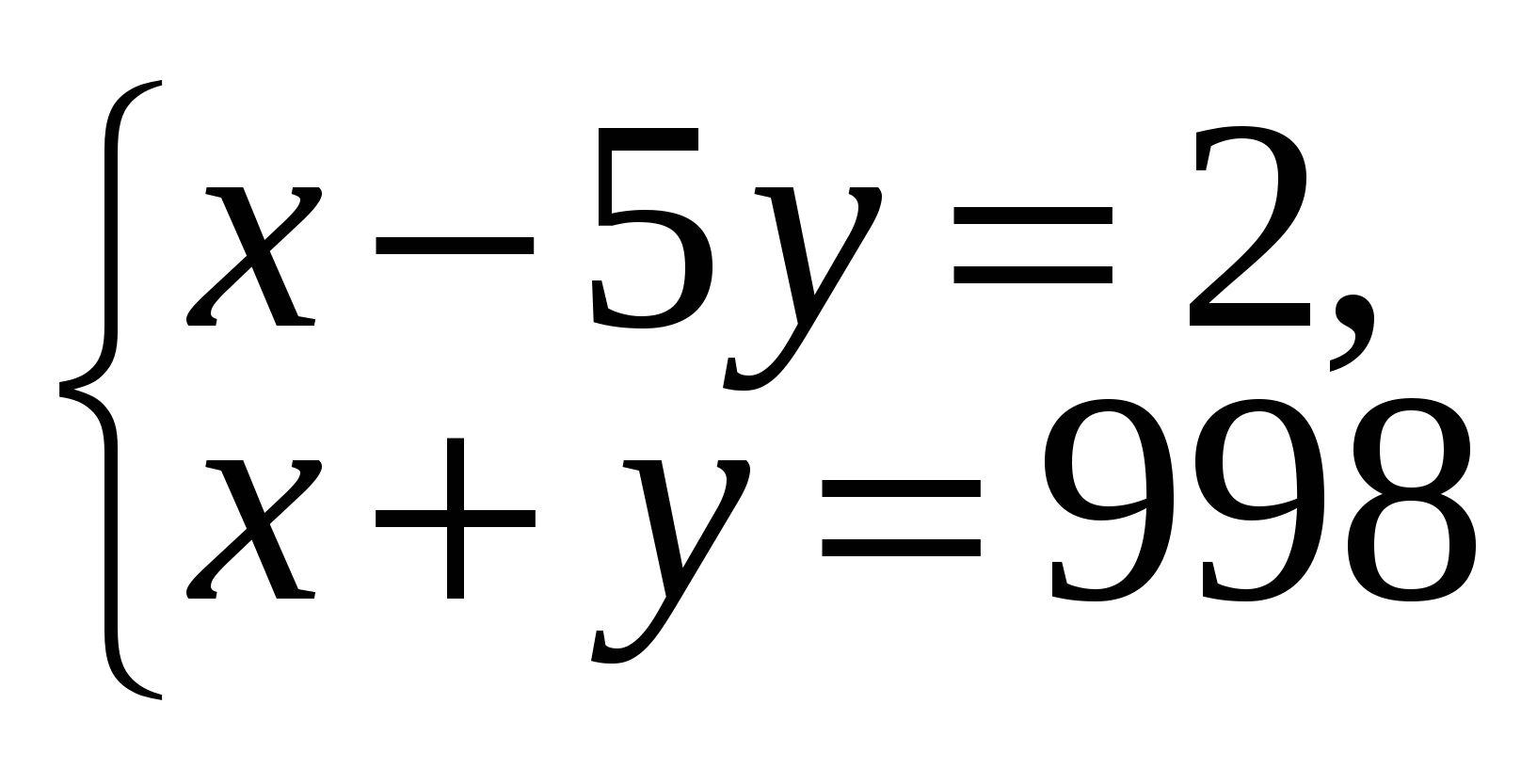или

(832; 166) решения в натуральных числах нет.

Ответ. x = 832, у = 166.

Задача № 25. Докажите, что система уравнений

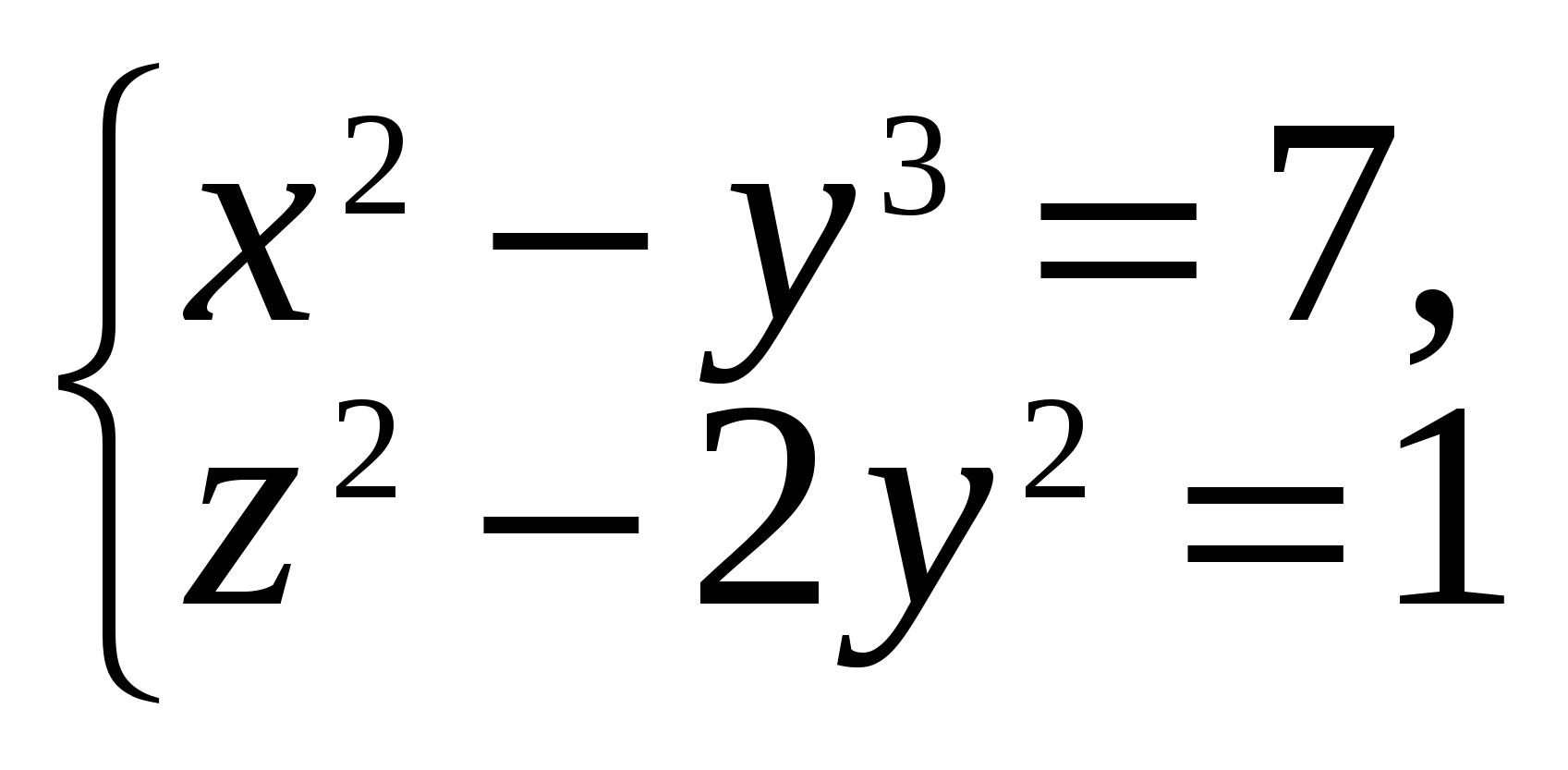
не имеет решений в целых числах.

Решение.

Предположим, что система разрешима. Из второго уравнения z²=2у²+ 1, то есть z²— нечетное число и z — нечетное, значит z = 2m + 1, m  Z.

Тогда y²= 2m²+ 2m, значит, y² — четное число и у — четное, y = 2n, n  Z.

Из первого уравнения: x²= 8n³+ 7, т. е. x² — нечетное число и x — нечетное число, х = 2k + 1, k  Z.

Подставим значения x и y в первое уравнение, получим

2(k² + k – 2n³) = 3, что невозможно, так как левая часть делится на 2, а правая нет.

Значит, наше предположение неверно, т. е. система не имеет решений в целых числах.

Задача № 26 (из «Арифметики» Диофанта)

Для числа 13 = 2² + 3² найти два других, сумма квадратов которых равна 13.

Решение.

Приведем решение самого Диофанта. Он полагает первое число (обозначим его через А) равным х + 2, а второе число B равным 2х – 3, указывая, что коэффициент перед x можно взять и другой.

Решая уравнение (x + 2)² + (2х – 3)² = 13, Диофант находит x = 1,6, откуда А = 3,6, В = 0,2.

Воспользуемся указанием Диофанта и возьмем произвольный коэффициент перед x в выражении для В. Пусть снова А = x + 2, а В = kx – 3, тогда из уравнения (x + 2)² + (kx – 3)² =13 получаем х = 2(3k – 2) : (k² + 1). Отсюда, A = 2(k²+ 3k – 1) : (k²+ 1), B = (3k²– 4k – 3) : (k²+ 1).

Теперь становятся понятными рассуждения Диофанта. Он вводит очень удобную подстановку A = х + 2, В = 2х – 3, которая с учетом условия 2²+ 3²= 13 позволяет понизить степень квадратного уравнения. Можно было бы с тем же успехом в качестве B взять (2х + 3) или еще проще (x ± 3), но тогда получаются отрицательные значения для B, чего Диофант не допускал. Очевидно k = 2 — наименьшее натуральное число, при котором A и B положительны. И хотя Диофант приводит решение задачи в конкретных числах, чувствуется, что он владеет общим методом.

Задача № 27 (из древнего китайского сборника)

Найти число, которое при делении на 3 дает остаток 2, при делении на 5 — остаток 3, а при делении на 7 — остаток 2.

Решение.

Рассмотрим решение этой задачи китайским математиком Сунь-цзы (III или IV век): «При делении на 3 остаток есть 2. Поэтому возьмем 140. При делении на 5 остаток есть 3, поэтому возьмем 63. При делении на 7 остаток есть 2, поэтому возьмем 30. Сложив их вместе, получим 233. Из этого вычтем 210 и получим ответ».

Разберем решение Сунь-цзы. Сначала он подбирает число 140, кратное 5 и 7, которое при делении на 3 дает остаток 2. Конечно, это не наименьшее натуральное число с такими свойствами: можно было бы взять число 35. Но это не столь важно для решения задачи. Затем берется число 63, кратное 3 и 7, дающее при делении на 5 остаток 3. Аналогично находится число 30. Очевидно, для числа 233 = 140 + 63 + 30 выполняются все условия задачи, а потому они выполняются для числа вида n = 1 05l + 233. В свою очередь 233 = 2 · 105 + 23, поэтому все натуральные решения можно записать формулой n = 105k + 23, где k = 0, 1, …

При k = 0 из нее получаем наименьшее натуральное решение, равное 23.

Задача № 28 (из «Арифметики» Диофанта)

Найти два числа, произведение которых, сложенное с каждым из данных чисел, составит куб некоторого числа.

Решение.

Рассмотрим решение самого Диофанта. Обозначим первое число в виде произведения x на куб некоторого числа, например на 2³ = 8, то есть первое число будет 8x. Положим второе число равным x² – 1. Ясно, что одно из условий задачи будет выполнено: произведение искомых чисел, сложенное с первым, равняется кубу некоторого числа. В самом деле, проверяя это, получим:

8х · (x² – 1) + 8х = 8x³.

Далее надо, чтобы выполнялось и другое условие, то есть, чтобы произведение искомых чисел, сложенное со вторым, равнялось также кубу некоторого числа. Для этого требуется, чтобы 8x^·(x² – 1) + x² – 1 было кубом некоторого числа. Полагая, что куб этого числа равняется (2х – 1)³, мы получим уравнение, из которого можно найти x:

8х · (x² – 1) + x² – 1 = (2x – 1)³,

откуда:

x = 14/13, следовательно, первое число будет: 8 · 14/13 = 112/13, а второе число будет равно: (14/13)²– 1= 196/169 – 1= 27/169. Проверьте, удовлетворяют ли найденные числа условию задачи.

Задача № 29. «После кораблекрушения»

Пять моряков высадились на остров и к вечеру собрали кучу кокосовых орехов. Дележ отложили на утро. Один из них, проснувшись ночью, пересчитал добычу, угостил одним орехом мартышку, а из остальных орехов взял себе точно 1/5 часть, после чего вновь лег спать и быстро уснул. За ночь так же поступили один за другим и остальные моряки; при этом каждый не знал о действиях своих предшественников. Наутро они поделили оставшиеся орехи поровну, но для мартышки в этот раз лишнего ореха не осталось. Сколько орехов собрали моряки?

Решение.

Обозначим искомое число орехов через х. Выражая последовательные действия моряков уравнениями, получаем x = 5а + 1; 4а = 5b + 1; 4b = 5c + 1;

4c = 5d + 1; 4d = 25y + 1 (обдумайте смысл предлагаемых уравнений).

Эта система сводится к одному неопределенному уравнению

256х = 2 101 + 15 625у.

Быстрое решение в целых числах этого громоздкого уравнения будет приятной наградой за терпеливое ознакомление с предложенными четырьмя способами — можно выбрать из них наиболее эффективный для данной задачи. Ответ в этой задаче таков: x = 3 121 — наименьшее из возможных натуральных значений х.

Замечание. В книге М. Гарднера «Математические головоломки и развлечения», в которой есть эта задача, написано, что она «принадлежит к числу наиболее часто решаемых, но наименее поддающихся решению, диофантовых головоломок». Когда эта задача в 1926 году появилась в одной газете (без решения и ответа), то 20 лет после этого не прекращался поток писем в газету либо с просьбой сообщить ответ, либо с вариантами собственных решений.

Заключение

Введение элективного курса «Десятая проблема Гильберта или уравнения Диофанта» необходимо учащимся как при подготовке к ГИА, ЕГЭ, так и к вступительным экзаменам в вузы. Владение различными приемами решения уравнений можно считать критерием знаний основных разделов школьной математики, уровня математического и логического мышления.

Решение задач и уравнений открывает перед учащимися значительное число эвристических приемов общего характера, ценных для математического развития личности, применяемых в исследованиях и на любом другом математическом материале. Именно такие задания играют большую роль в формировании логического мышления и математической культуры у школьников. Поэтому учащиеся, владеющие методами решения задач с помощью уравнений, успешно справляются и с другими задачами.

Приложение 1

Задачи

1. Найдите все пары натуральных чисел, которые являются решениями уравнения:

а) x + у = 11; б) 3х + 5у = 17.

2. Учащиеся 9 класса выполняли тест, содержащий задания по алгебре и геометрии. За каждый верный ответ на алгебраический вопрос выставлялось 3 балла, а на геометрический — 4 балла. Ученик верно ответил на все вопросы теста и получил 100 баллов. Сколько в тесте было заданий по алгебре и сколько по геометрии?

3. Ученики начальной школы на уроке математики выкладывают из палочек пятиугольники и шестиугольники. Всего в наборе 100 палочек. Сколько пятиугольников и сколько шестиугольников можно выложить, чтобы использованными оказались все палочки?

4. На неделю учащимся 9 класса было предложено для решения два списка задач: по алгебре и по геометрии. За каждую правильно решенную задачу по алгебре выставлялось 4 балла, а по геометрии — 5 баллов. Николай за выполненную им работу получил 80 баллов. Сколько задач по алгебре и сколько по геометрии решил Николай, если известно, что в каждом списке было 15 задач?

5.Из двух рублевых и пятирублевых монет составлена сумма в 23 р. Сколько среди этих монет двухрублевых?

6. Решить уравнение на множестве целых чисел:

а) 7х + 11у = 69; в) 5х + 29у = 39;

б) 3х + 17у = 143; г) 7х + 31у = 90.

7. Для газификации жилого дома требуется проложить газопровод длиной 150 м. Имеются трубы 13 м и 9 м длиной. Сколько требуется труб, чтобы не приходилось их разрезать при прокладке газопровода?

8. Туристическое бюро организует поездки на автомашинах двух типов: 23-местных автобусах и 6-местных автомобилях. Группа туристов состоит из 310 человек. Сколько машин того и другого типа следует выделить, чтобы не осталось свободных мест в салоне?

9. Транспортные организации имеют в наличие машины вместимостью 3,5 т и 4,5 т. Следует перевезти груз весом 53 т. Сколько машин нужно взять для одного рейса?

10. На 6 200 р. Школой было закуплено некоторое количество шахмат и шашек, стоимостью соответственно 460 и 190 р. Сколько комплектов шахмат и шашек можно купить, чтобы рационально использовать эти деньги?

11. Школа получила 1 млн руб. на приобретение 100 единиц учебного оборудования (на всю сумму без остатка). Администрации школы предложили, оборудование стоимостью 3 000, 8 000 и 12 000 р. За единицу. Сколькими способами школа может закупить это оборудование? Укажите один из способов.

12. Представьте дробь в виде цепной дроби:

а) 7/11; б) 3/8; в) 9/5; г) 17/3.

13. Несколько лет назад были входу монеты по 3 и 5 к. Сколькими способами можно набрать ими сумму в 10 р.?

14. Надо разлить 15 л жидкости в бутыли емкостью в 0,5 и 0,8 л так, чтобы все использованные бутыли были полными. Сколько потребуется бутылей той и другой емкости?

15. Сколько можно купить на 100 монет петухов, кур и цыплят, если всего надо купить 100 птиц, причем петух стоит 5 монет, курица — 4, а 4 цыпленка — одну монету?

16. Крестьянка несла на базар корзину яиц. Неосторожный всадник, обгоняя женщину, задел корзину, и все яйца разбились. Желая возместить ущерб, он спросил у крестьянки, сколько яиц было в корзине. Она ответила, что число яиц не знает, но когда она раскладывала их по 2, по 3, по 4, по 5 и по6, то каждый раз одно яйцо оставалось лишним, а когда она разложила по 7, лишних яиц не осталось. Сколько яиц несла крестьянка на базар?

17. «Продажа кур» (старинная задача).

Три сестры пошли на рынок с курами. Одна принесла для продажи 10 кур, другая — 16, третья — 26. До полудня они продали часть своих кур по одной и той же цене. После полудня, опасаясь, что не все куры будут проданы, они понизили цену и распродали оставшихся кур снова по одинаковой цене. Домой все трое вернулись с одинаковой выручкой: каждая сестра получила от продажи 35 р. По какой цене они продавали кур до и после полудня?

18. Решить способом измельчения в целых числах уравнение:

19. а) 5х + 8у = 39; б) 7х + 11у = 43.

20. Решить в целых числах 29х + 13у + 56z = 17.

21. Шехерезада рассказывает свои сказки великому правителю. Всего она должна рассказать 1 001 сказку. Сколько ночей потребуется Шехерезаде, чтобы рассказать все свои, если x ночей она будет рассказывать по

3 сказки, а остальные сказки по 5 за у ночей?

22. Найти целые решения уравнения 10х + 21у = 23 каждым из изученных способов.

23. Найти двузначное число, у которого увосьмеренное число единиц на 13 меньше утроенного числа десятков.

24. Некоторое число экскурсантов, разместившихся поровну в 5 автобусах (каждый автобус вмещает не более 54 человек), были доставлены на вокзал. Там к ним присоединились еще 7 человек, и все экскурсанты распределились поровну в 14 вагонах. Сколько всего было экскурсантов?

25. Решите в натуральных числах x² – 4ху – 5y² = 1 996.

Литература

Бабинская, И. Л. Задачи математических олимпиад [Текст] / И. Л. Бабинская. — М. : Просвещение, 1975.
Башмакова, И. Г. Диофант и диофантовы уравнения [Текст] / И. Г. Башмакова. — М. : Наука, 1972.
Белл, Э. Т. Творцы математики: Предшественники современной математики [Текст] : пособие для учителей / Э. Т. Белл ; пер. с англ. В. Н. Тростникова, С. Н. Киро, Н. С. Киро / под ред. и с доп. С. Н. Киро. — М. : Просвещение, 1979.
Варпаховский, Ф. П. О решении десятой проблемы Гильберта [Текст] / Ф. П. Варпаховский, А. Н. Колмогоров // Квант. — 1970. — № 7.
Груденов, Я. И. Совершенствование методики работы учителя математики [Текст] / Я. И. Груденов. — М. : Просвещение, 1990.
Дорофеев, Г. В. Математика. Алгебра. Функции. Анализ данных. 8 класс [Текст] : учеб. для общеобразоват. учеб. заведений / Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович [и др.] ; под ред. Г. В. Дорофеева. — М. : Дрофа, 2001.
Кордемский, Б. А. Этому виду задач более 1 600 лет [Текст] / Б. А. Кордемский // Квант. — 1973. — № 4. — С. 38—41.
Крафт, Х. Алгебраические кривые и диофантовы уравнения [Текст] / Х. Крафт // Живые числа : сб. ст. ; пер. с нем. — М. : Мир, 1986.
Перельман, Я. И. Занимательная алгебра [Текст] / Я. И. Перельман. — М. : Наука, 1976.
Фоминых, Ю. Ф. Диофантовы уравнения [Текст] / Ю. Ф. Фоминых // Математика в школе. — 1996. — № 6.
Чередов, М. М. Формы учебной работы в средней школе / М. М. Чередов. — М. : Просвещение, 1988.