Муниципальное образовательное учреждение
средняя общеобразовательная школа № 33
с углубленным изучением отдельных предметов
Дзержинского района города Волгограда
Программа элективного курса по алгебре для 9 классаРешение текстовых задач
составила
учитель математики
Кулик Татьяна Анатольевна
г. Волгоград
2012
Пояснительная записка
Данный элективный курс рассчитан в первую очередь на учащихся, желающих расширить и углубить свои знания по математике, сделать правильный выбор профиля обучения в старших классах и качественно подготовиться к ЕГЭ. Он поможет школьникам систематизировать полученные на уроках знания по решению текстовых задач и открыть для себя новые методы их решения, которые не рассматриваются в рамках школьной программы.
Полный минимум знаний, необходимых для решения всех типов текстовых задач, формируется в течение первых девяти лет обучения в школе, поэтому представленный элективный курс «Решение текстовых задач» рекомендуется вводить с 9-го класса.
Представленный элективный курс содержит 5 тем: «Задачи на движение», «Задачи на смеси, сплавы, растворы», «Задачи на работу», «Задачи на дроби и проценты», «Задачи на прогрессии» – закрепляют и дополняют знания учащихся, полученные на уроках. При раскрытии тем курса акцент должен быть сделан на выделение основных этапов решения текстовых задач и их назначение. Следует также обратить внимание учащихся на важность письменного оформления.
Провести занятия можно в форме обзорных лекций с разбором ключевых задач или в форме семинаров, нацелив учащихся на предварительную подготовку и самостоятельный поиск материалов с их последующим обсуждением.
Цели и задачи курса:
определить уровень способностей учащихся и уровень их готовности к профильному обучению в школе и вузе;
систематизировать ранее полученные знания по решению текстовых задач;
познакомить учащихся с разными типами задач, особенностями методики и различными способами их решения.
Ожидаемые результаты
После изучения курса учащиеся должны:
уметь определять тип текстовой задачи, знать особенности методики ее решения, использовать при решении различные способы;
уметь применять полученные математические знания при решении задач;
уметь использовать дополнительную математическую литературу.
Содержание курса.
Задачи на движение (2 ч)
Движение: план или реальность. Совместное движение. Задачи на закон сложения скоростей. Движение тел по течению и против течения. Равномерное и равноускоренное движение тел по прямой линии в одном направлении и навстречу друг другу. Составление таблицы данных задачи и ее значение для составления математической модели.
Задачи на работу (1 ч)
Совместная работа. Формула зависимости объема выполненной работы от производительности и времени ее выполнения. Особенности выбора переменных и методика решения задач на работу. Составление таблицы данных задачи и ее значение для составления математической модели.
Задачи на дроби и проценты(1 ч)
Три задачи на проценты. Задачи на банковские расчеты. Определение начальных вкладов. Составление таблицы данных задачи и ее значение для составления математической модели.
Задачи на сплавы, смеси, растворы (1 ч)
Формула зависимости массы или объема вещества от концентрации и массы или объема. Особенности выбора переменных и методика решения задач на сплавы, смеси, растворы. Составление таблицы данных задачи и ее значение для составления математической модели.
Задачи на прогрессии (2 ч)
Формула общего члена и суммы первых n членов арифметической и геометрической прогрессий. Особенности выбора переменных и методика решения задач на прогрессии.
Учебно – тематический план
№ п/п
Наименование тем курса
Количество часов
Формы контроля
всего
лекции
практикум
1
Задачи на движение
2
1
1
Проверка самостоятельно решенных задач
2
Задачи на работу
1
0,5
0,5
Проверка самостоятельно решенных задач
3
Задачи на проценты
1
0,5
0,5
Проверка самостоятельно решенных задач
4
Задачи на сплавы, смеси, растворы
1
0,5
0,5
Выполнение практических заданий
5
Задачи на прогрессии
2
1
1
Выполнение практических заданий
Приложения.
Содержание занятий курса.
Занятие 1.
На первом занятии учащимся сообщается цель и назначение элективного курса, рассматриваются способы решения текстовых задач, устанавливаются зависимости между величинами, выделяются этапы решения текстовой задачи.
1 тип задач на движение.
При решении таких задач полезно сразу переводить все данные в одни и те же единицы измерения.
Пример 1. На путь между двумя деревнями пешеход затратил на 4 ч 30 мин больше, чем мотоциклист. Скорость мотоциклиста 40 км/ч, скорость пешехода составляет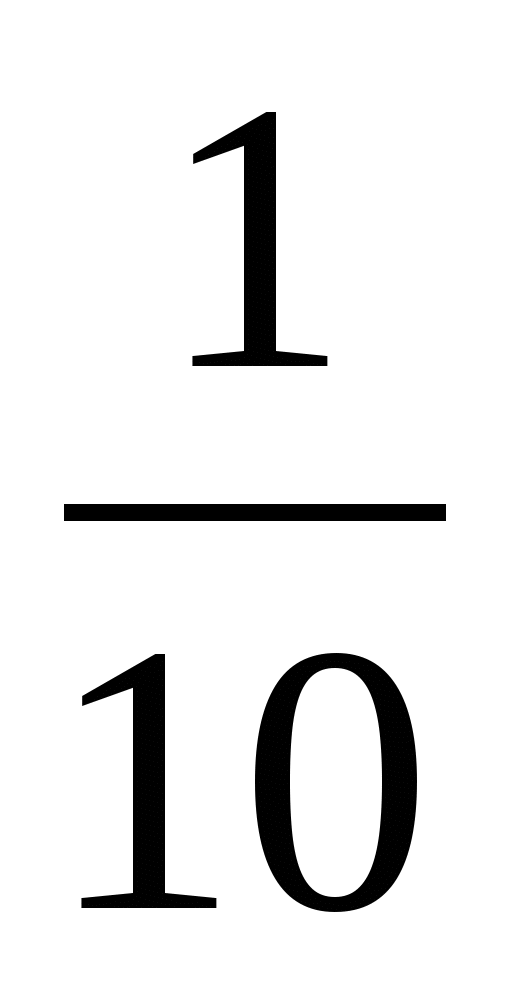 
скорости мотоциклиста. Найдите расстояние между деревнями.
Решение. Во-первых, найдем скорость пешехода. Она равна 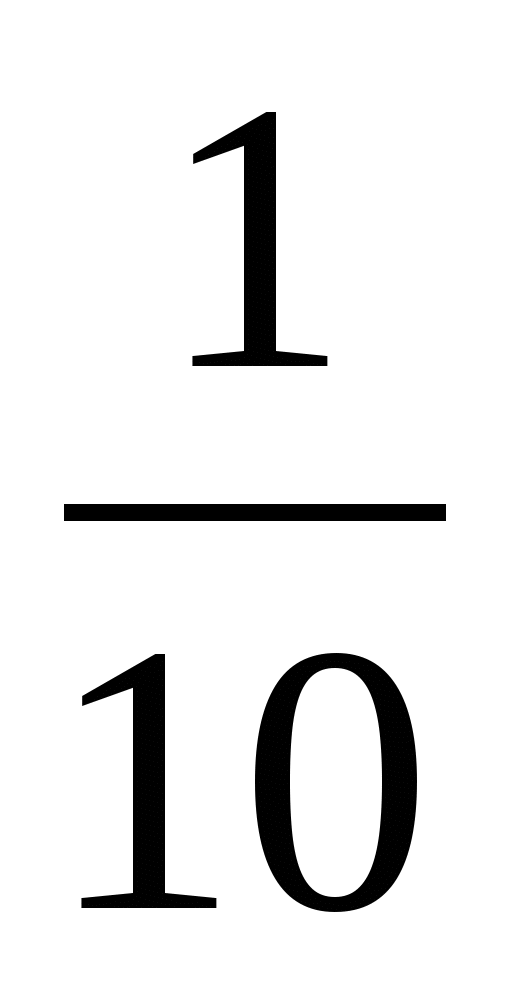· 40=4 км/ч.
Пусть мотоциклист может проехать расстояние между деревнями за х ч, тогда пешеход может пройти это расстояние за (х+4,5)ч. Таким образом, пешеход пройдет 4(х+4,5) км, мотоциклист проедет 40х км.
Так как по условию задачи эти величины равны, поучим уравнение
4(х+4,5) = 40х,
откуда х=0,5.
Следовательно, расстояние между деревнями равно 0,5·40=20(км).
Ответ: 20 км.
2 тип задач на движение.
В следующих задачах запланированные параметры движения (расстояние, скорость, время) сопоставляются с реальными.
Для решения подобных задач необходимо выразить через переменную расстояние, время и скорость на каждом из запланированных и реальных участков пути с момента отклонения от плана. После этого нужно найти в условии задачи еще не использованный факт и с его помощью составить уравнение.
Пример 2. Велосипедист должен был проехать весь путь с определенной скоростью за 2ч. Но он ехал со скоростью, превышающей намеченную на 3 км/ч, и поэтому на весь путь затратил 1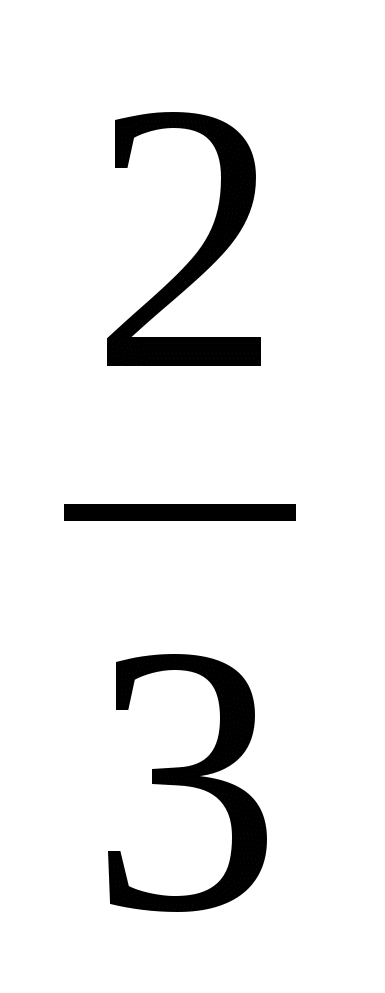
ч. Найдите длину пути.
Решение. При решении этой задачи полезно рассматривать как бы два участка пути – запланированный и реальный. Они, естественно, равны по длине, но отличаются временем и скоростью их прохождения.
По - плану: затраченное время 2ч, скорость обозначим х км/ч, расстояние равно 2х км/ч.
В реальности: скорость (х+3) км/ч, время 1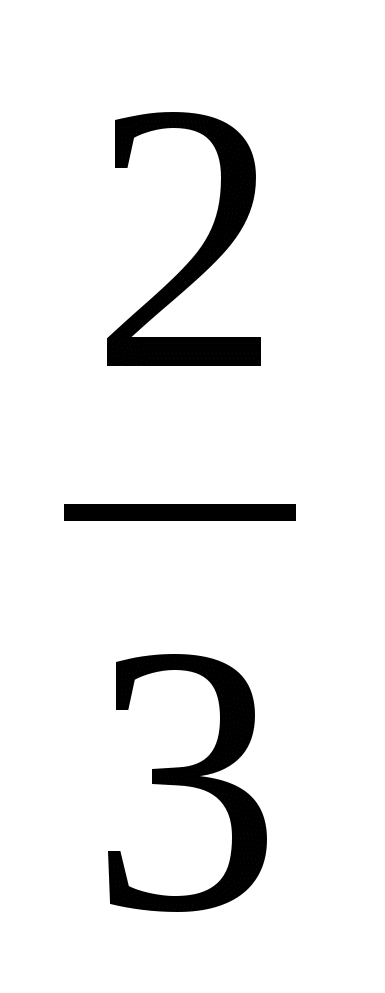ч, значит расстояние равно 1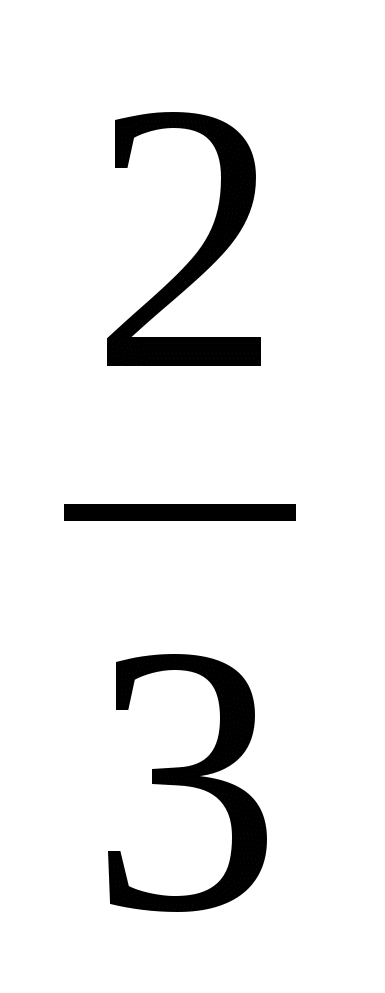(х+3) км.
Поскольку в реальности пройдено именно то расстояние, которое было запланировано, получаем уравнение 2х = 1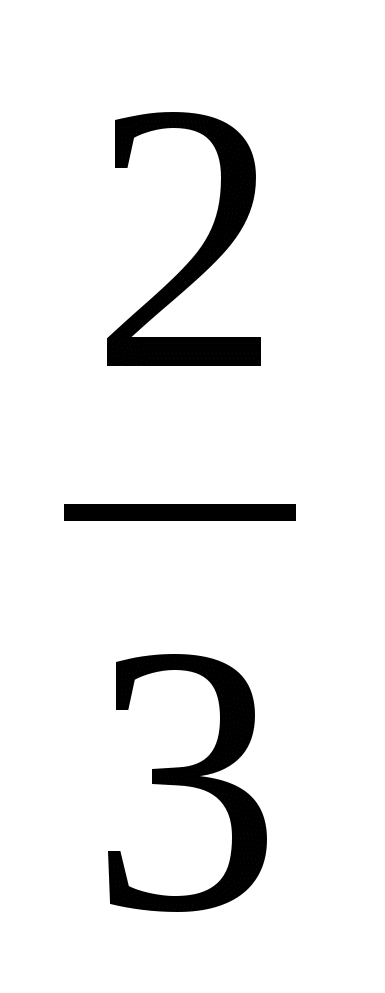(х+3),
откуда х=15.
Итак, велосипедист должен был за 2 ч со скоростью 15 км/ч проехать расстояние 2·15=30(км).
Ответ: 30 км.Пример 3. Автобус прошел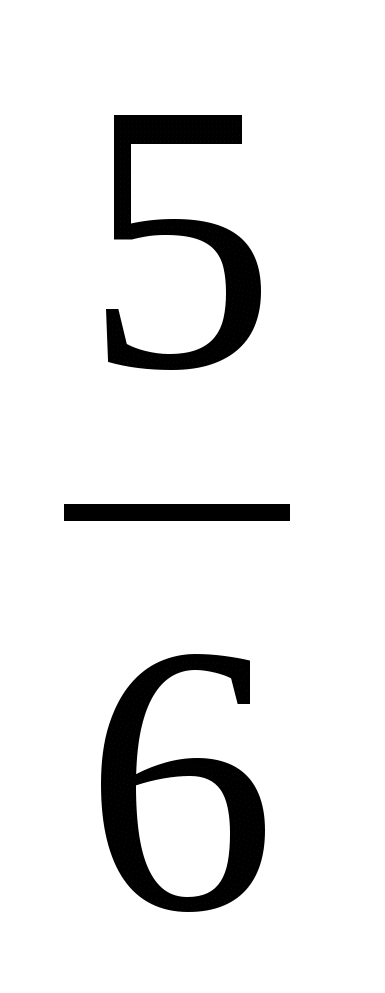 
пути со скоростью 50 км/ч, а затем задержался на 3 мин. Чтобы прибыть в конечный путь вовремя, оставшуюся часть пути он шел со скоростью 60 км/ч. Найдите путь, пройденный автобусом.
Решение. Отклонение от плана началось с момента остановки. Обозначим за х ч – время, за которое автобус должен был пройти оставшуюся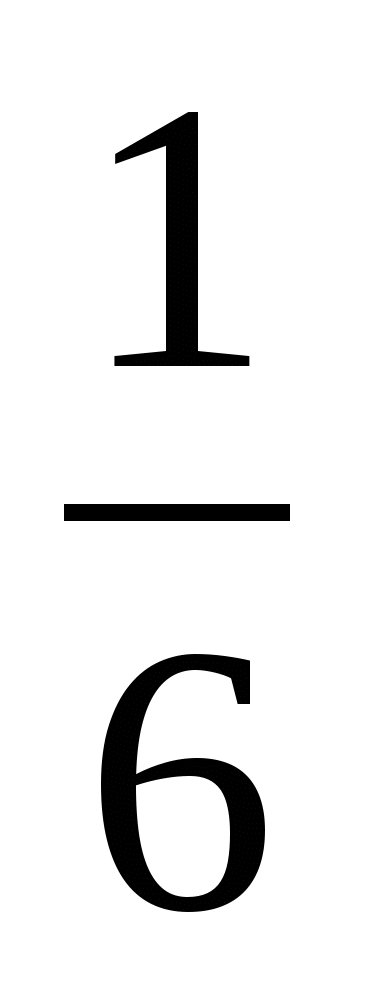 
часть пути. Тогда запланированное расстояние равно 50х км.
В реальности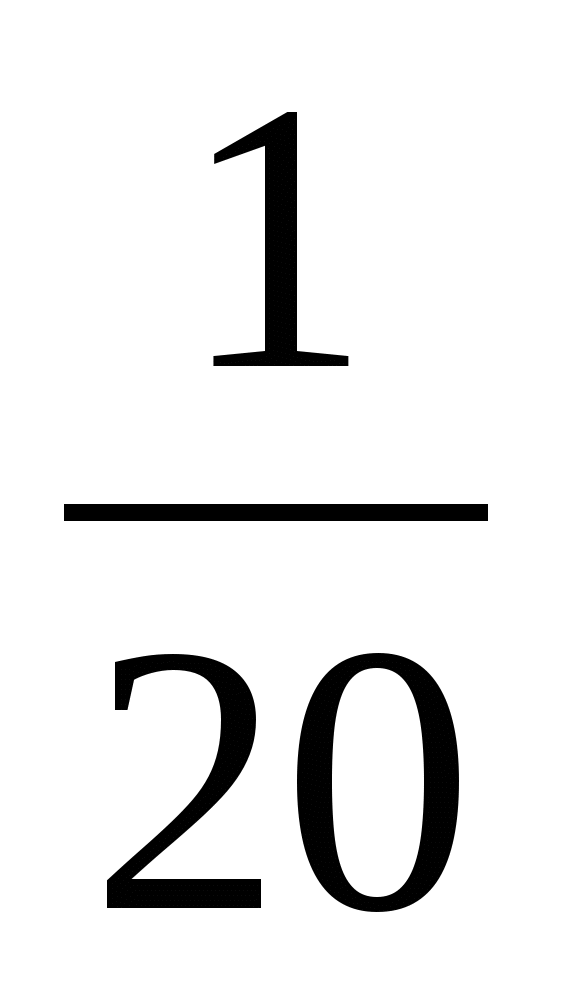 
ч автобус стоял, а оставшуюся часть пути прошел за (х -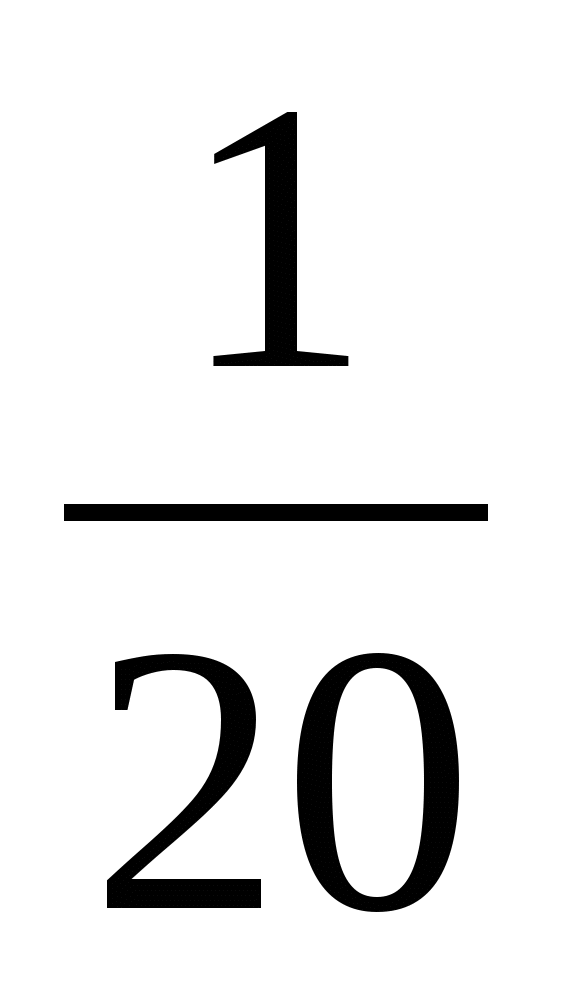) ч, то есть, реально пройденный путь равен 60(х -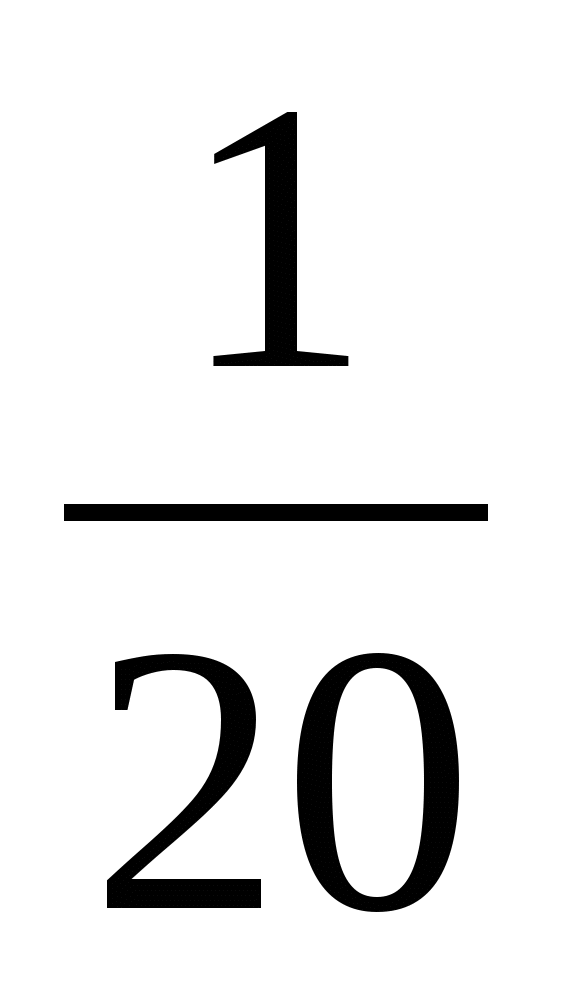) км. По условию задачи запланированное расстояние совпадает с реально пройденным, следовательно, получаем уравнение 60(х -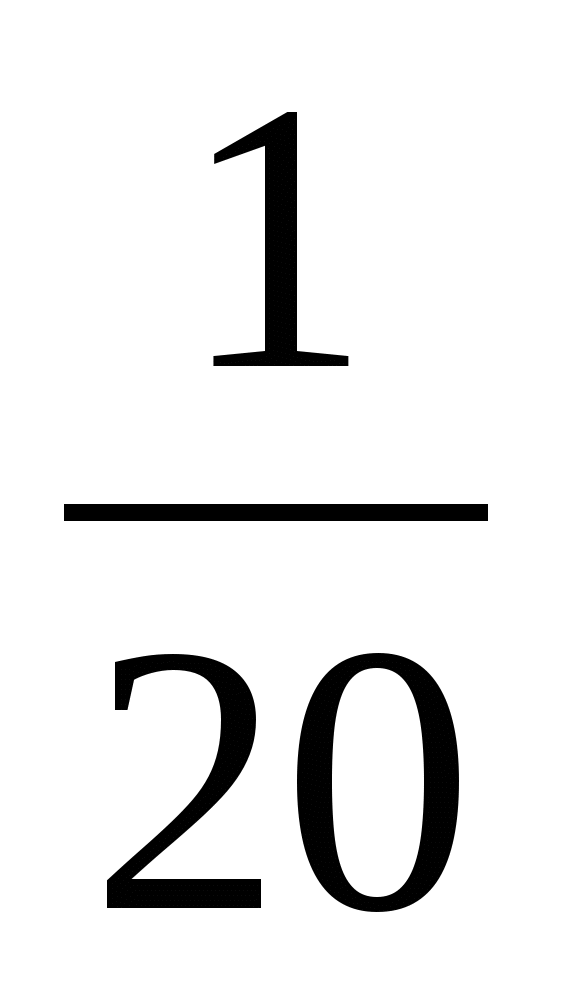) = 50х,
откуда х=0,3.
Таким образом, 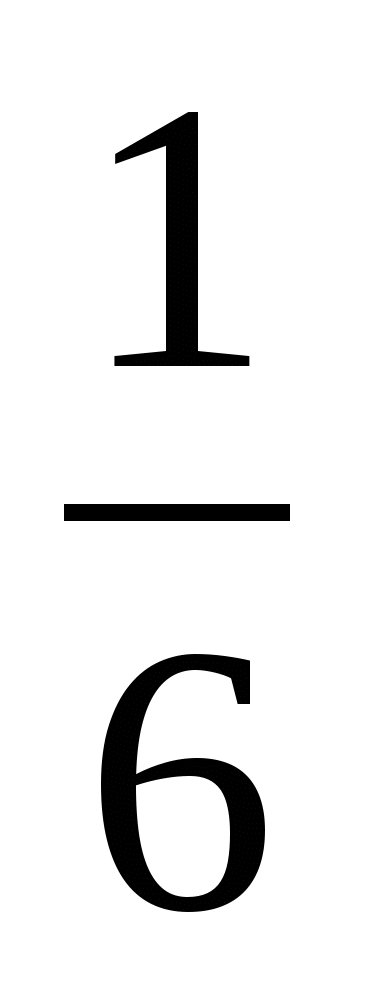часть пути равна 50·0,3=15(км), а весь путь равен 15·6=90(км).
Ответ: 90 км.
Дидактический материал для учащихся.
Почтальон проехал на мотоцикле от почты до села со скоростью 30 км/ч. Назад он возвращался пешком со скоростью, составляющей
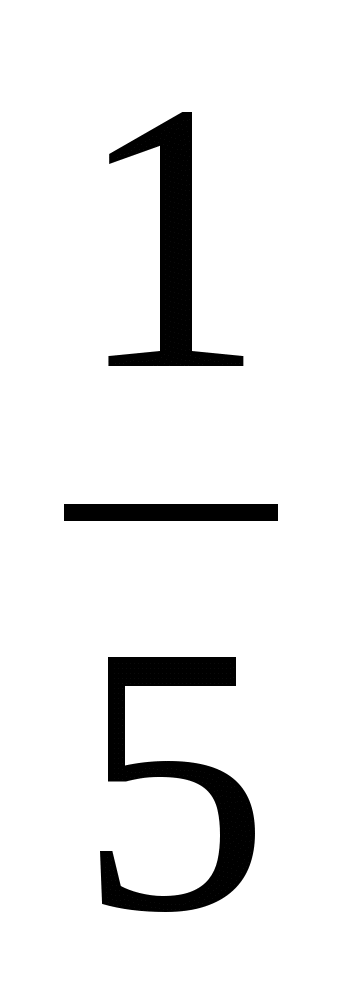
скорости его движения на мотоцикле. Поэтому на обратный путь он затратил на 1 ч 12 мин больше, чем от почты до села. Найдите расстояние от почты до села.Расстояние между деревней и поселком мотоциклист проезжает на 0,4 ч быстрее велосипедиста. Скорость мотоциклиста 18 км/ч, а скорость велосипедиста составляет
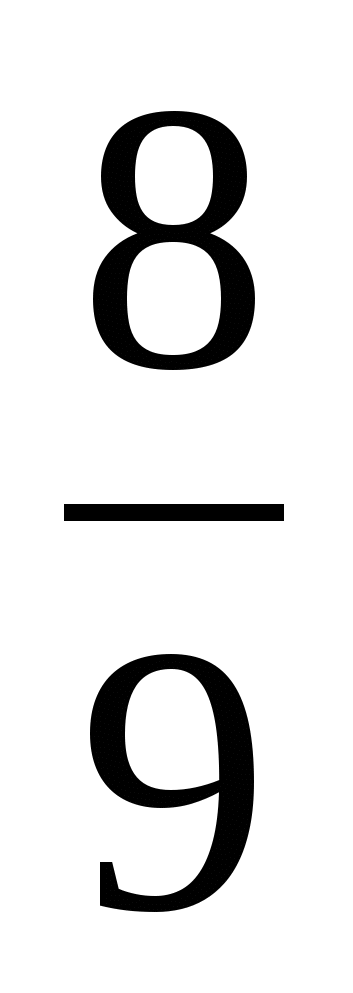скорости мотоциклиста. Найдите расстояние между деревней и поселком.Велосипедист каждую минуту проезжает на 800 м меньше, чем мотоциклист, поэтому на путь в 30 км он затратил времени на 2 ч больше, чем мотоциклист. Сколько километров в час проезжал мотоциклист?
Путь от А до В пешеход проходит за 2 ч. Если он увеличит скорость на 2 км/ч, то уже за 1,8 ч он пройдет на 3 км больше. Чем расстояние от А до В. Найдите расстояние от А до В.
Расстояние между двумя пунктами поезд проходит по расписанию с намеченной скоростью за 6 ч. Через 5 ч после отправления он был задержан в пути на 12 мин. Поэтому, чтобы прибыть на станцию назначения вовремя, поезд увеличил скорость на 15 км/ч. Найдите первоначальную скорость поезда.
Расстояние между двумя пунктами автомобиль должен был проехать за 4 ч. Первые 2 ч он ехал с намеченной скоростью, а затем снизил ее на 10 км/ч, поэтому в конечный пункт приехал на 20 мин позже, чем предполагал. Найдите первоначальную скорость автомобиля.
Расстояние между двумя пунктами автомобиль должен был пройти за 3 ч. Первые 2 ч он ехал с намеченной скоростью, а затем увеличил ее на 10 км/ч, поэтому в конечный пункт приехал на 12 мин раньше. Чем предполагал. Найдите расстояние между этими пунктами.
Занятие 2.
3 тип задач на движение. Совместное движение.
Рассмотрим задачи, описывающие движение двух участников. В задачах на совместное движение участники не всегда одновременно начинают движение и не всегда одновременно его заканчивают. Поэтому очень важно выделить участок или участки пути, на которых движение происходит действительно совместно. Кроме этого, в задачах имеются, как правило, такие участки пути, на которых передвигается один участник, в то время как другой еще не начал или уже закончил движение.
В некоторых задачах полезно найти скорость сближения (или удаления) участников – величину, показывающую, на сколько уменьшается (или увеличивается) расстояние между участниками в единицу времени.
Замечания.
Скорость сближения или удаления равна сумме скоростей участников при их движении в противоположных направлениях (навстречу друг другу или друг от друга).
При движении участников в одном направлении (один убегает, другой его догоняет) скорость сближения или удаления равна модулю разности их скоростей.
Пример 4. Из Смоленска в Москву вышел поезд со скоростью 70 км/ч. Спустя 1ч 40 мин из Москвы в Смоленск отправился поезд, скорость которого равна 60 км/ч. Через сколько часов после выхода поезда из Смоленска произойдет встреча, если расстояние между городами равно 420 км?
Решение. Совместное движение началось в момент выхода из Москвы первого поезда. К этому времени второй поезд прошел 70·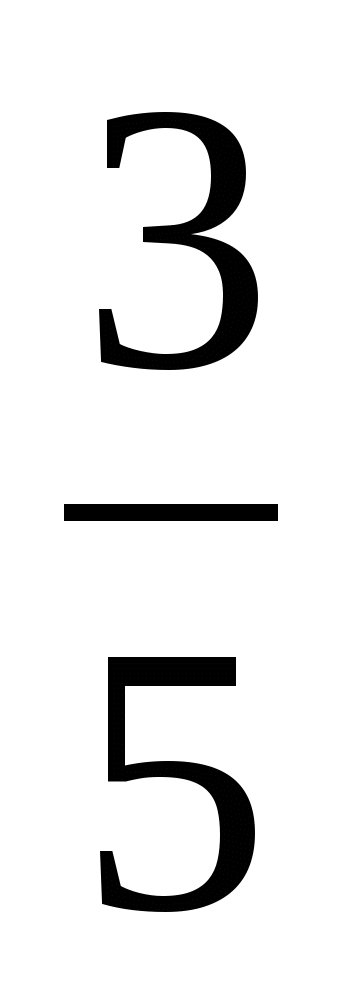
=
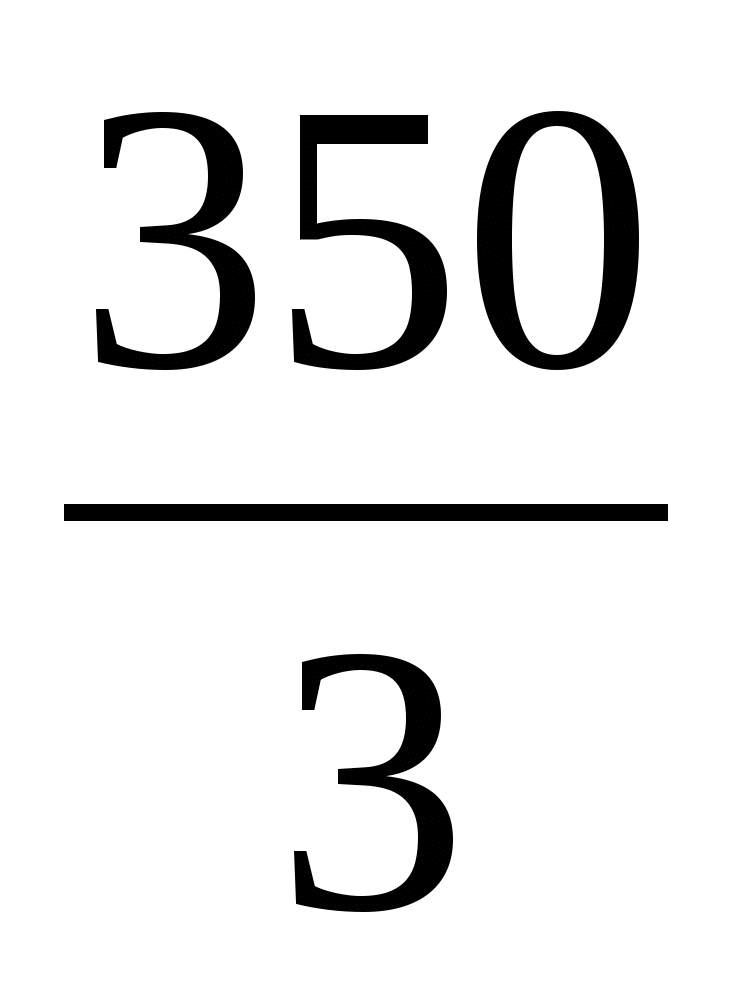=116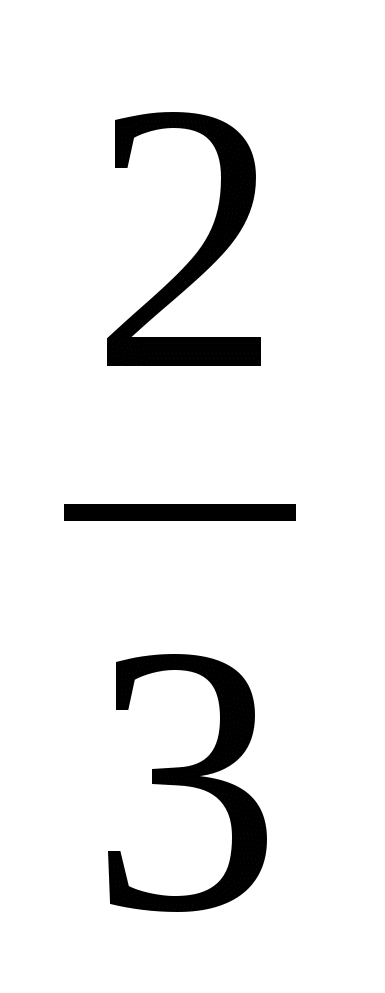(км) и расстояние между поездами сократилось до 420 - 116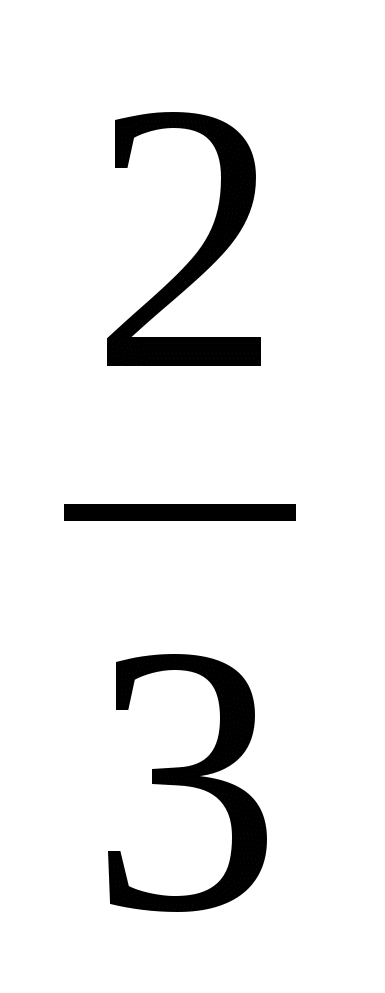=303
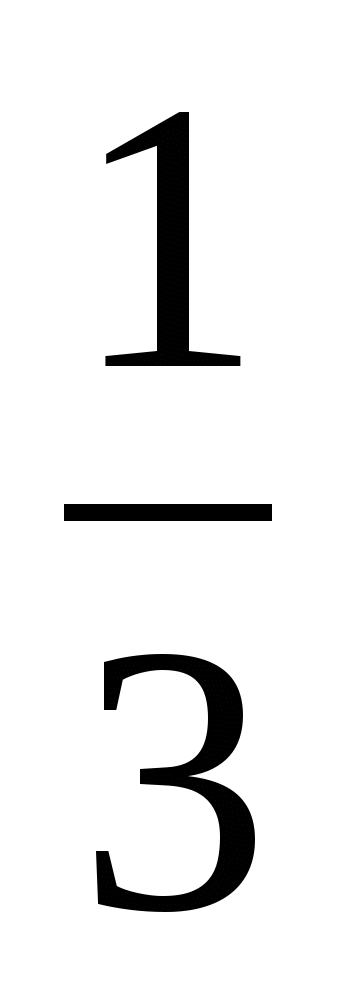(км)
Закончилось совместное движение их встречей. Итак, на расстоянии
303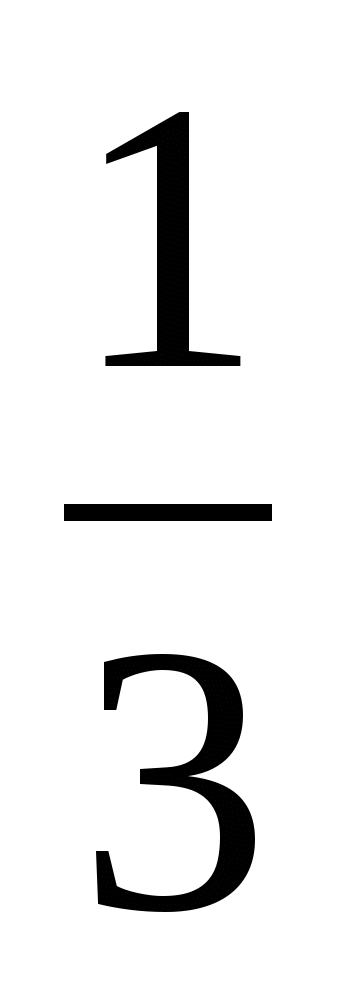км поезда сближались со скоростью 70+60=130(км/ч) и потратили на это 303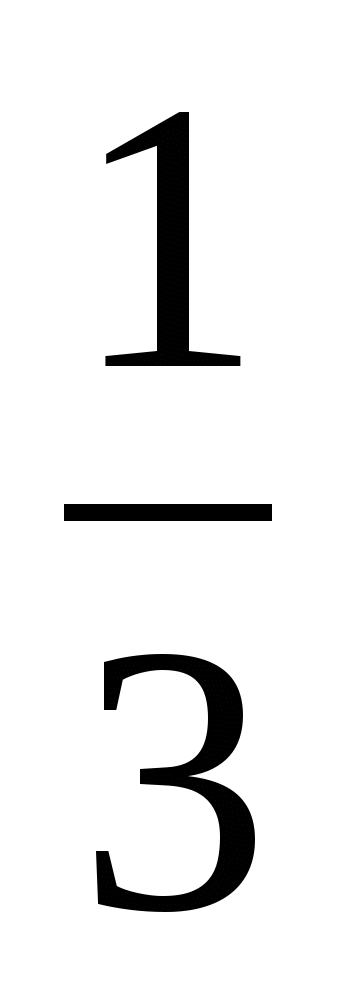:130=2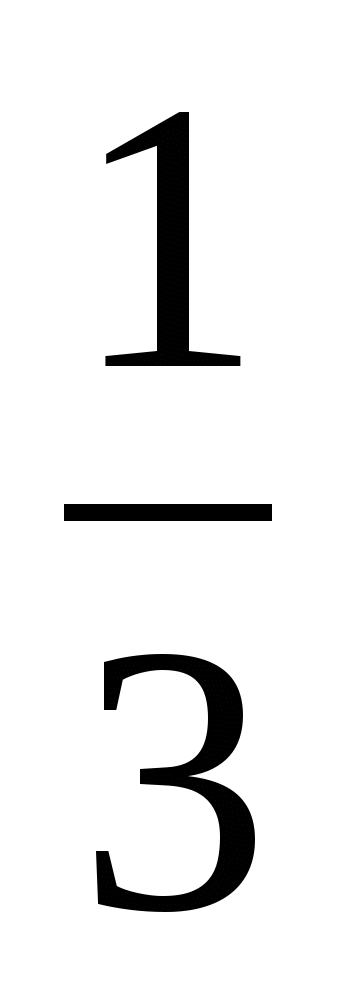(ч).
Тогда поезд до Смоленска шел до встречи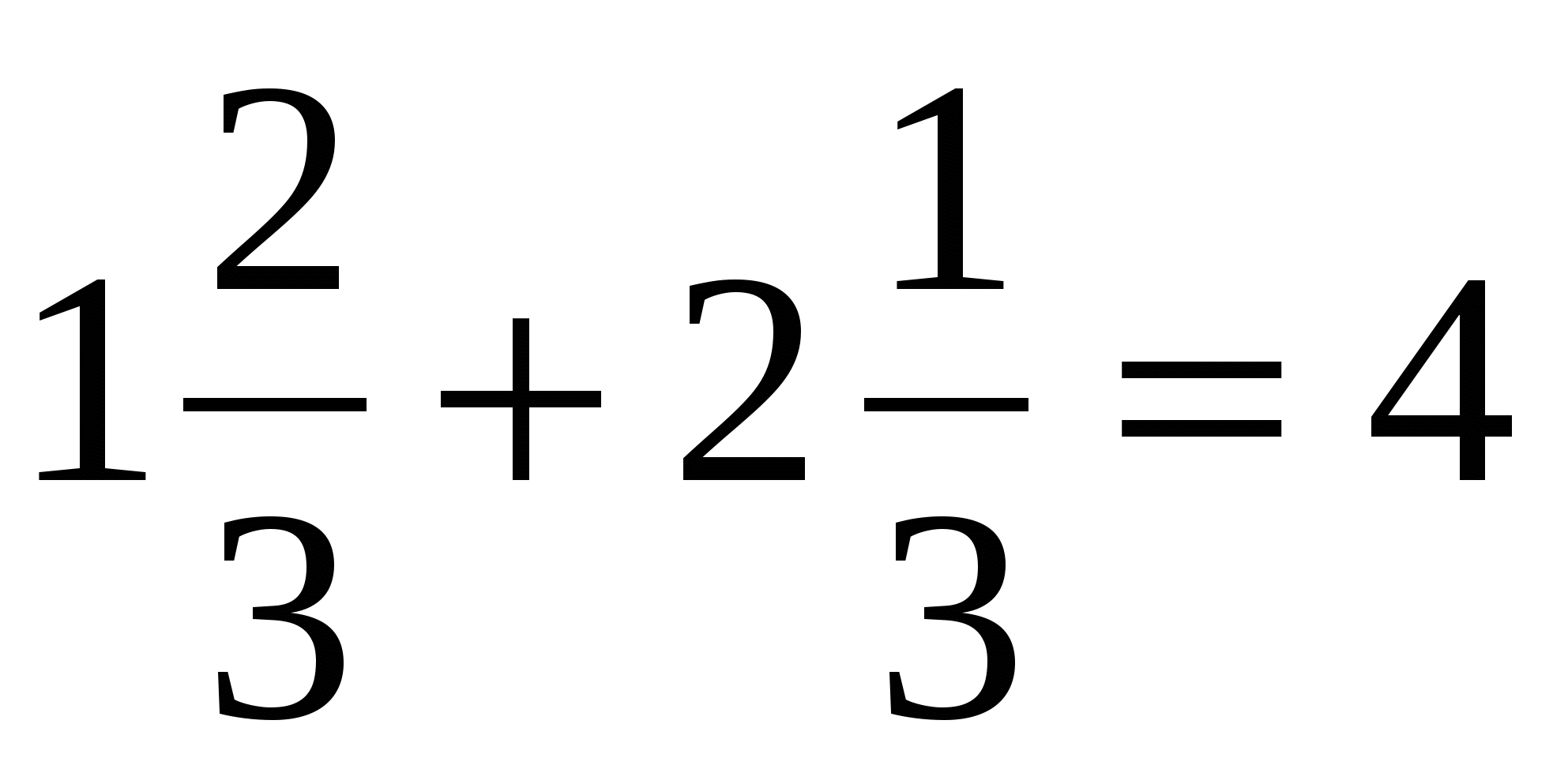 
(ч).
Ответ: 4 ч.
Пример 5. Из пункта А в пункт В выехал автобус со скоростью 40 км/ч. После того как автобус проехал 30 км, из пункта А со скоростью 60 км/ч выехал автомобиль, который прибыл в пункт В на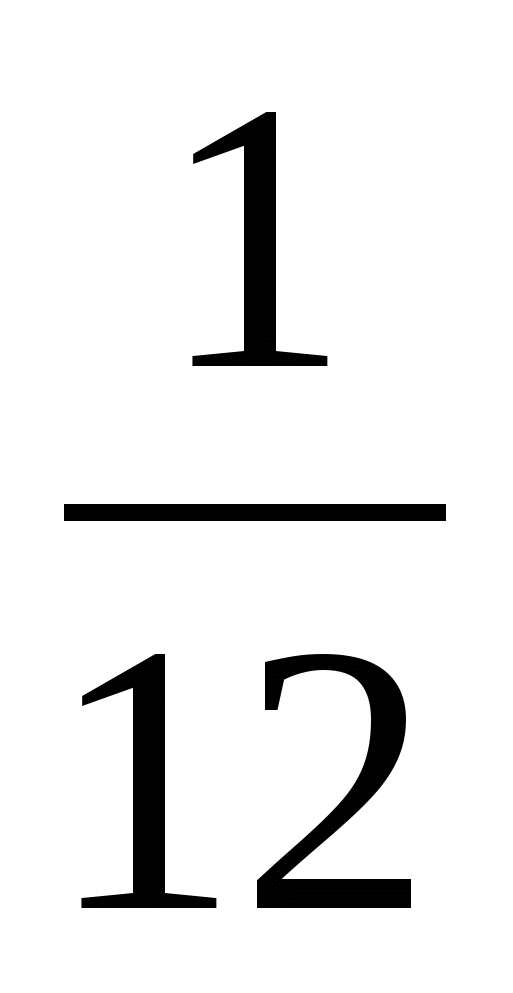 
ч позже автобуса. Найдите расстояние между пунктами.
Решение. Совместное движение началось в момент выхода автомобиля из пункта А. К этому времени автобус прошел 30 км со скоростью 40 км/ч за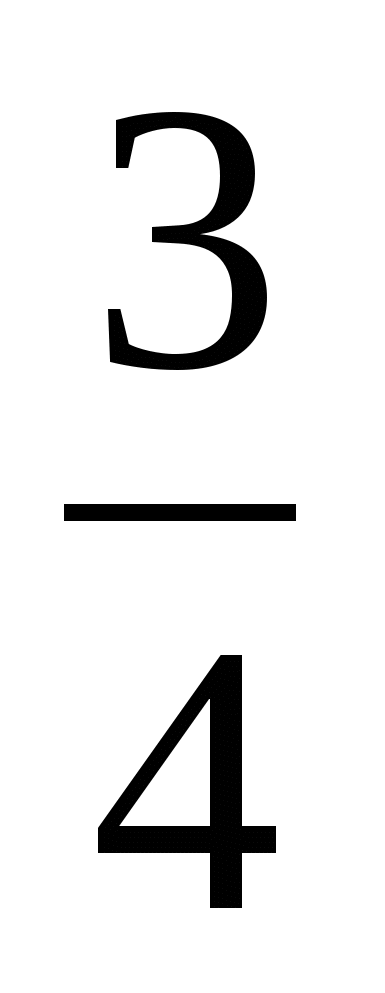 
ч (30:40=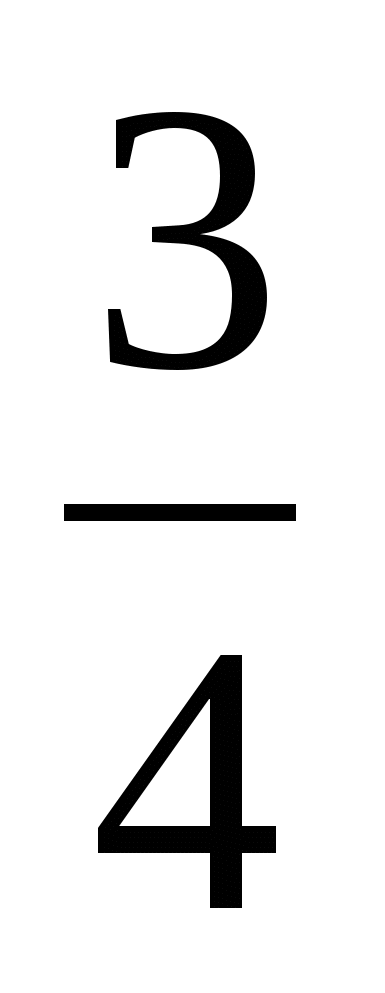) – это первый участок пути автобуса.
Второй участок пути автобуса начинается в 30 км от пункта А и заканчивается в пункте В.
Пусть второй участок пути автобус прошел за t ч. Так как скорость движения равна 40 км/ч, то в общей сложности от пункта А до пункта В автобус прошел (30+40t) км.
Закончилось совместное движение прибытием автобуса в пункт В. За t ч (время прохождения автобусом второго участка) автомобиль со скоростью 60 км/ч прошел 60t км, и до пункта В ему осталось пройти 60·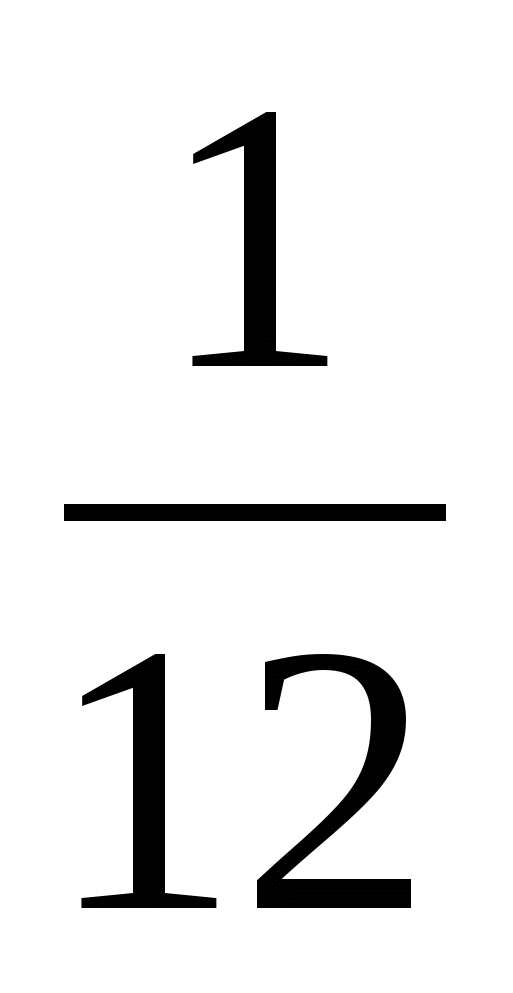=5(км). Таким образом, расстояние от пункта А до пункта В равно 60t+5(км). Составим уравнение: 30+40t=60t+5,
откуда t =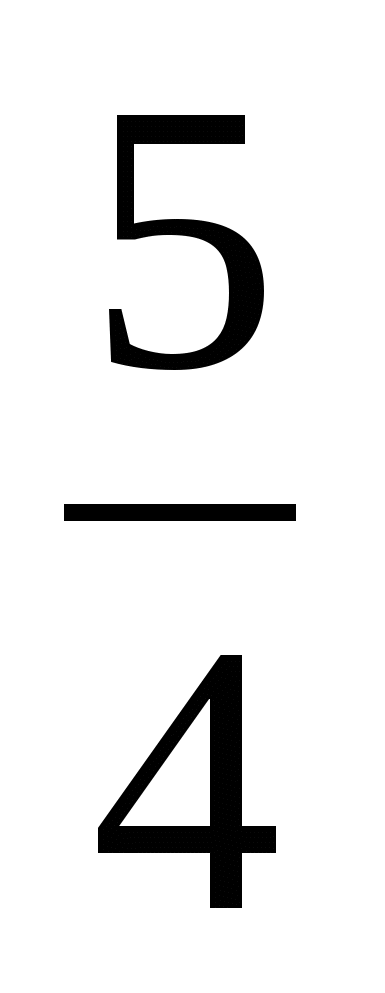
ч, тогда расстояние между пунктами А и В равно 30+40·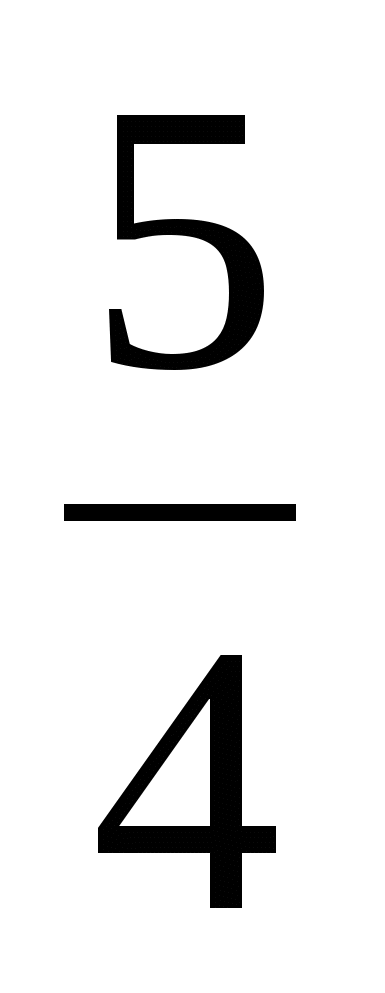=80 (км).
Ответ: 80 км.
4 тип задач на движение. Задачи на закон сложения скоростей.
В ряде задач на движение учитываются скорость ветра при движении самолетов, скорость течения при движении по реке. В задачах такого типа рассматриваются две основные скорости – собственная скорость самолета, корабля, лодки, создаваемая двигателем или усилием людей при работе на веслах, т.е. скорость движения при отсутствии ветра или в стоячей воде, и скорость ветра или течения. Как правило, если собственная скорость и скорость ветра (или течения) не даны, то именно их обозначают переменными. Две другие скорости – скорость по ветру или течению и скорость против ветра или течения – можно выразить через основные скорости (через сумму или разность). Далее решаем задачу, как любую другую задачу на движение.
Пример 6. Самолет пролетит по направлению ветра за 5,5 ч такое же расстояние, какое в обратном направлении за 6 ч при условии, что ни скорость, ни направление ветра не меняются. Найдите расстояние, которое пролетит самолет туда и обратно, если собственная скорость самолета равна 690 км/ч.
Решение. В данной задаче основные скорости – собственная скорость самолета, равная 690 км/ч, и скорость ветра, которая не дана. Обозначим ее за х км/ч.
Тогда при движении по направлению ветра самолет со скоростью (690+х) км/ч за 5,5 ч пролетит 5,5(690+х) км, а при движении против направления ветра самолет со скоростью (690-х) км/ч за 6 ч пролетит 6(690-х) км.
Учитывая, что по условию задачи самолет туда и обратно пролетает одно и тоже расстояние, составим уравнение 5,5(690+х)=6(690-х).
Решая уравнение, находим, что скорость ветра равна 30 км/ч. Далее вычислим расстояние: 6·(690-30)=3960(км).
Туда и обратно самолет пролетит 3960·2=7920(км).
Ответ: 7920 км.
Пример 7. Катер, собственная скорость которого равна 15 км/ч, прошел 60 км по реке от одной пристани до другой и вернулся обратно. За это же время спасательный круг, упавший за борт с катера, проплывет 25 км. Найдите время движения катера вверх по реке.
Решение. В данной задаче основные скорости – собственная скорость катера, равная 15 км/ч, и скорость течения, которая не дана. Обозначим ее за х км/ч.
Тогда на путь по течению катер со скоростью (15+х) км/ч затратит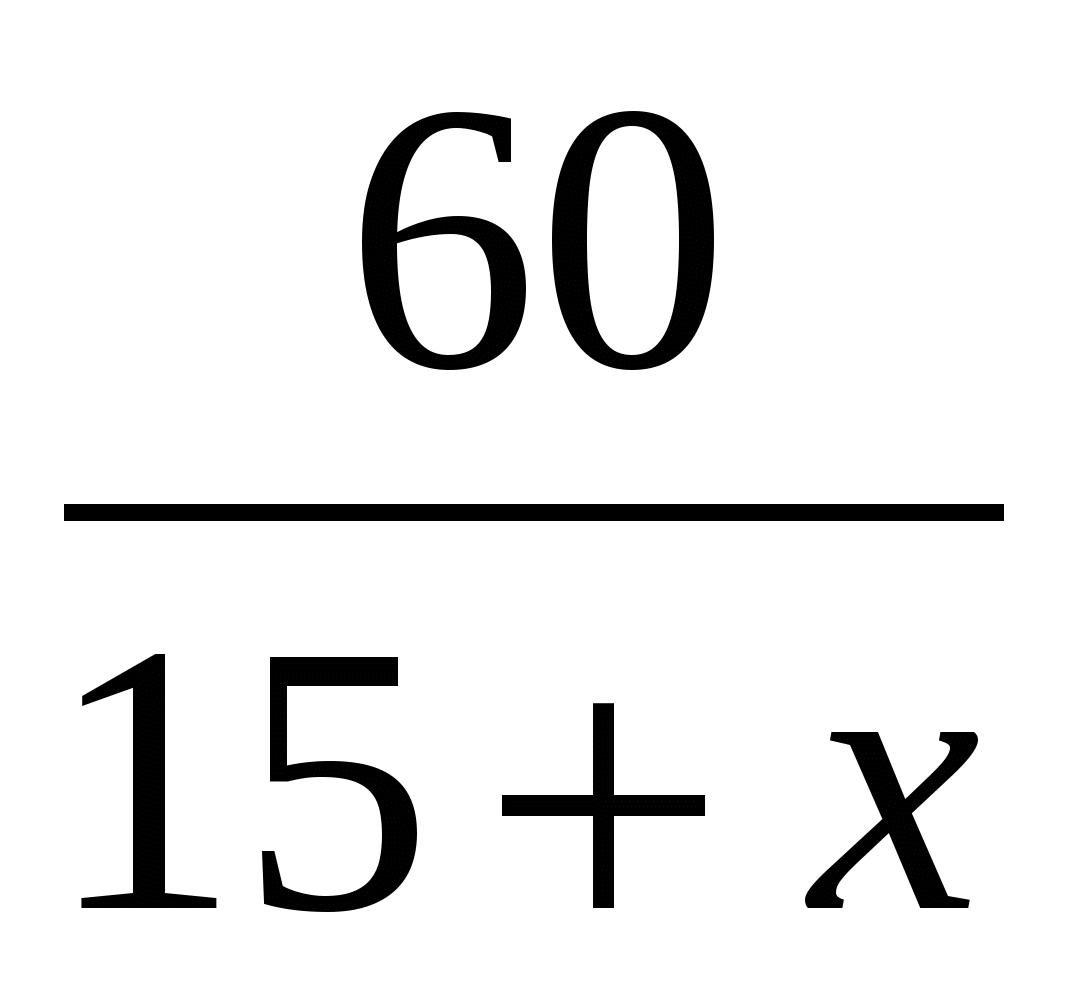 
ч, а на путь против течения катер со скорость (15-х)км/ч затратит 
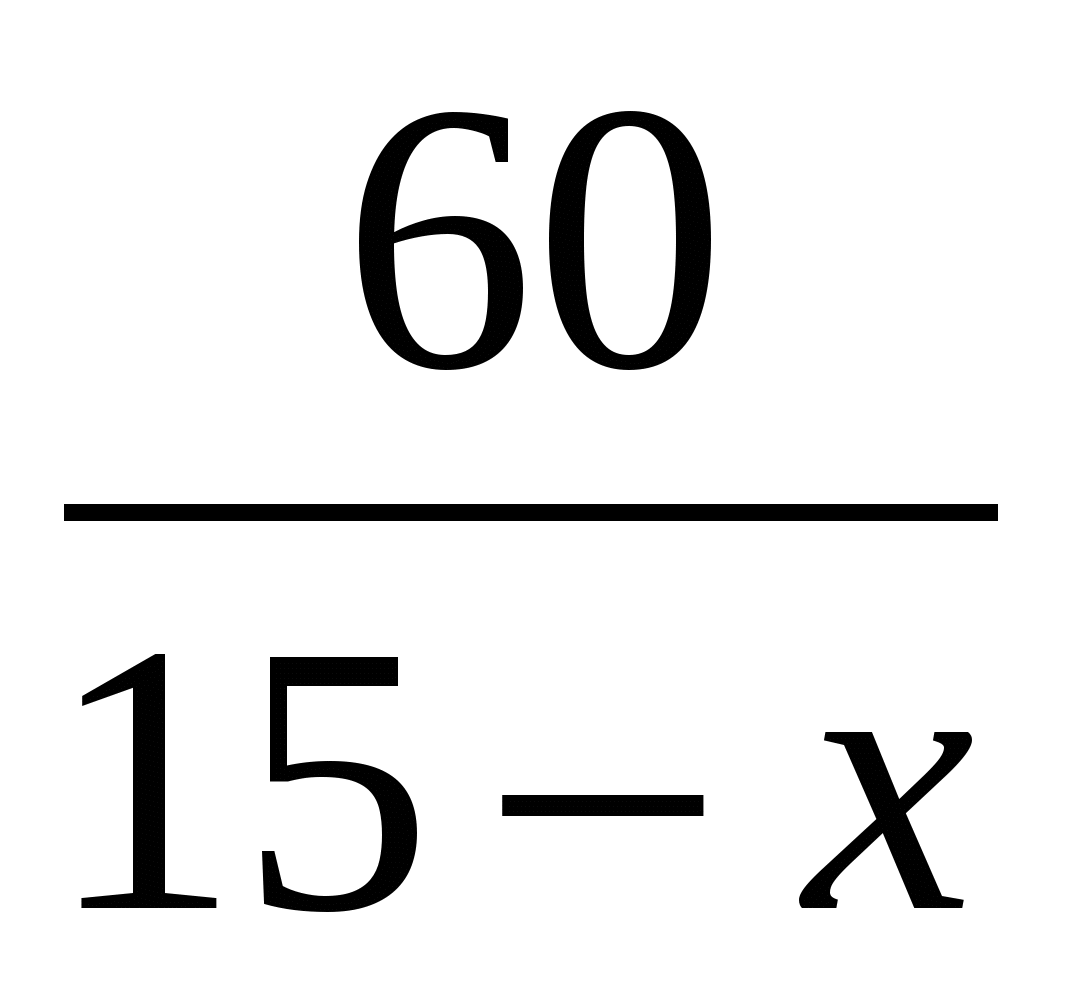ч.
Спасательный круг проплыл 25 км по течению реки за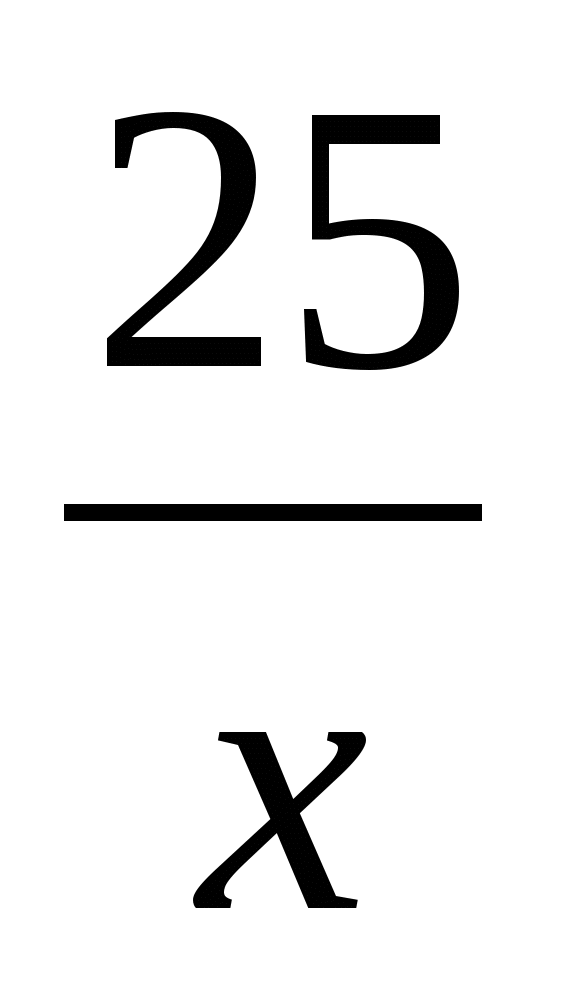 
ч. Учитывая, что по условию задачи на путь туда и обратно катер затратил такое же время, за какое спасательный круг поплыл 25 км, составим уравнение:
,
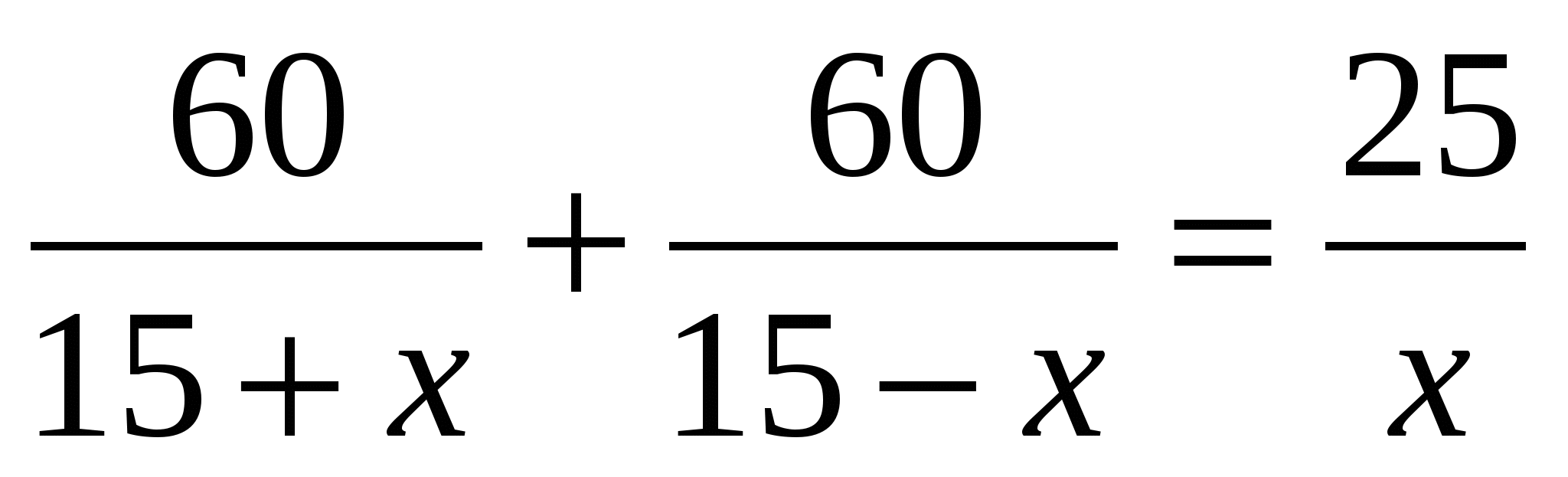далее получим х=3, х=-75.
Отрицательный корень не удовлетворяет условию задачи. Итак, скорость течения равна 3 км/ч. Далее узнаем время движения вверх по реке: 
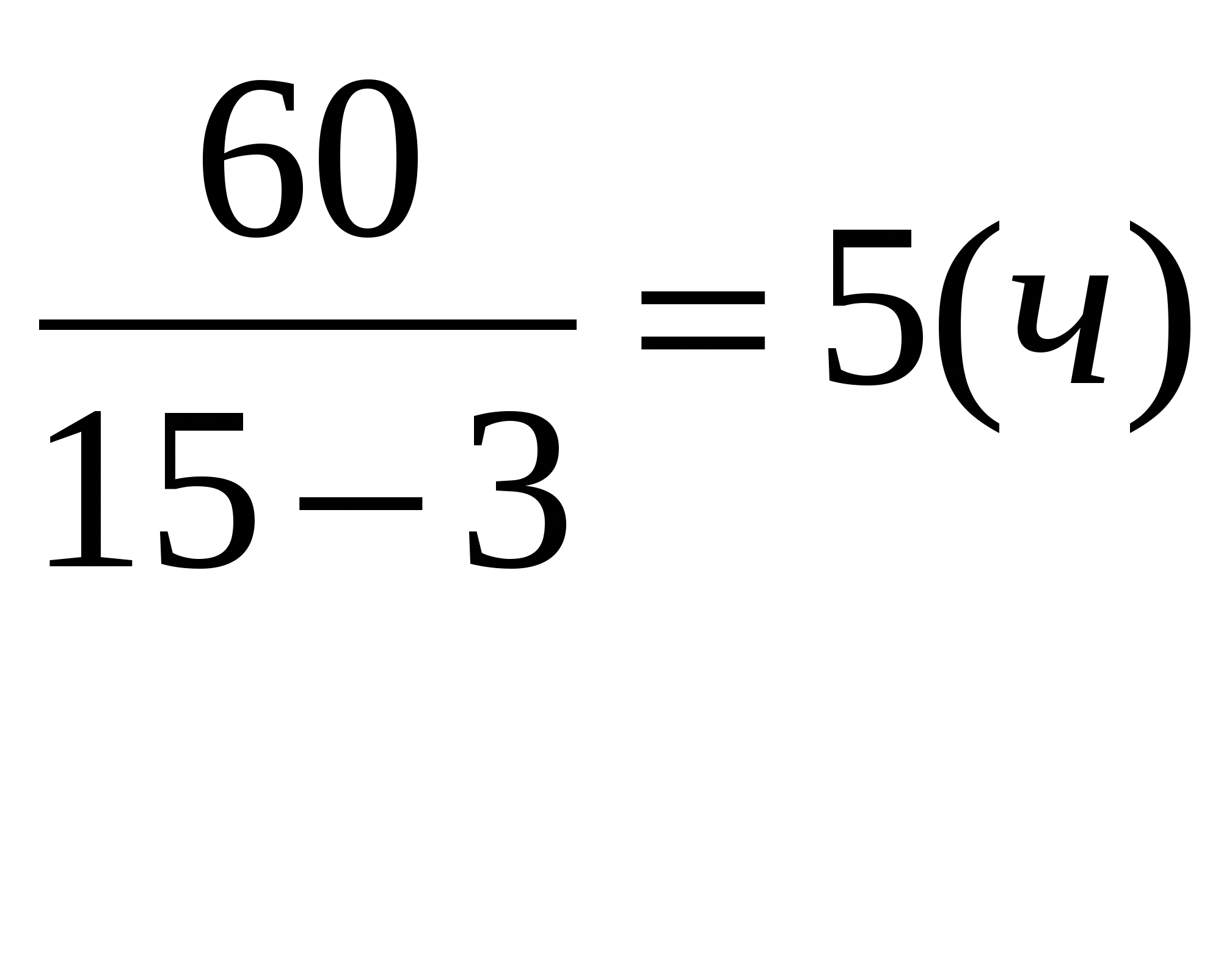
Ответ: 5 ч.
Дидактический материал для учащихся.
Из Москвы в Киев вышел поезд со скоростью 80 км/ч. Спустя 24 мин из Киева в Москву отправился поезд со скоростью 70 км/ч. Через сколько часов после выхода из Москвы произойдет встреча, если расстояние между городами равно 872 км?
Из города А в город в выехал грузовик со скоростью 45 км/ч. После того как грузовик проехал 15 км, из города А выехал со скоростью 60 км/ч автомобиль, который приехал в город В на
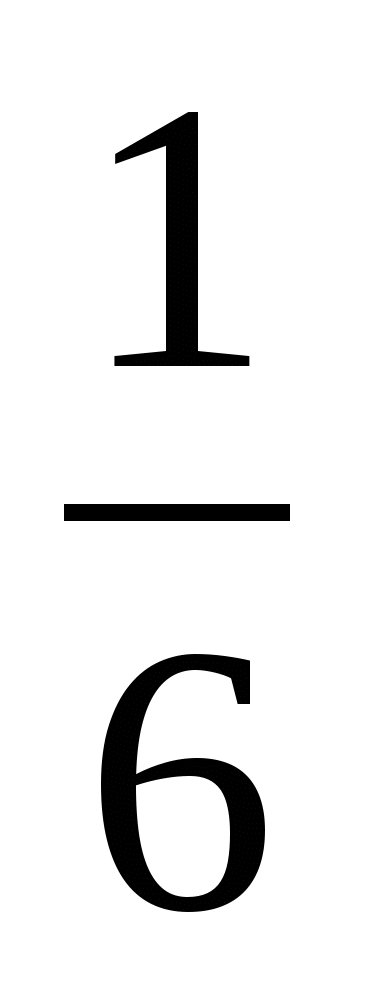раньше грузовика. Найдите расстояние между городами.Расстояние между городами А и В равно 50 км. Из города А в город В выехал велосипедист, а через 1ч 30 мин вслед за ним выехал мотоциклист. Обогнав велосипедиста, он прибыл в город В на 1 час раньше его. Найдите скорость мотоциклиста, если известно. Что она в 2,5 раза больше скорости велосипедиста.
Из двух пунктов А и В, расстояние между которыми равно 5 км, одновременно в одном направлении выехали велосипедист и легковой автомобиль. Легковой автомобиль все время был впереди велосипедиста, и через
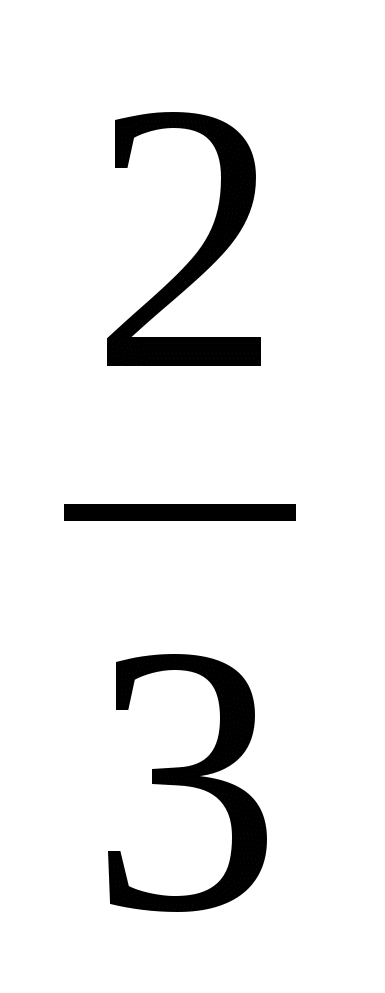ч расстояние между ними стало 35 км. Найдите скорость велосипедиста, если она в 4 раза меньше скорости легкового автомобиля.Из двух аэропортов, расстояние между которыми равно 1300 км, вылетели одновременно навстречу друг другу два самолета – один с поршневым, другой с реактивным двигателем. Через 30 мин им оставалось пролететь до встречи 800 км. Найдите скорость самолета с реактивным двигателем, если она в 3 раза больше скорости самолета с поршневым двигателем.
Два туриста отправились одновременно из пунктов А и В, расстояние между которыми равно 33 км, навстречу друг другу. Через 3ч 12 мин расстояние между ними сократилось до 1 км ( они еще не встретились), а еще через 2 ч 18 мин первому осталось пройти до пункта В втрое большее расстояние, чем второму до пункта А. Найдите скорость второго туриста.
Лодка проплывет за 3ч по течению такое же расстояние, какое за 4 ч против течения. Найдите расстояние, которое проплывет лодка вниз по течению, если собственная скорость лодки 14 км/ч.
Из пункта А вниз по течению реки движется лодка с собственной скоростью 17 км/ч. Ей навстречу из пункта В движется катер с собственной скоростью 26 м/ч. Лодка до встречи шла 2 ч, катер – 2,5 ч. Какое расстояние проплывет за 3 ч плот, если расстояние между пунктами А и В равно 74 км?
Катер, собственная скорость которого равна 21 км/ч, прошел вниз по реке от города А до города В 72 км и вернулся обратно. За это же время пустая канистра, упавшая с борта катера при отходе из города А, проплыла 21 км. Сколько времени понадобится канистре, чтобы доплыть от города А до города В?
Самоходная баржа, собственная скорость которой равна 20 км/ч , прошла по реке от одной пристани до другой 96 км и вернулась обратно. За это же время плот проплывет 40 км. Найдите время движения лодки вверх по реке.
Друзья отправились на пикник на лодке, а вечером вернулись обратно. Они проплыли в общей сложности 48 км, затратив на весь путь 2ч 48 мин. При этом каждые 3 км против течения им приходилось тратить столько же времени, сколько на 4 км по течению. Найдите собственную скорость лодки.
Занятие 3.
При решении задач на совместную работу следует помнить, следует помнить, что работа, как и равномерное движение , описывается формулой А=Р·T, где А-работа, Р- производительность труда (аналог скорости движения), Т-время работы (время движения), А-объем выполненной работы (пройденный путь).
Пример 8. Заказ по выпуску машин завод должен был выполнить за 20 дней. Но завод выпускал ежедневно по 2 машины сверх плана. А поэтому выполнил заказ за 18 дней. Сколько машин выпустил завод?
Решение. Пусть завод должен был выпускать х машин в день, тогда заказ составляет 20х машин.
На самом деле завод выпускал (х+2) машины в день и за 18 дней выпустил 18(х+2) машин.
Составим уравнение 20х=18(х+2), откуда х=18. таким образом. Завод выпустил 360 машин.
Ответ: 360 машин.
Пример 9. Одна труба подает в бассейн 1м³ воды на 4 мин быстрее, чем другая. Сколько кубических метров воды подаст вторая труба за 5 ч, если она подает за это время на 100 м³ меньше, чем первая?
Решение. Пусть первая труба подает в бассейн 1м³ за х мин, то есть за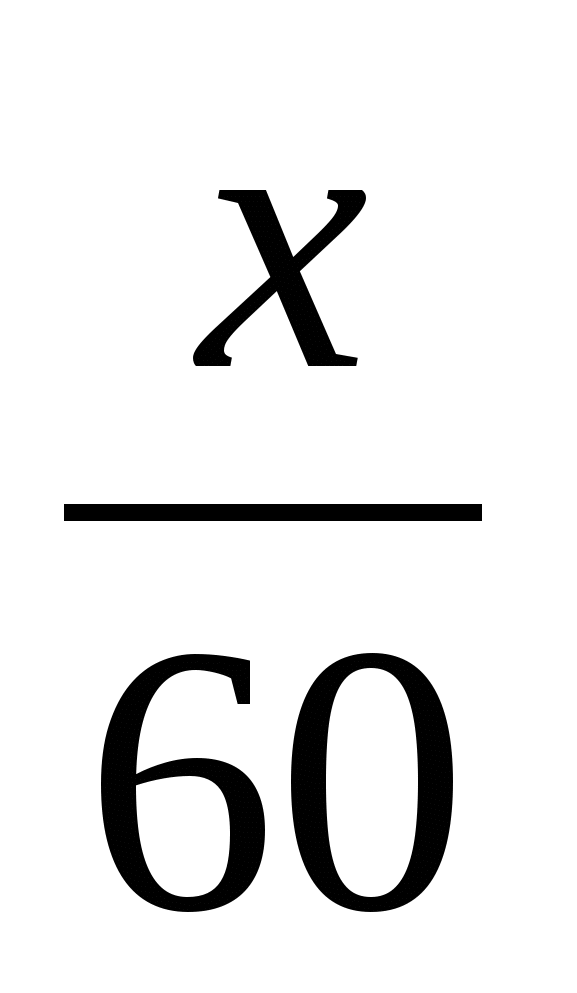 
ч, тогда вторая труба подает в бассейн 1м³ воды за (х+4) мин, то есть за 
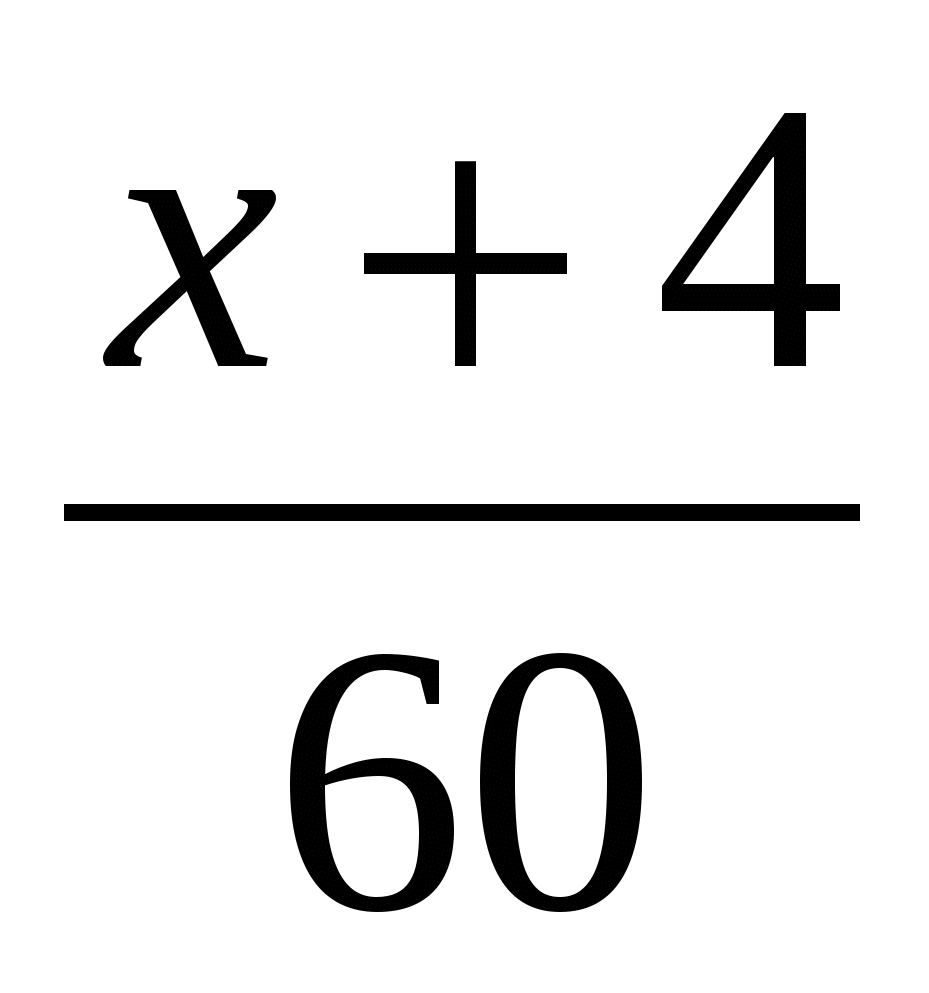ч.
Это означает, что за 1 час первая труба подает в бассейн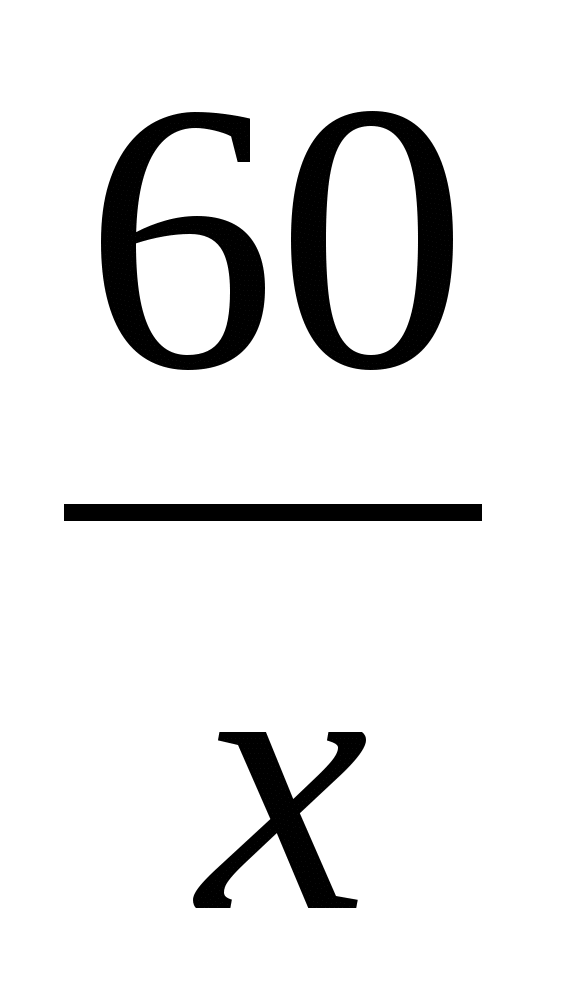 
м³ воды. А вторая труба подает в бассейн 
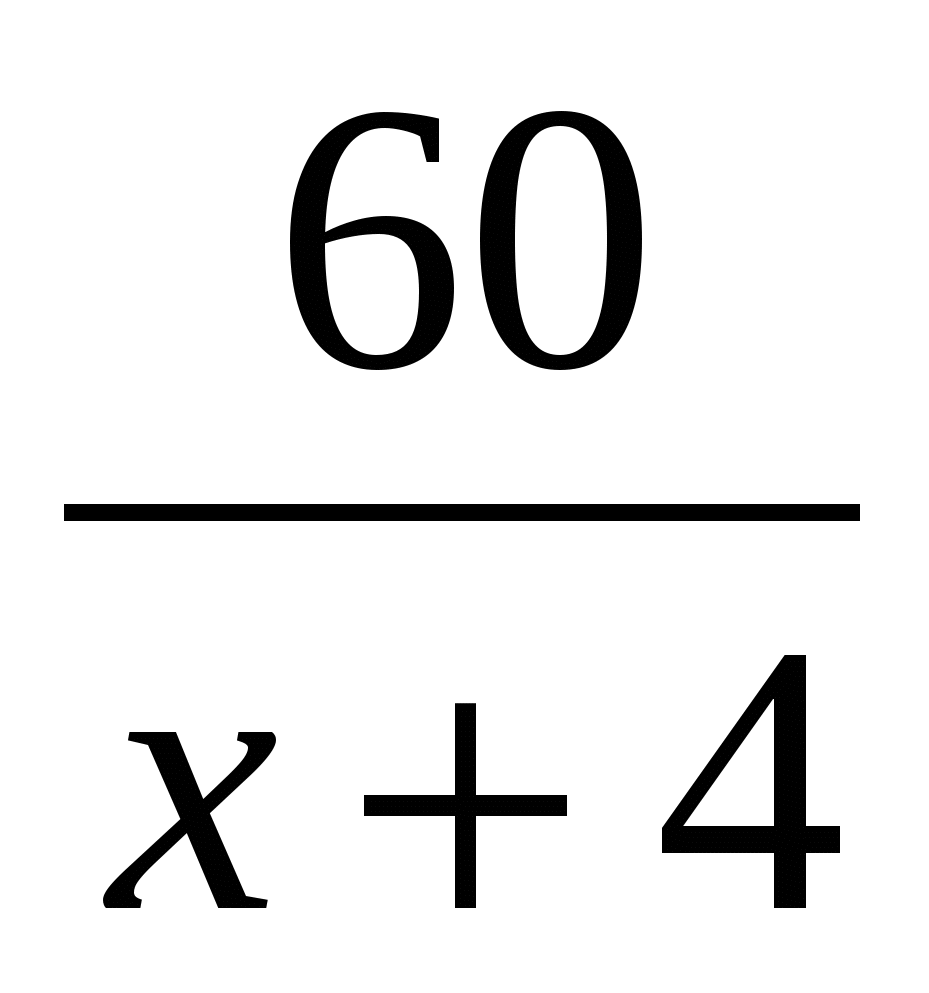м³ воды.
По условию задачи 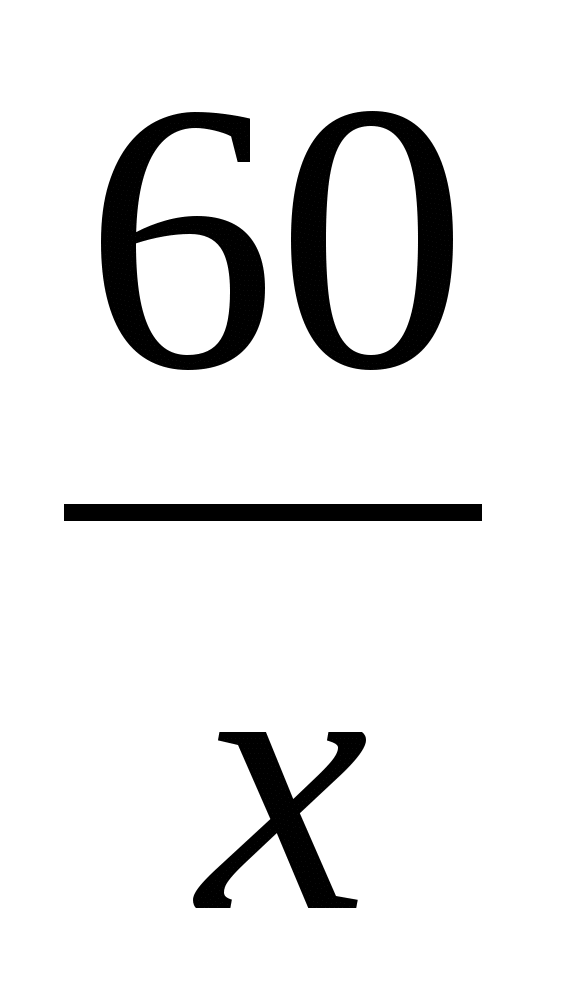м³ больше 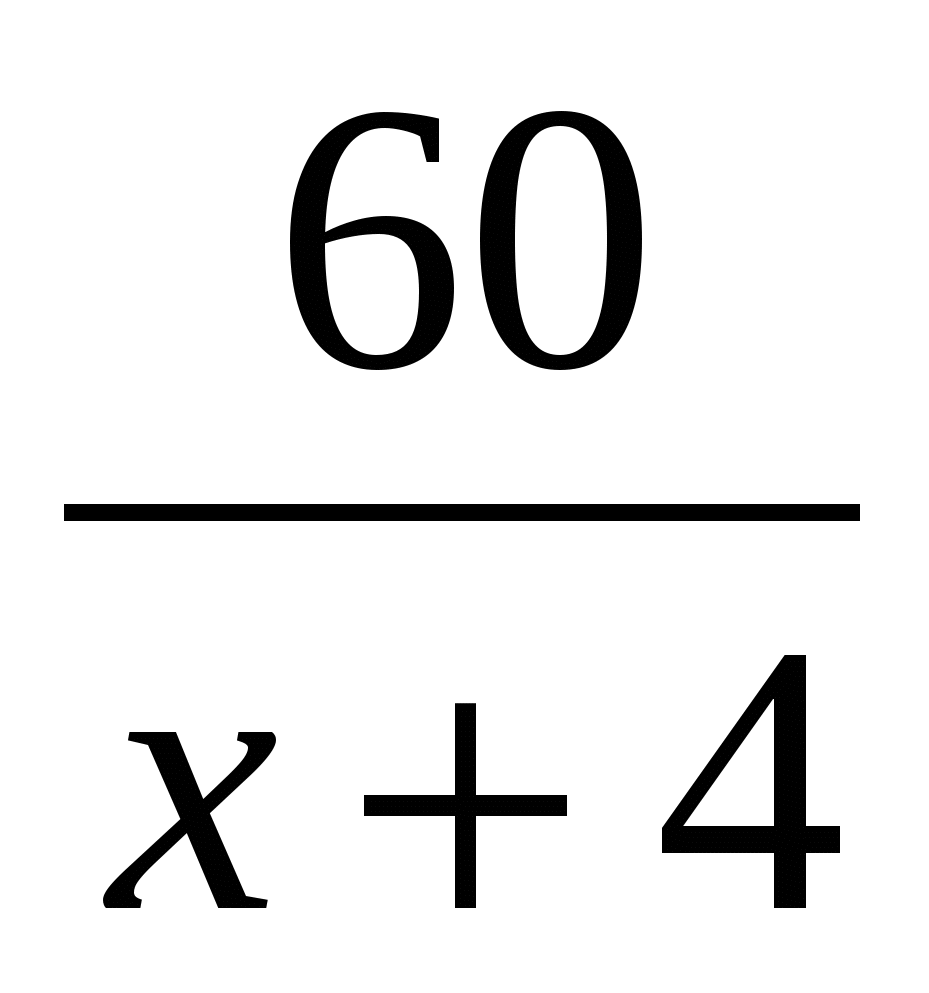м³ на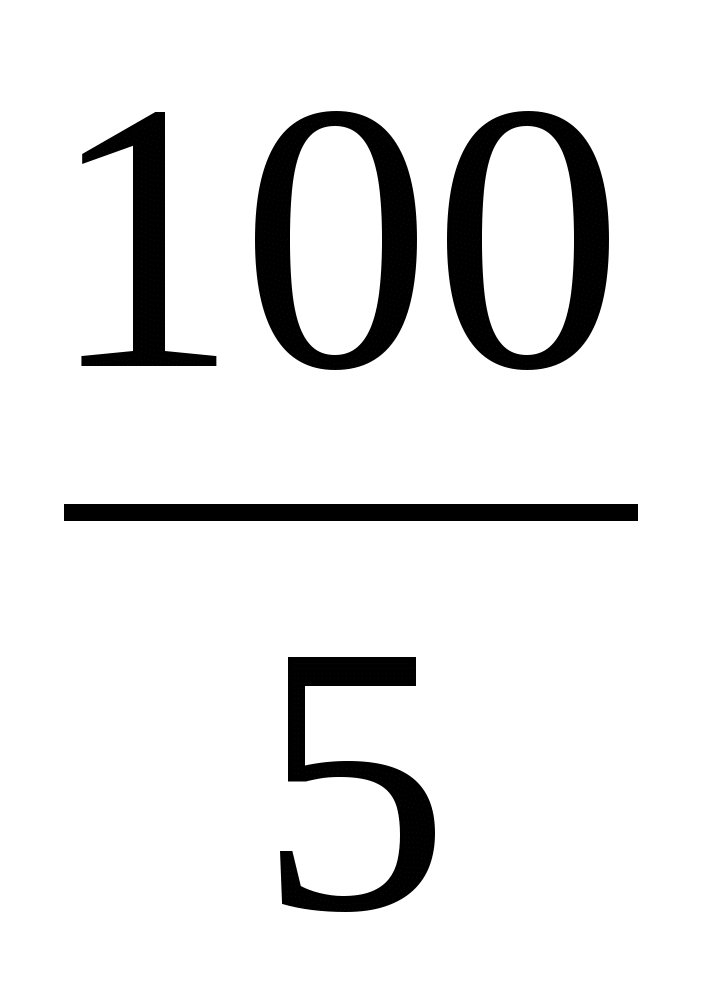 
=20(м³). Составим уравнение 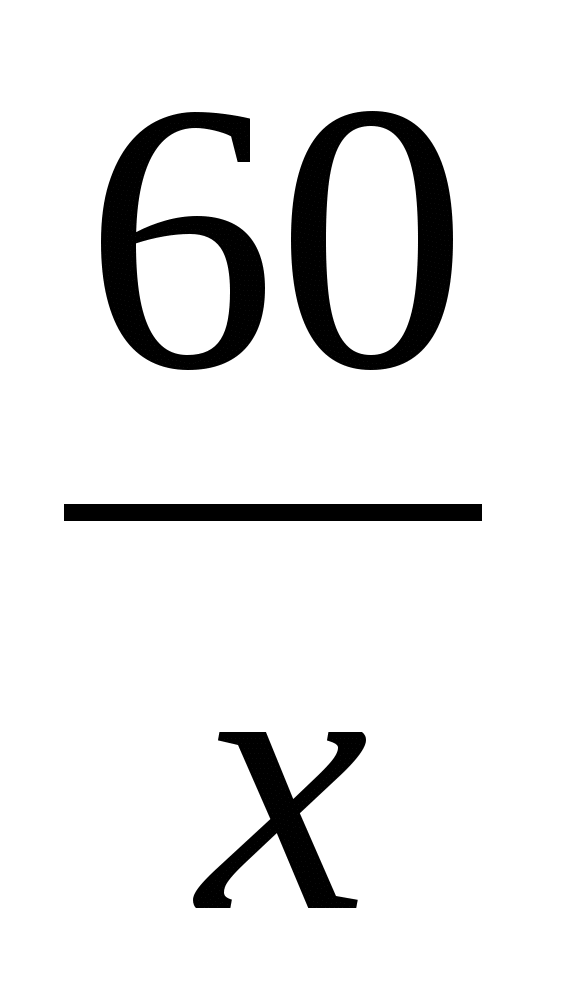- 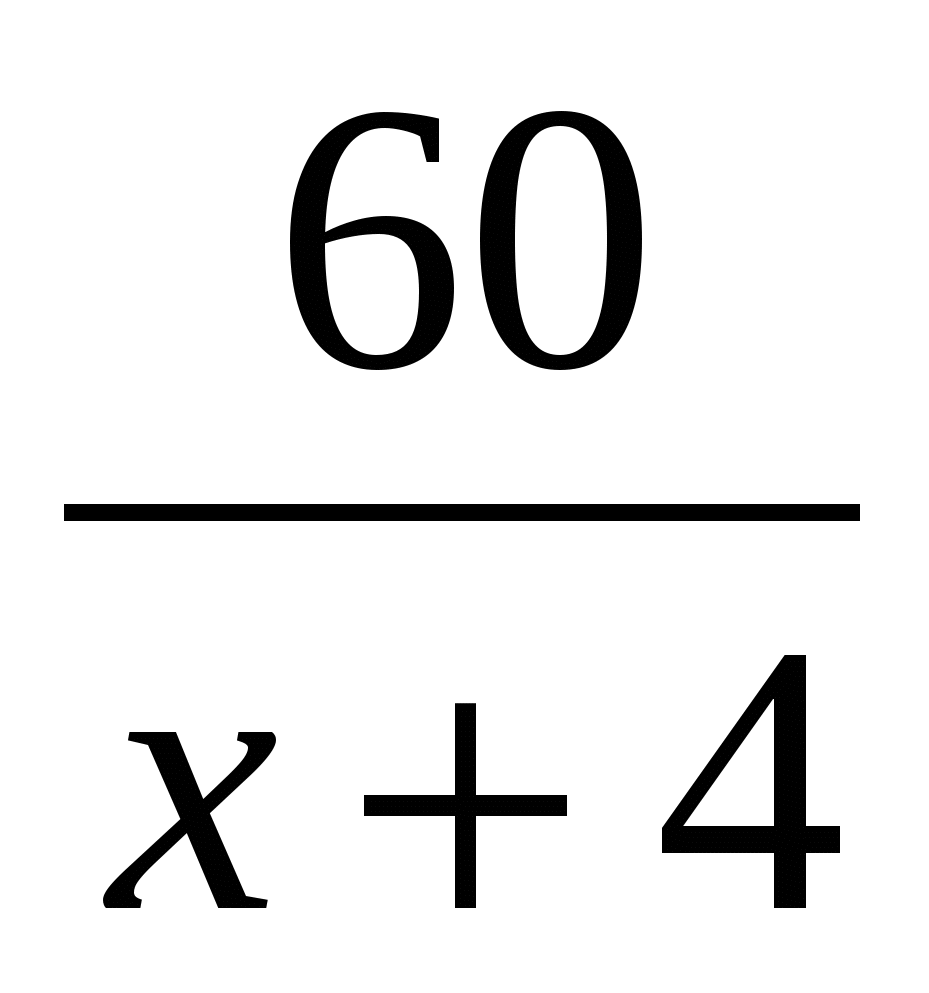= 20. Решая уравнение, получим х=2.Тогда вторая труба подает в бассейн 1м³ воды за 6 мин, за 1 час она подает в бассейн 10м³ воды. Значит вторая труба за 5 часов подает 50 м³ воды.
Ответ: 50м³
Пример 10. Два переводчика переводили рукопись. Первые 2ч работал первый переводчик, следующие 6 ч они работали вместе. За это время было переведено 80% рукописи. Сколько часов потребовалось бы первому переводчику, чтобы перевести всю рукопись, если известно, что ему потребуется на эту работу на 4 ч меньше, чем второму?
Решение. Примем объем рукописи за 1. Пусть первому переводчику для перевода всей рукописи нужно х ч, тогда второму переводчику для перевода всей рукописи нужно (х+4) ч. Производительность первого переводчика равна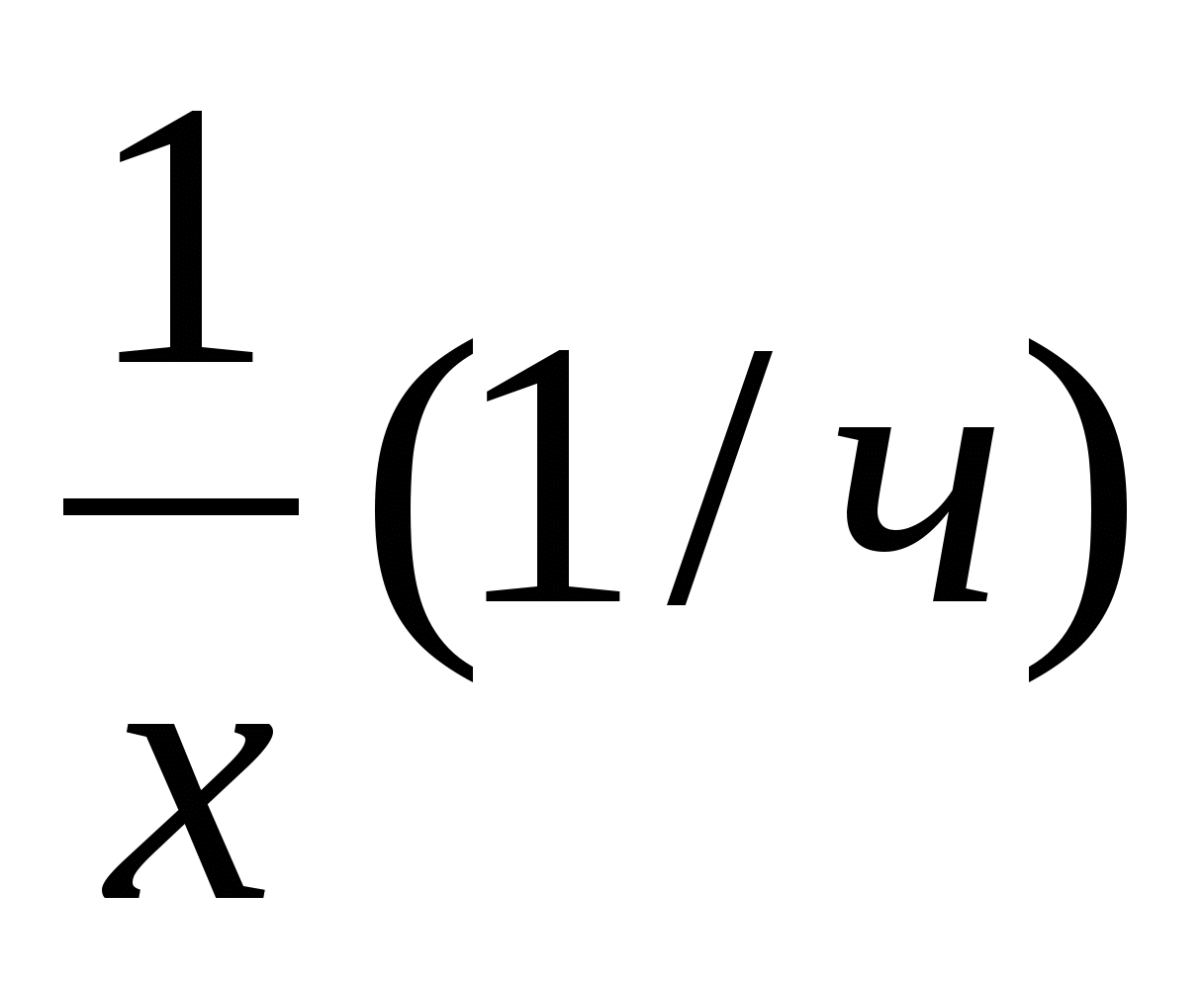 
, производительность второго переводчика равна 
.
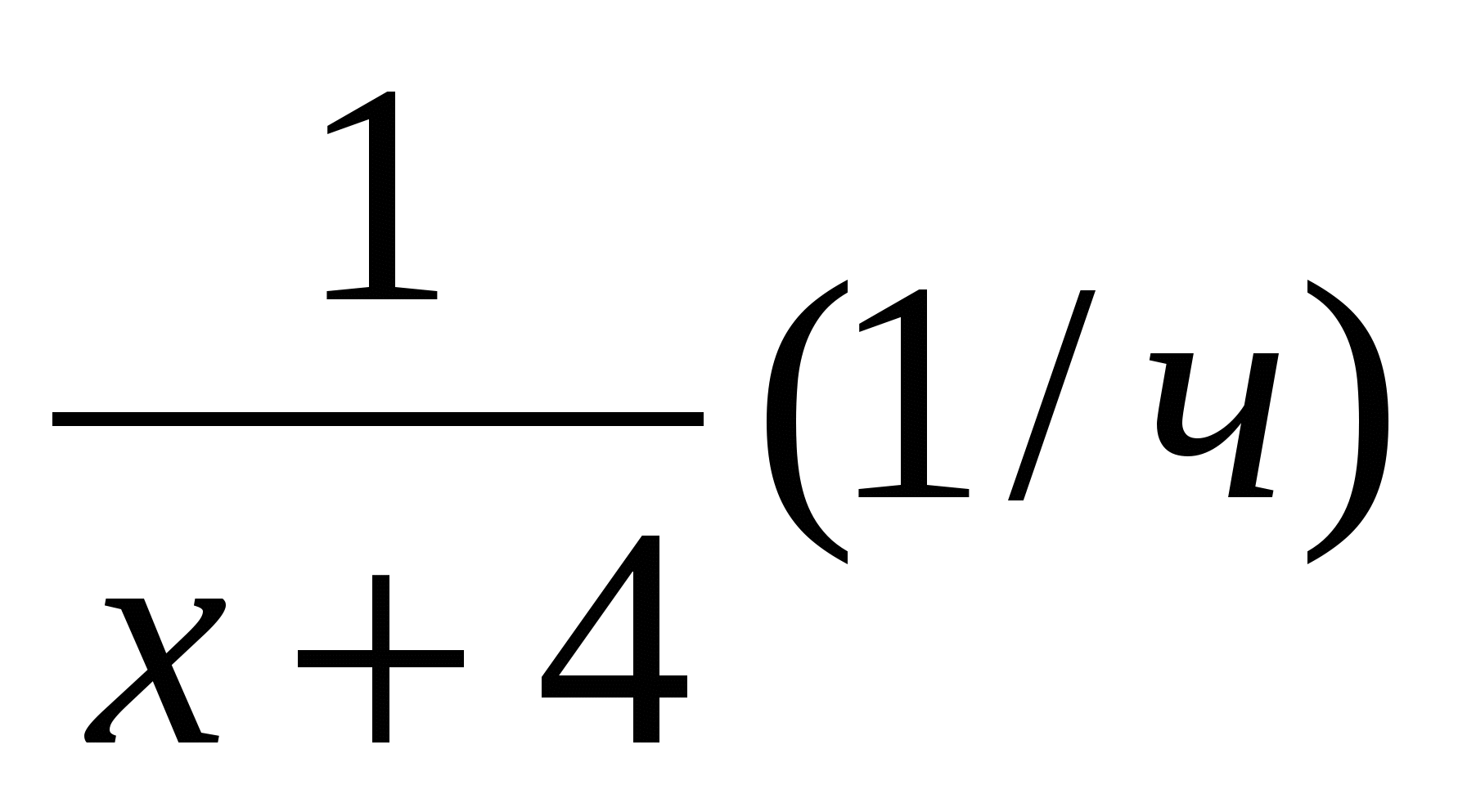За первые 2 ч было переведено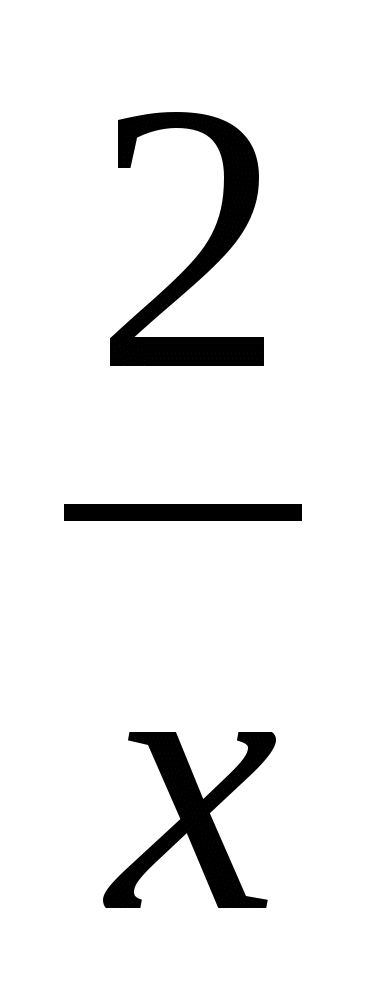 
рукописи, за следующие 6 ч было переведено 
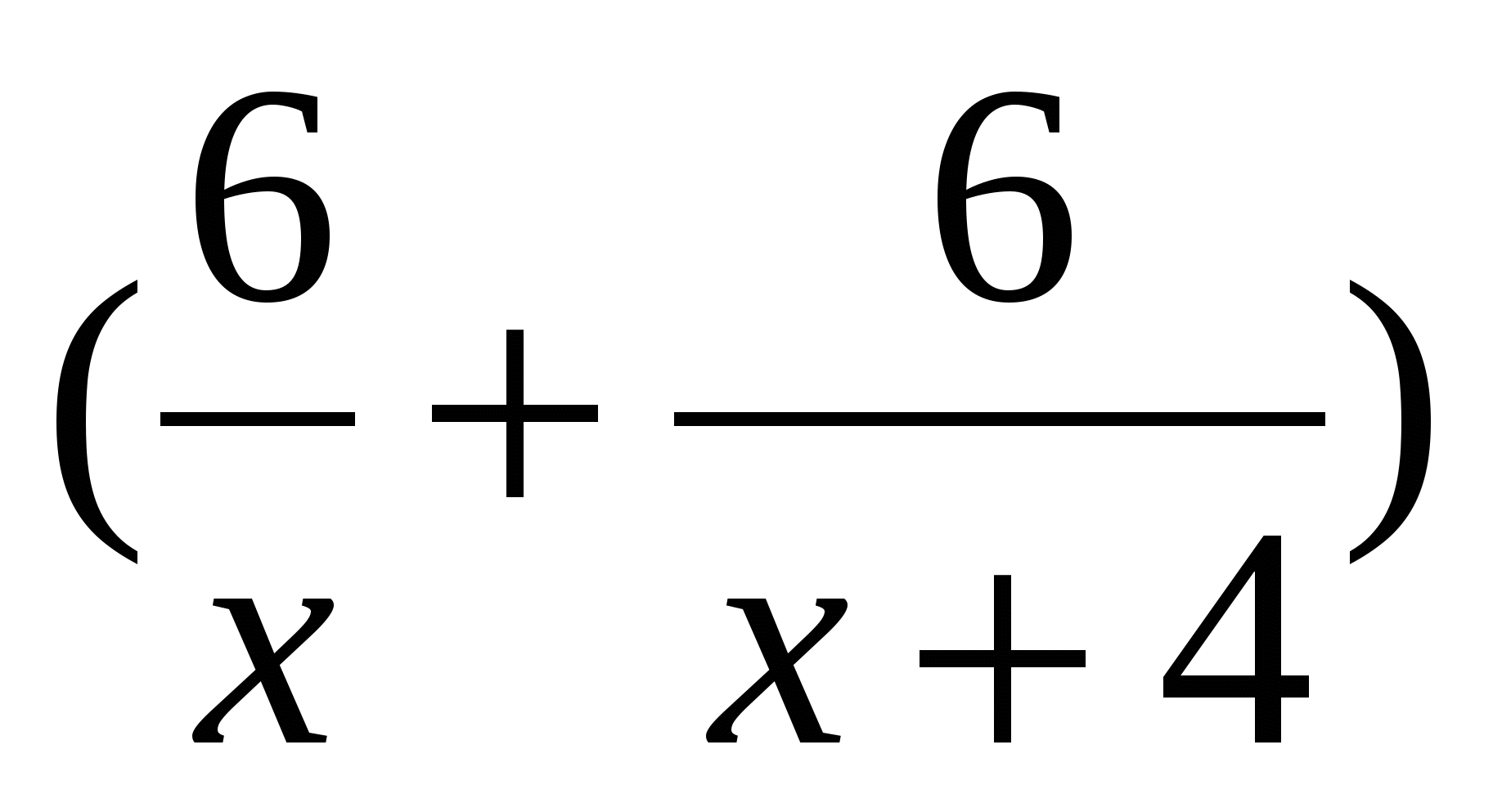рукописи. В общей сложности было переведено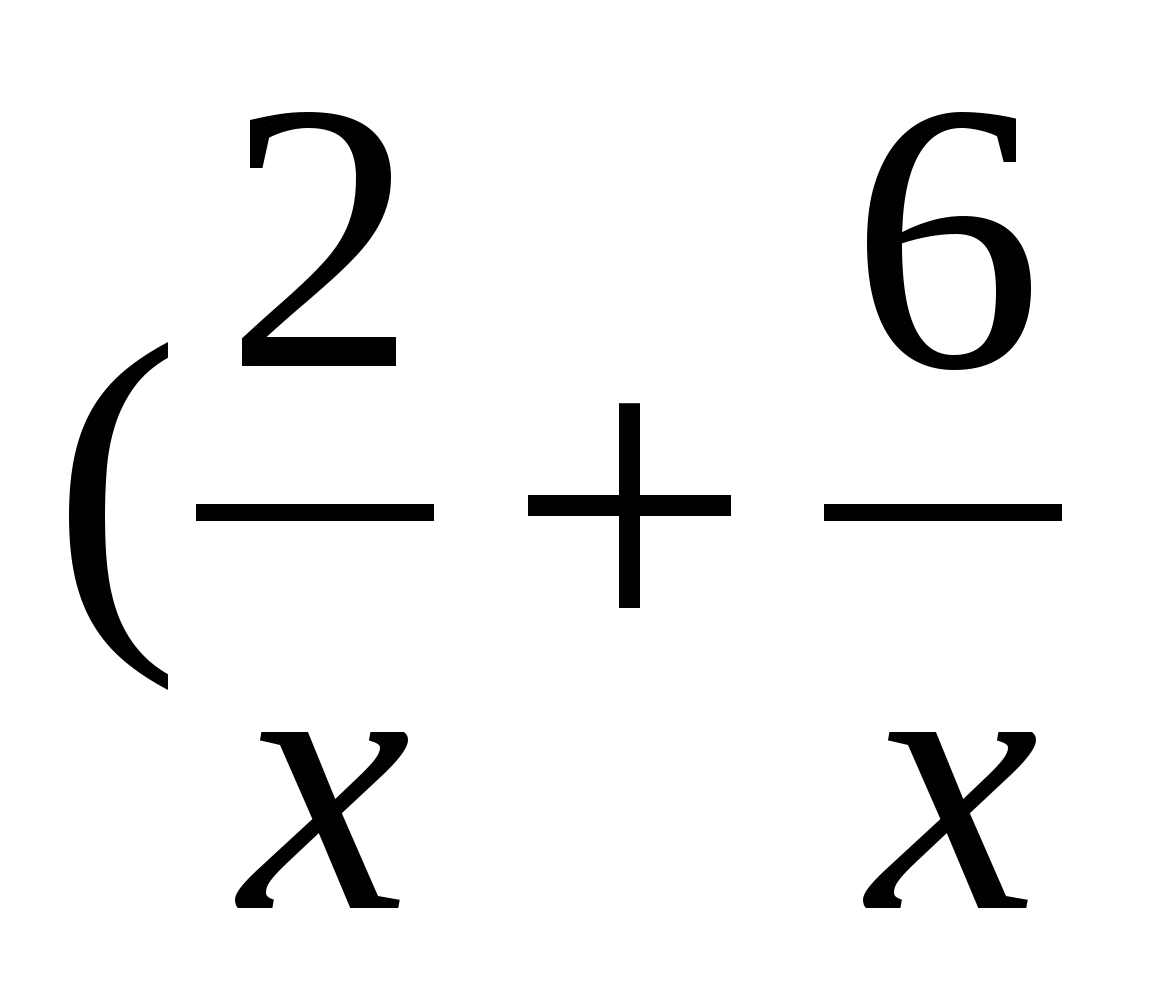 
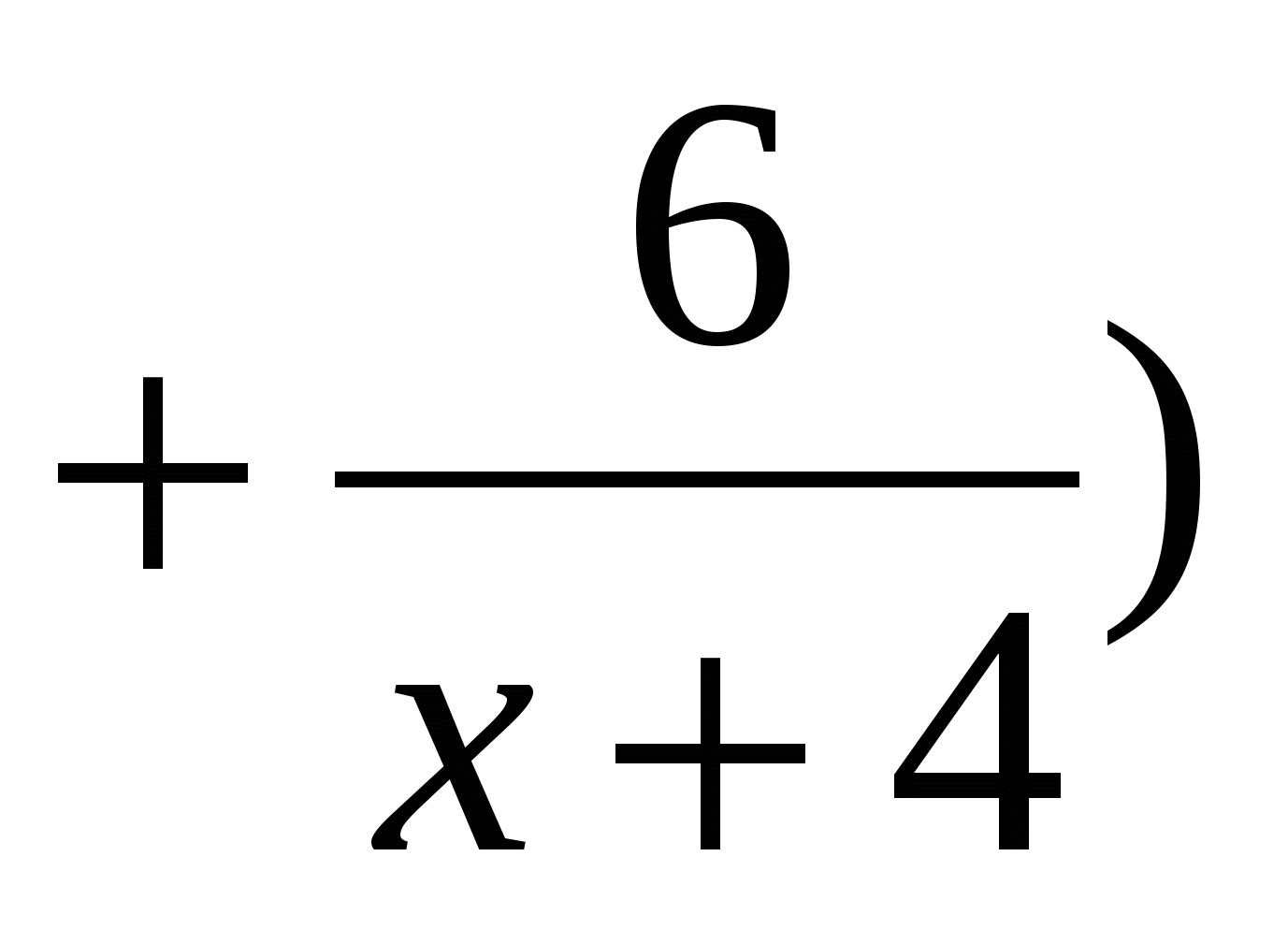рукописи, что по условию задачи составляет 80%, или 
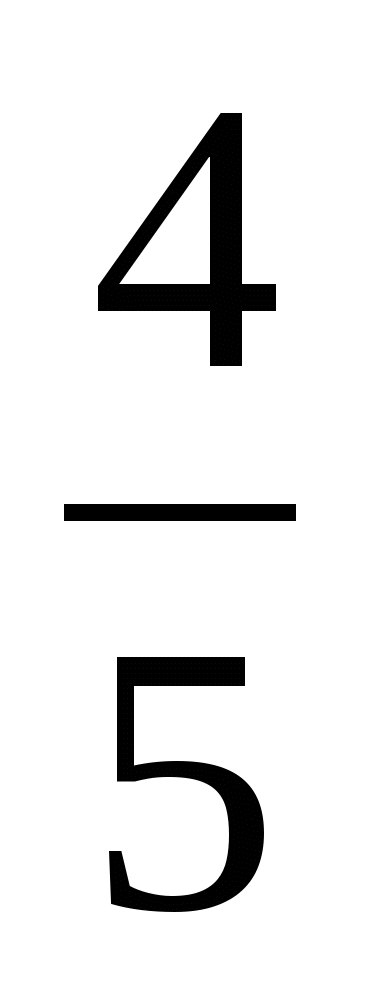рукописи.
Составим и решим уравнение:
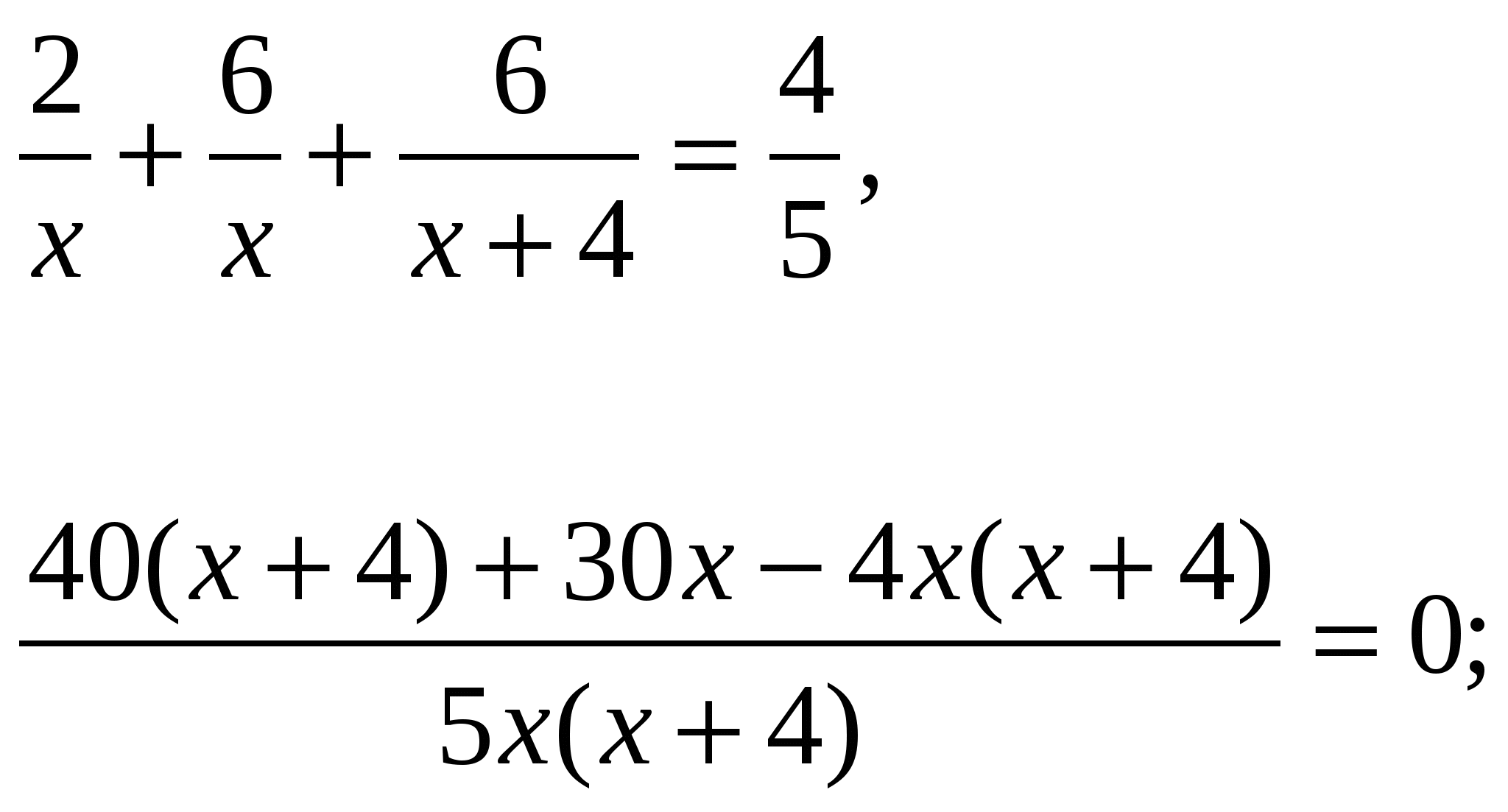
откуда х=-2,5 и х=16. По условию х должен быть положительным, значит х=16. Итак, первому переводчику на перевод рукописи потребовалось 16 часов.
Ответ: 16 часов.
Дидактический материал для учащихся.
Фермеры должны были закончить сев за 5 дней. Но, узнав о предстоящем ухудшении погоды, они засевали в день на 20 га больше, чем предполагалось по плану, и поэтому закончили сев за 4 дня. Сколько гектаров они засеяли?
На обработку одной детали один рабочий затрачивает на 1 мин меньше, чем другой. Сколько деталей обработает первый рабочий за 4 ч, если он обрабатывает за это время на 8 деталей больше, чем второй?
Бригада цветоводов должна была высадить в понедельник на центральных площадях города 7200 цветов. Однако три человека заболели, и каждому из вышедших на работу пришлось высадить на 400 цветов больше нормы, чтобы успеть вовремя. Сколько человек вышло на работу в понедельник?
Первая машинистка напечатала 270 страниц, печатая в день на 2 страницы больше второй машинистки, при этом работала она на 1 день меньше, чем вторая. Сколько страниц в день печатала вторая машинистка, если всего она напечатала 280 страниц?
Два секретаря должны были сделать по 120 звонков клиентам фирмы к определенному сроку. Один из них выполнил работу на 5 ч раньше второго, так как делал на 2 звонка в час больше второго. Скольким клиентам дозвонились во второй час работы оба секретаря?
Два помощника депутата так разделили между собой работу по редактированию доклада, что закончили каждый свою часть работы одновременно, через 12 часов. Первый помощник, работая один, мог бы отредактировать доклад на 10 часов быстрее второго. Сколько часов потребовалось бы второму помощнику для выполнения этой работы?
Для наполнения газгольдера сжатым газом имеется три компрессора. Второму компрессору для наполнения газгольдера требуется времени вдвое меньше, чем первому, и на 4 ч меньше, чес третьему. Три компрессора, работая вместе, наполнили бы газгольдер за 2ч, но по технологическим требованиям одновременно должны работать только два из них. Определите минимальное время (в минутах) наполнения газгольдера.
Для наполнения плавательного бассейна водой имеются три насоса. Первому насосу для наполнения бассейна требуется времени вдвое меньше, чем второму, и на 7 часов больше, чем третьему. Три насоса, работая вместе, наполнили бы бассейн за 4ч, но по условиям эксплуатации одновременно должны работать только два насоса. Определите минимальное время (в минутах) наполнения бассейна.
Для наполнения плавательного бассейна водой имеются три насоса. Первому насосу для наполнения бассейна требуется времени в три раза меньше, чем второму, и на 2 часа больше, чем третьему. Три насоса, работая вместе, наполнили бы бассейн за 3ч, но по условиям эксплуатации одновременно должны работать только два насоса. Определите минимальную стоимость (в рублях) наполнения бассейна, если 1 час работы любого из насосов стоит 140 рублей.
Занятие 4.
Существуют три основных вида задач «на проценты»:
Найти число а, составляющее n процентов от числа b.
Решение.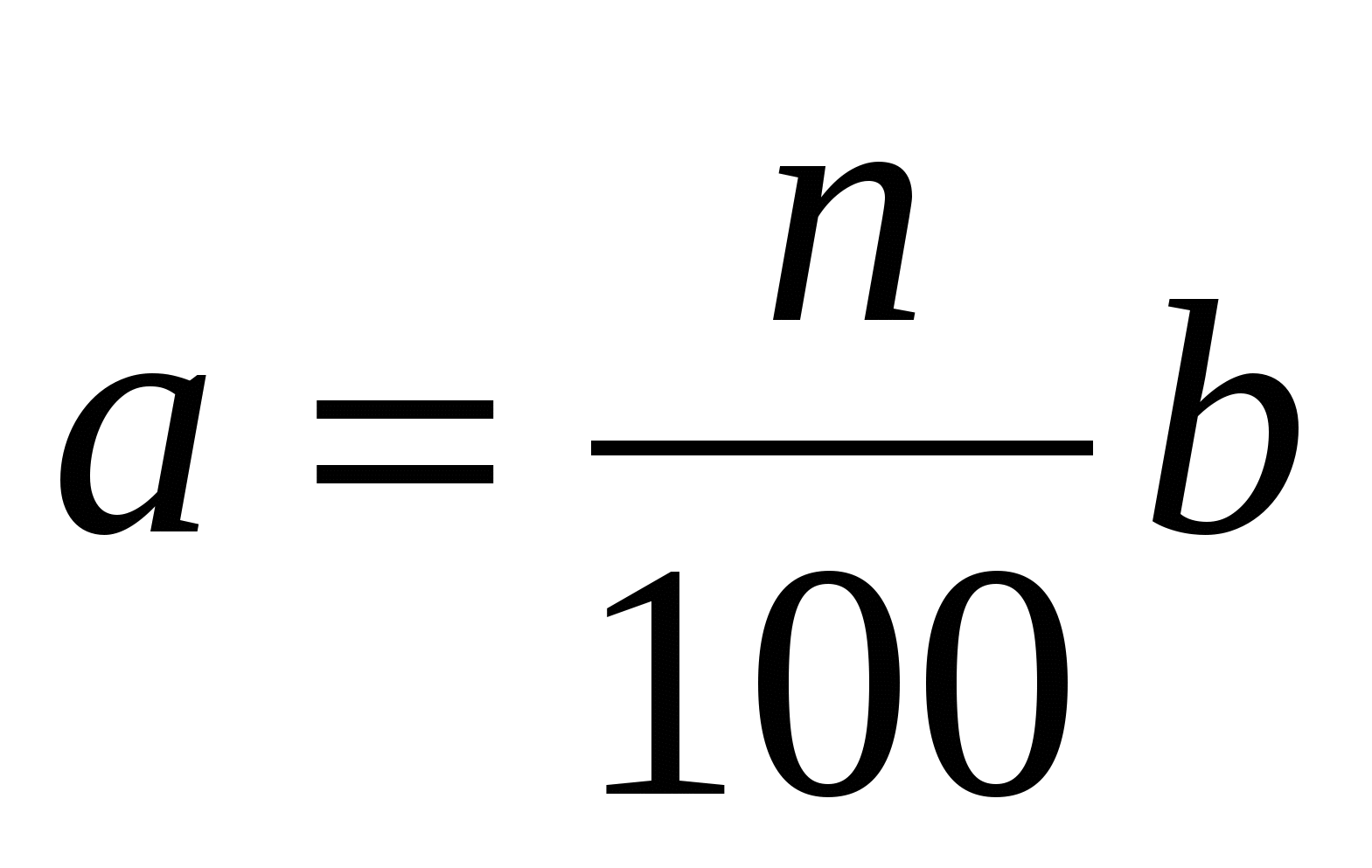 
.
Обратная задача: найти число b, если n процентов от него равно a.
Решение.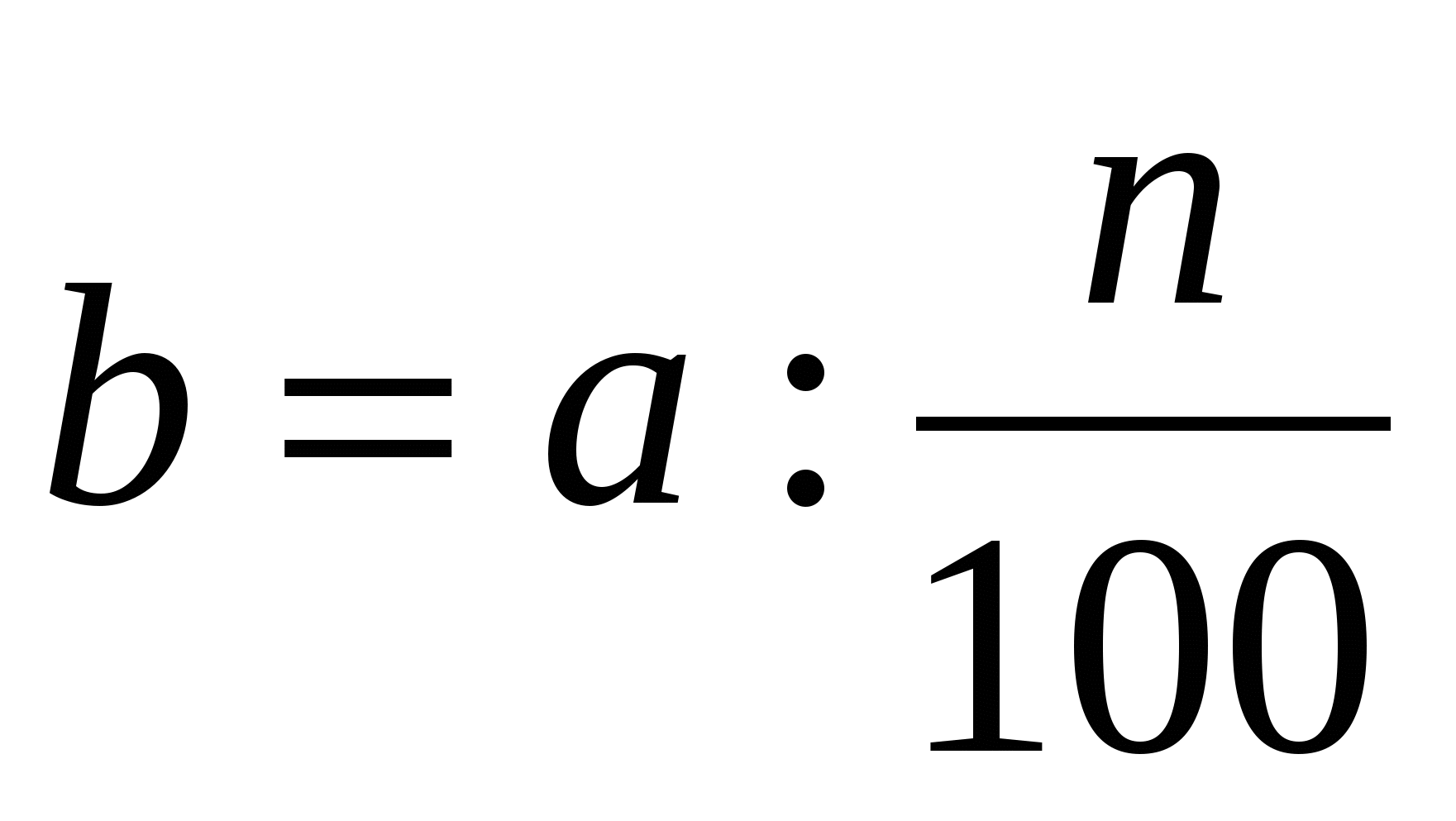 
.
Найдите, сколько процентов составляет число а от числа b.
Решение.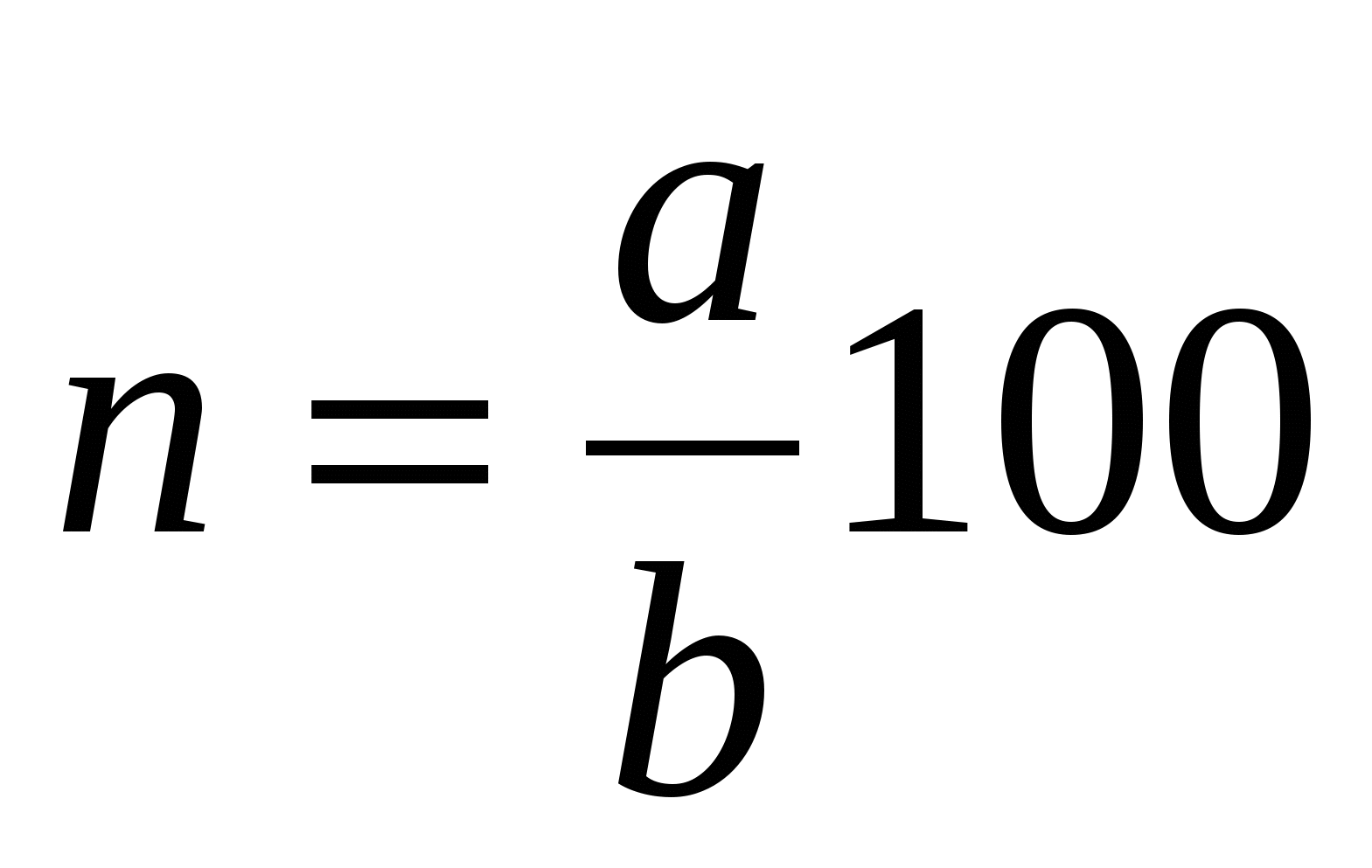 
.
Пример 11. В двух сараях сложено сено. В первом сена в три раза больше, чем во втором. После того, как из первого сарая взяли 20 т сена, а во второй добавили 20 т, оказалось, что во втором сарае масса сена равна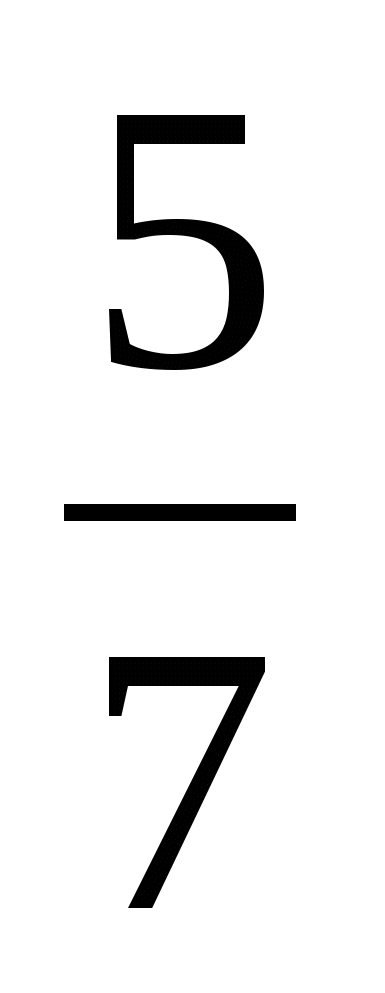 
массы сена, оставшегося в первом сарае. Сколько тонн сена было первоначально во втором сарае?
Решение. Пусть во втором сарае х т сена, тогда в первом сарае 3х т сена. После всех перемещений сена в первом сарае стало (3х-20) т , а во втором (х+20) т. Составим уравнение по условию задачи: х+20=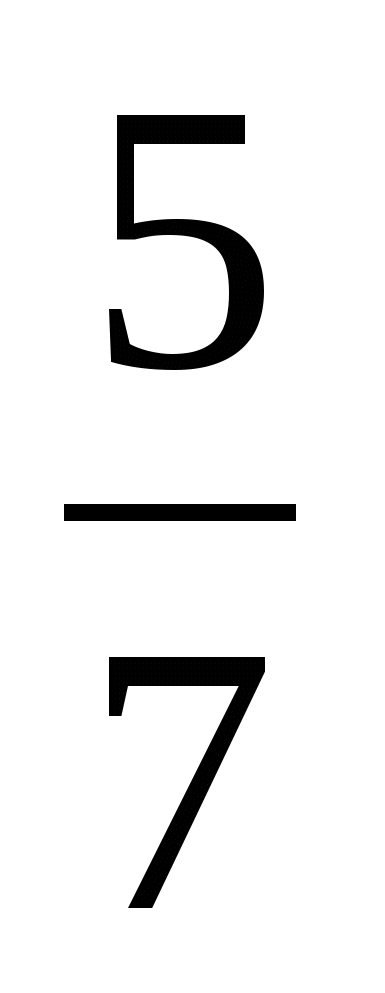(3х-20), откуда х=30. Итак, во втором сарае было первоначально 30 т сена.
Ответ: 30 т сена.
Пример 12. С двух участков ежегодно собиралось 500 т пшеницы. После проведения агротехнических мероприятий урожай на первом участке увеличился на 30%, а на втором – на 20%. Поэтому с двух участков собрали 630 т пшеницы. Сколько пшеницы собрали с первого участка первоначально?
Решение. Пусть с первого участка собрали х т пшеницы, тогда со второго – (500-х) т. После проведения агротехнических мероприятий с первого участка стали собирать 1,3х т пшеницы, а со второго - 1,2(500-х) т. С двух участков стали собирать (1,3х+1,2(500-х)) т, что по условию задачи составляет 630 т .
Составим и решим уравнение: 1,3х+1,2(500-х)=630, х=300. Таким образом, с первого участка до проведения агротехнических мероприятий собирали 300 т пшеницы.
Ответ: 300 т пшеницы.
Пример 13. Банк ежегодно увеличивает на одно и то же число процентов сумму, имеющуюся на вкладе к моменту начисления процентов. На сколько процентов ежегодно увеличивается сумма, если за два года она возросла с 2000 до 2420 рублей?
Решение. Пусть ежегодно имеющаяся на счете сумма увеличивается на х%. В первый раз за 100% мы должны принять сумму, имеющуюся на счете к началу нового года, т.е. 2000 рублей. Тогда через год на счете окажется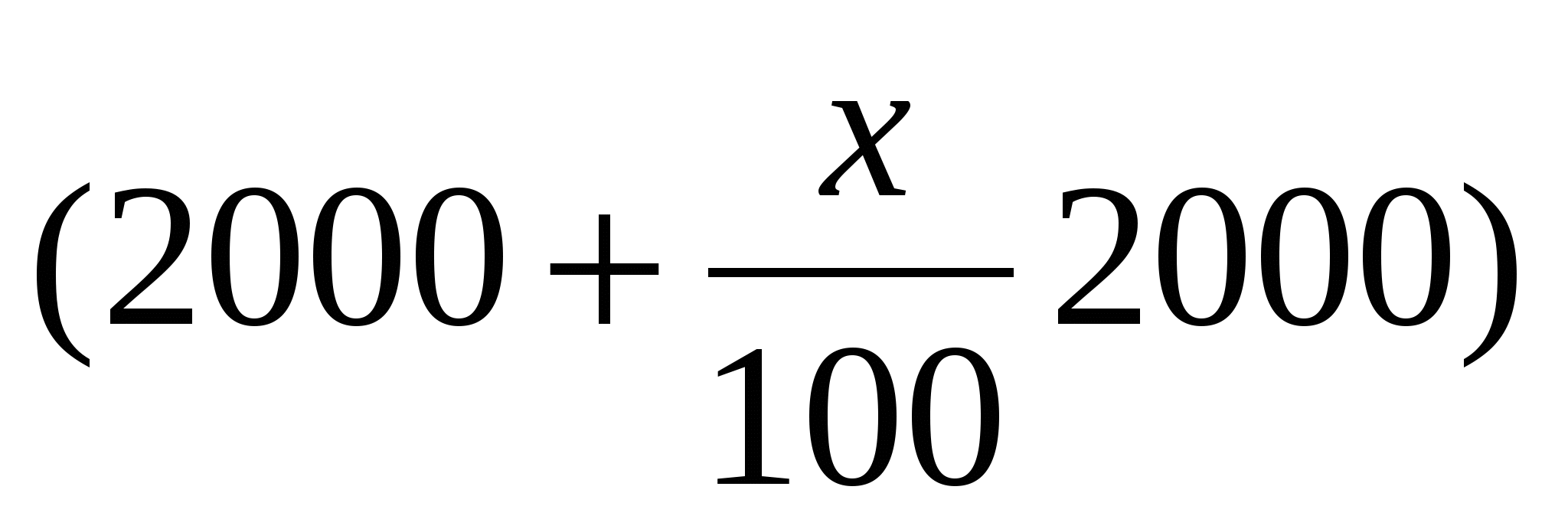 
рублей, т.е. (2000+20х) рублей.
Для расчета процентов за второй год мы должны принять за 100% уже сумму, имеющуюся на счете к началу года, т.е. (2000+20х) рублей. Тогда по прошествии второго года на счете окажется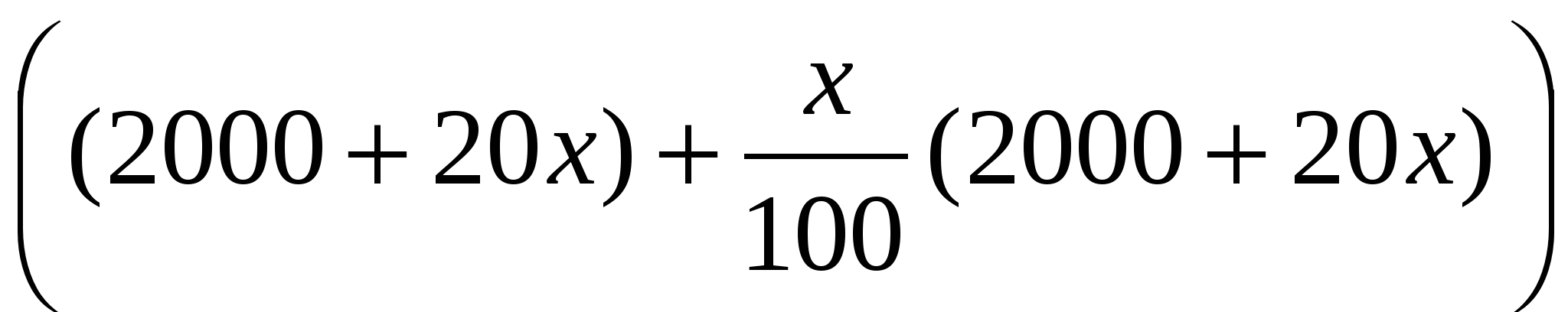 
рублей, т.е. (0,2х²+40х+2000) рублей. Что по условию задачи составляет 2420 рублей.
Составим и решим уравнение.
0,2х²+40х+2000=2420, х=-210, х=10.
Так как по условию задачи значение х должно быть положительным, то х=10. Итак, ежегодная сумма вклада увеличивалась на 10%.
Ответ: на 10%.
Дидактический материал для учащихся.
1. На одной котельной запасено на зиму в три раза меньше торфа, чем на второй. Если на первую котельную завести 680 т топлива, а на вторую 220 т, то торфа на обеих котельных станет поровну. Сколько всего топлива запасено на обеих котельных?
2. Один из хозяев двух равных по площади смежных участков решил купить у другого 2 га земли. В этом случае площадь участка продавца будет составлять 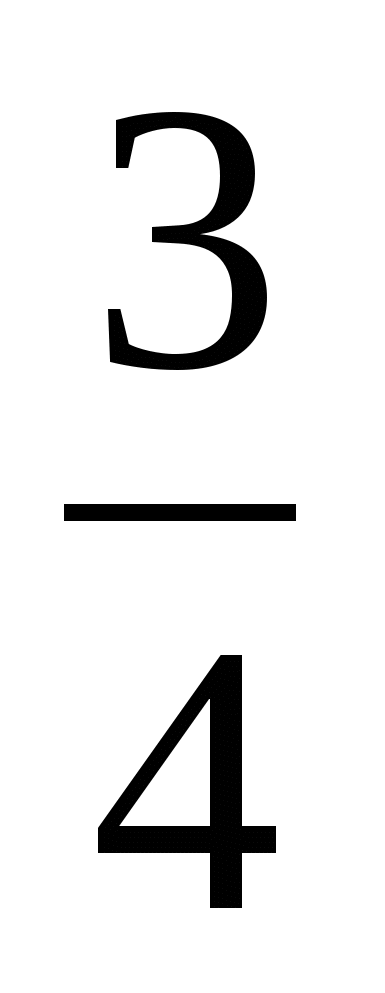площади участка покупателя. Какова первоначальная площадь каждого участка?
3. От трех библиотек университета поступили заявки на приобретение книг. Стоимость книг в заявке второй библиотеки составляет 50% от заявки первой, а стоимость книг в заявке первой библиотеки – 60% от заявки третьей. Стоимость книг в заявке третьей библиотеки превышает заявку второй на 27 тысяч рублей. Какова общая стоимость книг ( в тыс.руб.) в заявках трех библиотек?
4. При заключении договора с фирмой на изготовление и установку дверей заказчик заплатил 39000 рублей. Согласно договору в случае нарушения фирмой сроков доставки и монтажа дверей фирма обязуется за каждый просроченный день выплачивать заказчику 1,5% суммы договора. Сроки договора были нарушены фирмой, и она возвратила заказчику 2340 рублей. На сколько дней позже срока были установлены двери?
5. Писатель, получив гонорар 150 000 рублей, решил положить эти деньги в банк. Для уменьшения риска он разделил всю сумму на две части и положил их в два банка: в первый под 4% годовых, а во второй- под 3% годовых. Через год первый вклад принес доход в два раза больший, чем второй. Какую сумму положил писатель во первый банк?
6. Две картины, общей стоимостью 30 000 рублей продали на аукционе с прибылью в 40%, причем от продажи одной картины было получено 25% прибыли, а от другой 50%. Найдите стоимость боле дорогой картины.
7. Владелец дискотеки имел стабильный доход. В погоне за увеличением прибыли он повысил цену на билеты на 25%. Количество посетителей резко уменьшилось, и владелец стал нести убытки. Тогда он вернулся к первоначальной цене билетов. На сколько процентов владелец дискотеки снизил новую цену билетов, чтобы она стала первоначальной?
Для привлечения клиентов владельцы медицинского центра снизили стоимость услуг на 20%. По окончании рекламной акции они вернулись к старым расценкам. На сколько процентов для этого они повысили стоимость услуг в центре?
До распродажи мужской и женский костюмы стоили одинаково. В начале распродажи на 15% была снижена цена на мужской костюм, но покупателя не нашлось, поэтому еще раз снизили цену на 15%. На сколько процентов нужно однократно снизить цену на женский костюм, чтобы оба костюма снова стали стоить одинаково?
Занятие 5.
Пример 14. Сплавили 300 г сплава олова и меди, содержащего 60% олова, и 900 г сплава олова и меди, содержащего 80% олова. Сколько процентов олова в получившемся сплаве?
Решение. масса олова в первом сплаве равна 0,6·300=180(г), во втором – 0,8·900=720(г). Тогда масса олова в новом сплаве 180+720=900(г). Масса нового сплава равна 300+900=1200(г), процентное содержание в нем олова равно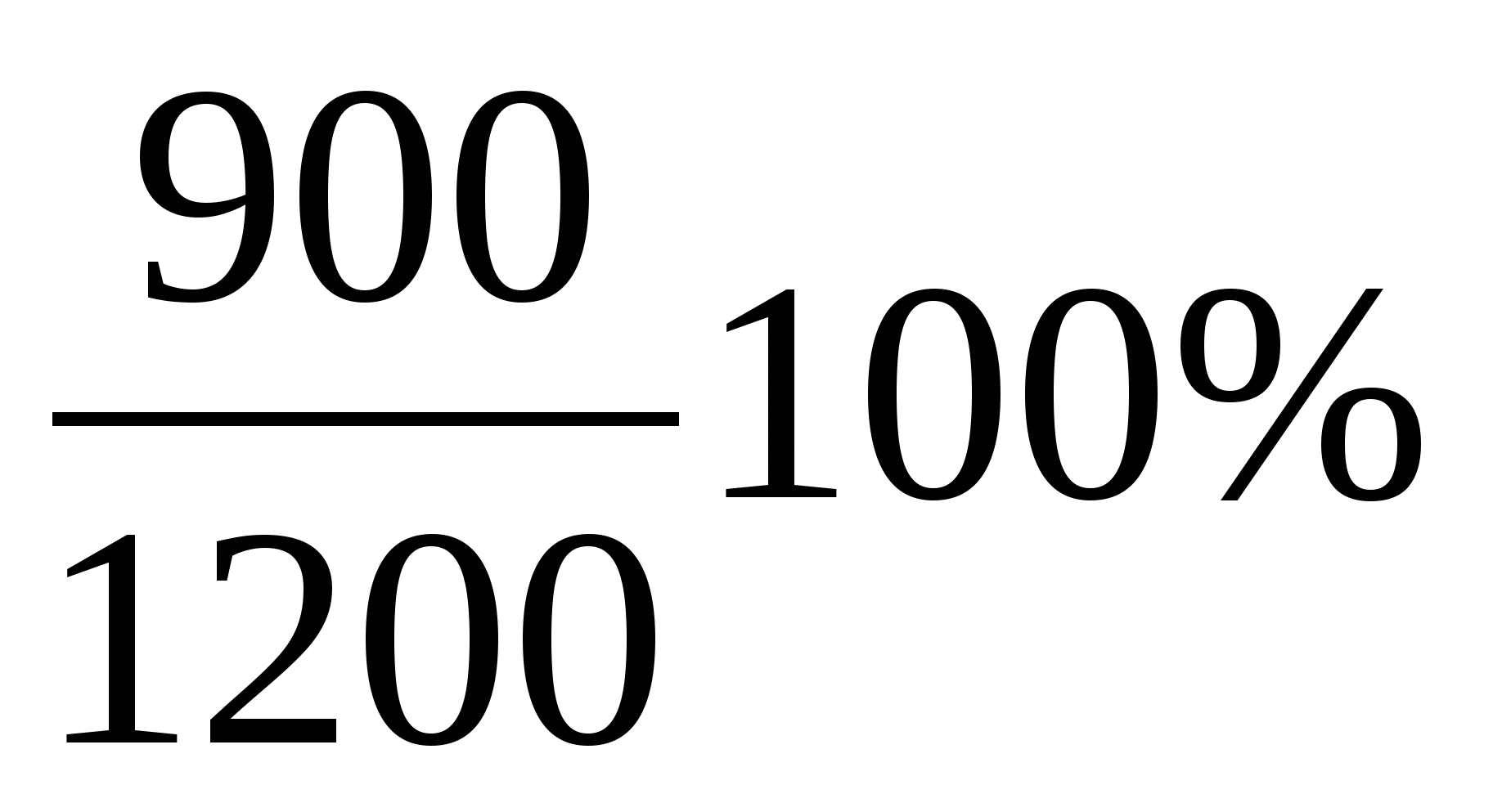 
=75%.
Ответ: 75%.
Пример 15. В смеси спирта и воды спирта в 4 раза меньше, чем воды. Когда к этой смеси добавили 20 л воды, получили смесь с содержанием спирта 12%. Сколько воды было в смеси первоначально?
Решение. Пусть в смеси было х л спирта, тогда объем воды в ней 4х л.
В новой смеси количество спирта осталось прежним х л, объем воды в ней (4х+20)л, объем смеси равен (х+4х+20) л, а процентное содержание спирта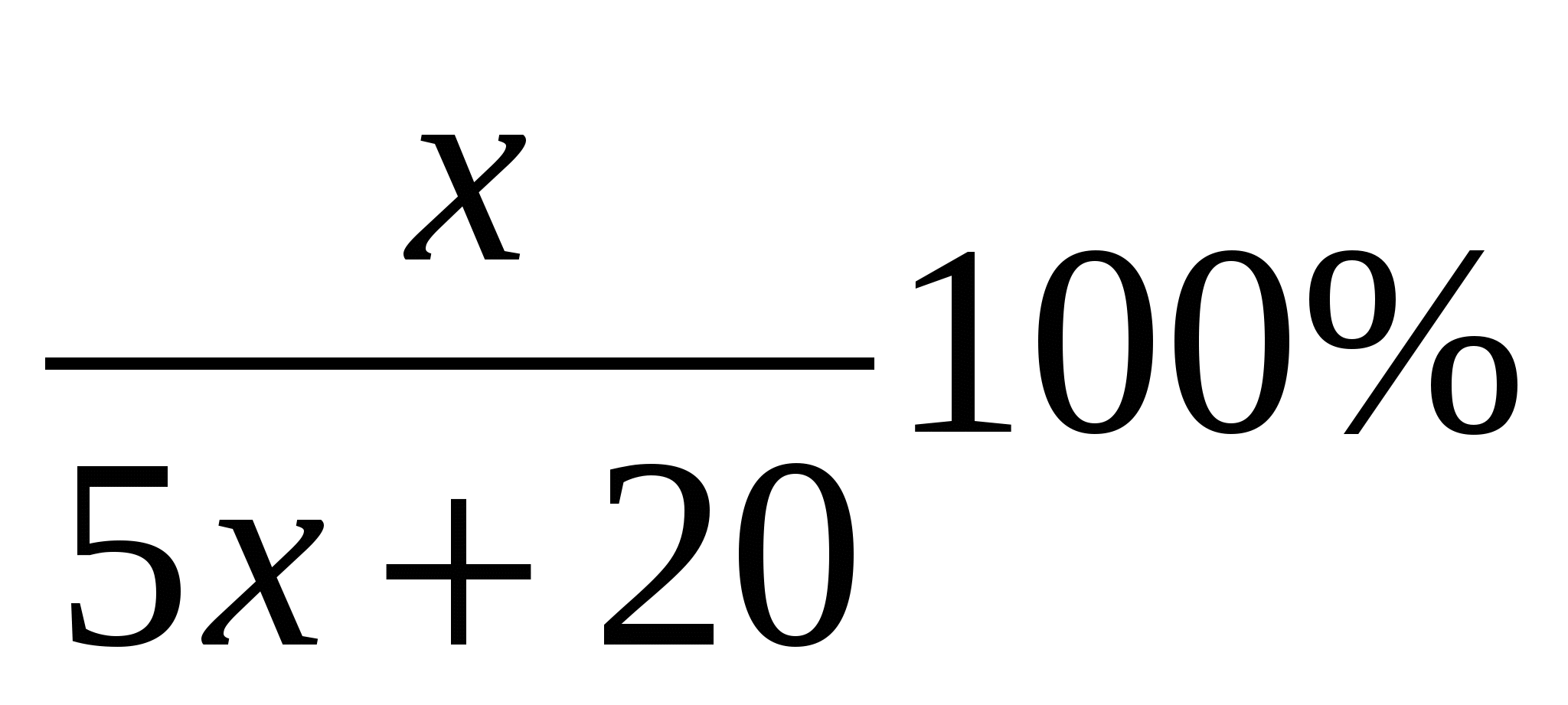 
, что по условию задачи составляет 12%. Составим и решим уравнение: 
;
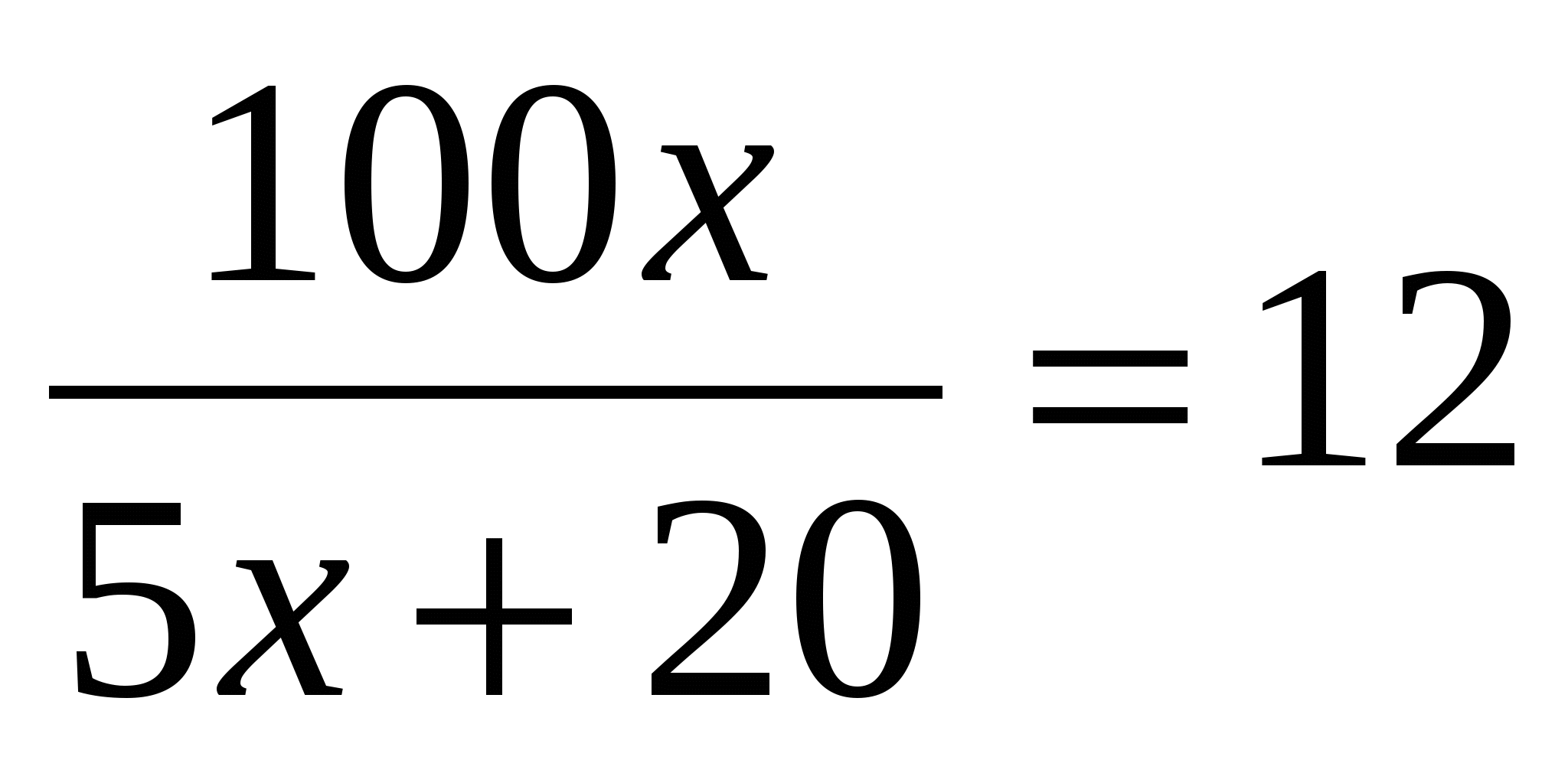100х=12(5х+20), х=6.
Итак, первоначально в смеси было 6 л спирта.
Дидактический материал для учащихся.
Сплавили 2 кг сплава цинка и меди, содержащего 20% цинка, и 6 кг сплава цинка и меди, содержащего 40% цинка. Найдите процентную концентрацию меди в получившемся сплаве.
Смешали 300 г 60%-ного раствора серной кислоты и 200 г 80%-ного раствора серной кислоты. Сколько процентов серной кислоты в этом растворе?
Имеется два сплава. Один содержит 2,8 кг золота 1,2 кг примесей, другой- 2,7 кг золота и 0,3 кг примесей. Отрезав по куску от каждого сплава и сплавив их , получили 2 кг сплава с содержанием золота 85%. Сколько килограммов металла отрезали от второго сплава?
Отношение массы олова к массе свинца в куске 2:3. Этот кусок сплавили с куском олова весом 3 кг и получили новый сплав с содержанием свинца 10%. Найдите массу олова в новом сплаве.
Для приготовления маринада необходим 2%-ный раствор уксуса. Сколько нужно добавить воды в 100 г 9%-ного раствора уксуса, чтобы получить раствор для маринада?
Для размножения водорослей вода в аквариуме должна содержать 2% морской соли. Сколько литров пресной воды нужно добавить к 80 л морской воды с 5%-ным содержанием соли, чтобы получить воду, пригодную для заполнения аквариума?
Огурцы содержат 99% воды. В магазин привезли 1960 кг свежих огурцов, но в результате неправильного хранения содержание воды в огурцах понизилось до 98%. Сколько килограммов огурцов поступило в продажу?
В ювелирной мастерской имеется два сплава золота различной пробы: с содержанием золота 58% и 95%. Сколько граммов сплава с 95%-ным содержанием золота надо взять, чтобы получить 37 г сплава с 70%-ным содержанием золота?
Занятие 6.
Арифметическая прогрессия.
Формула n-го члена арифметической прогрессии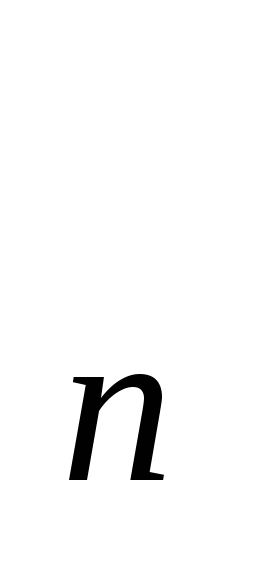: а
=а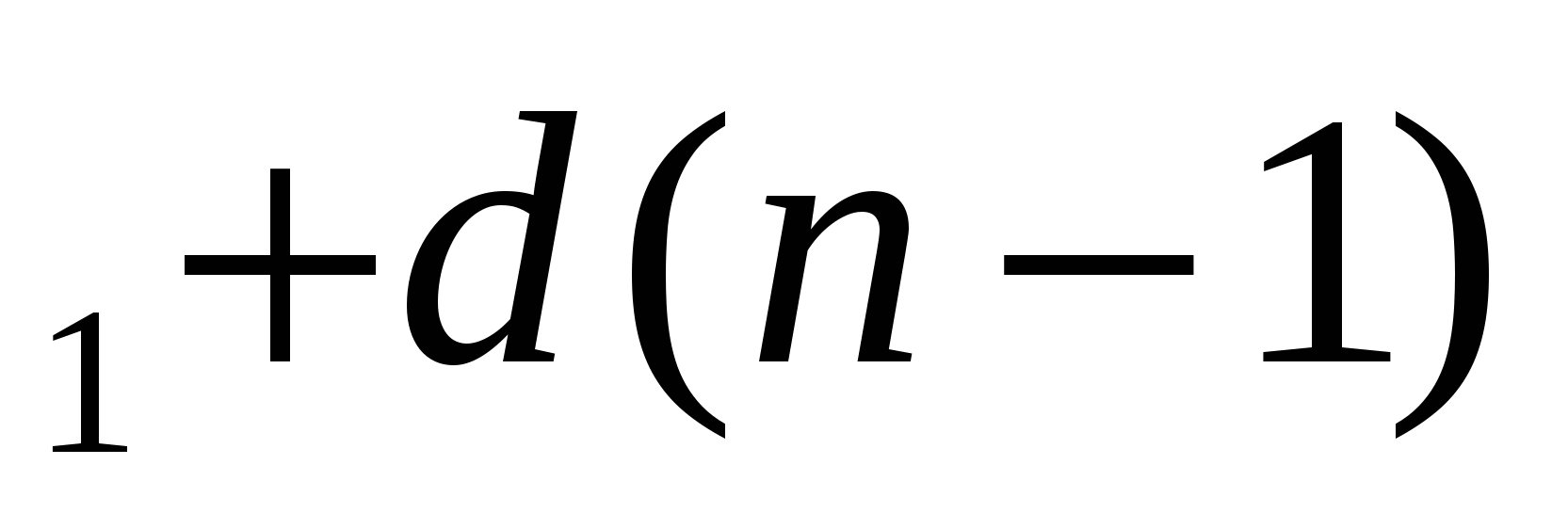
.
Формулы суммы n- первых членов арифметической прогрессии:
.
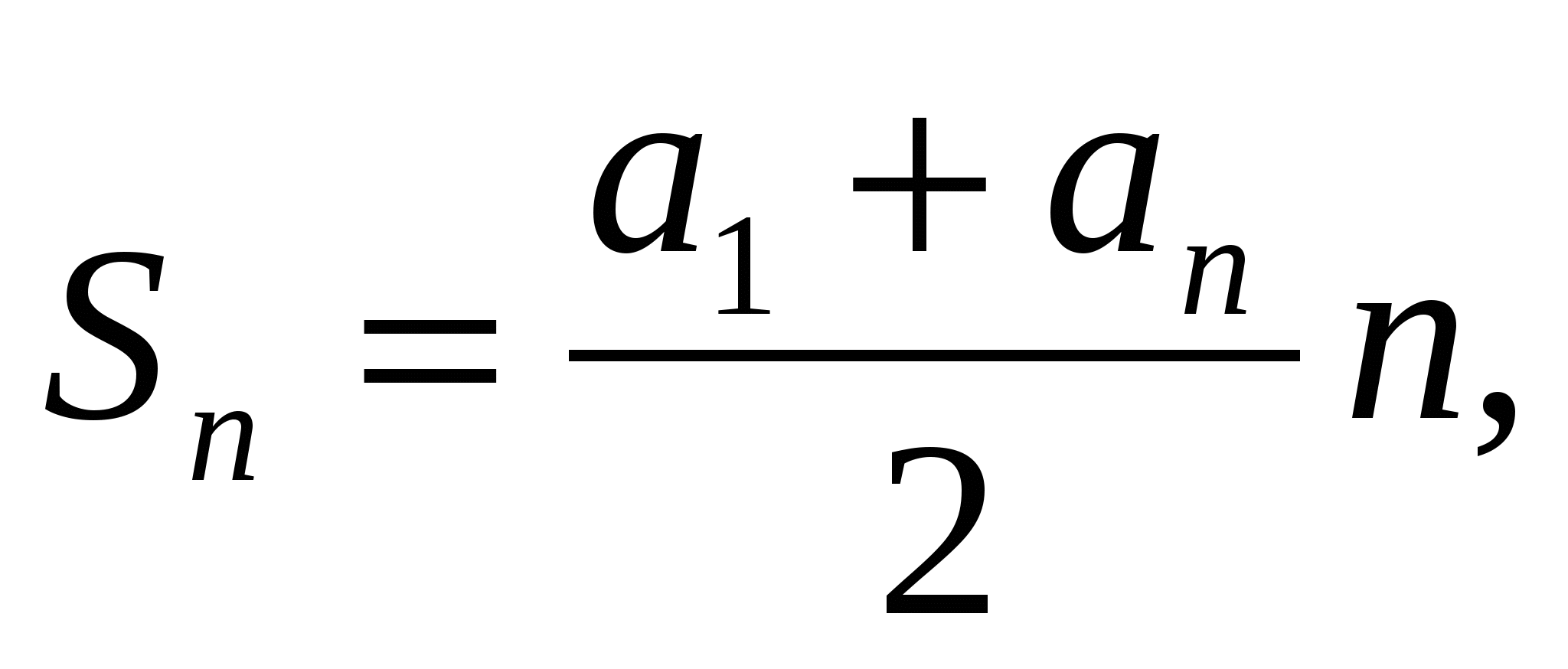
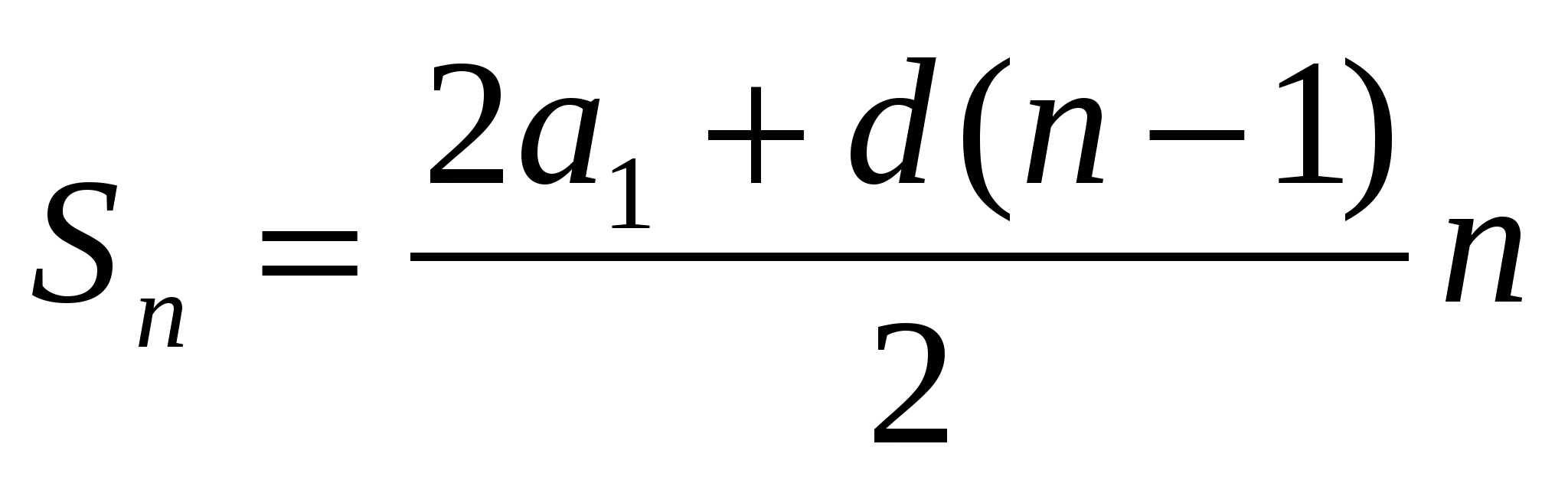Пример 16. Цена костюма снижалась несколько раз на одно и то же число рублей. После третьего снижения она составила 2460 рублей, а после одиннадцатого снижения- 1980 рублей. После скольких снижений цена костюма составит 50% первоначальной цены?
Решение. Последовательность цен на костюм – арифметическая прогрессия (а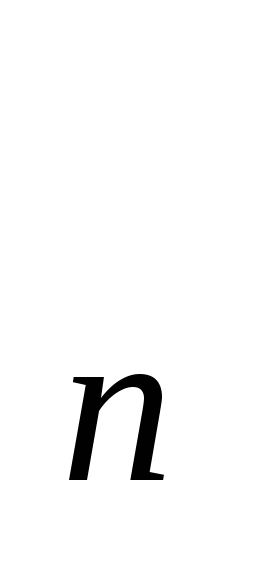). Ее первый член а
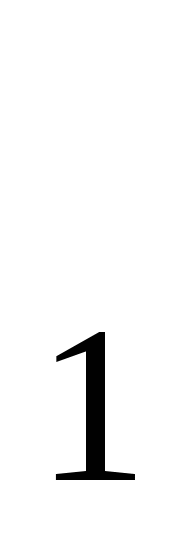- начальная цена костюма, а разность d- величина, на которую каждый раз уменьшалась цена костюма.
Обратите внимание, что цена после третьего снижения- четвертый член данной прогрессии, а цена после одиннадцатого снижения- двенадцатый член данной прогрессии. Так как а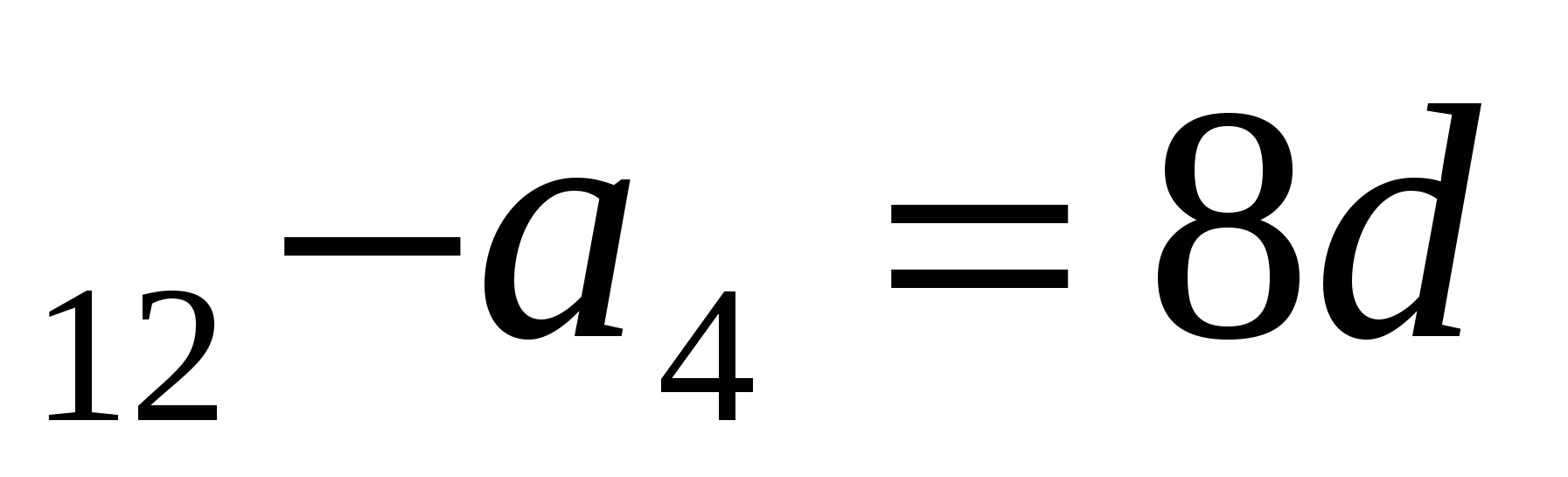
, то 8d=1980-2460, d=-60.
Узнаем теперь первоначальную цену костюма: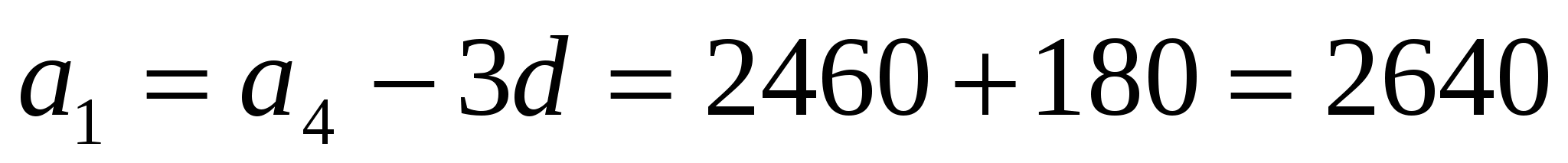 
. Начальная цена была равной 2640 рублей. Чтобы составить 50% от начальной, цена должна уменьшиться на 2640:2 =1320 (руб.).
Это произойдет за 1320:60=22 понижения.
Ответ: 22 понижения.
Пример 17. Во время распродажи с 21 июня по 30 июня количество проданных сервизов ежедневно увеличивалось на одно и то же число. При этом с 21 по 24 июня было продано 460 сервизов, а с 23 по 26 июня было продано 700 сервизов. Сколько сервизов было продано за все время распродажи?
Решение. Последовательность количества проданных за день сервизов – арифметическая прогрессия (а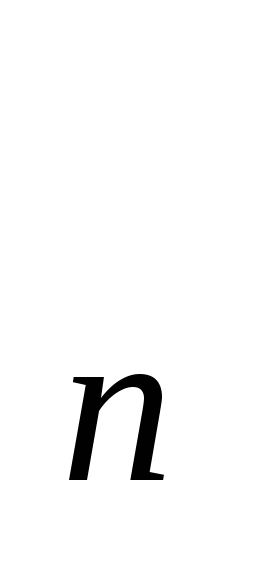). Ее первый член а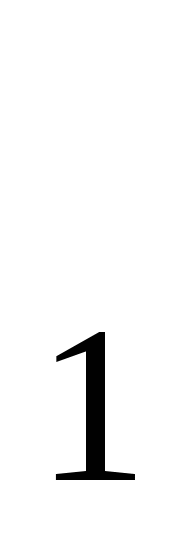-количество сервизов, проданных 21 июня, а разность d- величина, на которую каждый день увеличивалось количество проданных сервизов.
Количество проданных сервизов с 21 по 24 июня:
.
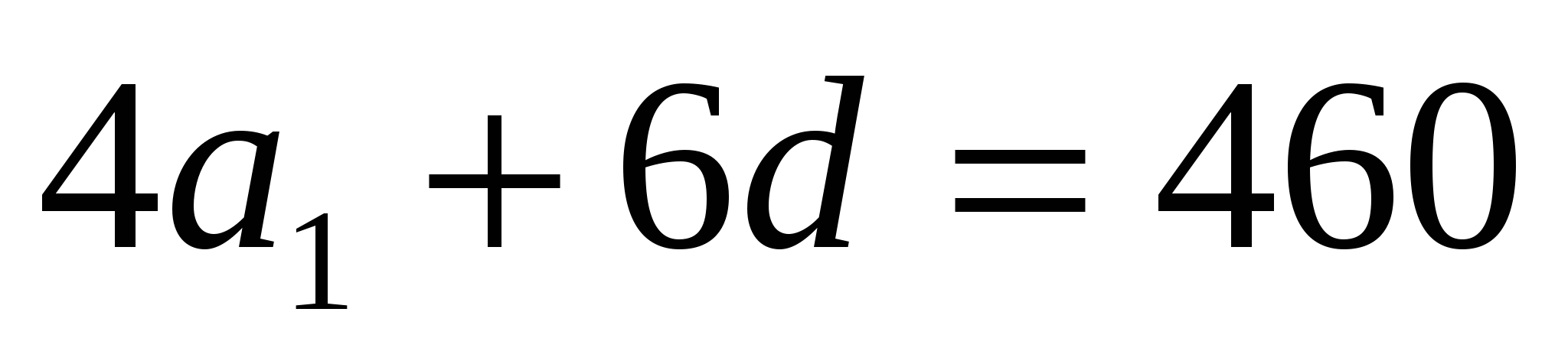Количество проданных сервизов с 23 по 26 июня:
.
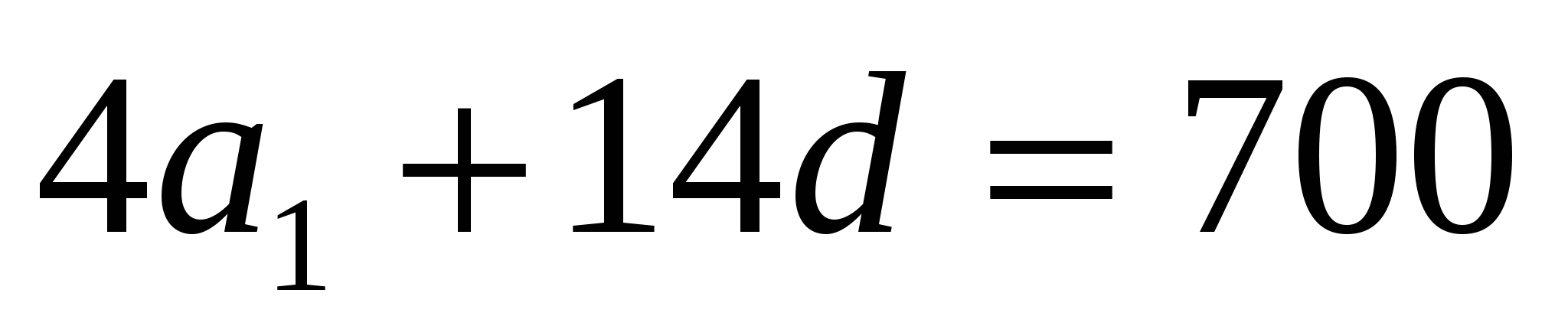Составим систему уравнений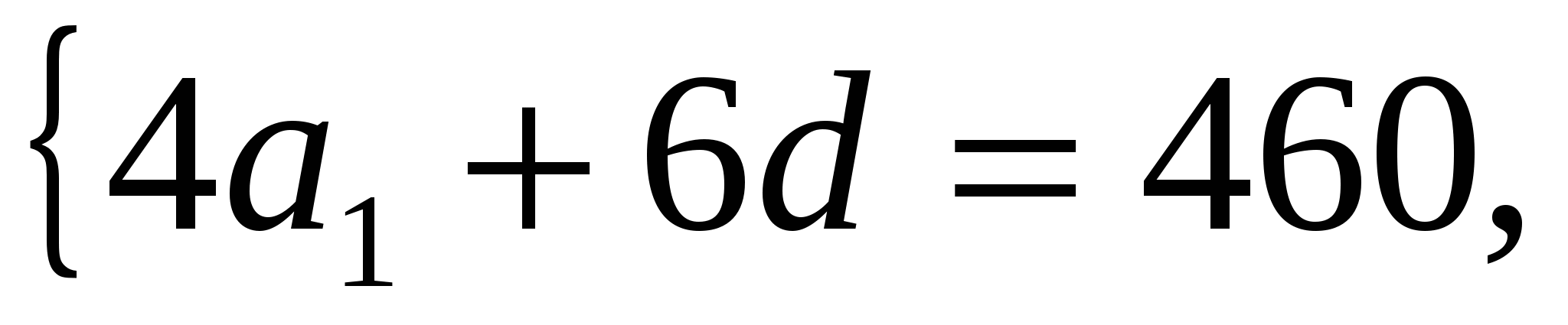 
.
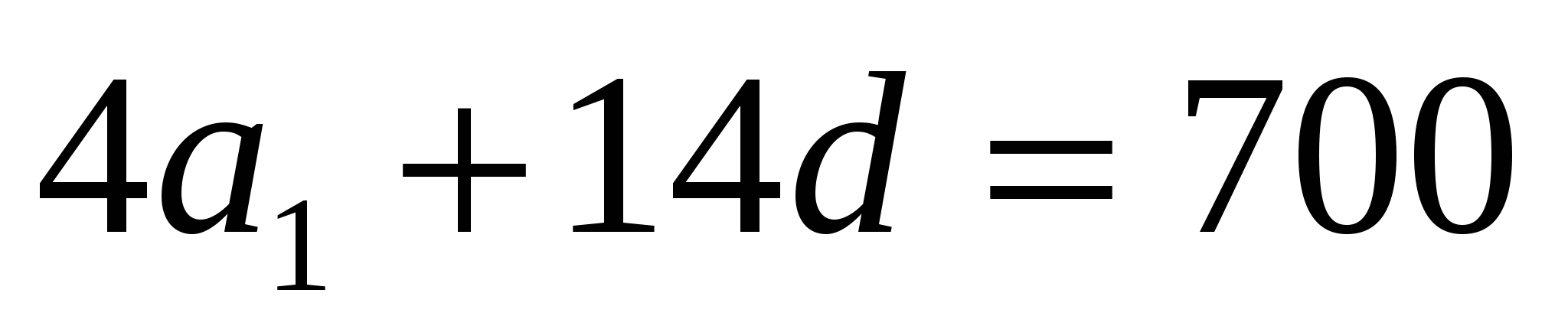Решая систему, получим а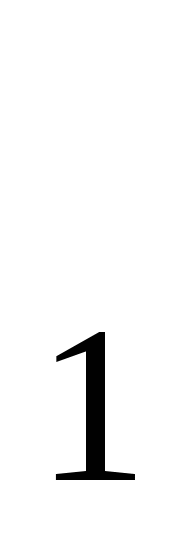=70, d=30. Количество проданных за время распродажи сервизов – сумма десяти первых членов данной арифметической прогрессии. 
.
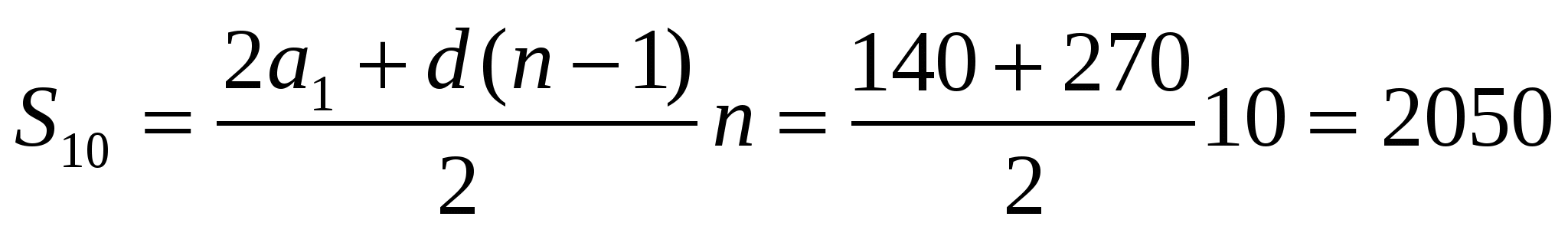Итак, за время распродажи было продано 2050 сервизов.
Ответ: 2050 сервизов.
Дидактический материал для учащихся.
1. В течение недели перед экзаменом ученик занимался 12 ч 15 мин, причем ежедневно он тратил на подготовку к экзамену на одно и то же число минут больше, чем в предыдущий день. В первые три дня он занимался в общей сложности 3 ч 45 мин. Сколько минут он занимался накануне экзамена?
2. В первые 7 дней марта количество продаваемых в парфюмерном магазине подарочных наборов увеличивалось на одно и то же число ежедневно. Сколько продали наборов за 7 дней, если во второй день продали 95 наборов, а в пятый – 140?
3. Фирма ежемесячно увеличивала выпуск пылесосов на одно и то же число. При этом за три летних месяца было изготовлено 2790 пылесосов, а за три осенних – 3060 пылесосов. Сколько пылесосов выпустила фирма с января по декабрь включительно?
4. Студенческая бригада подрядилась выложить керамической плиткой автостоянку рядом с летним кафе площадью 288 м². Приобретая опыт, студенты в каждый последующий день, начиная со второго, выкладывали на 2м² больше, чем в предыдущий, и запасов плитки им хватило ровно на 11 дней работы. Планируя, что производительность труда будет увеличиваться таким же образом, бригадир определил, что для завершения работы потребуется еще 5 дней. Сколько коробок с плитками ему надо заказать, если 1 коробки хватает на 1,2 м² покрытия, а для замены некачественных плиток понадобится 3 коробки?
Занятие 7.
Геометрическая прогрессия- числовая последовательность, в которой каждый член, начиная со второго, равен предыдущему, умноженному на одно и то же число q (знаменатель геометрической прогрессии): b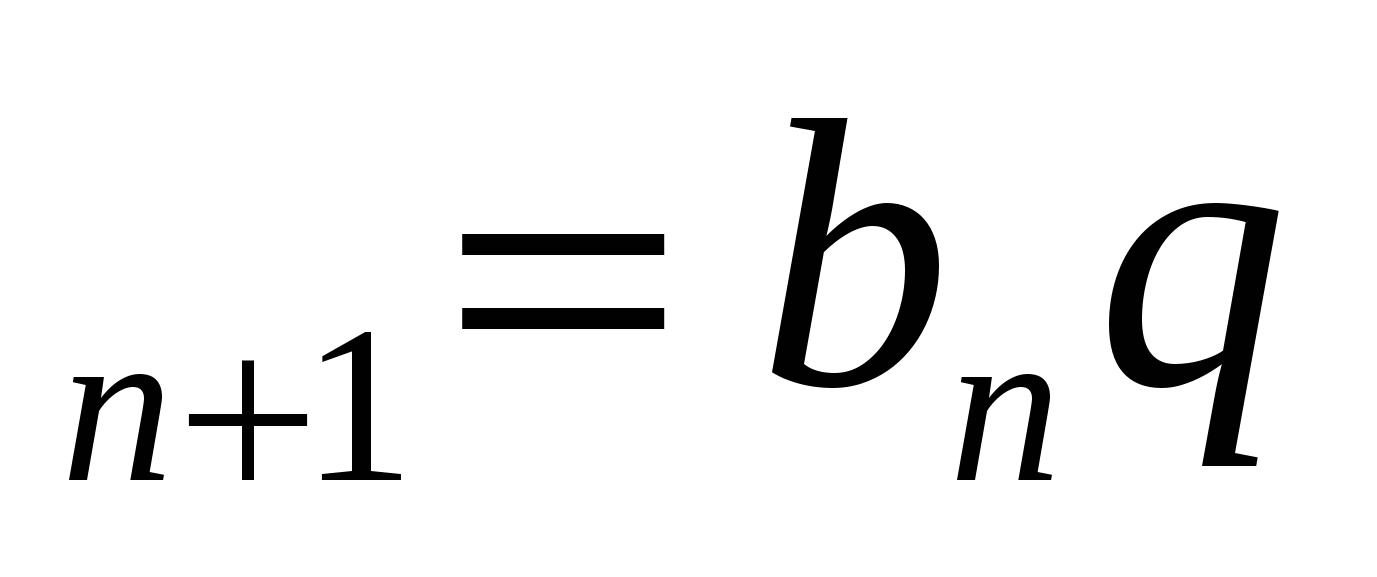
.
Формула n-го члена геометрической прогрессии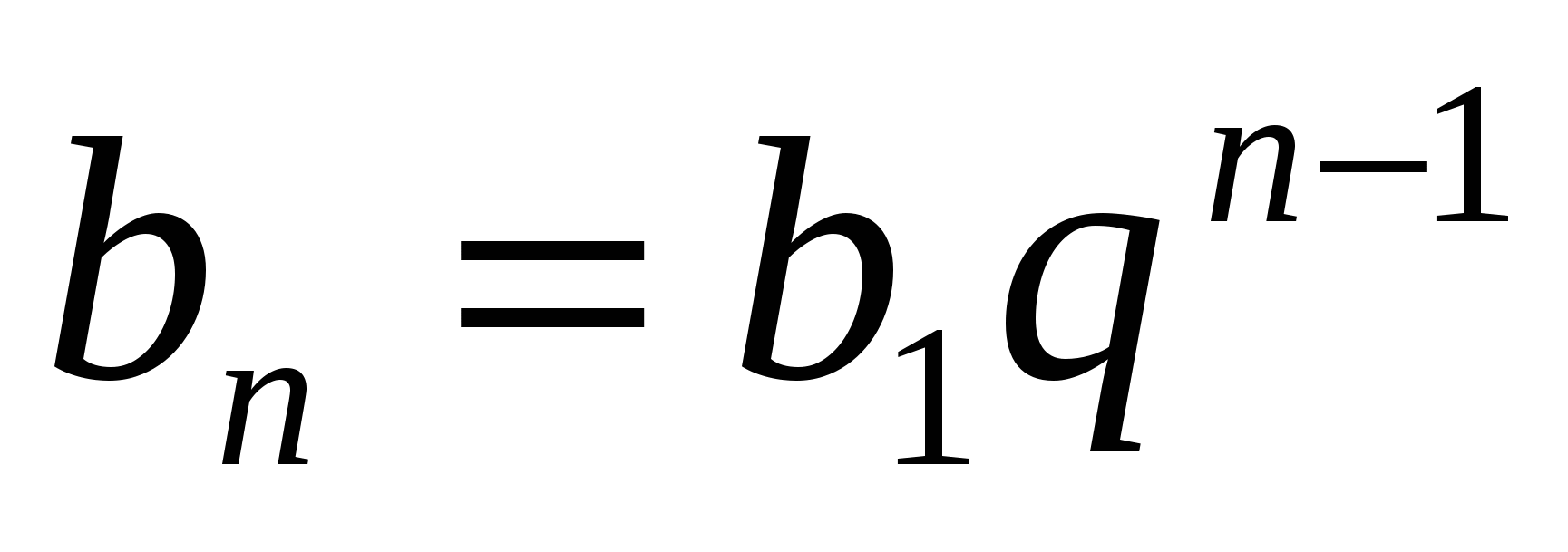 
.
Формула суммы n-первых членов геометрической прогрессии
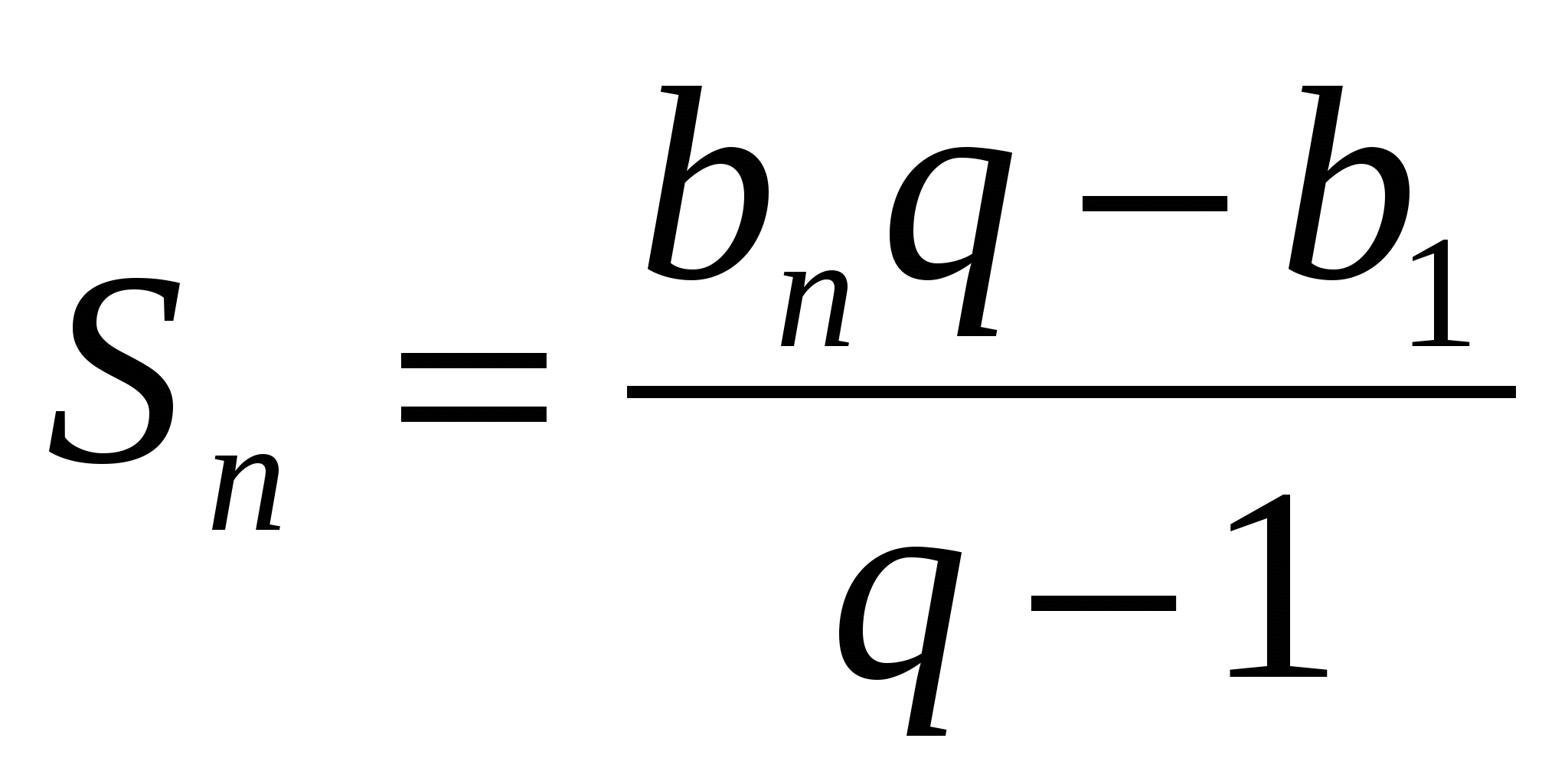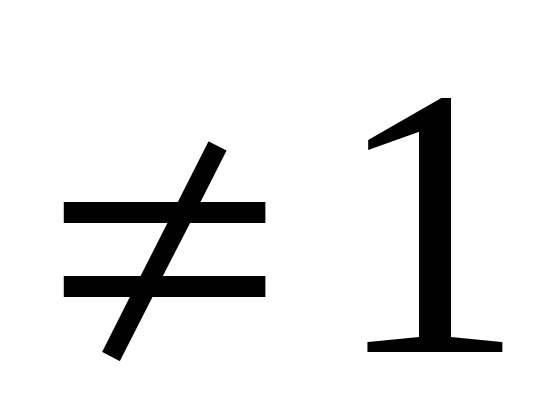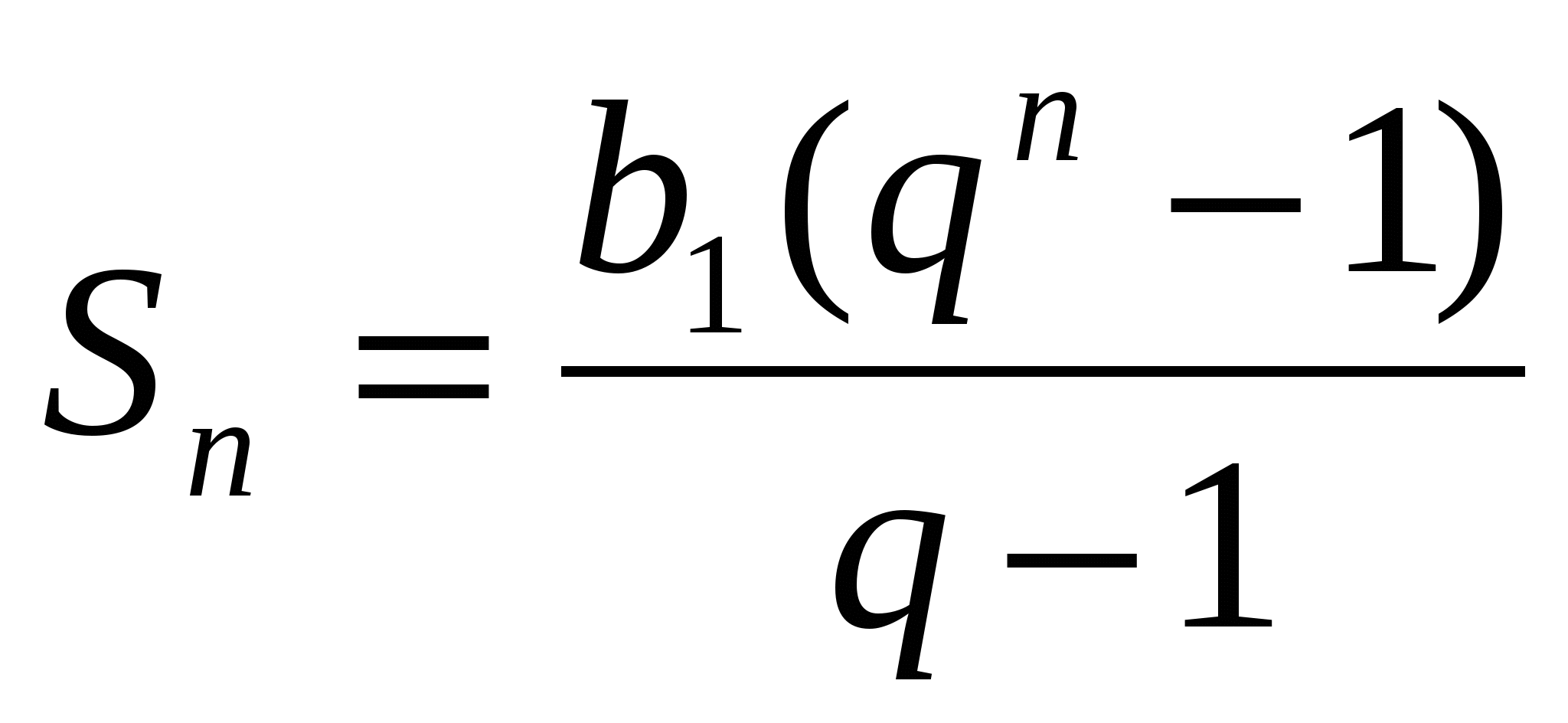, q
, 
, q.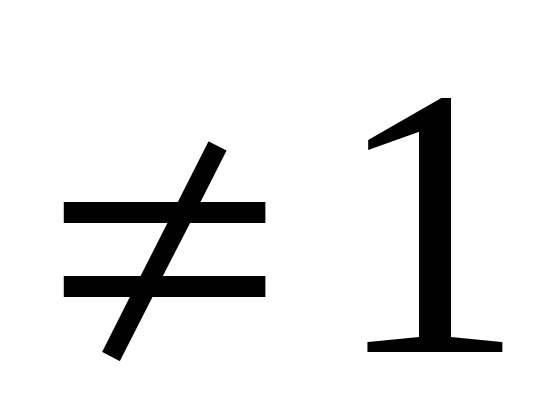
Пример 18. Число посетителей вновь открывшегося кафе в первые 8 дней работы увеличивалось ежедневно в одно и то же число раз. Сколько человек посетило кафе в восьмой день, если в третий день было 288 посетителей, а в пятый – 648?
Решение. Последовательность чисел, равных количеству посетителей кафе в каждый из восьми дней- геометрическая прогрессия. В ней известны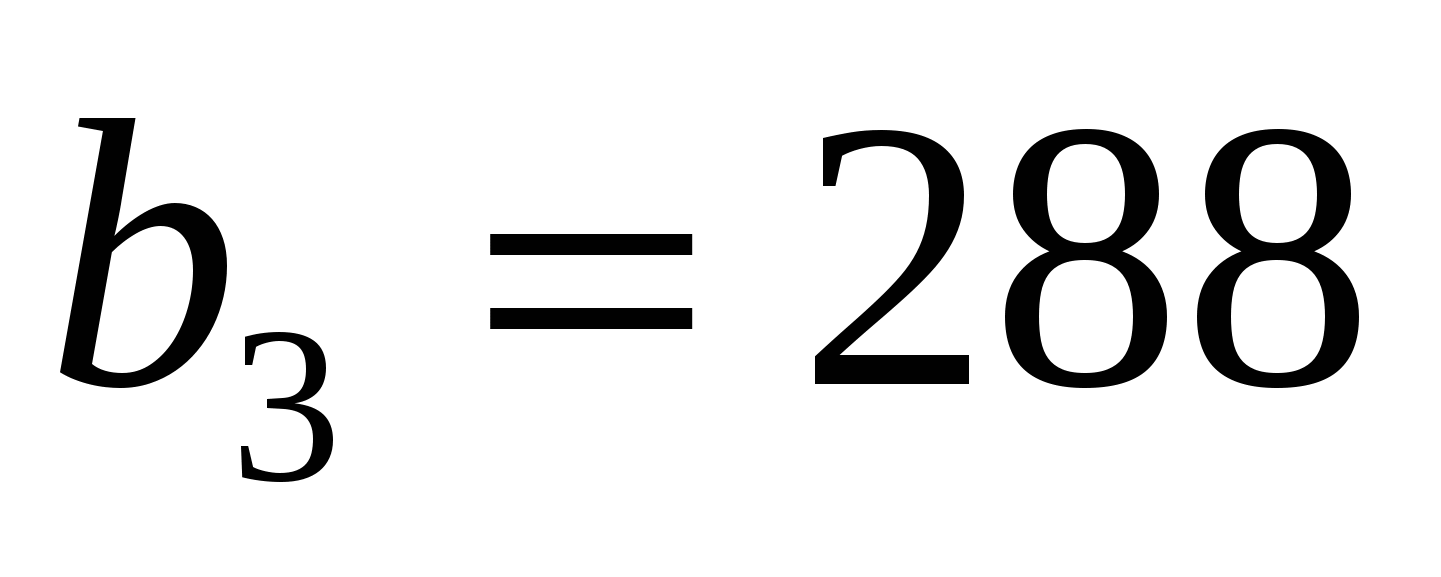 
, 
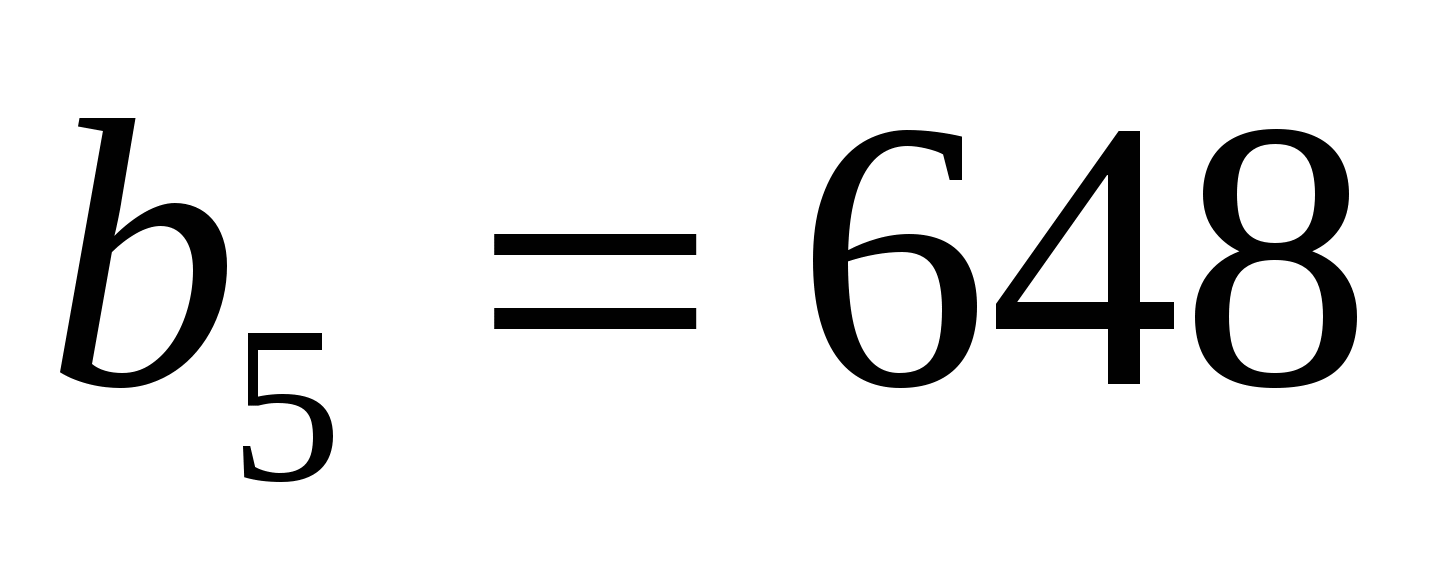, а найти нужно b
.
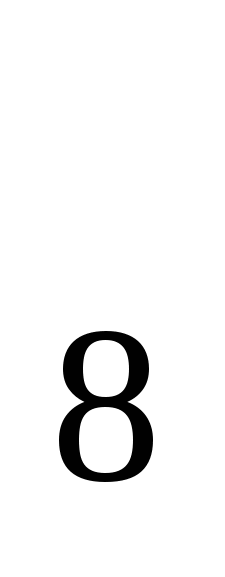Найдем знаменатель прогрессии q.
Так как q²=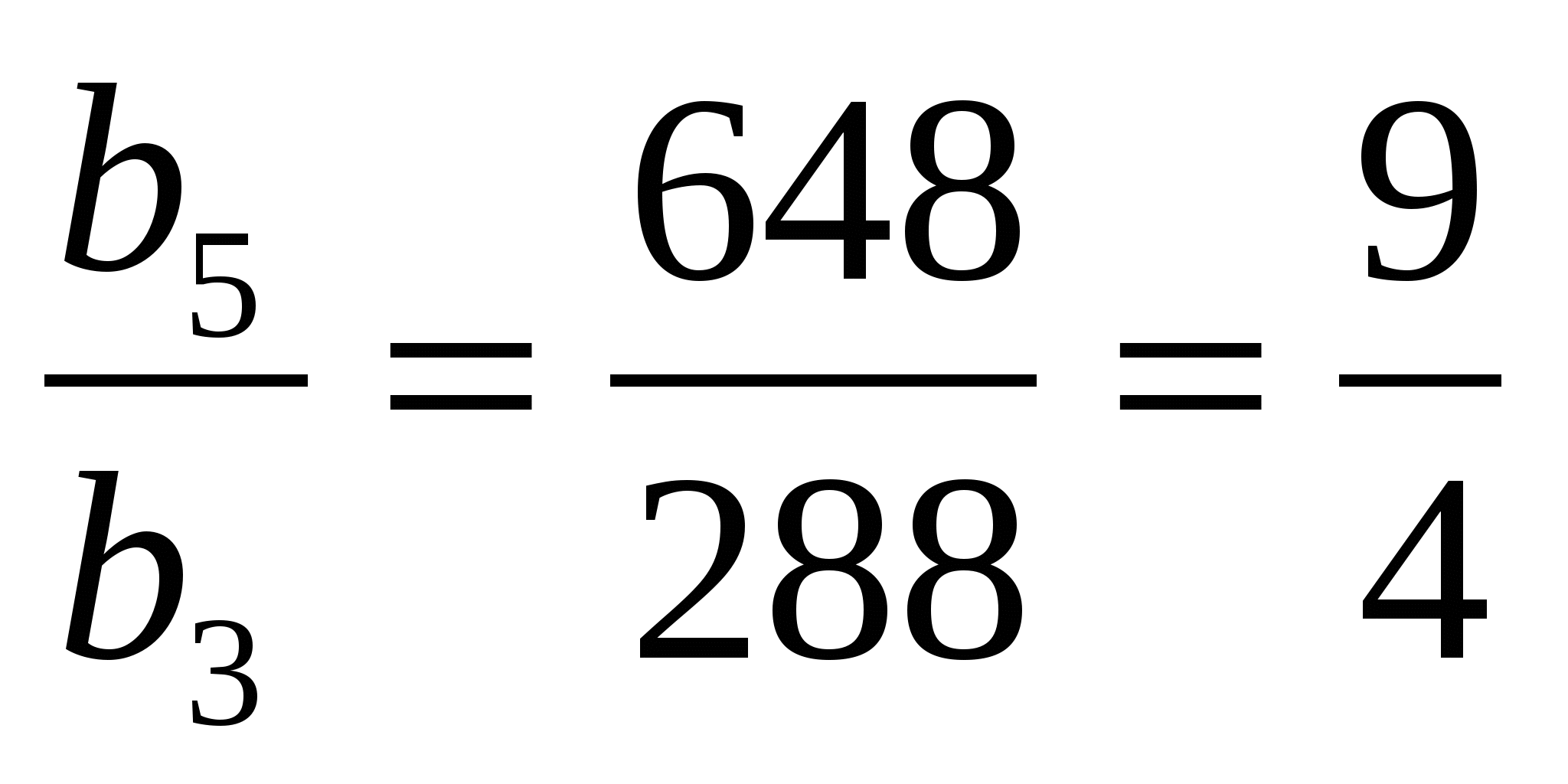
и q>0, то q=1,5. Тогда 
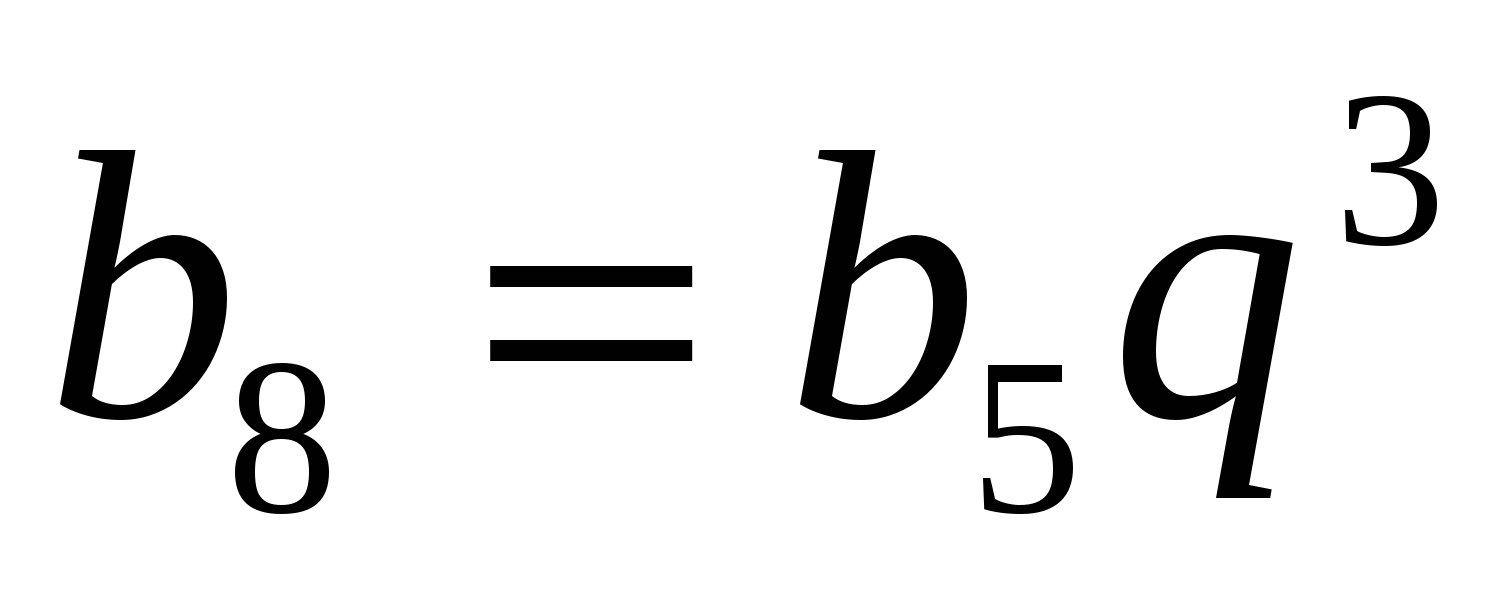=2187.
Итак, в восьмой день кафе посетило 2187 человек.
Ответ: 2187 человек.
Пример 19. В первую неделю работы очистных сооружений после их реконструкции количество вредных выбросов в реку ежедневно уменьшалось в одно и то же число раз. Сколько вредных веществ попало в реку за эту неделю, если во второй день в реку попало 128 м³ , а в пятый день-16 м³ вредных веществ?
Решение. Последовательность объемов выбросов в каждый из семи дней – геометрическая прогрессия, в которой даны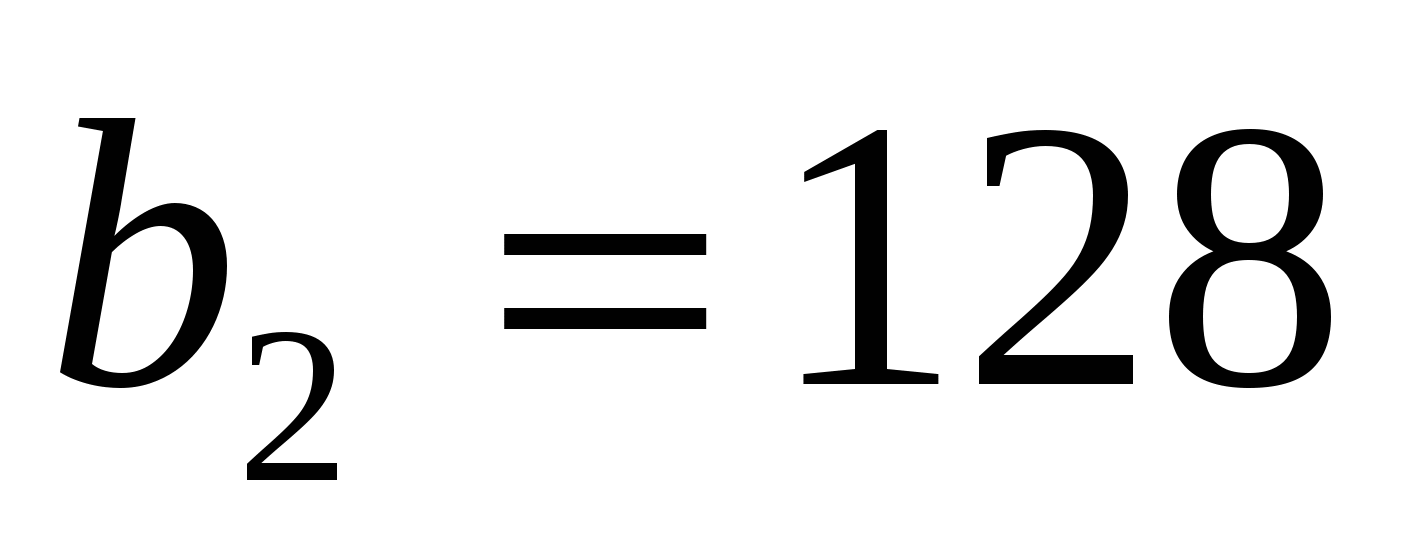 
, 
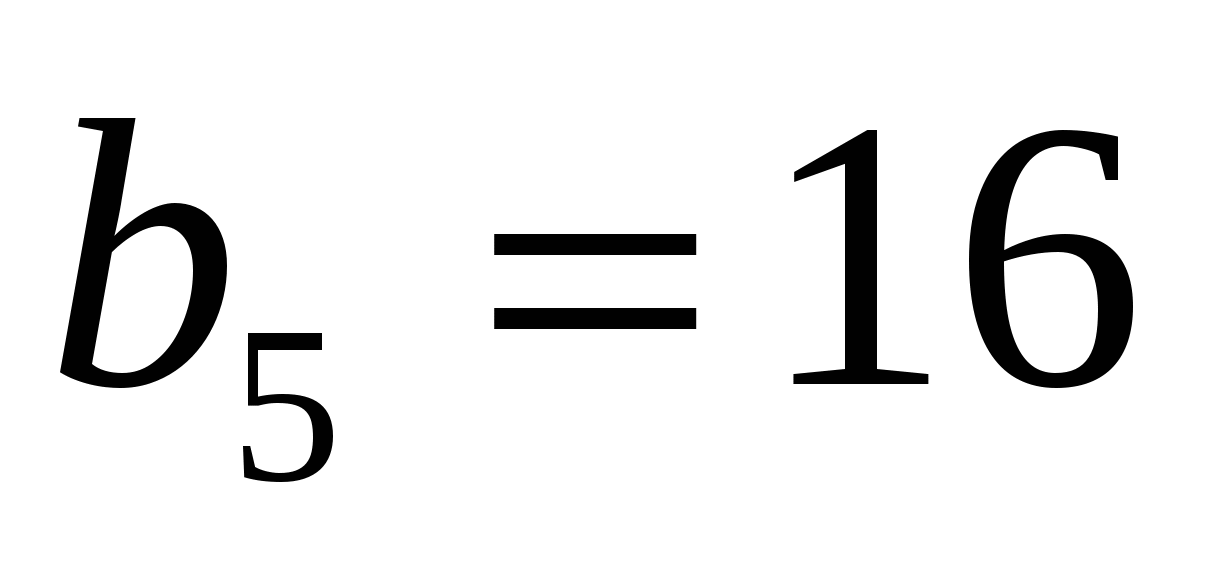. А найти нужно сумму первых семи ее членов S
.
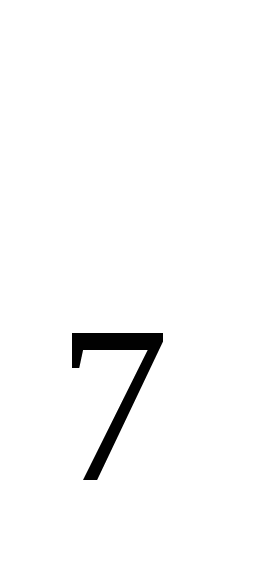Найдем знаменатель прогрессии q. Так как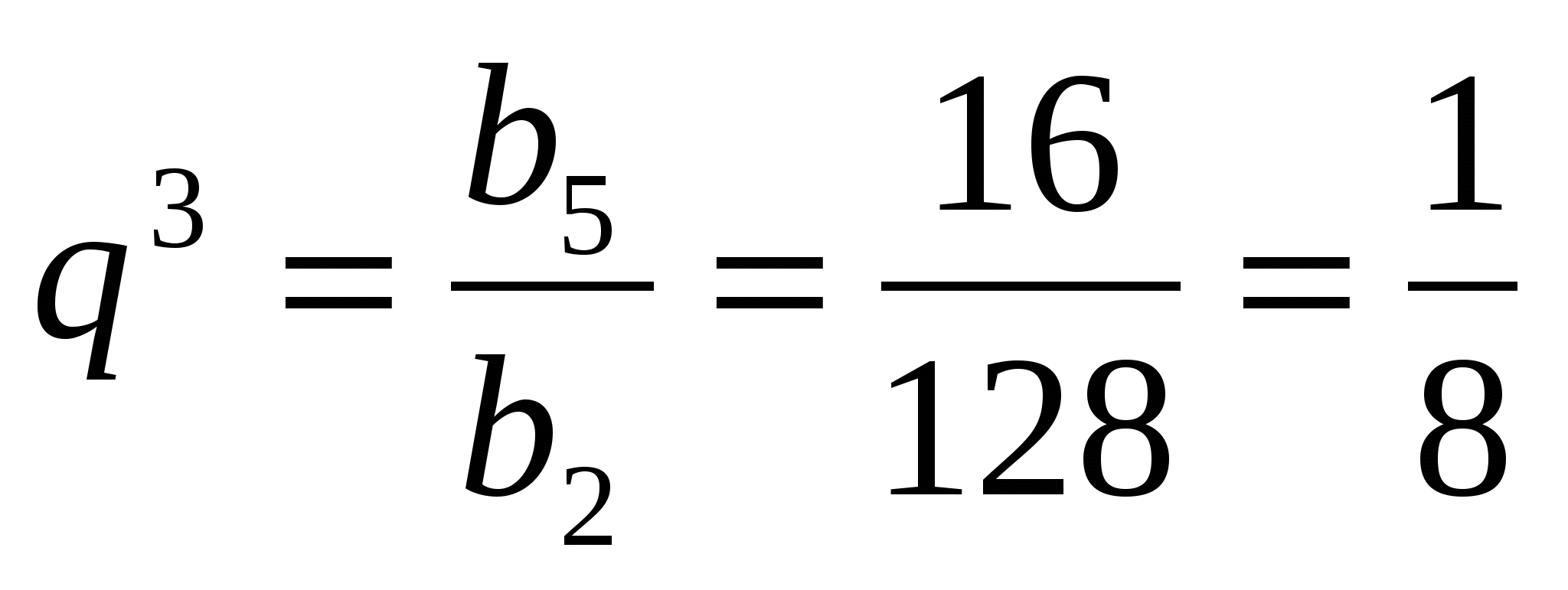 
, то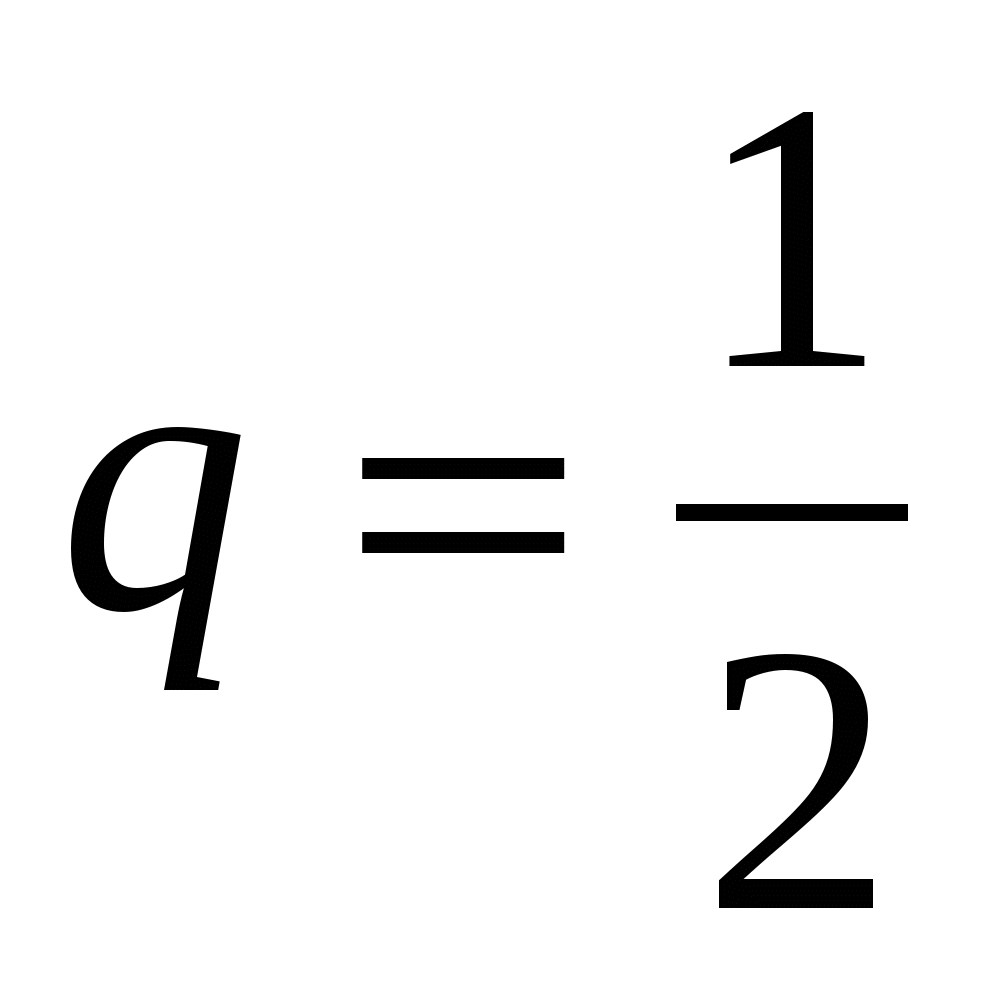 
. Тогда ,
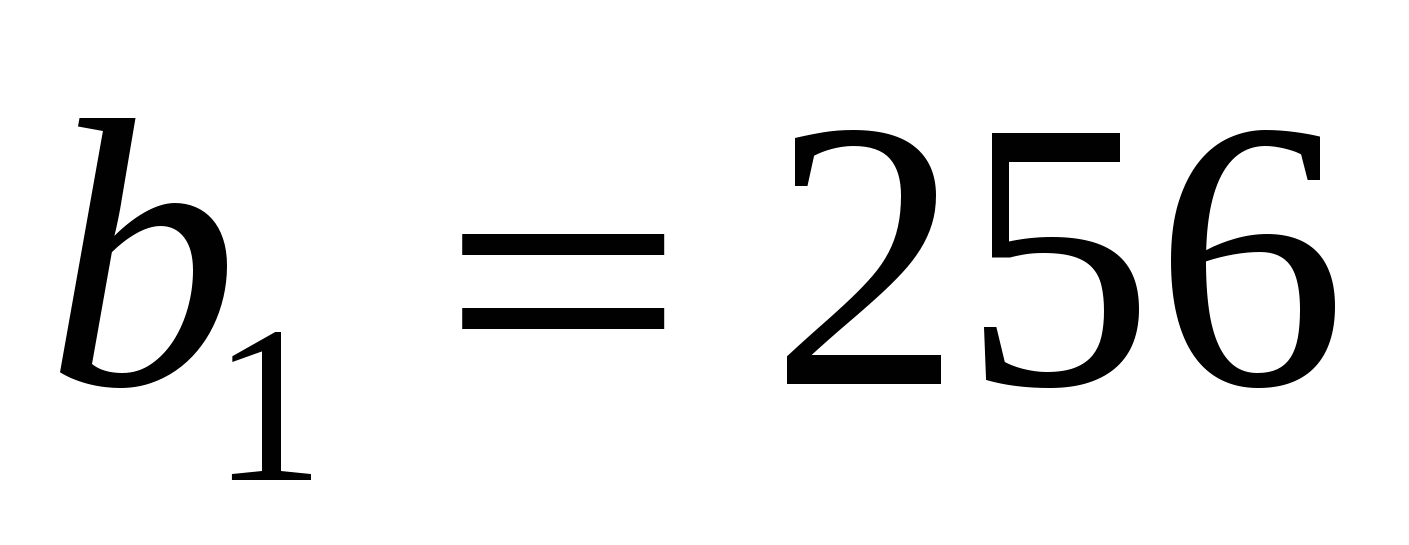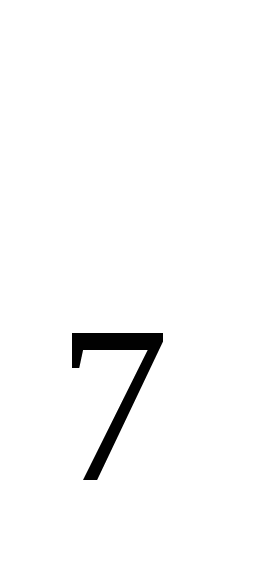, S=508.
Итак, за неделю в реку попало 508 м³ вредных веществ.
Ответ: 508 м³.
Дидактический материал для учащихся.
1. В последнюю неделю мая количество продаваемых надувных игрушек для плавания маленьких детей ежедневно увеличивалось в одно и то же число раз. Найдите отношение количества проданных игрушек 31 мая к количеству проданных игрушек 30 мая, если 27 мая было продано 45 игрушек, а 29 мая – 405 игрушек?
2. Производительность линии по производству йогуртов в первые пять дней после реконструкции ежедневно увеличивалась в одно и то же число раз. Сколько йогуртов было произведено в пятый день, если во второй день произвели 1200 кг йогуртов, а в четвертый – 1728 кг йогуртов?
3. Себестоимость выпускаемой на новом конвейере продукции в первые полгода ежемесячно уменьшалась в одно и то же число раз. Найдите себестоимость продукции во второй месяц этого полугодия ( в тыс. руб.), если в четвертый месяц она составила 512 тыс.руб., а в последний месяц – 327, 68 тыс.руб.
Список использованной литературы
Булынин В. Применение графических методов при решении текстовых задач// Математика, 2005, № 14.
Дорофеев Г.В., Потапов М.К., Розов Н.Х. Пособие по математике для поступающих в вузы (избранные вопросы элементарной математики). – М.: Наука, 1996.
Егоров В.К. и др. Сборник задач по математике для поступающих во ВТУЗы. – М.: Высшая школа, 1993.
Колесникова Т.В., Минаева С.С. Типовые тестовые задания 9 класс. М.: «Экзамен», 2007.
Кочагин В.В., Кочагина М.Н. Алгебра. Государственная итоговая аттестация по новой форме. 9 класс. М.: «Эксмо», 2010.
Куланин Е.Д., Норин В.П., Федин С.Н., Шевченко Ю.А. 3000 конкурсных задач по математике. – М.: Айрис-пресс, 2003.
Крайнева Л.Б. Сборник тестовых заданий для тематического и обобщающего контроля. Алгебра – 9. М.: «Интеллект - Центр», 2009.
Лурье М.В., Александров Б.И. Задачи на составление уравнений. – М.: Наука, 1990.
Цыпкин А.Г., Цыпкин А.И. Справочник по методам решения задач по математике для средней школы. – М.: Наука, 1989.