Проверочная работа по алгебре «Арифметическая прогрессия» 9 класс

Проверочная работа по алгебре для 9 класса

Тема: Арифметическая прогрессия.

Подготовила Кривошеева Светлана Александровна

учитель математики МБОУСОШ №40 города Тулы

Инструкция к выполнению.

Задания подобраны так, что ответ предыдущего является условием следующего (математическая эстафета).

Задания для первого варианта:

№1. Выпишите первые пять членов арифметической прогрессии (а_n): 6;3…

№2. В арифметической прогрессии (с_n) первый член равен (а₅) из задания №1, d=5. Найдите сумму первых двадцати членов этой прогрессии.

№3. Найдите номер члена арифметической прогрессии (b_n), если b₁=20, d=10, а b_n=S₂₀ из задания №2.

№4. Найти сумму всех натуральных чисел, не превосходящих n, где n-номер члена из задания №3.

№5. В арифметической прогрессии (х_n) первый член равен сумме из задания №4, а равность равна- 25. Для каких членов прогрессии выполняется условие х_n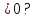

№6.Последовательность задана формулой y=5n-2. Найдите сумму n-первых членов этой последовательности, если n-номер наименьшего положительного члена арифметической последовательности из задания №5.

№7. Сумма первых ста членов арифметической прогрессии равна сумме арифметической прогрессии из задания №6. Найдите сумму первых ста членов такой арифметической прогрессии, каждый член которой на 3 больше соответствующего члена данной прогрессии.

Решение заданий первого варианта:

№1.

(a_n): 6;3;…, значит d=3-6=-3. Ответ: 6;3;0;-3;-6;-9;-12;… а₅=-6

№2.

(с_n)-арифметическая прогрессия, с₁=а₅=-6, d=5.

S_n=0,5n(2a₁+d(n-1)), S₂₀=830.

№3.

(b_n)-арифметическая прогрессия, (b₁)=20, d=10,b_n=S₂₀=830.

b_n=b₁+d(n-1), 20+10(n-1)=830,n=82.

№4.

b_n=n, n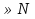, n=82. S_n=0,5n(2a₁+d(n-1)),S₈₂=3403.

№5.

x₁=3403, d=-25, x_n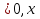

x_n=x₁+d(n-1), 3403-25(n-1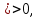

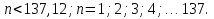
№6.

y_n=5n-2, n=137.Последовательность (у_n)-арифметическая прогрессия, т. к. d=у_n+1:у_n=5.

y₁=3, S_n=0,5n(2y₁+d(n-1)),S₁₃₇=46991.

№7

1.(a_n)-арифметическая прогрессия, S₁₀₀=46991

(a_n): a_1;a_2;a_;… S₁₀₀=0,5(2a₁+99d)100=(2a₁+99)50=46991

2.(b_n)- арифметическая прогрессия,

(b_n): b₁₌a₁+3; b₂=a₂+3;b₃=a₃+3;… S₁₀₀=0,5(2b₁+99d)100=

=(2(a₁+3)+99d)50=((2a₁+99d)+6)50=S₁₀₀+300=46991+300=

=47291

Конечный результат для первого варианта 47291.

Задания для второго варианта:

№1.Выпишите первые пять членов арифметической прогрессии 10;5;…

№2.В арифметической прогрессии(c_n) первый член равен a₅ из задания №1, d=5.Найдите сумму первых двадцати первых членов прогрессии.

№3.Найдите номер члена арифметической прогрессии(b_n), если b₁=20,d=10,а b₄=S₂₀ из задания №2.

№4. Найдите сумму всех натуральных чисел, не превосходящих n,где n-номер члена из задания №3.

№5. В арифметической прогрессии (x_n) первый член равен сумме из задания №4, а d=-25. Для каких членов прогрессии выполняется условие x_n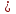 0?

№6. Последовательность задана формулой y_n=5n-2. Найдите сумму n-первых членов этой последовательности, если n –номер наименьшего положительного члена из задания №5.

№7. Сумма первых ста членов арифметической прогрессии равна сумме полученной в задании №6. Найдите сумму первых ста членов такой арифметической прогрессии, каждый член которой на 4 больше соответствующего члена данной прогрессии.

Решение заданий второго варианта:

№1. (a_n)-арифметическая прогрессия.

(a_n):10;5;… d=5-10=-5. Ответ: 10;5;0;-5;-10;…

№2.(c_n)-арифметическая прогрессия, с₁=-10, d=5.

S_n=0,5n(2c₁+d(n-1)), n=20,S₂₀=750.

№3. (b_n)-арифметическая прогрессия,b₁₌20,d=10, b_n=S₂₀=750

b_n=b₁+d(n-1), 20+10(n-1)=750, n=74.

№4.(a_n)=n, n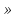N,n=74.

S_n=0,5n(2a₁+d(n-1)),S₇₄=2775.

№5.(x_n)-арифметическая прогрессия, x₁=2775, d=-25, x_n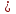 0

x_n=x₁+d(n-1), 2775-25(n-1)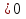_,n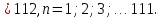

№6. Последовательность (у_n)-арифметическая прогрессия, т. к. d=у_n+1:у_n=5.

y₁=3, S_n=0,5n(2y₁+d(n-1)),S₁₁₁=30858.

№7. 1.(a_n)-арифметическая прогрессия, S₁₀₀=30858

(a_n): a_1;a_2;a_;… S₁₀₀=0,5(2a₁+99d)100=(2a₁+99)50=30858

2.(b_n)- арифметическая прогрессия,

(b_n): b₁₌a₁+4; b₂=a₂+4;b₃=a₃+4;… S₁₀₀=0,5(2b₁+99d)100=

=(2(a₁+4)+99d)50=((2a₁+99d)+8)50=S₁₀₀+400=30858+400=

=31258.

Конечный результат для второго варианта 31258.