РАБОЧАЯ ПРОГРАММА
по алгебре
на 2014-2015 ученый год
7 класс
Количество часов: 105ч
Учитель: Бажкова Юлия Петровна
Программа разработана на основе примерной программы по математике общего образования, авторской программы А.Г. Мордковича (2007)
Пояснительная записка.
Статус документа
Материалы для рабочей программы составлены на основе:
федерального компонента государственного стандарта общего образования,
примерной программы по математике основного общего образования,
федерального перечня учебников, рекомендованных Министерством образования Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях на 2014-2015 учебный год,
с учетом требований к оснащению образовательного процесса в соответствии с содержанием наполнения учебных предметов компонента государственного стандарта общего образования,
авторского тематического планирования учебного материала,
Общая характеристика учебного предмета.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
В ходе освоения содержания курса учащиеся получают возможность:
сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить логическое мышление и речь — умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В ходе преподавания алгебры в 7 классах, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Результаты обучения представлены в Требованиях к уровню подготовки, задающих систему итоговых результатов обучения, которые должны быть достигнуты всеми учащимися, оканчивающими 7 класс, и достижение которых является обязательным условием положительной аттестации ученика за курс 7 класса. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни».
Требования к уровню подготовки
В результате изучения ученик должен
знать/понимать:
существо понятия математического доказательства; приводить примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения, примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
уметь:
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с натуральными показателями, с многочленами; выполнять разложение многочленов на множители; выполнять тождественные преобразования выражений;
решать линейные уравнения и сводящиеся к ним, системы двух линейных уравнений;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой; определять координаты точки плоскости, строить точки с заданными координатами;
строить графики изученных функций;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять простейшие свойства функции по ее графику; применять графические представления при решении уравнении, систем, описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
интерпретации графиков зависимостей между величинами.
Место предмета в базисном учебном плане
Согласно федеральному базисному учебному плану на изучение математики в 7 классе отводится не менее 170 часов из расчета 5 ч в неделю, при этом разделение часов на изучение алгебры и геометрии может быть следующим: 105 по алгебре, 70 по геометрии
Количество часов – 105
Количество часов в неделю – 3
Тематическое и примерное поурочное планирование представлены в материалах для второго варианта и сделаны в соответствии с учебником «Алгебра», Мордкович А.Г., М.:Мнемозина, 2008
Литература
А. Г. Мордкович Алгебра . 7 класс. Учебник - М.: Мнемозина 2008 г.;
А. Г. Мордкович, Л. О. Денищева, Т. А. Корешкова, Т. Н. Мишустина, Е. Е. Тульчинская Алгебра . 7 класс. Задачник – М: Мнемозина 2008 г.;
А. Г. Мордкович Алгебра 7-9 класс. Пособие для учителей М.: Мнемозина 2009г.;
Содержание учебного предмета
Рациональные числа. Арифметические действия с рациональными числами. Степень с натуральным показателем, свойства степени с натуральным показателем. Числовые выражения, порядок действий в них, использование скобок. Законы арифметических действий: переместительный, сочетательный, распределительный.
Текстовые задачи. Решение текстовых задач арифметическим способом. Представление зависимости между величинами в виде формул.
Алгебраические выражения. Буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных, входящих в алгебраические выражения. Подстановка выражений вместо переменных. Равенство буквенных выражений. Тождество, доказательство тождеств. Преобразования выражений. Свойства степеней с натуральным показателем.
Многочлены. Многочлены с одной переменной. Степень многочлена Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности. Формула разности квадратов, формулы суммы кубов и разности кубов. Разложение многочлена на множители.
Алгебраическая дробь. Сокращение дробей.
Уравнения. Уравнение с одной переменной. Линейное уравнение. Уравнение с двумя переменными; решение уравнения с двумя переменными. Система уравнений; решение системы. Система двух линейных уравнений с двумя переменными; решение подстановкой и алгебраическим сложением. Уравнение с несколькими переменными. Переход от словесной формулировки соотношений между величинами к алгебраической. Решение текстовых задач алгебраическим способом.
Числовые функции. Понятие функции. Область определения функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции, нули функции, промежутки знакопостоянства Чтение графиков функций.
Функции, описывающие прямую пропорциональную зависимости её график. Линейная функция, ее график, геометрический смысл коэффициентов. Использование графиков функций для решения уравнений и систем.
Координаты. Изображение чисел точками координатной прямой. Числовые промежутки: интервал, отрезок, луч. Формула расстояния между точками координатной прямой.
Декартовы координаты на плоскости; координаты точки. Уравнение прямой, угловой коэффициент прямой, условие параллельности прямых.
Графическая интерпретация уравнений с двумя переменными и их систем.
Тематическое планирование учебного материала.
Тематическое планирование составлено к УМК А.Г. Мордковича «Алгебра», 7 класс, М. «Мнемозина», 2008 года на основе федерального компонента государственного стандарта общего образования с учетом авторского тематического планирования учебного материала Программы Математика 5 -6 классы, алгебра 7 – 9 классы алгебра и начала анализа 10 – 11 классы, Мнемозина 2009 г.
Примерное распределение часов по темам, 3 часа в неделю всего 105 учебных часов
п/п
содержание учебного материала
Глава и
№ параграфа
количество часов по примерной программе
количество часов по рабочей программе
1
Математический язык. Математическая модель
Гл 1 №1-5
13
13
2
Линейная функция
Гл2 №6-10
11
11
3
Системы двух линейных уравнений с двумя
переменными.
Гл 3 №11-14
13
13
4
Степень с натуральным показателем и её свойства
Гл 4 №15 - 19
6
6
5
Одночлены. Арифметические операции над
одночленами
Гл.5№20-23
8
8
6
Многочлены. Арифметические операции над
многочленами.
гл 6 №24 – 29
15
15
7
Разложение многочленов на множители.
Гл7 №30- 36
18
18
8
Функция y=x2.
Гл 8 №37_39
9
9
9
Итоговое повторение.
12
12
Календарно – тематическое планирование
№урока
содержание учебного материала
цель урока
Планируемый результат обучения
Домашнее задание
дата
Глава 1 Математический язык. Математическая модель. 13ч
1
Числовые выражения.
Формирование новых знаний и умений
Знать: буквенные выражения (выражения с переменными). Числовое значение буквенного выражения. Допустимые значения переменных, входящих в алгебраическое выражение. Подстановка выражений вместо переменных. Равенство буквенных выражений. Тождество. Доказательство тождеств. Преобразование выражений.
Уметь:Составлять буквенные выражения и формулы по условиям задач, осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные.
стр.6 П1 №1.9, 1.141
2
Значение числового выражения.
Формирование новых знаний и умений
стр10 П1 №1.33, 1.43
3
Алгебраические выражения Допустимые значения переменных.
Формирование и совершенствование новых знаний
стр.10 П1 31.35,1.36стр12 П22.9,2.14
4
Что такое математический язык.
Формирование новых знаний и умений
стр.14 П2 22.19, 2.21
5
Что такое математический модель?
Формирование новых знаний и умений
Стр.15 П3№б3.4,3,63.17
6
Составление математической модели
Формирование и совершенствование новых знаний
стр.17П3№3.183.21,
7
Составление математической модели. Закрепление знаний
закрепление и совершенствование новых знаний
стр21. П3 №3.41,3.47
8
Линейное уравнение с одной переменной
Формирование новых знаний и умений
стр.23.П4 №4.5 4.8 4.10
9
Закрепление знаний по теме: линейное уравнение с одной переменной
Формирование и совершенствование новых знаний
стр23 П4№ 4.204.39
10
Координатная прямая
Формирование новых знаний и умений
стр27 П5 5.2,5.11-5.14
11
Закрепление знаний по теме: Координатная прямая
Формирование и совершенствование новых знаний
дом к/р № 1-7
12
Вводная к/р
13
Контрольная работа №1 по теме Математический язык. Математическая модель
Глава 2. Линейная функция. 11 ч
14
Координатная плоскость
Формирование новых знаний и умений
Знать: линейная функция, ее график, геометрический смысл коэффициентов. Функции описывающие прямую зависимость, их графики. Алгоритм нахождения координат точки на плоскости и отыскания точки по ее координатам. Алгоритм построения графика уравнения ах+ву+с=0.
Уметь: решать линейные уравнения. Решать задачи с помощью уравнений с двумя переменными. Строить и читать график функции у=kx+b, y=kx. Определять взаимное расположение графиков линейных функций
стр35№6.7,6.106.24
15
Закрепление знаний по теме: Координатная плоскость
Применение знаний на практике
стр38№6.31,6.39а
16
Линейное уравнение с двумя переменными и его график.
Формирование новых знаний и умений
стр40 №7.5,7.117.17
17
Линейное уравнение с двумя переменными и его график.
Формирование и совершенствование новых знаний
стр43 №7.237.28
18
Линейное уравнение с двумя переменными и его график.
Формирование новых знаний и умений
стр44 №7.33 7.36
19
Линейная функция
Формирование новых знаний и умений
стр45 №8.11, 8.23.8.30
20
Линейная функция и её график
Применение знаний на практике
стр48 №8.34,8.45
21
Закрепление знаний по теме: Линейная функция и её график
Совершенствование знаний, умений и навыков
стр49 №8.478.598.66
22
Линейная функция у = кх
Формирование и совершенствование новых знаний
стр 53 №9.119.18
23
Взаимное расположение графиков линейных функций
Совершенствование знаний, умений и навыков
стр58 №10.2,10.1210.17
24
Контрольная работа №2 по теме Линейная функция
Глава 3 Системы двух линейных уравнений с двумя переменными 13ч
25
Основные понятия
Формирование новых знаний и умений
Знать: графический метод решения систем уравнений. Метод подстановки и алгебраического сложения.
Уметь: решать системы двух линейных уравнений методом подстановки, алгебраического сложения. Применять системы линейных уравнений при решении задач. Решать текстовые задачи алгебраическим методом, интерпретировать полученные результаты, проводить отбор решений, исходя из формулировки задачи. Находить значения аргумента по значению функции, заданной графиком или таблицей. Определять свойства функции по ее графику
стр64.№11.10, 11.13
26
Основные понятия
стр 65 №11.14, 11.20
27
Метод подстановки
Формирование новых знаний и умений
стр66 №12.4, 12.8
28
Закрепление знаний по теме: Метод подстановки
Формирование и совершенствование новых знаний
стр68 №12.17, 12.20
29
Практикум по теме: Метод подстановки
стр68. №12.21 12.27
30
Метод алгебраического сложения
Формирование новых знаний и умений
стр71 №13.3, 13.7
31
Метод алгебраического сложения
Совершенствование знаний, умений и навыков
стр72 №13.12, 13.10
32
Практикум по теме: Метод алгебраического сложения
Применение знаний на практике
стр73 №13.15, 1318
33
Системы двух лин. уравнений с двумя переменными как мат модели реальных ситуаций
Формирование новых знаний и умений
стр.75 №14.5,14.8
34
Закрепление знаний по теме: Системы двух лин. уравнений с двумя переменными как мат модели реальных ситуаций
Применение знаний на практике
стр 76№14.1314.15
35
Практикум по теме: Системы двух лин. уравнений с двумя переменными как мат модели реальных ситуаций
Применение знаний на практике
стр77 №14.1914.23
36
Повторительно – обощающий урок, подготовка к к/р
Совершенствование знаний, умений и навыков
стр79 вариант1 дом к/р
37
Контрольная работа №3 по теме Системы двух линейных уравнений с двумя переменными
Глава 4 Степень с натуральным показателем 6ч
38
Что такое степень с натуральным показателем
Формирование и совершенствование новых знаний
Знать: понятие степени с натуральным показателем. Компоненты степени. Свойства степеней с целым показателем.
Уметь: читать степени любых чисел с любым натуральным показателем и выполнять операцию возведения в степень. Составлять таблицы основных степеней и пользоваться ими при вычислении и нахождении значений выражений. Выполнять основные действия со степенями
стр84 №15.20,15.36,37
39
Таблица основных степеней
Формирование и совершенствование новых знаний
стр 87 №1616-16. 18
40
Свойства степени с нат показателем
Формирование новых знаний и умений
стр 89 №17.917.23
17.24
41
Закрепление знаний по теме: Свойства степени с нат показателем
Применение знаний на практике
стр.91 №1732,17 3317.36,17.42
42
Умножение и деление степеней с одинаковыми показателями
Совершенствование знаний, умений и навыков
сто94 №18.18,18.20,18.24
43
Степень с нулевым показателем
Формирование новых знаний и умений
стр 95 №19.6, 19.719.12
Глава 5 Одночлены. Операции над одночленами 8ч
44
Понятие одночлена. Стандартный вид одночлена
Формирование новых знаний и умений
Знать: понятие одночлена. Правила сложения, вычитания, умножения и деления одночленов. Стандартный вид одночлена. Коэффициент и буквенная часть.
Уметь: приводить примеры и определять является ли выражение одночленом, а также указывать его коэффициент и буквенную часть. Приводить одночлены к стандартному виду. Выполнять основные действия с одночленами.
стр100 №20.13,20.15, 20.10
45
Сложение и вычитание одночленов
Формирование новых знаний и умений
стр103 321.16,21.17
46
Закрепление знаний по теме: Сложение и вычитание одночленов
Применение знаний на практике
стр103 321.23, 21.2421.31
47
Умножение одночленов. Возведение в натуральную степень
Формирование новых знаний и умений
стр.106 №22.7, 22.16,22.18
48
Закрепление знаний по теме Умножение одночленов. Возведение в натуральную степень
Применение знаний на практике
стр109 №22.32, 22.33
49
Деление одночлена на одночлен
Формирование новых знаний и умений
стр.110 №23.10, 23.12, 23.18
50
Закрепление знаний по теме Деление одночлена на одночлен
Совершенствование знаний, умений и навыков
стр112 вариант2 дом к/р
51
Контрольная работа №4 по теме Одночлены. Операции над одночленами
Глава 6 Многочлены. Арифметические действия над многочленами 15ч
52
Основные понятия
Формирование новых знаний и умений
Знать: понятие многочлена. Правила сложения, вычитания, умножения и деления многочленов. Формулы сокращенного умножения. Стандартный вид многочлена. Степень многочлена.
Уметь: приводить примеры многочленов и определять, является ли выражение многочленом. Определять степень многочлена. Выполнять основные действия над многочленами. Выносить за скобки множитель. Уметь применять формулы сокращенного умножения
стр 114№24.12 24.14
53
Сложение и вычитание многочленов
Формирование новых знаний и умений
стр117 №25.4, 24.19
54
Закрепление знаний по теме Сложение и вычитание многочленов
Формирование и совершенствование новых знаний
стр118 25.6, 25.11
55
Умножение многочлена на одночлен
Формирование новых знаний и умений
стр120 №26.6, 26.8
56
Закрепление знаний по теме Умножение многочлена на одночлен
Применение знаний на практике
стр121 №26.14, 26.15
57
Умножение многочлена на многочлен
Формирование новых знаний и умений
стр 124 №27.8, 27.11,
58
Закрепление знаний по теме Умножение многочлена на многочлен
закрепление и совершенствование знаний
стр 125 №27.14, 27.17
59
Практикум по теме:Умножение многочлена на многочлен
Применение знаний на практике
стр 126 №27.21, 27.24, 27. 27
60
Формулы сокращённого умножения
Формирование новых знаний и умений
стр127 №28.3, 28.8
61
Формула квадрата суммы и разности
Формирование новых знаний и умений
стр130 №28.50 28.59
62
формула разности квадратов
закрепление и совершенствование знаний
стр127 №28.1828.26
63
формулы суммы и разности кубов
Применение знаний на практике
стр.128 №28.3128.53
64
Деление многочлена на одночлен
Применение знаний на практике
стр 133 №29.929.10
65
Повторительно – обобщающий урок Подготовка к к/р
Совершенствование знаний, умений и навыков
стр 136 дом к/р вариант2
66
Контрольная работа№5 по теме: Многочлены. Арифметические действия над многочленами
Глава 7 Разложение многочленов на множители 18ч
67
Что такое разложение и зачем оно нужно
Формирование новых знаний и умений
Знать: понятие многочлена. Правила сложения, вычитания, умножения и деления многочленов. Формулы сокращенного умножения. Стандартный вид многочлена. Степень многочлена.
Уметь: приводить примеры многочленов и определять, является ли выражение многочленом. Определять степень многочлена. Выполнять основные действия над многочленами. Выносить за скобки множитель. Уметь применять формулы сокращенного умножения
стр.30.5,30.6,30.14
68
Вынесение общего множителя за скобки
Формирование новых знаний и умений
стр140 №31.18 31.20
69
Закрепление знаний по теме Вынесение общего множителя за скобки
Совершенствование знаний, умений и навыков
стр141 №31.23, 31.25
70
Способ группировки
Формирование новых знаний и умений
стр142 №32.4, 32.6
71
Способ группировки
Совершенствование знаний, умений и навыков
стр 143 №32.16, 32.12
72
Разложение на множители с помощью ФСУ
Формирование новых знаний и умений
стр 144 33.7 33.10 33.14
73
Закрепление знаний по теме Разложение на множители с помощью ФСУ
Формирование и совершенствование новых знаний
стр 145 №33.2333.27,33.35
74
Закрепление знаний по теме Разложение на множители с помощью ФСУ
Применение знаний на практике
стр145 33.34, 33.36
75
Практикум по теме: Разложение на множители с помощью ФСУ
Применение знаний на практике
стр147 №33.41, 33.44
76
Практикум. Самостоятельная работа
Совершенствование знаний, умений и навыков
стр14733.4633.48
77
Разложение с помощью комбинации различных методов
Формирование новых знаний и умений
стр149 №34.6, 34.9,34.10
78
Закрепление знаний по теме:Разложение с помощью комбинации различных методов
Совершенствование знаний, умений и навыков
стр150 №34.12, 34.13,34.15
79
практикум по теме:Разложение с помощью комбинации различных методов
Совершенствование знаний, умений и навыков
стр.150№34.21, 34.23,34.25
80
Сокращение алгебраических дробей
Формирование новых знаний и умений
стр152 №35.12,35.15
81
Закрепление знаний по теме Сокращение алгебраических дробей
Применение знаний на практике
стр153 №35.22, 35.23,35.29
82
Тождества
Формирование новых знаний и умений
стр 15736.12,36.13
83
Повторительно – обощающий урок Подготовка к к/р
Совершенствование знаний, умений и навыков
стр160 вариант2 дом к/р
84
Контрольная работа №6 по теме: Разложение многочленов на множители
Глава 8 Функция у=х2 9ч
85
Функция у=х2 и её график
Формирование новых знаний и умений
Знать: квадратичная функция, ее график, парабола. Область определения функции, непрерывность функции.
Уметь: строить и читать график функции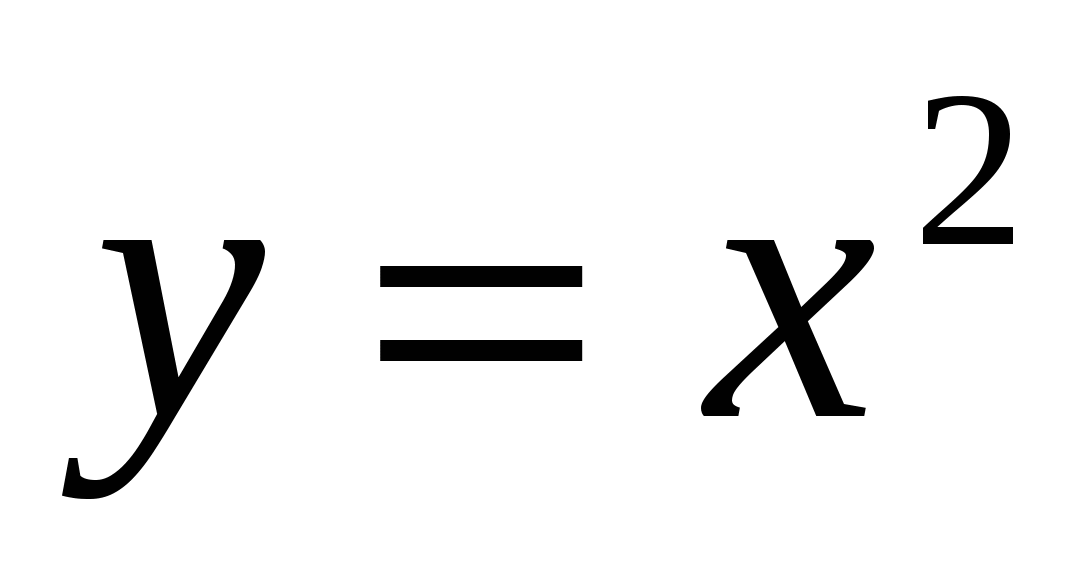
. Применять основные алгоритмические приемы графического решения уравнений. Находить значения функции, заданной формулой, таблицей, графиком по ее аргументу, находить значение аргумента по значению функции, заданной графиком или таблицей. Определять свойства функции по ее графику, применять графические представления при решении уравнений
стр161 №37.8,37.13
86
Закрепление знаний по теме Функция у=х2 и её график
Применение знаний на практике
стр167 №37.28, 37.31
87
Практикум по теме:Функция у=х2 и её график
Совершенствование знаний, умений и навыков
стр.169 337.55,37.49
88
Графическое решение уравнений
Формирование новых знаний и умений
стр 170 №38.2, 38.3
89
Практикум по теме Графическое решение уравнений
Применение знаний на практике
стр170 №38.10, 38.13
90
Что означает в математике запись у =f(х)
стр.171 №39.2,39.9
91
Закрепление знаний по теме Что означает в математике запись у =f(х)
Совершенствование знаний, умений и навыков
стр173 339.15, 39.16, 39.19
92
Практикум по теме Что означает в математике запись у =f(х)
стр 183 вариант 2 дом к/р
93
Контрольная работа №7 по теме: Функция у=х2
Итоговое повторение 12ч
94
Функции и графики
Совершенствование знаний, умений и навыков
Применение знаний на практике
стр 185 № 10,11
95
Линейная функция
стр 186 № 14,19
96- 97
Системы двух линейных уравнений с двумя
переменными.
стр 196 №84, 87
98
Степень с натуральным показателем и её свойства
стр199 №121, 122
99
Одночлены. Арифметические операции над
одночленами
стр200 №134,155,161
100
Многочлены. Арифметические операции над
многочленами.
стр 204№ 180, 184
101
Итоговая контрольная работа №8
102-105
Решение задач.
Учебно – методическое и материально – техническое обеспечение образовательного процесса
Основная литература:
1.Александрова Л.А. «Контрольные работы. Алгебра -7» - М.: Мнемозина, 2009
2.Александрова Л.А. «Самостоятельные работы. Алгебра -7» - М.: Мнемозина, 2009
3.Крайнева Л.Б. «Алгебра 7.Практикум.Готовимся к ГИА.- М.: Интеллект – Центр,2013
4.Мартышева Л.И. «КИМ.Алгебра:7 класс» - М.: ВАКО,2010
5.Мордкович А.Г. «Алгебра 7: методическое пособие для учителя» - М.: Мнемозина, 2008
6.Мордкович А.Г. «Алгебра-7» часть 1 , учебник – М.: Мнемозина, 2008
7.Мордкович А.Г. «Алгебра-7» часть 2, задачник – М.: Мнемозина, 2008
Дополнительная литература:
«Нестандартные задания по математике 5 – 11 классы», В.В. Кривоногов.
«Математика, итоговые уроки 5-9 классы», О.В. Бощенко.
«Математические олимпиады в школе 5-11 классы», А.В. Фарков.
Тесты по математике 5-11 классы, М.А. Максимовская и др.
«Учитесь мыслить нестандартно», Б.М. Абдрашитов и др.
6.«Тесты для промежуточной аттестации 7-8 классы», Ф.Ф. Лысенко, 2007 г.
7.«Я иду на урок математики, 7 класс, алгебра», библиотека «Первого сентября», 2001 г.
8.ГИА 3000 задач.математика, Семенов, Ященко
Интернет ресурсы:
http://uchitmatematika. ucos. ru/
http:// mikhatoval. edum. ru/
http://yroki. net
http:// rusedi.ru/
http://www.zavuch.info/
http://mathgia.ru/
Технические средства обучения
Компьютер, медиапроектор, интерактивная доска
Результаты освоения учебного курса
Для оценки достижений учащихся применяется пятибалльная система оценивания.
Нормы оценки:
Оценка письменных контрольных работ обучающихся по алгебре.
Ответ оценивается отметкой «5», если:
1) работа выполнена полностью;
2) в логических рассуждениях и обосновании решения нет пробелов и ошибок;
3) в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится, если:
1) работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
2)допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2.Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4»,
если удовлетворяет в основном требованиям на оценку «5»,
но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя
-
СОГЛАСОВАНО
Протокол заседания методического совета МБОУ СОШ № 3
от 2014 года №
Заместитель директора по УВР
_______________ ФИО
Подпись____________2014 года
СОГЛАСОВАНО
_______________
подпись руководителя МК
_______________ФИО
___________________дата