Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа № 6 г. Буденновска Будённовского района»
«Рассмотрено»
Руководитель МО
__________ С.В.Романенко
Протокол № _____ от «_____»_____________2014г.
«Согласовано»
Заместитель директора по УВР
_____________Г.Р.Алферова
«___»______________2014г.
«Утверждаю»
Директор МОУ СОШ №6 ___________ С.И.Иванова
Приказ № _____ от «____»____________2014г.
Рабочая учебная программа
по алгебре
9 класc
(базовый уровень)
Составитель:
Романенко С.В.
учитель математики,
высшая квалификационная категория
г. Буденновск
2014-2015 учебный год
Пояснительная записка
Рабочая программа по алгебре для 9 класса составлена на основе:
1. Государственного стандарта начального общего, основного общего и среднего (полного) общего образования. Приказ Министерства образования РФ от 05.03.2004 г № 1089.
2. Приказа Минобразования России от 31 января 2012 г. № 69 "О внесении изменений в федеральный компонент государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования, утвержденный приказом министерства образования Российской Федерации от 5 марта 2004 г. № 1089".
3. Программы общеобразовательных учреждений по алгебре 7–9 классы, к учебному комплексу для 7-9 классов (авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.Н. Нешков, С.Б. Суворова Ю.Н., составитель Т.А. Бурмистрова – М: «Просвещение», 2010. – с. 36-40).
Изучение алгебры в 9 классах направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии;
развитие вычислительных и формально-оперативных алгебраических умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов (физика, химия, основы информатики и вычислительной техники), усвоение аппарата уравнений и неравенств как основного средства математического моделирования прикладных задач, осуществление функциональной подготовки школьников. В ходе изучения курса обучающиеся овладевают приёмами вычислений на калькуляторе.
Основные задачи
При изучении курса математики на базовом уровне продолжаются и получают развитие содержательные линии: «Числа и вычисления», «Выражения и их преобразования», «Функции», «Уравнения и неравенства», «Геометрия», «Элементы комбинаторики, теории вероятностей, статистики и логики».
В рамках указанных содержательных линий решаются следующие задачи:
развитие представление о числе и роли вычислений в человеческой практике; формирование практических навыков выполнения устных, письменных, инструментальных вычислений, развитие вычислительной культуры;
овладение символическим языком алгебры, выработка формально-оперативные алгебраических умений и применение их к решению математических и нематематических задач;
изучение свойств и графиков элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развитие пространственных представлений и изобразительных умений, освоение основных фактов и методов планиметрии, знакомство с простейшими пространственными телами и их свойствами;
получение представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развитие логического мышления и речи – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
формирование представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
В результате изучения курса алгебры 9 класса обучающиеся должны:
знать
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
Арифметика
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь — в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений;
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы;
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследований построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Элементы логики, комбинаторики,статистики и теории вероятностей
уметь
проводить несложные доказательства, получать простейшие следствия из известных или
ранее полученных утверждений, оценивать логическую правильность рассуждений,
использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять
таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов,
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические
данные;
использовать приобретенные знания и умения в практической деятельности и повседневной
жизни для:
- выстраивания аргументации при доказательстве (в форме монолога и диалога);
- распознавания логически некорректных рассуждений;
- записи математических утверждений, доказательств;
- анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
- решения практических задач в повседневной и профессиональной деятельности с
использованием действий с числами, процентов, длин, площадей, объемов, времени,
скорости;
- решения учебных и практических задач, требующих систематического перебора
вариантов;
- понимания статистических утверждений.
Место предмета в базисном учебном плане
Согласно Федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение алгебры в 9 классе отводится 102 часа из расчёта 3 часа в неделю. На изучение курса в соответствии с авторской программой Бурмистровой Т. А. «Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель Бурмистрова Т.А., М.: Просвещение, 2011»
Содержание курса алгебры 9 класса включает следующие тематические блоки:
-
№
Тема
Количество часов
Контрольных работ
1
Повторение материала 7-8 класса
2
2
Квадратичная функция
22
2
3
Уравнения и неравенства с одной переменной
14
1
4
Уравнения и неравенства с двумя переменными и их системы
17
1
5
Прогрессии
15
2
6
Элементы комбинаторики и теории вероятностей
13
1
Повторение. Решение задач по курсу алгебры 7-9
10
Контрольные работы по тексту администрации:
-входной контроль
-промежуточный контроль
-пробный ГИА
итоговая контрольная
1
2
5
1
1
1
1
1
Итого
102
11
Характеристика основных содержательных линий
1.Квадратичная функция, 22 ч
1) Функция. Возрастание и убывание функции. Квадратный трехчлен. Разложение квадратного трехчлена на множители. Решение задач путем выделения квадрата двучлена из квадратного трехчлена. Функция y=ax2 + bx + с, её свойства, график. Простейшие преобразования графиков функций. Решение неравенств второй степени с одной переменной. [Решение рациональных неравенств методом интервалов.]
Цель – выработать умение строить график квадратичной функции и применять графические представления для решения неравенств второй степени с одной переменной.
Знать основные свойства функций, уметь находить промежутки знакопостоянства, возрастания, убывания функций
Уметь находить область определения и область значений функции, читать график функции
Уметь решать квадратные уравнения, определять знаки корней
Уметь выполнять разложение квадратного трехчлена на множители
Уметь строить график функции у=ах2 , выполнять простейшие преобразования графиков функций
Уметь строить график квадратичной функции y=ax2 + bx + с, выполнять простейшие преобразования графиков функций, находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения.
Уметь находить точки пересечения графика квадратичной функции с осями координат.
Уметь раскладывать квадратный трёхчлен на множители.
Уметь решать квадратное неравенство ах2 +вх+с.≥0 алгебраическим способом. Уметь решать квадратное неравенство с помощью графика квадратичной функции
Уметь решать квадратное неравенство методом интервалов и на основе свойств квадратичной функции.
2) Четная и нечетная функции. Функция y=xn, Определение корня n-й степени.
Цель – ввести понятие корня n-й степени.
Знать определение и свойства четной и нечетной функций, определение корня n- й степени; при каких значениях а имеет смысл выражение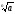 
. Знать, что степень с основанием, равным 0 определяется только для положительного дробного показателя и знать, что степени с дробным показателем не зависят от способа записи r в виде дроби; свойства степеней с рациональным показателем.
Уметь строить график функции у=хn , знать свойства степенной функции с натуральным показателем, уметь решать уравнения хn=а при: а) четных и б)нечетных значениях n. Выполнять простейшие преобразования и вычисления выражений, содержащих корни, применяя изученные свойства арифметического корня n-й степени. Уметь выполнять преобразования выражений, содержащих степени с дробным показателем.
В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область определения функции, график. Даются понятия о возрастании и убывании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа.
Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трехчлене и его корнях, выделении квадрата двучлена из квадратного трехчлена, разложении квадратного трехчлена на множители.
Изучение квадратичной функции начинается с рассмотрения функции у=ах2, её свойств и особенностей графика, а также других частных видов квадратичной функции – функции у=ах2+n, у=а(х-m)2. Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции у = ах2 + bх + с может быть получен из графика функции у = ах2 с помощью двух параллельных переносов. Приёмы построения графика функции у = ах2 + bх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы.
При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак.
Учащиеся знакомятся со свойствами степенной функции у=хn при четном и нечетном натуральном показателе n.. Вводится понятие корня n-й степени. Обучающиеся должны понимать смысл записей вида
, 
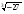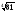. Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.
2.Уравнения и неравенства с одной переменной, 14 ч
Целое уравнение и его корни. Биквадратные уравнения. Дробные рациональные уравнения. Решение неравенств второй степени с одной переменной. Решение неравенств методом интервалов.
Цель – выработать умение решать простейшие уравнения заменой переменной и неравенства с одной переменной методом интервалов.
Знать методы решения уравнений
Уметь решать целые уравнения методом введения новой переменной и неравенства методом интервалов.
В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях. Вводятся понятия дробного рационального уравнения и его степени. Учащиеся знакомятся с решением уравнений третьей степени и четвертой степени с помощью разложения на множители и введения вспомогательной переменной. Метод решения уравнений путем введения вспомогательных переменных будет широко использоваться дальнейшем при решении тригонометрических, логарифмических и других видов уравнений.
Расширяются сведения о решении дробных рациональных уравнений. Учащиеся знакомятся с некоторыми специальными приемами решения таких уравнений.
Формирование умений решать неравенства вида ах2 + bх + с>0 или ах2 + bх + с<0, где а
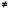0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей, ее расположение относительно оси Ох).Учащиеся знакомятся с методом интервалов, с помощью которого решаются несложные рациональные неравенства.
3.Уравнения и неравенства с двумя переменными и их системы, 17 ч.
Уравнение с двумя переменными и его график. Графический способ решения систем уравнений. Решение систем содержащих одно уравнение первой, а другое второй степени. Решение текстовых задач методом составления систем. Неравенства с двумя переменными. Системы неравенств с двумя переменными. Уравнение окружности. Решение систем двух уравнений второй степени с двумя переменными.
Цель – выработать умение решать простейшие системы, содержащие уравнения второй степени с двумя переменными, и решать текстовые задачи с помощью составления таких систем.
Знать методы решения уравнений:
а) разложение на множители;
б) введение новой переменной;
в)графический способ.
Уметь решать целые уравнения методом введения новой переменной
Уметь решать системы 2 уравнений с 2 переменными графическим способом
Уметь решать уравнения с 2 переменными способом подстановки и сложения
Уметь решать задачи «на работу», «на движение» и другие составлением систем уравнений.
В данной теме завершаемся изучение систем уравнений с двумя. переменными. Основное внимание уделяется системам, в которых одно из уравнений первой степени, а другое второй. Известный учащимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к решению квадратного уравнения.
Ознакомление обучающихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени, должно осуществляться с достаточной осторожностью и ограничиваться простейшими примерами.
Привлечение известных обучающимся графиков позволяет привести примеры графического решения систем уравнений. С помощью графических представлений можно наглядно показать обучающимся, что системы двух уравнений с двумя переменными второй степени могут иметь одно, два, три, четыре решения или не иметь решений.
Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач, решаемых с помощью систем уравнений.
Изучение темы завершается введением понятия неравенства и системы неравенств с двумя переменными. Сведения о графиках уравнений с двумя переменными используется при иллюстрации множеств решений некоторых простейших неравенств с двумя переменными и их систем.
4. Прогрессии, 15 ч
Последовательности. Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы n первых членов прогрессии.
Цель – дать понятие об арифметической и геометрической прогрессиях как числовых последовательностях особого вида.
Добиться понимания терминов «член последовательности», «номер члена последовательности», «формула n –го члена арифметической прогрессии»
Знать формулу n –го члена арифметической прогрессии, свойства членов арифметической прогрессии, способы задания арифметической прогрессии
Уметь применять формулу суммы n –первых членов арифметической прогрессии при решении задач.
Знать, какая последовательность является геометрической, уметь выявлять, является ли последовательность геометрической, если да, то находить q
Уметь вычислять любой член геометрической прогрессии по формуле, знать свойства членов геометрической прогрессии
Уметь применять формулу при решении стандартных задач
Уметь применять формулу S=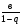
при решении практических задач
Уметь находить разность арифметической прогрессии
Уметь находить сумму n первых членов арифметической прогрессии. Уметь находить любой член геометрической прогрессии. Уметь находить сумму n первых членов геометрической прогрессии.
Уметь решать текстовые задачи.
При изучении темы вводится понятие последовательности, разъясняется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий.
Работа с формулами n-го члена и суммы первых n членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем.
Рассматриваются характеристические свойства арифметической и геометрической прогрессий, что позволяет расширить круг предлагаемых задач.
5. Элементы комбинаторики и теории вероятностей, 13 ч.
Примеры комбинаторных задач. Перестановки, размещения, сочетания. Относительная частота случайного события. Равновозможные события и их вероятность.
Цель: ознакомить учащихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события.
Знать формулы числа перестановок, размещений, сочетаний и уметь пользоваться ими.
Уметь пользоваться формулой комбинаторики при вычислении вероятностей.
Изучение темы начинается с решения задач, в которых требуется составить те или иные комбинации элементов и. подсчитать их число. Разъясняется комбинаторное правило умножения, которое исполнятся в дальнейшем при выводе формул для подсчёта числа перестановок, размещений и сочетаний.
При изучении данного материала необходимо обратить внимание обучающихся на различие понятий «размещение» и «сочетание», сформировать у них умение определять, о каком виде комбинаций идет речь в задаче.
В данной теме учащиеся знакомятся с начальными сведениями из теории вероятностей. Вводятся понятия «случайное событие», «относительная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание обучающихся на то, что классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными.
6. Повторение. Решение задач по курсу алгебры 7-9 кл , 10 ч
Тождественные преобразования алгебраических выражений. Решение уравнений. Решение систем уравнений. Решение текстовых задач. Решение неравенств и их систем. Прогрессии. Функции и их свойства (курс алгебры 9
Критерии и нормы оценки знаний, умений и навыков
обучающихся по алгебре.
1. Оценка письменных контрольных работ обучающихся по алгебре.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Отметка «1» ставится, если:
работа показала полное отсутствие у обучающегося обязательных знаний и умений по проверяемой теме или значительная часть работы выполнена не самостоятельно.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
2. Оценка устных ответов обучающихся по алгебре.
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала;
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Отметка «1» ставится, если:
ученик обнаружил полное незнание и непонимание изучаемого учебного материала или не смог ответить ни на один из поставленных вопросов по изученному материалу.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
нерациональные приемы вычислений и преобразований;
небрежное выполнение записей, чертежей, схем, графиков.
Формы промежуточной и итоговой аттестации:
Освоение образовательных программ основного общего образования завершается обязательной итоговой аттестацией выпускников.
Государственная итоговая аттестация выпускников школы осуществляется в соответствии с Положением о государственной (итоговой) аттестации выпускников общеобразовательных учреждений, утвержденным Министерством образования и науки Российской Федерации.
Промежуточная аттестация проводится в форме тестов, контрольных, самостоятельных работ.
На основании результатов промежуточной аттестации выставляются итоговые оценки.
Календарно-тематическое планирование по алгебре 9 класс (3 часа в неделю)
Дата по плану
Дата факти-
ческая
№
урока
Тема урока
Колич.часов
Требования к уровню
подготовки
обучающихся
Примечание
Повторение материала 7-8 класса
1
Повторение материала 7-8 класса
1
Повторение материала 7-8 класса
1
4.
Диагностическая контрольная работа по тексту администрации
1
Глава I. Квадратичная функция. (22 час)
§1. Функции и их свойства. (5 час)
5
п.1. Функция. Область определения и область значений функции.
1
Знать определение функции, основные свойства функций.
Уметь находить ООФ, МЗФ, промежутки знакопостоянства, возрастания, убывания функций.
6.
п.1. Функция. Область определения и область значений функции.
1
7.
п.2. Свойства функций.
1
8.
п.2. Свойства функций.
1
9.
п.2. Свойства функций.
1
§2. Квадратный трёхчлен. (4 час) + 1 ч к/р № 1 по плану
10.
п.3. Квадратный трёхчлен и его корни.
1
Знать определение квадратного трёхчлена и его корней.
Уметь выполнять разложение квадратного трехчлена на множители.
11.
п.4. Разложение квадратного трёхчлена на множители.
1
12.
п.4. Разложение квадратного трёхчлена на множители.
1
13.
Контрольная работа № 1 «Функции и их свойства. Квадратный трёхчлен».
1
§3. Квадратичная функция и её график. (8 час)
14.
п.5. Функция y=ax2, её график и свойства.
1
Знать: определение квадратичной функции, её свойства.
Уметь: строить график квадратичной функции y=ax2 + bx + с, выполнять простейшие преобразования графиков функций, находить по графику нули функции, промежутки, где функция принимает положительные и отрицательные значения. Уметь находить точки пересечения графика квадратичной функции с осями координат.
15.
п.5. Функция y=ax2, её график и свойства.
1
16.
п.6. Графики функций y=ax2 + n и y=a(x-m)2 .
1
17.
п.6. Графики функций y=ax2 + n и y=a(x-m)2 .
1
18.
п.6. Графики функций y=ax2 + n и y=a(x-m)2 .
1
19.
п.7. Построение графика квадратичной функции.
1
20.
п.7. Построение графика квадратичной функции.
1
21.
п.7. Построение графика квадратичной функции.
1
§4. Степенная функция. Корень n-й степени. (3 час) + 1 ч к/р № 2 по плану
22.
п.8. Функция y=axn
1
Знать: определение степенной функции с натуральным показателем и его свойства; определение корня n - й степени; при каких значениях а имеет смысл выражение 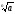, свойства корня n-степени и арифметического корня n-й степени. Знать, что степень с основанием, равным 0 определяется только для положительного дробного показателя и знать, что степени с дробным показателем не зависят от способа записи n в виде дроби; свойства степеней с рациональным показателем.
Уметь: решать уравнения хn=а при: а) четных и б) нечетных значениях n. Выполнять простейшие преобразования и вычисления выражений, содержащих корни, применяя изученные свойства арифметического корня n-й степени. Уметь выполнять преобразования выражений, содержащих степени с дробным показателем.
23.
п.9. Корень n-й степени.
1
24.
п.9. Корень n-й степени.
1
25.
Контрольная работа № 2 «Квадратичная функция и её график».
1
Глава II. Уравнения и неравенства с одной переменной. (14 час)
§5. Уравнения с одной переменной. (8 час)
26.
п.12. Целое уравнение и его корни.
1
Знать определение степени уравнения, методы решения уравнений; определение дробного рационального уравнения.
Уметь решать целые уравнения методом введения новой переменной и неравенства методом интервалов; решать дробно-рациональные уравнения.
27.
п.12. Целое уравнение и его корни.
1
28.
п.12. Целое уравнение и его корни.
1
29
п.12. Целое уравнение и его корни.
1
30
п.13. Дробные рациональные уравнения.
1
31.
п.13. Дробные рациональные уравнения.
1
32.
п.13. Дробные рациональные уравнения.
1
33.
п.13. Дробные рациональные уравнения.
1
§6. Неравенства с одной переменной. ( 5 час) + 1 ч к/р № 3 по плану
34.
п.14. Решение неравенств второй степени с одной переменной.
1
Знать: определение неравенства второй степени с одной переменной.
Уметь: решать неравенства методом интервалов и с помощью графика квадратичной функции.
35.
п.14. Решение неравенств второй степени с одной переменной.
1
36.
п.14. Решение неравенств второй степени с одной переменной.
1
37.
п.15. Решение неравенств методом интервалов.
1
38.
п.15. Решение неравенств методом интервалов.
1
39.
Контрольная работа №3 «Уравнения и неравенства с одной переменной».
1
Глава III. Уравнения и неравенства с двумя переменными. (17 час)
§7. Уравнения с двумя переменными и их системы. (12 час) + 2 ч диагностическая работа ИМЦ
40.
п.17. Уравнение с двумя переменными и его график.
1
Знать определение решения уравнения с двумя переменными; методы решения уравнений:
а) разложение на множители;
б) введение новой переменной;
в) графический способ.
Уметь решать целые уравнения методом введения новой переменной
Уметь решать системы 2 уравнений с 2 переменными графическим способом
Уметь решать уравнения с 2 переменными способом подстановки и сложения
Уметь решать задачи «на работу», «на движение» и другие составлением систем уравнений.
41.
п.17. Уравнение с двумя переменными и его график.
1
42.
п.18. Графический способ решения систем уравнений.
1
43.
п.18. Графический способ решения систем уравнений.
1
44.
п.19. Решение систем уравнений второй степени.
1
45-46.
Двухчасовая диагностическая контрольная работа
2
47.
п.19. Решение систем уравнений второй степени.
1
48.
п.19. Решение систем уравнений второй степени.
1
49.
п.19. Решение систем уравнений второй степени.
1
50.
п.20. Решение задач с помощью систем уравнений второй степени.
1
51.
п.20. Решение задач с помощью систем уравнений второй степени.
1
52.
п.20. Решение задач с помощью систем уравнений второй степени.
1
53.
п.20. Решение задач с помощью систем уравнений второй степени.
1
§8. Неравенства с двумя переменными и их системы. (4 час) + 1 ч к/р № 4 по плану
54.
п.21. Неравенства с двумя переменными.
1
Знать определение решения неравенства с двумя переменными; методы решения неравенства.
Уметь решать неравенства различными способами
55.
п.21. Неравенства с двумя переменными.
1
56.
п.22. Системы неравенств с двумя переменными.
1
57.
п.22. Системы неравенств с двумя переменными.
1
58.
Контрольная работа № 4 "Уравнения и неравенства с двумя переменными".
1
Глава IV. Арифметическая и геометрическая прогрессии. (15 час)
§9. Арифметическая прогрессия. (7 час) + 1 ч к/р № 5 по плану
59.
п.24. Последовательности
1
Знать формулу n –го члена арифметической прогрессии, свойства членов арифметической прогрессии, способы задания арифметической прогрессии
Уметь применять формулу суммы n –первых членов арифметической прогрессии при решении задач.
60
п.25. Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии.
1
61.
п.25. Определение арифметической прогрессии. Формула n-го члена арифметической прогрессии.
1
62.
п.26. Формула суммы первых n членов арифметической прогрессии.
1
63.
п.26. Формула суммы первых n членов арифметической прогрессии.
1
64.
п.26. Формула суммы первых n членов арифметической прогрессии.
1
65.
п.26. Формула суммы первых n членов арифметической прогрессии.
1
66.
Контрольная работа №5 "Арифметическая прогрессия".
1
§10. Геометрическая прогрессия. (6 час) + 1 ч к/р № 6 по плану + 5 ч пробный ГИА
67.
п.27. Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии.
1
Знать, какая последовательность является геометрической, уметь выявлять, является ли последовательность геометрической, если да, то находить q; свойства членов геометрической прогрессии, применять формулу при решении стандартных задач, применять формулу S=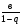 при решении практических задач
Уметь вычислять любой член геометрической прогрессии по формуле; находить разность арифметической прогрессии, сумму n первых членов арифметической прогрессии; находить любой член геометрической прогрессии; уметь находить сумму n первых членов геометрической прогрессии; решать текстовые задачи.
68-72.
Пробный экзамен в формате ГИА
5
73.
п.27. Определение геометрической прогрессии. Формула n-го члена геометрической прогрессии.
1
74.
п.28. Формула суммы первых n членов геометрической прогрессии.
1
75.
п.28. Формула суммы первых n членов геометрической прогрессии.
1
76.
п.28. Формула суммы первых n членов геометрической прогрессии.
1
77.
п.28. Формула суммы первых n членов геометрической прогрессии.
1
78.
Контрольная работа № 6 "Геометрическая прогрессия".
1
Глава V. Элементы комбинаторики и теории вероятностей. (13 час)
§11. Элементы комбинаторики. (9 час)
79.
п.30. Примеры комбинаторных задач.
1
Знать формулы числа перестановок, размещений, сочетаний и уметь пользоваться ими.
Уметь пользоваться формулой комбинаторики при вычислении вероятностей.
80.
п.30. Примеры комбинаторных задач.
1
81.
п.31. Перестановки.
1
82.
п.31. Перестановки.
1
83.
п.32. Размещения.
1
84.
п.32. Размещения.
1
85.
п.33. Сочетания.
1
86.
п.33. Сочетания.
1
87.
п.33. Сочетания.
1
§12. Начальные сведения из теории вероятностей. (3 час) + 1 ч к/р № 7 по плану
88.
п.34. Относительная частота случайного события.
1
Знать: классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными.
89.
п.35. Вероятность равновозможных событий.
1
90.
п.35. Вероятность равновозможных событий.
1
91.
Контрольная работа № 7 "Элементы комбинаторики и теории вероятности".
1
Итоговое повторение. (10 часов) + 1 ч итоговая контрольная работа
92.
Повторение. Тождественное преобразование алгебраических выражений.
1
93.
Повторение. Решение уравнений.
1
94.
Повторение. Решение систем уравнений.
1
95.
Повторение. Решение текстовых задач.
1
96.
Повторение. Решение неравенств и их систем.
1
97.
Повторение. Решение неравенств и их систем.
1
98.
Повторение. Прогрессии.
1
99.
Повторение. Прогрессии.
1
100.
Повторение. Функции и их свойства.
1
101.
Итоговая контрольная работа.
1
102.
Комплексное повторение.
1
Учебно-методический комплект:
Учебник.
Алгебра. Учебник для 9 кл. общеобразовательных учреждений / Ю. Н, Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворова; Под ред. С. А. Теляковского. – 15-е изд. Дораб.– М.: Просвещение, 20011. – 272 с.
Дополнительная литература:
1. Дидактические материалы по алгебре 9 класс / Ю.Н.Макарычев, Н.Г.Миндюк, Л.Б.Крайнева.М.: Просвещение, 2011.
2. Сборник заданий для подготовки к государственной итоговой аттестации в 9 классе
Л.В. Кузнецова, С.Б. Суворова и др. / М: Просвещение, 2009 – 240с.
3. Изучение алгебры в 7-9 классах: пособие для учителей. Макарычев Ю.Н., Миндюк Н.Г., Суворова С.Б., Шлыкова И.С. 4-е изд. - М.: «Просвещение» 2011. - 304 с
4. Уроки алгебры в 9 классе. Пособие к учебнику Макарычева Ю.Н. и др. Жохов В.И., Крайнева Л.Б. М.: 2001. - 96 с.
Интернет-ресурсы:
1. Федеральный институт педагогических измерений www.fipi.ru2. Федеральный центр тестирования www.rustest.ru3. РосОбрНадзор www.obrnadzor.gov.ru4. Российское образование. Федеральный портал edu.ru5. Федеральное агенство по образованию РФ ed.gov.ru6. Федеральный совет по учебникам Министерства образования и науки Российской Федерации http://fsu.edu.ru
7. Открытый банк заданий по математике http://www.mathgia.ru:8080/or/gia12/Main.html?view=TrainArchive
8. Сайт Александра Ларина http://alexlarin.net/
9. Сеть творческих учителей http://www.it-n.ru/
Контрольная работа № 1
В а р и а н т 1
1. Разложите на множители квадратный трехчлен:
а) х2 – 14х + 45; б) 3у2 + 7у – 6.
2. Постройте график функции у = х2 – 2х – 8. Найдите с помощью графика:
а) значение у при х = –1,5;
б) значения х, при которых у = 3;
в) нули функции;
г) промежутки, в которых у > 0 и в которых у < 0;
д) промежуток, в котором функция возрастает.
3. Сравните:
а) 
и 
; в) (–4,1)11 и (–3,9)11;
б) (–1,3)6 и (–2,1)6; г) 
и 0,0114.
4. Вычислите:
а) 
; б) 
; в) 
.
5. Сократите дробь 
.
6. Найдите наименьшее значение квадратного трехчлена х2 – 6х + 11.
В а р и а н т 2
1. Разложите на множители квадратный трехчлен:
а) х2 – 10х + 21; б) 5у2 + 9у – 2.
2. Постройте график функции у = х2 – 4х – 5. Найдите с помощью графика:
а) значение у при х = 0,5;
б) значения х, при которых у = 3;
в) нули функции;
г) промежутки, в которых у > 0 и в которых у < 0;
д) промежуток, в котором функция убывает.
3. Сравните:
а) (–1,7)5 и (–2,1)5; в) 4,79 и 
;
б) 
и 
; г) 5,712 и (–6,3)12.
4. Вычислите:
а) 
; б) 
; в) 
.
5. Сократите дробь 
.
6. Найдите наибольшее значение квадратного трехчлена –х2 + 4х + 3.
В а р и а н т 3
1. Разложите на множители квадратный трехчлен:
а) х2 – 12х + 35; б) 7у2 + 19у – 6.
2. Постройте график функции у = х2 – 6х + 5. Найдите с помощью графика:
а) значение у при х = 0,5;
б) значения х, при которых у = –1;
в) нули функции;
г) промежутки, в которых у > 0 и в которых у < 0;
д) промежуток, в котором функция возрастает.
3. Сравните:
а) 
и 
; в) (–2,3)6 и (–4,1)6;
б) (–1,7)3 и (0,4)3; г) 
и (–1,4)10.
4. Вычислите:
а) 
; б) 
; в) 
.
5. Сократите дробь 
.
6. Найдите наименьшее значение квадратного трехчлена х2 – 8х + 7.
В а р и а н т 4
1. Разложите на множители квадратный трехчлен:
а) х2 – 18х + 45; б) 9х2 + 25х – 6.
2. Постройте график функции у = х2 – 8х + 13. Найдите с помощью графика:
а) значение у при х = 1,5;
б) значения х, при которых у = 2;
в) нули функции;
г) промежутки, в которых у > 0 и в которых у < 0;
д) промежуток, в котором функция возрастает.
3. Сравните:
а) 3,411 и 4,211; в) 
и (–0,7)9;
б) и (–1,2)8; г) (–2,4)4 и 1,24.
4. Вычислите:
а) 
; б) 
; в) 
.
5. Сократите дробь 
.
6. Найдите наибольшее значение квадратного трехчлена –х2 + 6х – 4.