Разработка к уроку алгебры для 7 класса «Умножение и деление степеней» | Лучшие рефераты, дипломные, курсовые работы

Тема: «Степень с натуральным показателем»

из учебника Ю.Н. Макарычева «АЛГЕБРА 7 класс»

Тип урока: объяснение нового материала.

Цели урока:

а) образовательные: научить умножать и делить степени;

б) развивающие: научить наблюдать, выводить закономерности, проводить рассуждения по аналогии;

в) воспитательные: воспитать интерес к математике.

Оборудование : компьютер, проектор, экран

Задачи урока: сформировать навыки сложения чисел с разными знаками.

Образовательные задачи урока (формирование познавательных УУД):

познакомить учащихся со степенью с натуральным показателем;
тренировать способность к использованию выведенного алгоритма;
организовать деятельность учащихся по приобретению необходимых умений и навыков;
повторить и закрепить;

Воспитательные задачи урока ( формирование коммуникативных и личностных УУД):

содействовать развитию познавательного интереса учащихся к предмету;
прививать учащимся навыки организации самостоятельной работы;
умение слушать и вступать в диалог, участвовать в коллективном обсуждении проблем, интегрироваться в группу сверстников и строить продуктивное взаимодействие, воспитывать ответственность и аккуратность.

Развивающие задачи урока: (формирование регулятивных УУД)

развивать умения учащихся анализировать, делать выводы, определять взаимосвязь и логическую последовательность мыслей;

Структура урока:

Организационный момент.
Актуализация.
Историческая справка
Формирование новых способов и действий.
Закрепление ЗУН

I.Итоги урока

II.Домашнее задание

III.Дополнительное задание

Ход урока

Организационный момент.

Здравствуйте учащиеся! (проверка наличия учеников и выполнение домашнего задания). Сегодня мы с вами продолжим работать со степенями. Внимательно посмотрели на экран.(Слайд 1)

Актуализация.

Чтобы продолжить нам урок нужно ответить на следующие вопросы: (слайд 2)

Сформулируйте определение степени числа с натуральным показателем.
Приведите примеры и назовите в каждом из них основание и показатель степени.
Каким числом (положительным или отрицательным) является:

Степень положительного числа, приведите примеры;
Степень отрицательного числа с чётным показателем, приведите примеры;
Степень отрицательного числа с нечётным показателем, приведите примеры.

Сравните с нулём квадрат произвольного числа. Ответ запишите в виде неравенства.

Работа устно: (слайд 3)

1. Найдите значение выражения.

а) 4³; б) (0,7)²; в) ; г) 0¹²; д) (–6)²; е) (–0,3)⁴; ж) (–1)⁸; з)

2. Сравните с нулем значение выражения.

а) (–25)¹² · (–25)⁹;

б) (–4)¹⁹ : (–4)⁷;

в) (–12)¹³ · (–12)⁸.

3. Замените звездочку степенью с основанием а так, чтобы стало верным равенство:

а) а⁴ · * = а¹²; б) * · а = а⁴;

в) а¹⁴ : * = а⁷; г) * : а⁹ = а¹⁰.

(слайд 4 )

Упростить: аааааа=? (-2)(-2)(-2)=? -2∙2∙2=?
Вычислить: 2³= 4²= 7²= 5³=

(-3)³= 12²= 2,4²= (-0,9)²=

Представьте 64 в виде степени с основанием 2; -2; -8.
Куб какого числа равен 64?
Существует ли еще какой-нибудь способ представления числа 64 в виде степени с натуральным показателем?

Историческая справка

(Слайд 5)Найдите верные неравенства. Из соответствующих им букв получите фамилию архитектора, по проекту которого в 1825 г. было построено здание Большого театра в Москве:

Я : (- 15)¹⁰ < 0
С : (- 3,2)¹³ > 0
Б : -4,1¹² < 0
М : -(- 2)⁶² >0
О : (-6,5)⁴ > (-8,4)³
В : (-3,4)² > -3,4²
Д : (-7)¹⁰¹ ∙ (-8)²¹ < 0
Е: (-15)⁴ / (-15⁴) < 0

(Слайд 6)

Осип Иванович Бове (1784 — 1834) архитектор, знаменитый реконструкцией Москвы после пожара 1812 года. Сочетание в лице Бове прекрасного организатора и первоклассного архитектора, знатока строительного дела и тонкого художника было одним из решающих обстоятельств, так необычайно благоприятствующих появлению в Москве архитектуры большого стиля.

Список основных сооружений
1814—1815 Торговые ряды напротив Кремля (не сохранились)
1820—1822 Кремлёвский (Александровский) сад с гротом
1824—1825 Манеж
1818—1824 Театральная площадь
1821—1824 Большой театр
1827—1834 Триумфальные ворота у Тверской заставы (ныне у парка Победы)
1828—1833 Градская больница (ныне Городская больница № 1 им. Н. И. Пирогова)
Дом во владении жены в Петровском переулке (бывшем Богословском)
Дом Н. С. Гагарина (позднее Книжная палата) на Новинском бульваре
1821 Церковь Николая Чудотворца в Котельниках
1822 Церковь Михаила Архангела в имении жены в Архангельском
1825—1828 Покровская церковь
1825—1828 Церковь Екатерины Великомученицы в Екатерининской больнице
1820-е гг. Торговые ряды на Таганке (не сохранились)
1830 Церковь Большое Вознесение у Никитских Ворот (доработка проекта Ф. М. Шестакова 1829 года, достроен после смерти Бове А. Г. Григорьевым)
1832 Перестройка Церкви Всех Скорбящих Радости
1833 Церковь Троицы Живоначальной в Даниловском монастыре

(Слайд 7) «Большой театр», (Слайд Центральный выставочный зал в Москве «Манеж», (Слайд 9) «Триумфальные ворота», (Слайд 10) «Александровский сад», (Слайд 11) «Александровский сад в Москве – Вечный огонь»

Формирование новых способов и действий.

Учитель: Тема нашего урока «Умножение и деление степеней». (Слайд 12)

Рассмотрим примеры

а² ∙ а³ = (аа) ∙ (ааа) = ааааа = а⁵

в³ ∙ в⁴ =

с⁴∙ с⁵ =

После рассмотрения примеров, учащиеся должны сделать вывод и самостоятельно сформулировать правило умножения степеней с одинаковыми основаниями. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней складываются

a^m· aⁿ= a^m⁺ⁿ

2. Аналогично и с делением степеней. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели степеней вычитаются

a^m:aⁿ= a^{m — n}, где, m > n, a ≠ 0

например: а)х⁶:х⁴=х^6-4=х²

б)3⁴ : 3² = 3^4-2 = 3²=9

в) (-3)⁴ : (-3)² = (-3)^4-2 = (-3)²=9

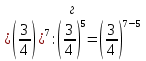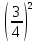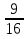
Степень с нулевым показателем не была определена и считают, что при а≠0

а⁰=1

например: 13⁴ : 3⁴ =13^4-4 = 13⁰=1

а¹ =а

например:

50¹=50,

3∙3⁴=3¹⁺⁴=3⁵

Закрепление ЗУН.

Учитель: (Слйд 13) Для закрепления новой темы выполним упражнения № 408 и 414. Упражнения решаются как в тетрадях, так и у доски. Учащиеся выполняют примеры у доски, выходя по цепочке.

(Слайд 14) Ну а сейчас выполним задания на экране, найденные ответы подставим в таблицу и узнаем два популярных высказывания.

будь: х⁵ ∙ х² =

быть: х³ ∙ х =

что: х² ∙ х³∙ х⁴ =

не: х ∙ х⁴∙ х⁵ =

им: х¹⁰ ÷ х⁸ =

хочешь: х⁷ ÷ х⁶ =

плачем: х¹² ÷ х =

имеем: х² ÷ х³ =

потерявши: х⁰ ∙ х²∙ х³÷ х⁵ =

храним: х³ ∙ х⁴∙ х⁵÷ х¹⁴ =

счастливым: ( х ∙ х⁵) / (х⁴ ÷ х) =

будь: х⁵ ∙ х² = х⁷

быть: х³ ∙ х = х⁴

что: х² ∙ х³∙ х⁴ = х⁹

не: х ∙ х⁴∙ х⁵ = х¹⁰

им: х¹⁰ ÷ х⁸ = х²

хочешь: х⁷ ÷ х⁶ = х

плачем: х¹² ÷ х = х¹¹

имеем: х² ÷ х³ = 1/х

потерявши: х⁰ ∙ х²∙ х³÷ х⁵ = х⁰ =1

храним: х³ ∙ х⁴∙ х⁵÷ х¹⁴ = 1/ х²

счастливым: ( х ∙ х⁵) / (х⁴ ÷ х) = х²

Используя найденные ответы, запишите в таблицах два высказывания Козьмы Пруткова

(Слайд 16)

Х⁹

1/ х

Х¹⁰

1/ х²

Х¹¹

что

имеем

не

храним

потерявши

плачем

(Слайд 17)

Х⁴

Х²

Х⁷

Х²

хочешь

быть

счастливым

будь

им

(Слайд 18-20) Историческая справка о Козьме Пруткове и его знаменитые высказывания.

Портрет работы трех художников: Льва Михайловича Жемчужникова, Александра Егоровича Вейдемана и Льва Феликсовича Лагорио. 1853 г.

Козьма Петрович Прутков (родился 23 апреля, 11-го по старому стилю 1801 года или 1803 года "в деревне Тентелевой близ Сольвычегодска"; умер 25 января, 13-го по старому стилю 1863 года в Петербурге) - вымышленный писатель и поэт, литературную личность и произведения которого создали: граф Алексей Константинович Толстой, Алексей Михайлович Жемчужников и Владимир Михайлович Жемчужников.

Философские мысли

Нельзя объять необъятное.

Глядя на мир, нельзя не удивляться.

Самый отдаленный пункт земного шара к чему-нибудь да близок, а самый близкий от чего-нибудь да отдален.

Вопросы

Что скажут о тебе другие, коли ты сам о себе ничего сказать не можешь?

Как же подданному знать мнение правительства, пока не наступила история?

Единожды солгавши, кто тебе поверит?

Если...

Если хочешь быть счастливым, будь им.

Если у тебя есть фонтан, заткни его: дай отдохнуть и фонтану.

Если на клетке слона прочтешь надпись "буйвол", - не верь глазам своим.

Если хочешь быть красивым, поступи в гусары.

Иногда достаточно обругать человека, чтобы не быть им обманутым!

Наблюдения о жизни и нравах

Что имеем - не храним; потерявши - плачем.

На беспристрастном безмене истории кисть Рафаэля имеет одинаковый вес с мечом Александра Македонского.

Гони любовь хоть в дверь, она влетит в окно.

Век живи - век учись! И ты, наконец, достигнешь того, что, подобно мудрецу, будешь иметь право сказать, что ты ничего не знаешь.

Специалист подобен флюсу: полнота его одностороння.

Многие люди подобны колбасам: чем их начинят, то и носят в себе.

Все говорят, что здоровье дороже всего; но никто этого не соблюдает.

Добрые советы

Даже летом, отправляясь в вояж, бери с собою что-либо теплое, ибо можешь ли ты знать, что случится в атмосфере?

Не робей перед врагом: лютейший враг человека - он сам.

Не все стриги, что растет.

Усердие все превозмогает.

Люби ближнего, но не давайся ему в обман!

Итоги урока. Урок подходит к завершению. Учитель выставляет оценки с комментариями. Спрашивает как прошел урок, понравилось ли его содержание и все ли усвоили новую тему.