РАЗРАБОТКА МОДУЛЯ ПО АЛГЕБРЕ В 9 КЛАССЕ ПО ТЕМЕ: «ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ»

РАЗРАБОТКА МОДУЛЯ ПО АЛГЕБРЕ

В 9 КЛАССЕ ПО ТЕМЕ:

«ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ»

РАЗРАБОТАЛА:

учитель математики 1 категории

МОКУ «ЛАРБИНСКАЯ СОШ»

ХИЖАК АЛЛА АЛЕКСЕЕВНА

2013 г.

ТЕМА: ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ.

ЦЕЛЬ: 1. Обобщить и систематизировать сведения о целых уравнениях, способах их

решений.

2. Способствовать формированию умений применять приемы сравнения, обобщения, выделения главного, переноса знаний в новую ситуацию.

3. Развитие творческих способностей учеников путем решения уравнений.

ОБОРУДОВАНИЕ: экран, магнитная доска, схемы 1-3, индивидуальные оценочные листы, карточки с заданиями.

Вся работа на уроках №26, 27, 28 сопровождается индивидуальным оценочным листом.

ОЦЕНОЧНЫЙ ЛИСТ УЧАЩЕГОСЯ

ФАМИЛИЯ____________

ИМЯ_________________

Этапы

Задания

Количество баллов

1

№1

№2

№3

11

№1

№2

№3

№4

№5

№6

№7

№8

№9

№10

№11

№12

111

№1,2,3

№4,5

Итоговое количество баллов: Оценка:

Каждое задание оценивается в 1 балл. Оценка зависит от суммы набранных баллов. Оценка «5» - 14 баллов; «4» - 11-13 баллов; «3» - 9-10 баллов; «2» - менее 9 баллов.

Устная работа.

1. Какова степень многочлена: а) х² – 3х⁵ +2; б) у⁶ – у + 5; в) 4х-8 – 2(3х+4)?

2. Является ли число 0; -1; 1 корнем уравнения: а) х²-1=0; б) х⁴+х²=-2?

3. Разложите на множители: а) 169-х²; б) 1-6х+9х²; в) 5х-х².

4. Какое из выражений является целым: х ; 3 ; х-2 ; 5х-3

3 х 2х 8 ?

ИЗУЧЕНИЕ НОВОГО МАТЕРИАЛА.

П Л А Н :

1. Понятие целого уравнения. Степень уравнения.

Целым уравнением с одной переменной называется уравнение, левая и правая часть которого – целые выражения. Привести примеры.

Работа с учебником п.12 стр.73 (определение степени уравнения), №265 (устно).

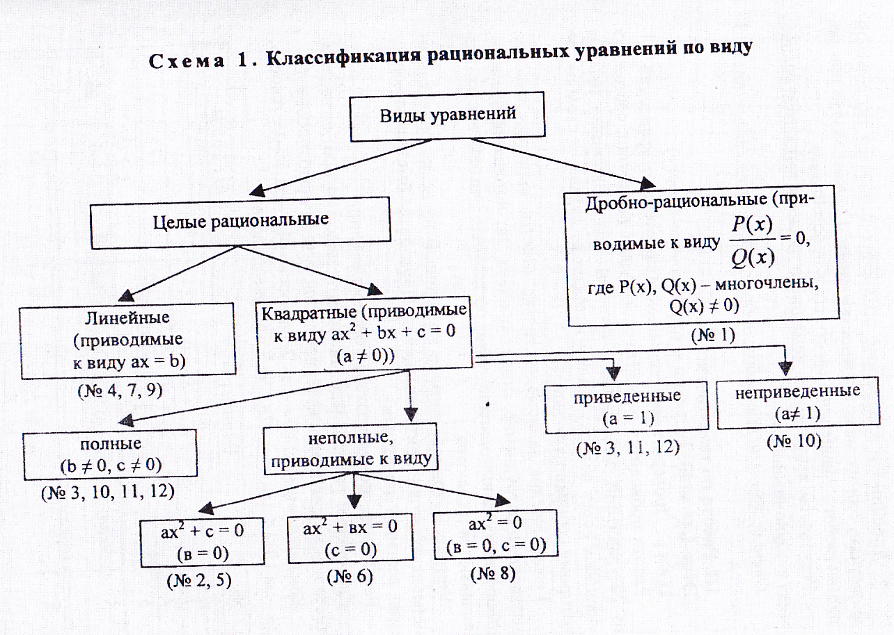
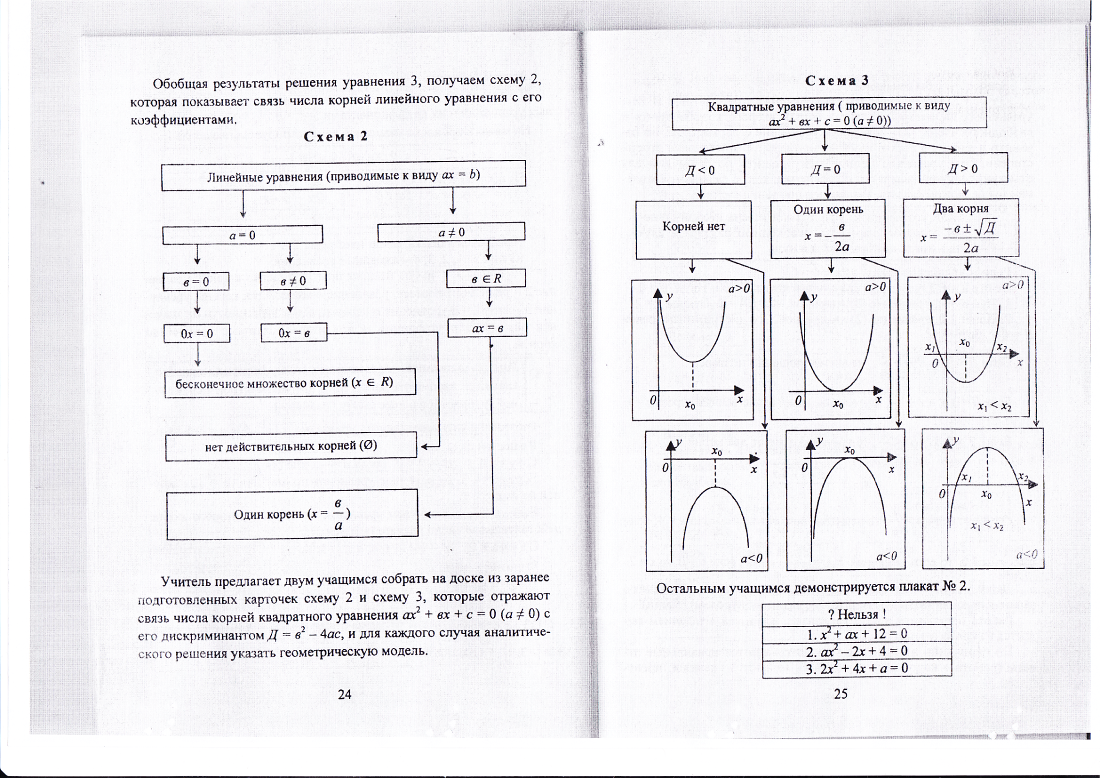
1. Виды целых уравнений: линейные (первой степени), квадратные (второй степени), высших степеней. (Смотреть схема №1, классификация рациональных уравнений по виду; схема №2, линейные уравнения; схема №3, квадратные уравнения.)

2. Методы решения целых уравнений: разложение на множители; введение новой переменной; графический способ. Примеры решений.

ЗАКРЕПЛЕНИЕ ИЗУЧЕННОГО МАТЕРИАЛА.

Задание 1. Решить уравнения 1-12 и провести классификацию уравнений по виду (схема №1)

1. (х-5)² + 9х= 5х²-х³ + 25. Ответы: х=3.

Х

1. 1/2х² + 0,7 = 0. Нет действительных корней.

2. (х-5) (х+3) = 9 х = -4, х = 6.

3. 5х _ х-3 = 1 + х-5

2 3 6 . х = -5/12.

1. (х-5) (х+3) = 1-2х. х_1,2 = +4.

2. (х-5) (х+3) = 3(х-5) . х=0, х=5.

3. 2(х+1) – 1 = 3 – (1-2х). Нет действительных корней.

4. 1 – 2х + 4х² = х² – 2х + 1. 0.

5. 3(1 – х) + 2 = 5 – 3х. Бесконечное множество корней.

6. 2х² + 3х + 4. Нет действительных корней.

7. х² + 6х + 4 = 0. х₁= -3 – 5, х₂= -3 + 5 .

8. 25х² – 30х + 9 = 0. х₁=х₂ = 3/5.

Задание 2. Подготовить одну физическую задачу, показывающую, что целые уравнения могут служить математическими моделями реальных ситуаций. (У доски разбирается наиболее интересный пример.)

В результате обсуждения заданий 1, 2 выясняем сущность решения уравнений

ИТОГ УРОКА.

В ы в о д ы: 1.Уравнения являются математическими моделями очень многих физических и иных явлений. Поэтому решение различных практических задач сводится к решению уравнений.

2. Областью определения уравнения называется множество всех значений х, при которых определены обе части уравнения.

3. Корнем или решением уравнения называется значение неизвестного, при подстановке которого в уравнение получается верное числовое равенство. Решить уравнение – значит найти все его корни или доказать, что их нет.

В о п р о с ы: 1. Какое уравнение называется целым? Примеры.

2. Что называется степенью уравнения?

3. Сколько корней может иметь уравнение, если его степень равна 1, 2, 3, 4, n ?

4. Составьте какое либо уравнение: а) первой степени, имеющее корень -5; б)второй степени, имеющее корни 2 и 3; в) третьей степени, имеющее корни 1, 2, 3.

5. Каков знак дискриминанта квадратного уравнения, если оно имеет: а) один корень; б) два корня; в) не имеет корней?

Домашнее задание: п.12, № 266 (а), 272 (в). Закончить решения уравнений из задания 1.

ТЕМА: ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ.

ЦЕЛЬ: 1. Продолжить формирование навыков по решению целых уравнений.

2. Сформировать умение решать целые уравнения методом введения новой переменной.

3. Способствовать развитию наблюдательности, умения анализировать, сравнивать, делать выводы.

4. Побуждать учеников к само-, взаимоконтролю, вызывать у них потребность в обосновании своих высказываний.

Оборудование: экран, магнитная доска, карточки с заданиями тестов, индивидуальные оценочные листы.

Оценка за урок зависит от суммы набранных балов по всем заданиям. Оценка «5» - 14 баллов; «4» - 11-13 баллов; «3» - 8 баллов; «2» - менее 8 баллов.

Фамилия Задания Количество баллов

Имя

Этап 1

№266(а)

№272(в)

Устная работа

Этап 11

№278 (г)

№278(в)

Этап 1У

А1

А2

А3

А4

В1

В2

С1

Итоговое количество баллов

Оценка

Психологическая установка учащимся.

1. Продолжаем отрабатывать навыки решения целых уравнений; учимся решать биквадратные уравнения методом введения новой переменной; формируем математическую интуицию, которая поможет ориентироваться в способах решения целых уравнений.

2. На уроке можно ошибаться, сомневаться, консультироваться.

3. Дать самому себе установку: «понять и быть первым, который увидит ход решения».

ЭТАП 1. Проверка домашнего задания (комментирование).

Устная работа.

1. Что называется областью определения уравнения?

2. Что называется корнем уравнения?

3. Какова степень уравнения: а) х² – зх⁵ + 2 =0; б) х (х – 1)(х + 2) = 0; в) (х² – 3)² – 5х?

4. Назвать способы решения целых уравнений.

5. Какие из чисел -3; -2; -1; 0; 1; 2; 3 являются корнями уравнения х⁴ – 13х² + 36?

ЭТАП 2. Научиться решать биквадратное уравнение методом введения новой переменной.

1.Работа с учебником. П.12 , стр. 75, пример 3.

2.Решить биквадратное уравнение х⁴ – 6х² + 5 = 0. Ответ: -1; 1; - 5; 5.

3. Решить № 278 (в,г).

ЭТАП 3. Домашнее задание №278 (а, б), 266(в). Для тех кто хочет знать больше №284.

ЭТАП 4. Тест.

Работа проводится по карточкам в двух вариантах, состоящих из 7 заданий. Вопросы и задания тестов разделены на три уровня сложности А, В, С. Уровень А – базовый. Он содержит 4 вопроса, каждый из которых имеет 4 варианта ответа (правильный только один). Уровень В является более сложным (2 вопроса). Уровень С включает задания повышенной сложности (1 вопрос). На выполнение работы отводится 15 минут. Критерии оценки ответов: За каждое верно выполненное задание части А начисляется 0,5 балла, в части В – 1 балл, в части С – 2 балла. Оценка «3» - 2 балла; оценка «4» - 3 балла; оценка «5» - 4 балла. ( смотри тест №5. Целое уравнение и его корни).

ТЕМА: ЦЕЛОЕ УРАВНЕНИЕ И ЕГО КОРНИ.

ЦЕЛЬ: 1.Обобщить, углубить знания учеников по изучаемой теме;

2.Способствовать формированию умений переноса знаний в новую ситуацию;

развитию творческих способностей учеников путем решения уравнений с параметром.

Оборудование: экран, индивидуальные оценочные листы, карточки с заданиями, схема №3.

Работа учащихся состоит из четырех этапов. Результаты каждого этапа урока ученики заносят в индивидуальные оценочные листы.

Фамилия

Имя

Этапы

Задания

Количество баллов

1

№266(в)

№278 (а,б)

№284

11

№1

№2

№3

№4

№5

№6

№7

№8

111

№2

№3

1У

№1(а)

№1(б)

№1(в)

№1(г)

№2

№3

№4

Итоговое количество баллов: Оценка:

Оценка за урок зависит от суммы набранных баллов по всем заданиям. Оценка «5» - 24 балла; «4» - 20-23 балла; «3» - 14-19 баллов; «2» - менее 14 баллов.

Этап 1. Проверка домашнего задания. Анализ результатов теста №5 и работа над ошибками.

Найди ошибку: х(х+3) = 2х, х+3 =2, х= -1. Ответ: х= -1.

В результате неравносильных преобразований в уравнении потерян один корень х=0. Как же не попасть в подобные ловушки? Прежде всего нужно четко понимать, какие действия нужно выполнять в ходе решения уравнения. Сегодня на уроке мы повторим, обобщим, приведем в систему изученные виды, методы и приемы решения целых уравнений.

Этап 2. Виды целых уравнений: линейные, квадратные, высших степеней.

Решить уравнения: 1) (у+2) – (3у-4) = -4; 2) 9х² + х + 1= 0;

3) х⁴-12х² +32=0; 4) х²-25=0;

5) у²-2х=0; 6) х³+4х=5х².

7. Какие из этих уравнений являются: а) линейными; б) квадратными; в) высших степеней?

8. Какие методы решения целых уравнений вы использовали?

Каждое задание оценивается 1 баллом. Критерии оценок: «5» - 8 баллов; «4» - 6 баллов; «3» - 4 балла.

Этап 3. Квадратные уравнения с параметром.

1.Учащимся демонстрируется плакат ( смотри схема №3 ). Вопрос: Что бы это означало? Ответ. Квадратные уравнения с параметром. В этих уравнениях параметр а входит в состав второго коэффициента (1), в состав коэффициента при х² (2), в состав свободного члена (3). Эти уравнения нельзя сразу решить по формулам для отыскания корней квадратного уравнения, т.к. о заданном уравнении мы не можем сказать, квадратное оно или линейное. Решить уравнение (2) ах² -2х+4=0. Решение. Рассмотрим два случая, когда а=0 и когда а не равняется 0. 1. При а=0, уравнение линейное -2х+4=0. Откуда х=2. 2. При а не равно 0, уравнение квадратное. Его дискриминант равен Д=4-16а. Если дискриминант меньше нуля, то уравнение не имеет корней. Уравнение имеет один корень, если дискриминант равен нулю. Если дискриминант больше нуля, то уравнение имеет два корня.

2. При каких значениях в уравнение 2х²+6х+в=0 имеет: а) один корень; б) два корня? (2балла)

3. При каких значениях с уравнение 6х²+сх+6=0 имеет: а) один корень; б) два корня? (2 балла)

Этап 4. Самостоятельная работа (закончить дома).

1 вариант 2 вариант

1. Решите уравнение:

а) х³-81х =0; а) х³-25х =0;

б) х²-1 _ 3х-1₌₂ ; б) х²+6 _ 8-х_=1;

2 4 5 10

в) х⁴-19х+48=0; в) х⁴-4х²-45=0;

г) (х²-2)² +3(х²-2) +2=0. г) (х²+3)²- 7(х²+3)+12=0.

2. При каких значениях t уравнение

3х²+ tх+3=0 имеет два корня? 2х² +tх+8=0 не имеет корней?

3.Решите графически и аналитически уравнение

х² = х³ х²= -2х.

1. Решите графически уравнение

12₌ х² -4х 6 ₌х² -7

х х .

Критерии оценивания: 1а,б – 1 балл; 1в,г; 2 - 2 балла; 3 – 3 балла; 4 – 4 балла. Оценка «5» - 10 баллов; «4» - 8 баллов; «3» - 6 баллов; «2» - менее 6 баллов.

ЛИТЕРАТУРА:

1. Ю.Н.Макарычев и др., Алгебра, 9 класс, Москва,изд-во «Просвещение», 2012 .

2. С.С.Минаева, Л.О.Рослова, Алгебра, 9 класс, Тематические тренировочные задания, Москва, изд-во «Экзамен», 2009.

3. Алгебра, Открытые уроки, автор-составитель С.Н.Зеленская, изд-во «Учитель», Волгоград, 2007.

4. Контрольно-измерительные материалы, Алгебра 9 класс, составитель Л.И.Мартышова, Москва:ВАКО, 2011.

5. Уроки математики в 9 классе, Поурочные планы ч.1, составитель Ковалева Г.И., Волгоград, изд-во «Братья Гринины», 2009

6. Миндюк М.Б., Миндюк Н.Г. Разноуровневые дидактические материалы по алгебре, 9 класс, Москва, 2007.