

























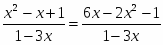 Разработка программы для итогового повторения курса 7-9 классов по алгебре, а также для подготовки к ГИА.
Разработка программы для итогового повторения курса 7-9 классов по алгебре, а также для подготовки к ГИА.
Выполнила: Климова Алиса Сергеевна,
учитель МАОУ СОШ №153
Программа включает в себя 2 модуля: календарно-тематическое планирование повторения и серия тематических тестов (5) плюс итоговый тест за курс 7-9 класса.
Модуль1: Разработка системы итогового повторения курса алгебры 7-9 классов.
Примерное планирование программы(18 часов).
Кол-во часов
Тема
Форма
2
Числовые и алгебраические вычисления, иррациональные числа и выражения, сравнение чисел
Повторение
Тестирование и разбор теста (тест№1)
2
Алгебраические дроби и рациональные уравнения. Решение текстовых задач.
2
Функции, их виды, исследование функций, построение графиков
Повторение
Тестирование и разбор теста (Тест №2)
2
Решение уравнений и систем уравнений графическим способом
2
Решение уравнений и систем уравнений алгебраическим способом
Повторение
Тестирование и разбор теста (Тест №3)
2
Решение иррациональных уравнений, равносильность уравнений.
3
Последовательности и прогрессии
Повторение
Тестирование и разбор теста (Тест №4)
3
Неравенства и системы неравенств
Повторение, Тестирование и разбор теста (Тест №5)
2
Итоговая работа
Тест
Тест №1
№
Задание
Варианты ответа
1
Расположить в порядке возрастания числа: 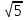 ,
,  , 2.6 ,
, 2.6 , 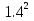
А)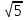 ,
,
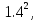 2.6 Б)
2.6 Б) ,
, , 2.6
, 2.6
В) , 2.6,
, 2.6,  Г)
Г)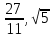 , 2.6,
, 2.6, 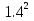
2
Расположить числа в порядке возрастания:
0, -0.01, 0.2, -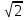
А) 0, -0.01, 0.2,
0, -0.01, 0.2,  Б)-
Б)-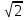 , -0.01, 0.2, 0
, -0.01, 0.2, 0
В)-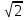 , -0.01, 0, 0.2 Г)
, -0.01, 0, 0.2 Г)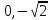 , -0.01, 0.2
, -0.01, 0.2
3
Найти значение выражения:
 +
+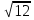 -
- 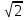 - 2
- 2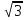 =
=
А) 0 Б)
0 Б) -2
-2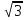 В)5
В)5 -
- 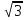 Г)2
Г)2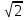
4
Упростить выражение:
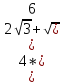
А) 2
2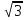 Б)
Б) В)
В)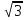 +
+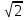 Г)
Г)
5
Сократить дробь:
А)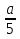 Б)а-1 В)
Б)а-1 В)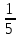 (а+1) Г)
(а+1) Г)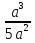
6
Выбрать, что является тождеством:
А) =
= 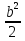 Б)
Б)  =
= 
В) =
=  Г)
Г) =
=
7
Найти корни уравнения:
 –
– = 1
= 1
А)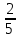 Б)
Б)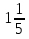 В)
В)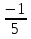 Г)
Г)
8
Найти корни уравнения:
 +
+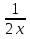 = -1
= -1
А) 0, -
0, -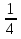 Б)нет корней В)
Б)нет корней В) , -
, - 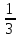 Г) 1, -
Г) 1, - 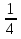
9
Найти модуль разности корней уравнения:  + 4
+ 4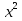 - 5 = 0
- 5 = 0
А) 0 Б) 6 В) 4 Г) 2
0 Б) 6 В) 4 Г) 2
10
Найти сумму квадратов корней уравнения:
0.5 +2(x-2) - 6 = 0
+2(x-2) - 6 = 0
А) 0 Б) 40 В) 32 Г) -32
0 Б) 40 В) 32 Г) -32
11
Найти p, если один из корней уравнения
равен -1
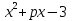 =0
=0
А) Б) 2 В) -2 Г) -3
Б) 2 В) -2 Г) -3
12
Какая математическая модель удовлетворяет условию задачи:
Катер прошёл 30 км по течению реки и 13 км против течения, затратив на весь путь 1 ч 30 мин. Какова собственная скорость катера, если скорость течения реки равна 2 км/ч?
А) 30*(х+2)-13*(х-2)=1,5
30*(х+2)-13*(х-2)=1,5
Б) 30/(х+2)+13/(х-2)=1,3
В) 30/(х+2)-13/(х-2)=1,5
Г) 30/(х+2)+13/(х-2)=1,5
13
Из одного и того же пункта одновременно в противоположных направлениях вышли два пешехода. Через 2 часа расстояние между ними стало 16 км. Найдите скорость второго пешехода, если скорость первого была 5 км/ч.
А) Б)
Б) 
В)  Г)
Г) 
14
Числитель обыкновенной дроби на 1 меньше её знаменателя. Если из числителя и знаменателя вычесть 1, то дробь уменьшится на 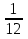 . Найдите эту дробь.
. Найдите эту дробь.
А) Б)
Б) 
В) 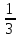 Г) не хватает данных
Г) не хватает данных
Тест №2
Задания теста 1-6 оцениваются в 1 балл
Задания 7-10 оцениваются в 2 балла
Задания 11-12 оцениваются в 3 балла
(макс. 20 баллов)
Для получения «5» нужно набрать 15-20 баллов
«4» - 10-14 баллов, «3» - 5-9 баллов
№
Задание
Варианты ответа
1
Определить какой знак имеет дискриминант и коэффициенты а и b функции
 , если
, если
её график имеет вид
А) D>0,a>0,b>0 Б) D<0,a<0,b>0
D>0,a>0,b>0 Б) D<0,a<0,b>0
В) D=0,a<0,b>0 Г) D>0,a<0,b<0
D>0,a<0,b<0
2
Определить, сколько корней имеет система уравнений, графики которых изображены на рисунке
А) 0 Б) 1 В) 2 Г)
0 Б) 1 В) 2 Г) 3
3
3
bbbbbb
Определить какому уравнениюсоответствует график
А)y= 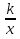 +b В)y=
+b В)y=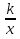 - b
- b
Б)y= -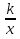 +b Г)y= -
+b Г)y= -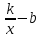
4
Определить какому уравнению
b
a
соответствует графикА)y= +a В) y=
+a В) y=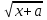 - b
- b
Б) y=  - b Г)y=
- b Г)y=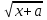 +b
+b
5
Определить какой вид имеют функции
y= -2x+1 и y= 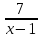
А) убывающая и возрастающая
убывающая и возрастающая
Б) обе функции убывающие
В) обе функции возрастающие
Г) возрастающая и убывающая
6
Найти минимальное и максимальное значение функции
y = -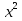 +4 на промежутке [-2; 3]
+4 на промежутке [-2; 3]
А)-5, 4 Б) -4, 5
В) 0, 4 Г)-5, 0
7
Найти корни системы уравнений, используя графический
y = х метод
y= -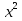 +2x-1
+2x-1
А)2, -1 Б) 2, 1
В) -2, 1 Г)нет корней
8
Решить уравнение
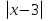 -1= 0
-1= 0
А) Б) 2,4
Б) 2,4
В) 2 Г)нет корней
9
Решить систему уравнений
y=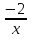
y= x+2
А)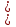 1;-1)
1;-1)
Б) (-1;1)
В) (-1;-1)
Г)нет корней
10
Сколько корней имеет система уравнений?
y + = 1
= 1
y = 
А) Б) 2 В) 3 Г)нет корней
Б) 2 В) 3 Г)нет корней
11
Какой математической модели соответствует задача?
На школьной математической олимпиаде было предложено 8 задач. За каждую решенную задачу засчитывалось 5 очков, а за каждую неправильную задачу списывалось 3 очка. Сколько задач правильно решил ученик, если он получил 24 очка?
А) 5х + 3·(8 - х)=24;
Б) 5·(8 - х) - 3x=24
В) 5х - 3·(8+x)=24;
Г) 5х-3·(8 - х)=24.
12
Найти все значения k, при которых система имеет корни
y=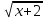
y=  +k
+k
А) Б) k
Б) k 2
2
В) k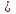 2 Г)k –любое
2 Г)k –любое
Тест №3
№
Задание
Варианты ответа
1
Найти промежуток, которому принадлежит корень уравнения: 2(x-5) – 3(1-x) = 7
А) (0;1) Б)[2;3) В)(3;4] Г) (4;5]
(0;1) Б)[2;3) В)(3;4] Г) (4;5]
2
Определить какому промежутку принадлежит положительный корень уравнения
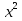 + 3x – 7 =0
+ 3x – 7 =0
А) (0;1) Б)(2;3) В)(1;2) Г) (3;4)
(0;1) Б)(2;3) В)(1;2) Г) (3;4)
3
Решить систему уравнений: x+y = 2
x- y = 4
А) (3;-1) Б)(-1;3) В)(1;1) Г) (1;3)
(3;-1) Б)(-1;3) В)(1;1) Г) (1;3)
4
Найти корни уравнения :
А)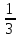 ; 2 Б) 2 В)
; 2 Б) 2 В) 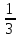 Г) 0;
Г) 0; 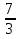
5
Найти пару чисел, которая является решением системы: 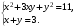
А) (1;- 2) Б) (-1;-2)
В) (2; 1) Г) (-2;-1).
6
Найти одну пару чисел, удовлетворяющих уравнению:

А) (4;2)
(4;2)
Б) (-2; 4)
В) (-4; 2)
Г)(-2; -4)
7
Решить уравнение:
А) Б) 0;7 В)7 Г) нет корней
Б) 0;7 В)7 Г) нет корней
8
Найти корни уравнения:
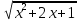 =
=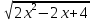
А) 1 Б)3 В)1;3 Г) нет корней
1 Б)3 В)1;3 Г) нет корней
9
Решить уравнение:
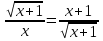
А) 1 Б)-1 В) 1;-1 Г) нет корней
1 Б)-1 В) 1;-1 Г) нет корней
10
Какой математической модели соответствует задача:
Расстояние между двумя городами скорый поезд проходит на 4 часа быстрее товарного и на 1 час быстрее пассажирского. Найти скорости товарного и скорого поездов, если известно, что скорость товарного поезда составляет 5/8 от скорости пассажирского и на 50 км/ч меньше скорости скорого.
А) 8/5 х(у+1) = х(у+4)
8/5 х(у+1) = х(у+4)
(х-50)у = х(у-4).
Б) 8/5 х(у-1) = х(у-4)
(х+50)у = х(у+4).
В) 5/8 х(у+1) = х(у+4)
(y+50)x = y(x+4).
Г) 8/5 х(у+1) = х(у+4)
(х+50)у = х(у+4).
11
Найти значение а при котором система имеет решение: х + (а2 – 3)у = а,
х + у = 2.
А) 2,-2
2,-2
Б) 2
В) -2
Г) любое число
Тест №4
Задания теста 1-4, 9 оцениваются в 1 балл
Задания 5-6, 10-12 оцениваются в 2 балла
Задания 7-8 оцениваются в 3 балла.
Максимальное количество баллов 21.
Для получения «5» нужно набрать 16-21 балл
«4» - 10-15 баллов, «3» - 5-9 баллов.
№
Задание
Варианты ответа
1
Какой формулой задана последовательность, если её члены  = 2,
= 2,  = 4,
= 4,  = 8,
= 8, 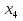 =16…,
=16…, 
А) =
= 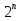 Б)
Б) =
= 
В) 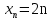 Г) Числа не являются членами последовательности
Г) Числа не являются членами последовательности
2
Какой формулой задана последовательность, если её члены  =
=  ,
,  =
= 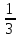 ,
,  =
=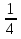 ,
, 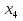 =
=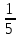 …,
…,
А)
 =1 +
=1 + 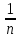 Б)
Б)  =
=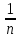
В)  =
=  Г) Числа не являются членами последовательности
Г) Числа не являются членами последовательности
3
Членами какой прогрессии являются числа 3, 6, 9, 12.
А) Геометрической
Б) В) Числа не являются членами прогрессии
В) Числа не являются членами прогрессии
4
Найти сумму десяти первых членов арифметической прогрессии, где  =2,
=2, 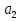 = 3.2
= 3.2
А)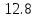 Б) 84 В) 148 Г)74
Б) 84 В) 148 Г)74
5
Найти разность арифметической прогрессии если  ,
, 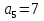
А)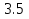 Б) 5.25 В) 10.5 Г) 1.75
Б) 5.25 В) 10.5 Г) 1.75
6
Найти седьмой член арифметической прогрессии,
если 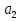 = -1, d= 1.5
= -1, d= 1.5
А) Б) 7 В) 6.5 Г) 4.5
Б) 7 В) 6.5 Г) 4.5
7
Найти  арифметической прогрессии, если
арифметической прогрессии, если  .
.
А) Б) 220 В) 440 Г)30
Б) 220 В) 440 Г)30
8
Дан треугольник, длины сторон которого образуют арифметическую прогрессию. Найти длину средней стороны, если периметр треугольника равен 12.
А)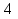 Б) 6
Б) 6
В) 2 Г)не хватает данных
9
Найти знаменатель геометрической прогрессии,
если 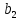 = -1,2 ,
= -1,2 , 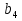 = -4,8
= -4,8
А) Б) 2 В)- 1.8 Г)1.5
Б) 2 В)- 1.8 Г)1.5
10
Найти сумму восьми первых членов геометрической прогрессии, если первый член равен 1, а второй равен 1.5
А) Б) 127 В) 255 Г)128
Б) 127 В) 255 Г)128
11
Первый член геометрической прогрессии равен 2, а знаменатель геометрической прогрессии равен 1,5. Найти
4-й член этой прогрессии.
А)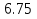 Б) 6.5 В) 4.75 Г)9
Б) 6.5 В) 4.75 Г)9
12
Найти сумму первых пяти членов геометрической прогрессии (bn), в которой второй член равен 2, а знаменатель геометрической прогрессии 3.
А) Б) 162 В) 243 Г)242
Б) 162 В) 243 Г)242
Тест №5
№
Задание
Варианты ответа
1
Какому промежутку принадлежит корень уравнения: 5x – 1 = 3 ?
А) Б) [0.8; 4]
Б) [0.8; 4]
В) (-2;0) Г)[0;0.8)
2
Решить неравенство: 6(2х + 7) < 15(х + 2)
А)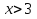 Б) x > 4 В) x>
Б) x > 4 В) x>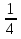 Г) x< 4
Г) x< 4
3
Решить неравенство: 
А) x
x
Б) (-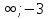 )
)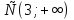
В) (-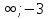 ]
]
Г)
4
Выбрать равносильную пару неравенств:
3x > 6
13-x> 2x-26
x-1 < 3x+3
7-3.5x < 0
А)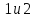
Б) 1 и 3
В) 1 и 4
Г) 2 и 4
5
Равносильны ли пары неравенств?
1) –17x < –51 и х > 3;
2) 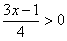 и 3х – 1 > 0;
и 3х – 1 > 0;
3) 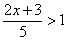 и 2х + 3 > 0?
и 2х + 3 > 0?
А) 1-да, 2 –да, 3 - нет
1-да, 2 –да, 3 - нет
Б) 1-да, 2 –нет, 3 - да
В) 1-нет, 2 –да, 3 - да
Г) 1-нет, 2 –нет, 3 - да
6
Решить неравенство: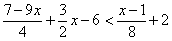
А) x> -7
x> -7
Б) x < 7
В) x > 7
Г) x < -7
7
Решить неравенство: (x-2)(x-5)(x-12)>0
А) (2;5)
(2;5)
Б) (12;+ )
)
В) (-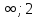 )
)
Г) (2;5)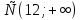
8
Решить неравенство:
А)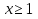
Б) x
В)
Г) (- )
)
9
Решить неравенство:

А) (2;3)
(2;3)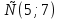
Б) (-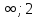 )
)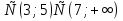
В) (-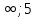 )
)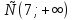
Г) (-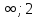 ]
]
10
Выбрать число, которое удовлетворяет решению системы неравенств: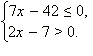
А)
Б) 3.5
В) 4
Г) 3
11
Найти решение системы неравенств: 5x – 10 > 15
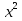 + x – 6
+ x – 6  0
0
А) [-3;5)
[-3;5)
Б) [-3;2]
В) [2;5)
Г) 
12
Найти количество целых точек, входящих в решение неравенства:
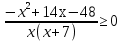
А)
Б) 11
В) 9
Г) бесконечно много
Итоговый тест
№
Задание
Варианты ответа
1
Расположить в порядке убывания числа:
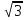 ,
,  , 1.65 ,
, 1.65 , 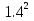
А) ,
, 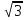 ,
, 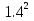
Б)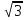 ,
,  , 1.65 ,
, 1.65 , 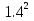
В) , 1.65,
, 1.65, 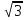
Г)
2
Упростить выражение:

А) 3 Б)
3 Б)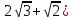
В)6 Г)
3
Сократить дробь: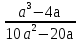
А)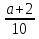 Б)
Б)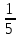
В) Г)
Г)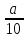
4
Найти корни уравнения:
 +
+ = 1
= 1
А) 2;
2;  Б) -
Б) -  ; -2
; -2
В) -1; 5 Г) -5; 1
5
Найти сумму квадратов корней уравнения:
4 +3(x+1) - 1 = 0
+3(x+1) - 1 = 0
А)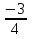 Б) - 2
Б) - 2
В)1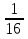 Г)
Г)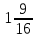
6
Найти минимальное и максимальное значение функции
y = 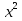 - 2 на промежутке [-2; 1]
- 2 на промежутке [-2; 1]
А) -2; 0
-2; 0
Б) -2; 2
В) -1; 0
Г) -1; 2
7
Найти корни уравнения:
 = 0
= 0
А) 1; 8 Б) -1; -8
1; 8 Б) -1; -8
В) 8; -1 Г) 1; -8
8
Найти абсциссы точек пересечения графиков функций:
y=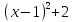
y= 3
А)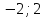 Б) 0.5; 3.5
Б) 0.5; 3.5
В) -2; 0 Г) 0; 2
9
Найти корни уравнения : 
А)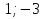 Б)-3
Б)-3
В) 1 Г) нет корней
10
Найти пару чисел, которая является решением системы: 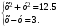
А) 0, -1
0, -1
Б) - 3.5, 0.5
В)-0.5, 3.5
Г) нет решений
11
Решить уравнение:
2x-1
x
4
7
А)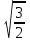 Б)
Б)
В) 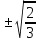 Г)
Г) 1.5
1.5
12
Решить уравнение:

А) 1; -2
1; -2
Б) 1
В) -1; 2
Г) нет корней
нет корней
13
Найти сумму восьми первых членов арифметической прогрессии, где  = -1,
= -1, 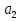 = 0.5
= 0.5
А) 8.5
8.5
Б) 9.5
В) 68
Г) 34
34
14
Найти седьмой член арифметической прогрессии,
если  = 6, d= 2.2
= 6, d= 2.2
А) 14.8
14.8
Б) 13.2
В) 15.2
Г) 14
14
15
Найти знаменатель геометрической прогрессии,
если  = 5 ,
= 5 , 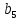 = 7.2
= 7.2
А) 1.2 Б) 1.44
1.2 Б) 1.44
В) 6.1 Г) 2.2
2.2
16
Первый член геометрической прогрессии равен 1.5, а знаменатель геометрической прогрессии равен -2. Найти
5-й член этой прогрессии.
А) -48
-48
Б) 12
В) -24
Г) 24
24
17
Решить неравенство: -3(3х + 1) < 5(1 - х )
А) x> 2
x> 2
Б) x< 2
В) x> - 2
Г) x< -2
x< -2
18
Решить неравенство:

А) [0.5; 2)
[0.5; 2)
Б) (-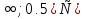
В) [1; 2)
Г) (-
(-
19
Найти решение системы неравенств: 2x – 1  x - 5
x - 5

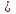 0
0
А) (-
(- ; 4]
; 4] 
Б) [-1 ; 12]
В) [-4; 12)
Г) (- 1; 12)
(- 1; 12)
20
Расстояние между городами A и B равно 435 км. Из города A в город B со скоростью 60 км/ч выехал первый автомобиль, а через час после этого навстречу ему из города B выехал со скоростью 65 км/ч второй автомобиль. На каком расстоянии от города A автомобили встретятся?
А) 310 км
310 км
Б) 240 км
В) 177.6 км
Г)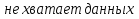
Информационные источники:
Завуч.инфо
Мифи.ру